Abstract
Nanopore-based sensing has emerged as a promising candidate for affordable and powerful DNA sequencing technologies. Herein, we demonstrate that nanopores can be successfully fabricated in Mg alloys via focused electron beam (e-beam) technology. Employing in situ high-resolution transmission electron microscopy techniques, we obtained unambiguous evidence that layer-by-layer growth of atomic planes at the nanopore periphery occurs when the e-beam is spread out, leading to the shrinkage and eventual disappearance of nanopores. The proposed healing process was attributed to the e-beam-induced anisotropic diffusion of Mg atoms in the vicinity of nanopore edges. A plausible diffusion mechanism that describes the observed phenomena is discussed. Our results constitute the first experimental investigation of nanopores in Mg alloys. Direct evidence of the healing process has advanced our fundamental understanding of surface science, which is of great practical importance for many technological applications, including thin film deposition and surface nanopatterning.
Similar content being viewed by others
Introduction
The last two decades have witnessed an explosion of nanopore technology, which has played a critical role in various biological applications, such as the detection and characterization of biomolecules1, DNA sequencing2,3,4 and medical diagnostics5. Kasianowicz et al.1 pioneered the first in vitro investigations of biomolecule transport through single nanopores by passing individual single-stranded RNA and DNA molecules through α-hemolysin protein pores. Recently, attention has shifted to non-biological solid-state nanopores6,7 and DNA origami nanopores8,9, which present clear advantages over their biological counterparts4,5, including superior stability and simple integration into devices. Functionally useful solid-state pores with nanometer dimensions have been successfully fabricated in silicon oxides10, silicon nitrides11, metal oxides12 and graphene13, via electron-beam drilling11,13 and ion-beam sculpting14.
Because the diameter of a nanopore can be nearly the same length and scale of the translocating species, extensive efforts have been dedicated to precisely control the nanopore size and various methods have been utilized10,12,15,16. A typical and effective approach is to apply a high-energy electron beam (e-beam), under which nanopores present in SiO2 thin films below a critical size (related to the sample thickness) shrink progressively and eventually disappear, resulting in an effective healing process10. In contrast, larger nanopores expand under e-beam irradiation. Without the e-beam, the nanopore would remain frozen and retain its original size. The healing process has been attributed to the surface tension effect of fluidized atoms10,17. Using transmission electron microscope (TEM) images, which provide real-time feedback during the healing process, allow for the precise control of pores with sub-nanometer sizes.
Although previous investigations on various materials10,11,12,13 have propelled the development of nanopore technology, to the best of our knowledge, experimental evidence concerning nanopores in metals or metal alloys, which exhibit good electrical and mechanical performance, have not yet been reported. Moreover, because solid-state nanopores can be employed in biological systems, the compatibility of these materials with biomaterials is crucial. Thus, Mg alloys, which possess good electrical conductivity, high mechanical strength and ductility18 and biocompatibility19, were examined in the current study.
In the present investigation, by applying in situ high-resolution transmission electron microscopy (HRTEM) techniques20,21, we obtained the first experimental evidence of the healing process of nanopores in Mg. First, the nanopores were successfully fabricated in a Mg substrate using a focused e-beam. Subsequently, we obtained unambiguous evidence that layer-by-layer growth of atomic planes at the nanopore periphery occurred when the e-beam was spread out, leading to the shrinkage and eventual disappearance of nanopores. Thus, the healing process was attributed to the e-beam-induced anisotropic diffusion of Mg atoms in the vicinity of nanopore edges. A plausible diffusion mechanism that dictates the observed phenomena is discussed in the present paper. The atomic-scale observation of morphology alterations at the nanopore periphery has implications in surface science, which is of great practical importance for many technological applications, including thin-film deposition and surface nanopatterning.
Results
The nanopores were directly drilled in a pure hexagonal-close-packed (HCP) Mg substrate (lattice parameter: a = b = 3.21 Å, c = 5.21 Å) by a focused e-beam (103–104 A cm−2) inside the TEM, as shown in Figs. 1a and 1b. The nanopores were created by removing Mg atoms via the knock-on mechanism22, which results from local exposure to the electron beam (the details of which will be discussed later). Depending on the thickness of the sample (10–50 nm), the drilling time varied from 5 to 30 s (thicker samples required longer drilling times). Interestingly, unlike circular nanopores fabricated in isotropic amorphous materials, such as SiO210 and Al2O312, the nanopores in Mg consistently exhibited an octagonal shape enclosed by four sets of parallel side-walls (Figs. 1b–1d) corresponding to the  ,
,  ,
,  and
and  crystal planes, as observed along the
crystal planes, as observed along the  zone axis. Because all of the planes in HCP metals23 are typical gliding planes with the lowest surface energies, such octagonal-shaped nanopores were easier to form due to energy considerations. The size of the nanopores, which was affected by both the converged beam size and drilling time, ranged from 3 to 8 nm (the size was calculated by averaging the perpendicular distances of four sets of parallel side-walls). Importantly, adjacent atoms around the nanopore periphery were well-ordered, implying that oxidation did not occur at this stage, in contrast to the results observed in Si nanopores24. The obtained nanopores may be applied in molecule analysis25 due to their relatively low surface charge.
zone axis. Because all of the planes in HCP metals23 are typical gliding planes with the lowest surface energies, such octagonal-shaped nanopores were easier to form due to energy considerations. The size of the nanopores, which was affected by both the converged beam size and drilling time, ranged from 3 to 8 nm (the size was calculated by averaging the perpendicular distances of four sets of parallel side-walls). Importantly, adjacent atoms around the nanopore periphery were well-ordered, implying that oxidation did not occur at this stage, in contrast to the results observed in Si nanopores24. The obtained nanopores may be applied in molecule analysis25 due to their relatively low surface charge.
To reduce the intensity to 101–102 A cm−2, we defocused the e-beam (Fig. 2) and subsequently studied each nanopore via in situ HRTEM. Strikingly, the nanopore with an original size of 3.3 nm shrank continuously (Figs. 2d and 2e) and finally disappeared (Fig. 2f) under e-beam irradiation (see also Supplementary Movie S1 online), which was indicative of a healing process. The entire procedure took only 48 s. When the e-beam was turned off, the nanopore retained its shape, suggesting an e-beam-assisted healing mechanism, which is consistent with the results of previous reports10. Additionally, the nanopore with a size of 6.0 nm (Fig. 2g), which was drilled in the vicinity of the nanopore shown in Figs. 2d and 2e, was not able to heal after a long period (701 s) of e-beam illumination. Simultaneously, the surface area may have become oxidized, as evidenced by the nucleation of the cubic MgO phase (indicated by arrow heads in Fig. 2i). A typical HRTEM image indicating the existence of MgO is also presented in Fig. S1. Noticeable expansion of the nanopore was not observed, which may be attributed to oxidation. Such size effects suggest that the surface-tension effect17 should be considered in the healing mechanism in Mg. However, the detailed relationship between the critical size and sample thickness is beyond the scope of the present study and will be studied in future research.
Nanopore dynamics under defocused e-beam irradiation.
(a–c) A schematic illustration showing the healing of a nanopore under wide-field electron beam irradiation. (d–f) Time-lapsed images illustrating the experimental observations of the healing process of a nanopore with an original size of 3.3 nm (Supplementary Movie S1). (g–i) Sequential images showing a nanopore with an original size of 6.0 nm under e-beam irradiation. The arrow heads indicate the existence of a MgO phase.
One distinguished advantage of studying the healing process of nanopores in crystalline materials is that it enables the direct visualization of atomic self-diffusion, which is an outstanding process in surface physics26,27 and is closely related to the intrinsic properties of the material. Atomic diffusion also provides one of the fundamental mechanisms for the equilibration of crystal surfaces, thin-film deposition and surface nanopatterning and is of great value in its own right28,29. Previous studies on nanopores in amorphous materials10, which indicated homogeneous contrasts in TEM, may fail to offer a detailed mechanism of atom diffusion. Figs. 3a–3f present sequential key HRTEM images during the healing procedure of a single nanopore (see also Supplementary Movie S2 online) and Figs. 3g–3l provide schematic illustrations related to Figs. 3a–3f, respectively. The white dots in Figs. 3a–3f represent actual atomic columns of Mg according to the simulated results shown in Figs. S2–S3. Due to nanopore symmetry, we only focused on the alteration of the four side-walls (corresponding to  ,
,  ,
,  and
and  crystal planes) throughout the entire process. Compared to the previous image, the arrow heads in Figs. 3h–3k refer to newly formed layers. For instance, in comparison to Fig. 3g, the growth of the
crystal planes) throughout the entire process. Compared to the previous image, the arrow heads in Figs. 3h–3k refer to newly formed layers. For instance, in comparison to Fig. 3g, the growth of the  layer is highlighted in Fig. 3h, which altered the surface morphology, as indicated by the disappearance of the
layer is highlighted in Fig. 3h, which altered the surface morphology, as indicated by the disappearance of the  facet (Figs. 3b and 3h). Interestingly, subsequent atom diffusion (Figs. 3c and 3i) led to the re-birth of the
facet (Figs. 3b and 3h). Interestingly, subsequent atom diffusion (Figs. 3c and 3i) led to the re-birth of the  side-wall. Later, the nucleation of
side-wall. Later, the nucleation of  and
and  layers again diminished the
layers again diminished the  facet (Figs. 3d and 3j), which re-nucleated, as indicated in Figs. 3e and 3k. Such periodic modulation of nanopore surface facets continued until the nanopore vanished completely.
facet (Figs. 3d and 3j), which re-nucleated, as indicated in Figs. 3e and 3k. Such periodic modulation of nanopore surface facets continued until the nanopore vanished completely.
The healing process of an individual nanopore.
(a–f) Sequential HRTEM images showing the alteration of nanopore morphology during continuous e-beam irradiation at a constant intensity and focus setting. (g–l) Schematic illustration corresponding to (a–f), respectively. The arrow heads point to newly nucleated layers compared to previous images.
To better illustrate the healing process, Fig. 4a presents the observed changes in the size of the nanopore shown in Fig. 3 along with the irradiation time. The nanopore width was measured along the  (d1),
(d1),  (d2),
(d2),  (d3) and
(d3) and  (d4) directions (perpendicular to
(d4) directions (perpendicular to  ,
,  ,
,  and
and  planes, respectively, as indicated in Fig. 1d), respectively and the width-time curves are represented by black, blue, pink and red lines. Moreover, Figs. 4b and 4c present the width-time curves of typical nanopores with original sizes of 4.5 and 3.3 nm, respectively. Initially, the curves were characterized by a remarkable stepwise width reduction, which was induced by the layer-by-layer growth of crystal planes via surface atom diffusion. Each growth event occurred fairly quickly, within 0.5 s (the limit of our acquisition time). Thus, each step height was related to the corresponding inter-planar spacing through multiples of integers. For instance, the step height Δd1 (Fig. 4a) corresponded to a single
planes, respectively, as indicated in Fig. 1d), respectively and the width-time curves are represented by black, blue, pink and red lines. Moreover, Figs. 4b and 4c present the width-time curves of typical nanopores with original sizes of 4.5 and 3.3 nm, respectively. Initially, the curves were characterized by a remarkable stepwise width reduction, which was induced by the layer-by-layer growth of crystal planes via surface atom diffusion. Each growth event occurred fairly quickly, within 0.5 s (the limit of our acquisition time). Thus, each step height was related to the corresponding inter-planar spacing through multiples of integers. For instance, the step height Δd1 (Fig. 4a) corresponded to a single  inter-planar spacing (2.61 Å). The curves consistently ended with a substantial decrease in the width (indicated by arrows in Figs. 4a–4c) (see Supplementary Movies S1–S2 online). Such nonlinear shrinking behavior is in contrast with knowledge revealed during the shrinkage of nanopores in SiO2, where the shrinking rate remained constant10,17.
inter-planar spacing (2.61 Å). The curves consistently ended with a substantial decrease in the width (indicated by arrows in Figs. 4a–4c) (see Supplementary Movies S1–S2 online). Such nonlinear shrinking behavior is in contrast with knowledge revealed during the shrinkage of nanopores in SiO2, where the shrinking rate remained constant10,17.
Anisotropic surface diffusion procedure.
(a) A plot of the pore width versus e-beam irradiation time of the nanopore shown in Fig. 3. The nanopore morphology at the moment marked as (b), (c), (d) and (e) is shown in Figs. 3b–3e, respectively. The black arrow heads point to the moment before new (0002) layers nucleated. (b–c) Width-time curves of two typical nanopores with original sizes of 4.5 and 3.3 nm. The insets (1)–(4) correspond to the nanopore morphology at the moment marked as (1)–(4), respectively. The width along the [0002],  ,
,  and
and  directions is represented by black, blue, pink and red lines, respectively. The arrows point to the observed decrease in width before the nanopore closed. (d) A schematic illustration of two independent jumps in an HCP crystal.
directions is represented by black, blue, pink and red lines, respectively. The arrows point to the observed decrease in width before the nanopore closed. (d) A schematic illustration of two independent jumps in an HCP crystal.
Another phenomenon observed in our experiments was that the growth of a new  layer typically initiated at a point (indicated by arrow heads in Fig. 4a) when the d1/di (i = 2,3,4) ratios were greater than one (see Supplementary Table S1 online). This effect was observed in all of the obtained datasets (see Supplementary Movies S1–S3 online), except when the original nanopore size was small (indicated by a red arrow head in Fig. 4c, where the initial pore size was 3.3 nm). Real-time HRTEM images provided in the insets (1)–(4) of Figs. 4b and 4c indicated that growth along the
layer typically initiated at a point (indicated by arrow heads in Fig. 4a) when the d1/di (i = 2,3,4) ratios were greater than one (see Supplementary Table S1 online). This effect was observed in all of the obtained datasets (see Supplementary Movies S1–S3 online), except when the original nanopore size was small (indicated by a red arrow head in Fig. 4c, where the initial pore size was 3.3 nm). Real-time HRTEM images provided in the insets (1)–(4) of Figs. 4b and 4c indicated that growth along the  ,
,  and
and  direction was easier to activate than growth along the [0002] direction, leading to an increase in the d1/di ratios. At certain points (d1/di ratios greater than one), the new (0002) layers began to nucleate, which often decreased the d1/di values to less than one. Interestingly, subsequent growth of the (0002) layer did not occur until the ratios increased to more than one (i.e., the nucleation of a (0002) layer always lagged behind than that of
direction was easier to activate than growth along the [0002] direction, leading to an increase in the d1/di ratios. At certain points (d1/di ratios greater than one), the new (0002) layers began to nucleate, which often decreased the d1/di values to less than one. Interestingly, subsequent growth of the (0002) layer did not occur until the ratios increased to more than one (i.e., the nucleation of a (0002) layer always lagged behind than that of  ,
,  and
and  layers), which was indicative of an anisotropic diffusion mechanism and can be explained as follows. Typically, for atom diffusion in an HCP crystal, the following two independent jumps occur, as shown schematically in Fig. 4d: (A) the jump of atoms to the nearest vacancy sites within the (0002) basal plane (indicated by the red arrow head), which contributed to the growth of
layers), which was indicative of an anisotropic diffusion mechanism and can be explained as follows. Typically, for atom diffusion in an HCP crystal, the following two independent jumps occur, as shown schematically in Fig. 4d: (A) the jump of atoms to the nearest vacancy sites within the (0002) basal plane (indicated by the red arrow head), which contributed to the growth of  ,
,  and
and  layers; (B) the jump of atoms to vacancy sites within the adjacent basal plane (indicated by the black arrow head), which accounted for the nucleation of a new (0002) layer, as previously discussed. Both the theoretical prediction30 and experimental measurements31 indicated that the energy barrier (theoretical: 0.47 eV; experimental: 0.57 eV) for jump A is lower than that of jump B (theoretical: 0.54 eV; experimental: 0.59 eV). That is, the growth of a (0002) layer is more difficult to achieve due to the higher energy barrier, which is consistent with the current experimental observations. Meanwhile, as the d1/di ratios increase, surface tension facilitates the growth of (0002) layers, which reduces the d1/di ratios and maintains stability.
layers; (B) the jump of atoms to vacancy sites within the adjacent basal plane (indicated by the black arrow head), which accounted for the nucleation of a new (0002) layer, as previously discussed. Both the theoretical prediction30 and experimental measurements31 indicated that the energy barrier (theoretical: 0.47 eV; experimental: 0.57 eV) for jump A is lower than that of jump B (theoretical: 0.54 eV; experimental: 0.59 eV). That is, the growth of a (0002) layer is more difficult to achieve due to the higher energy barrier, which is consistent with the current experimental observations. Meanwhile, as the d1/di ratios increase, surface tension facilitates the growth of (0002) layers, which reduces the d1/di ratios and maintains stability.
Discussion
The e-beam-induced temperature increase of the sample was estimated to be less than 1 K (see the Methods section for further information) under the current experimental conditions. Compared to the high melting point of Mg (923 K), such a small temperature increase is insufficient to explain the fast and spontaneous healing of nanopores observed in our experiments. Dynamic displacements of constituent atoms occurs under electron irradiation at high voltages, which promotes atom diffusion in crystalline and amorphous phases22. The amount of energy transferred by an electron to the nucleus of an atom can be estimated according to the following equations22:


where θ is the deflected angle of the electron in the field of the atom nucleus, Emax is the maximum energy transferred, E0 is the incident electron energy (in eV) and A is the atomic mass number. According to the equations, the maximum amount of energy (Emax) transferred to Mg nuclei by a 200-kV e-beam is 22 eV, whereas the energy required for the displacement of Mg atoms is 9–14 eV32. Therefore, knock-on damage occurs, which results in nanopore formation. In addition, the amount of energy transferred may be negligible when θ is very small. At lower energy beam intensities, once the energy barrier along the diffusion path has been overcome, atom sputtering is suppressed and nanopore shrinking is driven by surface atom diffusion at the vicinity of the nanopore periphery. As a result, the healed region (as indicated by arrows in Fig. 2f) with brighter contrast is thinner than the nearby areas, as evidenced in the simulated HRTEM images (Fig. S4).
In summary, we demonstrated that nanopores could be fabricated in Mg using a converged e-beam. Strikingly, real-time videos directly revealed that the healing process of nanopores with sizes of 3–5 nm is due to the layer-by-layer growth of lattice planes, which is related to the anisotropic self-diffusion of Mg atoms. The diffusion process can be initiated by surface tension-driven mass flow, which is activated by e-beam irradiation. The ability to fabricate nanopores with controlled sizes in Mg alloys makes the proposed method a viable alternative for potential applications in nanopore technology. Furthermore, the healing properties of Mg alloys have extended possible applications in irradiated environments, such as in outer space. Our work indicates that TEM may be an alternative to other techniques, such as scanning tunneling microscopy, in the race towards comprehensive investigations of surface science.
Methods
The nominal composition of the Mg alloy in the present experiment was 86 wt.% Mg, 9.0 wt.% Al, 1.0 wt.% Zn and 4.0 wt.% Sn. First, we made a slice with a thickness and width of nearly 500 μm and 3 mm, respectively (Fig. S5a), which was mechanically thinned to approximately 60 μm via mechanical grinding (Fig. S5b). Finally, the specimens were ion-milled using a Gatan precision ion polishing system at 5.0 kV. During this stage of the process, only the central part of the slice where the nanopores were directly drilled was thinned to the nanometer scale (Fig. S5c). Further details on the sample preparation method can be found in our previous paper33. The in situ HRTEM observations were performed in a JEOL JEM-2010 FEF (UHR) electron microscope (Tokyo, Japan) operated at a voltage of 200 kV.
The temperature increase under irradiation was calculated by Fisher's model34:  , where I is the beam current, κ is the thermal conductivity, e is the electron charge, b is the sample radius, r0 is the beam radius and ΔE is the total energy loss per electron in a sample with a thickness of d. Because energy losses in the sample were small compared to the initial energy (200 keV), the term ΔE/d was equal to the stopping power of electrons, dE/dx, which was calculated from the Bethe-Bloch equation35:
, where I is the beam current, κ is the thermal conductivity, e is the electron charge, b is the sample radius, r0 is the beam radius and ΔE is the total energy loss per electron in a sample with a thickness of d. Because energy losses in the sample were small compared to the initial energy (200 keV), the term ΔE/d was equal to the stopping power of electrons, dE/dx, which was calculated from the Bethe-Bloch equation35:

where Z is the atomic number of the target element, ρ is the atomic density, εo is the dielectric constant, m is the electron rest mass, υ is the electron velocity, c is the speed of light, E is the electron energy, Ie is the average excitation energy of electrons in the target and β = υ/c.
In the present study, the acceleration voltage was 200 kV; thus, β = 0.6946 and υ = 2.0837 × 108 m/s. For Mg, Z = 12, Ie = 8.8Z = 105.6, m = 9.3 × 10−31 kg, ρ = 4.44 × 1028 m−3 (the mass density is 1,770 kg m−3), e = 1.6 × 10−19 C, εo = 8.85 × 10−12 F/m, melting point = 923 K and thermal conductivity κ = 156 W/mK. The maximum temperature increase was estimated to be less than 1 K with I = 2.1 nA36, b = 1.5 mm and r0 = 100 nm.
References
Kasianowicz, J. J., Brandin, E., Branton, D. & Deamer, D. W. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. USA 93, 13770–13773 (1996).
Zwolak, M. & Di Ventra, M. Colloquium: Physical approaches to DNA sequencing and detection. Rev. Mod. Phys. 80, 141–165 (2008).
Clarke, J. et al. Continuous base identification for single-molecule nanopore DNA sequencing. Nat. Nanotechnol. 4, 265–270 (2009).
Derrington, I. M. et al. Nanopore DNA sequencing with MspA. Proc. Natl. Acad. Sci. USA 107, 16060–16065 (2010).
Calin, G. A. & Croce, C. M. MicroRNA signatures in human cancers. Nature Rev. Cancer 6, 857–866 (2006).
Dekker, C. Solid-state nanopores. Nat. Nanotechnol. 2, 209–215 (2007).
Venkatesan, B. M. & Bashir, R. Nanopore sensors for nucleic acid analysis. Nat. Nanotechnol. 6, 615–624 (2011).
Bell, N. A. W. et al. DNA Origami Nanopores. Nano Lett. 12, 512–517 (2012).
Wei, R., Martin, T. G., Rant, U. & Dietz, H. DNA Origami Gatekeepers for Solid-State Nanopores. Angew. Chem. Int. Ed. 51, 4864–4867 (2012).
Storm, A. J., Chen, J. H., Ling, X. S., Zandbergen, H. W. & Dekker, C. Fabrication of solid-state nanopores with single-nanometre precision. Nat. Mater. 2, 537–540 (2003).
Keyser, U. F. et al. Nanopore Tomography of a Laser Focus. Nano Lett. 5, 2253–2256 (2005).
Venkatesan, B. M. et al. Highly Sensitive, Mechanically Stable Nanopore Sensors for DNA Analysis. Adv. Mater. 21, 2771–2776 (2009).
Fischbein, M. D. & Drndic, M. Electron beam nanosculpting of suspended graphene sheets. Appl. Phys. Lett. 93, 113103–113107 (2008).
Li, J. et al. Ion-beam sculpting at nanometre length scales. Nature 412, 166–169 (2001).
Fang, D. Z., Striemer, C. C., Gaborski, T. R., McGrath, J. L. & Fauchet, P. M. Pore Size Control of Ultrathin Silicon Membranes by Rapid Thermal Carbonization. Nano Lett. 10, 3904–3908 (2010).
Van den Hout, M. et al. Controlling nanopore size, shape and stability. Nanotechnology 21, 115304 (2010).
Shin, J. W. et al. Irradiation-induced shrinkage and expansion mechanisms of SiO2 circle membrane nanopores. Nanotechnology 20, 075703 (2009).
Zhang, E. & Yang, L. Microstructure, mechanical properties and bio-corrosion properties of Mg–Zn–Mn–Ca alloy for biomedical application. Mater. Sci. Eng. A 497, 111–118 (2008).
Li, Z., Gu, X., Lou, S. & Zheng, Y. The development of binary Mg–Ca alloys for use as biodegradable materials within bone. Biomaterials 29, 1329–1344 (2008).
Zheng, H. et al. Discrete plasticity in sub-10-nm-sized gold crystals. Nat. Commun. 1, 144 (2010).
Zheng, H., Wang, J., Huang, J., Cao, A. & Mao, S. In Situ Visualization of Birth and Annihilation of Grain Boundaries in an Au Nanocrystal. Phys. Rev. Lett. 109, 225501 (2012).
Egerton, R. Radiation damage in the TEM and SEM. Micron 35, 399–409 (2004).
Matysina, Z. A. The relative surface energy of hexagonal close-packed crystals. Mater. Chem. Phys. 60, 70–78 (1999).
Drozdov, M., Kauffmann, Y., Carter, W. C. & Kaplan, W. D. Shape-controlled nanopores in single crystals. Nanotechnology 21, 475301 (2010).
Tabard-Cossa, V., Trivedi, D., Wiggin, M., Jetha, N. N. & Marziali, A. Noise analysis and reduction in solid-state nanopores. Nanotechnology 18, 305505 (2007).
Feibelman, P. Diffusion path for an Al adatom on Al(001). Phys. Rev. Lett. 65, 729–732 (1990).
Shang, S., Hector, L., Wang, Y. & Liu, Z. Anomalous energy pathway of vacancy migration and self-diffusion in hcp Ti. Phys. Rev. B 83, 224104 (2011).
Ehrlich, G. Atomic View of Surface Self-Diffusion: Tungsten on Tungsten. J. Chem. Phys. 44, 1039 (1966).
Wang, J., Huang, H. & Cale, T. S. Diffusion barriers on Cu surfaces and near steps. Modelling Simul. Mater. Sci. Eng. 12, 1209–1225 (2004).
Monti, A. M. & Savino, E. J. Calculation of the formation entropy and diffusivity constants for the vacancy in Mg. Phys. Rev. B 23, 6494–6502 (1981).
Combronde, J. & Brebec, G. Anisotropy for self diffusion in magnesium. Acta Metall. 19, 1393–1399 (1971).
Hossain, M. K. & Brown, L. M. Electron irradiation damage in magnesium. Acta Metall. 25, 257–264 (1977).
Zhao, D. et al. High-resolution electron microscopy observations of the microstructure of a rapidly solidified Mg–9.0 wt% Al–1.0 wt% Zn–4.0 wt% Sn alloy. Philos. Mag. 91, 2654–2660 (2011).
Fisher, S. B. On the temperature rise in electron irradiated foils. Radiat. Eff. Defects Solids 5, 239 (1970).
Jencic, I., Bench, M. W., Robertson, I. M. & Kirk, M. A. Electron-beam-induced crystallization of isolated amorphous regions in Si, Ge, GaP and GaAs. J. Appl. Phys. 78, 974–982 (1995).
Longo, D. M., Howe, J. M. & Johnson, W. C. Development of a focused ion beam (FIB) technique to minimize X-ray fluorescence during energy dispersive X-ray spectroscopy (EDS) of FIB specimens in the transmission electron microscope (TEM). Ultramicroscopy 80, 69–84 (1999).
Acknowledgements
This work was supported by the 973 Program (2011CB933300), the National Natural Science Foundation of China (51071110, 51271134, 40972044, J1210061), the China MOE NCET Program (NCET-07-0640), MOE Doctoral Fund (20090141110059) and the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Contributions
H.Z. and Y.L. carried out the TEM experiments and wrote the paper. H.Z., Y.L., F.C., S.W., S.J., A.C., D.Z. and J.W. contributed to the data analyses and paper revisions. The project was designed by J.W.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Video S1
Supplementary Information
Video S2
Supplementary Information
Video S3
Supplementary Information
supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Zheng, H., Liu, Y., Cao, F. et al. Electron beam-assisted healing of nanopores in magnesium alloys. Sci Rep 3, 1920 (2013). https://doi.org/10.1038/srep01920
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01920
This article is cited by
-
A Review on the Radiation Response of Nanoporous Metallic Materials
JOM (2018)
-
In situ heavy ion irradiation studies of nanopore shrinkage and enhanced radiation tolerance of nanoporous Au
Scientific Reports (2017)
-
Anelasticity of twinned CuO nanowires
Nano Research (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



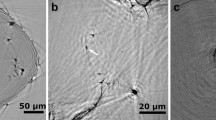

 ,
,  and
and  crystal planes.
crystal planes.

