Abstract
Preparing low energy liquid-repellant surfaces (superhydrophobic or superoleophobic) have attracted tremendous attention of late. In all these studies, the necessary liquid repellency is achieved by irreversible micro-nano texturing of the surfaces. Here we show for the first time that a glass surface, placed under water, can be made superoleophobic (with unprecedented contact angles close to 180 degrees and roll off angles only a few fractions of 1 degree) by merely changing the surfactant content of the water medium in which the oil (immiscible in water) has been dispersed. Therefore, we propose a paradigm shift in efforts to achieve liquid-repellant systems, namely, altering the solvent characteristics instead of engineering the surfaces. The effect occurs for a surfactant concentration much larger than the critical micelle concentration and is associated to strong adsorption of surfactant molecules at the solid surface, triggering an extremely stable Cassie-Baxter like conformation of the oil droplets.
Similar content being viewed by others
Introduction
Nature exhibits abundant examples of liquid-repellent surfaces1,2,3,4,5,6,7. The inherent microstructural features of these surfaces are often attributed for such characteristics. Buoyed by their overwhelming applications in several disciplines8,9,10, there have been an ever-increasing number of attempts to develop artificial liquid-repellant superhydrophobic surfaces by replicating such naturally occurring structural morphology11,12,13 on to a given substrate. The most common liquid-repellant surfaces are superhydrophobic (or water repelling) surfaces14,15,16,17,18,19,20,21,22. Of late, attempts have been made to prepare surfaces that may repel liquids other than water. For example, there has been substantial progress in developing superoleophobic substrates that repel oil23,24,25,26,27,28,29. Such surfaces are gaining large importance for their wide applications in several disciplines30,31.
To prepare either superhydrophobic or superoleophobic surfaces, one necessarily requires to engineer an irreversible artificial micro-nano-texturing of the surface. In this study, we demonstrate, on the contrary, that we can make a glass surface, placed inside water, superoleophobic by merely altering the properties of the water, i.e., by changing the surfactant concentration of the water (in which the oil is dispersed). Hence, it is possible to obtain surfaces with high liquid-repellency without requiring any permanent engineering of the substrate. Certain oils in dispersed state in de-ionized (DI) water exhibit obtuse contact angles on the glass27. There have been other studies, which report under-water superoleophobic surfaces with contact angles of more than 160° and roll off angles of few degrees23,24. However, in this study we demonstrate contact angles (~180°) that are significantly larger. In fact, we observe a close to perfect rolling behavior with modified roll-off angles of merely a few fractions of a degree. Here the liquid-repellency of the substrate is characterized by modified roll-off angle, which is somewhat different from the classical roll-off angle23,24. In the present case, on tilting the substrate, the oil drop, being under water, is subjected to a water advection force (on account of the pressure difference across the two sides of the oil drop). The height of the water column being much larger than the drop height, it is this advection force that triggers the roll-off behavior of the drop by overcoming the adhesion force between the drop and the substrate. Therefore, this roll-off behavior is slightly different from the conventional roll-off behavior that occurs due to the interplay between the gravitational force and the adhesion force. Here the effect of the gravitational force is implicitly present in triggering the pressure difference and the advection force. Therefore, we call this roll-off behavior as the modified roll-off behavior and the corresponding tilting angle as the modified roll-off angle.
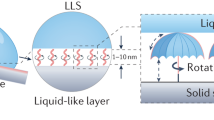
The fundamental reason for achieving such remarkably large contact angles is the surface adsorption of the surfactant molecules that induce “pillar” like structures (see Fig. 1e) with which the oil droplets interact to attain stable Cassie-Baxter (CB)32 conformations, triggering such unprecedented under-water superoleophobic behavior. At lesser surfactant concentrations, when such “pillar” densities are less, a transition from the CB to the Wenzel (Wn) state33,34,35,36 occurs over a finite time that is a function of the surfactant concentration, dictated by the possible entropic effects (steric stabilization37) and van der Waals (vdW) interactions. It is to be noted that even though there have been studies that illustrate the effect of surfactant on varying the substrate wettability (in particular for originally superhydrophobic surfaces38,39,40, illustrating a lowering in hydrophobicity with adsorption of the surfactant), this unique regime of attainment of surfactant-mediated extreme under-water superoleophobicity on originally untreated surfaces has not been explored.
Superoleophobic behavior of the glass.
(a) Snapshots of the equilibrium configurations of the oil drop for different surfactant concentrations c. Below each image of the drop we provide in parentheses the Δt values needed for the drop to attain the equilibrium state from its initial state (for cases where the initial and equilibrium states of the drop are identical, we do not provide this value). Instantly after the deposition, the drop corresponding to each c has the configuration identical to the equilibrium configuration corresponding to c = 200 μM. The equilibrium configuration for all c > 200 μM is same as that corresponding to c = 200 μM. (b) Variation of the contact angle of the oil drop with the surfactant concentration. (c) Variation of the spreading time (Δt) with the surfactant concentration. In [(b), (c)] we also show the corresponding standard error and the “rolling zone” (or the zone where the oil drop remains in stable CB state), where there is no spreading time and the contact angle is ~180°. (d) Schematic of the falling drop (with surfactant at the oil-water interface) on the solid (with adsorbed surfactant molecules). (e) Schematic showing the “pillar” formation (responsible for oil drop to be in CB state) and the droop δ. Possible deviations from such simplified “pillar” structures, on account of interplay of wettabilities of different segments (hydrophobic or hydrophilic) of the Tween 20 molecules with the solid wettability, or the structural characteristics of Tween 20 molecules, are discussed in Figs. S2 and S3 and Supplementary Information sections 2 and 3. (f) Schematic of the surfactant orientation in (top) interpenetration domain and (bottom) compressive domain, representing entropic interactions. Error bars [in (b) and (c)] are the standard errors obtained from the Standard Deviation analysis of the data. (g) Graphical formula of the Tween 20 molecule50.
Results
We first prepare a solution of non-ionic surfactant (using Tween 20 surfactant in DI water) of different concentrations c (ranging between 10 μM–800 μM; CMC or the critical micelle concentration for Tween 20 is 60 μM, see Figure 1g for the graphical formula of Tween 20). We put this surfactant solution inside a glass cuvette and place a thoroughly cleaned glass slide inside this solution at the bottom of the cuvette [see the figure in the inset (a) of Supp. Figure S1]. Depending on the concentration of the surfactant solution, there will be a given packing (and a resulting pattern) of the adsorbed surfactant molecules on this glass slide [see the AFM results in Figure 2, Suppl. Figures S4,S5; for a detailed discussion on how the Tween 20 structure and the wettability of the different segments of Tween 20 molecules (relative to the solid wettability) may affect present study, please refer to Supplementary Information sections 2 and 3]. We then dispense an oil drop of fixed volume of 2 μl (we keep the volume small so that the drop radius is substantially smaller than the corresponding capillary length calculated using the oil-water surface tension and the oil density) from the air-water interface of the cuvette, i.e., from a certain height h (~25 mm) (see Supp. Figure S1 and the Method section for the reason of selection of such an unconventional drop deposition method; also see Supplementary Movies 1 and 2 for the difficulties associated with the conventional drop deposition technique24 for the present case). The oil is silicon oil (density: 1100 kg/m3), which is heavier than water and hence the oil drop falls inside the liquid column and the velocity with which the drop impacts the glass substrate (and the resultant Weber number) is a function of the different forces acting on the falling oil drop. For the present case, the Weber number is small enough to ensure that after the impact, the drop does not bounce off, even though the surface has extremely low energy with respect to the impacting drop (see the Supplementary Information section 1 for the necessary calculations; also see Supplementary Movie 3). Alternatively, the impacting speed of the drop is small enough to ensure that the drop forms a composite interface41, or equivalently a CB state (see the Supplementary Information section 1). Therefore, a given drop first deposits and rests on the surfactant-covered glass substrate in a CB-state. This state gets triggered as the surfactants adsorbed at the glass and at the oil-water interface interact, forming hypothetical “pillar”-like structures on which the oil drop will rest (see Figs. 1d,e). Three things are not considered in the simplified picture of surfactant-mediated “pillar” formation. First, in Figs. 1d,e, we do not consider the relative orientation of the hydrophobic and the hydrophilic components of the surfactant molecules in conjunction with the wettability of the glass surface (in Supplementary Information section 2 and Supp. Figure S2, we illustrate this issue). Second, we do not account for the alteration of the structure of these “pillars” on account of the presence of three ethylene oxide side chains of the Tween 20 molecule (in Supplementary Information section 3 and Supp. Figure S3, we illustrate this issue). Third, mostly relevant for very large bulk surfactant concentration values (i.e., c ≫ cCMC), the surfactants may get adsorbed on the solid as hemi-micelles42, so that the hypothetical “pillar” structures would be different from that proposed in Figure 1e and Supp. Figures S2, S3. However, as has been discussed in Supplementary Information sections 2 and 3, even when such modifications are taken into account, the drop conforms to a CB-like state.
AFM results for glass substrates with adsorbed surfactant at different surfactant concentrations.
AFM height trace images (for 1 μm × 1 μm scan area) of glass substrates with adsorbed surfactants for (a) c = 0, (b) c = 30 μM, (c) c = 100 μM and (d) c = 400 μM. All the images are taken with the glass substrate immersed inside water.
The fact that the drop always attains a CB state at the outset ensures that it demonstrates a point contact at the start (see later for explanation) and then over a time Δt, spreads and attains the contact angle (see the Method section for more analysis on this transition; also see Supplementary Movie 3). In Figures 1a–c, we depict the equilibrium drop conformations, the contact angle and Δt for different surfactant concentrations. For lesser value of surfactant concentration (c < cCMC, or c ~ cCMC), there is a finite value of this time Δt (indicating that the drop spreads), whereas for larger surfactant concentration (c ≫ cCMC), there is no spreading at all (and hence no finite Δt). In fact, at such c values (c ≫ cCMC), the drop continues to remain in the CB state, i.e., at equilibrium it is in a conformation of close to a point contact and the corresponding modified roll off angle is only a few fractions (~1/12th) of a degree (for more details please refer to the Method section; also see Supplementary Movie 4).
Figures 2a–d show the AFM height trace images of the glass surface with adsorbed surfactants for different surfactant concentrations for a scan area of 1 μm × 1 μm (also see Supp. Figures S4–S6 and Supplementary Information section 5). All the AFM images are obtained with the glass substrate immersed inside the water. Increase in the surfactant concentration shows an increase in the average deposition, clearly depicting a more enhanced adsorption of the surfactant molecules. Surfactant molecules (at the solid and at the oil-water interface) are hypothesized to form pillar-like structures (see Figure 1e) that enforce the oil drop into CB-like conformation and the subsequent transition. Parameters pertaining to these hypothetical pillars that dictate these dynamics (see later) are pitch P, height H and width D (see Figure 1e). It is found that H < 1 nm or H ~ 1 nm for small and intermediate concentration (see Figures 2b,c and Supp. Figures S5,S6) and H > 1 nm for a very large concentration (see Figure 2d and Supp. Figure S4). The most important parameter is the pitch P, which dictates the droop height δ and accordingly the transition (or no-transition) behavior (see Figure 1e and discussions later). For a large surfactant concentration (c = 400 μM), P ~ 10 nm. But for a smaller concentration (c = 30 μM), the pitch values are around 1 μm (see Supp. Figure S6). In Supplementary Information section 5 and Supp. Figures S4–S6, we provide detailed analysis on the technique used to obtain these parameters from the AFM images.
Discussion
The key point to discuss here is the mechanism of such under-water superoleophobic behavior of a glass surface in presence of a surfactant-rich aqueous solution. Large bulk concentration of surfactant will lead to a significant surfactant adsorption at the glass surface. Also there will be surfactant molecules adsorbed on the oil-water interface (see Figure 1d). Irrespective of the surfactant concentration, when the oil drop touches the surface, it is always in a conformation of close to a point contact (i.e., the contact angle is very large ~180°) and there is no instantaneous spreading. This is primarily due to the triggering of a CB state, as depicted in Figure 1e. Figure 1e shows that the surfactants primarily adsorb on the glass surface as monomers and interact with the monomeric layer of surfactants at the oil-water interface to trigger hypothetical “pillar”-like structures that induce this CB state. There may be three different types of modifications, as compared to the simplified picture illustrated in Figure 1e. These modifications, occurring due to the consideration of interplay between the solid wettability and the wettabilities of the different parts of the Tween 20 molecule (see Supplementary Information section 2 and Supp. Figure S2), or the consideration of the branched structure of the Tween 20 molecule (see Supplementary Information section 3 and Supp. Figure S3), or the consideration of surfactant adsorbing on the glass as hemi-micelles for large values of bulk concentration (see Supplementary Information section 3 and Ref. 42) will also lead to CB states.
For the proposed “pillar” structure introduced by the interacting surfactant molecules (see Figure 1e), the CB state encountered by the oil drop can be characterized by the corresponding contact angle θCB, expressed as41:

where θY is the Young's contact angle and D and P are the parameters associated with the “pillar” configuration (see Figure 1e). Eq. (1) can be approximated to remain unaltered in case one accounts for the variation in the surfactant orientation due to the interplay between the solid wettability and the wettabilities of the different parts of the Tween 20 molecule (see Supplementary Information section 2 and Supp. Figure S2). Eq. (1), however, does not account for branched nature (containing 3 ethylene oxide side chains) of the Tween 20 molecule. Presence of such side chains would imply a modification of the proposed “pillar”-like structure (the pillars would now demonstrate hierarchical structures, as proposed by Bhushan et al.43), which would modify the expression for the contact angle θCB as (see Supplementary Information section 3 and Supp. Figure S3 for derivation):

where nsc is the number of side chains (for each Tween 20 molecule) and dsc and hsc are the dimensions of the hierarchical structures (of the hypothetical “pillars”) formed by these side chains (please see Supp. Figure S3). For all the cases studied here D ≪ P, dsc ≪ P and hsc ≪ P. Therefore, from either Eq. (1) or Eq. (2), we may write cosθCB ≈ −1. This indicates that at the CB state, which the drop invariably experiences immediately after coming in contact with the surface, the drop must have an extremely large contact angle (~180°), ensuring a conformation of close to a point contact. The drop continues to stay in this conformation for some finite duration before gradually spreading to attain its equilibrium configuration. Please note that such spreading indicates a transition from the CB state to the Wenzel (Wn) state. This transition (characterized by a finite transition time Δt) occurs for low to intermediate surfactant concentration (c ≤ 100 μM) (see Figure 1c). However, for larger concentration this initial CB state is extremely stable ensuring that the equilibrium configuration of the drop is this CB state with a contact angle ~180°, affirming the surfactant-mediated under-water superoleophobic picture. We shall discuss the detailed dynamics of this transition (or no transition) later. First, we shall explain the variation of contact angle (induced by the spreading or CB-to-Wn transition) as a function of the surfactant concentration. The Wn state of the oil drop on the glass substrate with the “pillar” structures proposed in Figure 1e or Supp. Figure S2, can be characterized by the corresponding contact angle θWn, expressed as41:

where, as in Eq. (1), D, P and H are the parameters associated with the “pillar” formation (see Fig. 1e). Like Eq. (1), Eq. (3) also does not account for the alteration in the “pillar”-like structure on account of the ethylene oxide side chains of the Tween 20 surfactant molecules. In case such structural details (which would lead to hierarchical “pillar”-like structures) are accounted for, contact angle θWn can be expressed as (see Supplementary Information section 3):

Therefore, for small concentration of surfactant (c < cCMC), where D ≪ P, H ≪ P, dsc ≪ P and hsc ≪ P, from either Eq. (3) or Eq. (4), we may write cosθWn≈ cosθY, i.e., the drop contact angle in the Wn state is identical to the Young's contact angle for the drop, which can be expressed as:

where γso, γsw and γow are the solid-oil, solid-water and oil-water interfacial surface tensions. For c < cCMC, increase in c decreases γow44,45 and accordingly decreases the obtuse angle value of θY. Therefore, for c < cCMC, increase in c decreases the angle (θWn≈θY) of the drop (see Figures 1a,b). However, for c > cCMC increase in c has no effect on γow. On the contrary, for such c values, increase in c decreases the pitch P. Accordingly, the prefactor (1 + πDH/P2) in Eq. (3) or the prefactor (1 + πDH/P2 + 2πnscdschsc/P2) in Eq. (4) increases, ensuring an increase in the obtuse angle value of θWn with c for c > cCMC (see Figures 1a,b). This monotonic increase of the contact angle for c > cCMC continues until the surfactant concentration is large enough to ascertain that there is no CB-to-Wn transition and the drop equilibrates at the under-water superoleophobic CB state. We would like to mention here that for very large values of surfactant bulk concentration (c ≫ cCMC, e.g., c = 400 μM), surfactants may adsorb on the under-water glass surface as hemi-micelles (as described in Ref. 42). In such a case the surfactant-mediated “pillar” configurations are not the same as illustrated in Fig. 1e and Supp. Figures S2, S3. Consequently, the quantification of the equilibrium Cassie-Baxter and Wenzel states would be different than that expressed in Eqs. (1–4), although the qualitative dependences of the angles on the different parameters pertaining to the “pillars” would remain unaffected, thereby ensuring that our theoretical hypothesis remains valid (see Supplementary Information section 3 for more relevant discussions).
The demarcation between the transition and the no-transition regimes (or wetting and rolling zones in Figures 1b,c) is characterized by the droop height δ in the initial CB conformation of the drop (see Figure 1e). This height can be expressed as41:

where R is the radius of the drop. This droop height remains independent of exact structural characteristic of the Tween 20 surfactant molecules, i.e., the hierarchical nature (caused by the presence of the ethylene oxide side chains) of the “pillar”-like structures formed by the surfactant molecules. The droop height is also independent of the possible alterations in the surfactant arrangement on account of interplay between the solid wettability and the wettabilities of the different parts of the surfactant molecules. There will be a transition from CB-to-Wn state if δ > H. At low surfactant concentrations, the pitch P is large and H is small, ensuring that the criterion δ > H is met and there is a transition. However, at higher concentrations (c ≫ cCMC) the pitch P is lowered and H is enhanced, thereby ensuring that δ < H and hence there is no transition. For example, for c = 30 μM, P ~ 1 μm (see Supp. Figure S6), so that δ ~ 1 nm (with R ~ 1 mm), whereas for c = 400 μM, P ~ 10 nm (see Supp. Figure S4), so that δ ~ 0.0001 nm. On the contrary, for c = 30 μM, H < 1 nm (see Supp. Figure S6), thereby ensuring that δ < H and hence there can be a transition. For c = 400 μM, H > 1 nm (see Supp. Figure S4), so that δ ≪ H and there is no transition. The values of these parameters, characterizing the surfactant-triggered “pillars”, are obtained from the AFM images and the involved procedure has been detailed in Supplementary Information section 5. However, this approach of demarcating the transition and the no-transition regimes, based on the relative variation of the droop height with respect to the height H of the “pillars”, cannot successfully explain the dependence of the spreading time Δt on the surfactant concentration c (Figure 1c). Rather Δt is obtained from the balance between the deforming Laplace pressure effects and the restoring forces on the oil drop. These restoring forces comprise of the van der Waals interactions and the entropic Steric stabilization effects37 (which has interpenetration and elastic contributions, see Figure 1f and Supplementary Information section 4) experienced by the surfactant molecules (see Figure 1f). This Δt can be expressed to scale as (see Supplementary Information section 4 for detail derivation):

where ρoil and Voil are the density and the volume of the oil drop, NA is the Avogadro number and kBT is the thermal energy. In Eq. (7), which quantifies the concentration dependence of Δt (see Figure 1c), the term γowδ represents the contribution of the driving Laplace pressure (causing the transition), whereas the term 10−3 NAkBTcR2 denotes the contribution of the net retardation effect experienced by the oil drop (caused by the competitive influences of the van der Waals and entropic Steric stabilization37 interactions experienced by the surfactant molecules, see Figure 1f). For an estimation of the magnitude of these two forces, please refer to Supplementary Information section 4. Eq. (7) demonstrates that the increase in c increases Δt, thereby establishing the observations in Figure 1c. Eq. (7) also suggests that beyond a critical c value, the steric interactions37 will outweigh the fluidic drive due to Laplace pressure thereby halting the CB-to-Wn transition. This is another reason for which one observes no transition beyond a certain surfactant concentration. Also for c < cCMC, increase in c reduces γow44,45, thereby leading to an increase in Δt. Typically, for c = 100 μM, γow ~ 0.01 N/m46 so that with ρoil ~ 1000 kg/m3 and Voil ~ 1 μl, we get Δt ~ 10 s, i.e., a time scale of similar order as predicted by the experiments (Figure 1c).
We would like to mention here that the Marangoni effect does not play any role in the spreading of the oil drop (which we conjecture to be a manifestation of CB-to-Wn transition) in our experiments. Surfactant-concentration-imbalance-driven Marangoni flow has been known to lead to spreading of drops47,48 – however, such spreading becomes possible only when there exists a precursor film and the drop has small (oleophilic or hydrophilic) contact angles47,48. Such a possibility being absent in the present case (since the oil drop exhibits a large oleophobic contact angle from outset), Marangoni flow is not affecting the drop spreading, or the possible redistribution of the coverage density of the surfactants close to the contact line.
We have demonstrated that a simple glass surface, placed inside water, can be made superoleophobic, with extremely large contact angles (~180°) and very small modified roll off angles (~1/12th of a degree) by merely changing the surfactant content of the water (in which the oil is dispersed). This occurs as the oil droplet (dispersed in water) experiences an extremely stable Cassie-Baxter state in presence of large concentration of adsorbed surfactant molecules at a surfactant content (of the water) much larger than the CMC. This is a new approach of creating low energy surfaces, in the light of the fact that such surfaces have earlier been invariably prepared by irreversible engineering (micro-nano texturing) of the substrates. On the contrary in this proposed approach, there is an inherent reversibility in the sense that one can regenerate the original glass surface by removing the adsorbed surfactant. Most importantly, the study demonstrates for the first time the possibility of achieving low energy surfaces by merely working with the solvent, without engineering/texturing the surface.
Methods
Materials
For the experiments, we use microscopic glass slides (Fisherbrand-12-550-A3), deionized (DI) water (PURELAB Ultra, ELGA), silicon oil (Cargille Inc., USA-20130) and Tween 20 surfactant (Sigma-Aldrich,-P7949).
Preparation of the glass substrates
We dice glass substrates of specific sizes (~25 mm × 25 mm) from the glass slides, clean them using Piranha solution (3:1 mixture H2SO4 with H2O2) and subsequently dry them using nitrogen gas. The standard piranha cleaning procedure has been used to clean the glass substrate49. After the piranha cleaning process, the glass substrate was placed in the dump rinser (Microkleen Rinse by WAFAB) for 5 cycles (with each cycle being approximately 3 minutes long) to rinse with the deionized water. Such elaborate rinsing procedure is necessary to ensure that there is no contamination on the glass.
Preparation of the surfactant solution
We prepare surfactant solutions of different concentrations by mixing appropriate quantities of Tween 20 with DI water. This DI water is prepared using the ELGA system.
Immersion of the glass substrate in surfactant solution
We pour 40 ml surfactant solution of a given concentration into a distortion-free cuvette (Krüss Germany, SC-02) of dimension 40 mm × 40 mm × 30 mm (see the inset of Supp. Figure S1). The surfactant solution level is maintained at a height of h ~ 25 mm inside the cuvette (see Supp. Figure S1). We carefully place the glass substrate inside the cuvette using a tweezer. Before starting the drop deposition, we allow sufficient time to ensure that the surfactant molecules had adsorbed on the glass substrate and equilibrium has been attained. Also after completing each set of experiments, we always wash and rinse the cuvette with DI water several times and subsequently dry it with nitrogen gas.
Drop deposition
We first fill a glass syringe (Krüss, Germany, SY20, volume = 500 μl) with silicone oil (Cargille Laboratories Inc., Cedar Grove, NJ, USA; ρoil = 1100 kg/m3). Then, we insert the stainless steel needle (Krüss, Germany, NE 43, diameter = 0.8 mm) of this syringe inside the cuvette that is filled with the surfactant solution. Subsequently, we generate an oil drop of volume of 2 μl at the tip of the needle. In this position, we gradually draw the needle out of the liquid bath (of the cuvette). The moment the tip of the needle hits the air-water interface, the oil drop gets detached from the needle and is deposited on the glass substrate (instantaneously after such deposition, the oil drop, irrespective of the surfactant concentration, is in a CB state with contact angle close to 180°, see main text for more discussions). We practice this method of drop deposition, primarily motivated by the immense difficulties associated with the conventional drop deposition technique24 for the present case (see Supplementary Movies 1 and 2). Such difficulties are primarily attributed to the extremely low surface energy of the substrate with respect to the oil drop. After the drop has been deposited (the drop does not bounce off, as the Weber number is substantially small, see Supplementary Movie 3 and Supplementary Information section 1), depending on the surfactant concentrations, it may start to spread (i.e., undergo a CB-to-Wn transition, see the main text and the Supplementary Movie 3) and achieve a contact angle (much lesser than 180°) over a finite time Δt, which varies with the surfactant concentration (see the main text). We capture this transition (a sample representation of this transition is provided in Supplementary Movie 3) using the imager (capture speed of 8 frames per second) and the drop shape analysis software of the DSA 100 (Krüss, Germany) Contact Angle Measurement System (see Supp. Figure S1 for the complete experimental set up).
Measurement of Δt and the contact angle
As discussed in the main text, depending on the surfactant concentrations, the oil drop after deposition may spread from the initial CB state to the Wn state over a finite time Δt and achieve a finite contact angle. For each value of the surfactant concentration, we measure both the contact angle and the Δt on two glass substrates, with ten readings for each of the glass substrates. The variations of these two parameters and the corresponding standard errors, are shown in Figures 1 b,c. In Supplementary Table S1, we provide the actual values of these measurements.
Estimation of modified roll off angles
Apart from the measurement of the contact angles, the under-water superoleophobic nature of the surface can be further quantified by determining the corresponding roll off angles24. In the present study, what we measure is the modified roll off angle (that is slightly different from the conventional roll-off angle). This is particularly useful for the case of large surfactant concentrations (200 μM, 400 μM and 800 μM), where the equilibrium state is the CB state, with contact angles ~180° (see Fig. 1). For these cases, it is difficult to calculate the exact values of the contact angle and therefore the additional quantification, provided by the corresponding modified roll off angles, is essential to establish the extent of the under-water superoleophobic behavior. For all of these concentration values (200 μM, 400 μM and 800 μM), we find an extremely small modified roll off angle of 1/12th of a degree (~5 minutes), which establish the under-water superoleophobic nature of the surface (see Supplementary Movie 4 for an illustration of the rolling). We achieve this extremely small inclination angle (which causes this roll off) by using special steel angle gauge blocks (Model-AG18TR, Webber Gage Division, Cleveland, Ohio, USA). We also attempted to check the modified roll off angles for oil droplet corresponding to the smaller surfactant concentrations [i.e., concentration values at which the oil drop spreads from the initial CB state to attain a finite contact angle (<180°)]. For all these cases, we tried up to an inclination of 5° and found no roll-off. Therefore, there is a distinct singularity in the roll-off behavior across an extremely narrow spectrum of the surfactant concentration values – the reason is identical to the apparent singularities in the variation of the contact angles and Δt values over the same narrow spectrum demarcating the transition and the no-transition (CB-to-Wn) regimes.
Atomic force microscopy (AFM)
To obtain the surface topography, we perform the contact mode AFM analysis using the MFP-3D AFM (Asylum Research Inc. Santa Barbara, CA). We have used the silicon cantilever (OMCL-AC240TS-W2) with aluminum reflex coating and a tip radius of 7 nm and scan area of 1 μm × 1 μm. All the AFM images are obtained with the glass substrate immersed inside the water, with or without the surfactant. The glass substrates, placed inside the water and having different surfactant coverage, are prepared in exactly the same manner as that in the main experiments (see above). We provide the AFM height trace images for these surfactant-covered surfaces, for different surfactant concentration values. For more discussions on the method of determining parameters pertaining to the hypothetical “pillars” from the AFM images and other related issues on AFM measurements kindly refer to Supplementary Information section 5.
References
Barthlott, W. & C. Neinhuis, C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 202, 1–8 (1997).
Herminghaus, S. Roughness-induced non-wetting. Europhys. Lett. 52, 165–170 (2000).
Gao, X. & Jiang, L. Water-repellent legs of water striders. Nature 432, 36 (2004).
Parker, A. R. & Lawrence, C. R. Water capture by a desert beetle. Nature 414, 33–34 (2001).
Autumn, K. et al. Adhesive force of a single gecko foot-hair. Nature 405, 681–685 (2000).
Genzer, J. & Efimenko, K. Recent developments in superhydrophobic surfaces and their relevance to marine fouling: A review. Biofouling 22, 339–360 (2006).
Extrand, C. W. Repellency of the lotus leaf: Resistance to water intrusion under hydrostatic pressure. Langmuir 27, 6920–6925 (2011).
Genzer, J. & Efimenko, K. Creating long-lived superhydrophobic polymer surfaces through mechanically assembled monolayers. Science 290, 2130–2133 (2000).
Singh, S., Houston, J., Swol, F. V. & Brinker, C. J. Superhydrophobicity: Drying transition of confined water. Nature 442, 526 (2006).
McHale, G., Newton, M. I. & Shirtcliffe, N. J. Immersed superhydrophobic surfaces: Gas exchange, slip and drag reduction properties. Soft Matter 6, 714–719 (2010).
Quere, D. Non-sticking drops. Rep. Prog. Phys. 68, 2495–2532 (2005).
Li, X.-M., Reinhoudt, D. & Crego-Calama, M. What do we need for a superhydrophobic surface? A review on the recent progress in the preparation of superhydrophobic surfaces. Chem. Soc. Rev. 36, 1350–1368 (2007).
Yan, Y. Y., Gao, N. & Barthlott, W. Mimicking natural superhydrophobic surfaces and grasping the wetting process: A review on recent progress in preparing superhydrophobic surfaces. Adv. Colloid Interface Sci. 169, 80–105 (2011).
Lafuma, A. & Quere, D. Superhydrophobic states. Nat. Mater. 2, 457–460 (2003).
Erbil, H. Y., Demirel, A. L., Avci, Y. & Mert, O. Transformation of a simple plastic into a superhydrophobic surface. Science 299, 1377–1380 (2003).
Vakarelski, I. U., Patankar, N. A., Marston, J. O., Chan, D. Y. C. & Thoroddsen, S. T. Stabilization of Leidenfrost vapour layer by textured superhydrophobic surfaces. Nature 489, 274–277 (2012).
Kwon, H. M., Paxson, A. T., Varanasi, K. K. & Patankar, N. A. Rapid deceleration-driven wetting transition during pendant drop deposition on superhydrophobic surfaces. Physical Review Letters 106, 36102 (2011).
Kwon, Y., Patankar, N., Choi, J. & Lee, J. Design of surface hierarchy for extreme hydrophobicity. Langmuir 25, 6129–6136 (2009).
Extrand, C. W. & Moon, S. I. Contact angles of liquid drops on super hydrophobic surfaces: Understanding the role of flattening of drops by gravity. Langmuir 26, 17090–17099 (2010).
Krumpfer, J. W., Bian, P., Zheng, P., Gao, L. & McCarthy, T. J. Contact angle hysteresis on superhydrophobic surfaces: An ionic liquid probe fluid offers mechanistic insight. Langmuir 27, 2166–2169 (2010).
Hozumi, A., Kim, B. & McCarthy, T. J. Hydrophobicity of perfluoroalkyl isocyanate monolayers on oxidized aluminum surfaces. Langmuir 25, 6834–6840 (2009).
Gao, L., Fadeev, A. Y. & McCarthy, T. J. Superhydrophobicity and contact-line issues. MRS Bulletin 33, 747–751 (2008).
Tuteja, A. et al. Designing superoleophobic surfaces. Science 318, 1618–1622 (2007).
Deng, X., Mammen, L., Butt, H.-J. & Vollmer, D. Candle soot as a template for a transparent robust superamphiphobic coating. Science 335, 67–70 (2012).
Tuteja, A., Choi, W., McKinley, G. H., Cohen, R. E. & Rubner, M. F. Design parameters for superhydrophobicity and superoleophobicity. MRS Bulletin 33, 752–758 (2008).
Xue, Z. et al. A novel superhydrophilic and underwater superoleophobic hydrogel-coated mesh for oil/water separation. Adv. Mater. 23, 4270–4273 (2011).
Su, B., Wang, S., Song, Y. & Jiang, L. Utilizing superhydrophilic materials to manipulate oil droplets arbitrarily in water. Soft Matter 7, 5144–5149 (2011).
Extrand, C. W. Modeling of ultralyophobicity: Suspension of liquid drops by a single asperity. Langmuir 21, 10370–10374 (2005).
Extrand, C. W. Criteria for ultralyophobic surfaces. Langmuir 20, 5013–5018 (2004).
Yao, X., Gao, J., Song, Y. & Jiang, L. Superoleophobic surfaces with controllable oil adhesion and their application in oil transportation. Adv. Funct Mater. 21, 4270–4276 (2011).
Zhang, L., Zhonghai, Z. & Peng, W. Smart surfaces with switchable superoleophilicity and superoleophobicity in aqueous media: toward controllable oil/water separation. NPG Asia Mater. 4, e8 (2012).
Quere, D. Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99 (2008).
Patankar, N. A. Consolidation of hydrophobic transition criteria by using an approximate energy minimization approach. Langmuir 26, 8941–8945 (2010).
Patankar, N. A. Hysteresis with regard to Cassie and Wenzel states on superhydrophobic surfaces. Langmuir 26, 7498–7503 (2010).
Patankar, N. A. Transition between superhydrophobic states on rough surfaces. Langmuir 26, 7498–7503 (2004).
Gao, L. & McCarthy, T. J. How Wenzel and Caasie were wrong. Langmuir 23, 3762–3765 (2007).
Napper, D. Steric stabilization. J. Colloid Interface Sci. 58, 390–407 (1977).
Mohammadi, R., Wassink, J. & Amirfazli, A. Effect of surfactants on wetting of super-hydrophobic surfaces. Langmuir 20, 9657–9662 (2004).
Ferrari, M., Ravera, F., Rao, S. & Liggieri, L. Surfactant adsorption at superhydrophobic surfaces. Appl. Phys. Lett. 89, 053104 (2006).
Ferrari, M. & Ravera, F. Surfactants and wetting at superhydrophobic surfaces: Water solutions and non aqueous liquids. Adv. Colloid Interface Sci. 161, 22–28 (2010).
Jung, Y. C. & Bhushan, B. Dynamic effects of bouncing water droplets on superhydrophobic surfaces. Langmuir 24, 6262–6269 (2008).
Schniepp, H. C., Snum, H. C., Saville, D. A. & Aksay, I. A. Surfactant aggregates at rough solid-liquid interfaces. J. Phys. Chem. B 111, 8708–8712 (2007).
Bhushan, B., Jung, Y. C. & Koch, K. Micro-, nano- and hierarchical structures for superhydrophobicity, self-cleaning and low adhesion. Phil. Trans. Roy. Soc. A 367, 1631–1672 (2009).
Wustneck, R., Miller, R., Kriwanek, J. & Holzbauer, H.-R. Quantification of synergistic interaction between different surfactants using a generalized Frumkin-Damaskin adsorption-isotherm. Langmuir 10, 3738–3742 (1994).
Fainerman, V. B., Miller, R., Wastneck, R. & Makievski, A. Adsorption isotherm and surface tension equation for a surfactant with changing partial molar area. 1. Ideal surface layer. J. Phys. Chem. 100, 7669–7675 (1996).
Raccurt, O., Berthier, J., Clementz, P., Borella, M. & Plissonnier, M. On the influence of surfactants in electrowetting systems. J. Micromech. Microeng. 17, 2217–2223 (2007).
Stoebe, T., Lin, Z., Hill, R. M., Ward, M. D. & Davis, H. T. Surfactant-enhanced spreading. Langmuir 12, 337–344 (1996).
Stoebe, T., Lin, Z., Hill, R. M., Ward, M. D. & Davis, H. T. Enhanced spreading of aqueous films containing ethoxylated alcohol surfactants on solid substrates. Langmuir 13, 7270–7275 (1997).
Madou, M. J. Fundamentals of Microfabrication. New York, CRC Press. (2002).
Shen, L., Guo, A. & Zhu, X. Tween surfactants: Adsorption, self-organization & protein resistance. Surf. Sci. 605, 494–499 (2011).
Acknowledgements
The authors are grateful to Dr. A. He and Dr. D. Karpuzov (Alberta Centre for Surface Engineering and Science, University of Alberta) for providing AFM training to PRW and to R. Marchand (Machine shop, Mechanical Engineering Department, University of Alberta) for providing steel angle gauges and other useful support. The authors also gratefully acknowledge Dr. T. Thundat and Dr. R. Gaikwad (Department of Chemical and Materials Engineering, University of Alberta) for many useful discussions. The authors also thank the Natural Sciences and Engineering Research Council of Canada (NSERC) for providing financial support and scholarship to S.D. in form of the Banting Postdoctoral Fellowship. The infrastructure support from Canada Foundation for Innovation (CFI) is also greatly appreciated.
Author information
Authors and Affiliations
Contributions
S.K.M. conceived the problem and supervised the project. P.R.W. designed the entire experimental set up and performed all the experiments of the drop dynamics and the AFM measurements. P.R.W. and S.D. made the mathematical modeling. S.D. and S.K.M. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Supplementary Information
Supplementary Movie 1
Supplementary Information
Supplementary Movie 2
Supplementary Information
Supplementary Movie 3
Supplementary Information
Supplementary Movie 4
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Waghmare, P., Das, S. & Mitra, S. Under-water superoleophobic Glass: Unexplored role of the surfactant-rich solvent. Sci Rep 3, 1862 (2013). https://doi.org/10.1038/srep01862
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01862
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.