Abstract
Measurement of a quantum system – the process by which an observer gathers information about it – provides a link between the quantum and classical worlds. The nature of this process is the central issue for attempts to reconcile quantum and classical descriptions of physical processes. Here, we show that the conventional paradigm of quantum measurement is directly responsible for a well-known disparity between the resources required to extract information from quantum and classical systems. We introduce a simple form of quantum data gathering, “coherent measurement”, that eliminates this disparity and restores a pleasing symmetry between classical and quantum statistical inference. To illustrate the power of quantum data gathering, we demonstrate that coherent measurements are optimal and strictly more powerful than conventional one-at-a-time measurements for the task of discriminating quantum states, including certain entangled many-body states (e.g., matrix product states).
Similar content being viewed by others
Introduction
Observation is at the heart of understanding physical phenomena. More broadly, it serves as the first step in information processing. In the canonical example, a classical observer gathers data about a quantum system by measuring it. This process yields classical information about the state, but at a high price – the observer's information gain is incomplete (it doesn't uniquely identify the state) and accompanied by an irreversible loss of information. It is typically further restricted by locality; most joint measurements on an N-component quantum system are practically impossible when the components are spatially delocalized. This has profound consequences for extracting information from multiple samples of a quantum state. Measuring them individually is strictly less powerful than a joint measurement on the whole ensemble. By contrast, in classical theories, measurement is a passive procedure with no accompanying information loss and complete information can be gathered from independent measurements of the samples. This implies a fundamental asymmetry between data-gathering in quantum and classical theories.
The conventional paradigm of quantum measurement comprises: (i) a controlled unitary interaction between a system  and an apparatus
and an apparatus  ; (ii) decoherence on
; (ii) decoherence on  , which forces its state into a mixture of “pointer basis” states1; and (iii) experimental readout of the classical result from
, which forces its state into a mixture of “pointer basis” states1; and (iii) experimental readout of the classical result from  (arguably accompanied by “collapse” of
(arguably accompanied by “collapse” of  state). But this prescription breaks down if any part of the observing apparatus can sustain coherence. A coherent apparatus has other, more powerful information-gathering strategies available to it. To demonstrate this in the context of traditional information processing, we allow
state). But this prescription breaks down if any part of the observing apparatus can sustain coherence. A coherent apparatus has other, more powerful information-gathering strategies available to it. To demonstrate this in the context of traditional information processing, we allow  to be a quantum information processor (QIP) – basically a very small (perhaps just 1 qubit) non-scalable quantum computer. We focus on the case where
to be a quantum information processor (QIP) – basically a very small (perhaps just 1 qubit) non-scalable quantum computer. We focus on the case where  is protected from decoherence until the very end of the protocol. What remains is a coherent measurement, a unitary interaction between
is protected from decoherence until the very end of the protocol. What remains is a coherent measurement, a unitary interaction between  and
and  that transfers information from
that transfers information from  to
to  .
.
To explore and demonstrate the power of coherent measurement, let us consider the specific problem of quantum state discrimination2,3: Given N quantum systems that were all prepared in one of K distinct states |ψ1〉,…,|ψK〉, decide in which state they were prepared. In principle, finding the optimal measurement is a straightforward convex program. But when N > 1 copies of |ψk〉 are available, this task (famously) requires joint measurement on all N copies, which is prohibitively difficult. Observing each of the N copies independently yields a strictly lower probability of success4,5. This contrasts starkly with the corresponding classical problem of distinguishing K distinct probability distributions, where one-at-a-time observations are completely sufficient. Discrimination thus provides an ideal scenario to test the information-processing utility of more general data gathering paradigms.
Results
Simple discrimination with N copies
Suppose we are given N quantum systems  with d-dimensional Hilbert spaces
with d-dimensional Hilbert spaces  and a promise that they were all identically prepared in one of K nonorthogonal states {|ψ1〉…|ψK〉}. Their joint state is
and a promise that they were all identically prepared in one of K nonorthogonal states {|ψ1〉…|ψK〉}. Their joint state is  , with k unknown. Identifying k with maximum success probability requires a joint measurement on all N samples. Non-adaptive, one-at-a-time measurement cannot achieve the optimal success probability. For K = 2 candidate states, there is an adaptive local measurement scheme that achieves the optimal success probability6, but no such protocol has been found for K > 2. It has recently been shown that for K = 3, there exist cases for which local measurements cannot achieve the optimal success probability, even with multiple rounds of classical communication7.
, with k unknown. Identifying k with maximum success probability requires a joint measurement on all N samples. Non-adaptive, one-at-a-time measurement cannot achieve the optimal success probability. For K = 2 candidate states, there is an adaptive local measurement scheme that achieves the optimal success probability6, but no such protocol has been found for K > 2. It has recently been shown that for K = 3, there exist cases for which local measurements cannot achieve the optimal success probability, even with multiple rounds of classical communication7.
All the information about k is contained in a K-dimensional subspace

So while the optimal measurement is a joint measurement, it does not need to explore the majority of  . We will implement it by rotating the entire subspace
. We will implement it by rotating the entire subspace  into the state space of our K-dimensional QIP
into the state space of our K-dimensional QIP  (the coherent measurement apparatus). We do so via sequential independent interactions between
(the coherent measurement apparatus). We do so via sequential independent interactions between  and each of the N samples
and each of the N samples  , “rolling up” all information about k into
, “rolling up” all information about k into  .
.
 is initially prepared in the |0〉 state. We bring it into contact with
is initially prepared in the |0〉 state. We bring it into contact with  and execute a SWAP gate between
and execute a SWAP gate between  and the {|0〉,…,|d − 1〉} subspace of
and the {|0〉,…,|d − 1〉} subspace of  . This transfers all information from the first sample into
. This transfers all information from the first sample into  , leaving
, leaving  in the |0〉 state.
in the |0〉 state.
Now we bring  into contact with
into contact with  . Their joint state is
. Their joint state is  , although we do not know k. But we do know that the state lies within
, although we do not know k. But we do know that the state lies within  , (see Eq. 1), whose dimension is at most K. A basis {|ϕj〉: j = 1…K} for this space can be obtained by Gram-Schmidt orthogonalization. We apply a unitary interaction between
, (see Eq. 1), whose dimension is at most K. A basis {|ϕj〉: j = 1…K} for this space can be obtained by Gram-Schmidt orthogonalization. We apply a unitary interaction between  and
and  ,
,

where we have defined U2 only on the subspace of interest (for completeness, it can be extended to the complement,  , in any convenient manner). It rotates
, in any convenient manner). It rotates  into
into  , which places all the information about k in
, which places all the information about k in  and decouples
and decouples  (
( is left with no information about k if and only if
is left with no information about k if and only if  is left with all the information about k.).
is left with all the information about k.).  is now in one of K possible states
is now in one of K possible states  , which (as a set) are unitarily equivalent to
, which (as a set) are unitarily equivalent to  – e.g.,
– e.g.,  .
.
The rest of the algorithm is now fairly obvious; we move on and interact  with
with  in the same way, etc, etc. At each step, when
in the same way, etc, etc. At each step, when  comes into contact with
comes into contact with  , their joint state is
, their joint state is  . These K alternatives reside in a K-dimensional space
. These K alternatives reside in a K-dimensional space  (see Eq. 1), spanned by a basis
(see Eq. 1), spanned by a basis  , which is then rotated into
, which is then rotated into  by applying
by applying

Each sample system is left in the |0〉 state, indicating that all its information has been extracted. After every sample has been sucked dry, we simply measure  to extract k. This final measurement can be efficiently computed via convex programming, since
to extract k. This final measurement can be efficiently computed via convex programming, since  is only K-dimensional.
is only K-dimensional.
The sequence of coherent measurement interactions is independent of what sort of discrimination we want to do – e.g., minimum-error4, unambiguous discrimination8,9,10,11, maximum-confidence12, etc. – because  is a sufficient statistic for any inference about k and our protocol simply extracts it whole, leaving the decision rule up to the final measurement on
is a sufficient statistic for any inference about k and our protocol simply extracts it whole, leaving the decision rule up to the final measurement on  . As in the classical case, data gathering can now be separated from data analysis.
. As in the classical case, data gathering can now be separated from data analysis.
As an example of the data gathering protocol, we consider now the K = 2 case and take the two possible initial states to be single qubit states, parametrized as follows


The joint state of the first n samples is given by

where |n,j〉 is a normalized equal superposition of all tensor product states with n − j systems in state |0〉 and j systems in state |1〉. A natural basis for the two-dimensional subspace  is then given by
is then given by


and the goal of the data gathering algorithm is to transfer the subspace spanned by these states into the processor  via sequential interactions with each of the samples
via sequential interactions with each of the samples  .
.
At the first step, as indicated above, we perform a SWAP gate between  and
and  . At the next step, the joint state of
. At the next step, the joint state of  and
and  is
is

where |0〉2, |1〉2 are joint  states, given by the n = 2 case of Eqs. 6 and 7. A two-qubit unitary acting as follows
states, given by the n = 2 case of Eqs. 6 and 7. A two-qubit unitary acting as follows


thus leaves  in state |0〉 while the processor, in state
in state |0〉 while the processor, in state

now holds all the information previously contained in the two samples read so far. Now suppose the processor has interacted with and processed the first n − 1 samples. Then we have performed a unitary which acts as follows on the relevant subspace:


Defining  and using Eqs. 5–7, the state of the processor is given by
and using Eqs. 5–7, the state of the processor is given by

and we wish to update this state through interaction with the nth sample. The basis states |0〉n, |1〉n spanning  are related to the corresponding basis states spanning
are related to the corresponding basis states spanning  and the basis |0〉, |1〉 of
and the basis |0〉, |1〉 of  as follows
as follows


Thus we wish to implement a 2-qubit unitary on the processor  and the nth sample, which acts as follows:
and the nth sample, which acts as follows:


This can be achieved by, e.g., performing a CNOT gate with  as the control and
as the control and  as the target, followed by a controlled unitary on
as the target, followed by a controlled unitary on  to rotate the residual state to |0〉, controlled on the state of
to rotate the residual state to |0〉, controlled on the state of  . Continuing in this way we can roll up all the information contained in the provided samples
. Continuing in this way we can roll up all the information contained in the provided samples  into the processor
into the processor  . Each step requires only a 2 qubit unitary, acting on the nth sample and the processor. During the course of this process all the information contained in the joint N qubit state is transferred to the processor, where a single qubit measurement is sufficient to perform any allowed data analysis operation.
. Each step requires only a 2 qubit unitary, acting on the nth sample and the processor. During the course of this process all the information contained in the joint N qubit state is transferred to the processor, where a single qubit measurement is sufficient to perform any allowed data analysis operation.
This protocol can be modified to discriminate non-symmetric product states, e.g.,  vs.
vs.  . A more general extension, however, is to discriminating many-body states of the matrix product form.
. A more general extension, however, is to discriminating many-body states of the matrix product form.
Matrix product state discrimination
The information about k can be “rolled up” using sequential interactions because it is contained in a subspace  with Schmidt rank at most K across any division of the N systems. By this we mean that, given any pure or mixed state ρ on
with Schmidt rank at most K across any division of the N systems. By this we mean that, given any pure or mixed state ρ on  , if we trace out
, if we trace out  , the reduced state for
, the reduced state for  has rank at most K. Low Schmidt rank is critical. Consider distinguishing between two states that are each maximally entangled between the first N/2 samples and the last N/2 samples. They lie in a 2-dimensional subspace, but it is not accessible through our protocol with a low-dimensional QIP. The first N/2 samples are maximally entangled with the rest, so their reduced state has rank dN/2. At least N log2 d/2 qubits would be needed to store the information extracted from the first N/2 samples.
has rank at most K. Low Schmidt rank is critical. Consider distinguishing between two states that are each maximally entangled between the first N/2 samples and the last N/2 samples. They lie in a 2-dimensional subspace, but it is not accessible through our protocol with a low-dimensional QIP. The first N/2 samples are maximally entangled with the rest, so their reduced state has rank dN/2. At least N log2 d/2 qubits would be needed to store the information extracted from the first N/2 samples.
But whenever the Schmidt rank condition is satisfied, a variation of our algorithm will work. For product states (above), each state has Schmidt rank 1 and the span of K such states has Schmidt rank at most K.
This property of low Schmidt rank is generalized by matrix product states (MPS)13,14. An N-particle MPS with bond dimension D is guaranteed to have Schmidt rank at most D across any division of the 1D lattice. Thus, the span of K such MPS, each with bond dimension ≤ D, has Schmidt rank at most DK. We denote such a subspace,

a matrix product subspace with bond dimension DK. Such a set of MPS can be distinguished optimally with coherent measurements and (log2 D + log2 K) qubits.
Our algorithm is a straightforward generalization of the one for product states and proceeds as shown in Figure 1. First, we represent the MP subspace  by its purification – a single MPS |Ψ〉 for
by its purification – a single MPS |Ψ〉 for  and a fictitious reference system R,
and a fictitious reference system R,

Information about k, which is contained in  , equates to correlation with the imaginary R.
, equates to correlation with the imaginary R.
Discrimination of MPS.
Our protocol represents an unknown MPS |ψk〉 from a set {|ψ1〉 … |ψK〉} by its purification – a single MPS |Ψ〉 involving a fictitious reference R. The algorithm then successively decorrelates each sample  from the rest, storing
from the rest, storing  correlations with the remainder of the lattice in the “apparatus”
correlations with the remainder of the lattice in the “apparatus”  . Ultimately, all existing information about k (i.e., its correlation with R) is contained in
. Ultimately, all existing information about k (i.e., its correlation with R) is contained in  , which can be measured.
, which can be measured.
Now, we initialize  in the |0〉 state, then SWAP its state with that of
in the |0〉 state, then SWAP its state with that of  (the first lattice site). This decouples
(the first lattice site). This decouples  , leaving
, leaving  in a matrix product state,
in a matrix product state,

with Schmidt rank no greater than DK.
Now, to roll up each successive site  , we find the Schmidt decomposition of the current state between
, we find the Schmidt decomposition of the current state between  and the remainder of the lattice, write it (generically) as
and the remainder of the lattice, write it (generically) as

and apply a unitary operation to  ,
,

which decouples  and leaves all the information previously in
and leaves all the information previously in  in
in  . As in Eq. 2, this unitary is specified only on the subspace of interest and can be completed in any convenient fashion. Doing this successively at each site decorrelates all the
. As in Eq. 2, this unitary is specified only on the subspace of interest and can be completed in any convenient fashion. Doing this successively at each site decorrelates all the  and we are left in the state
and we are left in the state

with all information about k in  , where it can be extracted by a simple measurement.
, where it can be extracted by a simple measurement.
Recent proposals for local tomography15 are also based on sequential interactions. Our protocol, with coherent measurements, offers a tremendous efficiency advantage (at the cost of requiring a small QIP!). It can distinguish near-orthogonal MPS states with a single copy, whereas local tomography requires O(N) copies. Distinguishing non-orthogonal states requires multiple (M) copies. To apply our algorithm, we simply line up the copies (they do not have to exist simultaneously) and treat them as a single NM-particle MPS of bond dimension D.
Mixed state discrimination and tomography
In the context of N-copy states, one may ask:
-
1
Can coherent measurement be used to discriminate mixed states, i.e.
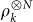 ?
? -
2
Can coherent measurement be used for full state tomography (rather than discrimination)?
The answer to both is “Yes, but it seems to require an O(log N)-qubit apparatus.” This is a very favorable scaling, but less remarkable (and less immediately useful) than the O(1) scaling for pure state discrimination.
This is possible because the order of the samples is completely irrelevant. As we scan through the samples, we can discard ordering information, keeping only a sufficient statistic for inference about ρ. The quantum Schur transform does this16. It is based on Schur-Weyl duality17, which states that because permutations of the N samples commute with collective rotations on them, the Hilbert space  can be refactored as
can be refactored as

The  factors are irreducible representation spaces (irreps) of SU(d), the
factors are irreducible representation spaces (irreps) of SU(d), the  factors are irreps of SN and λ labels the various irreps. The Schur transform can be implemented by a unitary circuit that acts sequentially on the samples, mapping N qudit registers into three quantum registers containing (respectively) λ,
factors are irreps of SN and λ labels the various irreps. The Schur transform can be implemented by a unitary circuit that acts sequentially on the samples, mapping N qudit registers into three quantum registers containing (respectively) λ,  and
and  :
:

The “ordering” register  accounts for nearly all the Hilbert space dimension of
accounts for nearly all the Hilbert space dimension of  and since it is irrelevant to inference it can be discarded as rapidly as it is produced. What remains to be stored in
and since it is irrelevant to inference it can be discarded as rapidly as it is produced. What remains to be stored in  is:
is:
-
1
a “label” register λ (a sufficient statistic for the spectrum of ρ),
-
2
a SU(d) register
 (a sufficient statistic for the eigenbasis of ρ).
(a sufficient statistic for the eigenbasis of ρ).
The λ register requires a Hilbert space with dimension ≥ the number of Young diagrams with N boxes in at most d rows, which is approximately

The  register must hold the largest N-copy irrep of SU(d), whose size can be calculated using hook-length formulae18 and upper bounded by
register must hold the largest N-copy irrep of SU(d), whose size can be calculated using hook-length formulae18 and upper bounded by

Together, these registers require O(d2 log N) qubits of memory (although for pure state tomography, O(d log N) qubits of memory are sufficient).
O(log N) memory appears to be necessary for optimal accuracy. Consider the simplest possible case – discrimination of two classical 1-bit probability distributions

The sufficient statistic is frequencies of “0” and “1”, {n, N −n}. For any given problem, there is a threshold value nc such that the answer depends only on whether n < nc, so only one bit of information is required. However, extracting that bit via sequential queries requires storing n exactly at every step (using O(log N) bits of memory). Any loss of precision could cause a ±1 error at the final step and thus a wrong decision. In this example, classical storage is sufficient. But in the general case, where the candidate ρk do not commute, no method is known to compress the intermediate data into classical memory without loss (previous work suggests it is probably impossible19).
Discussion
Quantum information science is rife with gaps between what is theoretically achievable and what is practically achievable. Our algorithm eliminates performance gaps for pure state discrimination with local measurements – but it requires a new kind of measurement apparatus with at least 1 controllable qubit of quantum storage. Its utility depends on its applications and on the difficulty of implementation.
One immediate application of our protocol is detection of weak forces and transient effects. A simple force detector (e.g., for magnetic fields) might comprise a large array of identical systems (e.g., |↓〉 spins). Each system is only weakly perturbed by the force, so information about the force is distributed across the entire array. Our algorithm efficiently gathers up that information with no loss – whereas local measurements with classical processing waste much information.
A more sensitive N-particle “antenna” would incorporate entanglement between the N particles20. High sensitivity can be achieved by simple MPS states with D = 2, like N00N states21,

Collective forces do not change D, so the final states to be discriminated are also MPS. Our approach can discriminate such states and it can be used to prepare them, by running the “rolling up” process in reverse22.
More ambitious applications include direct probing of many-body states, to test a particular MPS ansatz for a lattice system, or to characterize results of quantum simulations in optical lattices or ion traps. Without fully scalable quantum computers that can couple directly to many-body systems, coherent measurements may be the only way to efficiently probe complex N-particle states. Our protocol does not obviously scale to PEPS, the higher-dimensional analogues of MPS14. Like MPS, PEPS obey an area law – entanglement across a cut scales not with the volume of the lattice (N), but with the area of the cut. For a 1-dimensional MPS on N systems, any cut has area 1, so the Schmidt rank scales as O(1) and our algorithm requires an O(1) qubit QIP. Rolling up a general PEPS on an n-dimensional lattice would require  bits of quantum memory. However, some PEPS can be sequentially generated23 and are likely amenable to our protocol.
bits of quantum memory. However, some PEPS can be sequentially generated23 and are likely amenable to our protocol.
We note that the engineering requirements for a coherent measurement apparatus are achievable with near-future technology.  should be a clean K-dimensional quantum system with:
should be a clean K-dimensional quantum system with:
-
1
Universal local control,
-
2
Long coherence time relative to the gate timescale,
-
3
Controllable interaction with an external d-dimensional “sample” system,
-
4
Sequential coupling to each of N samples,
-
5
Strong measurements (which may be destructive).
Although adaptive local measurements can discriminate 2 states optimally, K = 2 is nevertheless sufficient for a proof of principle experiment demonstrating quantum data gathering. That a sufficient statistic for any desired measurement is stored as quantum data in the processor could be demonstrated by e.g. performing minimum error or unambiguous discrimination through eventual measurement on the processor in different runs of the same experiment. However, K ≥ 3 would be more exciting as optimal discrimination of 3 states via local, adaptive measurements is not possible in all cases7.
These requirements are much weaker than those for scalable quantum computing. Coherent measurement could be an early application for embryonic quantum architectures. Furthermore, scalability is not required, just a single K-dimensional system. Only local control has to be universal, since the interaction with external systems is limited. Error correction is not mandatory, for coherence need only persist long enough to interact with each of the N systems of interest. Since measurements are postponed until the end, they can be destructive.
We do require  to be portable – i.e., sequentially coupled to each of the N samples – whereas a quantum computer can be built using only nearest neighbor interactions. Fortunately, most proposed architectures have selective coupling either through frequency space (NMR, ion traps with a phonon bus) or physical motion of the qubits (some ion traps) or flying qubits (photonic architectures). Devices that are not viable for full-scale quantum computing may be even better for coherent measurement. For example, an STM might pick up and transport a single coherent atomic spin along an array of sample atoms, interacting sequentially with each of them.
to be portable – i.e., sequentially coupled to each of the N samples – whereas a quantum computer can be built using only nearest neighbor interactions. Fortunately, most proposed architectures have selective coupling either through frequency space (NMR, ion traps with a phonon bus) or physical motion of the qubits (some ion traps) or flying qubits (photonic architectures). Devices that are not viable for full-scale quantum computing may be even better for coherent measurement. For example, an STM might pick up and transport a single coherent atomic spin along an array of sample atoms, interacting sequentially with each of them.
There are broad implications stemming from the results above. Coherent measurements are a genuinely new way to gather information. We have not just removed collapse from standard quantum measurements! That kind of coherent measurement is used already in quantum error correction, where it's common to replace a measurement of X with a controlled unitary of the form

Such unitaries transfer information about a specific observable X from  to
to  . For appropriate
. For appropriate  and
and  , later measurements of
, later measurements of  produce exactly the same result as if
produce exactly the same result as if  had been measured directly. The coherent measurements in our discrimination protocols are not of this form. They do not measure (i.e., transfer information to
had been measured directly. The coherent measurements in our discrimination protocols are not of this form. They do not measure (i.e., transfer information to  about) a specific basis. For example, in N-copy state discrimination,
about) a specific basis. For example, in N-copy state discrimination,  interacts with the first sample by a SWAP operation, which has no preferred basis. Later interactions are also not of controlled-U form (Eq. 12).
interacts with the first sample by a SWAP operation, which has no preferred basis. Later interactions are also not of controlled-U form (Eq. 12).
One might ask where the “measurement” occurs, since the interaction between  and
and  is purely unitary. The essence of measurement is that an observer or apparatus gains information. Quantum measurements are usually construed as mysterious processes that consume quantum states and excrete specific, definite measurement outcomes. Quantum theories of measurements usually represent them as (i) unitary interaction, (ii) decoherence and superselection and finally (iii) wavefunction collapse or splitting of the universe. Our results suggest that unitary interaction (the only part of this sequence that is really understood) can stand alone as an information-gathering “measurement.” And by avoiding decoherence, we can gather information strictly more effectively.
is purely unitary. The essence of measurement is that an observer or apparatus gains information. Quantum measurements are usually construed as mysterious processes that consume quantum states and excrete specific, definite measurement outcomes. Quantum theories of measurements usually represent them as (i) unitary interaction, (ii) decoherence and superselection and finally (iii) wavefunction collapse or splitting of the universe. Our results suggest that unitary interaction (the only part of this sequence that is really understood) can stand alone as an information-gathering “measurement.” And by avoiding decoherence, we can gather information strictly more effectively.
Decoherence is ubiquitous in human experience. But in its absence, there is no compelling reason why gathering information must be accompanied by collapse or definite outcomes. The whole point of quantum information science is to produce devices that do not decohere and that can process information more efficiently than classical computers. The central message of this paper is that they can also gather information more efficiently. Unfettered by decoherence, they may still be constrained by locality. For such devices, coherent measurements are the natural way to gather information.
References
Zurek, W. H. Decoherence, einselection and the quantum origins of the classical. Rev. Mod. Phys. 75, 715–75 (2003).
Chefles, A. Quantum state discrimination. Contemp. Phys. 41, 401–424 (2000).
Barnett, S. M. & Croke, S. Quantum state discrimination. Adv. Opt. Photon. 1, 238–278 (2009).
Helstrom, C. W. Quantum detection and estimation theory (Academic Press Inc. (New York), 1976).
Peres, A. & Wootters, W. K. Optimal detection of quantum information. Phys. Rev. Lett. 66, 1119–1122 (1991).
Acín, A., Bagan, E., Baig, M., Masanes, L. & Muñoz Tapia, R. Multiple-copy two-state discrimination with individual measurements. Phys. Rev. A 71, 032338 (2005).
Chitambar, E. & Hsieh, M.-H. A return to the Optimal Detection of Quantum Information. arxiv:1304.1555. (2013).
Ivanovic, I. D. How to differentiate between non-orthogonal states. Phys. Lett. A 123, 257–259 (1987).
Dieks, D. Overlap and distinguishability of quantum states. Phys. Lett. A 126, 303–306 (1988).
Peres, A. How to differentiate between non-orthogonal states. Phys. Lett. A 128, 19–19 (1988).
Jaeger, G. & Shimony, A. Optimal distinction between two non-orthogonal quantum states. Phys. Lett. A 197, 83–87 (1995).
Croke, S., Andersson, E., Barnett, S. M., Gilson, C. R. & Jeffers, J. Maximum confidence quantum measurements. Phys. Rev. Lett. 96, 070401 (2006).
Fannes, M., Nachtergaele, B. & Werner, R. Finitely correlated states on quantum spin chains. Commun. Math. Phys. 144, 443–490 (1992).
Verstraete, F., Murg, V. & Cirac, J. Matrix product states, projected entangled pair states and variational renormalization group methods for quantum spin systems. Adv. Phys. 57, 143–224 (2008).
Cramer, M. et al. Efficient quantum state tomography. Nat. Commun. 1, 149 (2010).
Bacon, D., Chuang, I. L. & Harrow, A. W. Efficient Quantum Circuits for Schur and Clebsch-Gordan Transforms. Phys. Rev. Lett. 97, 170502 (2006).
Harrow, A. W. Applications of coherent classical communication and the Schur transform to quantum information theory. Ph. D. thesis, Massachusetts Institute of Technology, Cambridge, MA, 2005 (2005).
Georgi, H. Lie algebras in particle physics (Westview Press, 1999).
Koashi, M. & Imoto, N. Quantum information is incompressible without errors. Phys. Rev. Lett. 89, 097904 (2002).
Bartlett, S. D., Rudolph, T. & Spekkens, R. W. Reference frames, superselection rules and quantum information. Rev. Mod. Phys. 79, 555–609 (2007).
Dowling, J. P. Quantum optical metrology – The lowdown on high-N00N states. Contemp. Phys. 49, 125–143 (2008).
Schön, C., Solano, E., Verstraete, F., Cirac, J. I. & Wolf, M. M. Sequential generation of entangled multiqubit states. Phys. Rev. Lett. 95, 110503 (2005).
Bañuls, M. C., Pérez-García, D., Wolf, M. M., Verstraete, F. & Cirac, J. I. Sequentially generated states for the study of two-dimensional systems. Phys. Rev. A 77, 052306 (2008).
Acknowledgements
We are grateful for comments by semi-anonymous QIP 2012 referees. This work was supported by the US Department of Energy through the LANL/LDRD program (RBK and MPZ), as well as by Perimeter Institute for Theoretical Physics (RBK and SC). Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research & Innovation.
Author information
Authors and Affiliations
Contributions
R.B.K., S.C. and M.Z. contributed equally to this work.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Blume-Kohout, R., Croke, S. & Zwolak, M. Quantum data gathering. Sci Rep 3, 1800 (2013). https://doi.org/10.1038/srep01800
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01800
This article is cited by
-
Energy and bandwidth efficiency optimization of quantum-enabled optical communication channels
npj Quantum Information (2022)
-
Simulations of Closed Timelike Curves
Foundations of Physics (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


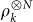 ?
?  (a sufficient statistic for the eigenbasis of ρ).
(a sufficient statistic for the eigenbasis of ρ).