Abstract
The sum of the Holevo quantity (that bounds the capacity of quantum channels to transmit classical information about an observable) and the quantum discord (a measure of the quantumness of correlations of that observable) yields an observable-independent total given by the quantum mutual information. This split naturally delineates information about quantum systems accessible to observers – information that is redundantly transmitted by the environment – while showing that it is maximized for the quasi-classical pointer observable. Other observables are accessible only via correlations with the pointer observable. We also prove an anti-symmetry property relating accessible information and discord. It shows that information becomes objective – accessible to many observers – only as quantum information is relegated to correlations with the global environment, and, therefore, locally inaccessible. The resulting complementarity explains why, in a quantum Universe, we perceive objective classical reality while flagrantly quantum superpositions are out of reach.
Similar content being viewed by others
Introduction
There is now overwhelming evidence that the Universe we inhabit is made out of quantum “stuff” and therefore quantum to the core. This suggests that we should routinely encounter superpositions. Yet, the world we perceive is resolutely classical. This contrast between quantum expectations and everyday classical reality sets up the problem that puzzled Bohr, Einstein and many others since the inception of quantum physics1,2,3,4,5.
Decoherence6,7,8 changed our view of the quantum-classical correspondence by explaining the stability of pointer states that are selected in the presence of the environment9,10. Their nature – in particular, their persistence – made them obvious candidates for “classical states”: It was natural to expect that predictably evolving states are good candidates for our everyday “classical reality”. Yet, the underlying question – “Why do we, observers, perceive pointer states?” – remains unanswered even after recognizing the role of decoherence in suppressing non-local superpositions. The stability of pointer states fulfills the expectation of predictability built on the daily experience of the classical realm, but it does not address the obvious question: Why is it that observers choose to measure the Universe in a way that reveals pointer states? The key premise of this paper can be summed-up by saying that the choice is made not by observers, but by the medium through which we perceive the Universe.
Quantum Darwinism11,12,13,14,15,16,17,18,19,20,21,22,23,24,25 recognizes that the same environment that is responsible for decoherence serves also as a channel through which information about systems reaches observers, see Fig. 1. We obtain most of our data from the photon environment. The focus of Quantum Darwinism is the redundancy – the presence of multiple copies – of data about certain observables achieved at the expense of the information about complementary observables. Thus, the decohering environment serves not just as a disposal for uncomfortably quantum evidence, but plays a role analogous to a communication channel, an advertising medium in which multiple copies of selected states of the system are present.
The environment as a communication channel.
A system,  , interacts with an environment,
, interacts with an environment,  , composed of many different fragments,
, composed of many different fragments,  . While the system decoheres (as indicated by the loss of phase coherence, which is illustrated at the bottom of the figure by the decay of the off-diagonal elements of the density matrix in the pointer basis), the environment fragments each acquire information about
. While the system decoheres (as indicated by the loss of phase coherence, which is illustrated at the bottom of the figure by the decay of the off-diagonal elements of the density matrix in the pointer basis), the environment fragments each acquire information about  that can then be transmitted to observers. To learn about the state of the system, each observer intercepts a different fragment.
that can then be transmitted to observers. To learn about the state of the system, each observer intercepts a different fragment.
Here we show that recognizing the environment as a communication channel is far more than an allegory. Rather, it leads to a precise split of the quantum mutual information between the system and the environment into two components in proportions that depend on the observable of the system: The (maximum) amount of the accessible information about an observable is given by the Holevo quantity that sets an upper limit on the capacity of a quantum channel to transmit classical data26. The information that is there in principle, but cannot be found out from the environment alone is given by the quantum discord27,28,29 that characterizes the quantumness of correlations. The Holevo quantity is largest for the pointer observable and decreases for other observables, nearly vanishing for observables that are complementary. Quantum discord makes up the difference between the mutual information (that remains constant) and the Holevo quantity. Thus, under very general conditions this yields a conservation law: While the classically accessible information and quantum discord depend on the observable of the system, their sum does not.
This division of the mutual information between the Holevo quantity and the quantum discord allows one to understand why the data about the system accessible to observers are effectively limited to the pointer observable. We show that the Holevo quantity for other observables decreases depending on the degree of “misalignment” between them and the eigenstates of the pointer observable. Furthermore, we prove an anti-symmetry relation between discord and the Holevo quantity. This shows that whenever objective, classical information about a system is present, quantum information, as measured by the discord, about this system is out of reach for observers without access to nearly the whole environment and the system – a situation that can occur, at best, only in controlled laboratory experiments.
Observers typically learn about a system of interest,  , indirectly. That is, the environment
, indirectly. That is, the environment  interacts with the system and its fragments acquire information about
interacts with the system and its fragments acquire information about  . What the fragment
. What the fragment  and
and  know about each other is quantified by the mutual information
know about each other is quantified by the mutual information

which measures the total correlations present30. Here, H is the von Neumann entropy of the reduced density matrices of  ,
,  and
and  . One of the main quantities of interest in Quantum Darwinism is the typical fragment size needed by an observer to learn about the system. That is, what typical fragment size
. One of the main quantities of interest in Quantum Darwinism is the typical fragment size needed by an observer to learn about the system. That is, what typical fragment size  contains 1 − δ of the missing information
contains 1 − δ of the missing information  about the system,
about the system,

decreasing the remaining entropy to  . The parameter δ is the information deficit, which quantifies the error tolerance of the observers. All entropic quantities that depend on the fragment are averaged with respect to all fragments of the same size, i.e.,
. The parameter δ is the information deficit, which quantifies the error tolerance of the observers. All entropic quantities that depend on the fragment are averaged with respect to all fragments of the same size, i.e.,  .
.
We will, on occasion, use a definition of the fragment size  that replaces
that replaces  in (2) with Holevo quantity χ. We will show, in the case of pointer states, that unless the fragment encompasses almost all of
in (2) with Holevo quantity χ. We will show, in the case of pointer states, that unless the fragment encompasses almost all of  ,
,  is essentially equivalent to χ.
is essentially equivalent to χ.
When an observer can acquire information about the system from a small fragment of the environment, this means information is redundant – not only can a single observer learn about the system, but many observers can do so independently and hence objectively. The redundancy is given by

where fδ is the fraction size needed to satisfy Eq. (2). The redundancy depends on how the information about  is stored in
is stored in  . Obviously, its magnitude is contingent on the information deficit δ and the total size of the environment,
. Obviously, its magnitude is contingent on the information deficit δ and the total size of the environment,  . When many environment components independently interact with the system – such as photons with an object in space –
. When many environment components independently interact with the system – such as photons with an object in space –  shown in the central plot of Fig. 2 appears as a consequence. The form of this curve indicates the presence of redundant information, as indicated in the figure.
shown in the central plot of Fig. 2 appears as a consequence. The form of this curve indicates the presence of redundant information, as indicated in the figure.
Accessible information and quantum discord.
The central plot shows the quantum mutual information versus the size of the fragment (given as the fraction  of the environment) for a pure
of the environment) for a pure  state, where
state, where  has decohered
has decohered  . For this and the other figures, we take the system to be two-dimensional (spin-1/2 like) and the interaction Hamiltonian to be diagonal in the σz basis (so the eigenstates of σz are “pointer”). (a) The initial steep rise is attributable to
. For this and the other figures, we take the system to be two-dimensional (spin-1/2 like) and the interaction Hamiltonian to be diagonal in the σz basis (so the eigenstates of σz are “pointer”). (a) The initial steep rise is attributable to  , i.e., classical information about the pointer states of
, i.e., classical information about the pointer states of  being communicated by the environment. Due to the anti-symmetry of the mutual information, the purely quantum information about
being communicated by the environment. Due to the anti-symmetry of the mutual information, the purely quantum information about  is encoded in global correlations with the environment. (b–d) Rotation by an angle µ = π/6, 2π/6, 3π/6 of the observable (i.e., the basis given by
is encoded in global correlations with the environment. (b–d) Rotation by an angle µ = π/6, 2π/6, 3π/6 of the observable (i.e., the basis given by  ) will eventually exchange
) will eventually exchange  and
and  . This gradual change between the plot of the Holevo quantity and quantum discord illustrates their complementarity in the setting of the Quantum Darwinism: Information that is locally accessible is maximized for the pointer observable of
. This gradual change between the plot of the Holevo quantity and quantum discord illustrates their complementarity in the setting of the Quantum Darwinism: Information that is locally accessible is maximized for the pointer observable of  . Accessible information about the other observables decreases and nearly disappears for the complementary observable. Meanwhile, the quantum discord
. Accessible information about the other observables decreases and nearly disappears for the complementary observable. Meanwhile, the quantum discord  increases, so that the sum
increases, so that the sum  is constant, independent of the system observable.
is constant, independent of the system observable.
There is a natural connection between Quantum Darwinism and decoherence – in particular, the existence of pointer states. These states survive decoherence with minimal loss of purity and thus “live on” to proliferate information about themselves into the environment.
An operational definition of pointer states (introduced in Refs. 31,32,33 and known as the “predictability sieve”) is based on an intuitive idea: Pointer states become minimally entangled with the environment in the course of decoherence. The predictability sieve criterion is a way to quantify this: For every initial pure state, one measures the entanglement generated dynamically between the system and the environment by computing the entropy or some other measure of predictability from the reduced density matrix of the system. The entropy is a function of time and a functional of the initial state. Pointer states are obtained by minimizing entropy over the initial states and demanding that the answer be robust when varying the decoherence time.
Pointer states are important in determining what information is deposited in the environment. In addition to this connection, the main themes of this work will be how  naturally separates into classical and quantum components and the implications for the emergence of the classical world.
naturally separates into classical and quantum components and the implications for the emergence of the classical world.
Results
The Holevo quantity and discord
We start with a straightforward rewrite of the definition of quantum discord in the setting suitable for Quantum Darwinism: We consider a system  that is decohered by the environment
that is decohered by the environment  . We focus on a fragment
. We focus on a fragment  of
of  . Quantum discord (from
. Quantum discord (from  to
to  ) is then defined as
) is then defined as

for the POVM  . The asymmetric mutual information
. The asymmetric mutual information  is given by
is given by

The conditional entropy  depends on the density matrices
depends on the density matrices  of the fragments
of the fragments  conditioned on the outcomes s for the POVM. The asymmetric mutual information is equal to
conditioned on the outcomes s for the POVM. The asymmetric mutual information is equal to  when Bayes' rule relating joint and conditional probabilities holds, as it does for classical systems34.
when Bayes' rule relating joint and conditional probabilities holds, as it does for classical systems34.
As a result of decoherence the system correlates with the environment. For a two dimensional system,

where  and
and  are the conditional states of the environment generated by interaction with the system. The extent of the coherence between 0 and 1 states of the system will depend on the overlap between the corresponding states of
are the conditional states of the environment generated by interaction with the system. The extent of the coherence between 0 and 1 states of the system will depend on the overlap between the corresponding states of  ,
,  . In the course of decoherence, the environment also acquires a record of the system's state. Orthogonal conditional states of the environment perfectly record the state of the system. Thus, there is a correspondence between decoherence and the acquisition of a record. As we will see below, in common decoherence scenarios such records are redundant and nearly complete when 0, 1 is the pointer basis. Moreover, the environment then acts as a communication channel, broadcasting the record into the larger world.
. In the course of decoherence, the environment also acquires a record of the system's state. Orthogonal conditional states of the environment perfectly record the state of the system. Thus, there is a correspondence between decoherence and the acquisition of a record. As we will see below, in common decoherence scenarios such records are redundant and nearly complete when 0, 1 is the pointer basis. Moreover, the environment then acts as a communication channel, broadcasting the record into the larger world.
This is not just an analogy. The asymmetric mutual information in Eq. (5) is the well-known Holevo quantity

where ps is the probability of outcome s occurring (see Methods). The Holevo quantity bounds the amount of classical information transmittable over a quantum channel, i.e., the classically accessible information. In the example above, this information is about the states 0 or 1 (more generally, the POVM  ). With the recognition that J and χ are identical, we can now write
). With the recognition that J and χ are identical, we can now write

This is the conservation law that we now employ in the discussion of Quantum Darwinism. It is illustrated in Fig. 2. Its salient feature is the fact that its left hand side does not depend on what is of interest to an observer via the set  , while the ingredients – the classical and quantum components – on the right hand side do.
, while the ingredients – the classical and quantum components – on the right hand side do.
In the above discussion, we have implicitly assumed that arbitrary POVMs are allowed. In most prior discussions of quantum discord,  is usually (although not always) taken as a set of orthogonal states. However, Datta35 has shown that quantum discord can always be minimized by using rank one projectors. We accept this generalization to arbitrary POVMs.
is usually (although not always) taken as a set of orthogonal states. However, Datta35 has shown that quantum discord can always be minimized by using rank one projectors. We accept this generalization to arbitrary POVMs.
In the study of discord there is also a natural temptation to extremize (usually, minimize)  with respect to the set
with respect to the set  . We are interested in what happens to χ and
. We are interested in what happens to χ and  as the measurement characterized by
as the measurement characterized by  is varied. This requires a departure from the usual temptations and a consistent – but more general – interpretation of discord.
is varied. This requires a departure from the usual temptations and a consistent – but more general – interpretation of discord.
The sharp division of the whole information present in the  correlations into classical, locally accessible χ and quantum
correlations into classical, locally accessible χ and quantum  (that can be accessed only globally by measurements involving both
(that can be accessed only globally by measurements involving both  and
and  ) puts immediately to rest the concern that was raised in the early discussions of decoherence36,37, where the common criticism was that “one has to ignore the environment to justify the emergence of the pointer observable”. Our discussion demonstrates that – by virtue of Holevo's theorem – no measurement of the environment alone can reveal more than
) puts immediately to rest the concern that was raised in the early discussions of decoherence36,37, where the common criticism was that “one has to ignore the environment to justify the emergence of the pointer observable”. Our discussion demonstrates that – by virtue of Holevo's theorem – no measurement of the environment alone can reveal more than  – the missing part of the information about the quasi-classical pointer states
– the missing part of the information about the quasi-classical pointer states  . Only global measurement of
. Only global measurement of  and all of
and all of  can detect phase coherence that is a quantum “leftover” from the phase coherence in the initial state of
can detect phase coherence that is a quantum “leftover” from the phase coherence in the initial state of  .
.
Thus, classicality that emerges from decoherence does not rest on the assumption of ignoring the environment, but on the realization that the measurements available to the observer are local – that they do not involve global observables with eigenstates that are entangled states of  and the whole of
and the whole of  . Indeed, even this (already outlandish) requirement does not suffice: To reveal global coherence one would have to measure the state of
. Indeed, even this (already outlandish) requirement does not suffice: To reveal global coherence one would have to measure the state of  in such a way that it would not collapse – i.e., one would have to choose a priori a global observable that has that (unknown) entangled state as an eigenstate. A number of well-known facts (including, e.g., the no-cloning theorem38,39) make this impossible.
in such a way that it would not collapse – i.e., one would have to choose a priori a global observable that has that (unknown) entangled state as an eigenstate. A number of well-known facts (including, e.g., the no-cloning theorem38,39) make this impossible.
Anti-symmetry and the emergence of classicality
Let us now analyze the consequences of this split into quantum and classical information. Given an arbitrary rank one POVM and a pure, but otherwise arbitrary, state  , the quantum discord and the Holevo quantity on complementary fragments of the environment (i.e.,
, the quantum discord and the Holevo quantity on complementary fragments of the environment (i.e.,  and the rest of
and the rest of  ,
,  ) are related by
) are related by

where we started with Eq. (8). The second to last line used that, for a globally pure state, the conditional state of  with respect to a rank one POVM element is also pure. The latter implies
with respect to a rank one POVM element is also pure. The latter implies  since
since  and
and  is a bipartite split of the conditional state of
is a bipartite split of the conditional state of  , just as
, just as  .
.
The relation, Eq. (9), implies that when classical information about  is available from small fragments of the environment,
is available from small fragments of the environment,  , then quantum information is banished to global correlations with the environment,
, then quantum information is banished to global correlations with the environment,  . Therefore, local observers – even when they can intercept the rest of the environment,
. Therefore, local observers – even when they can intercept the rest of the environment,  – will not have access to it and will never detect superpositions. The reverse is also true for pure
– will not have access to it and will never detect superpositions. The reverse is also true for pure  states – when quantum information is contained in global correlations, then classical information will be present in small fragments of the environment.
states – when quantum information is contained in global correlations, then classical information will be present in small fragments of the environment.
It is worth reflecting on this statement further. Figure 3 shows the results of Eq. (9) rewritten to pivot about  :
:

This shows that increasing the redundant (classical) information stored in a small fragment  decreases the quantum information in the much larger fragment
decreases the quantum information in the much larger fragment  . In other words, a world where objective information is present is also a world with quantum information inaccessible to all but the most encompassing observer. The loss or inaccessibility of any tiny component of the environment will preclude the retrieval of this quantum information.
. In other words, a world where objective information is present is also a world with quantum information inaccessible to all but the most encompassing observer. The loss or inaccessibility of any tiny component of the environment will preclude the retrieval of this quantum information.
Anti-symmetry of discord and the Holevo quantity for a pure  state and rank one POVM
state and rank one POVM  .
.
This symmetry relates discord between  and the remainder of the environment
and the remainder of the environment  and the Holevo quantity between
and the Holevo quantity between  and fragment
and fragment  . As the Holevo quantity increases – i.e., as the classical information transmitted by the environment increases – the discord on the opposite side of the axis decreases. Since the discord is monotonically increasing with f, this means that the quantum information about
. As the Holevo quantity increases – i.e., as the classical information transmitted by the environment increases – the discord on the opposite side of the axis decreases. Since the discord is monotonically increasing with f, this means that the quantum information about  is pushed into correlations with the global environment as redundant (classical) information is increased. Thus, a state which has redundant information will have quantum information encoded in the environment, implying that Quantum Darwinism is in action.
is pushed into correlations with the global environment as redundant (classical) information is increased. Thus, a state which has redundant information will have quantum information encoded in the environment, implying that Quantum Darwinism is in action.
For arbitrary  states, including mixed states, Eq. (9) is replaced by the inequality (see Methods)
states, including mixed states, Eq. (9) is replaced by the inequality (see Methods)

Thus, it can be stated unequivocally that whenever redundant information is present, quantum information is relegated to global correlations with the environment. We can, as well, examine what happens in particular mixed states. If only  is mixed, for instance, the discord will just be further suppressed – not only is it contained solely in global correlations, but it can be totally absent (see, e.g., Ref. 21). In the cases studied in Refs. 18,21, the initial mixedness of
is mixed, for instance, the discord will just be further suppressed – not only is it contained solely in global correlations, but it can be totally absent (see, e.g., Ref. 21). In the cases studied in Refs. 18,21, the initial mixedness of  reduced the redundancy but quantum information stayed banished to global correlations.
reduced the redundancy but quantum information stayed banished to global correlations.
Branching states and surplus decoherence
To “set the baseline” for physical application of these results, we simplify the rest of our study to the two scenarios that accurately approximate commonly encountered situations – the emergence of branching states via decoherence13,14,40 and what we will call “surplus decoherence”. Branching happens when the evolution of the decohering system does not create transitions between its pointer states and the imprints of these states on the environment components are unaffected by the evolution of the remaining  . This is a good approximation of what happens when the photon environment scatters from a heavy object: Subsystems of the environment (photons) individually interact with the system, each pushing
. This is a good approximation of what happens when the photon environment scatters from a heavy object: Subsystems of the environment (photons) individually interact with the system, each pushing  closer to a localization, but they do not interact with each other22,24. Fragments
closer to a localization, but they do not interact with each other22,24. Fragments  consist of collection of such subsystems. On a more formal level, the situation will give rise to Eq. (6) where
consist of collection of such subsystems. On a more formal level, the situation will give rise to Eq. (6) where  . Branching states can also occur approximately, at times shorter than the dissipation timescale15 or the mixing timescale of environment components25.
. Branching states can also occur approximately, at times shorter than the dissipation timescale15 or the mixing timescale of environment components25.
Surplus decoherence occurs when a part of  suffices to decohere
suffices to decohere  – i.e., when both the environment
– i.e., when both the environment  and the environment without some fragment
and the environment without some fragment  completely decohere the system. In other words, the environment is so large that the state of the system and a fragment will have the form
completely decohere the system. In other words, the environment is so large that the state of the system and a fragment will have the form

where  is the conditional state of the fragment given the state
is the conditional state of the fragment given the state  . That is, there is some orthogonal basis
. That is, there is some orthogonal basis  of the system – the pointer basis – such that
of the system – the pointer basis – such that  will decohere even the joint state of
will decohere even the joint state of  giving a discord-free form. In many situations (but not always) branching will give rise to surplus decoherence. Together, these two cases accurately approximate commonly encountered system-fragment states generated by decoherence. Thus, it is enlightening to study what are the consequences of these conditions for the division of the mutual information into classical and and quantum components.
giving a discord-free form. In many situations (but not always) branching will give rise to surplus decoherence. Together, these two cases accurately approximate commonly encountered system-fragment states generated by decoherence. Thus, it is enlightening to study what are the consequences of these conditions for the division of the mutual information into classical and and quantum components.
For the final part of the paper, we will mostly make use of pure, branched  states, which have the form
states, which have the form

where  indicates a pointer state. For these states,
indicates a pointer state. For these states,  has the shape characteristic of Quantum Darwinism, see Fig. 2: It raises steeply from
has the shape characteristic of Quantum Darwinism, see Fig. 2: It raises steeply from  at
at  , the size of
, the size of  , to a plateau of
, to a plateau of  – to the level of the entropy of the system. This plateau is in many ways the dominant feature of
– to the level of the entropy of the system. This plateau is in many ways the dominant feature of  that arises in Quantum Darwinism.
that arises in Quantum Darwinism.
Pointer states minimize discord
When  is decomposed into χ and
is decomposed into χ and  , the initial rise is attributable to the channel capacity χ that reveals the state of the pointer basis. The mutual information continues then at the level
, the initial rise is attributable to the channel capacity χ that reveals the state of the pointer basis. The mutual information continues then at the level  until
until  where the fragment becomes so large that it encompasses essentially all of the environment. For a state of the form in Eq. (13), the discord is
where the fragment becomes so large that it encompasses essentially all of the environment. For a state of the form in Eq. (13), the discord is

where the second line follows from the fact that the states of  conditional on a pointer state on
conditional on a pointer state on  are pure (just a pure
are pure (just a pure  state will suffice to ensure the conditional state on
state will suffice to ensure the conditional state on  ,
,  , is pure so
, is pure so  in Eq. (5) vanishes). The second term in Eq. (14) is positive but zero for the pointer basis and thus the pointer basis minimizes the discord. Using the conservation law, when the discord is minimized, the Holevo quantity is maximized. Therefore, the maximum accessible quantum information is largest for the pointer basis.
in Eq. (5) vanishes). The second term in Eq. (14) is positive but zero for the pointer basis and thus the pointer basis minimizes the discord. Using the conservation law, when the discord is minimized, the Holevo quantity is maximized. Therefore, the maximum accessible quantum information is largest for the pointer basis.
Moreover, for branched states, including ones evolved from initially mixed states of  , the discord is given
, the discord is given  , i.e., a difference of the system entropy decohered by the full environment
, i.e., a difference of the system entropy decohered by the full environment  and by the remainder of the environment
and by the remainder of the environment  (see Eq. (17) of Ref. 21). For initially mixed states, the pointer basis will not necessarily minimize the discord. However, the discord with respect to the pointer basis is exponentially small in the size of the environment and we have the state approximately given by Eq. (12). Thus, for all practical purposes, one has
(see Eq. (17) of Ref. 21). For initially mixed states, the pointer basis will not necessarily minimize the discord. However, the discord with respect to the pointer basis is exponentially small in the size of the environment and we have the state approximately given by Eq. (12). Thus, for all practical purposes, one has

This equality is equivalent to the assumption of surplus decoherence. While the surplus decoherence condition can be framed independently of the dynamics/Hamiltonian, we know that the physically relevant scenario of many environment components interacting independently with the system (e.g., the photon environment) leads naturally to surplus decoherence. If one removed a small fragment of the photon environment, systems would still be rapidly decohered. In fact, in this scenario, Eq. (12) is true up to corrections  , where |dk| < 1 is the decoherence factor from environment component k. Yet, the state resulting from surplus decoherence has a deep implication: The mutual information between
, where |dk| < 1 is the decoherence factor from environment component k. Yet, the state resulting from surplus decoherence has a deep implication: The mutual information between  and
and  contains only classical information about the pointer basis,
contains only classical information about the pointer basis,  .
.
For a pure state of  and
and  , the resulting
, the resulting  is antisymmetric with respect to
is antisymmetric with respect to  and
and  . This means that the initial rise to the plateau must be matched by the steep rise from the plateau to
. This means that the initial rise to the plateau must be matched by the steep rise from the plateau to  as the size of
as the size of  approaches the size of the whole of
approaches the size of the whole of  . This final rise is caused by the rapid increase of
. This final rise is caused by the rapid increase of  from 0 to
from 0 to  .
.
The physical implications of these runs of χ and  are straightforward and appealing: The information that can be obtained from the environment about the pointer observable of
are straightforward and appealing: The information that can be obtained from the environment about the pointer observable of  by measurement of a fragment
by measurement of a fragment  quickly saturates to the value set by its entropy
quickly saturates to the value set by its entropy  . Moreover, only χ of information can be obtained from
. Moreover, only χ of information can be obtained from  no matter how large is the fragment
no matter how large is the fragment  . This follows from Holevo's theorem26: χ is an upper bound on the information that can be extracted from the quantum channel. The rapid rise of
. This follows from Holevo's theorem26: χ is an upper bound on the information that can be extracted from the quantum channel. The rapid rise of  at the very end is then completely due to discord – due to the quantum information that can be accessed only via global measurements that involve both
at the very end is then completely due to discord – due to the quantum information that can be accessed only via global measurements that involve both  and
and  .
.
This consideration implies that when many environment components interact independently with the system, only classical information will be transferred into the environment: There is a basis chosen by the environment's interaction with the system that is proliferated into the environment. In this sense, the generation of branching states will always proliferate information about the pointer basis. Incidentally, this is the world in which we live, where photons interact independently with systems, proliferating redundant – and therefore objective – information and conveniently hiding quantum information. We can take this latter step forward and show that one can only – in a way that will be clear in a moment – find out about the pointer states.
Only pointer states can be redundant
We now consider an attempt to extract, from fragments of  , information about σy, which is complementary to the pointer observable σz (see Fig. 2). Success would imply detection of evidence of quantumness – catching Schrödinger's cat in a superposition of dead and alive. The plot of quantum mutual information
, information about σy, which is complementary to the pointer observable σz (see Fig. 2). Success would imply detection of evidence of quantumness – catching Schrödinger's cat in a superposition of dead and alive. The plot of quantum mutual information  is, of course, independent of the observable of
is, of course, independent of the observable of  . The two contributions, though, “change places”. Now it is the discord that raises rapidly (a feature that we address below), its graph matching the plot of χ in the previous pointer observable case. By contrast, χ remains close to zero until the very end, where measurement of all of
. The two contributions, though, “change places”. Now it is the discord that raises rapidly (a feature that we address below), its graph matching the plot of χ in the previous pointer observable case. By contrast, χ remains close to zero until the very end, where measurement of all of  could in principle reveal the eigenstate of σy with which
could in principle reveal the eigenstate of σy with which  is entangled. Still, there is no information about σy that can be gleaned from any fraction of
is entangled. Still, there is no information about σy that can be gleaned from any fraction of  – the whole of
– the whole of  is needed to get σy (if it is available at all).
is needed to get σy (if it is available at all).
An intermediate case – spin at an angle µ from σz – is an obvious next case to consider. Now the plateau of the corresponding  is lower than the missing information about the “intermediate” observable,
is lower than the missing information about the “intermediate” observable,  . Under surplus decoherence and when
. Under surplus decoherence and when  holds a perfect record of the pointer states, χ for another observable is given by
holds a perfect record of the pointer states, χ for another observable is given by

Figure 4 shows the Holevo quantity versus the fragment size and the angle for the example system under consideration. When  , redundant records of the observable
, redundant records of the observable  can not exist – at most “there can be only one” copy. When δ is small, but non-zero, only states that are very nearly the pointer states can be determined. An equivalent result to Eq. (16) was obtained in Ref. 12. We show in the Methods how to extend it to imperfect records.
can not exist – at most “there can be only one” copy. When δ is small, but non-zero, only states that are very nearly the pointer states can be determined. An equivalent result to Eq. (16) was obtained in Ref. 12. We show in the Methods how to extend it to imperfect records.
Observable dependence of the classical information and its redundancy.
(a) Plot of the Holevo quantity versus basis (defined by the angle µ) and fragment size for the representative spin model. Here, the off-diagonal elements of the reduced state of the system,  , are suppressed by the decoherence factor
, are suppressed by the decoherence factor  , where
, where  is the action (in units of
is the action (in units of  ) that results from the coupling of a single environment spin to the system. The plot shows the Holevo quantity for
) that results from the coupling of a single environment spin to the system. The plot shows the Holevo quantity for  ,
,  and a symmetric and pure environment state. The white line parallel to the fragment size axis demarcates where redundancy is no longer possible for δ = 0.1. The other white line plots Eq. (16) for the plateau value of
and a symmetric and pure environment state. The white line parallel to the fragment size axis demarcates where redundancy is no longer possible for δ = 0.1. The other white line plots Eq. (16) for the plateau value of  . Note that the discord versus basis would be a similar figure, but larger on the side µ = π/2, as it is given by
. Note that the discord versus basis would be a similar figure, but larger on the side µ = π/2, as it is given by  . (b) Redundancy versus µ and
. (b) Redundancy versus µ and  computed by finding
computed by finding  such that
such that  . Compared to Eq. (2), this calculation of
. Compared to Eq. (2), this calculation of  drops terms that are exponentially small. For the example case here, the missing information is
drops terms that are exponentially small. For the example case here, the missing information is  , with H(pµ) the binary entropy of the new probability distribution. The probabilities of detecting the spin in the “+/−” directions along the axis defined by µ are p+ = p0 cos2[µ/2] + p1 sin2[µ/2] and p− = 1 − p+, where p0,1 = 1/2 are the probabilities of the pointer states occurring. The conditional entropy is given by
, with H(pµ) the binary entropy of the new probability distribution. The probabilities of detecting the spin in the “+/−” directions along the axis defined by µ are p+ = p0 cos2[µ/2] + p1 sin2[µ/2] and p− = 1 − p+, where p0,1 = 1/2 are the probabilities of the pointer states occurring. The conditional entropy is given by  .
.
The Holevo quantity for pointer  is the discord for a complementary
is the discord for a complementary 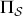
Continuing from the above results, as χµ is reduced,  must make up the difference due to the conservation law. In case of surplus decoherence, this means
must make up the difference due to the conservation law. In case of surplus decoherence, this means

When the basis  is complementary to the pointer basis
is complementary to the pointer basis  the plateau in the Holevo quantity is zero and the accessible information about the pointer basis turns into the complementary discord. We define a complementary POVM
the plateau in the Holevo quantity is zero and the accessible information about the pointer basis turns into the complementary discord. We define a complementary POVM  as one where all elements satisfy
as one where all elements satisfy

where qs is independent of the pointer state  . That is, each πs is unbiased with respect to any pointer state
. That is, each πs is unbiased with respect to any pointer state  . An example would be the σy basis when σz is pointer.
. An example would be the σy basis when σz is pointer.
Assuming a state of the form in Eq. (12), the conditional state with respect to the outcome s is

yielding ps = qs. In other words, the conditional states are just the reduced states of  . Then, however,
. Then, however,

where the second line follows from the surplus decoherence condition and also Eq. (19). Thus, the plot of  will follow that of
will follow that of  . When one does not exactly have surplus decoherence, the corrections will depend on the magnitude of the off-diagonal elements in
. When one does not exactly have surplus decoherence, the corrections will depend on the magnitude of the off-diagonal elements in  . For many environment components independently decohering the system these elements become exponentially small in the environment size (exponentially small in
. For many environment components independently decohering the system these elements become exponentially small in the environment size (exponentially small in  ).
).
Discussion
We have demonstrated that the quantum mutual information naturally separates into classical and quantum components. We proved that a world containing redundant information about a system necessarily implies that quantum information is inaccessible. In other words, when information about some basis has been proliferated into the environment (making it “objective”), then the quantum information – information about superpositions of that basis (e.g., of the initial state of the system) – is suppressed. This information cannot be obtained by observers intercepting only a fragment of the environment. Rather, they need the whole environment and the system to retrieve it. Furthermore, the information proliferated into the environment is not destroyed by further change/monitoring of the system. Once the system has deposited multiple copies of its information, they are “here to stay”.
Although discord is often studied these days, questions remain about its fundamental significance. This work suggests that discord has a robust role to play in defining what quantum information means. We have explored it in a specific context of the quantum-to-classical transition in the setting of Quantum Darwinism, but some of our conclusions are clearly relevant more generally41. Our results also help draw a distinction between the more flagrant aspects of the “quantumness of correlations” captured by entanglement and the quantumness of correlations that are separable – devoid of entanglement – and yet not completely classical.
Methods
The Holevo quantity and discord
The quantum discord (from  to
to  ) is
) is

given the POVM  ,
,  , where πs are the elements of
, where πs are the elements of  . The quantum mutual information is
. The quantum mutual information is  , where H is the von Neumann entropy of the of the density matrices
, where H is the von Neumann entropy of the of the density matrices  ,
,  and
and  that one obtains by tracing out “the rest”, i.e.,
that one obtains by tracing out “the rest”, i.e.,  ,
,  , …. All entropic quantities are averaged with respect to all fragments of the same size, e.g.,
, …. All entropic quantities are averaged with respect to all fragments of the same size, e.g.,  . Most results hold without averaging and it will be stated when averaging is necessary.
. Most results hold without averaging and it will be stated when averaging is necessary.
The state of  conditional on outcome s on
conditional on outcome s on  is
is

where ps is the probability of obtaining outcome s. Denoting the entropy of  given outcome s as
given outcome s as  , the asymmetric mutual information is
, the asymmetric mutual information is

The last line used

which follows from the cyclic property of the partial trace (with the identity acting on  ). Even though the POVM does not uniquely set the post-measurement state of
). Even though the POVM does not uniquely set the post-measurement state of  , it will for
, it will for  . Equation (22) is of course the equation for the Holevo quantity χ, which we denote as
. Equation (22) is of course the equation for the Holevo quantity χ, which we denote as  since it depends on the POVM
since it depends on the POVM  . The similarity with the Holevo quantity was also noticed in Ref. 29.
. The similarity with the Holevo quantity was also noticed in Ref. 29.
Anti-symmetry and the emergence of classicality
Assuming a pure  state, the mutual information,
state, the mutual information,  (designated by
(designated by  ), is antisymmetric about the point
), is antisymmetric about the point  (see Ref.14). That is,
(see Ref.14). That is,

and  . This is shown readily by writing out the mutual information
. This is shown readily by writing out the mutual information

where we used that  is in a pure state to relate entropies across a bipartite split (e.g.,
is in a pure state to relate entropies across a bipartite split (e.g.,  ). Equation (24) holds regardless of whether averaging is done. However, only when the mutual information refers to the average of all fragments of a given size does it imply that the mutual information versus
). Equation (24) holds regardless of whether averaging is done. However, only when the mutual information refers to the average of all fragments of a given size does it imply that the mutual information versus  is antisymmetric about its midpoint (at
is antisymmetric about its midpoint (at  ,
,  from Eq. (24) when averaged). This is easy to see by examining, e.g., the mutual information in the state
from Eq. (24) when averaged). This is easy to see by examining, e.g., the mutual information in the state

where only a single environment spin is correlated with the system. If ordering is maintained in the environment spins, the mutual information is clearly not anti-symmetric, even though Eq. (24) holds. It becomes so only when averaging is performed and the mutual information then depends on the (typical) fragment size only.
In the main text, we derived a stronger result

for an arbitrary rank one POVM  and a pure state of
and a pure state of  . Averaging is not required for Eq. (26). More generally,
. Averaging is not required for Eq. (26). More generally,

for an arbitrary rank one POVM  and arbitrary, potentially mixed, state of
and arbitrary, potentially mixed, state of  . To show this, consider any state
. To show this, consider any state  and purify the state to
and purify the state to  . Starting with the conservation law,
. Starting with the conservation law,

where we used that for a rank one POVM the conditional state of  is pure and therefore
is pure and therefore  . From the data processing inequality42, if we trace out the purifying environment
. From the data processing inequality42, if we trace out the purifying environment  , then this reduces the Holevo quantity
, then this reduces the Holevo quantity

and gives Eq. (27). We note that, in addition to pure states, there are cases of interest here where equality holds in Eq. (28) (i.e., when  is mixed but only within disjoint subspaces that are correlated with
is mixed but only within disjoint subspaces that are correlated with  ).
).
Only pointer states can be redundant
We have seen that the pointer states minimize discord for pure, branching states (and for surplus decoherence) and that branching states lead to surplus decoherence up to exponentially small corrections. Let's see what happens to transmitted information for surplus decoherence. Consider the case where a perfect record of the pointer basis exist in a fragment of the environment,

i.e., suppose that the conditional states  are orthogonal for the PVM
are orthogonal for the PVM  . Now consider a POVM
. Now consider a POVM  , that we can define by the quantities
, that we can define by the quantities

which give the conditional probabilities for s to occur given  . For the state
. For the state  in Eq. (12), the probability of outcome s is
in Eq. (12), the probability of outcome s is

Further, since the  are conditional probabilities, they obey
are conditional probabilities, they obey

which is readily obtained by using that  is a POVM. This also gives
is a POVM. This also gives

for the probabilities for s to occur.
The Holevo quantity for the communication of (classical) information about s is given by

where we used Eq. (23). Taking Eq. (12) and the assumption that for the pointer basis the classical information is at the plateau value, i.e., that there is a perfect record, one obtains

for the plateau value of the classical information about s deposited in the environment: Its value is suppressed by the conditional entropy of  with respect to the pointer basis
with respect to the pointer basis  , i.e., the misalignment of
, i.e., the misalignment of  from
from  .
.
The presence of redundant information requires that

where  measures the amount of missing information. This can not be satisfied when
measures the amount of missing information. This can not be satisfied when

which makes it clear that when the POVM is rotated away from the pointer basis, eventually redundant information cannot be present in the environment. Furthermore, even for an environment with an infinite number of components, whether or not there is redundant information about the POVM depends on the accuracy required: All POVMs that are not the pointer basis will not be redundantly encoded if one requires a small information deficit. In this sense, we say that only pointer states can be found out.
Of course, one can also start from the expression Eq. (14) for branched states and use the conservation law to get

Thus, the Holevo quantity will be reduced for all POVMs that are not the pointer basis. As the generation of the branched state gives rise to surplus decoherence and the fragment starts to acquire a perfect record, Eq. (38) will approach Eq. (35).
We can quantify this approach for imperfect records. We assume surplus decoherence and that the pointer states are correlated with nearly distinguishable states  , i.e., that one is very near the classical plateau. The latter implies that there exists a POVM Λ on
, i.e., that one is very near the classical plateau. The latter implies that there exists a POVM Λ on  , with elements
, with elements  , such that
, such that  and
and  for
for  , where
, where  gives the error probability for distinguishing the states. Let the measurement be carried out by apparatus
gives the error probability for distinguishing the states. Let the measurement be carried out by apparatus  . We can apply this to studying the Holevo quantity with respect to some arbitrary POVM on
. We can apply this to studying the Holevo quantity with respect to some arbitrary POVM on  :
:

where first  and then a unitary acts on
and then a unitary acts on  , with its relevant action defined by
, with its relevant action defined by  , to get
, to get  , neither of which change the Holevo quantity. Then, however, the positive operator
, neither of which change the Holevo quantity. Then, however, the positive operator  has the property
has the property

Thus, the state

has

by the gentle measurement lemma43,44. The analysis leading to Eq. (35) holds as  and
and  are perfectly correlated in the state
are perfectly correlated in the state  . We can then apply the Alicki-Fannes' inequality45
. We can then apply the Alicki-Fannes' inequality45

where DΠ is the number of outcomes for the POVM  . Thus, the reduction in the classical information about non-pointer
. Thus, the reduction in the classical information about non-pointer  is due to
is due to  up to small corrections. For the case of branching states, these corrections are exponentially small in the size of the fragment.
up to small corrections. For the case of branching states, these corrections are exponentially small in the size of the fragment.
The surplus decoherence assumption can be similarly relaxed, i.e., by assuming  is near to the discord-free state. For branching states,
is near to the discord-free state. For branching states,  is exponentially close in the size of environment to a discord free state. Thus, the
is exponentially close in the size of environment to a discord free state. Thus, the  above, while small, dominates how close the exact
above, while small, dominates how close the exact  is to the perfect record case. The case of imperfect records but mixed states extends the results of Ref. 12.
is to the perfect record case. The case of imperfect records but mixed states extends the results of Ref. 12.
References
Bohr, N. The quantum postulate and the recent development of atomic theory. Nature 121, 580–590 (1928).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Bohr, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 48, 696–702 (1935).
Schrödinger, E. Die gegenwärtige situation in der quantenmechanik. Naturwissenschaften 23, 807–812 (1935).
Bohr, N. Atomic Physics and Human Knowledge (Wiley, New York, 1958).
Joos, E. et al. Decoherence and the Appearance of a Classical World in Quantum Theory (Springer-Verlag, Berlin, 2003).
Zurek, W. H. Decoherence, einselection and the quantum origins of the classical. Rev. Mod. Phys. 75, 715–775 (2003).
Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition (Springer-Verlag, Berlin, 2008).
Zurek, W. H. Pointer basis of quantum apparatus: Into what mixture does the wave packet collapse? Phys. Rev. D 24, 1516 (1981).
Zurek, W. H. Environment-induced superselection rules. Phys. Rev. D 26, 1862 (1982).
Ollivier, H., Poulin, D. & Zurek, W. H. Objective properties from subjective quantum states: Environment as a witness. Phys. Rev. Lett. 93, 220401 (2004).
Ollivier, H., Poulin, D. & Zurek, W. H. Environment as a witness: Selective proliferation of information and emergence of objectivity in a quantum universe. Phys. Rev. A 72, 042113 (2005).
Blume-Kohout, R. & Zurek, W. H. A simple example of quantum Darwinism: Redundant information storage in many-spin environments. Found. Phys. 35, 1857–1876 (2005).
Blume-Kohout, R. & Zurek, W. H. Quantum Darwinism: Entanglement, branches and the emergent classicality of redundantly stored quantum information. Phys. Rev. A 73, 062310 (2006).
Blume-Kohout, R. & Zurek, W. H. Quantum Darwinism in quantum brownian motion. Phys. Rev. Lett. 101, 240405 (2008).
Bennett, C. H. The second law and quantum physics. AIP Conf. Proc. 1033, 66–79 (2008).
Brunner, R., Akis, R., Ferry, D. K., Kuchar, F. & Meisels, R. Coupling-induced bipartite pointer states in arrays of electron billiards: Quantum Darwinism in action? Phys. Rev. Lett. 101, 024102 (2008).
Zwolak, M., Quan, H. T. & Zurek, W. H. Quantum Darwinism in a mixed environment. Phys. Rev. Lett. 103, 110402 (2009).
Zurek, W. H. Quantum Darwinism. Nat. Phys. 5, 181–188 (2009).
Paz, J. P. & Roncaglia, A. J. Redundancy of classical and quantum correlations during decoherence. Phys. Rev. A 80, 042111–042116 (2009).
Zwolak, M., Quan, H. T. & Zurek, W. H. Redundant imprinting of information in nonideal environments: Objective reality via a noisy channel. Phys. Rev. A 81, 062110 (2010).
Riedel, C. J. & Zurek, W. H. Quantum Darwinism in an everyday environment: Huge redundancy in scattered photons. Phys. Rev. Lett. 105, 020404 (2010).
Burke, A. M. et al. Periodic scarred states in open quantum dots as evidence of quantum Darwinism. Phys. Rev. Lett. 104, 176801 (2010).
Riedel, C. J. & Zurek, W. H. Redundant information from thermal illumination: Quantum Darwinism in scattered photons. New Journal of Physics 13, 073038 (2011).
Riedel, C. J., Zurek, W. H. & Zwolak, M. The rise and fall of redundancy in decoherence and quantum darwinism. New Journal of Physics 14, 083010 (2012).
Holevo, A. S. Bounds for the quantity of information transmitted by a quantum communication channel. Probl. Peredachi Inf. 9, 3–11 (1973).
Zurek, W. H. Einselection and decoherence from an information theory perspective. Ann. Phys.-Leipzig 9, 855–864 (2000).
Ollivier, H. & Zurek, W. H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2002).
Henderson, L. & Vedral, V. Classical, quantum and total correlations. J. Phys. A: Math. Gen. 34, 6899 (2001).
Groisman, B., Popescu, S. & Winter, A. Quantum, classical and total amount of correlations in a quantum state. Phys. Rev. A 72, 032317 (2005).
Zurek, W. H., Habib, S. & Paz, J. P. Coherent states via decoherence. Phys. Rev. Lett. 70, 1187–1190 (1993).
Zurek, W. H. Preferred states, predictability, classicality and the environment-induced decoherence. Prog. Theor. Phys. 89, 281 (1993).
Paz, J. P. & Zurek, W. H. Environment-induced decoherence and the transition from quantum to classical. 72nd Les Houches Summer School on “Coherent Matter Waves”, arXiv:quant-ph/0010011 (2000).
Cover, T. M. & Thomas, J. A. Elements of information theory (Wiley-Interscience, New York, 2006).
Datta, A. Studies on the role of entanglement in mixed-state quantum computation. Ph. D. Thesis, arXiv::0807.4490 (2008).
Greenberger, D. & YaSin, A. “Haunted” measurements in quantum theory. Found. Phys. 19, 679–704 (1989).
Carmichael, H. J., Kochan, P. & Tian, L. Coherent states and open quantum systems: A comment on the Stern-Gerlach experiment and Schrödinger's cat. In Feng D., Klauder J. R., & Strayer M. R., (eds.) Proceedings of the International Symposium on Coherent States, Past, Present and Future 75–91 (World Scientific, Singapore, 1994).
Wootters, W. K. & Zurek, W. H. A single quantum cannot be cloned. Nature 299, 802–803 (1982).
Dieks, D. Communication by EPR devices. Physics Letters 92A, 271–272 (1982).
Everett, H. “Relative state” formulation of quantum mechanics. Rev. Mod. Phys. 29, 454 (1957).
Streltsov, A. & Zurek, W. H. Quantum discord cannot be shared, arXiv:1304. 2914 (2013).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, UK, 2000).
Winter, A. Coding theorem and strong converse for quantum channels. Information Theory, IEEE Transactions on 45, 2481–2485 (1999).
Ogawa, T. & Nagaoka, H. Making good codes for classical-quantum channel coding via quantum hypothesis testing. Information Theory, IEEE Transactions on 53, 2261–2266 (2007).
Alicki, R. & Fannes, M. Continuity of quantum conditional information. J. Phys. A: Math. Gen. 37, L55 (2004).
Acknowledgements
This research is supported in part by the U.S. Department of Energy through the LANL/LDRD Program and in part by the John Templeton Foundation. We would also like to thank the Center for Integrated Quantum Science and Technology (IQST), Universität Ulm, where part of this work was carried out.
Author information
Authors and Affiliations
Contributions
M.Z. and W.H.Z. both contributed to this research and the writing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplemental Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Zwolak, M., Zurek, W. Complementarity of quantum discord and classically accessible information. Sci Rep 3, 1729 (2013). https://doi.org/10.1038/srep01729
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01729
This article is cited by
-
Quantum correlation of microwave two-mode squeezed state generated by nonlinearity of InP HEMT
Scientific Reports (2023)
-
Enhancing quantum correlation at zero-IF band by confining the thermally excited photons: InP hemt circuitry effect
Optical and Quantum Electronics (2023)
-
Demonstration of quantum Darwinism on quantum computer
Quantum Information Processing (2022)
-
Secure quantum remote state preparation of squeezed microwave states
Nature Communications (2019)
-
Lower bound of local quantum uncertainty for high-dimensional bipartite quantum systems
Science China Physics, Mechanics & Astronomy (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






 is the discord for a complementary
is the discord for a complementary