Abstract
Here we show theoretically that the history of solid growth during “rapid” solidification must be S-shaped, in accord with the constructal law of design in nature. In the beginning the rate of solidification increases and after reaching a maximum it decreases monotonically as the volume of solid tends toward a plateau. The S-history is a consequence of four configurations for the flow of heat from the solidification front to the subcooled surroundings, in this chronological order: solid spheres centered at nucleation sites, needles that invade longitudinally, radial growth by conduction and finally radial lateral conduction to interstices that are warming up. The solid volume (Bs) vs time (t) is an S-curve because it is a power law of type Bs ~ tn where the exponent n first increases and then decreases in time (n = 3/2, 2, 1, …). The initial portion of the S curve is not an exponential.
Similar content being viewed by others
Introduction
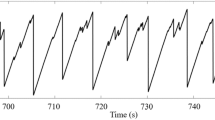
An extremely common phenomenon in nature is the S-shaped history of areas and volumes swept by spreading flows and collecting flows. Examples of S-curve spreading histories are the growth of populations1, the spreading of technologies2 and the spreading of news and information3, Fig. 1. The histories of collecting flows also exhibit S curves: examples are mining and the extraction of minerals, such as the Hubbert peak of oil extraction4.
Rapid solidification is another common phenomenon, where the S-curve history is about the growth of solid in a subcooled liquid or gas. This phenomenon is classical textbook material in materials science5,6,7 and has generated a voluminous body of research dedicated to explaining the S-shaped history. The classical explanation is based on the Johnson-Mehl-Avrami (JMA) model of solidification8,9,10,11,12,13, which consists of postulating solidification as a swarm of uniformly distributed spheres of solid that grow from initial nucleation sites, such that initially the solid volume increases exponentially. Although this model leads to a formula with two empirical constants that can be used to correlate experimental measurements, the S-curve remains a theoretical puzzle, while the theoretical basis of the sphere model is being questioned8: the physical meaning of the two empirical constants is not known.
In this paper we go back to the state of knowledge that existed before the JMA model and show how to predict the S-curve of solidification purely theoretically. The starting idea is to see solidification as a “spreading flow” like the flows exhibited in Fig. 1 and to recognize that this spreading flow has the same natural tendency as all the inanimate and animate flow systems that morph freely into configurations that provide greater access to what flows, over time. This natural tendency is summarized as the constructal law14,15. Here, we ask two questions:
First, what flow is spreading during solidification? It is not the solid, because the solid and its subcooled surroundings are motionless. The spreading flow is the flow of heat, which emanates from the solid surface and flows in all directions into the surroundings.
Second, what is the configuration of the heat flow system? We do not postulate the configuration (e.g. spheres in the JMA model). Instead, we rely on the physics principle14,15 that the flow system generates and evolves its flow architecture in order for the solidification process to be the more “rapid” at every stage in its history. We show that although the solidification is triggered as small spheres around nucleation sites, at longer times the greater solidification rate is associated with needles and dendrites, in accord with common observations (e.g. Fig. 216).
Dendritic solidification of Inconel 625 in the region close to the melt pool16.
Results
Solidification begins at point-size nucleation sites around which the solid grows as tiny spheres. As shown later in the Discussion section, the spherical growth slows down and is replaced by needle-shaped growth, which is faster. The transition from spherical to needle-shaped growth is in accord with the constructal law and defines the early part of the S. Because most of the S-shape of the solidification curve is due to needle solidification, we start by examining the needle configuration.
Needle invasion
Consider the solidification of a volume of pure substance that is initially in a subcooled liquid state of temperature Tf, which is lower than the solidification temperature Ts. Along the axis of this volume grows a solid needle with a speed (V) that increases monotonically with the degree of subcooling (Ts − Tf) and which has been documented extensively (e.g. Refs. 17,18,19,20,21). The instantaneous length of the needle is x and the length of the volume is L (Fig. 3).
Because of solidification, the needle grows in length and its older portions become thicker. In every stationary cross-section, the volume of solid is isothermal at Ts and is proportional to the volume of liquid heated by the latent heat of solidification released on the solidification front,

In other words, the latent heat of solidification (hsf) that was released on the periphery of the disc of solid is now the sensible heat of the annulus of heated liquid,

The scaling relation (2) is based on the assumption that Df ≫ Ds and it yields the constant factor in the proportionality of Eq. (1), namely

The objective of this analysis is to predict the evolution of the solidification process, which means to predict the history of the volume of solid  . Because of Eq. (3), the solid volume is proportional to the liquid volume heated by the heat of solidification,
. Because of Eq. (3), the solid volume is proportional to the liquid volume heated by the heat of solidification,  . Consequently, the shape of the history function Bs(t) is the same as the shape of Bf(t), where in accord with Eq. (3),
. Consequently, the shape of the history function Bs(t) is the same as the shape of Bf(t), where in accord with Eq. (3),

where b is constant. The time during which the liquid and solid thicknesses grow to the length scales Df (t) and Ds (t) is

During this time, the liquid thickness grows by thermal diffusion,

where αf is the liquid thermal diffusivity. From Eqs. (5) and (6) follows the history of the volume of heated liquid,

The first conclusion is that Bf and Bs increase in proportion with t2, along the needle “invasion” curve shown in Fig. 4. The volume increase is accelerated in time, but it is not exponential. This behavior lasts until the needle invades the entire liquid volume, x ~ L, which happens during the invasion time

when the liquid volume length scale is  with the corresponding solid volume Bsi derived from Eq. (4).
with the corresponding solid volume Bsi derived from Eq. (4).
Consolidation
Beyond the invasion time ti, the solid and liquid volumes continue to grow in proportion with each other, but they grow radially laterally until Df spreads over the entire subcooled liquid. This is the “consolidation” process. The growth of the liquid thickness is in accord with the solution to the problem of thermal diffusion around a line heat source of uniform and constant temperature (the needle, Ts) embedded in an infinite conducting medium (Tf)22:


where R(t) is the radius of the solid cylinder, t = 0 is the start of the needle solidification process and T(r, t) is the temperature in the liquid. The cylindrical geometry to which Eqs. (9) and (10) refer is visualized in the x = constant cut through the solid shown in Fig. 3. Ei is the exponential integral function

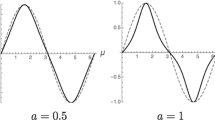
while λ is a monotonic function of the liquid subcooling Stefan number [Ste = cf (Ts − Tf)/hsf], as shown in Fig. 5:

The temperature distribution in the subcooled liquid is plotted in Fig. 5 for the case Ste = 1. The abscissa shows that the radial length scale (r) of the heated liquid increases as 2(αft)1/2. The volume of liquid heated during the consolidation increases in proportion with the cross-sectional area of the annulus of heated liquid, namely π (r2 − R2), which has the scale αft.
The second conclusion is that the growth of Bf (or Bs) during consolidation process is proportional to t, which is slower than the t2 growth during the invasion process. This accounts for the inflexion of the S curve, which is the beginning of the slowdown of solidification, Fig. 4.
Plateau
The liquid volume has two dimensions, the longitudinal length L aligned with the needle and the lateral (radial) dimension Y, across the interstices. The time when the radial dimension of the heated liquid reaches Y is the consolidation time tc,

which follows from writing r ~ Y, where r ~ (αft)1/2. After this event, the heated liquid (already Y thick) becomes warmer at a progressively smaller rate, as its average temperature rises to match the solidification temperature Ts. This final arc of the S-curve of solidification can be predicted as follows.
The heat current flows from the solidification front across the Y-thick liquid of average temperature Tl(t) and has the scale kfπDs(Ts − Tl)/Y, where it is assumed that Y ≫ Ds. The heat current is equal to the rate at which the energy of the liquid layer increases, namely ρfcfπY2dTl/dt. Integrating the resulting equation and invoking the initial condition  at
at  , we obtain the decelerating rise of the liquid temperature,
, we obtain the decelerating rise of the liquid temperature,

where tp is the time scale of reaching the Ts plateau:

The heat current released at the solidification front is proportional to the temperature gradient across the Y-layer, therefore it has the same exponential decay as in Eq. (14). The same behavior belongs to the rate of solidification dBs/dt and consequently the history of the solid volume Bs(t) has the flattening tendency sketched in Fig. 4.
Discussion
In summary of the preceding analysis, the history of needle solid volume is composed of three successive periods (invasion, consolidation, plateau), each with its own time scale: ti, tc and tp. The analysis began with the needle invasion process and it was based on the assumption that the solid is needle shaped, i.e. it is slender, not spherical. Why and under what conditions this assumption is correct is the foundation of the S-curve of solidification and it is demanded by the constructal law.
Solidification begins at point-size nucleation sites and for this reason the earliest shape of the solid is spherical, of diameter Ds(t). The sphere is surrounded by an annulus of heated liquid of outer diameter Df(t), which increases in proportion with (αft)1/2. Equation (2) is replaced by

and leads to the conclusion that Ds(t) and Df(t) increase proportionally and

The solid volume Bs,sphere (of order  ) increases as
) increases as

The needle is the alternative configuration, which competes with the sphere. During the same time interval (0 – t), the needle would acquire the volume [cf. Eq. (7)]

The intersection of Eqs. (18) and (19) reveals the time scale of needle onset,

where as shown in Fig. 6,


The complete S curve of solidification.
Note the early competition between the sphere and needle configurations in the pursuit of more rapid solidification. The last three regions (invasion, consolidation, plateau) are log-log representations of the S curve shown in Fig. 4.
In conclusion, in the evolution of configuration the sphere is first and the needle next. Not the other way around. In accord with the constructal law, this sequence of heat flow designs facilitates more effectively the flow of heat toward equilibrium, i.e. this is the evolutionary design in which the solidification is more rapid.
The succession of four heat-flow configurations (Fig. 6) is why the history of the solidified volume is S shaped. The S curve is a power law Bs ~ tn, where the exponent varies over time in this sequence: n = 3/2, 2, 1 and finally n < 1. The early part of the S-curve is not an exponential.
References
Pearl, R. The growth of populations. Quarterly Review of Biology 51 (50th Anniversary Special Issue, 1926–1976), 6–24 (1976).
Easterly, W. The White Man's Burden (London, Penguin Books, 2006).
Bejan, A. & Lorente, S. The physics of spreading ideas. International Journal of Heat and Mass Transfer 55, 802–807 (2012).
Hubbert, M. K. Energy from fossil fuels. Science 109, 103–109 (1949).
Avrami, M. Kinetics of phase change II: transformation-time relations for random distribution of nuclei. Journal of Chemical Physics, 8, 212 (1940).
Christian, J. W. Theory of transformation in Metals and Alloys, 2nd Ed. (Oxford, UK, Pergamon Press, ch. 10, p. 473, 1969).
Chen, H. S. Glassy metals. Reports on Progress in Physics 43, 354–432 (1980).
Málek, J. The applicability of Johnson-Mehl-Avrami model in the thermal analysis of crystallization kinetics of glasses. Thermochmica Acta 267, 61–73 (1995).
Zener, C. Theory of growth of spherical precipitates from solid solutions. Journal of Applied Physics 20, 950–953 (1949).
Wert, C. A. Precipitation from solid solutions of C and N in α – iron. Journal of Applied Physics 20, 943–949 (1949).
Turnbull, D. & Treaftis, H. N. Kinetics of precipitation of tin from lead - tin solid solutions. Acta Metallurgica 3, 43–54 (1955).
Cahn, J. W. The kinetics of grain boundary nucleated reactions. Acta Metallurgica 4, 449–459 (1956).
Aaron, H. B., Fainstein, D. & Kotler, G. R. Diffusion-limited phase transformations: a comparison and critical evaluation of the mathematical approximations. Journal of Applied Physics 41, 4404–4410 (1970).
Bejan, A. Advanced Engineering Thermodynamics, 2nd ed. (New York, Wiley, 1997), ch. 13.
Bejan, A. & Lorente, S. The constructal law and the evolution of design in nature. Physics of Life Reviews 8, 209–240 (2011).
Taha-al, Z. Y., Hashmi, M. S. J. & Yilbas, B. S. Effect of WC on the residual stress in the laser treated HVOF coating. Journal of Materials Processing Technology 209, 3172–3181 (2009).
Powell, G. L. F., Colligan, G. A., Surprenant, V. A. & Urquhart, A. The growth rate of dendrites in undercooled tin. Metallurgical Transactions A 8, 971–973 (1977).
Huang, S.-C. & Glicksman, M. E. Fundamentals of dendritic solidification—II Development of sidebranch structure. Acta Metallurgica 29, 717–734 (1981).
Liu, F. & Goldenfeld, N. Linear stability of needle crystals in the boundary-layer model of dendritic solidification. Physical Review A 38, 407–417 (1988).
Ben Amar, M. Dendritic growth rate at arbitrary undercooling. Physical Review A 41, 2080–2092 (1990).
Liu, Z.-K. & Chang, Y. A. On the applicability of the Ivantsov growth equation. Journal of Applied Physics 82, 4838–4841 (1997).
Carslaw, H. S. & Jaeger, J. C. Conduction of Heat in Solids (Oxford UK, Oxford University Press, 1959).
Acknowledgements
The authors acknowledge the Deanship of Scientific Research, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia, for funding the project IN111042 during the course of this work.
Author information
Authors and Affiliations
Contributions
A.B. did the research work in collaboration with the other three co-authors, wrote the manuscript and made Figures 1, 3, 4 and 6. S.L. did the research work in collaboration with the other three co-authors, wrote the manuscript and made Figures 1, 3, 4 and 6. B.S.Y. did the research work in collaboration with the other three co-authors, wrote the manuscript and made Figure 2. A.Z.S. did the research work in collaboration with the other three co-authors, wrote the manuscript and made Figure 5.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Bejan, A., Lorente, S., Yilbas, B. et al. Why solidification has an S-shaped history. Sci Rep 3, 1711 (2013). https://doi.org/10.1038/srep01711
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01711
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.