Abstract
Quantum information science promises transformative impact over a range of key technologies in computing, communication and sensing. A prominent example uses entangled photons to overcome the resolution-degrading effects of dispersion in the medical-imaging technology, optical coherence tomography. The quantum solution introduces new challenges: inherently low signal and artifacts, additional unwanted signal features. It has recently been shown that entanglement is not a requirement for automatic dispersion cancellation. Such classical techniques could solve the low-signal problem, however they all still suffer from artifacts. Here, we introduce a method of chirped-pulse interferometry based on shaped laser pulses and use it to produce artifact-free, high-resolution, dispersion-cancelled images of the internal structure of a biological sample. Our work fulfills one of the promises of quantum technologies: automatic-dispersion-cancellation interferometry in biomedical imaging. It also shows how subtle differences between a quantum technique and its classical analogue may have unforeseen, yet beneficial, consequences.
Similar content being viewed by others
Introduction
Quantum information science promises powerful and unconventional capabilities across a broad range of technologies. An important example relates to the imaging technology, optical coherence tomography (OCT). OCT can noninvasively reconstruct the 3-dimensional structure of tissue with micron resolution1; it is emerging as an important clinical tool with diverse medical applications. OCT can diagnose retinal diseases such as glaucoma, analyze artherosclerotic tissues within arteries and detect early-stage cancerous lesions in breast tissue2,3. In addition, OCT has found application in precision laser machining4. Since OCT relies on low-coherence interferometry, its axial resolution is limited by the coherence length of the light, inversely proportional to the bandwidth. The coherence length determines ultimate resolution, however, material dispersion can limit the practical one.
Fundamental studies in quantum optics showed that interference with energy-time entangled photon pairs5 exhibits inherent robustness against unbalanced dispersion6,7. Even-order effects of dispersion, including the dominant group-velocity dispersion, are automatically cancelled, effectively solving the dispersion problem. This dispersion cancellation is automatic since one does not need to precisely measure and compensate the dispersion. When energy-time entanglement is strong, but not perfect, the effect is more accurately described as automatic even-order dispersion reduction since the dispersion is dramatically reduced, not cancelled8. OCT based on entangled-photon interferometry was proposed to harness automatic dispersion cancellation9. This quantum-optical coherence tomography (QOCT) has two significant barriers to practical implementation. Firstly, the reliance on producing and resolving individual photon pairs places stringent limits on the QOCT signal using state-of-the-art systems10,11. Secondly, in samples with multiple interfaces, QOCT produces a signal for each interface and an additional, artifact feature for each unique pair of interfaces9,12,13; the number of artifacts grows quadratically with the number of interfaces, cluttering the image of complex samples. QOCT was first used to perform an axial scan of a coverslip13 and later applied to measure the surface topography of a gold-coated onion sample14. The gold coating was essential to increase reflectivity but rendered the technique impractical for in vivo applications; furthermore, it prevented imaging the sample's internal structure, which is one of the main benefits of OCT and necessary for most medical applications.
Recently, several different approaches have shown that dispersion cancellation does not require entanglement, but can also be observed in classical systems15,16,17,18,19. While all of these methods could, in principle, solve the low-signal problem of QOCT, each suffers from unwanted artifacts. Here, we focus on one of these techniques, chirped-pulse interferometry (CPI). A method for identifying artifacts in CPI has been demonstrated, but it requires multiple axial scans of a sample and is thus inherently slow25.
In the present work, we describe and demonstrate a new method for CPI using a single beam of shaped laser pulses. Our method produces background-free, dispersion-cancelled signals, completely free of artifacts without the need for multiple scans. We apply this technique to image a biological sample, demonstrating dispersion cancellation and observing the sample's internal structure. CPI overcomes both limitations of QOCT while retaining its advantages, demonstrating its potential for future practical application.
Results
Theoretical description
CPI uses classical light with strong frequency anti-correlations. To create these anti-correlations, we constructed a 4-F pulse shaper with a spatial light modulator (SLM)20,21. In CPI, this method has distinct advantages over pulse-stretching techniques with bulk optics22,23, including: straightforward optimization of the chirp parameter8, better stability and efficiency and more complex pulse shapes. We apply a frequency-dependent phase shift to the laser pulses, ϕ(ω) = −A(ω − ω0)|ω − ω0|, where A is a positive constant. The absolute value distinguishes this from the quadratic phase leading to linear chirp: ϕ(ω) applies a linear chirp to red-shifted frequencies (ω < ω0) and an equal, opposite chirp (antichirp) to blue-shifted frequencies (ω > ω0). The resulting pulse has frequency ω0 at its lagging edge and instantaneous frequencies in the preceding part of the pulse obey the function  . These are the frequency anti-correlations needed for CPI.We refer to this as a Blue-Antichirped-Red-Chirped (BARC) pulse.
. These are the frequency anti-correlations needed for CPI.We refer to this as a Blue-Antichirped-Red-Chirped (BARC) pulse.
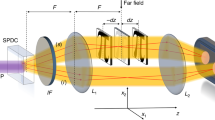
CPI can be understood by considering the schematic in Figure 1a. Light in the upper arm of the interferometer travels through a dispersive material of length L as well as a distance L1 − L through free space; light in the lower arm travels a distance L2 through free space. The dispersive material in the upper arm has a wavevector of light that can be expanded about frequency ω0 as k(ω) = k(ω0) + α(ω − ω0) + β(ω − ω0)2 + …, where α and β describe the group delay and group velocity dispersion, respectively. At any time, two laser beams with frequencies ω0 + Δ and ω0 − Δ enter the interferometer with corresponding amplitudes E(Δ) and E(−Δ). After travelling through the interferometer they overlap at the nonlinear crystal for sum-frequency generation (SFG). Two paths produce SFG with frequency 2ω0; either blue-shifted light travels the upper arm and red-shifted light travels the lower arm, or vice versa. The amplitudes for these two paths interfere to give a signal S(Δ, τ) = |E(Δ)E(−Δ)|2 (1 + cos [ϕ+(Δ, τ) − ϕ−(Δ, τ)]), where τ = (L2 − L1 + L)/c is the time delay between the two paths18. To second order in the wave-vector and ignoring a global phase, the respective phases of the two paths are,  . The final signal results from integrating Δ over the pulse bandwidth, forming a peak at τ = αL26. Since unbalanced dispersion contributes the same phase βΔ2 to each path, the effect cancels out of the final signal; this is automatic dispersion-cancellation. With imperfect anti-correlations, dispersion cancellation persists if the unbalanced dispersion is much less than the chirp parameter, A (see ref. 8).
. The final signal results from integrating Δ over the pulse bandwidth, forming a peak at τ = αL26. Since unbalanced dispersion contributes the same phase βΔ2 to each path, the effect cancels out of the final signal; this is automatic dispersion-cancellation. With imperfect anti-correlations, dispersion cancellation persists if the unbalanced dispersion is much less than the chirp parameter, A (see ref. 8).
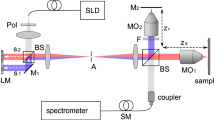
An optical-coherence-tomography system based on chirped-pulse interferometry.
(a) A simplified schematic of CPI. A pair of classical beams in the same spatial mode and with anticorrelated frequencies impinges on a beamsplitter and the two resulting paths overlap in a β-barium borate (BBO) crystal for sum-frequency generation (SFG) after one path experiences a variable delay, τ and the other passes through a dispersive material with a frequency-dependent wave-vector k(ω). The frequency offset, Δ, is swept over the bandwidth of the input pulses. The CPI signal then is the intensity of the SFG light near 2ω0 as a function of τ. This signal is inherently robust against unbalanced dispersion. (b) The experimental implementation. Broadband pulses from a titanium: sapphire laser pass through a 4-F pulse-shaper20,21, the light is then split into a beam that reflects from the sample in the focus of a lens and a beam that travels a variable-length delay. The delay and the x- and y-positions of the sample are motorized. A stack of BK7 glass in the reference arm introduces dispersion equal to that of the static optical elements in the sample arm, including the BK7 window and water layer in the sample holder, but excluding the samples themselves. The pulse shaper compensates for this static, balanced dispersion throughout the experiment such that the laser pulse is transform limited at the nonlinear crystal. The pulse shaper can add an additional phase shift, ϕ(ω), to produce the BARC pulse shape at the crystal. Inserting an extra 3-mm-thick BK7 window in the sample arm introduces a controlled amount of unbalanced dispersion. Light from the two interferometer arms is focused onto a nonlinear crystal and undergoes non-collinear SFG. The SFG light passes through a spatial filter and a monochromator and the signal is measured as a function of time delay using a photomultiplier. Illustration of the cross-sections of the two samples, (c) microscope coverglass slides and (d) a piece of onion. Each sample was held in a lens tube and placed behind a layer of distilled water and a 1-mm-thick BK7 window; the 2.7 mm water layer prevented drying of the onion sample.
Ideally, each interference signal would correspond to an interface in the sample. However, in both QOCT13 and CPI25 an additional artifact signal appears halfway between the signals arising from each pair of interfaces. In complex samples, artifacts can outnumber the features from real interfaces, seriously impeding reconstruction and interpretation. The origin of the artifacts in these two techniques are subtly, but importantly different (see Supplementary Fig. S1 online). Artifacts in CPI are a result of interference in the SFG light at frequencies blue-shifted or red-shifted from the operating frequency, 2ω0, by an amount Δω = Δτ/(4A), where Δτ is the time-delay difference between the two sample interfaces. Spectral filtering of the SFG can remove all artifacts arising from pairs of interfaces separated by more than some minimum delay. The analogous method of artifact removal in QOCT requires coincidence detection with tens of femtoseconds time-resolution, which is extremely difficult in practice.
Experimental setup and characterization
Our experimental setup is shown in Figure 1b. We used this system to image a stack of two microscope coverglass slips (Figure 1c) and an onion (Figure 1d). First, we focus on the coverglass sample to benchmark our system performance. We measure the SFG power as a function of time delay, τ, with two types of pulses, a transform-limited (TL) pulse and the BARC pulse. Using the TL pulse is equivalent to OCT with background-free autocorrelation24, which does not suffer from artifacts but is not dispersion cancelling. In order to remove artifacts from signals acquired with BARC pulses, the SFG signal is sent through a 0.35-nm-bandwidth filter. See Methods for more details.
The data measured using TL and BARC pulses are shown in Figures 2a and b, respectively. Black (red) lines show data without (with) unbalanced dispersion from 3-mm BK7 in the sample arm, where the light passes twice through the glass. The left-most four peaks correspond to the front and back surfaces of the first and second coverglass pieces. The average delay between the first (second) two peaks is 248 ± 4 μm (236 ± 4 μm). Dividing by the group index ng = 1.517 of the coverglass gives thicknesses of 163 μm and 156 μm for the two slides, in good agreement with 164 ± 3 μm and 157 ± 3 μm measured with a caliper. We subtracted a constant 1.6 mm from the delay-arm motor position in the unbalanced-dispersion data to compensate for the group delay from the additional glass so corresponding peaks could be overlayed for comparison.
Axial scans of the coverglass sample using (a) transform-limited pulses and (b) BARC pulses.
Each set of data shows five distinct peaks; the left-most four arise from the front and back surfaces of each of the two coverglass slides while the final right-most peak is from the BK7 base of the sample holder. Each peak is associated with a real interface and the BARC-pulse signal shows no additional features as compared with (a). Thus any artifacts have been effectively removed by our filtering technique. The black (red) data were taken without (with) the removable 3-mm BK7 in the sample arm. The numerical labels denote each peak width in microns (FWHM). The peaks in (a) from the transform-limited pulses were broadened by 106% from the unbalanced dispersion, while that in (b) from the BARC pulses were broadened by just 7%. Dispersive broadening can be observed directly by zooming in on the pair of peaks near motor position 0.25 mm shown in the insets. These data demonstrate automatic dispersion cancellation in our chirped-pulse interferometer.
Figures 2a and b show that no additional artifact features arise going from a TL to a BARC pulse. In the online Supplementary Information, we show the maximum layer separation giving rise to artifacts is 3 μm, narrower than the peak widths, 4.2 μm. As expected, any resolvable artifacts are filtered out of our signal.
The average signal peak width for the TL pulses is 3.6 ± 0.2 μm (FWHM) which broadened by 106% to 7.4 ± 0.6 μm by the dispersion. Uncertainties represent the standard deviations of the five peak widths. In contrast, the BARC-pulse produced average signal widths of 4.2 ± 0.1 μm that broadened by only 7% to 4.5 ± 0.2 μm, demonstrating dispersion cancellation. The measured peak widths for the TL and BARC pulses are in good agreement with the theoretical calculations of 3.4 μm and 4.1 μm, respectively, using the 60 nm acceptance bandwidth of our system. The peak width of the BARC-pulse signal is broadened compared to the TL pulses as a result of the narrow filtering of the SFG; if a broader bandwidth was measured instead, the widths would become equal, but artifacts can reappear. The dispersion cancellation observed cannot be explained by the slightly broader BARC-pulse signal in the balanced dispersion case. If one used a TL pulse yielding a 4.2 μm peak width in the absence of dispersion, equal to the width to our BARC-pulse signal, we calculate that two passes through 3-mm BK7 glass would broaden the signal to 5.8 μm, a 38% increase. Our BARC-pulse signal is broadened by 7%, thus the dispersion cancellation is significant even when compared with this conservative benchmark.
Dispersion-cancelled biological imaging
We prepared a sample of onion as depicted in Figure 1d and took a set of axial (z) scans, moving the sample in the y-direction between scans. The data are displayed in Figure 3, where the four panels a, b, d and e show cases with and without dispersion (3-mm BK7) for both TL and BARC pulses. The vertical axes are the delay-arm motor positions and the horizontal axes show the transverse y-positions. The images show the cellular structure of the onion deep into the sample and are artifact-free. Beside each image, we show a single axial scan taken at the y-position marked by the red line in each plot. The TL-pulse signal peaks are dramatically broadened when unbalanced dispersion is added, but the BARC-pulse peak widths are unchanged, directly demonstrating automatic dispersion cancellation in our image. In order to compare the effect of dispersion over the entire images produced by the TL pulses and BARC pulses, we extracted the widths of signal peaks throughout the images and display corresponding histograms in Figures 3c and f. The TL-pulse peaks broadened by 61% from an average of 3.6 ± 0.5 μm to 5.7 ± 1.2 μm, where uncertainties are the standard deviations of each distribution. The BARC-pulse peak widths increased by only 4% from 4.2 ± 0.8 μm to 4.3 ± 0.6 μm, less than the standard deviation. Hence, dispersion is cancelled througout the BARC-pulse images.
Two-dimensional images of an onion sample.
Panel (a) was taken with the TL pulse with no unbalanced dispersion, (b) TL pulse with 3 mm of BK7 in the sample arm for unbalanced dispersion (d) BARC pulse, no dispersion and (e) BARC pulse with unbalanced dispersion. The colour-bar represents the natural logarithm of the number of counts per delay-arm motor step recorded by the photomultiplier. The internal cellular structure of the onion is visible deep into the sample in all four images and comparing the images we see that no artifacts are introduced by using BARC pulses. A single axial scan at the transverse position indicated by the red vertical line in each image are plotted on a linear scale beside each corresponding image; the labels represent the widths of each peak FWHM in micrometres. The addition of dispersion significantly broadens the TL-pulse peaks while in contrast the BARC-pulse peaks are dispersion cancelled. Peak widths over each entire image are plotted as histograms shown in panels (c) and (f), for the TL and BARC pulses respectively; the black bars are used for no unbalanced dispersion and the red for unbalanced dispersion. The peak widths for the TL pulses broadened by 61% with the addition of dispersion, while those from the BARC pulses broadened only by 4%. Dispersion cancellation is thus achieved over the entire image.
To further show the capability of our method, we took a set of axial (z) scans over a grid of x- and y-positions of a different onion sample prepared in the same manner as before, using the BARC pulses with no unbalanced dispersion. From this data, we extracted 2D cross-sections of the sample shown in Figures 4a–c and the 3D cell wall structure of the top layer of cells is shown in Figure 4d. Thus CPI, with its inherent dispersion cancellation, is suitable for practical 3D imaging of biological samples.
A three-dimensional image of an onion sample.
Using BARC pulses with no unbalanced dispersion, we took a set of axial (z) scans at a grid of x- and y-positions on an onion sample. Panels (a), (b) and (c) show 2D cross-sectional images of our 3D data in the xz, yz and xy planes depicting the cellular structure. In panel (d), we show a 3D rendering of the surface layer of cells extracted from our data. The grid spacing is 50 μm and the transparent red planes correspond to the slices shown in panels (a), (b) and (c).
Discussion
We have demonstrated dispersion-cancelled, artifact-free, optical-coherence-tomography imaging of a biological sample. For future work, incorporating a nonlinear material with larger nonlinearity and acceptance bandwidth24,27 will improve the system, increasing acquisition rates and image resolution. Dispersion-cancelled OCT with chirped-pulse interferometry draws upon insights from quantum information science. Exploiting subtle differences in the analogous roles played by different physical parameters between the techniques allowed problems inherent to the quantum scheme to be solved in the classical technology; extraction of artifacts is very hard, or even technologically impossible, in the quantum device, yet becomes straightforward in CPI. Our results remove the technological barriers to dispersion-cancelled biological imaging and underscore the importance of understanding classical analogues to quantum mechanical effects.
Methods
Pulses from a titanium:sapphire laser (808 nm, 90 nm FWHM) pass through a 4-F pulse shaper incorporating a spatial light modulator (CRi SLM-640-D-VN)20,21, also see ref. 28 for details. The SLM served two purposes, compressing the pulses by compensating for balanced dispersion in the setup and applying the BARC-phase ϕ(ω) = −A(ω − ω0)|ω − ω0|, where A = 2500 fs2 and λ0 = 2πc/ω0 = 809.60 nm. The shaped pulses were split on a beamsplitter with 16 mW sent to the sample and 24 mW into a variable-delay line (a retroreflector on a motorized stage). A 3-mm-thick BK7 glass window could be inserted into the sample arm to introduce unbalanced dispersion of β = 132 fs2. A small onion sample was placed inside a 1″ lens tube, submerged in water, covered with a 1-mm-thick BK7 window (Figure 1d) and mounted on a motorized x-y stage. A washer separated the onion and BK7 window by 2.7 mm. A 19-mm achromatic lens on a motorized stage focused the beam inside the sample to a spot size of approximately 6 μm. The delay-arm and sample-arm beams were focused using a 75-mm achromatic lens onto a 0.5-mm BBO crystal, cut for type-I SFG. The beam separation at the lens was 14 mm. The SFG signal was collimated and sent through a monochromator (Princeton Instruments Acton Advanced SP2750A) and detected with a single-photon-counting photomultiplier (Hamamatsu H10682-210). The monochromator was centred at 404.80 nm when the TL-pulse was used and 404.64 nm when the BARC-pulse was used, to account for a small shift in the signal frequency induced by the added dispersion (see Supplementary Fig. S2 online). The acceptance bandwidth of the monochromator was 0.35 nm in both cases. This filtering of the SFG light was performed in order to remove artifacts from signals acquired with BARC pulses.
Axial depth scans were taken by moving the retro-reflector and recording the photomultiplier signal every 0.4 μm. For the coverglass samples, the delay-stage speed was 0.5 mm/s and the delay stage scanned a range of 700 μm. For the 2D onion data, axial scans were taken over an 800 μm range in the y-direction with one scan every 4 μm. The delay-stage speed was 0.1 mm/s and it was scanned over a total range of 600 μm. The acquisition time per image was 1 hour.
For the histograms in Figure 3, all peaks from each axial scan were fitted provided their amplitudes were between 250 and 6000 counts per delay-stage step, so that their widths were not obscured by noise or detector saturation. Each histogram was fit with a Gaussian peak to estimate the mean and variation of the peak widths in each image.
The 3D onion data was taken over a range of 300 μm, 500 μm and 350 μm in the x, y and z directions, respectively. One axial scan was taken every 10 μm in the x and y directions. Every five data points in the z direction were binned to provide a point every 2 μm. Smoothing and threshold algorithms were applied to the raw data to create the 2D images. The 3D structure was visualized with the Imaris (Bitplane, Inc.) software after an FFT bandpass filter was applied. The delay-stage speed was 0.3 mm/s and data acquisition took 2.5 hours.
References
Povazay, B. et al. Submicrometer axial resolution optical coherence tomography. Opt. Lett. 27, 1800–1802 (2002).
Fercher, A. F., Drexler, W., Hitzenberger, C. K. & Lasser, T. Optical coherence tomography — principles and applications. Rep. Prog. Phys. 66, 239–303 (2003).
Zysk, A. M., Nguyen, F. T., Oldenburg, A. L., Marks, D. L. & Boppart, S. A. Optical coherence tomography: a review of clinical development from bench to bedside. J. Biomed. Opt. 12, 051403 (2007).
Webster, J. L. P., Muller, M. S. & Fraser, J. M. High speed in situ depth profiling of ultrafast micromachining. Opt. Express 15, 14967–14972 (2007).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of Subpicosecond Time Intervals between Two Photons by Interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Steinberg, A. M., Kwiat, P. G. & Chiao, R. Y. Dispersion cancellation and high-resolution time measurements in a fourth-order optical interferometer. Phys. Rev. A 45, 6659–6665 (1992).
Steinberg, A. M., Kwiat, P. G. & Chiao, R. Y. Dispersion Cancellation in a Measurement of the Single-Photon Propagation Velocity in Glass. Phys. Rev. Lett. 68, 2421–2424 (1992).
Resch, K. J., Kaltenbaek, R., Lavoie, J. & Biggerstaff, D. N. Chirped-pulse interferometry with finite frequency correlations. Proc. of SPIE 7465, 74650N (2009).
Abouraddy, A. F., Nasr, M. B., Saleh, B. E. A., Sergienko, A. V. & Teich, M. C. Quantum-optical coherence tomography with dispersion cancellation. Phys. Rev. A 65, 053817 (2002).
Altepeter, J., Jeffrey, E. & Kwiat, P. Phase-compensated ultra-bright source of entangled photons. Opt. Express 13, 8951–8959 (2005).
Fedrizzi, A. et al. High-fidelity transmission of entanglement over a high-loss free-space channel. Nature Phys. 5, 389–392 (2009).
Strekalov, D. V., Pittman, T. B. & Shih, Y. H. What we can learn about single photons in a two-photon interference experiment. Phys. Rev. A 57, 567–570 (1998).
Nasr, M. B., Saleh, B. E. A., Sergienko, A. V. & Teich, M. C. Demonstration of Dispersion-Canceled Quantum-Optical Coherence Tomography. Phys. Rev. Lett. 91, 083601 (2003)
Nasr, M. B. et al. Quantum optical coherence tomography of a biological sample. Opt. Commun. 282, 1154–1159 (2009).
Erkmen, B. I. & Shapiro, J. H. Phase-conjugate optical coherence tomography. Phys. Rev. A 74, 041601(R) (2006).
Banaszek, K., Radunsky, A. S. & Walmsley, I. A. Blind dispersion compensation for optical coherence tomography. Opt. Commun. 269 152–155 (2007).
Resch, K. J., Puvanathasan, P., Lundeen, J. S., Mitchell, M. W. & Bizheva, K. Classical dispersion-cancellation interferometry. Opt. Express 15, 8797–8804 (2007).
Kaltenbaek, R., Lavoie, J., Biggerstaff, D. N. & Resch, K. J. Quantum-inspired interferometry with chirped laser pulses. Nature Phys. 4 864–868 (2008).
Le Gouët, J., Venkatraman, D., Wong, F. N. C. & Shapiro, J. H. Experimental realization of phase-conjugate optical coherence tomography. Opt. Lett. 35, 1001–1003 (2010).
Weiner, A. M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Inst. 71, 1929–1960 (2000).
Légaré, F. L., Fraser, J. M., Villeneuve, D. M. & Corkum, P. B. Adaptive compression of intense 250-nm-bandwidth laser pulses. Appl. Phys. B 74(Suppl.), S279–S282 (2002).
Martínez, O. E. Matrix Formalism for Pulse Compressors. IEEE J. Quantum Electron. 234, 2530–2536 (1988).
Pessot, M., Maine, P. & Mourou, G. 1000 times expansion/compression of optical pulses for chirped pulse amplification. Opt. Commun. 62, 419–421 (1987).
Pe'er, A., Bromberg, Y., Dayan, B., Silberberg, Y. & Friesem, A. Broadband sum-frequency generation as an efficient two-photon detector for optical tomography. Opt. Express 15, 8760–8769 (2007).
Lavoie, J., Kaltenbaek, R. & Resch, K. J. Quantum-optical coherence tomography with classical light. Opt. Express 17, 3818–3825 (2009).
Kaltenbaek, R., Lavoie, J. & Resch, K. J. Classical Analogues of Two-Photon Quantum Interference. Phys. Rev. Lett. 102, 243601 (2009).
Nasr, M. B. et al. Ultrabroadband Biphotons Generated via Chirped Quasi-Phase-Matched Optical Parametric Down-Conversion. Phys. Rev. Lett. 100, 183601 (2008).
Schreiter, K. Optical pulse shaping for chirped pulse interferometry and bio-imaging. M. Sc. Thesis. University of Waterloo, Canada. (2011).
Acknowledgements
We thank Jonathan Lavoie, Kostadinka Bizheva, Donna Strickland and Rolf Horn for helpful discussions. Sellmeier coefficients for the coverglass slides were provided by Corning Inc. We are grateful for financial support from NSERC, OCE, CFI, QuantumWorks, Industry Canada and MRI ERA. R.P. acknowledges support from the FWF (J2960-N20), MRI, the VIPS Program of the Austrian Federal Ministry of Science and Research and the City of Vienna as well as the European Commission (Marie Curie, FP7-PEOPLE-2011-IIF). R.K. acknowledges support from the Austrian Academy of Sciences (APART) and support from the European Commission (Marie Curie, FP7-PEOPLE-2010-RG).
Author information
Authors and Affiliations
Contributions
K.J.R. and R.K. conceived of the experiment. K.M.S., R.K. and R.P. set up the pulse shaper and cross correlator and performed preliminary experiments. K.M.S. wrote the control software and calibrated the SLM. M.D.M. modified the setup and performed the experiments and simulations presented here and along with R.P. analyzed the data. M.D.M. and K.J.R. wrote the first draft of the manuscript. All authors contributed to the final version.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Dispersion-cancelled biological imaging with quantum-inspired interferometry-Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Mazurek, M., Schreiter, K., Prevedel, R. et al. Dispersion-cancelled biological imaging with quantum-inspired interferometry. Sci Rep 3, 1582 (2013). https://doi.org/10.1038/srep01582
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01582
This article is cited by
-
Moderate-coherence sensing with optical cavities: ultra-high accuracy meets ultra-high measurement bandwidth and range
Communications Engineering (2024)
-
Interference effects in quantum-optical coherence tomography using spectrally engineered photon pairs
Scientific Reports (2019)
-
Quantum enhancement of accuracy and precision in optical interferometry
Light: Science & Applications (2017)
-
Experimental Demonstration of Spectral Intensity Optical Coherence Tomography
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.