Abstract
We address the general question of the extent to which the hydrodynamic behaviour of microscopic freely fluctuating objects can be reproduced by macrosopic rigid objects. In particular, we compare the sedimentation speeds of knotted DNA molecules undergoing gel electrophoresis to the sedimentation speeds of rigid stereolithographic models of ideal knots in both water and silicon oil. We find that the sedimentation speeds grow roughly linearly with the average crossing number of the ideal knot configurations and that the correlation is stronger within classes of knots. This is consistent with previous observations with DNA knots in gel electrophoresis.
Similar content being viewed by others
Introduction
Gel electrophoresis of knotted DNA molecules revealed that DNA molecules of the same length, but forming different knot types, separate into specific bands1,2,3. More complex knots migrated quicker than less complex ones and the migration speed was increasing linearly with the average crossing number (ACN) of the corresponding knots in their ideal configurations4,5. Ideal knots are defined as axial paths of shortest possible unit-radius cylindrical tubes that can still form a knot of a given type6,7,8,9,10,11,12. The average crossing number for a rigid curve in space is defined as the average number of crossings perceived when that curve is observed from all possible directions13. For a randomly fluctuating curve in space, such as the axial path of a DNA molecule undergoing a thermal motion, the average crossing number can be obtained by averaging over many independent configurations observed from a randomly chosen direction. Of course, thermally fluctuating DNA knots do not take ideal shapes, but can be considered as fluctuating around their ideal configuration. Monte Carlo simulations of fluctuating polymer chains forming different knot types revealed, for example, that the average writhe of a polymer forming a given knot is practically the same as the writhe of the corresponding ideal knot6 and their migration distance in simulations of gel electrophoresis also correlates with their ACN14,15.
Although the ACN of freely fluctuating polymers increases with their length, if DNA molecules with the same length form two different knots, the difference in their average crossing number is practically the same as the difference between average crossing numbers of the corresponding ideal knots6. The average crossing number is a frequently used and studied descriptor in the field of polymer topology as its value is scale invariant16,17,18,19. It is intuitively clear that the higher the average crossing number of a polymer chain of a given length the higher is the compaction of the polymer. The average crossing number is a good measure of polymer compaction since for simulated DNA molecules of the same length, but forming different knot types, their respective average crossing numbers were proportional to their calculated sedimentation coefficients5.
Since rigid ideal configurations of knots seem to capture several characteristics of freely fluctuating knots of the same type, such as their mean writhe6, we decided to use stereolithography technique to manufacture macroscopic models of various knots consisting of a rod of circular cross section centered at axial trajectories of corresponding ideal knots in order to study their hydrodynamic behavior while sedimenting in liquids of various viscosities. Although DNA knots that revealed the linear dependence between their electrophoretic mobility and their average crossing number had the length diameter ratio on the order of one thousand, in our models we set this ratio to 60. This permitted us to have objects that were relatively sturdy and thus were not breaking when removing them from the viscous silicon oil. Usage of relatively large diameter (0.5 cm) of cylinders following the axial trajectories of ideal knots permitted us also to diminish the relative error in shape rendering by the stereo-lithography. Having a small relative error and thus small relative differences of weight between different knots was important for us to be able to associate the observed differences of sedimentation speeds of different knots just to their different average crossing number and not to other factors like their weight differences, for example. In addition, we wanted to investigate whether the linear relation between average crossing number of various knots and their sedimentation speed is more general and thus extends also to knots made out of relatively thick tubes.
Results
By trying different starting orientations, we identified at least one stable hydrodynamic axis for the majority of the knots. Several knots showed two different stable axes, which they could take depending on the starting orientation of their fall in the tank (see Fig 2). For the ideal knots 31, 41, 51, 61, 71 and 77 that were the subject of an analytical study aimed to predict their hydrodynamic axes20, we were pleased to notice that the orientations observed in our experiments corresponded to the predicted one (Supplementary movies S1 and S2 show the knot 51 sedimenting along two different stable axes).
The knot 41 was somewhat peculiar because it was flipping continuously from one metastable position to another one (see movie S3). We noted also that some of the ideal knots did not show any rotation during the sedimentation, such as the knot 818 (see movie S4). This is presumably the consequence of the fact that the ideal configuration of this achiral knot is identical to its mirror image. Chirality and rotation during sedimentation are correlated. Moreover, we also observed that right- and left-handed 31 knots were rotating in opposite directions when sedimenting along the corresponding hydrodynamic axes (see movie S5). The movements of right- and left-handed ideal 31 knots just looked like mirror images of each other. We also studied the rotation of ideal composite knots with 31 right-handed (31R) and left-handed (31L) knots: 31L#31R (square knot) and respectively 31R#31R (granny knot). We observed that the achiral composite knot 31L#31R did not rotate (see movie S6) whereas that the chiral one 31R#31R showed a quick rotation (see movie S7). Note that similar to 818 knot, the ideal configuration of 31L#31R is superimposable with its mirror image.
Table 1 lists sedimentation speeds of different knots in water and silicon oil, respectively. As aforementioned, some knots were observed to adopt two different stable orientations during sedimentation, where the two orientations usually resulted in a different specific speed. In Table 1 these knots have three characteristic speed values, where vs and vf denote the speeds in orientations resulting in a slower and faster sedimentation, respectively and va denote the average speed between the former two speeds. For knots for which we observed only one preferential orientation, we treat the observed speed as the average speed (va) for a given knot. The same applies to knots that did not reach a stable orientation during sedimentation and constantly tumbled during the fall.
 and oil
and oil 
Obviously, the sedimentation speed is much larger in water than in viscous silicon oil, however we are rather interested here in the ratio of sedimentation speeds of different knots in the same medium. We therefore normalize the reported velocities by the average velocity va of the unknot in a given medium. Figure 3.a,b shows the relationship between the normalized average sedimentation speeds of different knots in water and oil, respectively and the ACN of the corresponding knots. We find that the sedimentation speed increases with the average crossing number (see Fig. 3). As could be expected, the differences of normalized speeds of different knots are much larger in oil than in water but the general trend is similar.
Relationship between the relative sedimentation speeds and the average crossing numbers of ideal knot models sedimenting in water (a) and silicon oil (b), respectively.
The relative sedimentation speed is the ratio between the average sedimentation speed of a given knot and the average sedimentation speed of unknot in the same liquid.
Discussion
Comparing our experimental results with numerical simulations of the sedimentation process for the shapes of ideal knots, reported by Gonzalez et al.20, we see a somewhat larger scattering of the data around the linear trend (see Fig. 5 in Ref. 20). Presumably the main source of discrepancy is that our average sedimentation speed was obtained by a straightforward average over speeds obtained in two stable orientations, whereas Gonzalez et al. in their simulations were able to take into account the relative frequency with which the two stable orientations were attained. However, if we take into account only the knots analyzed by Gonzalez et al.20, i.e. 31, 41, 51, 61, 71 and 77, the latter knots agree significantly better with a linear relation with the ACN than some of the other knots we analyzed.
Also in the gel electrophoresis experiments that gave rise to the observation that the electrophoretic migration speeds of various DNA knots increases with their ACN, the studied knots belonged only to two families of knots, i.e. torus and twist knots, which include 31, 41, 51, 52, 61, 71, 72, 81, 91, 92 and 101 knots5. If we look only at the speeds of the 31, 41, 51, 52, 61, 71, 72, 81, 91, 92 knots, they also show a much smaller scatter around the linear relation. The slow mean speed of 91 knot in oil (see Fig. 3.b) was due to the fact that the faster hydrodynamic axis was unstable and we measured only the speed resulting from the orientation resulting in a slower sedimentation. Also the slow speed of 821 in water most likely resulted from the fact that its faster hydrodynamic was unstable.
Our experiments showed that there is a general correlation between the sedimentation speed of rigid ideal knots and their ACN. However, this correlation applies better to knots belonging to the same family, like twist knots for example, as supported also by further simulations of ideal knots21, where knots belonging to the same family like 31, 51, 61 and 71 show a nearly perfect linear relation between their sedimentation speed and their ACN.
An interesting question is whether the quasi-linear relation between sedimentation speed and average crossing number of ideal knots would also hold for models with vanishing thickness. We expect it to be the case. Our expectation is based on the fact that knotted DNA molecules show linear increase of gel migration with their ACN and knotted DNA molecules are very thin and thus have a much larger length to diameter ratio than our models. In addition, in simulation studies aimed to reproduce sedimentation of knotted DNA molecules the sedimentation coefficient was increasing linearly with the ACN of the modeled DNA molecules with the same chain length5.
Methods
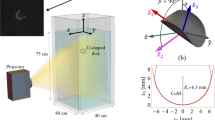
The models were made of a rigid epoxy resin of density 1.2 g/ml. The tubes forming knots of different topological types, had the same length (30 cm) and diameter (0.5 cm) and hence the same volume (5.89 cm3) and weight (7 g). The stereolithography technique of manufacture using epoxy resin has an error at the surface of less than 2–3% of the diameter of the tube. The small imperfections of the stereolithography led to a measured weight dispersion smaller than 1%. The ideal knot models were immersed and gently released into a transparent plexiglass tank (see Fig 1g) that was filled either with water or with a silicon oil. The individual models were released in orientations that were close to analytically predicted stable axes of sedimentations for a given knot20. The majority of investigated knots quickly reached a stable orientation along one of their hydrodynamic axes. We observed which of the hydrodynamic axes coincided with the direction of the sedimentation and measured sedimentation speeds. To avoid spurious pressure effects induced by the vicinity of the sedimenting model to the bottom of the tube and to avoid the initial accelerating phase and perturbation due to the release, we discarded the first and last 20 cm of every run. For knots that end up in a stable orientation during the sedimentation, the 20 cm distance was sufficient to reach this orientation. Sedimentation runs were captured by two digital cameras, which were placed at the top and on the side of the tube.
We have used two fluids for the sedimentation experiments: water, where the Reynolds number for the speed considered in this work is estimated to be around the laminar flow regime (≈ 2000) and a silicon oil, with a density close to water and kinematic viscosity of ν = 1000 ctS with Reynolds number of approximately 0.01, which is below the Stokes flow regime (Re ≈ 0.1). In order to further quantify the proximity to the Stokes regime for experiments performed with silicon oil, we used a sphere of epoxy resin (same weight and volume as the ideal knot models) that we released in silicon oil. In the limit of a Stokes flow and in an infinite medium, the speed of a sphere is: v = 2gr2 (ρsphere − ρoil)/ϑηoil, where ηoil is the dynamical viscosity of the oil, r the radius of the sphere, g the gravitational acceleration. Using the appropriate constants, we get a theoretical prediction in the Stokes regime of v = 5.7426 cm/s (with a 1000 ctS oil) and it compares extremely well to the measurement v = 5.69(2) cm/s, which confirms that we are close to the Stokes regime. We also note that the velocity of the sphere is much greater than the ideal knot sedimentation velocities, due to its much smaller gyration radius.
References
Dean, F. B., Stasiak, A., Koller, T. & Cozzarelli, N. R. Duplex DNA knots produced by Escherichia-Coli Topoisomerase-I - structure and requirements for formation. Journal of Biological Chemistry 260, 4975–4983 (1985).
Crisona, N. J., Kanaar, R., Gonzalez, T. N., Zechiedrich, E. L., Klippel, A. & Cozzarelli, N. R. Processive recombination by wild-type Gin and an enhancer-independent mutant. Insight into the mechanisms of recombination selectivity and strand exchange. J. Mol. Biol. 243, 437–457 (1994).
Kanaar, R., Klippel, A., Shekhtman, E., Dungan, J. M., Kahmann, R. & Cozzarelli, N. R. Processive recombination by the phage mu gin system: implications for the mechanisms of DNA strand exchange, DNA site alignment and enhancer action. Cell 62, 353–366 (1990).
Stasiak, A., Katritch, V., Bednar, J., Michoud, D. & Dubochet, J. Electrophoretic mobility of DNA knots. Nature 384, 122 (1996).
Vologodskii, A. V., Crisona, N. J., Laurie, B., Pieranski, P., Katritch, V., Dubochet, J. & Stasiak, A. Sedimentation and electrophoretic migration of DNA knots and catenanes. J Mol Biol 278(1), 1–3 (1998).
Katritch, V., Bednar, J., Michoud, D., Scharein, R. G., Dubochet, J. & Stasiak, A. Geometry and physics of knots. Nature 384, 142–145 (1996).
Moffatt, H. K. Pulling the knot tight. Nature 384, 114–114 (1996).
Gonzalez, O. & Maddocks, J. H. Global curvature, thickness and the ideal shapes of knots. Proc. Natl. Acad. Sci. USA 96, 4769–4773 (1999).
Litherland, R. A., Simon, J., Durumeric, O. & Rawdon, E. Thickness of knots. Topology Appl. 91, 233–244 (1999).
Cantarella, J., Kusner, R. B. & Sullivan, J. M. On the minimum ropelength of knots and links. Invent. Math. 150, 257–286 (2002).
Rawdon, E. J. Can computers discover ideal knots? Exp. Math. 12, 287–302 (2003).
Ashton, T., Cantarella, J., Piatek, M. & Rawdon, E. J. Knot tightening by constrained gradient descent. Exp. Math. 20, 57–90 (2011).
Freedman, M. H. & He, Z.-X. Divergence-free fields: Energy and asymptotic crossing number. Annals of Mathematics 134, 189–229 (1991).
Weber, C., Stasiak, A., De Los Rios, P. & Dietler, G. Biophys J 90, 3100–3105 (2006).
Weber, C., De Los Rios, P., Dietler, G. & Stasiak, A. Simulations of electrophoretic collisions of DNA knots with gel obstacles. Journal of Physics: Condensed Matter 18(14), S161 (2006).
Arteca, G. A. Overcrossing spectra of protein backbones: characterization of three-dimensional molecular shape and global structural homologies. Biopolymers 33, 1829–1841 (1993).
Arteca, G. A. & Tapia, O. Characterization of fold diversity among proteins with the same number of amino acid residues. J Chem Inf Comput Sci 39, 642–649 (1999).
Diao, Y., Dobay, A., Kusner, R. B., Millett, K. & Stasiak, A. The average crossing number of equilateral random polygons. Journal of Physics A: Mathematical and General 36, 11561 (2003).
Arsuaga, J., Borgo, B., Diao, Y. & Scharein, R. The growth of the mean average crossing number of equilateral polygons in confinement. J. Phys. A-Math. Theor. 42, 9 (2009).
Gonzalez, O., Graf, A. B. A. & Maddocks, J. H. Dynamics of a rigid body in a Stokes fluid. J. Fluid Mech. 519, 133–160 (2004).
Mathias Carlen. Analysis and Simulation of Stokes Flow of Knotted Filaments. Master thesis, EPFL (2010).
Acknowledgements
We are grateful to J. Dubochet, O. Gonzalez and J. Maddocks for useful discussions throughout this project. EJR was supported by National Science Foundation grant number 1115722. AS was supported by SNSF grant number 31003A 138367.
Author information
Authors and Affiliations
Contributions
G.D., A.S. and C.W. conceived and designed the experiment, C.W. and M.C. carried out the experiment, E.J.R. provided coordinates of ideal knots, C.W., A.S. and G.D. analysed the data, C.W., A.S., G.D. and E.J.R. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Video - Knot 5.2 first axis
Supplementary Information
Video - Knot 5.2 second axis
Supplementary Information
Video - Knot 4.1
Supplementary Information
Video - Knot 8.18
Supplementary Information
Video - 3.1 right and left handed
Supplementary Information
Video - Achiral composite 3.1 knot
Supplementary Information
Video - Chiral composite 3.1 knot
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Weber, C., Carlen, M., Dietler, G. et al. Sedimentation of macroscopic rigid knots and its relation to gel electrophoretic mobility of DNA knots. Sci Rep 3, 1091 (2013). https://doi.org/10.1038/srep01091
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01091
This article is cited by
-
Knot Energy, Complexity, and Mobility of Knotted Polymers
Scientific Reports (2017)
-
Conservation of writhe helicity under anti-parallel reconnection
Scientific Reports (2015)
-
Subknots in ideal knots, random knots and knotted proteins
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.