Abstract
The birth and decline of disciplines are critical to science and society. How do scientific disciplines emerge? No quantitative model to date allows us to validate competing theories on the different roles of endogenous processes, such as social collaborations and exogenous events, such as scientific discoveries. Here we propose an agent-based model in which the evolution of disciplines is guided mainly by social interactions among agents representing scientists. Disciplines emerge from splitting and merging of social communities in a collaboration network. We find that this social model can account for a number of stylized facts about the relationships between disciplines, scholars and publications. These results provide strong quantitative support for the key role of social interactions in shaping the dynamics of science. While several “science of science” theories exist, this is the first account for the emergence of disciplines that is validated on the basis of empirical data.
Similar content being viewed by others
Introduction
Understanding the dynamics of science as a human endeavor — the birth, evolution and decline of disciplines — is of critical importance for allocating resources and planning toward positive societal impact. For example, the emergence of new fields such as bioinformatics, nanophysics, quantum computing and data science promises “converging technologies” with unparalleled potential to influence our lives. Efforts to describe, explain and predict different aspects of science have intensified in recent years1,2,3 spanning a wide range of theoretical, mathematical, statistical and computational approaches. This paper is about modeling the dynamic evolution of scientific disciplines.
Definitions of scientific discipline encompass complex mixtures of bodies of knowledge, norms, methods and organizations. Correspondingly, these shared elements emerge from the collaborations among groups of scholars in a discipline. What drives the birth of these communities? Quantitative work on modeling the emergence of disciplines is lacking to date, owing in part to the difficulty of formally defining the notion of scientific field and the consequent sparsity of data to inform and validate models. Many theories have been inspired by Kuhn's seminal notion of paradigm shifts triggered by unexplained observations4. Some models of science dynamics have attributed the evolution of fields to branching, caused by growth and new discoveries5,6 or specialization and fragmentation7. Examples of this kind of branching include nanophysics and molecular biology. Other models focus on the synthesis of elements of preexisting disciplines8, as in bioinformatics and quantum computing. All of these models point to the self-organizing development of science exhibiting growth and emergent behavior9,10,11.
No matter the cause or specific dynamics leading to the birth of a new discipline, such an event is reflected in the social community of scholars12. New journals emerge, new collaborations are established and new departments are created. Some theories emphasize the formation of social groups of scientists as the driving force behind the evolution of disciplines13,14,15.
Here we offer a first quantitative model to describe the various dynamics of discipline evolution independently of their underlying causes. We assume a purely social dynamics of science, without explicit references to exogenous events such as scientific discoveries, technological advances and availability of new data or methods. In our model, agents represent scholars who choose their collaborators, while groups of collaborating scholars represent scientific disciplines16. The key idea behind our model is that new scientific fields emerge from splitting and merging of these social communities. Splitting can account for branching mechanisms such as specialization and fragmentation, while merging can capture the synthesis of new fields from old ones. The birth and evolution of disciplines is thus guided mainly by the social interactions among scientists.
The proposed approach falls within the class of agent-based models17. While agent-based models have been used to study science dynamics18,19,20, the focus was primarily on coauthorship, publication and citation behavior rather than the emergence of disciplines. A key advantage of agent-based models is the capability to generate macroscopic predictions from micro-level mechanisms guiding the behavior of individuals, thus providing testable hypotheses about the emergence of disciplines. The social model of science proposed here will be validated against independent empirical datasets about the relationships between disciplines, scholars and publications.
Results
The critical assumption of our model is the correspondence between the social dynamics of scholar communities and the evolution of scientific disciplines. To illustrate this intuition, let us look at the coauthorship network for papers published by the American Physical Society (APS). Using journals as proxies for scholarly communities, we can track the changes in community structure over time. Fig. 1 plots the modularity21 of the partition induced by the journals; higher values indicate a more clustered structure (see Methods). To gauge the significance of the network modularity, we construct a null model by shuffling the edges of the co-authorship network in such a way that the degree sequence of the network is preserved.
Modularity Q of APS journal-induced scholar communities (solid blue line).
For each year t, we build a collaboration network based on the papers published in the 5-year time interval between t − 2 and t + 2. Such a network snapshot consists only of active scholars, who published at least one paper in that time window. If a scholar published papers in more than one journal, we select the first journal in that period. The grey areas correspond to the introduction of major new journals. The dashed red line plots the modularity obtained from a shuffled version of the collaboration network that preserves the degree of every node.
We observe noticeable changes in modularity around the introduction of new journals. Some of these changes suggest a scenario in which a new field emerges (e.g., quantum mechanics in the late 1920's) and a new journal captures the corresponding scholar community, leading to an increase in modularity. Interdisciplinary interactions across established areas lead to a decrease in modularity (e.g., prior to the introduction of Physical Review E in the 1990's). Note that the modularity baseline of the shuffled network is significantly lower and does not display clear spikes in proximity of the introduction of new journals. This suggests that the birth of new scholar communities reflects the introduction of new journals and cannot be explained solely by the increased number of nodes and edges. An alternative, suggestive visualization of the emergence of topics can be obtained by tracking communities over time in the citation network22. These observations motivate the use of community detection algorithms in a model of discipline evolution.
Model description
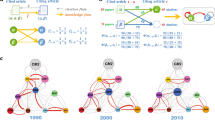
In the proposed model, which we call SDS (Social Dynamics of Science), we build a social network of collaborations whose nodes represent scholars, linked by coauthored papers as illustrated in Fig. 2(a). Each scholar is represented by a list of disciplines indicating the scientific fields they have been working on and every discipline has a list of papers. Similarly, each link is represented by a list of disciplines with associated papers describing the collaborations between two scholars. The social network starts with one scholar writing one paper in one discipline. The network then evolves as new scholars join, new papers are written and new disciplines emerge over time.
(a) Illustration of the social network structure. Nodes and edges represent scholars and their collaborations. They are annotated with lists of (co)authored papers grouped by scientific fields. For example, scholar b has five papers including four in computer science (CS) and one in Math. Papers 1 and 2 are coauthored with a, papers 5 and 6 with c and paper 5 with d. Paper 4 is authored by b alone. (b) Illustration of the random walk mechanism to select authors. For the new paper 7, the first author a is chosen randomly and then walks to b and c, stopping at d. These four authors become connected to each other if they have not collaborated before; for example, new edges connect a to c and d. Paper 7 acquires topics CS, Math and Physics (Phy). The main (majority) field of the paper, CS, diffuses across the collaborators, including d who joins this discipline as a result.
At every time step, a new paper is added to the network. Its first author is chosen uniformly at random, so that every scholar has the same chance to publish a paper. In modeling the choice of collaborators, we aim to capture a few basic intuitions: (i) scholars who have collaborated before are likely to do so again; (ii) scholars with common collaborators are likely to collaborate with each other; (iii) it is easier to choose collaborators with similar than dissimilar background; and (iv) scholars with many collaborations have higher probability to gain additional ones23,24. We model these behaviors through a biased random walk25, illustrated in Fig. 2(b). The random walk traverses the collaboration network starting at the node corresponding to the first author. At each step, the walker decides to stop at the current node i with probability pw, or to move to an adjacent node with probability 1 – pw. In the latter case a neighbor j is selected according to the transition probability  where wij is the weight of the edge connecting scholars i and j, that is, the number of papers that i and j have coauthored. Each visited node becomes an additional collaborator. Note that the walk may result in a single author.
where wij is the weight of the edge connecting scholars i and j, that is, the number of papers that i and j have coauthored. Each visited node becomes an additional collaborator. Note that the walk may result in a single author.
Each paper is characterized by one main topic and possibly additional, secondary topics. The discipline that is shared by the majority of authors is selected as the main topic of the paper. Each coauthor acquires membership in this main topic, to model exposure of scholars to new disciplines through collaboration. Additionally, a paper with authors from multiple disciplines inherits the union of these disciplines as topics. This choice is motivated by a desire to capture highly multidisciplinary efforts that are likely to lead to the emergence of new fields. This mechanism could be modified to reflect a more conservative notion of discipline by adopting a stricter rule for discipline inheritance.
At every time step, with probability pn, we also add a new scholar to the network. The parameter pn regulates the ratio of papers to scholars. The new scholar is the first author of the paper created at that time step. To generate other collaborators, an existing scholar is first selected uniformly at random as the first coauthor. Then the random walk procedure is followed to pick additional collaborators. The new scholar acquires the main topic of the paper.
We introduce a novel mechanism to model the evolution of disciplines by splitting and merging communities in the social collaboration network. The idea, motivated by the earlier observations from the APS data, is that the birth or decline of a discipline should correspond to an increase in the modularity of the network. Two such events may occur at each time step with probability pd. The process is illustrated in Fig. 3.
Discipline evolution.
(a) The collaboration network of discipline D1 is split into two disciplines D2 and D3. The modularity increases from Q = 0 to Q = 0.4. The dashed line indicates the partition of the network suggested by the community detection algorithm. Some nodes in the new discipline D3 have also published papers with scholars in D2 and therefore belong to both disciplines. (b) Two collaboration networks of disciplines D4 and D5 are merged into new discipline D6. For scholars in both original disciplines, we pick one based on the number of papers published in each discipline. The dashed line shows the resulting partition, with very low modularity Q = −0.1. The merged community D6 has still low, but higher mudularity Q = 0.
For a split event we select a random discipline with its collaborator network and decide whether a new discipline should emerge from a subset of this community. We partition the collaboration network into two clusters (see Methods). If the modularity of the partition is higher than that of the single discipline, there are more collaborations within each cluster than across the two. We then split the smaller community as a new discipline. For papers labeled with the discipline corresponding to the smaller community in the split, this discipline label may be updated; all other labels remain unchanged. In particular, the papers whose authors are all in the new community are relabeled to reflect the emergent discipline. Borderline papers with authors in both old and new disciplines are labeled according to the discipline of the majority of authors. Some authors may as a result belong to both old and new discipline.
For a merge event we randomly select two disciplines with at least one common author. If the modularity obtained by merging the two groups is higher than that of the partitioned groups, the collaborations across the two communities are stronger than those within each one. The two are then merged into a single new discipline. In this case, all the papers in the two old disciplines are relabeled to replace the old discipline with the new one; other labels of those papers remains unchanged.
Empirical validation
To evaluate the predictive power of the SDS model we consider a number of stylized facts, i.e., broad empirical observations that describe essential characteristics of the dynamic relationships between disciplines, scholars and publications. Our model provides an explanation for the evolution of scientific fields if it can reproduce these empirical observations. The complex interactions of a changing group of scientists, their artifacts and their disciplinary aggregations can be captured by the broad empirical distributions of six quantitative descriptors: the number of authors per paper AP (collaboration size); the number of papers per scholar PA (scholar productivity); the number of scholars per discipline AD (discipline popularity); the number of disciplines per scholar DA (scholar interdisciplinary effort); the number of papers per discipline PD (discipline productivity); and the number of disciplines per paper DP (publication breadth).
To validate the SDS model, one would ideally require a single real-world dataset mapping the three-way relationships between scholars, publications and disciplines. Unfortunately, no such dataset is available to date. One possibility would be to use a dataset such as those derived from Web of Science or Scopus and attempt to infer associations between subjects, papers and authors based on the subject categories of the journals in which the papers are published. However, such an inference approach is necessarily arbitrary. A less biased validation approach is to trade off the single dataset in exchange for multiple ones that capture the desired associations explicitly. We therefore adopt three large datasets that each map a binary projection of the three-way relationships: NanoBank26 to validate the relationship between scholars and papers, Scholarometer27 to study the relationship between scholars and disciplines and Bibsonomy28 to analyze the relationship between papers and disciplinary topics. The datasets are described in the Methods section. The parameters pn, pw and pd of our model are tuned to fit the quantitative descriptors of each dataset (see Methods).
Fig. 4 presents a compelling fit between the real data and the predictions of our model. SDS reproduces the stylized facts about the relationships between scholars, publications and disciplines, characterized by these six distributions.
Stylized facts characterizing relationships between scholars, papers and disciplines.
We plot the distributions of (a) authors per paper, (b) papers per scholar, (c) scholars per discipline, (d) disciplines per scholar, (e) papers per discipline and (f) disciplines per paper. Circles represent the SDS predictions, while other symbols represent the empirical data from the three datasets. The results of the model are averaged over 10 runs.
These results focus on the relationships between disciplines, scholars and papers, for which there is little prior quantitative analysis. The collaboration network, on the other hand, has been studied extensively in the past29,30. As shown in Fig. 5, the SDS model generates collaboration networks whose long-tailed degree distributions are consistent with the empirical data, as well as with those in the literature.
Degree distribution of the collaboration network generated by the SDS model, compared to the empirical distribution from the Bibsonomy dataset.
A few papers with more than 100 authors were excluded as they generate an anomaly in the tail; each such paper generates at least 100 nodes with degree at least 100. A similar match is also observed for other datasets.
Discussion
The match between the predictions of our model and the empirical distributions describing the relationships between scholars, publications and disciplines (Fig. 4) deserves further discussion. The exponential distribution of AP is captured by the random walk process. The broad distribution of scholar productivity PA is well accounted for by the bias in the random walk, which incorporates a kind of preferential attachment mechanism regulated by prior collaborations. The distributions of discipline popularity AD and productivity PD also display heavy tails, which cannot be attributed to a specific mechanism in the model; they emerge from the non-trivial interactions between (i) merging and splitting of the discipline communities and (ii) knowledge diffusion from the collaborations. The distribution of publication DP shows that there is a continuum in the breadth of papers, rather than a sharp separation between disciplinary and interdisciplinary work.
The prediction is not as good for DA: our model produces a relatively large number of highly interdisciplinary scholars. One could correct this effect, for example, by requiring more than one paper in a discipline as a condition for membership. However, this would require an additional parameter and thus a more complicated model.
Another possible modification of the model would be to alter the random walk process with occasional jumps, allowing scholars to go beyond their close collaborators with a finite probability. Such a mechanism could facilitate interdisciplinary papers by creating shortcuts across different fields. While we leave this extension for future work, we do not expect significant changes in the results as far as the jumps are not too common, given the small diameter of the co-authorship network. For high jump probability, the weaker locality would lead to a more random and therefore inherently less clustered network. By definition one would still find and possibly split communities, but the resulting clusters would be much less meaningful.
In summary, we introduced an agent-based model to simulate the evolution of science as a process driven only by social dynamics. Our model captures for the first time major stylized facts about the complex socio-cognitive interactions of a changing group of scholars, publications and scientific communities. The model is relatively simple when one considers the complexity of the science dynamics process being studied, yet powerful in its capability to reproduce the emergence of patterns similar to those observed in three real datasets about scientific production and fields.
The SDS model provides us with strong quantitative support for the key role of social dynamics in shaping the birth, evolution and decline of scientific disciplines. Future “science of science” studies will have to gauge the role of scientific discoveries, technological advances and other exogenous events in the emergence of new disciplines against this purely social baseline.
Methods
Modularity
Modularity21 measures the strength of a network partition into clusters of nodes. It compares the number of edges falling within groups with the expected number in an equivalent network from a null model with the same degree sequence but shuffled edges. Larger values indicate stronger community structure. For Fig. 1 we consider the weighted extension of modularity. Let wij be the weight of an edge (number of coauthored papers) between nodes i and j and Wij its expected value. The weighted modularity is defined as

where δ(gi, gj) = 1 if gi = gj (i and j are in the same group) and 0 otherwise; m is the sum of all edge weights in the network. Wij is computed as

where si is the strength or weighted degree of node i,  .
.
When splitting and merging disciplines in the model, we compare the merged and split partitions and select the option with higher modularity. Although the modularity measure does not allow to detect very small communities31, the advantages of this simple and intuitive approach outweigh those of more sophisticated algorithms. In practice, we use the leading eigenvector method32 based on the (non-weighted) modularity matrix, as an efficient and effective algorithm to split a collaboration network into two groups.
Datasets
The APS dataset (Fig. 1) was made available by the American Physical Society (publish.aps.org/datasets/). We consider the papers appearing in eight journals during the period of 1913–2000: Physical Review (PR) 1913–1955, Review of Modern Physics (RMP) 1929–2000, Physical Review Letters (PRL) 1958–2000, Physical Review A, B, C, D (PRA-D) 1970–2000 and Physical Review E (PRE) 1993–2000.
The SDS model is validated against three datasets:
NanoBank (version Beta 1, released on May 2007)26,33 is a digital library of bibliographic data on articles, patents and grants related to nanotech-nology. Articles in NanoBank were selected from the Science Citation Index Expanded, Social Sciences Citation Index and Arts and Humanities Citation Index produced by the Institute for Scientific Information (ISI, now Thomson Reuters). Unlike most disciplinary datasets that are selected by subject categories of journals and are therefore rather narrow in their focus, NanoBank was constructed by selecting articles containing a large number of terms. This resulted in a database that is very multidisciplinary in nature34, containing articles belonging to 226 out of 245 ISI JCR subject categories, from humanities and social science to core nano subjects such as the applied physics and material science. In that respect the database has enough variety to cover a wide range of authoring practices, from mostly single-authored papers in humanities and mathematics to extremely large teams in biosciences and physics, including high-energy physics. We used this dataset to validate the relationship between authors and papers.
Scholarometer (scholarometer.indiana.edu) is a social tool for scholarly services developed at Indiana University, with the goal of exploring the crowdsourcing approach for disciplinary annotations and cross-disciplinary impact metrics35,27. Users provide discipline annotations (tags) for queried authors, which in turn are used to compare scholar impact across disciplinary boundaries. The annotations of an author must include at least one discipline from a predefined list (ISI JCR subject categories) and may include any additional free-style tags. This accomplishes a tradeoff between quality and flexibility of disciplinary annotations. The data collected by Scholarometer is available via an open API. We use this data to study the relationship between scholars and disciplines.
Bibsonomy (www.bibsonomy.org) is a system for sharing bookmarks and literature lists28. Users freely annotate papers with tags, resulting in a folksonomy, or emergent ontology. To deal with the noise inherent in these annotations, we removed the tags associated with fewer than 3 papers or more than 6,000 papers, amounting to 4% of the tags and 2.5% of the annotations. These thresholds were selected manually to maximize the signal to noise ratio. The data is publicly available for research purposes. We analyze the relationship between papers and disciplines from a dataset including data until 2012-01-01.
Model calibration
The SDS model has three parameters. The value of pn is set to the empirical ratio of scholars to papers. The value of pw is set by matching the expected length of the random walk to the empirical average number of authors per paper; in doing so we assume that the random walk does not visit the same node twice. Finally, pd is the frequency of network split and merge events. Since our different datasets rely on different notions of disciplines, we explore a range of values for pd and select the one yielding the best match to the empirical number of disciplines for each dataset. Note that, even if we used a fixed ontology of disciplines, such as APS PACS or PubMed MeSH, one could select different granularity levels yielding different numbers of disciplines; each level of granularity would require a different value of pd.
Table 1 reports the main properties of the three empirical datasets and the model parameters used to generate predictions from numerical simulations of the model. For each dataset we run the simulations until the empirical number of papers or scholars is reached (shown in bold). As shown in Table 2, the SDS model is capable of approximating the basic statistics of the empirical data.
References
Börner, K. & Scharnhorst, A. Visual conceptualizations and models of science. J. Informetrics 3, 161–172 (2009).
Börner, K., Glänzel, W., Scharnhorst, A. & den Besselaar, P. V. Modeling science: studying the structure and dynamics of science. Scientometrics 89, 347–348 (2011).
Scharnhorst, A., Borner, K. & Besselaar, P. Models of Science Dynamics: Encounters Between Complexity Theory and Information Sciences (Springer Verlag, 2012).
Kuhn, T. S. The structure of scientific revolutions (University of Chicago Press, 1996).
Price, D. Little science, big science (Columbia University Press, 1986).
Mulkay, M. Three models of scientific development. The Sociological Review 23, 509–526 (1975).
Dogan, M. & Pahre, R. Creative marginality: Innovation at the intersections of social sciences (Westview Press, 1990).
Etzkowitz, H. & Leydesdorff, L. The dynamics of innovation: from national systems and “Mode 2” to a Triple Helix of university-industry-government relations. Research Policy 29, 109–123 (2000).
Noyons, E. C. M. & van Raan, A. F. J. Monitoring scientific developments from a dynamic perspective: Self-organized structuring to map neural network research. Journal of the American Society for Information Science 49, 68–81 (1998).
van Raan, A. F. J. Fractal dimension of co-citations. Nature 347, 626 (1990).
van Raan, A. F. J. On growth, ageing and fractal differentiation of science. Scientometrics 47, 347–362 (2000).
Bettencourt, L. M., Kaiser, D. I. & Kaur, J. Scientific discovery and topological transitions in collaboration networks. Journal of Informetrics 3, 210–221 (2009).
Crane, D. Invisible colleges: Diffusion of knowledge in scientific communities (University of Chicago Press, 1972).
Guimera, R., Uzzi, B., Spiro, J. & Amaral, L. Team assembly mechanisms determine collaboration network structure and team performance. Science 308, 697–702 (2005).
Wagner, C. The new invisible college: Science for development (Brookings Institution Press, 2008).
Palla, G., Barabasi, A. & Vicsek, T. Quantifying social group evolution. Nature 446, 664–667 (2007).
Payette, N. Agent-based models of science. Models of Science Dynamics 127–157 (2012).
Gilbert, N. A simulation of the structure of academic science. Sociological Research Online 2 (1997).
Börner, K., Maru, J. & Goldstone, R. The simultaneous evolution of author and paper networks. Proc. Nat. Acad. Sci. USA 101, 5266–5273 (2004).
Watts, C. & Gilbert, N. Does cumulative advantage affect collective learning in science? An agent-based simulation. Scientometrics 89, 437–463 (2011).
Newman, M. E. J. Modularity and community structure in networks. Proc. Nat. Acad. Sci. USA 103, 8577–8582 (2006).
Lancichinetti, A. & Fortunato, S. Consensus clustering in complex networks. Scientific Reports 2, 336 (2012).
Merton, R. The Matthew effect in science. Science 159, 56–63 (1968).
Barabási, A. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Lovász, L. Random walks on graphs: A survey. Combinatorics, Paul Erdos is Eighty 2, 1–46 (1993).
Zucker, L. G. & Darby, M. R. Nanobank data description, release 1.0 (betatest). UCLA Center for International Science, Technology and Cultural Policy and Nanobank (2007).
Kaur, J. et al. Scholarometer: A Social Framework for Analyzing Impact across Disciplines. PLoS ONE 7, e43235 (2012).
Benz, D. et al. The social bookmark and publication management system bibsonomy. The VLDB Journal 19, 849–875 (2010).
Newman, M. E. J. The structure of scientific collaboration networks. Proc. Nat. Acad. Sci. USA 98, 404–409 (2001).
Newman, M. E. J. Coauthorship networks and patterns of scientific collaboration. Proc. Nat. Acad. Sci. USA 101, 5200–5205 (2004).
Fortunato, S. & Barthelemy, M. Resolution limit in community detection. Proc. Nat. Acad. Sci. USA 104, 36–41 (2007).
Newman, M. E. J. Finding community structure in networks using the eigenvectors of matrices. Physical Review E 74, 036104 (2006).
Zucker, L., Darby, M., Furner, J., Liu, R. & Ma, H. Minerva unbound: Knowledge stocks, knowledge flows and new knowledge production. Research Policy 36, 850–863 (2007).
Milojević, S. Multidisciplinary cognitive content of nanoscience and nanotechnology. Journal of Nanoparticle Research 14, 1–28 (2012).
Hoang, D. T., Kaur, J. & Menczer, F. Crowdsourcing scholarly data. In Proc. Web Science Conference: Extending the Frontiers of Society On-Line (WebSci) (2010).
Acknowledgements
The work presented in this paper was performed while Xiaoling Sun was visiting the Center for Complex Networks and Systems Research (cnets.indiana.edu) at the Indiana University School of Informatics and Computing. Thanks to Diep Thi Hoang, Mohsen JafariAsbagh and Lino Possamai for Scholarometer system development and helpful discussions; to Emilio Ferrara and John McCurley for comments and editing assistance; and to two anonymous referees for their constructive suggestions. We acknowledge support from Hongfei Lin at Dalian University of Technology, the China Scholarship Council, the Lilly Endowment and NSF (award IIS-0811994) for funding the computing infrastructure that hosts the Scholarometer service.
Author information
Authors and Affiliations
Contributions
All authors contributed to empirical analysis, model design and evaluation and manuscript preparation. XS implemented the model and produced the figures.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Sun, X., Kaur, J., Milojević, S. et al. Social Dynamics of Science. Sci Rep 3, 1069 (2013). https://doi.org/10.1038/srep01069
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01069
This article is cited by
-
Collaboration and topic switches in science
Scientific Reports (2024)
-
Network patterns of university-industry collaboration: A case study of the chemical sciences in Australia
Scientometrics (2023)
-
Evolution and structure of research fields driven by crises and environmental threats: the COVID-19 research
Scientometrics (2021)
-
On knowledge-transfer characterization in dynamic attributed networks
Social Network Analysis and Mining (2020)
-
The evolution of scientific disciplines in applied sciences: dynamics and empirical properties of experimental physics
Scientometrics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.