Abstract
Colloidal particles with strongly attractive interactions snap on contact and form permanent, but disordered aggregates. In contrast, AC electric fields allow directional assembly of chains or crystals from repulsive particles by dielectrophoresis (DEP), but these structures fall apart once the field is switched off. We demonstrate how well-organized, permanent clusters and chains of micron-sized particles can be assembled by applying DEP to mixtures of oppositely charged microspheres. We found that the length of the formed chains depends on size ratio as well as the number ratio of the two species and formulated a statistical model for this assembly mechanism, which is in excellent agreement with the experimental results. The assembly rules resulting from this study form a basis for tailoring new classes of permanent supracolloidal clusters and gels.
Similar content being viewed by others
Introduction
Colloidal assembly is a major route to fabricate materials with tailored functionality resulting from the organization of the particles1,2,3. While colloidal crystals with their promising applications in photonics4 have occupied much of the focus of interest, linear assemblies are somewhat overlooked, in spite of a broad range of potential applications. For example, linear arrays of colloidal particles could find applications in structures for single-nanowire light emitting diodes5, single-electron transistors6, flexible artificial flagellum7 and in microfuidics8. Linear chains of nanoparticles dispersed in liquid media can cause interesting viscosity anomalies9. One rapid and controllable way of making linear and multidimensional structures is the “directed” colloidal assembly, which can be achieved by internal fields (induced by surfactants10 and by dynamic self-assembly11) or by applying an external field (e.g., magnetic12, or electric13, or light14). AC-field driven DEP induces a long-range dipolar interaction between randomly distributed particles13,14,15,16, which forces them to align into long chains along the direction of the applied field17. This effect has been used for one-dimensional18 and two-dimensional19 assembly, as well as for particle (or cell) capturing20. However, DEP-induced structures formed from a single type of particles disassemble as soon as the field is switched off, due to the repulsive electrostatic interactions that keep the particles in a stable suspension.
Here we report how micron and submicron-sized positive and negative particles can be co-assembled rapidly into permanent long-range organized chains by applying an AC electric field to the freshly-mixed dispersions. In contrast to biparticle assembly into crystalline arrays21,22, where the charge on the particles has to be tuned to low values to avoid irreversible aggregation, we use a binary mixture of highly charged particles, with attractive interaction energies well in excess of the thermal energy. These particles stick irreversibly when they come in contact. In the absence of the field, the heteroaggregation between positive and negative particles in water is driven by Brownian diffusion dynamics and leads to fractal-like disordered aggregate structures23,24. Electric fields have been used previously for assembling microwires from metal particles18,25. However, that mechanism is vastly different from the present chain assembly of dielectric particles. The rapid deployment of an external electric field enables us to align the dielectric particles in chains irrespective of their charge due to the long-range induced polarization interaction. Thus, by directing the heteroaggregation by means of DEP we can form linear structures of unprecedented length and order. The systems investigated include permanent chains of binary systems of particles of equal and unequal sizes. We propose an explanation for the pronounced effects of the size ratio and number ratio of the particles and on this basis formulate assembly rules for tailoring the length of the permanent biparticle chains.
Results
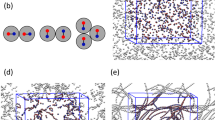
The schematic of the on-chip setup used for assembling microparticles in the presence of an electric field is shown in Fig. 1a. It consists of two coplanar gold electrodes 2 mm apart connected to a function generator and amplifier. The water-borne biparticle dispersion is placed in a microchamber (thickness 100 μm) over the electrodes. The assembly patterns of two pairs of latex microparticles of opposite surface charge were investigated by bright-field and fluorescence microscopy. The particle sizes, surface functional groups, fluorescence absorption and emission and zeta potential (at pH 3) of the two pairs are given in Table 1. The charge of the particles at given pH is dependent on the nature of their surface functional groups and the zeta potential is a proxy of the surface charge on the particles. The suspensions of positive and negative particles were mixed rapidly and immediately subjected to the unidirectional electric field for 1 min, leading to field-induced chaining.
Experimental setup and proposed steps of the biparticle chaining process.
(a) Schematic of the setup used in the DEP experiments; (b) Sketch of the two-step chaining process of equal-sized particles; (c) Sketch of the three-step process leading to permanent chaining of unequal-sized particles (in (b) and (c) green and red spheres represent the positively and negatively charged particles); (d) Bright-field and fluorescence images of composite structures formed between the 0.9 μm (positive) and 4 μm (negative) latex particles of System 2 (Table I) upon application of a 40 V/mm, 10 kHz electric field. Only the small (positive) particles are seen in the fluorescence micrograph. The chain assemblies shown in (d) correspond to structure C2 in (c).
The two different sequences of events leading to biparticle chaining of equal-sized and different-sized latex microspheres are sketched in Fig. 1b and 1c. The size ratio of the particles matters because the long-range drag experienced by them in the electric field is strongly dependent on their diameter D (FDEP ∝ D3)26. If the size of positive and negative particles is similar (Fig. 1b), all particles experience nearly the same DEP force and are dragged with equal probability into a given position in the chains. Accordingly, we expect a random sequence of positive (green) and negative (red) particles in the chains formed in the DEP field (structure B1). When the field is switched off, all contacts between equally charged neighbors will break due to the repulsive interaction and only short chains of alternating positive and negative particles will persist (permanent structures B2 in Fig. 1b).
In contrast, when the sizes of the positive and negative particles are significantly different, as in System 2, a much greater DEP force is exerted on the large particles than on the small ones during the field-induced chaining due to the large difference in particle volume. Accordingly, only the large particles (red) participate in the rapid primary chain formation (transient structure C1). In a slower secondary process, while the field is still on, the small particles (green) are drawn into the high-field-intensity regions between the pairs of the large particles by DEP attraction20, forming the structure C2. When the field is subsequently switched off, the small particles remain bound between the large particles of opposite charge and serve as links between the large particles. Accordingly, the chains will break only at those junctions where no small particle “binder” has been captured (permanent structures C3 in Fig. 1c). Composite chains of the kind sketched as C2 in Fig. 1c have been visualized experimentally by a combination between bright field and fluorescence microscopy as shown in Fig. 1d for the pair of 4 μm and 0.9 μm latex particles. Here the 0.9 μm particles appear green when observed in fluorescence mode of the microscope while the 4 μm particles were not fluorescent.
Equal-sized particles
Examples of permanent structures formed by co-assembly of similar-sized particles (System 1, Dsmall/Dlarge = 0.91) for equal numbers of positive and negative particles (NB = NA; number fraction x = NB/(NA + NB)) are shown in the fluorescence microscope images in Fig. 2a. Data for the chain length distribution are shown in Fig. 2 (b and c), where Xn represents the number of entities consisting of n particles, related to the total number of A and B particles (Fig. 2b) and Φn = nXn gives the fraction of A and B particles contained in aggregates of length n (Fig. 2c). The number of discrete chains formed including the monomers is always less than the total number of NA+NB particles, hence  . The experimental chain length distribution is compared with the distribution expected on the basis of the model sketched in Fig. 1b. The probability of finding a chain of n particles in alternating sequence of A and B depends on the number fractions x and 1 − x and is proportional to xm(1 − x)n−m, where m = (n±1)/2 (for n = 1,3,5 …) and m = n/2 (for n = 2, 4 …). For a stoichiometric composition of A and B particles (
. The experimental chain length distribution is compared with the distribution expected on the basis of the model sketched in Fig. 1b. The probability of finding a chain of n particles in alternating sequence of A and B depends on the number fractions x and 1 − x and is proportional to xm(1 − x)n−m, where m = (n±1)/2 (for n = 1,3,5 …) and m = n/2 (for n = 2, 4 …). For a stoichiometric composition of A and B particles ( ) this combinatorial mathematics approach yields normalized numbers of n-mer chains as (see Supporting Information),
) this combinatorial mathematics approach yields normalized numbers of n-mer chains as (see Supporting Information),

(for all n) and the respective fraction of particles in n-mer chains Φn = nXn. As can be seen in Fig. 2 (b and c) this chain breaking statistics is in agreement with the experimental results. The mean chain length for this stoichiometric composition from eq. 1 is  . Interestingly, these (relatively short) chains are the longest linear clusters that may assemble in a system of similarly sized heterocoagulating particles. Experiments with an excess of either A or B particles (
. Interestingly, these (relatively short) chains are the longest linear clusters that may assemble in a system of similarly sized heterocoagulating particles. Experiments with an excess of either A or B particles ( ) yield assemblies with even shorter chain lengths, in agreement with the model applied to non-stoichiometric mixtures (not shown).
) yield assemblies with even shorter chain lengths, in agreement with the model applied to non-stoichiometric mixtures (not shown).
Microscope images and chain length distribution of permanent structures for System 1 (Dsmall/Dlarge = 0.91).
(a) Fluorescence images of chains formed by application of DEP to a suspension containing equal numbers of 2.2 μm positive (green) and 2.0 μm negative (red) latex particles; insets show specific aggregates at higher magnification (structures equivalent to B2 in Fig. 1b). (b) Normalized numbers of n-mer aggregates, Xn, as a function of n. (c) The same results expressed by Φn, the fractions of particles existing in form of n-mers. In (b) and (c) the points represent the experimental data, the lines represent the statistical model (eq 1). In (b) the error bars are no larger than the symbol size.
Unequal-sized particles
The DEP co-assembly in System 2 (Dsmall/Dlarge = 0.225) was investigated for particle number ratios r = NB/NA ranging from 1 to 24. Results of the chain length analysis are presented in Fig. 3. For this system we define chain length n as the number of large (A type) particles in the aggregates and the respective number of chains, Nn, is normalized as Xn = Nn/NA. The microscope images for r = 1, 2.5, 12 and 24 (Fig. 3a–d) illustrate how longer chains of A-type particles are formed when the small particles (B) are present in excess. This is most pronounced for the highest number ratio (r = 24), for which a distribution including very long chains was found, some extending over the entire length of the microscope image. Closer inspection of the enlarged bright-field and fluorescence images reveals that several small particles may be captured in the gap between two large particles. As seen in Fig. 3, not all of the small particles are captured in the gaps and some B particles remain free, especially in samples with a high excess of such particles (insets in Fig. 3a–d). Broadly similar DEP entrapment of small particles between larger ones was reported by Gupta et al.27, where the capture of micron-sized latex particles in the junctions between 5 μm yeast cells has been observed and interpreted as field-gradient sequestration. This has allowed forming permanent linear structures through short-range binding of the Concanavalin-A conjugated to the particles to the polysaccharide functional groups on the yeast cell membranes. Our new data show that field-driven attraction of the small particles in the gaps between large ones is a universal phenomenon that can play a role even in irreversible strongly attractive systems with submicron particles.
Microscope images of permanent structures formed in System 2 (Dsmall/Dlarge = 0.225).
(a–d) Bright-field microscope images for r = 1, 2.5, 12 and 24, respectively. The insets show magnified images of chain structures in bright field and fluorescence mode (structures equivalent of C3 in Fig. 1c), indicating the location of the binding sites of small particles in the aggregates. The chain length increases with r. Chains longer than the length of the microscope field of imaging were obtained at r = 24.
The chain length distributions observed in System 2 can be interpreted on the basis of the mechanism sketched in Fig. 1c. The model assumes that each contact point in the chain of large particles (A) formed in the primary DEP chaining process can serve as a binding site for the positively charged small particles (B), which form a permanent bond between the two A particles. If S- S0 out of the S binding sites in the primary chain of A particles are occupied by B particles and S0 sites remain vacant, the primary chain will break up into S0+1 fragments when the field is switched off. The resulting permanent chain length distribution Xn can be expressed by the fraction of vacant sites in the primary chain, S0/S. To account for the observation that more than one B particle can be accommodated per binding site, we adopted a reaction-type model of sequential random binding events that relates the fractions of binding sites occupied by j-1 and j particles. This leads to a chain length distribution which depends solely on the number ratio of A and B particles (see Supporting Information),

When comparing the predicted distribution with the experimental findings one has to take into account that not all B particles are captured in the chains. Starting from the experimental chain-length distribution we used eq. 2 to determine an effective particle number ratio reff of A and B particles in the chains. By accounting for this effective particle number ratio, eq. 2 gives a good representation of the experimental chain length distribution Xn for particle number ratios up to r = 12, as shown in Fig. 4a. At higher number ratios the data analysis is unreliable because the resulting assemblies are in the form of few chains extending over the whole length of the microscope field (forming an effectively percolated structure). Fig. 4b illustrates the effect of increasing particle number ratio r on the fraction of A particles contained in chains of n segments, Φn = nXn. For equal numbers of A and B particles (r = 1) and for moderate excess of B (r = 2.5) we find that reff is close to or even somewhat larger than the experimental r. For a larger excess of B, however, reff becomes significantly smaller than r, indicating that a decreasing fraction of B particles is incorporated in the chains (less than 50% for r = 24). The increase of the mean chain length  with the effective particle number ratio is shown in Fig. 4c. The variation of effective particle ratio (reff) with r shows a similar trend to the one of
with the effective particle number ratio is shown in Fig. 4c. The variation of effective particle ratio (reff) with r shows a similar trend to the one of  . Interestingly, we find a linear increase of
. Interestingly, we find a linear increase of  with reff (Fig. 4d).
with reff (Fig. 4d).
Chain-length distributions for System 2 (Dsmall/Dlarge = 0.225).
(a) Normalized numbers of linear aggregates containing n large particles, Xn, as a function of n for different particle number ratios r. The points represent the experimental data as derived from the bright-field images, the solid lines show fits by the proposed model; the values of r and reff given in the plots represent the experimental (overall) particle number ratio and the effective number ratio corresponding to the best fit of eq 2. (b) Fraction of A-type particles, Φn, that exists in form of n-mer chains. The values of r and corresponding reff are given in the plot. The figure illustrates the pronounced shift in the distribution to larger n values as the number ratio reff increases. (c) Mean chain lengths  plotted as the function of the experimental number ratio r. (d) Mean chain length as a function of the effective number ratio reff.
plotted as the function of the experimental number ratio r. (d) Mean chain length as a function of the effective number ratio reff.
Discussion
The above results show how models based on combinatorial mathematics and reaction kinetics can be employed to predict results of permanent supracolloidal assembly initiated by external fields. Two assembly rules emerge from the study: Permanent chains of significant length are obtained only if (1) the positive and negative particles have significantly different sizes and (2) the small particles are present in considerable excess. The importance of using particles of different sizes for forming long “particle polymers” is underscored by the fact that for equally sized particles, an excess of positive or negative particles leads not to an increase but a decrease of the mean chain length. In both cases, however, the large opposite charge of the two types of particles leads to the formation of permanent chains. In this respect our work differs from earlier studies of particle pattern formation in AC electric fields, such as the work on sterically stabilized binary suspensions of oppositely charged microparticles28 where the lanes formed upon application of the external field were temporary and disassembled on removing the electric field.
The present findings open up a new direction for studies in AC-field induced supracolloidal permanent assembly. They show an efficient and simple way of directed permanent assembly of supracolloidal structures of defined size and periodicity in a single step, rapid and controllable process. The statistical interpretation developed can provide guidance for the synthesis of linear clusters of controlled lengths, which can be tuned experimentally by adjusting the particle size and number ratios. Permanent chains of polymer particles with adjustable lengths suspended in liquid medium can find application in novel types of biparticle gels and chain fluids exhibiting unusual directional rheology response. Aligned linear clusters of well-defined morphology immobilized on surfaces may also be used as bio-scaffold matrices in tissue engineering. Liquid-borne, or permanently immobilized materials containing oriented chain clusters from inorganic or metal particles will exhibit anisotropy in heat and electrical conductance that may lead to potential uses in microdevice heat management and wiring.
Methods
The polystyrene particles were washed several times with deionized water in order to minimize the ionic strength of the dispersion and to remove any trace of surfactant. pH of the dispersions was adjusted to 3.0 using 0.01 M HCl. The biparticle dispersion was prepared by mixing pre-sonicated aliquots of the constituent single-particle dispersions in a vial; it was then rapidly transferred into the hydrophobically sealed chamber (< 10 s) and the electric field was employed instantaneously. The particle dispersion was subjected to a square wave AC electric field (40 V/mm, 10 kHz), using parallel electrodes. The assembly process was observed using an Olympus BX-61 microscope both in bright-field and fluorescence mode. Several images of the linear chain structures were taken for further analysis. The chain length of a linear aggregate was defined by counting the number of constituent particles of a given chain. The chain length distribution was determined by analyzing at least 5 microscope images for given values of Dsmall/Dlarge and r.
References
Velev, O. D. & Gupta, S. Materials fabrication by micro- and nanoparticle assembly – The challenging path from science to engineering. Adv. Mater. 21, 1897–1905 (2009).
Tang, Z. & Kotov, N. A. One-dimensional assemblies of nanoparticles: Preparation, properties and promise. Adv. Mater. 17, 951–962 (2005).
Li, F., Josephson, D. P. & Stein, A. Colloidal assembly: The road from particles to colloidal molecules and crystals. Angew. Chem. Int. Ed. 50, 360–388 (2011).
Yethiraj, A., Thijssen, J. H. J., Wouterse, A. & Blaaderen, A. v. Large-area electric-field-induced colloidal single crystals for photonic applications. Adv. Mater. 16, 596–600 (2004).
Gudiksen, M. S., Lauhon, L. J., Wang, J., Smith, D. C. & Lieber, C. M. Growth of nanowire superlattice structures for nanoscale photonics and electronics. Nature 415, 617–620 (2002).
Thelander, C. et al. Single-electron transistors in heterostructure nanowires. Appl. Phys. Lett. 83, 2052–2054 (2003).
Dreyfus et al. Microscopic artificial swimmers. Nature 437, 862–864 (2005).
Terray, A., Oakey, J. & Marr, D. W. M. Fabrication of linear colloidal structures for microfluidic applications. Appl. Phys. Lett. 81, 1555–1557 (2002).
Mackay et al. Nanoscale effects leading to non-Einstein-like decrease in viscosity. Nature Mater. 2, 762–766 (2003).
Sharma, K. P., Kumaraswamy, G., Ly, I. & Mondain-Monval, O. Self-assembly of silica particles in a nonionic hexagonal mesophase. J. Phys. Chem. B 113, 3423–3430 (2009).
Grzybowski, B. A., Stone, H. A. & Whitesides, G. M. Dynamic self-assembly of magnetized, millimeter-sized objects rotating at a liquid-air interface. Nature 405, 1033–1036 (2000).
Zerrouki, D., Baudry, J., Pine, D., Chaikin, P. & Bibette, J. Chiral colloidal clusters. Nature 455, 380–382 (2008).
Gangwal, S., Cayre, O. J. & Velev, O. D. Dielectrophoretic assembly of metallodielectric janus particles in AC electric fields. Langmuir 24, 13312–13320 (2008).
Piech, M., George, M. C., Bell, N. S. & Braun, P. V. Patterned colloidal assembly by grafted photochromic polymer layers. Langmuir 22, 1379–1382 (2006).
Jones, T. B. Electromechanics of Particles, Cambridge University Press, Cambridge 1995.
Techaumnat, B., Eua-arporn, B. & Takuma, T. Electric field and dielectrophoretic force on a dielectric particle in a chain parallel plate electrode system. J. Phys. D: Appl. Phys. 37, 3337–3346 (2004).
Velev, O. D. & Bhatt, K. H. On-chip micromanipulation and assembly of colloidal particles by electric fields. Soft Matter 2, 738–750 (2006).
Hermanson, K. D., Lumsdon, S. O., Williams, J. P., Kaler, E. W. & Velev, O. D. Dielectrophoretic assembly of electrically functional microwires from nanoparticle suspensions. Science 294, 1082–1086 (2001).
Lumsdon, S. O., Kaler, E. W. & Velev, O. D. Two-dimensional crystallization of microspheres by coplanar AC electric field. Langmuir, 20, 2108–2116 (2004).
Gupta, S., Alargova, R. G., Kilpatrick, P. K. & Velev, O. D. On-chip dielectrophoretic coassembly of live cells and particles into responsive biomaterials. Langmuir 26, 3441–3452 (2010).
Leunissen et al. Ionic colloidal crystals of oppositely charged particles. Nature 437, 235–240 (2005).
Vutukuri, H. R., Stiefelhagen, J., Vissers, T., Imhof, A. & Blaaderen, A. v. Bonding assembled colloids without loss of colloidal stability. Adv. Mater. 24, 412–416 (2012).
Bharti, B., Meissner, J. & Findenegg, G. H. Aggregation of silica nanoparticles directed by adsorption of lysozyme. Langmuir 27, 9823–9833 (2011).
Lin, W. et al. Heteroaggregation of binary mixtures of oppositely charged colloidal particles. Langmuir 22, 1038–1047 (2006).
Sapozhnikov, M. V., Aranson, I. S., Kwok, W.-K. & Tolmachev, Y. V. Self-assembly and vortices by microparticles in weak electrolytes. Phys. Rev. Lett. 93, 084502 (1–4) (2004).
Stoy, R. D. Interactive dipole model for two-sphere system. J. Electrostatics 33, 385–392 (1994).
Gupta, S., Alargova, R. G., Kilpatrick, P. K. & Velev, O. D. On-chip electric field driven assembly of biocomposites from live cells and functionalized particles. Soft Matter 4, 726–730 (2008).
Vissers, T., Blaaderen, A. v. & Imhof, A. Band formation in mixtures of oppositely charged colloids driven by an ac electric field. Phys. Rev. Lett. 106, 228303 (1–4) (2011).
Acknowledgements
We are grateful for the financial support of this study from US-NSF via the Triangle MRSEC on Programmable Soft Matter (DMR-1121107) and from the Deutsche Forschungsgemeinschaft (DFG) in the framework of IRTG-1524.
Author information
Authors and Affiliations
Contributions
B.B. performed all experiments and analyzed the data. O.D.V. conceived and designed the experiment and G.H.F. developed the statistical model. All authors participated in writing and reviewing the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Details of the proposed statastical models
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Bharti, B., Findenegg, G. & Velev, O. Co-Assembly of Oppositely Charged Particles into Linear Clusters and Chains of Controllable Length. Sci Rep 2, 1004 (2012). https://doi.org/10.1038/srep01004
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01004
This article is cited by
-
Formation of printable granular and colloidal chains through capillary effects and dielectrophoresis
Nature Communications (2017)
-
Nanocapillarity-mediated magnetic assembly of nanoparticles into ultraflexible filaments and reconfigurable networks
Nature Materials (2015)
-
Rapid identification of bacteria utilizing amplified dielectrophoretic force-assisted nanoparticle-induced surface-enhanced Raman spectroscopy
Nanoscale Research Letters (2014)
-
Self-assembled tunable networks of sticky colloidal particles
Nature Communications (2014)
-
Rapid (<5 min) Identification of Pathogen in Human Blood by Electrokinetic Concentration and Surface-Enhanced Raman Spectroscopy
Scientific Reports (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.