Abstract
Experiments show that simple diffusion of nutrients and waste molecules is not sufficient to explain the typical multilayered structure of solid tumours, where an outer rim of proliferating cells surrounds a layer of quiescent but viable cells and a central necrotic region. These experiments challenge models of tumour growth based exclusively on diffusion. Here we propose a model of tumour growth that incorporates the volume dynamics and the distribution of cells within the viable cell rim. The model is suggested by in silico experiments and is validated using in vitro data. The results correlate with in vivo data as well and the model can be used to support experimental and clinical oncology.
Similar content being viewed by others
Introduction
Early in their development, solid tumours form avascular nodules. In the absence of blood vessels, these nodules can grow to a size of a few millimetres and develop a central core of dead cells, surrounded first by a layer of viable but quiescent cells and then by proliferating cells. Any further growth depends on the ability of tumours to stimulate angiogenesis, i.e. the formation of new blood vessels that deliver oxygen and nutrients to tumour cells1. Even in vascularized tumours it is still possible to recognize layered structures, called tumour cords, around blood vessels, where active layers of cells wrap around the vessels, while deeper layers are mostly necrotic2,3. Similar structures can be observed and studied in vitro with 3-dimensional aggregates of tumour cells called multicell tumour spheroids (MTS)4,5, which are excellent experimental models. Most importantly, these multi-layered structures determine relevant biological properties of solid tumours such as growth kinetics and sensitivity to therapeutic treatments4,5.
Given their simple, nearly spherical geometry, MTS have long been a target of biophysical and biomathematical modelling, in the hope of turning such models into useful tools to understand tumours and their dynamics. The work of Araujo and McElwain6 is a comprehensive review, which also includes some more complex tumour models that try to capture the effects of vascularization. Many of these mathematical models are based on the seminal work of Greenspan7, who related the formation of the multi-layered structure in nodular carcinomas to the limited diffusion of nutrients such as oxygen and glucose and of waste molecules in the tumour tissue. As a result it has been generally accepted that the onset of central necrosis in MTS and tumour cords is due to molecular diffusion. Consequently, modellers have mostly turned their attention to other complex aspects of tumours such as cell migration and metastasis, biomechanics, vascularization, etc. However, experimental data collected with multicellular tumor spheroids over two decades or more by different research groups challenge the simple diffusive model (this evidence is reviewed in refs. 5,8). Experiments show that the formation of the central necrotic region in MTS is uncorrelated with hypoxia and indicate that cell death in the central region is due to a combination of several factors that have not yet been fully characterized5,8. Recently, Tindall et al.9,10 have constructed phenomenological mathematical models to explore the effects of known factors, such as cell cycling, possible different pathways to cell death and the accumulation dynamics of dead materials in the inner layers, which also hint that simple diffusion of nutrients and waste molecules alone cannot explain the structure of solid tumours, whether they are vascularized or not.
Here we describe a new analytical model of solid tumour growth, where growth depends on the distribution of live cells in the tumour mass. In turn, growth determines the distribution of live cells, so that there is a mutual influence between growth and live cell distribution. The model is suggested by experiments carried out in silico with a recently developed multi-scale computer model of MTS11,12 and is validated using data from in vitro experiments. The computer model is lattice-free – i.e., cells are free to move and are not constrained on a fixed grid as it happens in models where cells are represented by cellular automata – and is based on a detailed description of the complex molecular network that regulates metabolism, of the cell cycle and cell death at the single cell level and of cell-cell forces. The metabolic network implemented in the model of individual cells includes the dynamics of oxygen, glucose and related chemical species, amino acids, ATP and drives the synthesis of DNA and of some selected proteins, especially those that regulate the cell cycle (pRB and cyclins). The model of individual cells also includes dynamical checkpoints – controlled by cyclins – and discrete events like cell division and cell death. Cell death is determined by several factors, but the most important in this context is the high level of metabolites – represented globally by lactate in the computer model – that poisons and stifles cells by downmodulating facilitated diffusion processes in the cell membrane, even when oxygen and nutrients are available. Biomechanics also plays a role, as the mechanical rearrangement of spheroids produces flows of both dead and live cells. Eventually the live cell distribution is the product of all these interacting factors. In previous papers13,14,15 we showed that this computer model provides good quantitative estimates of biochemical and biological variables, so that it is reasonable to trust the simulation results and use the program to study features that are still unobserved in the laboratory.
Results
An aggregate of tumour cells grows because individual cells proliferate. At the very early stages of tumour growth, when no limiting factors act upon cells, the process of cell division displays a simple exponential dynamics. If N(t) is the cell number at time t and if vc is the mean cell volume, then the overall volume of the cell cluster is V (t) = vcN(t) and the early growth dynamics obeys the simple law:

where α = ln 2/T and T is the average duration of the cell cycle. However this exponential growth is soon kept in check by other processes and most notably by cell death and by the subsequent cell shrinking – a well documented process, see ref. 16 – and also by the mechanical rearrangement of cells, if the structure is initially very disordered. Since cells mostly die in the deeper tumour layers, shrinking affects mainly the bulk of a solid tumour rather than its surface.
If F is the fraction of live cells in the tumour cluster, so that the volume occupied by live cells is Va = F V, then dead cells and empty spaces correspond to the volume fraction 1 − F = (V − Va)/V, they do not absorb nutrients and keep shrinking. This means that the differential equation for the total MTS volume must include a term that takes into account dead cells and empty spaces as well:

where δ sets the timescale for the shrinking of dead cells. Using Va = F V we can find an equivalent equation for the dynamics of live cells

which shows that in this model the rates of proliferation and death are both time-dependent (see the supplementary text for a straightforward derivation of equation (2)). For a nearly spherical shape, the total MTS volume is a simple function of MTS radius r:V ≈ 4πr3/3 and from equation (1) we find the corresponding evolution equation for MTS radius

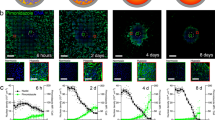
where F is a function of the MTS radius r, which is itself a function of time, so that F = F[r(t)]. The problem now lies in the determination of the fraction of live cells F = Va/V: it is less likely to find live cells deep inside a MTS or in a real solid tumour and there is no sharp boundary between layers, but the exact distribution of live cells as a function of the distance from the MTS surface, or from blood vessels in real tumours, is unknown. However, the simulation program11 tracks the fate of every single cell and we know at all times the number of live and dead cells in a simulation run and hence the live-cell fraction F. Since we have access to the full cell record as well, we can also observe the fractional density f(s) of live cells – i.e., the fraction of live cells per unit volume – as a function of the distance s from the surface of the cell cluster and we find that f(s) can be well approximated by an exponential function with decay length λ (see figures 1a–b):

Using the exponential fractional density (4) we find that the total volume taken by live cells in a spherical tumour cluster is

The resulting F(r) is well approximated by

(see the supplementary text for further details) and using the approximate live-cell fraction (6), the complete evolution equations are

for the cluster radius and

for the total cluster volume. The computer simulations also indicate that λ – and thus the distribution of live cells – depends weakly on cluster radius (see figure 1c):

The live fraction F(r) can be measured in actual experimental MTS and we find that expression (7) with the decay length (9) provides an excellent description of data in the literature, which have never been modelled before (see figure 2). Data in Freyer and Sutherland17 were taken with spheroids obtained from EMT6/Ro cells grown under standard oxygen and glucose concentrations (the original data are shown in the top panel of figure 3 in17). Each measurement is the mean of 20–25 spheroids of the same size. Data in Kunz-Schughart et al.18 were taken with single spheroids of a given size obtained from both Rat1-T1 and MR1 cells (the original data are shown in panel C of figure 2 in ref. 18). The viable cell rim thickness was measured by careful histologic analysis of serial sections. We have estimated the total fraction of live cells F(r) from these experimental data by calculating the ratio between the measured rim thickness of viable cells and spheroid diameter. These estimates are rather rough, however they provide interesting hints on model behaviour. Figure 2 shows the Bayesian regressions of expression (6) both with constant and with variable λ. According to the classification in table S2 – which reports standard criteria for model comparison – there is very weak evidence to prefer the variable-lambda model over the constant-lambda one. The Bayes factor of 6.63 corresponds to a “Not worth more than a bare mention” category of evidence support, although there is slightly stronger support for the model with variable-lambda.
a. Simulation data closely follow the exponential function (4). The plot shows f(s) for a simulated MTS, at about 28.5 days from the start of the numerical experiment with a single initial cell. In this numerical experiment the cell duplication time is about one day. The solid red line is a least-squares exponential regression, which in this case yields λ = 52.7 ± 1.0 μm. b. Simulation data for the same MTS at different times (roughly equally spaced, starting at 12.8 days of simulated time, when about 50% of the cells are still alive near the MTS center; different colors map different times, increasing from blue to dark red) with log vertical scale. In this representation true exponentials should display as straight lines: the straight line is drawn to guide the eye and corresponds to an exponential with λ = 80 μm. At large depth there is a marked deviation from the exponential behavior, but this is not important in determining the growth law, because the fraction of live cells is very low there and greater depths also mean spherical shells with smaller volume, which weigh less in the growth law. c. Estimated values of λ from the data in panel b. λ changes slowly as the MTS grows; the solid line is a fit with expression (9).
Total fraction of live cells F(r) estimated from actual experimental data in refs. 17 and 18.
Circles represent the aggregate measurements of individual MTS obtained with Rat1-T1, MR1 and EMT6/Ro cells. The solid black line is the estimate obtained from expression (6), assuming variable λ as defined by equation (9) – Maximum a posteriori (MAP) values are: λ0 = 48.96 ± 0.05 μm, λ1 = 77.48 ± 0.05 μm, ζ = 48.96 ± 0.05 μm – while the dashed line is the estimate obtained with constant λ (MAP value: λc = 54.64 ± 0.05 μm).
Bayesian analysis of experimental data.
Top panels: representative growth data (circles) of individual tumour MTS obtained with cell lines 9l, U118 and MCF7. The lines show the predictive posteriors computed by Bayesian inference with our model at the following percentile levels: 2.5% (orange), 25% (red), 50% (green), 75% (cyan), 97.5% (blue). Deviation of the data from these model predictions was identified as observation error. Bottom panels: box-plots of the Bayes factor that compares the new model with constant λ and the Gompertz model. The Bayes factors are calculated for n individual MTS and the box plots represent their distributions. The Bayes factors are always greater than 1 and always favor our model, sometimes strikingly so. The background colored bands show levels of evidence to prefer our model: red, weak evidence; orange, positive evidence; green, strong evidence; blue, very strong evidence (levels are chosen according to the suggestion of Kass and Raftery23, see the supplementary text). In this analysis we also obtain Maximum a posteriori (MAP) estimates of the model parameters; we find the following mean values from populations of MAP estimates with constant λ: λc = 15.3 ± 1.7 μm (9l); λc = 19.3 ± 1.9 μm (U118); λc = 16.2 ± 1.9 μm (MCF7).
What happens if the cell cluster is not spherical, as a tumour cord? In this case we can still write V = Ax3, where x is some characteristic length of the tumour, like a chord that joins two recognizable, fixed features on the tumour surface and where we assume that the tumour shape remains roughly the same as the tumour grows. Then, assuming the same kind of exponential fractional density f(s), the total volume occupied by the live cells is

which this leads to the same F function introduced above.
It is interesting to notice that the growth model (8) can be recast as a differential system. We rewrite first the defining equation (8) as

where γ(t) is the time-dependent total rate of change of the MTS volume

with the initial condition γ(0) = α. A straightforward but lengthy calculation (reported in the supplementary text) shows that

The differential system for V and γ can be compared with the similar differential system for the phenomenological Gompertz model19,20,21:


with γG(t) = αGe−βGt and αG = γG(0). The term in square brackets in equation (10) is actually quite close to a constant over a wide range of r/λ values, so that βG loosely corresponds to (α + δ) [(r(t)/3λ + 1) F(t)−1] and we see that the phenomenological Gompertz model – widely regarded as a sort of “golden standard” for the description of tumour volume growth20,21,22 – naturally arises as an approximation of the new model (8).
To assess the validity of the growth model and to frame more precisely its relationship with the time-tested Gompertz model, we turned to real data obtained in vitro with tumour MTS. As explained in the methods section, we collected data from spheroids obtained with three different cell lines: 9l, from a rat glioblastoma; U118, from a human glioblastoma; MCF7, from a human breast carcinoma. The analysis of experimental data was carried out with the Bayesian techniques described in the methods section and in the supplementary text and we estimated both the model parameters and the Bayes factors for model selection23. Here we consider the results obtained with these three cell lines and some of them are shown in figure 3. The full set of figures is in the supplementary text.
9l cell line
We considered the 32 individual spheroids of the 9l cell line as separate data sets. Consequently, we derived 32 independent posterior parameter distributions and computed the Bayes factor for comparing both variants of the new model to the classical Gompertz model separately, 32 times. This allowed us to analyze the stability of our conclusions in the light of evidence coming from independent biological replicates of the experiment.
Predictive posteriors for data coming from the 32 separate spheroids are depicted in Figure S5. Generally, model predictions are similar for both the Gompertz model and the two variants of the new model, with a somewhat “stronger nonlinearity” of the predictions drawn from the new model.
Parameter posteriors for all 32 spheroids are located quite compactly for the Gompertz model, see, for example, the posterior marginals for the first spheroid displayed in Figure S6. At the same time, the new model allows for a wider variation of the posteriors, as depicted in Figures S7 and S8 This is an expected result, as the new model is more complex than the traditional Gompertz model and as there are more parameters in this model, therefore there are more degrees of freedom. Natural identifiability problems with the new model are tackled properly in this case, by considering complete parameter posteriors instead of only the maximum likelihood estimate of model parameters.
The Bayesian framework handles uncertainty about particular parameter values properly by considering the parameter posteriors as multivariate distributions. Consider marginal distributions for parameters δ and λ in Figure S7. On their own, when the rest of the parameters are marginalized out, these parameters have wide and vague posteriors, that hardly diverge from the corresponding priors. However, when considered together, we observe large and significant a posteriori correlation between these parameters (correlation coefficient is 0.996 in this case). If the value of δ is selected, the appropriate value for λ follows almost deterministically. This is a property of the new model detected without any prior knowledge, purely on the basis of the experimental data, which shows the deep connection between the shape of the distribution of live cells and the dead-cell shrinking rate.
At the same time, the observation noise with variance σ2 considered in both models, was found to be almost independent a posteriori from other model parameters, with the largest correlation coefficient for Gompertz model of 0.07 (correlation of σ and αG) and the largest correlation coefficient for the new model of 0.059 (correlation of σ and α) and the largest correlation coefficient for the new model with variable λ of −0.024 (correlation of σ and δ).
Plots of the parameter posterior marginals, samples from multivariate parameter posteriors and correlation coefficients for other spheroids in our complete data set, as well as the code to replicate our data analysis, can be obtained from the authors on request. The results presented in the supplementary text are selected to represent a typical outcome of the inferential experiment. There were no spheroids in this data set that produce qualitatively different results.
We also performed evidential model comparison, to check which of the considered models is better supported by our experimental data and if the difference of evidence support is significant. We computed the Bayes factor to compare evidence support for the new model versus the evidence support for the Gompertz model as discussed in the supplementary text. The Bayes factor was computed 32 times, separately for every spheroid. We found that in every single case the new model was preferred to the traditional Gompertz model by the experimental evidence. The sample of 32 computed Bayes factors comparing Gompertz model to the new model with constant λ is depicted in Figure S9. The weakest Bayes factor in this sample – for spheroid 31, predictions depicted in the penultimate plot of Figure S5 – qualified the category of evidence support as ‘positive’ while for every other spheroid the preference for the new model was ‘very strong’.
There is much smaller evidence to prefer the new model with variable λ over the one with constant λ. Corresponding Bayes factors are depicted in Figure S10. Assuming equal a priori probabilities of our three alternative models, we can compute the a posteriori odds of each of the models to be the preferred one. Corresponding bar charts are depicted in Figure S11.
Bayesian analysis of this data set demonstrates that the new model of tumour growth not only gives biological interpretation to model parameters, but also provides better quality of predictions and is better supported by the experimental evidence.
U118 cell line
The inference results for the data obtained from U118 cell line are qualitatively similar to the results for the 9l cell line. Model parameters, of course, may have slightly different values to reflect the specific growth characteristics for the tumours of the U118 line. Predictive posteriors for 8 data sets, collected from separate spheroids of this type, are depicted in Figure S12.
Parameter posteriors obtained using the data from U118 spheroids demonstrate the same qualitative properties as the parameter posteriors for the 9l cell line discussed in the previous section. At the same time, the values of the parameters quantitatively shift a little to reflect differences in cell line phenotypes. See the marginals to the parameter posteriors computed from the first spheroid data in Figures S13, S14 and S15.
We computed the Bayes factor for preferring the new model with constant λ over the traditional Gompertz model. The Bayes factor was computed 8 times, separately for every spheroid. We found that in every single case the new model was very strongly preferred to the traditional Gompertz model by the experimental evidence. In every case, the scale of the Bayes factor suggested extremely strong evidential support for the new model in comparison to the Gompertz model. The sample of 8 computed Bayes factors is depicted in Figure S16. At the same time, the Bayes factor for preferring the new model with variable λ over the new model with constant λ, while showing some preference for variable λ, has a much lower scale of the evidence, see Figure S17. Assuming equal a priori probabilities of our three alternative models, we can compute the a posteriori odds of each of the models to be the preferred one. Corresponding bar charts are depicted in Figure S18.
Again, Bayesian analysis of data obtained from the U118 cell line demonstrates better predictive power of the new model. Evidence in our experimental data very strongly supports preference of the new model over the traditional Gompertz model.
MCF7 cell line
The inference results for the data obtained from MCF7 cell line are qualitatively similar to the results for the 9l and U118 cell lines. Model parameters may have slightly different values to reflect the specific growth characteristics for the tumours of the MCF7 line. Predictive posteriors for 5 data sets, collected from separate spheroids of this type, are depicted in Figure S19.
Predictive posteriors in Figure S19 display prominently the capability of the new model to demonstrate more flexible dynamic behaviour. Left hand side plots, produced using Gompertz model, in most cases match the data much worse than the right hand side plots produced with the new model.
Parameter posteriors obtained using the data from MCF7 spheroids demonstrate the same qualitative properties as the parameter posteriors for the U118 cell line discussed in the previous section. At the same time, the values of the parameters quantitatively shift a little to reflect differences in cell line phenotypes. See the marginals to the parameter posteriors computed from the first spheroid data in Figures S20, S21 and S22.
We computed the Bayes factor for preferring the new model with constant λ over the traditional Gompertz model. The Bayes factor was computed 5 times, separately for every spheroid. We found that in every single case the new model was very strongly preferred to the traditional Gompertz model by the experimental evidence. In every case, the scale of the Bayes factor suggested extremely strong evidential support for the new model in comparison to the Gompertz model. The sample of 5 computed Bayes factors is depicted in Figure S23. At the same time, the new model with variable λ is preferred to the model with constant λ, corresponding Bayes factors are depicted in Figure S24. Assuming equal a priori probabilities of our three alternative models, we can compute the a posteriori odds of each of the models to be the preferred one. Corresponding bar charts are depicted in Figure S25.
The Bayesian analysis of the data obtained from MCF7 cell line demonstrates the greater predictive power of the new model. Evidence in our experimental data very strongly supports preference of the new model over the traditional Gompertz model.
Distribution of λ in the experimental tumour spheroids
In the analysis reported above, we find that there is little difference between the full 3-parameter expression for variable λ and the simplified version with a fixed, effective λc – the more complex expression has only a weak advantage over the fixed λ model. We also find that the estimates of λ fluctuate in a limited region. Figure 4 shows box plots that summarize the distributions of the MAP estimates of λc for the model with constant λ, for the three cell lines. Correspondingly, figure 5 shows box plots that summarize the distributions of the MAP estimates of λ0 and λ1 for the model with variable λ.
Discussion
The λ function that describes the thin layer of viable cells around the central necrotic core observed in experimental tumour MTS, has a special role in the new models. Using data from both in silico and in vitro experiments we find that λ roughly spans the range 10–150 μm (see figures 1, 2, 4 and 5), in agreement with independent visual observations carried out on MTS tissue sections (see e.g. refs. 17 and 24) and on tumour cords from rodent and human vascularized solid tumours3. This also supports the idea that the model applies to non-spherical tumours as well.
In the computational environment, λ is not an input, but emerges from the combined dynamics of growth with diffusion and the individual biochemistry of cells. This parameter can be measured independently from tissue sections and thus the model could be used to predict tumour growth. Conversely, λ can be estimated by nonlinear fit of tumour growth data and contribute to the biological classification of tumours. We conjecture that this shall help in determining the aggressiveness and the growth potential of solid tumours and thus assist both experimental and clinical oncology.
Methods
Experimental methods: cell lines and spheroid culture
We used the following established tumour cell lines: 9l, from a rat glioblastoma; U118, from a human glioblastoma; MCF7, from a human breast carcinoma. Data obtained with 9l and U118 spheroids and the experimental procedure have been described previously25. Data obtained with MCF7 cells are new. The 9l and U118 cells were obtained from ATCC. The MCF7 cells were purchased from ECACC and used to obtain spheroids from monoclonal cells.
All cells were cultured at 37°C in a 5% carbon dioxide atmosphere in RPMI-1640 medium supplemented with 10% heat-inactivated fetal bovine serum (FBS), antibiotics and passaged weekly. In the case of 9l and U118 cells, 106 cells were inoculated in 10 ml complete medium in Petri dishes on a thin layer of agar (10 ml of a 0.75% w/v solution of agar in complete medium). Spheroids of about 200 μm of diameter were isolated by micromanipulation and grown individually into the wells of 24-well culture plates containing 1 ml of agar and filled with 1 ml of medium. In this case the first growth phase of tumour spheroids could not be observed and for this reason we turned to the spheroids from cloned MCF7 cells. The cells were seeded at the limiting dilution of 0.1 cells/well into the wells of five 96-well culture plates filled with 100 μl of agar and grown in an equal volume of complete medium.
The presence of single cells in the wells was carefully checked by visual inspection using a digital microscope EVOSci (AMG, Bothell, WA, U.S.A.). Spheroid radius was then measured from digital photomicrographs using the image analysis software ImageJ64-1.45i (http://imagej.nih.gov), calculating the spheroid projected areas and assuming a spherical shape.
Parameter inference
For parameter inference and model comparison we use Bayesian methods that are reviewed in the supplementary text. Here we describe those details that apply to the data analysis reported above.
The choice of priors and the likelihood
We assumed independent distributions of all of the priors for model parameters

and we assumed normal observation noise with unknown variance σ2. As we consider the variance of the observation noise as an additional parameter, we defined an independent prior over σ

in the case of 9l cells, where the original measurements are reported as volumes; similarly

in the case of U118 and MCF7 cells, where the original measurements are reported as radii. Here exp(a) denotes an exponential distribution with mean a.
We employed the same exponential distribution as the prior for the model parameters as well, as it is wide enough to be uninformative, while still expressing our preference for smaller parameter values in the resulting solution.

where ui are the units associated to the i-th parameter.
We assumed the same scale of the observation noise over all of the observed time points and therefore we define our likelihood as

where there are N data points, Xi is the time when the size of the spheroid Di was measured, φ(θ,Xi) is a prediction drawn from the considered model produced by solving a corresponding initial value problem with parameters θ and Xi.  denotes the Gaussian probability density function.
denotes the Gaussian probability density function.
Change history
03 April 2014
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Ribatti, D., Vacca, A. & Dammacco, F. The role of the vascular phase in solid tumor growth: a historical review. Neoplasia (New York, NY) 1, 293 (1999).
Tannock, I. The relation between cell proliferation and the vascular system in a transplanted mouse mammary tumour. British Journal of Cancer 22, 258 (1968).
Moore, J., Hasleton, P. & Buckley, C. Tumour cords in 52 human bronchial and cervical squamous cell carcinomas: inferences for their cellular kinetics and radiobiology. British journal of cancer 51, 407 (1985).
Sutherland, R. Cell and environment interactions in tumor microregions: the multicell spheroid model. Science 240, 177–184 (1988).
Mueller-Klieser, W. Tumor biology and experimental therapeutics. Critical reviews in oncology/hematology 36, 123–139 (2000).
Araujo, R. & McElwain, D. A history of the study of solid tumour growth: the contribution of mathematical modelling. Bulletin of mathematical biology 66, 1039–1091 (2004).
Greenspan, H. Models for the growth of a solid tumor by diffusion. Stud. Appl. Math 51, 317–340 (1972).
Mueller-Klieser, W. Three-dimensional cell cultures: from molecular mechanisms to clinical applications. American Journal of Physiology-Cell Physiology 273, C1109–C1123 (1997).
Tindall, M., Please, C. & Peddie, M. Modelling the formation of necrotic regions in avascular tumours. Mathematical biosciences 211, 34–55 (2008).
Tindall, M., Dyson, L., Smallbone, K. & Maini, P. Modelling acidosis and the cell cycle in multicellular tumour spheroids. Journal of Theoretical Biology (2011).
Milotti, E. & Chignola, R. Emergent properties of tumor microenvironment in a real-life model of multicell tumor spheroids. PLoS One 5, e13942 (2010).
Chignola, R. & Milotti, E. Bridging the gap between the micro-and the macro-world of tumors. AIP Advances 2, 011204 (2012).
Chignola, R. & Milotti, E. A phenomenological approach to the simulation of metabolism and proliferation dynamics of large tumour cell populations. Physical Biology 2, 8 (2005).
Chignola, R., Fabbro, A., Pellegrina, C. & Milotti, E. Ab initio phenomenological simulation of the growth of large tumor cell populations. Physical Biology 4, 114 (2007).
Milotti, E., Del Fabbro, A. & Chignola, R. Numerical integration methods for large-scale biophysical simulations. Computer Physics Communications 180, 2166–2174 (2009).
Bortner, C. & Cidlowski, J. Apoptotic volume decrease and the incredible shrinking cell. Cell death and differentiation 9, 1307 (2002).
Freyer, J. & Sutherland, R. Regulation of growth saturation and development of necrosis in emt6/ro multicellular spheroids by the glucose and oxygen supply. Cancer research 46, 3504–3512 (1986).
Kunz-Schughart, L., Doetsch, J., Mueller-Klieser, W. & Groebe, K. Proliferative activity and tumorigenic conversion: impact on cellular metabolism in 3-d culture. American Journal of Physiology-Cell Physiology 278, C765–C780 (2000).
Gompertz, B. On the nature of the function expressive of the law of human mortality and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London 115, 513–583 (1825).
Laird, A. Dynamics of tumour growth. British Journal of Cancer 18, 490 (1964).
Laird, A. Dynamics of tumour growth: comparison of growth rates and extrapolation of growth curve to one cell. British Journal of Cancer 19, 278 (1965).
Bajzer, Ž. & Pavlović, S. New dimension in gompertzian growth. Computational and Mathematical Methods in Medicine 2, 307–315 (2000).
Kass, R. E. & Raftery, A. E. Bayes factors. Journal of the American Statistical Association 90, 773–795 (1995).
Freyer, J. Role of necrosis in regulating the growth saturation of multicellular spheroids. Cancer Res. 48, 2432 (1988).
Chignola, R. et al. Oscillating growth patterns of multicellular tumour spheroids. Cell Prolif. 32, 39–48 (1999).
Acknowledgements
The authors wish to acknowledge support from INFN, MIUR-PRIN2009 and from the HPC CASPUR Standard Grant 2011.
Author information
Authors and Affiliations
Contributions
The experimental work was carried out by M.S. and R.C. The model was developed by E.M. Statistical analysis of experimental data through Bayesian inference methods was performed by V.V. Simulations were carried out by E.M. and R.C. All authors wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary text for Interplay between distribution of live cells and growth dynamics of solid tumors
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Milotti, E., Vyshemirsky, V., Sega, M. et al. Interplay between distribution of live cells and growth dynamics of solid tumours. Sci Rep 2, 990 (2012). https://doi.org/10.1038/srep00990
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00990
This article is cited by
-
The control of acidity in tumor cells: a biophysical model
Scientific Reports (2020)
-
Fine-grained simulations of the microenvironment of vascularized tumours
Scientific Reports (2019)
-
Improving the Subcutaneous Mouse Tumor Model by Effective Manipulation of Magnetic Nanoparticles-Treated Implanted Cancer Cells
Annals of Biomedical Engineering (2018)
-
Pulsation-limited oxygen diffusion in the tumour microenvironment
Scientific Reports (2017)
-
Allometric scaling in-vitro
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.