Abstract
Graphene has attracted much interest in both academia and industry. The challenge of making it semiconducting is crucial for applications in electronic devices. A promising approach is to reduce its physical size down to the nanometer scale. Here, we present the surface-assisted bottom-up fabrication of atomically precise armchair graphene nanoribbons (AGNRs) with predefined widths, namely 7-, 14- and 21-AGNRs, on Ag(111) as well as their spatially resolved width-dependent electronic structures. STM/STS measurements reveal their associated electron scattering patterns and the energy gaps over 1 eV. The mechanism to form such AGNRs is addressed based on the observed intermediate products. Our results provide new insights into the local properties of AGNRs and have implications for the understanding of their electrical properties and potential applications.
Similar content being viewed by others
Introduction
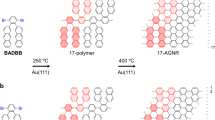
Graphene, a single sheet of sp2-bonded carbon atoms arranged in a honeycomb lattice, exhibits extraordinary electrical and mechanical properties. For applications in electronic devices, graphene needs to be semiconducting. Reducing its physical size down to the nanometer scale is a promising approach. Theoretically, free-standing armchair graphene nanoribbons (AGNRs) can behave as either metals or semiconductors, depending on their widths1,2,3. GNRs fabricated by top-down methods generally possess uncontrolled and atomically imperfect edges, precluding detailed studies on finite size and edge effects4,5,6. Recently, the fabrication of 7-AGNRs (Fig. 1b, the number before “AGNR” indicates its width, that is, the number of carbon-pair lines in the direction perpendicular to AGNR axis, as sampled in Fig. 1d) from 10,10’-dibromo-9,9’-bianthryl (DBBA, Fig. 1a) via polyanthracene has been demonstrated7,8. The GNR topology, width and edge periphery are predefined by the DBBA precursor molecule. Density functional theory (DFT) calculations suggest that dehydrogenation takes place in a domino-like fashion and is more favourable at sites between anthracene monomers than at their head sites9. This limits the formation of wider AGNRs such as 14- and 21-AGNRs (Fig. 1c and 1d), which can be regarded as two and three 7-AGNRs conjugated side-by-side via dehydrogenation at the head sites, respectively.
Schematic of surface-assisted bottom-up synthesis of atomically precise AGNRs from DBBA.
a) side view of a ball-and-stick model of DBBA monomer, whose chemical structure is inserted; b) 7-AGNR; c) 14-AGNR; d) 21-AGNR. The number before “AGNR” indicates its width, that is, the number of carbon-pair lines in the direction perpendicular to AGNR axis, as sampled in Fig. 1d. In Fig. 1b, the yellow hexagon highlights an edged benzene-ring, the red arrows for the location between two benzene-rings edges.
Fabrication of atomically precise AGNRs with varying widths provides a unique opportunity to investigate quantum confinement and edge effects on them. In this article, we present the surface-assisted bottom-up fabrication of a series of atomically precise AGNRs from DBBA on Ag(111), such as 7-, 14- and 21-AGNRs, as well as their spatially resolved width-dependent electronic structures. Their typical vibration modes are measured by Raman spectroscopy. The associated electron scattering patterns (ESPs) which arise from intervalley electron backscattering at both armchair edges10,11 are visualized by scanning tunneling microscopy (STM). The local density of states (LDOS) on each AGNRs observed by scanning tunneling spectroscopy (STS) reveal the presence of energy gap over 1 eV. The mechanism to form such AGNRs is addressed based on the observed intermediate products. Our results are a significant step towards understanding the local properties of AGNRs and provide us with design guidelines for the fabrication of edge-precise graphene nanoribbons for potential device applications.
Results
To provide a general characterization of the prepared AGNRs/Ag(111) sample, ex situ Raman measurements were carried out at ambient atmosphere. Fig. 2a shows an average Raman spectrum from ten spots. Six representative modes in the range from ~350 cm−1 to ~1700 cm−1 are observed and identified as G (~1610 cm−1), D (~1350 cm−1), the edge-phonon modes (~1220 cm−1 and ~1260 cm−1) and radial-breathing-like-mode (RBLM) (~396 cm−1) as well as its third overtone RBLM3 (~960 cm−1)12. Remarkably, the intensity ratio between modes D and G (ID/IG) is ~0.90, which is about twice that of AGNRs on Au(111)7. (also refer to Fig. S1) For polycrystalline graphite, the ID/IG ratio correlates with the effective crystallite size (La) as La2 for La < 2 nm: due to increasing fraction of sp2 carbons, which contribute to the G band but not to the D band13,14. According to Ref 14, the ID/IG ratio is ~0.3 for 7-AGNR (0.74 nm) and ~1.2 for 14-AGNR. Thus, the larger ID/IG ratio on AGNRs/Ag(111) suggests the coexistence of wider AGNRs such as 14-AGNRs or 21-AGNRs with 7-AGNRs. Besides these six modes, the spectrum exhibits a sharp peak at ~2000 cm−1, as highlighted in the middle inset, originating from the localized width-independent mode generated by the vibration of the atoms at the edge of AGNRs15. Notably, only when the AGNRs are at least partially H-free, that is, when C≡C bonds exist at their armchair edges, can the localized mode be observed15. This gives evidence for the dehydrogenation at the head sites and the formation of AGNRs with multiple integer widths of 14-, 21-AGNRs and so on.
a) Raman spectrum on AGNRs/Ag(111) under ambient conditions. Besides mode D (1350 cm−1) and mode G (1610 cm−1), some other vibration modes appear due to the finite width and low symmetry of the nanoribbons, such as RBLM (396 cm−1), RBLM3 (961 cm−1). The peak at 2000 cm−1 as highlighted in the middle inset arises from the vibration mode of the C-atoms at the edge of AGNRs. The inserted typical STM image (70 nm × 40 nm, VT = −2.0 V) at the upper-right corner shows straight AGNRs with varying widths. b) line-profiles taken perpendicularly across the 7-, 14-, 21- and 28-AGNRs, respectively. c) STM image (8 nm × 10 nm, VT = −0.5 V) showing the electron scattering patterns in 7- (lower) and 21-AGNRs (upper). The 21-AGNR is imperfect at the lower end.
The STM image inserted in the upper-right corner in Fig. 2a clearly shows the randomly distributed AGNRs with varying widths on Ag(111). The green rectangles highlight one 7-14-7-AGNR and one 14-21-AGNR heterojunction, where the π-conjugation at the junction interface is preserved. The line profiles taken perpendicularly across 7-, 14-, 21- and 28-AGNRs axes reveal the corresponding widths of ~1.5 nm, ~2.4 nm, ~3.3 nm and ~4.2 nm respectively and an apparent height of ~0.19 nm, as shown in Fig. 2b. These values vary slightly depending on tip conditions. For such AGNRs the widths measured are larger than those from the corresponding atomic structure models. For example, the model of 7-AGNR (Fig. 1b) shows a smaller width of 0.741 nm. This could be attributed to the finite size of STM tip. The highly-resolved STM image taken at 77 K in Fig. 2c shows ESPs in 7- and 21-AGNRs, which arise from the intervalley electron backscattering at both armchair edges10,11.
Discussion
We first discuss the two Raman peaks located at ~2608 cm−1 and ~2690 cm−1 in Fig. 2. A previous report shows Raman 2D peak splitting upon deposition of Au onto single layer graphene, which come from the graphene with and without Au and is not the case in this work16. Recent theoretical and experimental investigations reveal that the Raman 2D peak of single layer graphene splits into two peaks under homogeneous uniaxial strain and both redshift significantly depending on the direction and magnitude of the strain applied17,18,19,20,21. In particular, the shift rates are up to −67.8 cm−1/% and −26.0 cm−1/% for strain applied along the zigzag directions17. Accordingly, the average strain in the direction perpendicular to the AGNR axis is at least 2%. In this work, the mismatch between AGNRs and Ag(111) may induce strain. However, we do not observe obvious deformation of AGNRs along its zigzag direction. Furthermore, uniaxial strain-induced redshift of the peak at ~2690 cm−1 is not observed. We also note that the 2D peak of GNRs formed by CNT unzipping is observed at ~2659 cm−16. Thus, strain-induced Raman 2D peak splitting is highly unlikely. We performed comparative Raman measurement on AGNRs of different widths. The Raman measurements on 7-AGNRs on Au(111) is shown in Fig. S1, where one peak is observed at ~2603 cm−1 accompanied by a shoulder at ~2685 cm−1. On Au surface, 7-AGNRs dominate and the Raman peak at ~2603 cm−1 is attributed to 7-AGNRs. The shoulder at 2685 cm−1 appears to have the same origin as the peak at ~2690 cm−1 for AGNRs on Ag(111). Wider AGNRs such as 14- and 21-AGNRs are observed on Ag(111) compared to that on Au(111). Hence, from our empirical observations, we suggest that the peak at ~2690 cm−1 is attributed to wider AGNRs. Further calculations are required to support this postulate.
Fig. 3 displays STM images of ESPs in 7-, 14- and 21-AGNRs (left column) as well as the corresponding DFT simulations (right column), respectively. Figs. 3a and 3c are enlarged from Fig. 2c. ESPs in 7-AGNR form localized ring-like shapes with a (√3 × √3)R30° unit cell, in good agreement with the calculated charge density plots of the conduction bands of 7-AGNR (filled red part in left panel in Fig. 3a)7 and with our DFT simulations (right panel in Fig. 3a). Such ESPs are attributed to the electronic states in the vicinity of the armchair edge where the incident and reflected waves interfere with each other due to intervalley scattering10,11. A piece of ball and stick model of 7-AGNR is superimposed in the STM image of Fig. 3a, with the red dots highlighting each centre of the ESPs. This suggests that ESPs centres at both armchair edges of 7-AGNR are located not at but between the benzene-ring edges. One edged benzene-ring and the location between two adjacent benzene-ring edges are highlighted in Fig. 1b by a yellow hexagon and red arrows, respectively. ESPs in 21-AGNR are similar to those in 7-AGNR, in a localized ring-like shape with a (√3 × √3)R30° unit cell, as marked by a red parallelogram. It is worth noting that there is a dislocation line parallel to the 21-AGNR axis, as highlighted by the green dash-dotted line. Given that 21-AGNR has the same lateral mirror symmetry as 7-AGNR and that the armchair edges have the same scattering effect on the incident electrons, we extend the above-mentioned calculated charge density plots of the conduction bands from 7-AGNR to 21-AGNR. The red (blue) dots indicate the ESP centres due to electron backscattering at the lower (upper) edge, as shown in the overlaid 21-AGNR ball and stick model in the left panel in Fig. 3c. Using geometrical considerations, ESPs from opposite armchair edges will be misaligned in the direction 60° off the lateral direction of 21-AGNR (parallel to the √3 direction as indicated by the red parallelogram), which will result in the observed dislocation. This is consistent with the DFT simulations in the right panel in Fig. 3c. The dislocation shifts to a lower position at the left end of the AGNR because of defects (see Fig. 2c, the lower end of 21-AGNR).
ESPs (left column, a: 3.5 nm × 2 nm, VT = −0.5 V; b: 5 nm × 3 nm, VT = −0.5 V; c: 5.5 nm × 3.5 nm, VT = −0.5 V) and corresponding DFT simulations (right column) in 7-, 14- and 21-AGNRs.
Parameter J in panel b is an integer that marks the position of carbon-pair lines in AGNRs. The red parallelogram in Fig 3c marks the (√3 × √3)R30° unit cell, the green dash-dotted line for dislocation, which shifts due to the defects at left end (see Fig. 2c). Red and blue dots: ESP centres.
ESPs in 14-AGNR are significantly different, as shown in the left panel in Fig. 3b. One-dimensional (1D) delocalized striped patterns were observed parallel to its axis with equal-spacing of ~0.38 nm, in good agreement with the Fermi wavelength of graphene of 3a/2 = 0.37 nm, where a = 0.246 nm is the lattice constant of graphene. Such ESPs arise from the intervalley electron backscattering at both armchair edges of metallic AGNRs3 and depend not on the electron energy but only on the edge structure, as observed at the armchair edge of epitaxial graphene on SiC(0001)22. A piece of ball and stick model of 14-AGNR is overlaid to show the registration between the ESPs and C chains. This model matches perfectly with the prediction3: the probability density for a state near the Dirac singularity disappears at J = 3i (i.e. 3, 6, 9, 12……), where i is an integer and J is introduced to mark the position of carbon-pair lines in AGNRs, as shown in Fig. 3b. The good match with the DFT calculations in the right panel of Fig. 3b confirms the 1D metallic nature of 14-AGNR due to quantum confinement effects3.
In order to acquire more detailed information about the electronic structures of AGNRs, dI/dV measurements were performed at 4.7 K. These conductance measurements are directly proportional to the LDOS within the Tersoff-Harmann approximation23,24,25,26. The dI/dV spectra in Figs. 4, 5 and S2 reveal the electronic properties of such AGNRs. Fig. 4 summarizes the typical dI/dV spectra from the centres of three neighbouring AGNRs, which are shown in the inserted STM image. The bottom spectra taken from clean Ag(111) terrace clearly show the surface states at ~66 mV below Fermi energy level (EF, 0 V in the spectrum), as marked by a short cyan solid line, verifying the good tip conditions. The position of AGNR EF as indicated by the green dash-dotted line is shifted toward their unoccupied bands. This is attributed to the smaller work function of Ag(111) (~4.4 eV) and a hybridization between Ag d band and graphene 2p27,28. The spectra exhibit a sharp peak at ~−240 mV for 21-AGNR, a broad peak at ~−400 mV for 14-AGNR and a broader peak at ~−800 mV for 7-AGNR, as marked by green arrows, respectively.
STS data showing the unoccupied states of clean Ag(111) and centers of 7-, 14- and 21-AGNRs, as marked on the inserted STM image (7 nm × 8 nm, VT = 1.5 V) as 1, 2 and 3 respectively, clearly show that electronic properties of AGNRs are significantly related to their widths.
Offset vertically for clarity. The green dash-dotted line indicates EF and the short cyan solid line for the surface states of clean Ag(111) at ~66 mV. The green arrows indicate the typical peaks in STS spectra.
Fig. 5 shows dI/dV spectra acquired perpendicularly across AGNRs. In each panel, the black spectra were taken from the adjacent Ag(111) surface, while the red (blue) ones are from the AGNRs edges (centre) at equal spacing. The inserted differential STM images show the typical AGNRs respectively. For 7-AGNR, dI/dV spectra exhibit a broad peak at ~−850 mV at the edges and is almost featureless in the centre, as shown in Fig. 5a. Taking the substrate influence into account28, it is in consistence with the recent report by Ruffieux et al.29 that the conduction band minimum of Au(111)-supported 7-AGNR is located at 1.6 eV above EF at its armchair edges. It is also in good agreement with the recent report by Koch M. that the HOMO and LUMO of Au(111)-supported 7-AGNRs delocalized along their armchair edges with an energy gap of 2.7 eV30. Detailed inspection reveals that the unoccupied bands of 7-AGNR is shifted below EF and thus becomes partially occupied, indicating a weak chemisorption nature31. On the contrary, while the featureless spectra are partially occupied at the edges, those in centre remain unoccupied and exhibit a broad (sharp) peak at ~−380 mV (~−240 mV) for 14-AGNR (21-AGNR), as highlighted by solid green lines in Fig. 5 respectively. The spatially resolved spectra indicate that the electronic structures are heavily influenced when AGNRs adsorbed on Ag(111). For 0 V < VT < 1.0 V, the LDOS of all the AGNRs are finite and similar to that of exposed Ag(111) (for the case of 21-AGNR see Fig. S2). This suggests that in the energy gap of AGNRs the local density of states from underlying Ag(111) could not be excluded in STS measurements. Due to the charge transfer between AGNRs and Ag(111), the corresponding valence band maximum of AGNRs shifts out of the measurement range and could not be detected with our experimental settings. Applying Ruffieux’s method29, the energy gap of semiconducting 7-AGNRs is deduced to be over 1.8 eV, in good agreement with recent experimental reports29,30,32,33. For 21-AGNRs, the energy gap is over 1.2 eV. For metallic 14-AGNRs, the observed peak at −380 meV might be the first Van Hove singularity (VHS) at the unoccupied states, which is broadened due to the hybridization with Ag(111)28,34. The first VHS gap of metallic 14-AGNR is calculated to be close to 2 eV35 and is also out of the measurement range. Further experiments and simulations are required to accurately measure the energy gaps.
For heterojunctions such as 7-14-AGNRs, 14-21-AGNRs, the spectra taken along the ribbons exhibit the previously mentioned characteristics of each AGNR when measured in their respective regions (Fig. 4). The change in spectra across the boundary (< 1 nm) is very sharp, having no transitional spectra. This is similar to the case of metallic intramolecular heterojunctions in CNT36, confirming that the electronic properties of AGNRs are significantly width-dependent.
Why do AGNRs with varying widths form on Ag(111)? To answer this question, a submonolayer DBBA on Ag(111) annealed at ~450 K for 30 min was investigated. Unexpectedly, instead of anthracene polymers, isolated planar products are observed, as shown in Fig. 6, indicating that dehydrogenation has taken place for DBBA monomers on Ag(111) at this stage37. The carbon backbone of an isolated molecular product is inserted at the upper-right corner of Fig. 6a. More theoretical simulations are required to determine how many hydrogen atoms dissociate from one DBBA molecule and its final configuration. Two such structural units are tentatively superimposed on the high resolution STM image in Fig. 6d. Fig. 6b shows the line profile taken along the white line in Fig. 6a and Fig. 6c shows the corresponding fast Fourier transform (FFT) pattern from Fig. 6a, revealing that isolated planar molecular products form a hexagonal arrangement with a nearest neighbour distance of 1.5±0.1 nm. This is much larger than that of ~1.15 nm for monolayer coronene on Ag(111)38, indicating a strong adsorbate-substrate interaction at 77 K. Some short rod-like features of two or three connected intermediate products are observed in the area enclosed by white dash-dotted curve, indicating that such planar products act as intermediates for AGNRs. The growth mechanism of AGNRs on Ag(111) is proposed in Fig. S3, which is significantly different with that on Au(111)7. It may be related to the different catalytic reactivities of Au(111) and Ag(111), which induce different self-assembly behaviour of DBBA at room temperature, as shown in Fig. S4.
Dehydrogenation of DBBA on Ag(111) at ~450 K.
a) STM image (VT = −1.0 V) showing that most of the products are isolated in a hexagonal arrangement, as revealed by the corresponding FFT pattern in panel c; while some are connected together as short rods, as highlighted by the white dash-dotted curve. The carbon backbone of the isolated product is inserted at the upper right corner. b) the line-profile taken along the white line in panel a, showing an average intermolecular distance of 1.5±0.1 nm. d) zoomed-in STM image (VT = −0.01 V) showing the isolated product lies flat on Ag(111). Two molecular unit structures are superimposed. Such planar products are believed to be the intermediates for AGNRs in varying widths.
In summary, we have succeeded in fabricating ultra-narrow atomically precise 7-, 14- and 21-AGNRs and observed their associated ESPs using LT-STM. The observed ESPs are in good agreement with theoretical predictions. The dI/dV spectra reveal the width-dependent electronic properties of the AGNRs. For the next step of our investigation, we plan to investigate the electronic properties of such AGNRs on insulating thin films. We expect that these initial investigations on the electronic properties of such AGNRs give us a better understanding of this extraordinary class of materials and help advance theoretical predictions on systems such as intraribbon quantum dots39, GNR switches40 and magnetic devices based on specific GNR edge states41.
Methods
Synthesis of AGNRs
The clean Ag(111) surface was achieved in situ by repeated cycles of Ar+ sputtering and subsequent annealing to ~750 K. DBBA (97%, St-Jean Photochemical Inc.) was evaporated from a K-cell (MBE-Komponenten, Germany) at a deposition rate of ~0.01 ML/min (ML: monolayer) at normal incidence onto Ag(111) at room temperature. After deposition, the sample was annealed at ~450 K and ~650 K for for 30 mins, respectively.
STM/STS measurements
Sample preparation and STM measurements were carried out in a custom-built multi-chamber ultra-high vacuum (UHV) system housing an Omicron LT-STM in the analysis chamber with a base pressure better than 6.0×10−11 mbar. All the STM images were recorded in constant current mode using chemically etched tungsten (W) tips. To reduce the thermal drift and noise level, differential conductance (dI/dV) measurements were performed at ~4.7 K in an open feedback loop mode using the lock-in technique with frequency 625 Hz and ac modulation of 20 meV and with set-point parameters of VT = 100 mV and I = 200 pA.
Raman measurements
Raman spectra were recorded with a Renishaw 1000 Raman Microscope at ambient. The excitation source was a 514 nm laser with power below 20 mW to avoid laser induced surface heating. The laser spot size was around 10 μm.
Simulation of the ESPs
Simulations of electron scattering patterns (ESPs) of pristine graphene nanoribbon were obtained by performing ab-initio pseudopotential density functional theory calculations. In Tersoff and Hamann approximation17, the tunneling current density between the STM tip and the sample is proportional to the local density of states (LDOS)

 is the wave function of pristine graphene nanoribbon. When a small bias voltage Vbias is applied, the numerical integration is carried out on the associated eigenvalues within this energy range below the Fermi level. This provides occupied (unoccupied) electronic states when a negative (positive) bias voltage is applied. The exchange-correlation functionals are described by the generalized gradient approximation (GGA) derived Perdew-Burke-Ernzerhof (PBE) approach18. The calculations were performed by using the SIESTA code19, together with a double-ζ polarized basis-set20, a real space mesh cutoff of 400 Ryd and norm conversing pseudopotential. The slab models include a vacuum thickness of 10 Å to reduce the influence of periodic images along the direction perpendicular to the GNR plane. The total energies converged well with respect to the sufficiently large k-point sampling of 90 × 1 × 1 in the Brillouin zone. The electronic structure calculations were carried out using fully relaxed structures where the structural optimization on the GNR atomic degrees of freedom was achieved until the residual forces on each atom are smaller than 0.01 eV/Å.
is the wave function of pristine graphene nanoribbon. When a small bias voltage Vbias is applied, the numerical integration is carried out on the associated eigenvalues within this energy range below the Fermi level. This provides occupied (unoccupied) electronic states when a negative (positive) bias voltage is applied. The exchange-correlation functionals are described by the generalized gradient approximation (GGA) derived Perdew-Burke-Ernzerhof (PBE) approach18. The calculations were performed by using the SIESTA code19, together with a double-ζ polarized basis-set20, a real space mesh cutoff of 400 Ryd and norm conversing pseudopotential. The slab models include a vacuum thickness of 10 Å to reduce the influence of periodic images along the direction perpendicular to the GNR plane. The total energies converged well with respect to the sufficiently large k-point sampling of 90 × 1 × 1 in the Brillouin zone. The electronic structure calculations were carried out using fully relaxed structures where the structural optimization on the GNR atomic degrees of freedom was achieved until the residual forces on each atom are smaller than 0.01 eV/Å.
References
Nakada, K., Fujita, M., Dresselhaus, G. & Dresselhaus, M. S. Edge State in Graphene Ribbons: Nanometer Size Effect and Edge Shape Dependence. Phys. Rev. B 54, 17954–17961 (1996).
Son, Y. W., Cohen, M. L. & Louie, S. G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 97, 216803 (2006).
Sasaki, K., Wakabayashi, K. & Enoki, T. Electron Wave Function in Armchair Graphene Nanoribbons. J. Phys. Soc. Jpn. 80, 044710 (2011).
Han, M. Y., Ozyilmaz, B., Zhang, Y. & Kim, P. Energy Band-Bap Engineering of Graphene Nanoribbons. Phys. Rev. Lett. 98, 206805 (2007).
Tapaszto, L., Dobrik, G., Lambin, P. & Biro, L. P. Tailoring the Atomic Structure of Graphene Nanoribbons by Scanning Tunneling Microscope Lithography. Nat. Nanotechnol. 3, 397–401 (2008).
Jiao, L. Y., Zhang, L., Wang, X. R.,. Diankov, G. & Dai, H. J. Narrow Graphene Nanoribbons from Carbon Nanotubes. Nature 458, 877–880 (2009).
Cai, J. M., Ruffieux, P., Jaafar, R., Bieri, M., Braun, T., Blankenburg, S., Muoth, M., Seitsonen, A. P., Saleh, M., Feng, X. L., Mullen, K. & Fasel, R. Atomically Precise Bottom-Up Fabrication of Graphene Nanoribbons. Nature 466, 470–473 (2010).
Blankenburg, S., Cau, J. M., Ruffieux, P., Jaafar, R., Passerone, D., Feng, X. L., Mullen, K., Fasel, R. & Pignedoli, C. S. Intraribbon Heterojunction Formation in Ultranarrow Graphene Nanoribbons. ACS Nano 6, 2020–2025 (2012).
Bjork, J., Stafstrom, S. & Hanke, F. Zipping Up: Cooperativity Drives the Synthesis of Graphene Nanoribbons. J. Am. Chem. Soc. 133, 14884–14887 (2011).
Niimi, Y., Matsui, T., Kambara, H., Tagami, K., Tsukada, M. & Fukuyama, H. Scanning Tunneling Microscopy and Spectroscopy of the Electronic Local Density of States of Graphite Surfaces near Monoatomic Step Edges. Phys. Rev. B 73, 085421 (2006).
Sakai, K., Takai, K., Fukui, K., Nakanishi, T. & Enoki, T. Honeycomb Superperiodic Pattern and its Fine Structure near the Armchair Edge of Graphene Observed by Low-Temperature Scanning Tunneling Microscopy. Phys. Rev. B 81, 235417 (2010).
Saito, R., Furukawa, M., Dresselhaus, G. & Dresselhaus, M. S. Raman Spectra of Graphene Ribbons. J. Phys: Condens. Matter 22, 334203 (2010).
Ryu, S., Maultzsch, J., Han, M. Y., Kim, P. & Brus, L. E. Raman Spectroscopy of Lithographically Patterned Graphene Nanoribbons. ACS Nano 5, 4123–4130 (2011).
Ferrari, A. C. & Robertson, J. Interpretation of Raman Spectra of Disordered and Amorphous Carbon. Phys. Rev. B 61, 14095–14107 (2000).
Zhou, J. & Dong, J. M. Vibrational Property and Raman Spectrum of Carbon Nanoribbon. Appl. Phys. Lett. 91, 173108 (2007).
Entani, S., Sakai, S., Matsumoto, Y., Naramoto, H., Hao,. T. &. Maeda, Y. Interface Properties of Metal/Graphene Heterostructures Studied by Micro-Raman Spectroscopy. J. Phys. Chem. C. 114, 20042–20048 (2010).
Yoon, D., Son, Y. W. & Cheong, H. Strain-Dependent Splitting of the Double-Resonance Raman Scattering Band in Graphene. Phys. Rev. Lett. 106, 155502 (2011).
Huang, M. Y., Yan, H., Heinz, T. F. & Hone, J. Probing Strain-induced Electronic Structure Change in Graphene by Raman Spectroscopy. Nano Lett. 10, 4074–4079 (2010).
Mohr, M., Maultzsch, J. & Thomsen, C. Splitting of the Raman 2D Band of Graphene subjected to Strain. Phys. Rev. B 82, 201409(R) (2010).
Frank, O., Mohr, M., Maultzsch, J., Thomsen, C., Riaz, I., Jalil, R., Novoselov, K. S., Tsoukleri, G., Parthenios, J., Papagelis, K., Kavan, L. & Galiotis, C. Raman 2D-Band Splitting in Graphene: Theory and Experiment. ACS Nano 5, 2231–2239 (2011).
Frank, O., Tsoukleri, G., Parthenios, J., Papagelis, K., Riaz, I., Jalil, R., Novoselov, K. S. & Galiotis, C. Compression Behavior of Single-Layer Graphenes. ACS Nano 4, 3131–3138 (2010).
Yang, H., Mayne, A. J., Boucherit, M., Comtet, G., Dujardin, G. & Kuk, Y. Quantum Interference Channeling at Graphene Edges. Nano Lett. 10, 943–947 (2010).
Tersoff, J. & Hamann, D. R. Theory and Application for the Scanning Tunneling Microscope. Phys. Rev. Lett. 50, 1998–2001 (1983).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Sánchez-Portal, D., Ordejón, P., Artacho, E. & Soler, J. M. Density Functional Method for Very Large Systems with LCAO Basis Sets. Int. J. Quantum Chem. 65, 453–461 (1997).
Junquera, J., Paz, Ó., Sánchez-Portal, D. & Artacho, E. Numerical Atomic Orbitals for Linear-Scaling Calculations. Phys. Rev. B 64, 235111–235119 (2001).
Wildoer, J. W. G., Venema, L. C., Rinzler, A. G., Smalley, R. E. & Dekker, C. Electronic Structure of Atomically Resolved Carbon Nanotubes. Nautre 391, 59–62 (1998).
Clair, S., Kim, Y. & Kawai, M. Energy Level Alignment of Single-walled Carbon Nanotubes on Metal Surfaces. Phys. Rev. B 83, 245422 (2011).
Ruffieux, P., Cai, J. M., Plumb, N. C., Patthey, L., Prezzi, D., Ferretti, A., Molinari, E., Feng, X. L., Mullen, K., Pignedoli, C. A. & Fasel, R. Electronic Structure of Atomically Precise Graphene Nanoribbons. Acs Nano, 6, 6930–6935 (2012).
Koch, M., Ample, F., Joachim, C. & Grill, L. Voltage-dependent Conductance of a Single Graphene Nanoribbon. Nat. Nanotechnol. 7, 713–717 (2012).
Norskov, J. K. Chemisorption on Metal Surface. Rep. Prog. Phys. 53, 1253–1295 (1990).
Linden, S., Zhang, D., Timmer, A., Aghdassi, N., Franke, J. H., Zhang, H., Feng, X., Mullen, K., Fuchs, H., Chi, L. & Zacharias, H. Electronic Structure of Specially Aligned Graphene Nanoribbons on Au(788). Phys. Rev. Lett. 108, 216801 (2012).
Bronner, C., Leyssner, F., Stremlau, S., Utecht, M., Saalfrank, P. Klamroth, T. & Tegeder, P. Phys. Rev. B 86, 085444 (2012).
Odom, T. W., Huang, J. L., Kim, P. & Lieber, C. M. Atomic Structure and Electronic Properties of Single-Walled Carbon Nanotubes. Nature 391, 62–64 (1998).
Long, M. Q., Tang, L., Wang, D., Wang, L. J. & Shuai, Z. G. Theoretical Predictions of Size-dependent Carrier Mobility and Polarity in Graphene. J. Am. Chem. Soc. 131, 17728–17729 (2009).
Ouyang, M., Huang, J. L., Cheung, C. L. & Lieber, C. M. Atomically Resolved Single-Walled Carbon Nanotube Intramolecular Junctions. Science 291, 97–100 (2002).
Treier, M., Pignedoli, C. A., Laino, T., Rieger, R., Müllen, K. Passerone, D. & Fasel, R. Surface-assisted Cyclodehydrogenation Provides a Synthetic Route towards Easily Processable and Chemically Tailored Nanographene. Nature Chem. 3, 61–67 (2011).
Lackinger, M., Griessl, S., Heckl, W. M. & Hietschold, M. Coronene on Ag(111) Investigated by LEED and STM in UHV. J. Phys. Chem. B 106, 4482–4485 (2002).
Prezzi, D., Varsano, D., Ruini, A. & Molinari, E. Quantum-Dot States and Optical Excitations on Edge-Modulated Graphene Nanoribbons. Phys. Rev. B 84, 041401 (2011).
Shi, Q. W., Wang, Z. F., Li, Q. X. & Yang, J. L. Chiral Selective Tunneling Induced Graphene Nanoribbon Switch. Front. Phys. China 4, 373–377 (2009).
Son, Y. W., Cohen, M. L. & Louie, S. G. Half-Metallic Graphene Nanoribbons. Nature 444, 347–349 (2006).
Acknowledgements
We acknowledge the financial support from NRF-CRP grants R-143-000-360-281: “Graphene and Related Materials and Devices” and R-144-000-295-281: “Novel 2D materials with tailored properties – beyond graphene”. Dr Dacheng Wei thanks the support from Lee Kuan Yew Post Doctoral Fellowship Grant (R-144-000-263-112).
Author information
Authors and Affiliations
Contributions
H.H., D.C.W. and A.T.S.W. planned the experiments. H.H. and S.L.W. collected and analyzed the data. J.T.S. and Y.P.F. performed the DFT calculations. H.H wrote the manuscript. A.T.S.W. supervised the project. A.H.C.N. provided theoretical insights and obtained funding for the project. All authors are involved in the revision of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Huang, H., Wei, D., Sun, J. et al. Spatially Resolved Electronic Structures of Atomically Precise Armchair Graphene Nanoribbons. Sci Rep 2, 983 (2012). https://doi.org/10.1038/srep00983
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00983
This article is cited by
-
Uncovering the magnetic response of open-shell graphene nanostructures on metallic surfaces at different doping levels
Science China Physics, Mechanics & Astronomy (2024)
-
Armchair and Zigzag Ising Nanoribbons with Bond Dilution
Journal of Superconductivity and Novel Magnetism (2023)
-
Graphene nanoribbons initiated from molecularly derived seeds
Nature Communications (2022)
-
Synthesis of oligoacenes using precursors for evaluation of their electronic structures
Photochemical & Photobiological Sciences (2022)
-
Tunneling current modulation in atomically precise graphene nanoribbon heterojunctions
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.