Abstract
Complex traits can require the accumulation of multiple mutations that are individually deleterious. Their evolution requires a fitness valley to be crossed, which can take relatively long time spans. A new evolutionary mechanism is described that accelerates the emergence of complex phenotypes, based on a “division of labor” game and the occurrence of cheaters. If each intermediate mutation leads to a product that can be shared with others, the complex type can arise relatively quickly as an emergent property among cooperating individuals, without any given individual having to accumulate all mutations. Moreover, the emergence of cheaters that destroy cooperative interactions can lead to the emergence of individuals that have accumulated all necessary mutations on a time scale that is significantly faster than observed in the absence of cooperation and cheating. Application of this mechanism to somatic and microbial evolution is discussed, including evolutionary processes in tumors, biofilms and viral infections.
Similar content being viewed by others
Introduction
Complex traits can arise from the interactions among multiple genes. They can emerge through different evolutionary pathways. In some cases, the evolution of complex traits involves the accumulation of several beneficial mutations. In other cases, however, their evolution requires the accumulation of multiple mutations, each of which is individually neutral or deleterious. A fitness advantage is only attained when all mutations have been acquired (sign epistasis). In such cases, evolution involves the crossing of a fitness valley1,2,3. While recombination can bring together multiple mutations within an organism, evolution in asexual populations depends on the sequential accumulation of mutations within a lineage. This can occur by two basic mechanisms. The complex trait can emerge following the sequential fixation of intermediate mutants by drift. This is only likely to occur in small populations where deleterious mutants have a chance to reach fixation. On the other hand, the advantageous type can reach fixation following temporary low level drift of intermediate mutants. This has been called “stochastic tunneling”4 and is likely to occur in larger populations where deleterious mutants cannot reach fixation. The dynamics of valley crossing depend on the mutational pathways and parameters, such as the number of intermediate mutants, their selective disadvantage and mutation rates. The rate at which the fitness valley is crossed and thus the time until the advantageous phenotype emerges, has been analyzed mathematically1,2,3,4,5,6,7,8,9.
In the context of asexual populations, the fitness valley crossing dynamics investigated so far require the sequential accumulation of mutations within individuals. However, if individuals share gene products as public goods, a form of parallel evolution can occur in which the complex trait arises not within one individual, but as an emergent property among cooperating individuals10 through “division of labor” dynamics11,12,13. Production of public goods is a well-known occurrence among microorganisms14,15 and has been documented to occur in tumor cell populations10,16,17,18. This paper examines fitness valley crossing dynamics in the context of division of labor, focusing on the time it takes for the complex trait to arise. It is found that the complex trait invades significantly faster as an emerging property of a cooperating population than through sequential evolution. Interestingly, the evolution of cheaters, which destroy the cooperation dynamics, enables all the mutations to accumulate within one individual on a time scale that is much faster than with sequential evolution. Applications of this accelerated crossing of fitness valleys are discussed in the context of somatic and microbial evolutionary processes.
Results
We consider an agent-based model that describes a habitat which can be occupied by maximally N asexual individuals, i.e. it contains N spots that are either occupied by an individual or empty. Each individual occupies a defined spot. At each time step, an individual reproduces with a given probability and a target spot for the offspring is chosen randomly from a neighborhood of K cells, defined by a “reproduction radius” (supplementary materials). A small radius corresponds to a spatially structured system while larger radii converge to a mass action assumption. Successful reproduction only occurs if the target spot is empty. Further, at each time step, an individual can die with a probability D. Since space is limited, individuals compete for empty spots. At the boundary, individuals are simply assumed to have fewer neighbors (although periodic boundary have conditions have also been implemented, without any qualitative changes in the results).
Several kinds of individuals are considered that differ in their genetic make-ups and replication kinetics. Consider the existence of m genes that express certain products. Wild-types carry un-mutated genes in all sites and have reproduction probability R. It is assumed that a mutation can occur in each of these sites, leading to the production of altered gene products. Further, if all m genes are mutated the individual gains a fitness advantage compared to the wild-type, i.e. it reproduces with a probability R+. However, if only a subset of the genes is mutated, the individual carries a fitness cost compared to the wild-type, reproducing with a probability R−.
In a division-of-labor scenario (Figure 1), we assume that these partial mutant types can share gene products and cooperate with each other through “public goods” to increase fitness. Hence, if within a defined “cooperation radius” (supplementary material), the missing products are provided by at least one individual per site, these can be utilized by the agent, conferring a fitness advantage compared to the wild-type. In this case, the enhanced fitness is an emergent property of a cooperating population. The size of the radius determines how many agents a given cooperator can help. Like the reproduction radius, the cooperation radius is also defined by a neighborhood of K cells and these two radii are assumed to be identical throughout the paper. Because producing public goods typically confers a fitness cost19,20, an amount f is subtracted from the fitness of an agent for each cooperating site. The model also takes account of cheating with respect to the individual sites. A cheater produces a gene product at reduced levels, only available to itself and thus avoids the fitness cost f. We explore two scenarios in which wild-types do and do not benefit from public goods. Both can be realistic, depending on the biological system. For reference, the parameters of this model are summarized in Table 1.
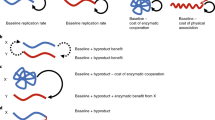
Selection-mutation diagram for the case m = 2.
The lower-case letters a and b denote the unmutated copy of the two genes. The capital letters are mutations giving rise to a cooperating phenotype with respect to the given site. For example, "Ab" denotes a cooperator with respect to the first site, with an unmutated second site. Star indicates a cheater with respect to the given site. The mutations are represented by arrows and the corresponding mutation rates are marked. For simplicity, in this diagram we omitted back-mutations. The fitness of all the types in the presence and in the absence of cooperation is given at the bottom of the diagram, underneath the specific types. For illustration purposes, we used the smaller number of loci, m = 2. A larger number of loci would make a graphical representation intractable. Most simulations were run with m>2.
We note that several variations in these assumptions can reasonably be assumed but that they do not influence the results reported here on a qualitative level. This is explored in the supplementary materials, where we considered the following variations: differences in the reproduction and cooperation radii; the occurrence of a fitness cost in relation to the amount of product that is being produced (leading to a small fitness cost for cheaters, a bigger cost for cooperators and none for wild-types); and the occurrence of a fitness penalty for each intermediate, deleterious mutation that is accumulated.
The simulations are started with all spots filled with wild-type individuals. Upon reproduction, for each site a mutation can lead to the expression of the altered gene product as a public good. Similarly, a mutation can generate a cheater with respect to this site, with lower expression. A cheating gene can further be generated from the corresponding cooperating gene. In each case, back-mutations can occur. These mutational processes are summarized in Figure 1 and equal mutation rates u are assumed for simplicity. For additional modeling details, see supplementary material.
The simplest case assumes no division of labor. In order for the fit m-hit mutant (complex trait) to arise the population must cross a fitness valley, a process that has been extensively studied mathematically and is not explored further3. We call this “sequential evolution”.
Next, assume the generation of cooperators, but the absence of cheaters for the case where wild-types do not benefit from public goods. Now, the complex trait can arise, not within one individual, but also as an emergent property of a cooperating population with enhanced fitness, which becomes dominant (Figure 2a, 3a). This happens significantly faster than the emergence of the m-hit mutant in sequential evolution (Figure 2a). The simultaneous presence of at least one cooperator for each site within the cooperation radius and thus a sufficiently large radius and mutation rate, are required for this to be possible. Note, however, that the m-hit mutant, cooperating at each site, will never invade because it carries the maximal fitness cost. If we assume that wild-types can also benefit from public goods, the complex phenotype cannot arise as an emerging property of cooperating individuals that become dominant (Figure 3b). This is because cooperation increases the wild-type fitness, while cooperating agents pay a cost and thus have a relative disadvantage. They are maintained by the wild-type through mutations. Because wild-type and cooperators enjoy increased fitness from the public goods, however, they still persist at significantly higher levels compared to the partial mutants in the sequential evolution scenario.
Distribution of times until the complex phenotype reaches 90% of the total population, based on repeated runs of the computer simulation.
(a) Scenario where wild-types do not benefit from shared goods. Time until emergence of the m-hit mutant is longest for the “sequential evolution” scenario. Cooperator-cheater dynamics significantly speed up the emergence of the m-hit mutant. In this case, even before the m-hit mutant arises, the complex phenotype arises as an emerging property among cooperating individuals. (b) Scenario where wild-types do benefit from shared goods. In this case, the complex phenotype cannot become dominant as an emergent property among cooperating individuals. Nevertheless, cooperator-cheater dynamics significantly accelerate the emergence of the m-hit mutant compared to the “sequential evolution” scenario. Parameters were chosen as follows. Grid size = 100×100; m = 5; R = 0.15; R+ = 0.5; R− = 0.135; D = 0.1; f = 1/70; u = 3.17×10−3; cooperation and replication radii = 10. (c,d) Assuming only 2 loci does not alter basic conclusions, shown for the scenario where wild-types do not benefit from shared goods. This is demonstrated in the context of smaller (c) and larger (d) radii. Parameters are as in (a) and (b), except the following: (c) m = 2; u = 2.52×10−5. (d) m = 2; cooperation and replication radii = 30; u = 2×10−5.
Time series arising from model simulations under different conditions.
Evolutionary dynamics are shown for the case where cooperation occurs through division of labor without and with the presence of cheaters. The color code is as follows: Wild-type = red; Partial mutant individuals with at least one cooperating site = blue; Partial mutant individuals containing only cheating sites = pink; m-hit cheater mutants = green. (a) Wild-types do not benefit from shared goods. (b) Wild-types do benefit from shared goods. Each graph represents the result of a single implementation of the model. Parameters were chosen as follows. Grid size = 100×100; m = 5; R = 0.15; R+ = 0.5; R− = 0.135; D = 0.1; f = 1/70; u = 3.17×10−3; cooperation and replication radii = 10.
Next, assume the generation of cheaters. In this case the dynamics are similar regardless of whether the wild-type cells benefit from public goods. Since cheating at a given locus increases fitness relative to the cooperating phenotype, cheaters quickly become more dominant (Figure 3). Cooperators are maintained by cheaters and wild-types through mutation, at a level given by

per site per cooperating neighborhood (this approximation is valid if  ). If the level Nc is relatively low, the cooperating phenotype at any given locus goes extinct frequently within the local interaction radius through stochastic effects. The lower the level of Nc, the higher the frequency of extinction events. The local extinction leads to a local crisis of the cooperators/cheaters, their average fitness plunging from R+ to R−. If at this time, an m-hit mutant is present, this reduction in average fitness will allow it to be selected for and to quickly become the dominant population (Figure 3). In this setting the m-hit mutant arises significantly faster than in the sequential evolution scenario (Figure 2). It does so for two reasons: (1) High level replication of cooperators/cheaters ensures fast generation of mutants. While with sequential evolution intermediate mutants replicate at relatively low levels, they replicate at much higher levels in the cooperator/cheater scenario, allowing mutations to be accumulated faster. This is quantified in a Figure 4a. (2) Cheaters reduce the average fitness of the cooperator/cheater population, thus conferring a selective advantage to the m-hit mutant, without which it would not surge to dominance. This point is demonstrated further in Figure 4b, which depicts the emergence of various cell populations in time and space and which shows that the m-hit mutants emerge in local areas where fitness of the agents has been reduced by cheating.
). If the level Nc is relatively low, the cooperating phenotype at any given locus goes extinct frequently within the local interaction radius through stochastic effects. The lower the level of Nc, the higher the frequency of extinction events. The local extinction leads to a local crisis of the cooperators/cheaters, their average fitness plunging from R+ to R−. If at this time, an m-hit mutant is present, this reduction in average fitness will allow it to be selected for and to quickly become the dominant population (Figure 3). In this setting the m-hit mutant arises significantly faster than in the sequential evolution scenario (Figure 2). It does so for two reasons: (1) High level replication of cooperators/cheaters ensures fast generation of mutants. While with sequential evolution intermediate mutants replicate at relatively low levels, they replicate at much higher levels in the cooperator/cheater scenario, allowing mutations to be accumulated faster. This is quantified in a Figure 4a. (2) Cheaters reduce the average fitness of the cooperator/cheater population, thus conferring a selective advantage to the m-hit mutant, without which it would not surge to dominance. This point is demonstrated further in Figure 4b, which depicts the emergence of various cell populations in time and space and which shows that the m-hit mutants emerge in local areas where fitness of the agents has been reduced by cheating.
Mechanisms underlying the accelerated emergence of m-hit mutants in the cooperator/cheater scenario, using the model where wild-types do not benefit from shared goods.
(a) Quantification of replication events of intermediate mutants. The number of replication events of intermediate mutants was counted both for the sequential evolution scenario (dashed line) and for the cooperator/cheater scenario (solid line). Significantly more replication events are seen for the cooperator/cheater scenario once the complex phenotype arises as an emerging property. (b) Evolutionary dynamics in space and time. Each image is a snapshot of the grid status at 10 successive time points. Red indicates wild-type individuals with fitness R; blue indicates mutants with at least one cooperating site, with base fitness R+ minus the appropriate cost for cooperation; yellow indicates partial mutant individuals containing only cheating sites with fitness R+; cyan indicates any individual with fitness R−; green indicates m-hit cheating mutants, with fitness R+; grey indicates an empty spot. Initially, the population is dominated by wild-type individuals (red) and partial mutants have low fitness R− due to absence of cooperation (cyan). Over time, all public goods become available within the required radius due to cooperation and individuals with enhanced fitness R+ emerge. This includes both individuals that contain cooperating sites (blue) and those that only contain cheating sites (yellow). This population grows to dominate the grid. Due to cheating, relatively large areas containing individuals with reduced fitness, R−, appear. Within these areas, the m-hit cheater mutants (green) can thrive if they are generated, because in this environment, the m-hit cheater mutants enjoy a fitness advantage relative to the cooperator/cheater cloud. This occurs in snapshot 7. The areas of reduced fitness in which the m-hit cheater mutants grow are indicated by circles. In the remaining areas, where the fitness of the individuals is higher, the m-hit cheaters do not initially grow because they are not advantageous compared to the existing cooperator/cheater cloud. Over time, the m-hit cheaters take over the grid. Parameters were chosen as follows. Grid size = 100×100; m = 5; R = 0.15; R+ = 0.5; R− = 0.135; D = 0.1; f = 1/70; u = 3.17×10−3; cooperation and replication radii = 10.
Note that while our results have been presented in the context of five loci, they are not dependent on assuming a relatively large number of loci. Figures 2c&d show that results hold true even for the smallest number of loci, i.e. two.
An obvious requirement for the occurrence of the accelerated evolution through cooperation/cheating is that the m-hit mutant does not arise almost instantly during sequential evolution, which would occur if the mutation rate were too high relative to the number of involved loci. In this case, the two evolutionary pathways would not be discernible. To explore the effect of further parameters, Figure 5 shows how the outcome depends on parameters K and R+. The results of numerical simulations show that division of labor dynamics accelerate evolution for relatively small parameters R+ and K. This is in agreement with formula (1) (see solid lines in figure 5), which states that for larger R+ and K the number of cooperators in each individual neighborhood becomes too large and is unlikely to go extinct stochastically. Since it is frequent extinction events that allow the m-hit mutant to dominate the population of cheaters/cooperators, the number Nc in equation (1) must be relatively small to ensure the rapid emergence of the m-hit mutants. It further follows from formula (1) that the number of cooperators in a given neighborhood is proportional to the product of u, the mutation rate and K, the neighborhood size. Thus increasing u or K will have a similar effect on the dynamics of cooperation. Other aspects of parameter dependence of our results are discussed in the supplementary materials. In all cases, the defining condition for the accelerated emergence of m-hit mutants is that the number of cooperators in the individual neighborhoods must be sufficiently low, such that stochastic extinction is likely.
Parameter dependence of the division of labor dynamics compared with the sequential evolution scenario.
Varied are parameters K (the neighborhood size, defining the cooperation and reproduction radii) and R+ (the enhanced fitness of cooperators). Crosses and snowflakes show results of numerical simulations. Crosses correspond to the cases where m-hit mutant is created significantly faster in the division-of-labor scenario compared to the sequential evolution. Snowflakes correspond to the cases where division of labor does not accelerate the emergence of m-hit mutants. For each point, 10 simulations were run both under the division of labor and sequential evolution scenarios. Solid lines are theoretical results from equation (1), showing the levels of the quantity Nc, the number of cooperators per site per neighborhood. Other parameters are m = 5, f = 1/40, u = 3.17×10−3, R− = 0.135, R = 0.15, d = 0.1.
Discussion
Cooperation and division of labor is a common theme in biology, where interactions among independent agents can give rise to emergent properties21. Different individuals, belonging to the same or different species, can cooperate. Cells of an organism certainly cooperate in complex ways and a multitude of cooperative interactions are observed among single celled organisms, both prokaryotic and eukaryotic. An enormous literature in evolutionary biology has accumulated, analyzing such cooperative interactions (e.g. reviewed in22,23,24,25). Most of the literature concentrates on identifying conditions under which cooperation and division of labor can evolve11,13,14,20,22,23,24,25,26,27,28,29,30,31 and how it can persist in the face of cheaters19,20. Among game theoretic approaches, the prisoner's dilemma framework22 has been subject to much investigation and spatially restricted interactions have been shown to promote the resistance of cooperative dynamics against cheaters, due to formation of cooperator clusters32. In their insightful paper, Lehmann and Keller33 classify the conditions required for the evolution of altruism and cooperation.
Our study, in contrast, focuses on a different question. In our system, the conditions for cooperation / division of labor to emerge and persist are satisfied and we do not pose the question of whether cooperation can exist. Instead of examining the evolution of cooperation, we investigated how division of labor and cooperative interactions can give rise to emergent properties that influence other evolutionary processes, i.e. the emergence of a complex phenotype. In the division-of-labor game considered here, we showed that the occurrence of cooperation and cheating can contribute to and accelerate the evolution of complex traits. Cooperation may enable the complex trait to arise as an emerging property across different individuals on a relatively short time-scale. It also allows for higher-level replication of intermediate mutants, which contributes to the faster accumulation of multiple mutations by individuals. Cheating is essential to significantly speed up the invasion of the m-hit mutants compared to sequential evolution, because it lowers the fitness of the dominant cooperating populations and provides the m-hit mutant a relative fitness advantage. Without cheating, m-hit mutants would not enjoy a selective advantage over the dominant populations.
It is important to note that competition for reproduction sites is a crucial component of the model. In the sequential evolution scenario, the intermediate mutants are kept at a low selection-mutation balance, which very much contributes to the long time it takes for the m-hit mutant to arise in this case. Without competition, the intermediate mutants would not be maintained at the selection-mutation balance. Further, in the scenario where there is cooperation but no competition, we note that while the complex phenotype can arise as an emerging property, the m-hit mutant cannot invade because it does not have a fitness advantage over the “collection of cooperators”. Cheaters temporarily drive individual cooperators extinct, allowing the m-hit mutant to have a fitness advantage. All these processes are dependent on the presence of a fixed number of reproductive sites for which individuals compete.
The basic patterns of dynamics hold over a large part of the parameter space (see formula (1) and Supplementary materials) and also under alternative model assumptions regarding the costs associated with intermediate mutants, the penalties that can be associated with cooperating and cheating and the radii of cooperation and reproduction. We observed an acceleration of m-hit mutant emergence through cooperation and cheating both in spatially restricted and mass-action settings. Although restricted radii are more realistic because one individual likely can only provide a gene product to a limited number of others, the cooperation radius needs to be sufficiently large to enable all cooperators to be simultaneously present.
The dynamics described in this paper are likely applicable to somatic and microbial evolutionary processes. One example is the process of carcinogenesis, where tumor cells can either sequentially accumulate multiple mutations required for malignant growth, or individual mutations can be spread among different cooperating cell clones, specific examples of which are discussed in the literature10,16,17,18. Further, the presence of tumor cell clones that fit the definition of cheaters in this context has been documented34,35. Additional investigations and parameter measurements are needed to determine whether the cooperator-cheater dynamics can lead to the accelerated emergence of multi-hit mutants that are responsible for malignancy. Another relevant example are biofilms where cooperation and division of labor have been extensively documented in the literature15,30,36. Again, directed experimental work and parameter estimates are needed to examine whether the cooperator-cheater dynamics can speed up the crossing of fitness valleys in specific microbial systems. It is important to note that the theory presented here is essential to serve as a guide to identify specific instances in which cooperation/cheating can accelerate evolutionary processes in these biological systems. Our theory has identified a new evolutionary pathway and defined the conditions when it can apply and is thus essential for the design of experiments aimed at finding examples in nature.
While in most candidate cases found in the literature, lack of appropriate data prevents a detailed application and parameterization of the model for specific biological systems, there is one example where it is presently possible. This is the evolution of immune escape in human immunodeficiency virus (HIV) infection37, in particular the escape of the virus from cytotoxic T lymphocytes (CTL). They kill infected cells and are thought to be crucial for the control of HIV. Multiple parts of the virus (epitopes) can be simultaneously targeted by different CTL clones and this tends to occur in some patients that control the virus population at relatively low levels38,39,40. In order to escape multiple CTL clones, accumulation of mutations in multiple loci (epitopes) are required by the virus41. When all loci have been mutated (creating an m-hit mutant), the virus can grow unopposed and thus has a fitness advantage compared to the wild-type. When only a subset of loci are mutated, however, the virus can still be targeted by CTL and cannot grow unopposed. In fact, escape mutations have been shown to be associated with a fitness cost, in accordance with our assumptions38,42. Certain types of escape mutants (called T cell antagonists) not only gain a benefit for themselves, but also modulate the CTL, such that they do not kill cells infected with alternative virus strains that do not bear this mutation43,44. Hence, they show a degree of cooperation45. While cooperation or division of labor does not occur through secretion of a shared good, it occurs by negatively influencing a shared enemy, which has the same effect. The traditional types of escape mutants only provide an advantage for themselves by not being recognized and do not benefit other virus strains37. They can thus be considered cheaters in the context of our theory. The supplementary material describes an adaptation of our model to this system and discusses advantages and limitations of this approach. Importantly, estimates for most model parameters are available in the literature. The parameterized model suggests that the cooperator/cheater pathway might be significantly sped up and might in fact be essential for the emergence of an m-hit escape mutant. While further studies are required to examine these evolutionary dynamics in greater depth (see supplementary materials), this is the most detailed application that is currently possible according to our knowledge.
One aspect we have so far not explored in our model is the potential effect of recombination on the evolutionary dynamics. In many situations, this is not applicable because we consider asexual populations. However, recombination can occur in microbial systems and it can occur with HIV because it has a diploid genome46. The effect of recombination on the emergence of multi-hit mutants has been found to be complex and dependent on the particular scenarios and assumptions considered47,48,49,50. In our model, recombination can potentially affect the evolutionary dynamics both in the sequential evolution and in the cooperation/cheater scenarios. In the context of the main model analyzed here, we ran the simulations of Figure 3 with the assumption that recombination can occur. The results are shown in Figure 6 and the exact model assumptions are described in the figure legend. Recombination does not significantly change the time to emergence of the m-hit mutant with the sequential evolution scenario in this parameter regime, because intermediate mutants are kept at low levels and are unlikely to meet. On the other hand, recombination significantly speeds up the emergence of the m-hit mutant with the cooperation/cheater pathway. Cooperation allows the collection of intermediate mutants to attain high levels, facilitating recombination. Similar results are observed for the HIV scenario, which is shown in a figure in the supplementary materials. While recombination accelerates evolution in the context of the cooperator/cheater pathway, it actually slows it down in the context of sequential evolution. Thus, the notions described here hold in the context of recombination. Note, however, that a comprehensive study of recombination in the various scenarios and parameter regimes is beyond the scope of the current paper and subject of future work.
Effect of recombination.
The simulations of Figure 2a were re-run assuming that recombination can occur. This was done by assuming that per time step, there is a probability Rec1 that a “donor” agent meets a “recipient” agent within the reproduction radius. When they do meet, then there is a probability Rec2 for each locus in the recipient to be exchanged with the genotype of the donor. The histograms in (a) present the times until the m-hit mutant reached 90% of the total population under 4 scenarios: cooperation/cheating and sequential evolution, with and without recombination (600 runs per scenario). We observe that sequential evolution takes a lot longer to create m-hit mutants compared to the cooperation/cheating scenario, regardless of the presence of recombination. Panel (b) presents a more detailed picture of the cooperation/cheating scenario (30,000 runs per scenario) and shows that the generation of an m-hit mutant is accelerated in the presence of recombination (the mean times are 33.1 and 41.2, which are significantly different with p<10−10). Recombination introduces no statistically significant difference in the case of sequential evolution. Parameters are the same as in Figure 2a and in addition, Rec1 = 0.1 and Rec2 = 0.01.
Methods
Our results are based on the analysis of stochastic, agent-based models that follow specific rules, described in the main text. The models have been analyzed both by numerical simulations and analytical techniques. The model was coded in FORTRAN and run on a cluster of workstations. In addition, ordinary differential equations (ODEs) were formulated in order to describe aspects of this system and to obtain analytical insights regarding the equilibrium levels of the various populations under considerations and to understand the dynamics observed in the agent-based model. The ODEs were analyzed by standard techniques. Details of calculations are given in the Supplementary Materials.
References
Weinreich, D. M. & Chao, L. Rapid evolutionary escape by large populations from local fitness peaks is likely in nature. Evolution 59, 1175–1182 (2005).
Serra, M. C. & Haccou, P. Dynamics of escape mutants. Theor Popul Biol 72, 167–178 (2007).
Weissman, D. B., Desai, M. M., Fisher, D. S. & Feldman, M. W. The rate at which asexual populations cross fitness valleys. Theoretical Population Biology 75, 286–300 (2009).
Iwasa, Y., Michor, F. & Nowak, M. A. Stochastic tunnels in evolutionary dynamics. Genetics 166, 1571–1579 (2004).
Barton, N. H. & Rouhani, S. The Frequency of Shifts between Alternative Equilibria. Journal of Theoretical Biology 125, 397–418 (1987).
Carter, A. J. R. & Wagner, G. P. Evolution of functionally conserved enhancers can be accelerated in large populations: a population-genetic model. P Roy Soc Lond B Bio 269, 953–960 (2002).
Durrett, R. & Schmidtt, D. Waiting for Two Mutations: With Applications to Regulatory Sequence Evolution and the Limits of Darwinian Evolution. Genetics 180, 1501–1509 (2008).
Iwasa, Y., Michor, F. & Nowak, M. A. Evolutionary dynamics of invasion and escape. Journal of Theoretical Biology 226, 205–214 (2004).
Kimura, M. The role of compensatory neutral mutations in molecular evolution. Journal of Genetics 64, 7–19 (1985).
Axelrod, R., Axelrod, D. E. & Pienta, K. J. Evolution of cooperation among tumor cells. Proc Natl Acad Sci U S A 103, 13474–13479 (2006).
Wahl, L. M. Evolving the division of labour: generalists, specialists and task allocation. J Theor Biol 219, 371–388 (2002).
D'Orazio, A. E. & Waite, T. A. Incomplete division of labor: error-prone multitaskers coexist with specialists. J Theor Biol 250, 449–460 (2008).
Wahl, L. M. The division of labor: genotypic versus phenotypic specialization. Am Nat 160, 135–145 (2002).
Diggle, S. P., Gardner, A., West, S. A. & Griffin, A. S. Evolutionary theory of bacterial quorum sensing: when is a signal not a signal? Philos Trans R Soc Lond B Biol Sci 362, 1241–1249 (2007).
Nadell, C. D., Xavier, J. B., Levin, S. A. & Foster, K. R. The evolution of quorum sensing in bacterial biofilms. PLoS Biol 6, e14 (2008).
Bidard, F. -C., Pierga, J. -Y., Vincent-Salomon, A. & Poupon, M.-F. A. “class action” against the microenvironment: do cancer cells cooperate in metastasis? Cancer and Metastasis Reviews 27, 5–10 (2008).
Deisboeck, T. S. & Couzin, I. D. Collective behavior in cancer cell populations. Bioessays 31, 190–197 (2009).
Sprouffske, K. & Maley, C. C. Cancer Genetics (ed Andrei Thomas-Tikhonenko. ) 471–485 (Springer New York, 2010).
Nowak, M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006).
West, S. A., Griffin, A. S. & Gardner, A. Evolutionary explanations for cooperation. Curr Biol 17, R661–672 (2007).
Wingreen, N. S. & Levin, S. A. Cooperation among microorganisms. Plos Biology 4, 1486–1488 (2006).
Axelrod, R. & Hamilton, W. D. The evolution of cooperation. Science 211, 1390–1396 (1981).
Dugatkin, L. A. The evolution of cooperation. Bioscience 47, 355–362 (1997).
Sachs, J. L., Mueller, U. G., Wilcox, T. P. & Bull, J. J. The evolution of cooperation. Q Rev Biol 79, 135–160 (2004).
Nowak, M. A. & Highfield, R. SuperCooperators: Altruism, Evolution and Why We Need Each Other to Succeed., (Free Press, 2011).
Beshers, S. N. & Fewell, J. H. Models of division of labor in social insects. Annu Rev Entomol 46, 413–440 (2001).
Dugatkin, L. A., Mesterton-Gibbonsand, M. & Houston, A. I. Beyond the prisoner's dilemma: Toward models to discriminate among mechanisms of cooperation in nature. Trends Ecol Evol 7, 202–205 (1992).
Griffin, A. S., West, S. A. & Buckling, A. Cooperation and competition in pathogenic bacteria. Nature 430, 1024–1027 (2004).
Rossetti, V., Schirrmeister, B. E., Bernasconi, M. V. & Bagheri, H. C. The evolutionary path to terminal differentiation and division of labor in cyanobacteria. Journal of Theoretical Biology 262, 23–34 (2010).
West, S. A., Griffin, A. S., Gardner, A. & Diggle, S. P. Social evolution theory for microorganisms. Nat Rev Microbiol 4, 597–607 (2006).
Lion, S., Jansen, V. A. A. & Day, T. Evolution in structured populations: beyond the kin versus group debate. Trends in Ecology & Evolution 26, 193–201 (2011).
Nowak, M. A. & May, R. M. Evolutionary Games and Spatial Chaos. Nature 359, 826–829 (1992).
Lehmann, L. & Keller, L. The evolution of cooperation and altruism - a general framework and a classification of models. J Evolution Biol 19, 1365–1376 (2006).
Feldman, B. J. & Feldman, D. The development of androgen-independent prostate cancer. Nat Rev Cancer 1, 34–45 (2001).
Labrie, F. Blockade of testicular and adrenal androgens in prostate cancer treatment. Nat Rev Urol 8, 73–85 (2011).
Xavier, J. B. & Foster, K. R. Cooperation and conflict in microbial biofilms. Proc Natl Acad Sci U S A 104, 876–881 (2007).
McMichael, A. J. & Phillips, R. E. Escape of human immunodeficiency virus from immune control. Annual Review of Immunology 15, 271–296 (1997).
Crawford, H. et al. Evolution of HLA-B*5703 HIV-1 escape mutations in HLA-B*5703-positive individuals and their transmission recipients. J Exp Med 206, 909–921 (2009).
Harrer, T. et al. Cytotoxic T lymphocytes in asymptomatic long-term nonprogressing HIV-1 infection. Breadth and specificity of the response and relation to in vivo viral quasispecies in a person with prolonged infection and low viral load. J Immunol 156, 2616–2623 (1996).
Chouquet, C. et al. Correlation between breadth of memory HIV-specific cytotoxic T cells, viral load and disease progression in HIV infection. AIDS 16, 2399–2407 (2002).
Nowak, M. A. & May, R. M. Virus dynamics. Mathematical principles of immunology and virology, (Oxford University Press, 2000).
Ganusov, V. V. & De Boer, R. J. Estimating Costs and Benefits of CTL Escape Mutations in SIV/HIV Infection. PLoS Comput Biol 2, e24 (2006).
Klenerman, P. et al. Cytotoxic T-cell activity antagonized by naturally occurring HIV-1 Gag variants. Nature 369, 403–407 (1994).
Meier, U. C. et al. Cytotoxic T lymphocyte lysis inhibited by viable HIV mutants. Science 270, 1360–1362 (1995).
Davenport, M. P. Antagonists or altruists: do viral mutants modulate T-cell responses? Immunol Today 16, 432–436 (1995).
Levy, D. N., Aldrovandi, G. M., Kutsch, O. & Shaw, G. M. Dynamics of HIV-1 recombination in its natural target cells. Proc Natl Acad Sci U S A 101, 4204–4209 (2004).
Bretscher, M. T., Althaus, C. L., Muller, V. & Bonhoeffer, S. Recombination in HIV and the evolution of drug resistance: for better or for worse? Bioessays 26, 180–188 (2004).
Fraser, C. HIV recombination: what is the impact on antiretroviral therapy? J R Soc Interface 2, 489–503 (2005).
Mostowy, R., Kouyos, R. D., Fouchet, D. & Bonhoeffer, S. The Role of Recombination for the Coevolutionary Dynamics of HIV and the Immune Response. Plos One 6 (2011).
Weissman, D. B., Feldman, M. W. & Fisher, D. S. The rate of fitness-valley crossing in sexual populations. Genetics 186, 1389–1410 (2010).
Acknowledgements
The authors wish to thank Brian Skirms, Donald Saari, Simon Levin and David Axelrod for helpful discussions. The work was funded by NIH grants 1R01AI093998-01A1 and 1R01CA129286.
Author information
Authors and Affiliations
Contributions
N.K. and D.W. designed the study and the model and performed analysis. E.U. performed computational analysis.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Komarova, N., Urwin, E. & Wodarz, D. Accelerated crossing of fitness valleys through division of labor and cheating in asexual populations. Sci Rep 2, 917 (2012). https://doi.org/10.1038/srep00917
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00917
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.