Abstract
Quantum coherence is one of the primary non-classical features of quantum systems. While protocols such as the Leggett-Garg inequality (LGI) and quantum tomography can be used to test for the existence of quantum coherence and dynamics in a given system, unambiguously detecting inherent “quantumness” still faces serious obstacles in terms of experimental feasibility and efficiency, particularly in complex systems. Here we introduce two “quantum witnesses” to efficiently verify quantum coherence and dynamics in the time domain, without the expense and burden of non-invasive measurements or full tomographic processes. Using several physical examples, including quantum transport in solid-state nanostructures and in biological organisms, we show that these quantum witnesses are robust and have a much finer resolution in their detection window than the LGI has. These robust quantum indicators may assist in reducing the experimental overhead in unambiguously verifying quantum coherence in complex systems.
Similar content being viewed by others
Introduction
Quantum coherence, or superposition, between different states is one of the main features of quantum systems. This distinctive property, coherence, ultimately leads to a variety of other phenomena, e.g., entanglement1,2. It is also thought to be the power behind several “quantum tools”, including quantum information processing3, metrology4, transport5 and recently, some functions in biological organisms6 (e.g., efficient energy transport).
Identifying quantum coherence and dynamics in an efficient way, given limited system access, is indispensable for ensuring reliable quantum applications in a variety of contexts. Furthermore, the question of whether quantum coherence can really exist in biological organisms in vivo, e.g., in a photosynthetic complex or in an avian chemical compass, surrounded by a hot and wet environment, has triggered a surge of interest into the relationship between quantum coherence and biological function7,8. In these cases, full-system access is often very limited and signatures of quantum coherence are often indirect.
The existing methods for identifying quantum coherent behavior can be generally classified into two types. The first type are based on imposing what can be thought of as a classical constraint9, such as macroscopic realism and non-invasive measurements in the Leggett-Garg inequality (LGI)10, or realism and locality in Bell's Inequality. Even though inequalities like the LGI were originally envisaged as a fundamental test of physical theories, a violation of the LGI can also be considered as a tool for classifying the behavior observed in experiment as quantum or classical. However, the Leggett-Garg inequality faces severe experimental difficulties when used as such a tool as it requires noninvasive measurements, e.g., via quantum nondemolition (QND) measurement11,12, weak measurement13, or quantum-gate-assisted ideal non-invasive measurements14. Because of this only a few tests of the LGI have been reported14,15,16,17,18.
The second type of test is based on deduction; do the results of a given experiment sufficiently correspond to the predictions of quantum theory (or classical theory, depending on the approach). Quantum witnesses can be considered as one such test, as they use the knowledge of a quantum state or of some quantum dynamics to determine whether an experimental system possesses quantum properties. Some examples that have been employed elsewhere include witnesses of entanglement19,20, direct measurement of coherence terms of density matrices, or the analysis of process tomography21 for non-classical state evolutions. The experimental realization of this kind of verification usually needs tomographic techniques and then the required experimental resources in terms of measurement settings increases exponentially with the system complexity19,21,22. Moreover, quantum state and process tomography are still difficult to implement in general systems and for general state evolutions, e.g., particularly in systems like charge transport through nanostructures, the transfer of electronic excitations in a photosynthetic complex, or systems where the state space is large.
In this work, we introduce two quantum witnesses to verify quantum coherence and dynamics in the time domain, both of which have various advantages and disadvantages. Both are efficient in the sense that there is no need to perform noninvasive measurements or to use quantum tomography, dramatically reducing the overhead and complexity of unambiguous experimental verification of quantum phenomena.
We apply these quantum witnesses to five examples: (1) electron-pair tunnelling in a Cooperpair box and coherent evolution of single-transmon qubit, (2) charge transport through double quantum dots, (3) non-equilibrium energy transfer in a photosynthetic pigment-protein complex, (4) vacuum Rabi oscillation in lossy cavities and (5) coherent rotations of photonic qubits. Furthermore, as we will illustrate in these examples, our quantum witnesses possess a finer detection resolution than the LGI.
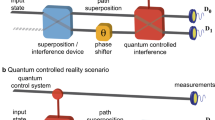
Both witnesses, which we will introduce shortly, involve the following steps: (Figure 1a) first, we prepare the system in a known product state with its environment (or reservoir, here we use both terms interchangeably) ρSR(0). We then let ρSR(0) evolve for a period of time t0, to reach the state ρSR(t0) (during which time one hopes the state has acquired significant coherence due to its internal dynamics). The second step is to implement a quantum witness using a “correlation check” between the state ρSR(t0) and its state at another later time t ≥ t0, ρSR(t) (see Figure 1b). The goal of this correlation check is to investigate non-classical properties in these two-time state-state correlations (see Figure 1c). If the state ρSR(t0) can be detected then by our quantum witness as having quantum properties, this implies that either the system state ρS(t0) = TrR[ρSR(t0)] possesses significant quantum coherence or that the state ρSR(t0) is an entangled system-bath state.
Detecting quantum coherence and dynamics.
Generic procedure for detecting quantum coherence: We need (a) state preparation and (b) a correlation check. With the freedom to manipulate the system state, the initial state of the total system can be reasonably prepared as a product state ρSR(0) = ρS(0)  ρR(0), where ρR(0) is the reservoir state. (b) and (c) show the correlation check, or measurements, we base our quantum witnesses on. Assuming the system state at time t0 is ρS(t0) = Qn(t0), the probability of being in a state Qm at later time t is determined by the n → m propagator Ωmn(t, t0). The general quantum correlator is defined by 〈Qm(t)Qn (t0)〉Q (upper green path) and the classical one is defined by pn(t0)Ωmn(t, t0) (lower brown track). In this expression, Ωmn(t, t0) is the probability of measuring the system in state m at time t given that it was in the state n at time t0. Both definitions describe the connections between Qn(t0) and Qm(t) for arbitrary states ρS(t0) with a distribution of state populations {pn(t0)}. As shown in the Methods, all classical dynamics should satisfy the relation, 〈Qm(t)Qn(t0)〉Q = pn(t0)Ωmn(t, t0). While our quantum witnesses are derived from this “correlation check”, the experimental requirements for each witness differ.
ρR(0), where ρR(0) is the reservoir state. (b) and (c) show the correlation check, or measurements, we base our quantum witnesses on. Assuming the system state at time t0 is ρS(t0) = Qn(t0), the probability of being in a state Qm at later time t is determined by the n → m propagator Ωmn(t, t0). The general quantum correlator is defined by 〈Qm(t)Qn (t0)〉Q (upper green path) and the classical one is defined by pn(t0)Ωmn(t, t0) (lower brown track). In this expression, Ωmn(t, t0) is the probability of measuring the system in state m at time t given that it was in the state n at time t0. Both definitions describe the connections between Qn(t0) and Qm(t) for arbitrary states ρS(t0) with a distribution of state populations {pn(t0)}. As shown in the Methods, all classical dynamics should satisfy the relation, 〈Qm(t)Qn(t0)〉Q = pn(t0)Ωmn(t, t0). While our quantum witnesses are derived from this “correlation check”, the experimental requirements for each witness differ.
Results
In order to find a signature of quantum dynamics we start by seeking characteristic features of classical dynamics or states23. All separable mixtures of system-reservoir states, with no coherent components, which we call classical states, obey the following relation for their two-time correlations:

See Methods for the proof. Succinctly put, equation (1) implies it is possible to define all future behavior based on only the system's instantaneous expectation values pn(t0). However, most quantum correlation functions also obey this relation under certain measurement conditions. For example, a correlation function constructed from two-time projective measurements has this form as the measurement at t0 destroys the coherence in the state at that time. Here Qi is an observable which measures if the system is in the state i. This state is assumed to have a classical meaning (e.g., localized charge state, etc) and the observable is normalized so that its expectation value is directly equal to the probability of observing the system in that state 〈Qi〉 = pi. The propagator Ωmn(t, t0) is the probability of measuring the system in state m at time t given that it was in the state n at time t0 (and which in principle depends on the state of the reservoir, so can include classical non-Markovian correlations, see Methods). Several other recent tests of quantumness18,24,25,26,27 rely on imposing Markovianity on Ωnm(t, t0). In our first witness we avoid taking that approach so that we can still distinguish quantum from classical non-Markovian dynamics. However we will use it in our second witness.
In principle, one could use Eq. (1) to construct a quantum witness of the form:

Where a non-zero result  , implies the state at t0 can be considered as quantum in that it contains quantum coherence which affects its future evolution. However, as mentioned above, most quantum correlation functions also obey equation (1), which will give
, implies the state at t0 can be considered as quantum in that it contains quantum coherence which affects its future evolution. However, as mentioned above, most quantum correlation functions also obey equation (1), which will give  . Is it ever possible to observe a non-zero
. Is it ever possible to observe a non-zero  ? In some cases coherence, or “amplitude”, sensitive correlation functions are encountered in quantum optics28 and in linear-response theory29. However, these are typically extracted from spectral functions in the steady state, or put in a symmetrized form, in which case any effect on the correlation function from the initial state coherence may be lost. In all the examples we consider in this work this witness
? In some cases coherence, or “amplitude”, sensitive correlation functions are encountered in quantum optics28 and in linear-response theory29. However, these are typically extracted from spectral functions in the steady state, or put in a symmetrized form, in which case any effect on the correlation function from the initial state coherence may be lost. In all the examples we consider in this work this witness  cannot be directly measured, as the initial coherence is of course destroyed by the first (projective) measurement. Fortunately,
cannot be directly measured, as the initial coherence is of course destroyed by the first (projective) measurement. Fortunately,  , via Eq. (1), gives us a way to develop a more generally applicable and valid witness.
, via Eq. (1), gives us a way to develop a more generally applicable and valid witness.
Witness 1
Our first practical witness (which is the main result of this work) can be derived from Eq. (1) by including normalization. Noting that all classical system-reservoir states obey,

where d is the number of states n in, or dimensionality of, the system state space, we define our first quantum witness as

If  , we can define the state at t0 as quantum. Compared with the witness
, we can define the state at t0 as quantum. Compared with the witness  and the tests of the LGI,
and the tests of the LGI,  can always be directly measured and ideal non-invasive measurements are not necessary. In experimental realizations, measuring the population-related quantities, or expectation values, 〈Qm(t)〉 and {pn(t0)}, is generally more feasible than constructing full correlation functions, particularly in systems which rely on destructive (e.g., fluorescence) measurements. Where correlation functions can be measured with projective measurements, the second term can of course be replaced with Σn pn(t0)Ωmn(t, t0) ≡ Σn〈Qm(t)Qn(t0)〉.
can always be directly measured and ideal non-invasive measurements are not necessary. In experimental realizations, measuring the population-related quantities, or expectation values, 〈Qm(t)〉 and {pn(t0)}, is generally more feasible than constructing full correlation functions, particularly in systems which rely on destructive (e.g., fluorescence) measurements. Where correlation functions can be measured with projective measurements, the second term can of course be replaced with Σn pn(t0)Ωmn(t, t0) ≡ Σn〈Qm(t)Qn(t0)〉.
However, determining all the propagators Ωmn(t, t0) with which to construct the witness requires, in principle, that we can prepare the system in each one of it states n exactly (or, alternatively if correlation functions constructed from projective measurements are available, it requires that we measure every possible cross-correlation Σn〈Qm(t)Qn(t0)〉). In the former case (where we use state preparation) we trade-off the need to do non-invasive state measurement with the need to perform ideal state preparation. In complex systems it may be difficult to prepare the system in each one of its states to construct these propagators and in some cases we may not even have knowledge of the full state-space of the system.
Importantly, this problem can be easily overcome by noticing that the individual terms in the sum in Eq. (4) are always positive. Thus when constructing the sum we can stop as soon as the witness is violated by this partial summation (i.e., when the terms in the summation together are larger than 〈Qm(t)〉), reducing the experimental overhead substantially (see Figure 4 for a practical example, where we show it is sufficient to include just one term in the sum of Eq. (4)).
Detecting quantum properties of the FMO complex.
Magnitude of the first witness  [Eq. (4) for t − t0 = τ] for the FMO complex assuming the final measurement is done on site m = 1 of the seven site FMO complex, for both (a) T = 77 K and (b) T = 300 K. A detection via our first witness is clearly visible for an initial evolution greater than t0 = 0.3 ps at 77 K. In comparison, for same parameters we employ for the witness, the LG inequality only reveals a violation for upto 0.035 ps44. (c) and (d) show the first witness with only limited access, i.e. with only state preparation and measurement on site 1. Quantum coherence is only detected when p1(t0)Ω11(t, t0) > 〈Q1(t)〉. In all figures the bath parameters used were γ−1 = 50 fs and λ = 35 cm−1 and the Hamiltonian is the same as that used in Ref. 8. For the Hierarchy calculation, we used the “Ishizaki-Tanimura” truncation scheme and truncation as taken at K = 0 and Nc = 8 (see Methods, or Ref. 8, for the meaning of these parameters).
[Eq. (4) for t − t0 = τ] for the FMO complex assuming the final measurement is done on site m = 1 of the seven site FMO complex, for both (a) T = 77 K and (b) T = 300 K. A detection via our first witness is clearly visible for an initial evolution greater than t0 = 0.3 ps at 77 K. In comparison, for same parameters we employ for the witness, the LG inequality only reveals a violation for upto 0.035 ps44. (c) and (d) show the first witness with only limited access, i.e. with only state preparation and measurement on site 1. Quantum coherence is only detected when p1(t0)Ω11(t, t0) > 〈Q1(t)〉. In all figures the bath parameters used were γ−1 = 50 fs and λ = 35 cm−1 and the Hamiltonian is the same as that used in Ref. 8. For the Hierarchy calculation, we used the “Ishizaki-Tanimura” truncation scheme and truncation as taken at K = 0 and Nc = 8 (see Methods, or Ref. 8, for the meaning of these parameters).
Note that with this witness we do not distinguish between just system-coherence or quantum correlations (entanglement) between system and bath/reservoir (see Methods). In addition, if there are classical correlations between system and reservoir, i.e., classical non-Markovian effects30, then some additional experimental overhead is needed to eliminate this from giving a “false positive”. If this overhead is ignored this represents a “loop-hole” in this witness and in some situations may be an obstacle for its unambiguous application. We will discuss this explicitly later with an example of a photosynthetic light-harvesting complex where the system and reservoir are strongly correlated both classically and quantum mechanically.
Witness 2
For our second witness we impose the extra condition that  for
for  , for any time interval τ. This assumption restricts us to a widely-studied subset of quantum processes where the system-bath/reservoir interaction is Markovian. We will show that, under the assumption that our system lies within this subset, quantum properties can be identified without needing to explicitly measure propagators (i.e., neither exact state initialization or non-invasive measurements are required). The trade-off in this case is that the witness cannot distinguish certain types of classical dynamics (e.g., classical non-Markovian), from quantum properties of the system. Still, this witness exceeds the tests proposed in earlier works under the same constraints which still required either non-invasive measurements or state preparation18,25.
, for any time interval τ. This assumption restricts us to a widely-studied subset of quantum processes where the system-bath/reservoir interaction is Markovian. We will show that, under the assumption that our system lies within this subset, quantum properties can be identified without needing to explicitly measure propagators (i.e., neither exact state initialization or non-invasive measurements are required). The trade-off in this case is that the witness cannot distinguish certain types of classical dynamics (e.g., classical non-Markovian), from quantum properties of the system. Still, this witness exceeds the tests proposed in earlier works under the same constraints which still required either non-invasive measurements or state preparation18,25.
This subset of quantum processes can be described as having weak coupling between system and reservoir so that system-reservoir state is always a product state and the bath/reservoir state does not evolve in time, i.e., ρR(t) = ρR(0). A large number of systems exist in this regime30, with well-developed models such as the master equation under the Born approximation operating within this class (see, e.g.30,31,32). For such cases, we can extend the first witness so that we replace the need to prepare the system state with that of needing to repeatedly measure expectation values (not correlation functions) a number of times that scales linearly with system size. To show this, we consider an extension of Eq. (3) involving a system of d linear equations represented in matrix multiplication form as follows:

where the d × d matrix Pj has elements [Pj]kn = pn(t0[j,k]) and Ωmj and Qmj are d × 1 column vectors with elements [Ωmj]n1 = Ωmn[j](τ) and [Q mj]k1 = 〈Qm(t[j,k])〉, respectively. Here, t0[j,k] and t[j,k] constitute the jth nontrivial time-domain set Tj:{t0[j,k], t[j,k]|t[j,k] – t0[j,k] = τ; k = 1, 2, …, d}. For a given time difference τ and a time pair (t0[j,k], t[j,k]) ∈ Tj, one can use the most experimentally-feasible method of measurement, i.e., invasive measurement, to obtain the information about the state populations, pn(t0[j,k]) and the expectation values 〈Qm(t[j,k])〉.
Given a set of measurement results to sufficiently describe the state populations, the vector Ωmj can be determined by simple algebraic methods. For nonzero determinant det(Pj), we have  , where
, where  is the matrix formed by replacing the nth column of Pj by Qmj. For an arbitrary pair of time-domain sets, say Tj and
is the matrix formed by replacing the nth column of Pj by Qmj. For an arbitrary pair of time-domain sets, say Tj and  , we impose an additional condition (not used in the earlier witnesses) that their propagators should be identical for all classical systems (within the subset described above):
, we impose an additional condition (not used in the earlier witnesses) that their propagators should be identical for all classical systems (within the subset described above):  . If the system and its environment are classically-correlated, i.e., they are not in a product state, this assumption does not hold. Any comparison between Ωmj and
. If the system and its environment are classically-correlated, i.e., they are not in a product state, this assumption does not hold. Any comparison between Ωmj and  can be considered as a quantum witness for this subset, such as the vector-element comparison:
can be considered as a quantum witness for this subset, such as the vector-element comparison:

If  and under the assumptions described earlier, we can again assume that some of the (set) of initial states are quantum. Since measuring
and under the assumptions described earlier, we can again assume that some of the (set) of initial states are quantum. Since measuring  requires the information about state populations only and can be performed with invasive observations, implementing
requires the information about state populations only and can be performed with invasive observations, implementing  can be more practical than implementing
can be more practical than implementing  (2) and
(2) and  (4).
(4).
Examples
To illustrate the effectiveness of our witnesses we now present five example systems where they could be applied. For each example we choose which ever witness is more appropriate, given the properties of that system.
Rabi oscillations in superconducting qubits
The oscillations of state populations are commonly thought of as a signature of quantum dynamics. The measurement of these kind of oscillations is widely employed for many experiments. The observation of such oscillations alone, however, is not definitive evidence for the existence of quantum coherent dynamics and can even be mimicked by the solutions of classical autonomous rate equations, e.g., Ref. 33,34.
As a first example of the application of our witnesses we apply  (6) to a two-level system composed of the two lowest-energy states in a single-Cooper-pair box35,36,37, Figure 2a. We can take n = 1, m = 2, for example together with the designation Tj: {t0[j,k] = (k + j – 1)t0, t[1,k] = (k + j – 1)t0 + τ|k = 1, 2} for j = 1, 2, Figure 2b illustrates that the quantum witness
(6) to a two-level system composed of the two lowest-energy states in a single-Cooper-pair box35,36,37, Figure 2a. We can take n = 1, m = 2, for example together with the designation Tj: {t0[j,k] = (k + j – 1)t0, t[1,k] = (k + j – 1)t0 + τ|k = 1, 2} for j = 1, 2, Figure 2b illustrates that the quantum witness  detects the presence of quantumness in the Cooper-pair tunneling. Since only information about state populations is required, this witness is easy to apply in practice with simple invasive measurements and can be readily applied to the existing experiments in the time domain36,37 without any additional experimental overhead.
detects the presence of quantumness in the Cooper-pair tunneling. Since only information about state populations is required, this witness is easy to apply in practice with simple invasive measurements and can be readily applied to the existing experiments in the time domain36,37 without any additional experimental overhead.
Detecting quantum oscillations.
(a) shows a schematic circuit of a single-Cooper-pair box36,37. Its Hamiltonian is described by HCB = EC(1–2ng)/2(|2〉〈2|−|1〉〈1|)−EJ/2(|1〉〈2|+ |2〉〈1|), where EJ and EC are the Josephson energy and the single-Cooper-pair charging energy of the box, respectively. The relative energy of the state with no excess Cooper pairs in the box |1〉 and the state with one excess Cooper pair |2〉, is controlled through the gate voltage, which is parametrized by ng. The resonance of the states |1〉 and |2〉 can be brought from the initial state |1〉 by the applied voltage pulse for ng = 0.5. (b), Detecting quantum dynamics in the resonance of the two charge states (ng = 0.5) with the quantum witness  . We use the realistic parameter EJ = 51.8 µeV. The positive regions are identified as the quantum areas.
. We use the realistic parameter EJ = 51.8 µeV. The positive regions are identified as the quantum areas.
One can also consider an application of our witnesses to single- and multiple-transmon qubits coupled to transmission lines in circuit quantum electrodynamics38,39, where qubit-state measurements are performed by monitoring the transmission through the microwave cavity39. For the simplest case of one-qubit rotation, the coherent evolution is driven by the Hamiltonian38

where ε(t) is the microwave pulse to induce transitions between qubit states |0〉 and |1〉 with an energy difference  ω. Through properly choosing the pulse ε(t), a reliable single-qubit gate, e.g., the Hadamard transformation (H), can be created. Here, we use the quantum-process-tomography-based optimal control theory40 to design the microwave pulse for such a gate (
ω. Through properly choosing the pulse ε(t), a reliable single-qubit gate, e.g., the Hadamard transformation (H), can be created. Here, we use the quantum-process-tomography-based optimal control theory40 to design the microwave pulse for such a gate ( ) with a process fidelity of about 94%. We use the first witness
) with a process fidelity of about 94%. We use the first witness  in the form:
in the form:

to show that the process  creates coherent rotations. When setting the input state as |0〉, the value of our witness is about
creates coherent rotations. When setting the input state as |0〉, the value of our witness is about  , which certifies the quantumness of
, which certifies the quantumness of  .
.
Quantum transport in quantum dots
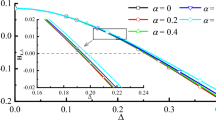
Experimentally distinguishing quantum from classical transport through nanostructure remains a critical challenge in studying transport phenomena and designing quantum electronic devices. As mentioned in the introduction, using time-domain methods to verify quantum coherence, such as by testing the Leggett-Garg inequality, can be very demanding. We illustrate here how our witnesses are valid in a non-equilibrium transport situation by modelling single-electron transport through double quantum dots (Figure 3a). Compared with the time periods identified by the Leggett-Garg-type approach25, the quantum witnesses  (Figure 3b) and
(Figure 3b) and  (Figure 3c) can detect a much larger quantum coherence window. For
(Figure 3c) can detect a much larger quantum coherence window. For  , we employ the settings Tj: {t0[j,k] = [k + c′(j – 1)]t0, t[1,k] = [k + c′(j – 1)]t0 + τ|k = 1, 2 , 3} for j = 1, 2. Here c′ is large such that the whole system is stationary in T2.
, we employ the settings Tj: {t0[j,k] = [k + c′(j – 1)]t0, t[1,k] = [k + c′(j – 1)]t0 + τ|k = 1, 2 , 3} for j = 1, 2. Here c′ is large such that the whole system is stationary in T2.
Detecting quantum transport through a double quantum dot.
(a) Schematic of a single-electron double quantum dot (DQD). Here we assume that the DQD is weakly coupled to leads under a large bias. Its Hamiltonian is HDQD = Δ(|L〉〈R| + |R〉〈L|) with the electron state basis {|L〉,|R〉,|0〉} where Δ is the tunnelling amplitude between the left-dot and right-dot electron states |L〉, |R〉. The transport between dots and leads is described by the self-energy,  , where sL = |0〉〈L|, sR = |R〉〈0| and ΓL and ΓR are the left and right tunnelling rates, respectively. We assume charge detectors (CDs) are used for the measurements, but invasive current measurements are also sufficient (not shown here). (b,c) Verifying quantum transport through DQD with
, where sL = |0〉〈L|, sR = |R〉〈0| and ΓL and ΓR are the left and right tunnelling rates, respectively. We assume charge detectors (CDs) are used for the measurements, but invasive current measurements are also sufficient (not shown here). (b,c) Verifying quantum transport through DQD with  [Eq. (4) for t − t0 = τ] and
[Eq. (4) for t − t0 = τ] and  [Eq. (6)], respectively. Here we define |0〉, |L〉 and |R〉 by |1〉, |2〉 and |3〉, respectively. For the setting ΓL = 4, ΓR = 0.1 and Δ = 1, the non-vanished
[Eq. (6)], respectively. Here we define |0〉, |L〉 and |R〉 by |1〉, |2〉 and |3〉, respectively. For the setting ΓL = 4, ΓR = 0.1 and Δ = 1, the non-vanished  and
and  indicate the quantum-transport regions, where c = (p1p2p3)−1 for the stationary state.
indicate the quantum-transport regions, where c = (p1p2p3)−1 for the stationary state.
Energy transfer in a light-harvesting complex
As an example of the effect of strong interactions with a bath we use a model from bio-physics; energy transport in the Fenna–Matthews–Olson (FMO) pigment-protein complex, where there is thought to be significant system-bath entanglement and coherence8. As mentioned earlier, this example enables to discuss the issue of whether classical-correlations between system and bath can cause a violation of our first witness  (the second witness is not valid in this regime).
(the second witness is not valid in this regime).
In the methods section we impose a classical condition based on an assumption of a class of classical states. States which violate this assumption possess coherences (either in the internal system degrees of freedom, or in the system-bath degrees of freedom, i.e., entanglement). However, to prevent classical correlations between system and bath from causing a false positive, the propagators Ωmn(t, t0) in our witness (4), which we construct by preparing the system in one (or more) of its states, must also capture the classical correlations between system and reservoir present at time t0. In the other examples we discuss in this work, this is trivial since the system and bath are always in a product state. However, in systems like the FMO complex we discuss here, this is not the case. Thus to account for these correlations when constructing Ωmn(t, t0) in a general case we must do the following: prepare the system-bath product state at t = 0, evolve to time t0 and perform a measurement on the system to project it, without preserving coherence, onto one of it states n. We then evolve again, retaining the post-measurement system-bath state and deduce the propagator by measuring the occupation of the state m at final time t. If we can do ideal projective (non-coherence preserving) measurements this accounts for the classical system-bath correlation loophole (as long as we can consistently prepare the t = 0 separable system-bath state). If we are doing destructive or invasive measurements then we must be able to re-prepare the destroyed system state, at time t0, on a time scale faster than the bath/environment dynamics. Since there is no need for measurements on superpositions of basis states, this procedure can be performed without quantum tomography.
We illustrate this with the FMO complex, a seven-site structure used by certain types of bacteria to transfer excitations from a light-harvesting antenna to a reaction center. It has been the focus of a great deal of attention due to experimental observation of apparent “quantum coherent oscillations” at both 77 K and room temperature. To fully capture the non-Markovian and non-perturbative system-bath interactions of this complex system we employ the Hierarchical equations of motion7,8, an exact model (given a bath with a Drude spectral density) valid for both strong system-bath coupling and long-bath memory time. We use the parameters used by Ishizaki and Fleming in Refs. 7,8 and in Figure 4 we show how this model is detected as quantum by our witness  , even at room temperature. We also show, in Figure 4c and 4d, how only partial information about the terms in propagator is needed to find a detection at small times, thus reducing the experimental overhead. In constructing the propagator terms for the sum in Eq. (4) in this case we discard all coherence terms in the physical density matrix but retain the state of the bath, as in43. In this way we account for the state of the bath at time t0, as discussed above. However, accounting for the classical correlations with the reservoir seems beyond the capability of current experiments. We also point out that the full witness detects coherence on timescales greater than t0 = 0.3 ps at 77 K, which is a much larger detection window than the Leggett-Garg inequality (0.035 ps) for the same parameters44.
, even at room temperature. We also show, in Figure 4c and 4d, how only partial information about the terms in propagator is needed to find a detection at small times, thus reducing the experimental overhead. In constructing the propagator terms for the sum in Eq. (4) in this case we discard all coherence terms in the physical density matrix but retain the state of the bath, as in43. In this way we account for the state of the bath at time t0, as discussed above. However, accounting for the classical correlations with the reservoir seems beyond the capability of current experiments. We also point out that the full witness detects coherence on timescales greater than t0 = 0.3 ps at 77 K, which is a much larger detection window than the Leggett-Garg inequality (0.035 ps) for the same parameters44.
Vacuum Rabi oscillation in a lossy cavity
We now consider a Rydberg atom placed in a single-mode cavity which is in resonance with an atomic transition frequency, ω0, for an adjacent pair of circular Rydberg states45 |e〉 and |g〉. Let us consider the case when the cavity field are initially prepared in the excited state |e〉 and the vacuum state |0〉p, respectively (denoted by |1〉 = |e〉 |0〉p). In this case, the atom-field state becomes |2〉 = |g〉 |1〉p due to spontaneous emission and then periodically oscillates between the states |e〉 |0〉p and |g〉 |1〉p at the vacuum Rabi frequency ωR. If the field irreversibly decays due to photon loss out of the cavity, the atomfield stochastically evolves to |3〉 = |g〉 |0〉p from |2〉. Summarizing the above, the time evolution of the atom-field state ρ can be described by the following master equation46

where  is the interaction Hamiltonian of the system. Here κ = ω0/Q and Q is the quality factor of the cavity.
is the interaction Hamiltonian of the system. Here κ = ω0/Q and Q is the quality factor of the cavity.
We now use our second witness to detect the vacuum-Rabi oscillation between the atom and cavity field states. Here we choose the time-domain set as Tj: {t0[j,k] = (k + j – 1)t0, t[1,k] = (k + j – 1)t0 + τ|k = 1, 2, 3} for j = 1, 2. Figure 5 shows the value of the witness for vacuum-Rabi oscillations in a high-Q cavity. Using the experimental parameters from47, where  , the damped coherent oscillations of the atom-cavity state are detected as quantum by our second witness. In comparison, for a low-Q cavity, where 2ωR < ω0/Q, irreversible spontaneous emission out of the cavity will dominate the state evolution. The value of the witness
, the damped coherent oscillations of the atom-cavity state are detected as quantum by our second witness. In comparison, for a low-Q cavity, where 2ωR < ω0/Q, irreversible spontaneous emission out of the cavity will dominate the state evolution. The value of the witness  is zero for this case. The measurements on atom states we require to construct the witness are experimentally available by using field-ionization detectors45 for selecting atom states |e〉 and |g〉.
is zero for this case. The measurements on atom states we require to construct the witness are experimentally available by using field-ionization detectors45 for selecting atom states |e〉 and |g〉.
Detecting vacuum Rabi oscillations in a lossy cavity.
Here we use the experimental data reported in Ref. 47 to illustrate coherence-verification using our second witness Eq. (6). The circular Rydberg states with principle quantum numbers 51 and 50 for transition ω0 = 51.1 GHz are considered as the states |e〉 and |g〉, respectively. The atom-field coupling is ωR/2π = 47 KHz. For a high-Q cavity with Q = 7 × 107, the vacuum Rabi oscillation is detected by use of  where m = n = 1. As a comparison we also checked the case when the Q-factor is so low that 2ωR < ω0/Q. For such a low-Q cavity (e.g., Q = 7 × 105), the state evolution is in the regime of irreversible transitions and obeys the classical constraint (3). Hence the value of the witness is zero.
where m = n = 1. As a comparison we also checked the case when the Q-factor is so low that 2ωR < ω0/Q. For such a low-Q cavity (e.g., Q = 7 × 105), the state evolution is in the regime of irreversible transitions and obeys the classical constraint (3). Hence the value of the witness is zero.
Coherent rotations of photonic quantum bits
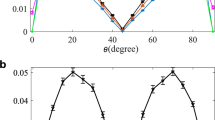
Photon polarization states |H〉 (horizontal) and |V〉 (vertical) have been widely used to achieve linear optical quantum information processing, quantum communication and quantum metrology3,48,49. As a qubit, polarization states can be coherently manipulated by half-wave plates (HWP) and quarter-wave plates (QWP). Arbitrary qubit rotations can be performed by using these linear optics elements. Here we will use our first quantum witness  to detect the quantum coherence of polarization states created by these rotations. The transformations of HWP and QWP can be represented by the following50:
to detect the quantum coherence of polarization states created by these rotations. The transformations of HWP and QWP can be represented by the following50:


As a concrete example, one can set a HWP at φ = π/8 to create a photonic Hadamard gate Hwp(π/8).
To detect the coherent rotations created by R(φ, θ) = Qwp(θ)Hwp(φ), we use the first quantum witness to probe the coherence between states |H〉 and |V〉. While the witness is originally constructed in the time domain, it can be rephrased in terms of the settings (φ, θ). Assuming that both the wave plates are perfect and there is no photon loss in the birefringent crystals of the wave plates, we have the following correspondences:

and

where ρ0 is some initial state created by R. Here m = H and n = V denote the different measurement basis for the horizontal and vertical polarizations. In this example, we set the initial state as ρ0 = R†(φ, θ) |m〉〈m| R(φ, θ) and then the witness becomes

Figure 6 shows this quantum witness for different prepared states ρ0, as a function of the angles θ and φ.
Detecting coherent rotations of photonic qubits.
The first witness  , Eq. (4), adapted from the time-domain to the domain of the angles of several applied transformations, detects quantum coherence in almost the whole range of the prepared states ρ0 (see text) as a function of different angle settings of wave plates (φ, θ): 0 ≤ φ ≤ π/4 and 0 ≤ θ ≤ π/2.
, Eq. (4), adapted from the time-domain to the domain of the angles of several applied transformations, detects quantum coherence in almost the whole range of the prepared states ρ0 (see text) as a function of different angle settings of wave plates (φ, θ): 0 ≤ φ ≤ π/4 and 0 ≤ θ ≤ π/2.
The usual approach to strictly probe the coherent superposition of states |H〉 and |V〉 is via quantum state tomography50. Compared to such tomographic measurements on single qubit states, which require three local measurement settings, only one setting of a local measurement is now sufficient to implement our first witness.
Discussion
In summary, we have formulated a set of quantum witnesses that allow the efficient detection of quantum coherence, without the restriction of non-invasive measurements. Compared to some of the existing methods, such as the Leggett-Garg inequality or employing general quantum tomography, our approach can drastically reduces the overhead and complexity of unambiguous experimental detection of quantum phenomena and has a larger detection window. As illustrated by the five physical examples, these witnesses are robust and can be readily used to explore the presence of quantum coherence in a wide-range of complex systems, e.g., transport in nanostructures, biological systems and perhaps even large-arrays of qubits used in adiabatic quantum computing51. After this paper went to press, we became aware of this preprint52, which has related results.
Methods
Proof of equation (1)
The quantum two-time state-state correlation 〈Qm(t)Qn(t0)〉Q is defined by31:

where ρSR(t0) is the system-reservoir state and U(τ) is the system-reservoir evolution operator for τ = t – t0. If ρSR(t0) is a classical state with no coherent components, then we have

where pn(t0) is the probability of measuring the system state n at time t0 for the classical mixture ρSR(t0) and R(t0) is the reservoir state at time t0 (which in principle depends on the measurement result Qn if the system and reservoir are classically correlated, i.e., are separable but in a mixture of product states). Then we have

The term describing the system's evolution trR[U(τ)Qn(0)R(t0)U†(τ)] can be described by the operator-sum representation21,30:

where  . The the reservoir state is assumed to be R(t0) = Σk prk |rk〉〈rk|. Hence the correlation 〈Qm(t)Qn(t0)〉Q for the system-reservoir classical mixture at the time t0 is
. The the reservoir state is assumed to be R(t0) = Σk prk |rk〉〈rk|. Hence the correlation 〈Qm(t)Qn(t0)〉Q for the system-reservoir classical mixture at the time t0 is

where  is the propagator, i.e., the probability of finding the state m at the time t when the state at an earlier time t0 is initialized at n.
is the propagator, i.e., the probability of finding the state m at the time t when the state at an earlier time t0 is initialized at n.
The Hierarchy model for FMO
The Hierarchy model was originally developed by Tanimura and Kubo41 and has been applied extensively to light-harvesting complexes7,8. We will not give a full description here, but will just summarize the main equation and parameters. It is always assumed that at t = 0 the system and bath are separable  and that the bath is in a thermal equilibrium state
and that the bath is in a thermal equilibrium state  . The bath is assumed to have a Drude spectral density
. The bath is assumed to have a Drude spectral density

where γj is the “Drude decay constant” and each site j is assumed to have its own independent bath. In addition, λj is the reorganisation energy and is proportional to the system-bath coupling strength. The correlation function for the bath is then given by,

where µj,0 = γj and  when m ≥ 1. The coefficients are
when m ≥ 1. The coefficients are

and

Under these assumptions, the Hierarchy equations of motion are given by,

The operator Qj = |j〉〈j| is the projector on the site j and for FMO there are seven sites, thus N = 7. The Liouvillian L describes the Hamiltonian evolution of the FMO complex. The label n is a set of non-negative integers uniquely specifying each equation; n = {n1, n2, n3, …, nN} = {{n10, n11, .., n1K}, .., {nN0, nN1, .., nNK}}. The density matrix labelled by n = 0 = {{0, 0, 0.…}} refers to the system density matrix and all others are non-physical density matrices, termed “auxiliary density matrices”. The density matrices in the equation labelled by  indicate that that density matrix is the one defined by increasing or decreasing the integer in the label n, at the position defined by j and m, by 1.
indicate that that density matrix is the one defined by increasing or decreasing the integer in the label n, at the position defined by j and m, by 1.
The hierarchy equations must be truncated, which is typically done by truncating the largest total number of terms in a label  . This value is termed the tier of the hierarchy. The choice of Nc should be determined by checking the convergence of the system dynamics. Here we also use the “Ishizaki-Tanimura boundary condition”42;
. This value is termed the tier of the hierarchy. The choice of Nc should be determined by checking the convergence of the system dynamics. Here we also use the “Ishizaki-Tanimura boundary condition”42;

This can be summed analytically, which for K = 0 gives,

References
Amico, L., Fazio, R., Osterloh, A. & Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 80, 517 (2008).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Pan, J.-W., Chen, Z.-B., Zukowski, M., Weinfurter, H. & Zeilinger, A. Multi-photon entanglement and interferometry. Rev. Mod. Phys. 84, 777 (2012).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330 (2004).
Brandes, T. Coherent and collective quantum optical effects in mesoscopic systems. Phys. Rep. 408, 315 (2005).
Cheng, Y.-C. & Fleming, G. R. Dynamics of light harvesting in photosynthesis. Annu. Rev. Phys. Chem. 60, 241 (2009).
Ishizaki, A. & Fleming, G. R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc. Natl Acad. Sci. 106, 17255 (2009).
Ishizaki, A., Calhoun, T. R., Schlau-Cohen, G. S. & Fleming, G. R. Quantum coherence and its interplay with protein environments in photosynthetic electronic energy transfer. Phys. Chem. Chem. Phys. 12, 7319 (2010).
Miranowicz, A., Bartkowiak, M., Wang, X., Liu, Y. X. & Nori, F. Testing nonclassicality in multimode fields: a unified derivation of classical inequalities. Phys. Rev. A 82, 013824 (2010).
Leggett, A. J. & Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 54, 857 (1985).
Caves, C. M., Thorne, K. S., Drever, R. W. P., Sandberg, V. D. & Zimmermann, M. On the measurement of a weak classical force coupled to a quantum-mechanical oscillator. I. Issues of principle. Rev. Mod. Phys. 52, 341 (1980).
Bocko, M. F. & Onofrio, R. On the measurement of a weak classical force coupled to a harmonic oscillator: experimental progress. Rev. Mod. Phys. 68, 755 (1996).
Aharonov, Y. & Vaidman, L. Properties of a quantum system during the time interval between two measurements. Phys. Rev. A 41, 11 (1990).
Knee, G. C. et al. Violation of a Leggett-Garg inequality with ideal non-invasive measurements. Nat. Commun. 3, 606 (2012).
Palacios-Laloy, A. et al. Experimental violation of a Bell's inequality in time with weak measurement. Nat. Phys. 6, 442 (2010).
Dressel, J., Broadbent, C. J., Howell, J. C. & Jordan, A. N. Experimental violation of two-party Leggett-Garg inequalities with semiweak measurements. Phys. Rev. Lett. 106, 040402 (2011).
Goggin, M. E. et al. Violation of the Leggett-Garg inequality with weak measurements of photons. Proc. Natl Acad. Sci. 108, 1256 (2011).
Waldherr, G., Neumann, P., Huelga, S. F., Jelezko, F. & Wrachtrup, J. Violation of a temporal Bell inequality for single spins in a diamond defect center. Phys. Rev. Lett. 107, 090401 (2011).
Gühne, O. & Toth, G. Entanglement detection. Phys. Rep. 474, 1 (2009).
Ma, J., Wang, X., Sun, C. P. & Nori, F. Quantum spin squeezing. Phys. Rep. 509, 89 (2011).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, 2000).
Li, C.-M., Chen, K., Reingruber, A., Chen, Y.-N. & Pan, J.-W. Verifying genuine high-order entanglement. Phys. Rev. Lett. 105, 210504 (2010).
Modi, K., Paterek, T., Wonmin, S., Vedral, V. & Williamson, M. Unified view of quantum and classical correlations. Phys. Rev. Lett. 104, 080501 (2010).
Huelga, S. F., Marshall, T. W. & Santos, E. Proposed test for realist theories using Rydberg atoms coupled to a high-Q resonator. Phys. Rev. A 52, R2497 (1995).
Lambert, N., Emary, C., Chen, Y.-N. & Nori, F. Distinguishing quantum and classical transport through nanostructures. Phys. Rev. Lett. 105, 176801 (2010).
Lambert, N., Chen, Y.-N. & Nori, F. Unified single-photon and single-electron counting statistics: from cavity-QED to electron transport. Phys. Rev. A 82, 063840 (2010).
Lambert, N., Johansson, J. R. & Nori, F. Macrorealism inequality for optoelectromechanical systems. Phys. Rev. B 84, 245421 (2011).
Gardiner, C. W. Quantum Noise (Springer, Berlin, 1991).
Mukamel, S. Principles of Nonlinear Optical Spectroscopy (Oxford University Press, 1995).
Breuer, H. P. & Petruccione, F. The Theory of Open Quantum Systems (Oxford University Press, 2007).
Carmichael, H. J. Statistical Methods in Quantum Optics 1: Master Equations and Fokker- Planck Equations (Springer, 2003).
Schlosshauer, M. A. Decoherence and the Quantum-to-Classical Transition (Springer, 2010).
Omelyanchouk, A. N., Shevchenko, S. N., Zagoskin, A. M., Il'ichev, E. & Nori, F. et al. Pseudo-Rabi oscillations in superconducting flux qubits in the classical regime. Phys. Rev. B 78, 054512 (2008).
Timm, C. Random transition-rate matrices for the master equation. Phys. Rev. E 80, 021140 (2009).
Bouchiat, V., Vion, D., Joyez, P., Esteve, D. & Devoret, M. H. Quantum coherence with a single Cooper pair. Physica Scripta 1998, 165 (1998).
You, J. Q. & Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 474, 589 (2011).
Nakamura, Y., Pashkin, Yu. A. & Tsai, J. S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 398, 786 (1999).
Chow, J. M. et al. Randomized benchmarking and process tomography for gate errors in a solid-state qubit. Phys. Rev. Lett. 102, 090502 (2009).
Reed, M. D. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382–385 (2012).
Hwang, C. C. et al. Engineering quantum logic gates with quantum process tomography. .submitted.
Tanimura, Y. & Kubo, R. Time evolution of a quantum system in contact with a nearly Gaussian-Markovian Noise Bath. J. Phys. Soc. Jpn. 58, 101 (1989).
Ishizaki, A. & Tanimura, Y. Quantum dynamics of system strongly coupled to low-temperature colored noise bath: reduced hierarchy equations approach. J. Phys. Soc. Jpn. 74, 3131 (2005).
Dijkstra, A. G. & Tanimura, Y. Non-Markovian entanglement dynamics in the presence of system-bath coherence. Phys. Rev. Lett. 104, 150401 (2010).
Wilde, M. M., McCracken, J. M. & Mizel, A. Could light harvesting complexes exhibit non-classical effects at room temperature? Proc. R. Soc. A 446, 1347 (2010).
Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565582 (2001).
Gerry, C. C. & Knight, P. L. Introductory Quantum Optics (Cambridge University Press, 2005).
Brune, M., Schmidt-Kaler, F., Maali, A., Dreyer, J., Hagley, E., Raimond, J. M. & Haroche, S. Quantum Rabi oscillation: a direct test of field quantization in a cavity. Phys. Rev. Lett 76, 1800 (2001).
Kok, P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135174 (2007).
O'Brien, J. L., Furusawa, A. & Vučković, J. Photonic quantum technologies. Nature Photonics 3, 687 (2009).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194 (2011).
Kofler, J. & Brukner, C. A condition for macroscopic realism beyond the Leggett-Garg inequalities. e-print arXiv: 1207, 3666 (2012).
Acknowledgements
We are grateful to Y. Ota and C. Emary for helpful comments. C.-M.L. acknowledges the partial support from the National Science Council, Taiwan, under Grant No. NSC 101-2112-M-006-016-MY3, No. NSC 101-2738-M-006-005 and No. NSC 103-2911-I-006 -301 and the National Center for Theoretical Sciences (south). Y.-N.C. is partially supported by the National Science Council, Taiwan, under Grant No. NSC 101-2628-M-006-003-MY3. This research was, in part, supported by the Ministry of Education, Taiwan. The Aim for the Top University Project to the National Cheng Kung University. F.N. acknowledges partial support from the Army Research Office, JSPS-RFBR Contract No. 09-02-92114, Grant-in-Aid for Scientific Research (S), MEXT Kakenhi on Quantum Cybernetics and Funding Program for Innovative R&D on S&T (FIRST).
Author information
Authors and Affiliations
Contributions
C.-M.L. devised the basic model. C.-M.L., N.L. and Y.-N.C. established the final framework. C.-M.L. and N.L. performed calculations and wrote the paper. G.-Y.C. attended the discussions. F.N. supervised the project and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Li, CM., Lambert, N., Chen, YN. et al. Witnessing Quantum Coherence: from solid-state to biological systems. Sci Rep 2, 885 (2012). https://doi.org/10.1038/srep00885
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00885
This article is cited by
-
Comparing the quantum witness, the entropic Leggett–Garg inequality and the NCGD
Scientific Reports (2024)
-
Uncertainty Relation of Quantum Coherence Measure Based on Hellinger Distance
International Journal of Theoretical Physics (2024)
-
Gaussian Rényi-2 correlations in a nondegenerate three-level laser
Quantum Information Processing (2024)
-
Remote creation of quantum coherence via indefinite causal order
Quantum Information Processing (2023)
-
Comparing various formulations of macrorealism
Quantum Information Processing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.