Abstract
Integrated photonic resonators are widely used to manipulate light propagation in an evanescently-coupled waveguide. While the evanescent coupling scheme works well for planar optical systems that are naturally waveguide based, many optical applications are free-space based, such as imaging, display, holographics, metrology and remote sensing. Here we demonstrate an active dielectric antenna as the interface device that allows the large-scale integration capability of silicon photonics to serve the free-space applications. We show a novel perturbation-base diffractive coupling scheme that allows a high-Q planer resonator to directly interact with and manipulate free-space waves. Using a silicon-based photonic crystal cavity whose resonance can be rapidly tuned with a p-i-n junction, a compact spatial light modulator with an extinction ratio of 9.5 dB and a modulation speed of 150 MHz is demonstrated. Method to improve the modulation speed is discussed.
Similar content being viewed by others
Introduction
Integrated photonic resonators are widely used to manipulate light propagation in an evanescently-coupled waveguide, resulting in various on-chip photonic devices including electro-optic modulators1,2, filters3,4,5, buffers6,7 and biosensors8,9,10. Their compact sizes, low power consumptions and CMOS-compatibility make low-cost and large-scale optoelectronic integration possible. The evanescent coupling scheme works well for planar optical systems that are naturally waveguide based, such as optical interconnection systems11,12. But many optical applications are free-space based, such as imaging, display, holographics, metrology and remote sensing. While the integrated optics field is focusing on building more complex photonic circuits on chip, the planar geometry will ultimately limit the capability of these circuits. In the two-dimensional (2D) setting, the massive multiplexing capability of optics, which roots from the fact that multiple light beams can propagate in the same space without affecting each other, is not taken full advantage of. Extending the dimension from a planar circuit to a 3D free-space circuit can significantly expand the capability and scalability of optical systems in data communications, processing and storage.
Here we show a new class of photonic device that can directly manipulate free-space waves. This type of device is a bridge for the impressive recent advancement in integrated photonics to be used for free-space optical applications and for building compact 3D optical systems. In particular, we demonstrate a silicon-based spatial light modulator (SLM) which is the key element in many free-space optical systems13. Compared to the existing SLMs14,15,16,17, this silicon-based device offers both high speed and the capability of large-scale integration.
Results
Diffractive coupling
Conventionally, high-Q optical resonators are designed specifically to prevent light from escaping the cavity. Optical coupling to free-space waves is minimized by creating wavevector mismatch between the cavity mode and the free-space waves. No matter how well the cavity is designed, however, light can escape to free space due to optical scattering caused by side-wall roughness. But the scattering is not strong in any particular direction due to the random nature of the roughness. Despite its low intensity, the scattered light can be detected from out-of-plane and the scattering spectrum can be used to determine the resonant wavelength18,19. Given the reciprocity in optics, a free-space wave can couple into the resonator through the reverse process. But the coupling efficiency is so low that it can hardly be seen on the transmission or reflection spectrum of the free-space wave. Special techniques, such as cross-polarization measurements need to be used to detect the resonance20 from out-of-plane. Obviously, this type of weak coupling cannot be used for SLM.
We developed a perturbation-based method to convert a photonic resonator to a dielectric antenna that strongly couple to free-space waves21 with coupling efficiency >90%. The design process starts with a conventional high-Q resonator as the base structure. First, the distribution of an in-plane component of the electric field (e.g. Ex) of the resonating mode is obtained from the numerical simulation. Then a perturbation to the base structure is introduced by adding the high-index material where Ex is positive and removing the high-index material where Ex is negative (or vice versa). This introduces a perturbation polarization  that has the same sign over the entire perturbed area. In the equation,
that has the same sign over the entire perturbed area. In the equation,  is the change in dielectric constant compared to the based structure. According to the coupled-mode theory22,23,
is the change in dielectric constant compared to the based structure. According to the coupled-mode theory22,23,  at each point can be thought as a source for a secondary wave. Since all the secondary waves are in-phase, they interfere constructively and create a strong radiation in the vertical direction. Given the reciprocity in optics, the reverse process couples a normal-incidence optical beam into the resonator. Here we call this coupling method diffractive coupling, which is fundamentally different from the evanescent coupling method currently used to optically access integrated resonators.
at each point can be thought as a source for a secondary wave. Since all the secondary waves are in-phase, they interfere constructively and create a strong radiation in the vertical direction. Given the reciprocity in optics, the reverse process couples a normal-incidence optical beam into the resonator. Here we call this coupling method diffractive coupling, which is fundamentally different from the evanescent coupling method currently used to optically access integrated resonators.
Device design and simulation
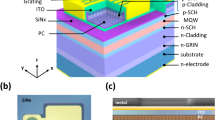
The base resonator structure we use to construct the SLM is a one-dimensional (1D) photonic crystal (PhC) cavity shown in Fig. 1b. The 1D PhC is formed by periodical silicon ribs on a thin silicon slab surrounded by SiO2 claddings and is designed for the TE mode. The silicon slab is used to inject free carriers (electrons and holes) into the cavity from the two sides. A high-Q resonating cavity is formed by gradually adjusting the lattice constant and thus the bandgap of the PhC24,25,26. With a reduced lattice constant in the middle of the PhC, as illustrated in Fig. 1a, the bandgap blue-shifts and a confined cavity mode is supported. The optical response of the device is simulated by the 3D finite-difference time-domain (FDTD) method. The top-view E-field distribution (the Ex component) of the resonant mode is shown in Fig. 1b. One can see that Ex has opposite signs in the neighboring ribs. Thus, to couple this cavity mode to a normal-incidence optical beam, we introduce a perturbation by slightly increasing the widths (in the y-direction) of the ribs by Δw in which Ex > 0 and slightly decreasing the widths of the ribs by Δw in which Ex < 0. The width perturbation of Δw is only applied in the cavity area where the lattice constant of the PhC is reduced.
(a) The band diagram of the 1D PhC cavity as its spatial period varies along the y-direction. The blue shaded area marks the bandgap. (b) Top-view of the PhC cavity where the dashed lines mark the positions of the silicon ribs. The color map shows Ex distribution of the resonant cavity mode. (c) The normal-incidence transmission spectra of the resonator without free carriers (red line) and with a free-carrier density 4×1017 cm−3 (blue line). The dimensions of the device in (b) and (c) are: the height of silicon slab is 50 nm; the height of silicon ribs is 200 nm; The length of the ribs (in the x direction) is 2.5 µm. the lattice constant of the PhC changes gradually from 320 nm outside of the cavity to 280 nm at the center of the cavity in 5 periods. Before introducing the perturbation, the rib width is 50% of the local lattice constant. A width perturbation of Δw = 4 nm is introduced inside the cavity region. The device is fully surrounded by SiO2. (d) The normal-incidence transmission spectra of devices with different perturbations strengths Δw as detailed in the legend. The dimensions for this device are: the height of silicon slab is 50 nm; the height of silicon ribs is 170 nm; The length of the ribs is 4 µm. the lattice constant of the PhC changes from 340 nm outside of the cavity to 290 nm at the center in 7 periods.
The width perturbation allows the cavity to strongly change the transmission and reflection of the normal-incidence waves around the resonant wavelength of the resonator. The red line in Fig. 1c shows the simulated normal-incidence transmission when Δw = 4 nm, which has a sharp dip with an extinction ratio (ER) of over 10-dB and a FWHM bandwidth of 0.2 nm (25 GHz). When free carriers with the density of 4×1017 cm−3 are injected into silicon, the reduction in refractive index causes a blue shift of the resonance1,31 as shown by the blue line and a >10-dB change in the optical transmission at the operation wavelength marked by the dashed line.
We simulated the transmission spectra with different perturbation strengths Δw, which are shown in Fig. 1d. As expected, very little resonance feature can be observed without the perturbation (Δw = 0). As Δw increases, the coupling rate between the cavity mode and the normal-incident beam increases. In this process, the cavity Q drops since the cavity mode escapes more quickly from the resonator, while the ER increases since the coupling rate becomes much higher than the intrinsic loss rate. In this set of simulations, the dimensions of the devices (see figure caption) are revised to match that of the fabricated devices shown below. Given the wafers on hand, the total thickness of the silicon layer is dropped to 220 nm, which results in a lower off-resonance transmission. In order to make optical alignment easier in the measurements, the fabricated devices are designed with a larger cavity area than that in previous simulations.
Performance determining factors
Compared to the micro-gear resonator we demonstrated previously21, this PhC cavity provides much higher ER and much lower insertion loss due to its sub-wavelength periodicity. The off-resonance transmission of the device is higher than 90% (resulting in a low insertion loss) because the silicon ribs with sub-wavelength periodicity do not scatter light. To the incident light with wavelength far from the resonant wavelength, the rib array acts essentially as a uniform effective medium. This is in contrast to the micro-gear resonator which acts as a scattering particle to the off-resonance light due to its wavelength-scale dimension. Besides scattering, off-resonance transmission also depends on layer thicknesses, which will be analyzed in the modeling section of this paper.
The high ER is achieved by eliminating higher-order diffractions21 introduced by the perturbation. For the resonating mode of the cavity, its far-field radiation pattern is determined by the 2D Fourier transform of the perturbation distribution function  , where the higher spatial frequency component of
, where the higher spatial frequency component of  creates radiation at a larger angle. The spatial frequency component with a period shorter than the wavelength do not create far-field radiation, therefore the radiation pattern is determined by the slow-varying profile of
creates radiation at a larger angle. The spatial frequency component with a period shorter than the wavelength do not create far-field radiation, therefore the radiation pattern is determined by the slow-varying profile of  .
.
In the micro-gear structure, the perturbation locates at the inner and outer edges of the rings with radii comparable to the wavelength. Its far-field radiation pattern obtained from 3D FDTD simulation is shown in Fig. 2(a). Besides the 0th-order diffraction that is used to couple the normal-incidence light, there is also a 1st-order diffraction that acts as an addition source of loss for the cavity which limits the extinction ratio of the resonance. In contrast,  in this PhC cavity distributes at the edges of the ribs with a deeply sub-wavelength periodicity. Therefore no higher-order diffraction is expected, which is confirmed by the far-field radiation pattern shown in Fig. 2(b). The optical Q of the PhC cavity is optimized when the cavity mode has a Gaussian profile27. Under that condition,
in this PhC cavity distributes at the edges of the ribs with a deeply sub-wavelength periodicity. Therefore no higher-order diffraction is expected, which is confirmed by the far-field radiation pattern shown in Fig. 2(b). The optical Q of the PhC cavity is optimized when the cavity mode has a Gaussian profile27. Under that condition,  introduced by a constant Δw also has a Gaussian profile and the far-field radiation pattern from the cavity matches well with that of a normal-incident Gaussian beam. This would maximize the coupling efficiency to the resonating mode and the extinction ratio on the transmission spectrum. If coupling to other types of beams is desired, a different distribution of Δw can be used.
introduced by a constant Δw also has a Gaussian profile and the far-field radiation pattern from the cavity matches well with that of a normal-incident Gaussian beam. This would maximize the coupling efficiency to the resonating mode and the extinction ratio on the transmission spectrum. If coupling to other types of beams is desired, a different distribution of Δw can be used.
Simulated far-field angular distribution of the transmitted light from a micro-gear resonator21 (a) or the perturbed 1-D PhC cavity (b) when they are on resonance.
The light-blue ring in (a) shows the 1st-order diffraction of the micro-gear resonator, which is absent from the radiation of the PhC cavity.
Measured spectra from fabricated devices
SLMs with different perturbation strengths Δw are fabricated on a silicon-on-insulator (SOI) substrate by deep-UV lithography in a CMOS photonics foundry (See Methods for details). As shown in Fig. 3a, a p-i-n junction is built across the PhC cavity to control the carrier density in the cavity. Fig. 3b shows an SEM picture of the device taken after the SiO2 top cladding layer is removed by HF wet etching. The design parameters for the fabricated devices are: the height of silicon slab is 50 nm; the height of silicon ribs is 170 nm; The length of the ribs (in the x direction) is 4 µm. The lattice constant of the PhC changes gradually from 340 nm outside the cavity region to 290 nm at the center of the cavity in 7 periods. Without perturbation, the rib width is 50% of the local lattice constant.
The measured normal-incidence transmission and reflection spectra of devices with different width perturbation Δw = 0 nm, 2 nm and 4 nm are shown in Fig. 4a and 4b respectively. As we expected, no resonance feature can be identified if no perturbation is introduced. On the other hand, even a perturbation as small as 2 nm can introduce a strong resonant feature that is clearly observed. The transmission drops over 90% at the resonant wavelength, showing that over 90% of optical power has been coupled into the resonator, which then escape through scattering or reflection. The device with a larger perturbation shows a stronger coupling, a broader bandwidth and a higher ER. The resonant spectra have an asymmetric shape due to the interference from the partial reflections at the multiple dielectric interfaces through the SOI substrate, which is not taken into consideration in the FDTD simulation.
Measured normal-incidence transmission and reflection spectra of the SLMs with different perturbation strengths Δw.
(a) The transmission spectra. (b) The reflection spectrum. In both panels, the symbols are the measured data with Δw = 0 nm (black dots), Δw = 2 nm (red circles) and Δw = 4 nm (blue dimonds). The solid lines are the fitted spectra using the theoretical model with Δw = 2 nm (red line) and Δw = 4 nm (blue line). The spectra are normalized to the transmission and reflection when the optical beam passes through a featureless area of the chip. The featureless area has a transmission of ~50% compared to air (i.e. when the chip is completely removed from the setup), which is mainly due to the reflection from the silicon substrate and optical scattering at the unpolished backside of the chip.
Fitting to theoretical model
The measured spectra agree well with those calculated from an analytical model based on the coupled-mode theory and the transfer matrix method. The device built on the SOI substrate can be modeled as a multilayer dielectric structure28 shown in Fig. 5a. The l-th dielectric interface is described by a transfer matrix  and the l-th layer is described by a transfer matrix (also called propagation matrix)
and the l-th layer is described by a transfer matrix (also called propagation matrix)  , where nl is the refractive index of the l-th layer and dl is the thickness of the l-th layer. The relationship between the amplitudes of the optical waves traveling downward and upward in the (l-1)-th layer and the l-th layer is thus
, where nl is the refractive index of the l-th layer and dl is the thickness of the l-th layer. The relationship between the amplitudes of the optical waves traveling downward and upward in the (l-1)-th layer and the l-th layer is thus  , where the ‘+’ and the ‘−’ signs mark the downward and upward travelling waves respectively. To model the non-resonant behavior of the silicon rib array, the rib layer is modeled as a homogeneous layer with an effective index neff that depends on the occupation ratio of the silicon ribs and the polarization of light.
, where the ‘+’ and the ‘−’ signs mark the downward and upward travelling waves respectively. To model the non-resonant behavior of the silicon rib array, the rib layer is modeled as a homogeneous layer with an effective index neff that depends on the occupation ratio of the silicon ribs and the polarization of light.
(a) A diagram of the multilayer dielectric model of the SLM. The multi-layer structure is described by the transfer matrics Pl and Tl, where l = 1,2..6. The resonant cavity is described by the transfer matrix Tc. (b) Off-resonance transmission versus the total thickness of the silicon layer and the thickness of the slab layer. The diamond and triangle symbols marks the thicknesses used in the FDTD simulations in Fig.1c and Fig.1d, respectively.
The resonance of the PhC cavity is modeled as a virtual interface in the middle of the rib array layer and is described by a transfer matrix Tc, which can be obtained from the coupled-mode theory. Due to the perturbation induced diffraction, the PhC cavity mode couples to both the upward and downward traveling optical beams. It can be express as a single-mode optical resonator coupled with two ports as shown in the inset figure of Fig. 5a. The dynamic equations for the amplitude of the resonance mode can be written as29,30



where ω is the frequency of the input wave and  is the resonant frequency of the PhC cavity. In these equations, s describes the amplitude of the input or output waves, which is normalized such that |s|2 is the power of the wave. a describes the amplitude of the resonant mode, which is normalized such that |a|2 is the energy in the cavity.
is the resonant frequency of the PhC cavity. In these equations, s describes the amplitude of the input or output waves, which is normalized such that |s|2 is the power of the wave. a describes the amplitude of the resonant mode, which is normalized such that |a|2 is the energy in the cavity.  is the intrinsic photonic lifetime of the cavity, which determines the intrinsic quality factor Qi as
is the intrinsic photonic lifetime of the cavity, which determines the intrinsic quality factor Qi as  .
.  and
and  are the field coupling coefficients associate with the downward (
are the field coupling coefficients associate with the downward ( ,
,  ) and upward (
) and upward ( ,
,  ) propagating waves. The coupling quality factor Qc is determined by the coupling coefficients as
) propagating waves. The coupling quality factor Qc is determined by the coupling coefficients as

Under the steady state ( ), the amplitude a of the resonant mode can be expressed as
), the amplitude a of the resonant mode can be expressed as

By plug Eq. (5) into Eq. (2) and (3), one can obtain the transfer matrix of the resonator Tc as .
.
As the propagation property of each layer and their interfaces are described by a (2×2) transfer matrix, the behavior of the entire multilayer structure is determined by the product of these matrices, from which the transmission and reflection spectra of the device are calculated. The ER of the resonance typically increases with the ratio  . The basic parameters of the resonator are obtained by fitting the calculated spectra to the measured ones. For the fabricated device with Δw = 2 nm, the coupling strength
. The basic parameters of the resonator are obtained by fitting the calculated spectra to the measured ones. For the fabricated device with Δw = 2 nm, the coupling strength  and
and  are found to be 1.02×1011 s−1 and 1.17×1011 s−1 respectively, which gives a coupling Q (Qc) of ~5,500. The intrinsic lifetime
are found to be 1.02×1011 s−1 and 1.17×1011 s−1 respectively, which gives a coupling Q (Qc) of ~5,500. The intrinsic lifetime  is 16.4 ps, corresponding to an intrinsic quality factor Qi of ~20,000. The coupled photon life time in the cavity is 3.6 ps, corresponding to a total Q of
is 16.4 ps, corresponding to an intrinsic quality factor Qi of ~20,000. The coupled photon life time in the cavity is 3.6 ps, corresponding to a total Q of  . When the width perturbation increases to be 4 nm, Qi and Qc decrease to 7,000 and 2,300 respectively.
. When the width perturbation increases to be 4 nm, Qi and Qc decrease to 7,000 and 2,300 respectively.
Based on this model, the off-resonance transmission for different thickness of the total silicon layer and slab layer is calculated, which is shown in Fig. 5b. The two marked points represent the two cases that are used in the simulations for Fig. 1c and Fig. 1d, respectively. One can see that the off-resonance transmission can be higher than 99% which optimal layer thicknesses.
High-speed modulation
When a forward bias voltage is applied on the p-i-n junction, free carriers are injected into the cavity which changes the refractive index of silicon and blue-shift the resonance1,31. For a device with Δw = 2 nm, the measured normal-incidence transmission and reflection spectra at different DC bias voltage are shown in Fig. 6a and Fig. 6b, respectively. With a low carrier density (VDC = 0.7 V), the transmission spectrum is the same as that at VDC = 0 V, which shows a resonant dip with an ER of 9.5 dB. When free carriers are injected into the p-i-n junction with a forward bias voltage of 1.0 V, the resonance blue-shifts. Fitting of the spectra gives a decreased intrinsic Q of 11,000 due to the free-carrier absorption effect, while the coupling Q does not change as one expects. The extinction ratio of the resonance drops due to the additional loss in the cavity from the free-carrier absorption effect. The resonances can be seen only when the input light is x-polarized (E-field parallel to the ribs), which interacts with the TE mode of the cavity. The y-polarized light does not couple to the resonant mode, therefore its transmission and reflection are nearly constant, as the dashed lines in Fig. 6a and 6b show. The transmission and reflection of the y-polarized light are different from the off-resonance transmission and reflection of the x-polarized light, because the effective index of the sub-wavelength grating as an effective medium is different for the two polarizations.
Measured normal-incidence transmission (a) and reflection (b) spectra of the SLM with a perturbation of Δw = 2 nm under different bias voltages VDC.
Blue line: VDC = 0.7 V; green line: VDC = 1.0 V; red line: VDC = 1.1 V. The solid lines are measured when the E-field of the normal-incidence light is parallel to the silicon slabs (x-polarized). The dashed black line is measured when the E-field is perpendicular to the silicon slabs (y-polarized). The spectra are normalized to the transmission and reflection when the optical beam passes through a featureless area of the chip.
Due to the asymmetrical line shape of the resonant spectra, the transition from low to high transmission happens in a wavelength range much narrower than the total Q of the resonator suggests. Here we define an effective Q to describe the sharpness of the transition edge, which determines the modulation efficiency of the SLM. In the measured device with Δw = 2 nm,  , where λ0 is the resonant wavelength and Δλ is the wavelength different between the minimal and maximal transmission points, as shown in Fig. 6a.
, where λ0 is the resonant wavelength and Δλ is the wavelength different between the minimal and maximal transmission points, as shown in Fig. 6a.
When the laser wavelength is fixed at 1547.4 nm and the bias voltage on the p-i-n junction is scanned, the transfer function is plotted in Fig. 7a. Transmission changes significantly when the bias voltage changes only 0.1 V. To show the high-speed modulation, a 150-MHz pseudo-random data sequence is applied on the p-i-n junction and the waveform of the transmitted optical signal is shown in Fig. 7b.
Discussion
The speed of the SLM is limited by the width of the p-i-n junction in this device where the intrinsic region is ~5-µm wide. The relatively wide intrinsic region limit the strength of the electric field inside the junction for carrier exaction and electrons have to travel a longer distance to go out of the wider junction. Since the optical field intensity is minimal in the areas between the silicon ribs, as shown in Fig. 1b, much narrower p-i-n junctions can be built without significantly increasing the cavity loss by extending the p- and n- doped regions in to these areas in an interleaving fashion. Multi-GHz modulation32 can be achieved with such a design.
The measured and simulated spectra of devices with different perturbation strengths are fitted with the theoretical model, from which the intrinsic Q (Qi) and coupling Q (Qc) are extracted and listed in Table 1. From the simulation results, one can see that the Qc roughly scales inversely with the square of perturbation strength (i.e.  ). This is consistent with the prediction of Eq. (4) where the field coupling efficiencies
). This is consistent with the prediction of Eq. (4) where the field coupling efficiencies  and
and  are expected to increase linearly with Δw. The intrinsic Q of the fabricated device is lower than that of the simulated one. This is mainly due to the scattering loss from the side-wall roughness and other fabrication imperfection.
are expected to increase linearly with Δw. The intrinsic Q of the fabricated device is lower than that of the simulated one. This is mainly due to the scattering loss from the side-wall roughness and other fabrication imperfection.
Besides that, there are two phenomena that are not expected from the basic theory. One is that Qi drops as the perturbation increases, which can be seen from both simulations and the experiments. We believe this drop is just an artifact from the fitting process. In the fitting process, the ratio  is adjusted to have the ER of the calculated spectra match that of the simulated or measured ones. In theory, ER increase with the ratio
is adjusted to have the ER of the calculated spectra match that of the simulated or measured ones. In theory, ER increase with the ratio  . However, ER in the simulated and measured spectra also depends on how well the far-field radiation pattern of the cavity matches the spatial profile of the input optical beam. The drop of ER due to an imperfect match caps
. However, ER in the simulated and measured spectra also depends on how well the far-field radiation pattern of the cavity matches the spatial profile of the input optical beam. The drop of ER due to an imperfect match caps  in the fitting process, so that Qi appears to decrease with Qc. The fabricated device with Δw = 8 nm shows a more significant drop in Qi. That is because the width of the narrowest trenches in this structure falls just below the resolution of the optical lithography process, so that some trenches are not completely cleared, which introduces extra optical loss in the cavity. The other unexpected phenomenon is that the diffractive coupling in the measured device is much stronger (represented by a lower Qc) than that obtained in the simulation with the same perturbation strength. It is yet to know whether this is due to a systematical under-estimation of the coupling strength in the simulation, or due to that the fabricated device has a larger perturbation than what is designed.
in the fitting process, so that Qi appears to decrease with Qc. The fabricated device with Δw = 8 nm shows a more significant drop in Qi. That is because the width of the narrowest trenches in this structure falls just below the resolution of the optical lithography process, so that some trenches are not completely cleared, which introduces extra optical loss in the cavity. The other unexpected phenomenon is that the diffractive coupling in the measured device is much stronger (represented by a lower Qc) than that obtained in the simulation with the same perturbation strength. It is yet to know whether this is due to a systematical under-estimation of the coupling strength in the simulation, or due to that the fabricated device has a larger perturbation than what is designed.
Methods
SLMs are fabricated in a CMOS photonics foundry at the Institute of Microelectronics of Singapore. The fabrication starts on an SOI wafer with a 220-nm-thick silicon layer and a 3-μm-thick buried oxide layer. To construct the 1D PhC cavities, silicon ribs with the height of 170 nm are patterned on a silicon slab with the thickness of 50 nm using 248-nm deep-UV lithography and inductively-coupled plasma etching. Following the etching, the p-i-n junctions are formed by patterned ion implantations with a dosage of 5×1014 cm−2 for both the p+ and n+ doping regions. A 2.1-μm-thick SiO2 layer is then deposited onto the wafer using plasma-enhanced chemical vapor deposition (PECVD). Finally, vias are opened on the ion-implanted areas and a 1.5-μm-thick aluminum layer is sputtered and etched to form the electric connections. The serial resistance of the diode is measured to be 105 Ω. After the fabrication process, the contact pads connecting to the p-i-n junction are wire-bonded to a SMA connector with a 50-ohms terminal resistor for impedance match.
The 3D FDTD simulations are done with commercial software Lumermical FDTD. A non-uniform grid is used which has a spatial resolution ~30 nm around the resonator. Even though perturbation we introduced is much smaller than the grid size, the software is capable of incorporate that in the simulation. When a dielectric interface (Si/SiO2) lies between two grid points, the program modifies the dielectric constant at the neighboring grid points according to the position of interface. This way, the small shift of the dielectric interface due to the width perturbation is taken into account in the simulation.
The transmission and reflection spectra are measured with a tunable laser whose fiber-coupled output is collimated to form a free-space optical beam. The polarization of the light is adjusted by a polarization controller. Then the optical beam is focused onto the device from top with an aspheric lens. The transmission through the back of the chip is collimated by a lens and measured with a photodetector. The reflection spectra are taken by inserting a beam splitter in the path of the incident light beam. Electro-optic modulation is achieved by applying DC and RF voltages on the p-i-n junctions through the SMA connector.
References
Xu, Q., Schmidt, B., Pradhan, S. & Lipson, M. Micrometre-scale silicon electro-optic modulator. Nature 435 (7040), 325–327 (2005).
Watts, M. R., Zortman, W. A., Trotter, D. C., Young, R. W. & Lentine, A. L. Vertical junction silicon microdisk modulators and switches. Opt. Express 19 (22), 21989–22003 (2011).
Rasras, M. S. et al. Demonstration of a Tunable Microwave-Photonic Notch Filter Using Low-Loss Silicon Ring Resonators. J. Lightwave Technol. 27 (12), 2105–2110 (2009).
Shen, H. et al. Eight-channel reconfigurable microring filters with tunable frequency, extinction ratio and bandwidth. Opt. Express 18 (17), 18067–18076 (2010).
Qing, L., Yegnanarayanan, S., Soltani, M., Alipour, P. & Adibi, A. A Temperature-Insensitive Third-Order Coupled-Resonator Filter for On-Chip Terabit/s Optical Interconnects. Photonics Technology Letters, IEEE 22 (23), 1768–1770 (2010).
Xu, Q., Dong, P. & Lipson, M. Breaking the delay-bandwidth limit in a photonic structure. Nature Phys 3 (6), 406–410 (2007).
Xia, F. N., Sekaric, L. & Vlasov, Y. Ultracompact optical buffers on a silicon chip. Nature Photonics 1 (1), 65–71 (2007).
Bailey, R. C., Washburn, A. L. & Gunn, L. C. Label-Free Quantitation of a Cancer Biomarker in Complex Media Using Silicon Photonic Microring Resonators. Analytical Chemistry 81 (22), 9499–9506 (2009).
Claes, T. et al. Label-Free Biosensing With a Slot-Waveguide-Based Ring Resonator in Silicon on Insulator. Ieee Photonics Journal 1 (3), 197–204 (2009).
Ramachandran, A. et al. A universal biosensing platform based on optical micro-ring resonators. Biosensors and Bioelectronics 23 (7), 939–944 (2008).
Ahn, J. et al. Devices and architectures for photonic chip-scale integration. Applied Physics A-Materials Science & Processing 95 (4), 989–997 (2009).
Shacham, A., Bergman, K. & Carloni, L. P. Photonic Networks-on-Chip for Future Generations of Chip Multiprocessors. IEEE Trans. Comput. 57 (9), 1246–1260 (2008).
Efron, U. Spatial light modulator technology: materials, devices and applications. (Marcel Dekker, 1994).
Wagner, E. P., Smith, B. W., Madden, S., Winefordner, J. D. & Mignardi, M. Construction and Evaluation of a Visible Spectrometer Using Digital Micromirror Spatial Light Modulation. Appl. Spectrosc. 49 (11), 1715–1719 (1995).
Ouyang, G., Wang, K., Henriksen, L. & Chen, X. Electroactive polymer-based spatial light modulator with high reliability and fast response speed. Opt. Eng. 50 (12), 124001–124004 (2011).
Sakarya, S., Vdovin, G. & Sarro, P. M. Spatial light modulators based on micromachined reflective membranes on viscoelastic layers. Sensors and Actuators A: Physical 108, 271–275 (2003).
Wang, X. et al. Performance evaluation of a liquid-crystal-on-silicon spatial light modulator. Opt. Eng. 43 (11), 2769–2774 (2004).
Qiu, C. Y., Shu, J., Li, Z., Zhang, X. Z. & Xu, Q. F. Wavelength tracking with thermally controlled silicon resonators. Opt. Express 19 (6), 5143–5148 (2011).
Portalupi, S. L. et al. Planar photonic crystal cavities with far-field optimization for high coupling efficiency and quality factor. Opt. Express 18 (15), 16064–16073 (2010).
Galli, M. et al. Light scattering and Fano resonances in high-Q photonic crystal nanocavities. App. Phys. Lett. 94 (7) (2009).
Qiu, C. & Xu, Q. Controlling normal incident optical waves with an integrated resonator. Opt. Express 19 (27), 26905–26910 (2011).
Yariv, A. Coupled-Mode Theory for Guided-Wave Optics. IEEE J. Quantum Electron. Qe 9 (9), 919–933 (1973).
Haus, H. A. & Huang, W. Coupled-mode theory. Proceedings of the Ieee 79 (10), 1505–1518 (1991).
Song, B.-S., Noda, S., Asano, T. & Akahane, Y. Ultra-high-Q photonic double-heterostructure nanocavity. Nat Mater 4 (3), 207–210 (2005).
Notomi, M., Kuramochi, E. & Taniyama, H. Ultrahigh-Q Nanocavity with 1D Photonic Gap. Opt. Express 16 (15), 11095–11102 (2008).
Deotare, P. B., McCutcheon, M. W., Frank, I. W., Khan, M. & LonCar, M. High quality factor photonic crystal nanobeam cavities. App. Phys. Lett. 94 (12), 121106–121103 (2009).
Akahane, Y., Asano, T., Song, B. S. & Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 425 (6961), 944–947 (2003).
Lee, W. & Degertekin, F. L. Rigorous Coupled-Wave Analysis of Multilayered Grating Structures. JOURNAL OF LIGHTWAVE TECHNOLOGY 22(10), 2359–2263 (2004).
Fan, S., Suh, W. & Joannopoulos, J. D. Temporal coupled-mode theory for the Fano resonance in optical resonators. JOSA A 20(3), 569–572 (2003).
Manolatou, C., Khan, M. J., Fan, S., Villeneuve, Pierre, R., Haus, H. A. & Joannopoulos, J. D. Coupling of modes analysis of resonant channel add-drop filters. IEEE JOURNAL OF QUANTUM ELECTRONICS 35(9), 1322–1331(1999).
Soref, R. A. & Bennett, B. R. Electrooptical effects in silicon. IEEE J. Quant. Electron. 23(1), 123–129 (1987).
Xu, Q., Manipatruni, S., Schmidt, B., Shakya, J. & Lipson, M. 12.5 Gbit/s carrier-injection-based silicon micro-ring silicon modulators. Opt. Express 15 (2), 430–436 (2007).
Acknowledgements
This work was partially supported by Air Force Office of Scientific Research (AFOSR grants FA9550-12-1-0261).
Author information
Authors and Affiliations
Contributions
Q. X. designed and simulated the device, supervised the project and prepared the manuscript. C. Q. and J. C. performed the experimental measurements. C. Q. analyzed the data, built the analytical model and contributed to the preparation of the manuscript. C. Q. and Y. X. took the SEM image of the device.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Qiu, C., Chen, J., Xia, Y. et al. Active dielectric antenna on chip for spatial light modulation. Sci Rep 2, 855 (2012). https://doi.org/10.1038/srep00855
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00855
This article is cited by
-
Nanoscale modeling of dynamically tunable planar optical absorbers utilizing InAs and InSb in metal-oxide-semiconductor–metal configurations
Discover Nano (2023)
-
A full degree-of-freedom spatiotemporal light modulator
Nature Photonics (2022)
-
Nano-electromechanical spatial light modulator enabled by asymmetric resonant dielectric metasurfaces
Nature Communications (2022)
-
Ultra-broadband spatial light modulation with dual-resonance coupled epsilon-near-zero materials
Nano Research (2021)
-
Coherence measure in terms of the Tsallis relative α entropy
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.