Abstract
Prediction and control of the dynamics of complex networks is a central problem in network science. Structural and dynamical similarities of different real networks suggest that some universal laws might accurately describe the dynamics of these networks, albeit the nature and common origin of such laws remain elusive. Here we show that the causal network representing the large-scale structure of spacetime in our accelerating universe is a power-law graph with strong clustering, similar to many complex networks such as the Internet, social, or biological networks. We prove that this structural similarity is a consequence of the asymptotic equivalence between the large-scale growth dynamics of complex networks and causal networks. This equivalence suggests that unexpectedly similar laws govern the dynamics of complex networks and spacetime in the universe, with implications to network science and cosmology.
Similar content being viewed by others
Introduction
Physics explains complex phenomena in nature by reducing them to an interplay of simple fundamental laws. This very successful tradition seems to experience certain difficulties in application to complex systems in general and to complex networks in particular, where it remains unclear if there exist some unique universal laws explaining a variety of structural and dynamical similarities found in many different real networks1,2,3,4,5,6,7. One could potentially remedy this situation by identifying a well-understood physical system whose large-scale dynamics would be asymptotically identical to the dynamics of complex networks. One could then try to use the extensively studied dynamical laws of that physical system to predict and possibly control the dynamics of networks. At the first glance, this program seems to be quite difficult to execute, as there are no indications where to start. Yet we show here that there exists a very simple but completely unexpected connection between networks and cosmology.
In cosmology, de Sitter spacetime plays a central role as the exact solution of Einstein's equations for an empty universe, to which our universe asymptotically converges. Here we show that graphs encoding the large-scale causal structure of de Sitter spacetime and our universe have structure common to many complex networks8,9,10 and that the large-scale growth dynamics of these causal graphs and complex networks are asymptotically the same. To show this, we describe the causal graphs first.
The finite speed of light c is a fundamental constant of our physical world, responsible for the non-trivial causal structure of the universe11. If in some coordinate system the spatial distance x between two spacetime events (points in space and time) is larger than ct, where t is the time difference between them, then these two events cannot be causally related since no signal can propagate faster than c (Fig. 1(a)). Causality is fundamental not only in physics, but also in fields as disparate as distributed systems12,13 and philosophy14.
Finite speed of light c and causal structure of spacetime.
In panel (a), a light source located at spatial coordinate x = 0 is switched on at time t = 0. This event, denoted by L in the figure, is not immediately visible to an observer located at distance x0 from the light source. The observer does not see any light until time t = x0/c. Since no signal can propagate faster than c, the events on the observer's world line, shown by the vertical dashed line, are not causally related to L until the world line enters the L's future light cone (yellow color) at t = x0/c. This light cone depicts the set of events that L can causally influence. An example is event P located on the observer's world line x = x0 at time t = t0 > x0/c. The past light cone of P (green color) is the set of events that can causally influence P. Events L and P lie within each other's light cones. Panel (b) shows a set of points sprinkled into the considered spacetime patch. The red and green links show all causal connections of events L and P in the resulting causet. These links form a subset of all the links in the causet (not shown). Eyes are (c) Pix by Marti - Fotolia.com
The main physical motivation for quantum gravity is that at the Planck scale (lP ~ 10–35 meters and tP ~ 10–43 seconds), one expects spacetime not to be continuous but to have a discrete structure15, similar to ordinary matter, which is not continuous at atomic scales but instead is composed of discrete atoms. The mathematical fact that the structure of a relativistic spacetime is almost fully determined by its causal structure alone16,17,18 motivates the causal set approach to quantum gravity19. This approach postulates that spacetime at the Planck scale is a discrete causal set, or causet. A causet is a set of elements (Planck-scale “atoms” of spacetime) endowed with causal relationships among them. A causet is thus a network in which nodes are spacetime quanta and links are causal relationships between them. To make contact with General Relativity, one expects the theory to give rise to causal sets which are constructed by a Poisson process, i.e. by sprinkling points into spacetime uniformly at random and then connecting each pair of points if they lie within each other's light cones (Fig. 1(b)). According to the theorem in Ref. 20, causets constructed by Poisson sprinkling are relativistically invariant, as opposed to regular lattices, for example. Therefore we will use Poisson sprinkling here to construct causets corresponding to spacetimes. An important goal in causal set quantum gravity (not discussed here) is to identify fundamental physical laws of causet growth consistent with Poisson sprinkling onto realistic spacetimes in the classical limit21,22.
In 1998 the expansion of our universe was found to be accelerating23,24. Positive vacuum energy, or dark energy, corresponding to a positive cosmological constant Λ in the Einstein equations (Supplementary Notes, Section II), is currently the most plausible explanation for this acceleration, even though the origin and nature of dark energy is one of the deepest mysteries in contemporary science25. Positive Λ implies that the universe is asymptotically (at late times) described by de Sitter spacetime26,27. We first consider the structure of causets sprinkled onto de Sitter spacetime, then quantify how different this structure is for the real universe and finally prove the asymptotic equivalence between the growth dynamics of de Sitter causets and complex networks.
Results
Structure of de Sitter causets
De Sitter spacetime is the solution of Einstein's field equations for an empty universe with positive cosmological constant Λ. The (1+1)-dimensional de Sitter spacetime (the first ‘1’ stands for the space dimension; the second ‘1’—for time) can be visualized as a one-sheeted 2-dimensional hyperboloid embedded in a flat 3-dimensional Minkowski space (Fig. 2(a)). The length of horizontal circles in Fig. 2(a), corresponding to the volume of space at a moment of time, grows exponentially with time t. Since causet nodes are distributed uniformly over spacetime, their number also grows exponentially with time, while as we show below, their degree decays exponentially, resulting in a power-law degree distribution in the causet.
Mapping between the de Sitter universe and complex networks.
Panel (a) shows the 1+1-dimensional de Sitter spacetime represented by the upper half of the outer one-sheeted hyperboloid in the 3-dimensional Minkowski space XY Z. The spacetime coordinates (θ, t), shown by the red arrows, cover the whole de Sitter spacetime. The spatial coordinate θ0 of any spacetime event, e.g. point P, is its polar angle in the XY plane, while P's temporal coordinate t0 is the length of the arc lying on the hyperboloid and connecting the point to the XY plane where t = 0. At any time t, the spatial slice of the spacetime is a circle. This 1-dimensional space expands exponentially with time. Dual to the outer hyperboloid is the inner hyperboloid—the hyperbolic 2-dimensional space, i.e. the hyperbolic plane, represented by the upper sheet of a two-sheeted hyperboloid. The mapping between the two hyperboloids is shown by the blue arrows. The green shapes show the past light cone of point P in the de Sitter spacetime and the projection of this light cone onto the hyperbolic plane under the mapping. Panel (b) depicts the cut of panel (a) by the YZ plane to further illustrate the mapping, shown also by the blue arrows. The mapping is the reflection between the two hyperboloids with respect to the cone shown by the dashed lines. Panel (c) projects the inner hyperboloid (the hyperbolic plane) with P's past light cone (the green shape) onto the XY plane. The red shape is the left half of the hyperbolic disc centered at P and having the radius equal to P's time t0, which in this representation is P's radial coordinate, i.e. the distance between P and the origin of the XY plane. The green and red shapes become indistinguishable at large times t0 as shown in panels (d,e,f) where these shapes are drawn for t0 = 5, 10, 15 using the exact expressions from Section II of Supplementary Notes. Assuming the average degree of  , these t0 times correspond to network sizes of approximately 40, 200 and 2000 nodes.
, these t0 times correspond to network sizes of approximately 40, 200 and 2000 nodes.
To obtain this result, we consider in Fig. 2(a) a patch of (1+1)-dimensional de Sitter spacetime between times t = 0 (the “big bang”) and t = t0 > 0 (the “current” time) and sprinkle N nodes onto it with uniform density δ. In this spacetime the element of length ds (often called the metric because its expression contains the full information about the metric tensor) and volume dV (or area, since the spacetime is two-dimensional) are given by the following expressions (Supplementary Notes, Section II):


where  is the angular (space) coordinate on the hyperboloid. In view of the last equation and uniform sprinkling, implying that the expected number of nodes dN in spacetime volume dV is dN = δ dV, the temporal node density ρ(t) at time
is the angular (space) coordinate on the hyperboloid. In view of the last equation and uniform sprinkling, implying that the expected number of nodes dN in spacetime volume dV is dN = δ dV, the temporal node density ρ(t) at time  is
is

where the last approximation holds for  .
.
Since links between two nodes in the causet exist only if the nodes lie within each other's light cones, the expected degree  of a node at time coordinate
of a node at time coordinate  is proportional to the sum of the volumes of two light cones centered at the node: the past light cone cut below at t = 0 and the future light cone cut above at t = t0, similar to Fig. 1. Denoting these volumes by Vp(t) and Vf(t) and orienting causet links from the future to the past, i.e. from nodes with higher t to nodes with lower t, we can write
is proportional to the sum of the volumes of two light cones centered at the node: the past light cone cut below at t = 0 and the future light cone cut above at t = t0, similar to Fig. 1. Denoting these volumes by Vp(t) and Vf(t) and orienting causet links from the future to the past, i.e. from nodes with higher t to nodes with lower t, we can write  , where
, where  and
and  are the expected out- and in-degrees of the node. One way to compute Vp(t) and Vf(t) is to calculate the expressions for the light cone boundaries in the (t, θ) coordinates and then integrate the volume form dV within these boundaries. An easier way is to switch from cosmological time t to conformal time26 η(t) = arcsec cosh t. After this coordinate change, the metric becomes conformally flat, i.e. proportional to the metric ds2 = –dt2 + dx2 in the flat Minkowski space in Fig. 1,
are the expected out- and in-degrees of the node. One way to compute Vp(t) and Vf(t) is to calculate the expressions for the light cone boundaries in the (t, θ) coordinates and then integrate the volume form dV within these boundaries. An easier way is to switch from cosmological time t to conformal time26 η(t) = arcsec cosh t. After this coordinate change, the metric becomes conformally flat, i.e. proportional to the metric ds2 = –dt2 + dx2 in the flat Minkowski space in Fig. 1,


so that the light cone boundaries are straight lines intersecting the coordinate (η, θ)-axes at 45°, as in Fig. 1 with (t, x) replaced by (η, θ). Therefore, the volumes can be easily calculated:


where approximations hold for  and where we have used η(t) = arcsec cosh t ≈ π/2 – 2e–t. For large times
and where we have used η(t) = arcsec cosh t ≈ π/2 – 2e–t. For large times  , the past volume and consequently the out-degree are negligible compared to the future volume and in-degree, which decay exponentially with time t,
, the past volume and consequently the out-degree are negligible compared to the future volume and in-degree, which decay exponentially with time t,

These results can be generalized to (d+1)-dimensional de Sitter spacetimes with any d and any curvature K = Λ/3 = 1/a2, where a, the inverse square root of curvature, is also known as the curvature radius of the de Sitter hyperboloid, or as its pseudoradius. Generalizing Eqs. (3,8), we can show that the temporal density of nodes and their expected in-degree in this case scale as  and
and  with α = β = d/a. In short, we have a combination of two exponentials, number of nodes ~ eαt born at time t and their degrees ~ e–βt. This combination yields a power-law distribution P(k) ~ k–γ of node degrees k in the causet, where exponent γ = 1 + α/β = 2.
with α = β = d/a. In short, we have a combination of two exponentials, number of nodes ~ eαt born at time t and their degrees ~ e–βt. This combination yields a power-law distribution P(k) ~ k–γ of node degrees k in the causet, where exponent γ = 1 + α/β = 2.
Structure of the universe and complex networks
The large-scale causet structure of the universe in the standard model differs from the structure of sparse de Sitter causets in many ways, two of which are particularly important. First, the universe is not empty but contains matter. Therefore it is only asymptotically de Sitter26,27, meaning that only at large times  , or rescaled times
, or rescaled times  , space in the universe expands asymptotically the same way as in de Sitter spacetime. In a homogeneous and isotropic universe, the metric is ds2 = –dt2 + R2(t)dΩ2, where dΩ is the spatial part of the metric and function R(t) is called the scale factor. In de Sitter spacetime, the scale factor is R(t) ~ cosh τ, while in a flat universe containing only matter and dark energy, R(t) ~ sinh2/3 (3τ/2). In both cases, R(t) ~ eτ at large times
, space in the universe expands asymptotically the same way as in de Sitter spacetime. In a homogeneous and isotropic universe, the metric is ds2 = –dt2 + R2(t)dΩ2, where dΩ is the spatial part of the metric and function R(t) is called the scale factor. In de Sitter spacetime, the scale factor is R(t) ~ cosh τ, while in a flat universe containing only matter and dark energy, R(t) ~ sinh2/3 (3τ/2). In both cases, R(t) ~ eτ at large times  , but at early times
, but at early times  the scaling is different. In particular, at τ → 0 the universe scale factor goes to zero, resulting in a real big bang. The second difference is even more important: the product between the square of inverse curvature a4 = 1/K2 and sprinkling density
the scaling is different. In particular, at τ → 0 the universe scale factor goes to zero, resulting in a real big bang. The second difference is even more important: the product between the square of inverse curvature a4 = 1/K2 and sprinkling density  (one causet element per unit Planck 4-volume) is astronomically huge in the universe, δa4 ~ 10244, compared to
(one causet element per unit Planck 4-volume) is astronomically huge in the universe, δa4 ~ 10244, compared to  in sparse causets with a small average degree. Collectively these two differences result in that the present universe causet is also a power-law graph, but with a different exponent γ = 3/4 (Fig. 3(a)).
in sparse causets with a small average degree. Collectively these two differences result in that the present universe causet is also a power-law graph, but with a different exponent γ = 3/4 (Fig. 3(a)).
Degree distribution in the universe.
Panel (a) shows the rescaled distribution Q(κ, τ0) = δa4P(k, t0) of rescaled degrees κ = k/(δa4) in the universe causet at the present rescaled time τ0 = t0/a = 0.85, where δ is the constant node density in spacetime and  . As shown in Section III of Supplementary Notes, the rescaled degree distribution does not depend on either δ or a, so we set them to δ = 104 and a = 1 for convenience. The size N of simulated causets can be also set to any value without affecting the degree distribution and this value is N = 106 nodes in the figure. The degree distribution in this simulated causet is juxtaposed against the numeric evaluation of the analytical solution for Q(κ, τ0) shown by the blue dashed line. The inset shows this analytic solution for the whole range of node degrees
. As shown in Section III of Supplementary Notes, the rescaled degree distribution does not depend on either δ or a, so we set them to δ = 104 and a = 1 for convenience. The size N of simulated causets can be also set to any value without affecting the degree distribution and this value is N = 106 nodes in the figure. The degree distribution in this simulated causet is juxtaposed against the numeric evaluation of the analytical solution for Q(κ, τ0) shown by the blue dashed line. The inset shows this analytic solution for the whole range of node degrees  in the universe, where δ ~ 10173 and a ~ 5 × 1017. Panel (b) shows the same solution for different values of the present rescaled time τ, tracing the evolution of the degree distribution in the universe in its past and future. All further details are in Section I of Supplementary Methods.
in the universe, where δ ~ 10173 and a ~ 5 × 1017. Panel (b) shows the same solution for different values of the present rescaled time τ, tracing the evolution of the degree distribution in the universe in its past and future. All further details are in Section I of Supplementary Methods.
However, the γ = 2 scaling currently emerges (Fig. 3(b)) as a part of a cosmic coincidence known as the “why now?” puzzle28,29,30,31. The matter and dark energy densities happen to be of the same order of magnitude in the universe today. This coincidence implies that the current rescaled time τ0 ≡ t0/a is approximately 1. Figure 3(b) traces the evolution of the degree distribution in the universe in its past and future. In the matter-dominated era with τ < 1, the degree distribution is a power law with exponent 3/4 up to a soft cut-off that grows with time. Above this soft cut-off, the distribution decays sharply. Once we reach times τ ~ 1, e.g. today, we enter the dark-energy-dominated era. The part of the distribution with exponent 3/4 freezes, while the soft cut-off transforms into a crossover to another power law with exponent 2, whose cut-off grows exponentially with time. The crossover point is located at kcr ~ δa4. Nodes of small degrees k < kcr obey the γ = 3/4 part of the distribution, while high-degree nodes, k > kcr, lie in its γ = 2 regime. At the future infinity τ → ∞, the distribution becomes a perfect double power law with exponents 3/4 and 2.
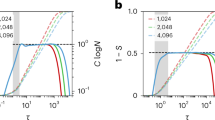
In short, the main structural property of the causet in the present-day universe is that it is a graph with a power-law degree distribution, which currently transitions from the past matter-dominated era (τ < 1) with exponent γ = 3/4 to the future dark-energy-dominated era (τ > 1) with γ = 2. In many (but not all) complex networks the degree distribution is also a power law with γ close to 28,9,10. In Fig. 4(a) we show a few paradigmatic examples of large-scale technological, social and biological networks for which reliable data are available and juxtapose these networks against a de Sitter causet. In all the shown networks, the exponent γ ≈ 2. This does not mean however that the networks are the same in all other respects. Degree-dependent clustering, for example (Fig. 4(b)), is different in different networks, although average clustering is strong in all the networks. Strong clustering is another structural property often observed in complex networks: average clustering in random graphs of similar size and average degree is lower by orders of magnitude8,9,10.
Degree distribution and clustering in complex networks and de Sitter spacetime.
The Internet is the network representing economic relations between autonomous systems, extracted from CAIDA's Internet topology measurements38. The network size is N = 23752 nodes, average degree  and average clustering
and average clustering  . Trust is the social network of trust relations between people extracted from the Pretty Good Privacy (PGP) data39; N = 23797,
. Trust is the social network of trust relations between people extracted from the Pretty Good Privacy (PGP) data39; N = 23797,  ,
,  . Brain is the functional network of the human brain obtained from the fMRI measurements in Ref. 40; N = 23713,
. Brain is the functional network of the human brain obtained from the fMRI measurements in Ref. 40; N = 23713,  ,
,  . De Sitter is a causal set in the 1 + 1-dimensional de Sitter spacetime; N = 23739,
. De Sitter is a causal set in the 1 + 1-dimensional de Sitter spacetime; N = 23739,  ,
,  . Panel (a) shows the degree distribution P(k), i.e. the number of nodes N(k) of degree k divided by the total number of nodes N in the networks, P(k) = N(k)/N, so that
. Panel (a) shows the degree distribution P(k), i.e. the number of nodes N(k) of degree k divided by the total number of nodes N in the networks, P(k) = N(k)/N, so that  . Panel (b) shows average clustering of degree-k nodes c(k), i.e. the number of triangular subgraphs containing nodes of degree k, divided by N(k)k(k – 1)/2, so that
. Panel (b) shows average clustering of degree-k nodes c(k), i.e. the number of triangular subgraphs containing nodes of degree k, divided by N(k)k(k – 1)/2, so that  . All further details are in Section I of Supplementary Methods.
. All further details are in Section I of Supplementary Methods.
Dynamics of de Sitter causets and complex networks
Is there a connection revealing a mechanism responsible for the emergence of this structural similarity? Remarkably, the answer is yes. This mechanism is the optimization of trade-offs between popularity and similarity, shown to accurately describe the large-scale structure and dynamics of some complex networks, such as the Internet, social trust network, etc32. The following model of growing networks, with all the parameters set to their default values, formalizes this optimization in Ref. 32. New nodes n in a modeled network are born one at a time, n = 1, 2, 3, …, so that n can be called a network time. Each new node is placed uniformly at random on circle  . That is, the angular coordinates θn for new nodes n are drawn from the uniform distribution on [0, 2π]. Circle
. That is, the angular coordinates θn for new nodes n are drawn from the uniform distribution on [0, 2π]. Circle  models a similarity space. The closer the two nodes on
models a similarity space. The closer the two nodes on  , the more similar they are. All other things equal, the older the node, the more popular it is, the higher its degree. Therefore birth time n of node n models its popularity. Upon its birth, new node n0 optimizes between popularity and similarity by establishing its fixed number m of connections to m existing nodes n < n0 that have the minimal values of the product nΔθ, where
, the more similar they are. All other things equal, the older the node, the more popular it is, the higher its degree. Therefore birth time n of node n models its popularity. Upon its birth, new node n0 optimizes between popularity and similarity by establishing its fixed number m of connections to m existing nodes n < n0 that have the minimal values of the product nΔθ, where  is the angular distance between nodes n and n0. One dimension of this trade-off optimization strategy is to connect to nodes with smaller birth times n (more popular nodes); the other dimension is to connect to nodes at smaller angular distances Δθ (more similar nodes). After placing each node n at radial coordinate rn = ln n, all nodes are located on a two-dimensional plane at polar coordinates (rn, θn). For each new node n0, the set of nodes minimizing nΔθ is identical to the set of nodes minimizing
is the angular distance between nodes n and n0. One dimension of this trade-off optimization strategy is to connect to nodes with smaller birth times n (more popular nodes); the other dimension is to connect to nodes at smaller angular distances Δθ (more similar nodes). After placing each node n at radial coordinate rn = ln n, all nodes are located on a two-dimensional plane at polar coordinates (rn, θn). For each new node n0, the set of nodes minimizing nΔθ is identical to the set of nodes minimizing  , where x is equal to the hyperbolic distance33 between nodes n0 and n if r, r0 and Δθ are sufficiently large. One can compute the expected distance from node n0 to its mth closest node and find that this distance is equal to
, where x is equal to the hyperbolic distance33 between nodes n0 and n if r, r0 and Δθ are sufficiently large. One can compute the expected distance from node n0 to its mth closest node and find that this distance is equal to  , where approximations hold for large n0. In other words, new node n0 is born at a random location on the edge of an expanding hyperbolic disc of radius r0 = ln n0 and connects to asymptotically all the existing nodes lying within hyperbolic distance r0 from itself. The connectivity perimeter of new node n0 at time n0 is thus the hyperbolic disc of radius r0 centered at node n0. The resulting connection condition x < r0, satisfied by nodes n to which new node n0 connects, can be rewritten as
, where approximations hold for large n0. In other words, new node n0 is born at a random location on the edge of an expanding hyperbolic disc of radius r0 = ln n0 and connects to asymptotically all the existing nodes lying within hyperbolic distance r0 from itself. The connectivity perimeter of new node n0 at time n0 is thus the hyperbolic disc of radius r0 centered at node n0. The resulting connection condition x < r0, satisfied by nodes n to which new node n0 connects, can be rewritten as

This model yields growing networks with power-law degree distribution P(k) ~ k–γ and γ = 2. The networks in the model also have strongest possible clustering, i.e. the largest possible number of triangular subgraphs, for graphs with this degree distribution. The model and its extensions describe the large-scale structure and growth dynamics of different real networks with a remarkable accuracy32. We next show that the described network growth dynamics is asymptotically identical to the growth dynamics of de Sitter causets.
To show this, consider a new spacetime quantum P that has just been born at current time t = t0 in Fig. 2. That is, assume that the whole de Sitter spacetime is sprinkled by nodes with a uniform density, but only nodes between t = 0 and t = t0 are considered to be “alive.” We can then model causet growth as moving forward the current time boundary t = t0 one causet element P at a time. By the causet definition, upon its birth, P connects to all nodes in its past light cone shown by green. As illustrated in Fig. 2, we then map the upper half of the outer one-sheeted hyperboloid representing the half of de Sitter spacetime  with t > 0, to the upper sheet of the dual two-sheeted inner hyperboloid, which is the standard hyperboloid representation of the hyperbolic space
with t > 0, to the upper sheet of the dual two-sheeted inner hyperboloid, which is the standard hyperboloid representation of the hyperbolic space  34. This mapping sends a point with coordinates (t, θ) in
34. This mapping sends a point with coordinates (t, θ) in  to the point with coordinate (r, θ) in
to the point with coordinate (r, θ) in  , where r = t. Since in the conformal time coordinates the light cone boundaries are straight lines intersecting the (η, θ)-axes at 45°, the coordinates (t, θ) of all points in P's past light cone satisfy inequality
, where r = t. Since in the conformal time coordinates the light cone boundaries are straight lines intersecting the (η, θ)-axes at 45°, the coordinates (t, θ) of all points in P's past light cone satisfy inequality  . If
. If  , then we can neglect the second term in the last expression and the coordinates (tn, θn) of existing causet nodes n to which new node P connects upon its birth are given by
, then we can neglect the second term in the last expression and the coordinates (tn, θn) of existing causet nodes n to which new node P connects upon its birth are given by

which is identical to Eq. (9) since rn = tn. In Section II of Supplementary Notes we fill in further details of this proof, extend it to any dimension and curvature and show that the considered mapping between de Sitter spacetime and hyperbolic space is relativistically invariant.
In short, past light cones of new nodes, shown by green in Fig. 2, are asymptotically equal (Fig. 2(d-f)) to the corresponding hyperbolic discs, shown by red. The green light cone bounds the set of nodes to which node P connects as a new causet element. The red hyperbolic disc bounds the set of nodes to which P connects as a new node in the hyperbolic network model that accurately describes the growth of real networks. Since these two sets are asymptotically the same, we conclude that not only the structure, but also the growth dynamics of complex networks and de Sitter causets are asymptotically identical.
Discussion
Geometrically, this equivalence is due to a simple duality between the two hyperboloids in Fig. 2. The inner hyperboloid represents the popularity×similarity hyperbolic geometry of complex networks; the outer hyperboloid is the de Sitter spacetime, which is the solution to Einstein's equations for a universe with positive vacuum energy. In that sense, Einstein's equations provide an adequate baseline description for the structure and dynamics of complex networks, which can be used for predicting network dynamics at the large scale. De Sitter spacetime is homogeneous and isotropic, as is the hyperbolic space, but if we take a real network, e.g. the Internet and map it to this homogeneous space, then after the mapping, the node density in the space is non-uniform35. In real networks, the space thus appears homogeneous only at the largest scale, while at smaller scales there are inhomogeneities and anisotropies, similar to the real universe, in which matter introduces spacetime inhomogeneities at smaller scales and leads to non-trivial coupled dynamics of matter density and spacetime curvature, described by the same Einstein equations. In view of this analogy, equations similar to Einstein's equations may also apply to complex networks at smaller scales. If so, these equations can be used to predict and possibly control the fine-grained dynamics of links and nodes in networks.
Our results may also have important implications for cosmology. In particular, de Sitter causal sets have exactly the same graph structure that maximizes network navigability36. Translated to asymptotically sparse causal sets, does this property imply that the expanding portion of de Sitter spacetime (t > 0) is the spacetime that maximizes the probability that two random Planck-scale events have an ancestor in their common past? If it does, then this uniqueness of de Sitter spacetime may lead to a different perspective on the cosmic coincidence problem, as well as on dark energy, possibly casting the latter as a phenomenon emerging from certain optimization principles encoded in the causal network structure.
The degree distributions in some complex networks deviate from clean power laws, the exponents of these power laws vary a lot across different real networks and so do clustering, correlation and many other structural properties of these networks8,9,10. Therefore it may seem unlikely that de Sitter causets can model the full spectrum of structural diversity observed in complex networks. Focusing on the trust network in Fig. 4 for instance, we have already observed that its degree-dependent clustering is quite different from the one in de Sitter causets. Yet, given that these causets are asymptotically identical to growing hyperbolic networks, this observation appears as a paradox, because the hyperbolic networks were shown to accurately match not only clustering peculiarities, but also a long list of other important structural properties of the same trust network, as well as of other networks32. The explanation of this paradox lies in the fact that the hyperbolic network model has parameters to tune the degree distribution exponent, clustering strength, node fitness and other network properties, while in de Sitter causets, only the number of nodes and average degree can be controlled. Do the hyperbolic network parameters have their duals in the de Sitter settings, what are the physical meanings of these dual parameters and do they lead to similar modeling versatility—all these questions are open.
We conclude with the observation that the node density in growing hyperbolic networks with the default parameters corresponding to de Sitter causets, is not uniform in the hyperbolic space32. This observation means that these networks are not random geometric graphs37 and that their structure does not exactly reflect the geometry of the underlying hyperbolic space. Informally, a random geometric graph is a coarse, discrete representation of a smooth geometric space. Our finding that asymptotically the same networks have a uniform node density in de Sitter spacetimes dual to hyperbolic spaces, strongly suggests that real networks are random geometric graphs that grow in spacetimes similar to the asymptotically de Sitter spacetime of our accelerating universe.
References
Barabási, A.-L. & Oltvai, Z. N. Network biology: understanding the cell's functional organization. Nat Rev Genet 5, 101–13 (2004).
Bullmore, E. & Sporns, O. Complex Brain Networks: Graph Theoretical Analysis of Structural and Functional Systems. Nat Rev Neurosci 10, 168–198 (2009).
Yamada, T. & Bork, P. Evolution of biomolecular networks: lessons from metabolic and protein interactions. Nat Rev Mol Cell Bio 10, 791–803 (2009).
Lazer, D. et al. Computational Social Science. Science 323, 721–723 (2009).
Vespignani, A. Predicting the behavior of techno-social systems. Science 325, 425–8 (2009).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. Nature 473, 167–173 (2011).
Simini, F., González, M. C., Maritan, A. & Barabási, A.-L. A universal model for mobility and migration patterns. Nature 484, 96–100 (2012).
Dorogovtsev, S. N. & Mendes, J. F. F. Evolution of Networks: From Biological Nets to the Internet and WWW (Oxford University Press, Oxford, 2003).
Newman, M. E. J. The Structure and Function of Complex Networks. SIAM Rev 45, 167–256 (2003).
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwanga, D.-U. Complex Networks: Structure and Dynamics. Phys Rep 424, 175–308 (2006).
Hawking, S. W. & Ellis, G. F. R. The Large Scale Structure of Space-Time (Cambridge University Press, Cambridge, 1975).
Mattern, F. Virtual time and global states of distributed systems. In Corsnard et al., M. (ed.) Proc Parallel and Distributed Algorithms, 215–226 (Elsevier, Amsterdam, 1988).
Korniss, G., Novotny, M. A., Guclu, H., Toroczkai, Z. & Rikvold, P. A. Suppressing roughness of virtual times in parallel discrete-event simulations. Science 299, 677–9 (2003).
Groff, R. (ed.) Revitalizing Causality: Realism about Causality in Philosophy and Social Science (Routledge, New York., 2008).
Kiefer, C. Quantum Gravity (Oxford University Press, New York, 2007).
Malament, D. B. The class of continuous timelike curves determines the topology of spacetime. J Math Phys 18, 1399 (1977).
Hawking, S. W., King, A. R. & McCarthy, P. J. A new topology for curved spacetime which incorporates the causal, differential and conformal structures. J Math Phys 17, 174 (1976).
Zeeman, E. C. Causality Implies the Lorentz Group. J Math Phys 5, 490 (1964).
Bombelli, L., Lee, J., Meyer, D. & Sorkin, R. Space-time as a causal set. Phys Rev Lett 59, 521–524 (1987).
Bombelli, L., Henson, J. & Sorkin, R. Discreteness without symmetry breaking: a theorem. Mod Phys Lett A 24, 2579–2587 (2009).
Rideout, D. & Sorkin, R. Classical sequential growth dynamics for causal sets. Phys Rev D 61, 024002 (1999).
Ahmed, M. & Rideout, D. Indications of de Sitter spacetime from classical sequential growth dynamics of causal sets. Phys Rev D 81, 083528 (2010).
Perlmutter, S. et al. Discovery of a supernova explosion at half the age of the Universe. Nature 391, 51–54 (1998).
Riess, A. G. et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron J 116, 1009–1038 (1998).
Albrecht, A. et al. Report of the Dark Energy Task Force. Report of the Dark Energy Task Force (2006).
Griffiths, J. B. & Podolský, J. Exact Space-Times in Einstein's General Relativity (Cambridge University Press, Cambridge, 2009).
Galloway, G. J. & Solis, D. A. Uniqueness of de Sitter space. Classical Quant Grav 24, 3125–3138 (2007).
Garriga, J., Livio, M. & Vilenkin, A. Cosmological constant and the time of its dominance. Phys Rev D 61, 023503 (1999).
Sorkin, R., Rajantie, A., Contaldi, C., Dauncey, P. & Stoica, H. Is the cosmological ”constant” a nonlocal quantum residue of discreteness of the causal set type? In AIP Conf Proc, vol. 957, 142–153 (AIP, 2007).
Barrow, J. & Shaw, D. New Solution of the Cosmological Constant Problems. Phys Rev Lett 106, 101302 (2011).
Harlow, D., Shenker, S., Stanford, D. & Susskind, L. Tree-like structure of eternal inflation: A solvable model. Phys Rev D 85, 063516 (2012).
Papadopoulos, F., Kitsak, M., Serrano, M. A., Boguñá, M. & Krioukov, D. Popularity versus similarity in growing networks. Nature 489, 537–540 (2012).
Bonahon, F. Low-Dimensional Geometry (AMS, Providence, 2009).
Cannon, J., Floyd, W., Kenyon, R. & Parry, W. Hyperbolic Geometry. In Levy, S. (ed.) Flavors of Geometry, 59–116 (MSRI, Berkeley, 1997).
Boguñá, M., Papadopoulos, F. & Krioukov, D. Sustaining the Internet with Hyperbolic Mapping. Nature Comms 1, 62 (2010).
Boguñá, M., Krioukov, D. & Claffy, K. Navigability of Complex Networks. Nature Physics 5, 74–80 (2009).
Penrose, M. Random Geometric Graphs (Oxford University Press, Oxford, 2003).
Claffy, K., Hyun, Y., Keys, K., Fomenkov, M. & Krioukov, D. Internet Mapping: from Art to Science. In Proceedings of the 2009 Cybersecurity Applications & Technology Conference for Homeland Security (CATCH 2009), Washington, DC, March 3-4, 2009, 205–211 (IEEE Computer Society, 2009).
Callas, J., Donnerhacke, L., Finney, H., Shaw, D. & Thayer, R. OpenPGP Message Format. IETF, RFC 4880. (2007).
Eguíluz, V., Chialvo, D., Cecchi, G., Baliki, M. & Apkarian, A. V. Scale-Free Brain Functional Networks. Phys Rev Lett 94, 018102 (2005).
Acknowledgements
We thank M.Á. Serrano, M. Norman, Z. Toroczkai, A.-L. Barabási, J. Garriga, A. Vilenkin, R. Sorkin, G. Gibbons, F. Papadopoulos, G. Bianconi, A. Petersen, L. Braunstein, F. Bonahon, kc claffy, M. Fomenkov, C. Carlson, L. Klushin, S. Paston, V.D. Lyakhovsky and A. Krioukov for useful discussions and suggestions. Special thanks to D. Chialvo for sharing his brain data with us. We also thank M. Norman for providing computing time at SDSC through the director's discretionary fund and to J. Cheng and B. Huffaker for their help with Fig. 1. This work was supported by DARPA grant No. HR0011-12-1-0012; NSF grants No. CNS-0964236 and CNS-1039646; Cisco Systems; Foundational Questions Institute grant No. FQXi-RFP3-1018; George W. and Carol A. Lattimer Campus Professorship at UCSD; MICINN project No. FIS2010-21781-C02-02; Generalitat de Catalunya grant No. 2009SGR838; and by the ICREA Academia prize, funded by the Generalitat de Catalunya.
Author information
Authors and Affiliations
Contributions
D.K., D.R., D.M. and M.B. designed research; D.K., M.K. and M.B. performed research; D.K., M.K., R.S. and M.B. analyzed data and performed simulations; D.K., D.R. and M.B. wrote the manuscript; all authors discussed the results and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information for Network Cosmology
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Krioukov, D., Kitsak, M., Sinkovits, R. et al. Network Cosmology. Sci Rep 2, 793 (2012). https://doi.org/10.1038/srep00793
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00793
This article is cited by
-
Greedy routing optimisation in hyperbolic networks
Scientific Reports (2023)
-
Emergent time, cosmological constant and boundary dimension at infinity in combinatorial quantum gravity
Journal of High Energy Physics (2022)
-
A cooperative game model for the multimodality of coauthorship networks
Scientometrics (2019)
-
Emergent Hyperbolic Network Geometry
Scientific Reports (2017)
-
Navigability of Random Geometric Graphs in the Universe and Other Spacetimes
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.