Abstract
Classical economic theories prescribe specialization of countries industrial production. Inspection of the country databases of exported products shows that this is not the case: successful countries are extremely diversified, in analogy with biosystems evolving in a competitive dynamical environment. The challenge is assessing quantitatively the non-monetary competitive advantage of diversification which represents the hidden potential for development and growth. Here we develop a new statistical approach based on coupled non-linear maps, whose fixed point defines a new metrics for the country Fitness and product Complexity. We show that a non-linear iteration is necessary to bound the complexity of products by the fitness of the less competitive countries exporting them. We show that, given the paradigm of economic complexity, the correct and simplest approach to measure the competitiveness of countries is the one presented in this work. Furthermore our metrics appears to be economically well-grounded.
Similar content being viewed by others
Introduction
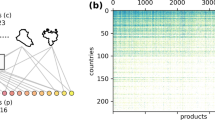
The analysis we present here has been triggered by recent studies1,2 that showed how the available data on world trade networks defies the standard economic approach3,4,5,6,7. Indeed, in the standard view, the wealthiest countries should produce only few products with a high degree of specialization. If we represent all the trading relations in a matrix M describing the bipartite network of countries and products, we should observe (once we suitably rearrange the various rows and columns) a mostly block diagonal matrix. On the contrary, data (See Supplementary Information for details) clearly show that countries tend to produce all the possible products they can, given their level of technology. As a result the shape of matrix M (when appropriately reordered), is approximately triangular (see Fig. 1 ).
Diversification vs Specialization.
According to the standard analysis the specialization of countries on few specific products should be an optimal strategy but this is valid only in a static situation. The strongly dynamical situation of the world market suggests that flexibility and adaptability are even more important to be the most competitive while the ones specialized on those few products exported by almost every country are the poorest. On this account mainstream theories would predict an almost diagonal binary country product matrix while, ordering rows and columns with respect to our metrics for countries' fitness and products' complexity we observe a triangular-shaped matrix. The matrix is built from the export flows of the year 2010 and the products are categorized according to the Harmonized System 2007 coding system at 4 digits level of coarse-graining.
A first attempt to define competitiveness in terms of diversification has been recently made by Hidalgo and Hausmann (HH) in2. However, we show here that this method suffers from a number of problems both conceptual and practical.
In this paper we propose a novel, non-linear, iterative approach able to capture efficiently the intrinsic link between the export basket of different countries and their industrial competitive-ness. We achieve this result by looking at the binary matrix representing the export basket of each country and combining iteratively measures on its rows and columns, in a spirit assimilable to Google's PageRank. An important difference with respect to the HH approach is that our theory is based on a highly non linear relationship to define the Complexity of products from the Fitness of countries which produce them. The observation that a product is made by a developed country gives a limited information on the complexity of the product itself because these countries export almost all products. On the other hand, when an underdeveloped country is able to export a given product, very likely this product requires a low level of sophistication. These observations lead to the following main argument behind the mathematical approach: while it is reasonable to measure the competitiveness and adaptability of a country through the sum of quality and complexity of its products, it is not possible to adopt the same approach to measure the quality and complexity of products. In particular the complexity of a product cannot be defined as the average of the fitnesses of the countries producing it9. It appears therefore natural, in the definition of the complexity of the product, to weight the complexity of the productive systems of its exporters in a highly nonlinear way, so that the information that such a product is produced by some scarcely competitive countries is sufficient to conclude that the complexity of the product is low. Consequently, the only possibility for a product to have a high qualitative level (or complexity) is to be produced only by highly competitive countries. In summary our method consists in coupled non-linear maps whose fixed point defines a new metrics for the Fitness of the countries and the Complexity of the products. In this method each iteration adds new information in the system and the distributions of the two metrics become broad Pareto-like. The new metrics for countries and products appear conceptually consistent and produce a wealth of new information in various directions. Their comparison with standard monetary indices can be interpreted as the potential for growth. The method represents a new approach to the fundamental analysis of countries' productive systems and it also introduces a non-monetary classification of product complexity. Furthermore we can define an effective measure for the Complexity of the products filtering out monetary biases from the product complexity definition such as labor cost, price market speculation, economical inefficiencies of commodities pricing, etc.
Results
The basic idea is to define an iteration process which couples the Fitness of a country Fc to the Complexity of a product Qp and then obtain the fixed point values. For the Fitness Fc it is natural that this is proportional to the sum of the products exported weighted by their complexity Qp. For Qp the situation is more subtle. To a first approximation, the complexity of a product is inversely proportional to the number of countries which export it. In addition, if a country has a high fitness this should reduce the weight in bounding the complexity of a product and the countries with low fitness should strongly contribute to the bound on Qp. These ideas9 are summarized in the iteration of Eqs. 1.

This iterative method is composed of two steps at each iteration: we first compute the intermediate variables  and
and  and then normalize them. The initial conditions are
and then normalize them. The initial conditions are  and
and  . The elements Mcp are the elements of the binary country-product matrix M: they are 1 if the country c exports the product p and 0 otherwise (see Methods for the mathematical definition of the matrix). We have tested numerically that the fixed point of this coupled maps is stable and not dependent on the initial condition.
. The elements Mcp are the elements of the binary country-product matrix M: they are 1 if the country c exports the product p and 0 otherwise (see Methods for the mathematical definition of the matrix). We have tested numerically that the fixed point of this coupled maps is stable and not dependent on the initial condition.
Given the fact that we want the less complex exporters to give a dominant contribution to the product complexity, the non-linearity of our coupled maps is a fundamental mathematical property that is unavoidable in view of the economic diversification problem. In particular, the definition of Q seems to us the simplest and most natural way to implement the desired behavior: the sum in the denominator is dominated by the producers with the lowest fitness and increases as the total number of exporter increases, thus considering the ubiquity of the product. Finally inverting the sum makes Q coherent with its positive meaning of complexity. In contrast, previous attempts2 were based on a linear iteration that, by construction, contracts the information and is inconsistent with the economic criteria of relating the complexity of a product to the complexity of its producers. The need of a non-linear framework was also preliminary indicated in8. At the end of this section we show a detailed comparison between the results of the two methods run on the same dataset and discuss how they are in favor of the non linear iterations.
Moving to the results, a preliminary comment is to be made. We show mainly how our results are more consistent, compared to those obtained with the linear method, with the framework of economic complexity which Hidalgo and Hausmann proposed. This is made by both formal arguments and a qualitative comparison to standard macroeconomical analysis of the economy of countries. However, a systematic validation, in terms of the ability of the algorithm to predict growth as a result of development, is a complex matter which deals with the heterogeneous dynamics to which economies in different phases are subject. We will enter in the details of such analysis in future works. The first result that we find through this approach is that we can more convincingly reproduce the difference between different countries (Fig. 2d) by broadening the distribution of Fc and Qp from the initial state towards a Pareto-like distribution as expected from experimental observations. In fact, as exemplified by the illustrative Fig. 2c, we expect that the iterative method, which adds more information about the complexity of products at each step, will tend to separate countries with respect to the starting point, differently from the procedure of HH. As an example we can consider USA and Nigeria. USA has a more diversified export basket with respect to Nigeria and likely, on average, the complexity of its products is higher than the one of Nigeria. Therefore the next iteration should necessarily increase the gap between Nigeria and USA with respect to the starting point. This way of reasoning holds for all the orders of the iterative method. On this account in Fig. 2d we show the evolution of the distributions of the variable kc (HH) and our countries' fitness. It is clear that only our method is consistent with the expected behavior shown in Fig. 2c.
The Bipartite Network of Countries and Products and the Non-Monetary Metrics.
In (a) we report a snapshot of the bipartite network for the most important countries; size of vertices is the fitness and the complexity we computed. In (b) we show the time evolution of the ranking of various country along the various years according to our metrics. In (c) we qualitatively show what is the effect on country fitness of our iterations (green) with respect to the method of HH (red). Finally in (d) we quantitatively show the evolution of country fitness' distribution (right panel) which is broaden by iterations as expected and compare it with the evolution of the variables of the method of HH (left panel). The distribution is in this case shrunk towards a delta-function by the iteration evolution. A similar effect is observed for the kp variable.
Another important element is that our method leads naturally to Pareto-like (power law) distributions which are an epitome of real Economic Complexity10,11. The fact that this type of results are a natural outcome of our theory is an important test of its validity. The Pareto-like features of our metrics are shown in Fig. 3a–b–c where we report the rank-size laws for the non-monetary fitnesses, the weighted fitnesses and the complexity of products in the binary and weighted case. By weighted fitness we mean the weighted version of our metrics which complements the results of the non-monetary case. The weighted fitness and complexity are obtained as the non-monetary partners by iterating eqs. 1 using the matrix W instead of M. The elements of W are defined as share of the country c of the world export of the product p (see Materials and Methods for further discussions). We point out that, while the non-monetary metrics gives a sort of intensive (or per capita) information on the level of competitiveness of a country, the weighted one instead partly represents an extensive piece of information of the country. In detail the countries are weighted according to the fraction of export within the set of exporters of a fixed product p, but we are still intensively treating the total export volume of different products since the sum of the weights over all the exporters of a product is equal to 1 for all products independently on the fraction of that product on the whole export.
Data Analysis: intensive and extensive metrics.
In (a) we show the rank-size law of the fitness as measured by the non-monetary metrics (solid black line). As discussed in the text this metrics corresponds to an intensive information, a sort of per capita fitness. Indeed we find a very good agreement with the rank-size for an per capita monetary indicator as the GPD per capita. Red lines in all panels represent a pure Zipf Law ~ 1/k. In (b) we show the rank size law of the weighted case and compare it with a extensive monetary indicator as the GDP. In panel c we show the comparison between the complexity of products in the intensive and extensive case. As expected we find that the complexity of products appears to be an intensive features of products independently on the analysis adopted.
Consistently with this observation we find that the rank size law of the intensive fitness is very broad but does not show a Zipfian behavior and instead matches the law observed for a per capita economic indicator, the GDP per capita (Fig. 3a). On the other hand the weighted (or extensive) metrics shows a Zipfian rank size law which closely follow the one of the total GDP, i.e. an extensive economic indicator. Finally in Fig 3c we show the comparison between the complexity of products in the intensive and extensive case. Within our framework we find that the complexity of products appears to be an intensive feature of products independently on the analysis adopted for countries. We consider this result as an important element of consistency.
In order to show the basic fundamental differences of our method with respect to HH, we consider a simplified world composed by only four countries USA, Austria, Mexico and Kazakhstan. We assign to them a fixed fitness Fc as reported in Table 1. We now perform a single step of the method of HH, thus evaluating their variables for products (kp = < F >) and a single step of our method:  . The average and the sums are performed only over the countries producing the p-th product. Finally, we compute Qp and kp for products made by every possible combination of the four countries.
. The average and the sums are performed only over the countries producing the p-th product. Finally, we compute Qp and kp for products made by every possible combination of the four countries.
From the results obtained in Table 2 we note that Qp (differently from kp) depends strongly on the worst producers. Furthermore Qp also reproduces hierarchically the importance of one product with respect to the others given their ubiquity preserving the ordering given by the worst producer. In this respect the variable kp misses this aspect predicting the highest complexity of the product with the highest ubiquity (USA, Austria, Mexico) among all the possible combinations of exporters, having Mexico as the worst country. In real data these features give rise to a more complex hierarchical behavior due to a richer distribution in countries' fitnesses.
Moving to economic aspects, the new metrics here introduced give now a method to measure the differences in the competitiveness of different countries. As an application of the potentiality of the metrics, we can discuss the case of BRIC countries (Brazil, Russia, India and China) in Fig. 2b. BRIC countries are usually considered as emerging countries whose economical systems have an high rate of growth. A conventional monetary analysis based on the GDP reveals that all these countries' GDP growth rate is higher than the ones of the western countries (US and Europe). For Brazil and even more Russia we measure that the Fitness is decreasing as shown in Fig. 2b. Therefore we conclude that their GDP growth is essentially fuelled by the increasing prices of raw materials. According to our analysis these two countries are not using their surplus of richness deriving from raw materials to develop their capabilities in order to give firm basis to their industrial economic system. On the other hand in the case of China and India the observed GDP growth reflects a genuine development of the capabilities and a real increase of the competitiveness of these two countries. In this sense the development of IC countries is economically well-grounded differently from BR countries, which appear to be boosted by the price bubble of the raw materials. The most spectacular growth, observed both in the GDP and in our fitness, is the case of China, for which the two data are in perfect agreement. According to our analysis from 1995 to 2010 the ranking of industrial competitiveness of China moved from the 13th position to the 2nd, just below Germany. The HH method instead ranks China in the 29th position in 2010 (The Atlas of Economic Complexity12, pag. 64), just above Panama which is 30th. However, the authors of12 provides different country rankings which are not consistent with each other (see2 and13). By reproducing the HH method on our data we find a ranking very close to the one of12, for instance China in 2010 is ranked in the position 34 and the discrepancies are due to the different data cleaning procedure adopted. For such reasons we choose to carry out all the comparisons with the results of this work. The position of China according to HH method is rather unrealistic since nowadays China always appears in the very top positions whatever economic indicator is adopted. In our metrics Panama (see Fig. 2) ranks 31st and the comparison of China and Panama is a clear example of the importance on one hand of the non-linear iteration and, on the other, of the role of diversification. In fact the variables representing the competitiveness of a country in the HH method are averages (see eq. 1 of2): for instance these variables at the first order of the iteration measure how ubiquitous are the products exported by a country on average. From this observation it follows that the country ranking of the HH method is only determined by the average quality of the products exported by a country, independently on the level of diversification and this is not consistent with the philosophy of the authors of the HH method. Conversely, according to our method, the fitness of a country is an extensive variable with respect to the number of product exported. Therefore the larger is the fitness of a country, the more diversified is its export and the larger is the quality of the exported products. China has one of the most diversified export baskets, but by measuring its competitiveness only by the average complexity of its products it is ranked in the 29th position (HH method), while taking into account both aspects - product complexity and diversification - China occupies the second position (our method). This also explains why Japan occupies the first position in the HH ranking (Japan has the export basket with the highest average complexity according to the method of HH) although Japan's diversification (about 300 products) is about 30–40% smaller than the one of China, Germany, Italy and USA (about 450–500 products). In other words, according to the mathematical framework of HH, the diversification is not an advantage in the sense that a country's fitness gets lowered if the country is diversified also in ubiquitous products: the averaging procedure corresponds to consider the export basket deteriorated by the presence of low complexity products. The export of low complexity products would represent an handicap instead of having a negligible effect or, as in our method, of giving a little but positive contribution to the fitness of a diversified country.
This observation also explains the rather unexpected results of Italy ranking over USA. Italy has a larger fitness than USA because, while the average complexity of the products exported by the two countries is very similar, according to the RCA criterion Italy's diversification is higher than the USA's one.
A more systematic comparison of the results yield by the two methods must also take into account the effects of nonlinearity in the determination of product complexity. The easiest way to do this is to scatter plot the two variables (fig 4 a). As expected the two variables have a negative correlation (being the HH's kp variable a generalized ubiquity, i.e. in some way the opposite of complexity). We consider a band having approximately a width of 10% of the total distribution of the logarithm of complexity: it is a rough estimate of where the dots should lay if the two variables had comparable values. It is now interesting to look at what kind of products fall on the two sides of the band. Red dots represent products whose complexity is overestimated by kp with respect to our measure. As reported in the figure, those are mainly raw materials, agriculture and oil-related products: no particular technological or industrial capability is required to be an exporter of such products. We would say it is more a matter of fate. Conversely, the blue dots correspond to products whose complexity is underestimated by kp: an inspection reveals that those are mostly related to light industry (portable electric lamps, vacuum flasks, etc.) and the textile sectors. These are not high-tech products (and they, correctly, do not top the ranking), but still an industrial development is required to produce them.
Comparison between our metrics and HH's.
In (a) we show a comparison of our product complexity measure against HH's kp. The band containing the black dots is based on a purely visual criterion: it has a width of about one tenth of the total distribution of the logarithm of complexity. Outside the band are the products that we consider having a significative difference with respect to the two measures: red ones are overestimated by HH's measure with respect to our definition of complexity, blue ones are underestimated. We indicate explicitly the category of some of these products. In (b) we show how the fitness ranking is mapped into the HH's kc ranking. Colors are assigned by the position in the fitness ranking.
Finally, the combined effects of the differences between the two methods are presented in fig. 4 b, where the rankings obtained are compared. The color scheme is given by the fitness ranking (left) and is an eye-guide to spot great differences in the (reconstructed) HH's ranking. Starting from top, we make just a few comments:
-
Malta and Ireland, two poorly diversified countries (respectively 71 and 100 products), make a significative jump of about 50 positions in the ranking.
-
China, India and Indonesia undergo a consistent drop of about 30–40 positions. We argue that this is an effect of the underestimation of textile and light industry, summed with the diversification issue. Remarkably Cyprus ends up ranked above China.
-
Among the BRIC countries, Russia is the only one experiencing an increase in its ranking: it is to be noted that Russia is the less diversified among BRIC countries with only 127 products in 2010, compared to the 191 of Brazil, 375 of India and 473 of China.
-
Oil exporters climb the ranking of more than 70 positions: is the case of Saudi Arabia, Quatar, Kuwait, Venezuela and others. This is clearly the effect of the overestimation of oil-related products.
The present study represents a new way to extract information from a bipartite network, providing a general new perspective with respect to the standard network studies14,15. In fact, in relation to the world trade web16,17,18, the analysis has been mostly focused on the network of total exchange between countries19,20, without explicitly taking into account the different products. Here instead we focus only on the export and we include all the products explicitly. For this bipartite network we introduce a novel approach for quantities which are related to importance and quality in a framework inspired by fundamental economics. The method resembles in some way the Google PageRank21 for directed networks, but it has the new feature of being suited for a bipartite network and of being intrinsically non-linear.
Discussion
In this paper we have presented a novel method to define a self-consistent and non-monetary metrics for the competitiveness of the countries and the complexity of the products in order to assess quantitatively the advantage of diversification. This method implements, in a non-linear self-consistent mathematical way, a basic economical observation related to the triangular structure of the country-product matrix M. Since developed countries export most of the products, the main information on the complexity of products is determined essentially by the worst of its producers. Mathematically this means that the fitness (i.e. competitiveness) of countries and complexity of products must interact in a non-linear way, with almost extremal mechanisms. We believe no linear coupling between these quantities is able to reproduce this effect.
With the introduction of our novel non-linear iterative algorithm for Fitnesses of countries (i.e. competitiveness) and Complexities of products, we are able to capture the very economical essence of the triangular structure of the matrix Mcp. It is exactly such an almost extremal interaction between the two sets of variables describing countries and products to determine the fixpoint economical properties of the market.
The new theory presented in this paper leads to a massive amount of results of which we have discussed few limited examples. All the information one can obtain has many other economic implications which we will consider in subsequent works. We believe that the present methodology, or its natural variants, could be useful also in a variety of other problems, characterized by bipartite networks also beyond the area of economics.
Methods
Datasets
We used data extracted from the BACI dataset22. In this dataset we have trading data about more than 200 countries and 5000 products classified according to a six digit code (categorization: Harmonized System 200723). We coarse-grained such classification by considering only the first 4 digits, obtaining a set of about 1200 products. The matrix M, whose elements are Mpc, is then built by transforming the flows qcp of US Dollars into unweighted links between countries and products. The criterion adopted in order to understand whether a country can be considered or not a producer of a particular product is the so-called Revealed Comparative Advantage (RCA)24 that is the fraction of export of the product p by country c with respect to the global export of p done by all countries. This quantity is then divided by the fraction of the total export of c with respect to the whole world export. I.e.

In order to build the binary matrix M from the RCA matrix, we consider Mcp = 1 if RCAcp ≥ 1 and zero otherwise.
As a consistency test of the robustness of this criterion, we can aggregate two or more countries and apply the RCA criterion to this macro-country. It is found that the diversification of this macro-country, i.e. the number of products for which the threshold condition is satisfied, is not the sum of the diversification of the single units (minus their intersection). The resulting diversification is generally of the same order of magnitude of the most diversified unit composing the macro-country. As an example, in 2010, by aggregating Germany, France, Italy, United Kingdom and Spain in a single country we find that this macro-nation exports about 600 products while the diversification of its units ranges from 400 to 500 and the simple union of these five countries would export almost all the products (about 950 products among 1160).
The non-monetary (intensive) metrics: the non-linear relationship
The above problems arise from the choice to link linearly the ubiquity of a product with the fitness of a country. A different and much more effective approach can be obtained by following these statements: the fitness of a country must be related to the average level of its products. The complexity of a product is dominated (i.e. it goes down) by less developed countries. We now deal with two sets of variables, non-linearly related, for which we define a metrics as the fix point solution of eqs. 1. As shown the iterative method is composed of two steps at each iteration, we first compute the intermediate variables  and
and  and then by normalizing them we define the countries' fitness and the products' complexity for each order n of the iteration. We recall that initial conditions are
and then by normalizing them we define the countries' fitness and the products' complexity for each order n of the iteration. We recall that initial conditions are  and
and  . The variable F is named fitness and measures the level of competitiveness of a country while the variables Q are the complexity of products. The elements Mcp are the elements of the binary country-product matrix M: the element Mcp is 1 if the country c exports the product p, 0 otherwise. The averages at the denominators are performed on all the intermediate values of fitness and complexity defined by eqs. 1. At each iteration both variables (fitness and complexity) are renormalized to keep constant the total export and the average complexity of products respectively. We introduce this renormalization procedure because our non linear equations have two trivial absorbing solutions in 0 and +∞. By the renormalization of the space in which the values of fitness and complexity lie we are able to grasp the non trivial, self-consistent and economically meaningful solution.
. The variable F is named fitness and measures the level of competitiveness of a country while the variables Q are the complexity of products. The elements Mcp are the elements of the binary country-product matrix M: the element Mcp is 1 if the country c exports the product p, 0 otherwise. The averages at the denominators are performed on all the intermediate values of fitness and complexity defined by eqs. 1. At each iteration both variables (fitness and complexity) are renormalized to keep constant the total export and the average complexity of products respectively. We introduce this renormalization procedure because our non linear equations have two trivial absorbing solutions in 0 and +∞. By the renormalization of the space in which the values of fitness and complexity lie we are able to grasp the non trivial, self-consistent and economically meaningful solution.
Firstly we note that the iterations do not change the meaning of the variables, each iteration only refines the information. As a second point, in the computation of the complexity of a product, the weight assigned to countries is inversely proportional to the fitness. The countries with small fitness dominate the sum in eqs. 1 as expected. As a final remark this version of our method can be seen as the intensive case since the matrix M is a binary matrix which does not take into account extensively the amount of export of a country. Thus the metrics deriving from the binary matrix is purely non-monetary: this metrics intensively measures the productive power of countries. The weighted (extensive) version of the method considering a weighted country-product matrix is discussed in the next section.
The extensive metrics: the weighted country-product matrix
The extensive metrics is simply obtained by replacing in eqs. 1 the matrix M with weighted matrix W whose elements Wcp ranges from 0 to 1 and are define as

According to this definition the weight Wcp is the fraction of export of product p held by the country c.
References
Hidalgo, C. A., Klinger, B., Barabási, A.-L. & Hausmann, R. The Product Space Conditions the Development of Nations. .Science 317, 482–487 (2007).
Hidalgo, C. A. & Hausmann, R. The building blocks of economic complexity. .Proceedings of the National Academy of Sciences 106, 10570–10575 (2009).
Smith, A. The Wealth of Nations. W. Strahan and T. Cadell, London (1776).
Ricardo, D. On the Principles of Political Economy and Taxation. John Murray (1817).
Romer, P. M. Endogenous technological change. Journal of Political Economy 98, 71–102 (1990).
Grossman, G. M. & Helpman, E. Quality ladders in the theory of growth. Review of Economic Studies 58, 43–61 (1991).
Flam, H. & Flanders, M. J. Heckscher-Ohlin Trade Theory. Cambridge, Mass.: MIT Press. (1991).
Caldarelli, G. et al. A network analysis of countries' export flows: towards non-linear metrics. arXiv,1108.2590 (2011).
Tacchella, A., Cristelli, M., Caldarelli, G., Gabrielli, A. & Pietronero, L. Economic complexity: a new metric for countries' competitiveness and products' complexity. submitted to JEDC (2012).
Pareto, V. Manual of Political Economy. Augustus M. Kelley Publishers, New York, (1906).
Zipf, G. K. Human Behavior and the Principle of Least Effort. Addison-Wesley, Cambridge, MA, (1949).
Hausmann, R. et al. The atlas of economic complexity. http://atlas.media.mit.edu/media/atlas/pdf/HarvardMIT_AtlasOfEconomicComplexity.pdf (2012).
Hidalgo, C. A. The Dynamics of Economic Complexity and the Product Space over a 42 year period. Center for International Development - Working Paper 189 (2009)
Caldarelli, G. Scale-Free Networks: Complex Webs in Nature and Technology. Oxford University Press, Oxford (2007).
Barrat, A., Barthélemy, M. & Vespignani, A. Dynamical Processes on Complex Networks. Cambridge University Press, Cambridge (2008).
Serrano, M.-A. & Boguñà, M. Topology of the world trade web. Physical Review E, 68 015101(R). (2003).
Garlaschelli, D. & Loffredo, M. I. Fitness-Dependent Topological Properties of the World Trade Web. Phys. Rev. Lett. 93, 188701 (2004).
Serrano, M.-A., Boguñà, M. & Vespignani, A. Patterns of dominant flows in the world trade web. Journal of Economic Interaction and Coordination 2, 111–124 (2007).
Squartini, T., Fagiolo, G. & Garlaschelli, D. Randomizing world trade. II. A binary network analysis. .Physical Review E 84, 046117 (2011).
Squartini, T., Fagiolo, G. & Garlaschelli, D. Randomizing world trade. I. A weighted network analysis. .Physical Review E 84, 046118 (2011).
Page, L., Brin, S., Motwani, R. & Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web. Technical Report. Stanford InfoLab (1999).
Gaulier, G. & Zignago, S. BACI: International Trade Database at the Product-level. Centre d'Etudes Prospectives et d'Informations Internationales (2010). http://www.cepii.fr/anglaisgraph/workpap/pdf/2010/wp2010-23.pdf.
http://www.wcoomd.org/ (Accessed: September 2012).
Balassa, B. Trade liberalization and ‘revealed’ comparative advantage. Manchester School 33, 99–123 (1965).
Acknowledgements
This work has been partly funded and supported by Italian PNR project CRISIS-Lab and FET Open project nr. 255987 “FOC”).
Author information
Authors and Affiliations
Contributions
A.T. and M.C. carried out the numerical simulations and data analysis. All authors devised the research, wrote and revised the main manuscript text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Tacchella, A., Cristelli, M., Caldarelli, G. et al. A New Metrics for Countries' Fitness and Products' Complexity. Sci Rep 2, 723 (2012). https://doi.org/10.1038/srep00723
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00723
This article is cited by
-
Network topology mapping of chemical compounds space
Scientific Reports (2024)
-
Aim high, shoot low? Product complexity and export survival in Latvia
Empirica (2024)
-
Technological paths and smart specialization: analysis of regional entry and exit in Turkey
Asia-Pacific Journal of Regional Science (2024)
-
Unpacking technology flows based on patent transactions: does trickle-down, proximity, and siphon help regional specialization?
The Annals of Regional Science (2024)
-
Symphony of sustainability: how technology similarity impacts international trade patterns in environmental goods
Environmental Science and Pollution Research (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.