Abstract
By combining complex network theory and data mining techniques, we provide objective criteria for optimization of the functional network representation of generic multivariate time series. In particular, we propose a method for the principled selection of the threshold value for functional network reconstruction from raw data and for proper identification of the network's indicators that unveil the most discriminative information on the system for classification purposes. We illustrate our method by analysing networks of functional brain activity of healthy subjects and patients suffering from Mild Cognitive Impairment, an intermediate stage between the expected cognitive decline of normal aging and the more pronounced decline of dementia. We discuss extensions of the scope of the proposed methodology to network engineering purposes and to other data mining tasks.
Similar content being viewed by others
Introduction
Many biological and man-made systems can suitably be endowed with a complex network description, allowing for the extraction of topological and dynamical information from the pattern of relations between their constituent elements1,2.
Complex network theory has proved very useful in representing not only systems where interactions have a physical support (like power grid networks, the Internet or World Wide Web, transportation networks, protein-protein interaction and metabolic networks, just to make a few examples), but also those other systems lacking such a support, as, for example, social networks3 or functional brain activity4. In the latter case, a multivariate data-set can conveniently be mapped into structured networks, where nodes represent individual time series and links are established based on some metrics assessing a relationship between them. For instance, when studying brain dynamics, nodes can represent the time series generated by brain activity recorded from individual sensors, or brain volumes and links between pairs of them are created if a relationship (e.g., correlation or synchrony) is detected in the recorded signals5. The generic result is a weighted clique, which needs to be further elaborated to access meaningful information.
While such a technique has allowed characterizing important features of economic structures and processes6,7,8, or functional brain activity in healthy brains4,9,10 and in neurological and psychiatric diseases11,12,13, the overall approach is plagued by three elements of arbitrariness. First, there is no objective criterion determining which metrics ought to be used (out of the great number of available ones) for the quantification of the relationships among nodes and the corresponding mapping of data into weighted cliques. Second, the transformation of the clique into a structured network (the so called functional network) generally requires a thresholding process (that ultimately leads to an adjacency matrix) and therefore crucially depends on the value of the adopted threshold. Finally, there is no criterion for establishing which feature, or set of features, of the functional network should be looked for and taken into account to extract the best information from the original system.
In this paper, we address the latter two issues. By starting from an external classification as ground truth (in our specific case the association of each network to a healthy status or an illness), we propose the use of the output of a data mining classification task as a proxy for the relevance of the network representation under study. This yields criteria for an optimal functional network representation relative to a given problem.
In what follows, we describe the proposed methodology and present an application to the analysis of networks corresponding to healthy subjects and patients suffering from Mild Cognitive Impairment (MCI), an intermediate stage between the expected cognitive decline of normal aging and the more pronounced decline of dementia and which is considered as the prodromal stage of Alzheimer14.
Results
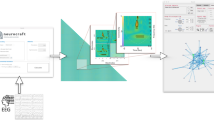
In our method, the four steps needed to transform raw data sets into a functional network representation are (see Fig. 1 Top) (i) creation of a weighted clique by means of a suitable metric, (ii) transformation of the clique to a set of structured networks with their corresponding threshold value, (iii) analysis of the resulting network topologies and the extraction of a set of features for each of them and (iv) the selection of the best threshold and the most significant set of features. We stress that we do not treat the first element of arbitrariness sketched above as we take the metrics used to establish the relationships between nodes as given. Nevertheless, an extension of the proposed methodology to cover this point is straightforward and some considerations about this are included in the final discussion.
Schematic representation of the network reconstruction process and examples of the obtained functional networks.
(Top) Sketch of the four phases of the reconstruction process. i) Creation of a weighted clique from multivariate time series, by means of some applicable metric; ii) Transformation of the weighted clique to a set of un-weighted adjacency matrices (representing functional networks) by means of different thresholds; iii) extraction of a set of features for each network and calculation of all classification scores; iv) selection of the best threshold to be used in step ii) and of the best combination of features. (Bottom) Examples of six networks extracted from the MCI data set (see Methods for details). Networks in green (in red) correspond to healthy (MCI) subjects. The functional networks are those obtained at three different thresholds: (a,d) τ = 0.19 (corresponding to a link density of 0.05), (b,e) τ = 0.1 (link density 0.2) and (c,f) τ = 0.069 (link density 0.43).
The initial information includes the raw data to be processed, composed of n time series for each one of the N subjects under study. In the standard approach, the output of the analysis is given by N networks, each composed of n nodes. We also assume prior knowledge of the initial labeling of each subject i to two non-overlapping classes ci = {0, 1}. For instance, subjects may be categorized as control and MCI subjects, or according to any other suitable categories.
Once a weighted clique W is created for each subject by means of a suitable metric (step (i) in Fig. 1 Top, see Methods section for details on the data and the adopted metric), the next step involves generating unweighted networks from it.
Instead of applying a single pre-determined threshold τ on W (i.e. defining an associated adjacency matrix A with elements ai,j = 1 whenever wi,j > τ and ai,j = 0 otherwise), we propose the use of a set of thresholds T = {τ1, τ2, …}, covering the whole range of applicable thresholds. Therefore, step (ii) yields |T| structured networks for each of the N subjects, ranging from sparsely to densely connected graphs. Examples of the resulting networks are sketched in Figure 1 Bottom, for healthy (in green) and MCI (in red) subjects and for high (a,d), intermediate (b,e) and low (c,f) values of the threshold τ.
The analysis of the topological properties of the resulting networks is usually performed by calculating and comparing a specific topological indicator, often chosen by the investigator based on his/her own experience. Instead, step (iii) of our procedure involves the extraction of a large set of measures M from each network, including the most relevant macro-, meso- and micro-scale topological features of a complex network (see Methods for the complete list of the features taken into account). At the end of the third step, the initial raw data are therefore converted into a large set of measures, specifically into N · |T| · |M| metrics, that represents a wide sample of the possible analyses that may be performed from a complex network perspective.
The problem is now that of identifying the optimal threshold and the subset of metrics that better characterize the system. This problem is tackled in step (iv) by means of a data mining classification task. Specifically, for each threshold τi and for each pair (or triplet) of metrics, subjects are classified using a Support Vector Machine (SVM) algorithm (see Methods for details on the classification and validation tasks); the percentage of subjects correctly classified is then used as a proxy of the relevance of such threshold and features.
Indeed, if a good classification is achieved, the used network metrics represent the structural differences between the two classes of subjects. Thus, the best classification corresponds to both the best set of metrics and to the corresponding best threshold.
To demonstrate the validity of the proposed approach, we consider a set of magneto-encephalographic data (MEG) and identify the features that better differentiate healthy subjects from patients suffering from MCI. The data set comprises MEG recordings from N = 38 subjects (19 MCI patients and 19 healthy controls). Information about the health status (i.e. the initial classification) was available through neuropsychological tests (see Methods for details).
Following the methodology proposed above, for each subject |T| = 178 networks are created, corresponding to the number of different thresholds chosen. For each of these networks, |M| = 72 different structural metrics are calculated. A classification task is ultimately performed for each pair and triplet of considered features. Fig. 2 reports the score (the percentage of correctly classified subjects) for the most representative pair (triplet, in red) of features, corresponding to each threshold. Specifically, at each threshold value, we consider the density of links resulting in the corresponding functional networks and report the best score (Figure 2) when adopting pairs (in black) and triplets (in red) of the measures of Table 1.
Classification score as a function of the link density.
Black (red) points indicate the best classification score obtained using pairs (triplets) of features. Best classification results appear at high link density, i.e., at rather dense networks, indicating that links associated to low correlations are actually codifying relevant information.
Several relevant conclusions can be derived from Figure 2. Firstly, the best classification rate (95%) is obtained for sufficiently low threshold values, i.e. including a great quantity of low-correlated links inside the analysis. Specifically, the maximum score corresponds to including about 40% of the links. Remarkably, the functional brain network literature typically generates networks using a 5% link density4,5. The increase in the number of links included in our optimization has a major consequence: allowing a better consideration of meso-scale structures (e.g. motifs), whose role is much less prominent at higher threshold values. As a consequence, the best classification is always obtained when explicitly including in the pairs or triplets of considered features the frequency (the Z-score) of a specific motif.
Secondly, an evaluation of the scores (from Figure 2) for a given threshold reveals no relevant increase when comparing a two-feature strategy with a three-feature approach. Therefore, in this particular example, one can define a |T| × |M| × |M| tensor of scores, where the first variable is the threshold value and the following two are a suitable combination of two measures extracted from the topological quantities definable on the reconstructed functional network. One then looks for the highest tensor component.
Thirdly, results corresponding to low link densities are much more unstable, as demonstrated by the leftmost part of the plot in Figure 2. Clearly, the addition, or deletion, of a few links has a major effect in the topology, changing the meaning of all metrics calculated on the top of it. Therefore, our results invite to reconsider many studies made in the Literature about functional brain network reconstruction.
We now discuss the relevance and stability of the obtained results. Figure 3a shows the histogram of the score values obtained at the best threshold (τbest = 0.069) for all possible pairs of measures specified in Table 1 of the Methods section. The Figure clearly shows that the best score (~ 0.95) only occurs for a very specific selection of the pair of features (namely, the Z –score of Motif 1 and the small-worldness), whereas a generic choice of a pair of measures leads to a much worse classification performance, with scores just above random classification level. In turn, this demonstrates the ability of the method to unveil which specific topological information one has to look for in order to gather the best information on the system under study and the best classification capability. This is confirmed by Figure 3b, where we report the value of the scores obtained when adopting the individuated best triplet (small-worldness, motif 1 ZScore and entropy of centrality distribution) for different values of the threshold τ. The classification ability of such a triplet is reflected by very stable high values of the score within a huge region of link densities around the optimal one.
Relevance and stability of the classification results.
(Left Panel) Histogram of the score values obtained with pairs of features for the best threshold value (0.069). (Right Panel) Score obtained with the best feature triplet (i.e., small-worldness, motif 1 ZScore and entropy of centrality distribution) at different thresholds.
Finally, Figure 4 helps visually understanding the power of the used classification technique. When adopting the best obtained threshold (τ = 0.069) and the best corresponding pair of topological features, each patient is then represented by a point in the corresponding plane of values, with green (red) points corresponding to healthy (MCI) patients.
Discussion
In conclusion, we proposed a method which, for a given (in our case a supervised classification) task, allows extracting objective criteria for the selection of the best functional network description of a generic multivariate data set. The proposed strategy allows identifying both the best descriptors of a given network and the best threshold to be used for functional network reconstruction. The effectiveness of the proposed approach is also confirmed by the score achieved in the classification task, close to a 95%.
From the specific functional neuroimaging point of view, our results show that the best threshold may be very different from those normally considered in the investigation of functional brain network and invite a debate on the significance of the choice of threshold values.
The method was applied to a biomedical classification task, but its validity is of absolute generality, as it can be applied to any kind of raw multivariate time series.
The scope of the proposed methodology is rather broad. For instance, the method naturally finds applications in the identification of the best synchronization metric to engineer a network and can easily be extended to the case of weighted networks, when considering the proper set of topological metrics to be analyzed. Furthermore, the method can be used in conjunction with other data mining tasks, as, for instance, finding the best regression between a network characteristic and an external value, or when performing unsupervised clustering tasks.
Methods
Magnetoencephalographic data
Magneto-encephalographic (MEG) recordings from nineteen Mild Cognitive Impairment (MCI) patients and nineteen healthy volunteers during a modified Sternberg's letter-probe task were analysed. All subjects were right-handed elderly volunteers recruited from the Geriatric Unit of the Hospital Universitario San Carlos, Madrid. The nineteen patients were as multi-domain MCI, according to the criteria proposed in Ref. 14. Nineteen age-matched, healthy elderly volunteers, without memory complaints, recruited for a project called Aging with Health, at the San Carlos Hospital in Madrid consented to participate in the study. This group undergoes a complete medical revision every year. To avoid possible differences due to the years of education, patients and controls were chosen so that the resulting average number of years of education was similar: 10 years for patients and 11 years for controls. Before the MEG recording, all participants or legal representatives gave informed consent to participate in the study. The study was approved by the local ethics committee.
Task
Participants were asked to memorize a set of five letters presented on a computer screen. After the presentation of the five letter set, a series of single letters (1000 ms in duration with a random ISI between 2–3 s) was presented one at a time and the participants were asked to press a button with their right hand when a member of the previous set was detected. All participants completed a training session before the actual test, which did not start until the participant demonstrated that he/she could remember the five letter set. The MEG signal was recorded with a 254 Hz sampling rate and a band pass filter between 0.5 to 50 Hz; the recording was performed using 148-channel whole head magnetometer, confined in a magnetically shielded room (MSR). An environmental noise reduction algorithm using reference channels at a distance from the MEG sensors was applied to the data. Thereafter, single trial epochs where visually inspected by an experienced investigator and epochs containing visible blinks, eye movements or muscular artifacts were excluded from further analysis. Artifact-free epochs from each channel were then classified into four different categories according to the subjects performance in the experiments: hits, false alarms, correct rejections and omissions, of which only hits were considered for further analysis. 35 1 second-long epochs were randomly chosen from each of participant.
A correlation matrix C{ωij} of size 148×148 was computed for each participant using the MEG time series. The correlation between each pair of sensors was calculated by means of a Synchronization Likelihood (SL) algorithm, as proposed in Ref. 15. In-house Fortran code was used to implement the SL algorithm. The SL was calculated for each of the 35 one-second epochs with 148*147/2 channel pairs and each subject (19 controls and 18 MCIs).
Complex network metrics used in the classification task
Table 1 reports the list of the topological indicators used in the study. Specifically, column 1 of the Table reports the name of the indicator, as it can be found in the Literature on network theory and column 2 of the Table indicates the symbol that is commonly used for denoting it. As for columns 3 and 4 of the Table, they contains a tic in all cases in which the used values were normalized, or Z-scored. Namely, for each considered network, we generated an ensemble of 500 random Erdös-Renyi (ER) graphs1, each one of them with the same number of nodes and links as in the original graph. A tic on column 3 indicates that the value of the indicator used in our computations was normalized to the corresponding average from the ensemble, while a tic on column 4 indicates that also the Z-score was considered in our computations (defined as the value of the indicator calculated on the original network minus the average of the value of the same indicator on the considered ER ensemble, divided by the standard deviation of the distribution of the indicator's value on the ER ensemble). Finally, the fifth column of the Table reports, when necessary, the Manuscript in the Literature where the full description and mathematical expression of the specific indicator can be found.
Classification task
The aim of a classification algorithm, also known as supervised learning, is, given a set of labeled examples, finding a model able to classify new non-labeled examples, i.e., find a model assigning the label attribute as a function of the rest of the attributes. In this paper we have chosen Support Vector Machines (SVM)21,24 as classification technique, which has lead to high performances in real appplications25.
SVMs are non-probabilitic linear binary classifiers21,22. Given a set of training subjects, each one described by s variables (features) and belonging to one of two previously known groups, the training phase consists in considering each subject as a point in a s-dimensional space and in finding the best hyperplane separating the two groups. New non-classified subjects are then mapped into that same space and predicted to belong to a category based on which side of the hyperplane they fall on.
To establish the accuracy of the model, the dataset is divided into training and test subsets, so that the model is built with the traning set and validated with the test set. Furthermore, to reduce variability on establising the accuracy, multiple rounds of cross-validation are performed using different partitions of the dataset. In this case and due to the limited size of the data set, we used leave-one-out cross validation, which involves the use of a single observation from the original sample as validation data and the remaining observations as the training data.
Classification was also attempted with other algorithms, including Naive Bayes27 and neural networks23,26 were used, producing qualitatively comparable results. Nevertheless, a comparison of classification methods is beyond the scope of the present paper.
References
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D. Complex networks: Structure and dynamics. Phys. Rep. 424, 175–308 (2006).
Amaral, L. A. N. & Ottino, J. M. Complex networks - Augmenting the framework for the study of complex systems. Eur. Phys. J. B 38, 147–162 (2004).
Castellano, C., Fortunato, S. & Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591 (2009).
Bullmore, E. T. & Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009).
Eguíluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M. & Apkarian, A. V. Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102 (2005).
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl. Acad. Sci. USA 99, 5766 (2002).
Llas, M., Gleiser, P. M., López, J. M. & Díaz-Guilera, A. Nonequilibrium phase transition in a model for the propagation of innovations among economic agents. Phys. Rev. E 68, 066101 (2003).
Guardiola, X., Díaz-Guilera, A., Pérez, C. J., Arenas, A. & Llas, M. Modeling diffusion of innovations in a social network. Phys. Rev. E 66, 026121 (2002).
Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, A., Apud, J. A., Weinberger, D. R. & Coppola, R. Cognitive fitness of cost-efficient brain functional networks. Proc. Natl. Acad. Sci. USA 106, 11747–11752 (2009).
Meunier, D., Lambiotte, R. & Bullmore, E. T. Modular and hierarchically modular organization of brain networks. Front. Neurosci. 4, 200 (2010).
Buldú, J. M., Bajo, R., Maestú, F., Castellanos, N., Leyva, I., Gil, P., Sendiña-Nadal, I., Almendral, J. A., Nevado, A., del-Pozo, F. & Boccaletti, S. Reorganization of functional networks in mild cognitive impairment. PLoS One 6, e19584 (2011).
Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M. & Scheltens, P. Small-world networks and functional connectivity in Alzheimers disease. Cereb. Cortex 17, 92–99 (2007).
Stam, C. J., de Haan, W., Daffertshofer, A., Jones, B. F., Manshanden, I., van Cappellen van Walsum, A. M., Montez, T., Verbunt, J. P., de Munck, J. C., van Dijk, B. W., Berendse, H. W. & Scheltens, P. Graph theoretical analysis of magnetoencephalographic functional connectivity in Alzheimer's disease. Brain 132, 213–224 (2009).
Petersen, R. C. Mild cognitive impairment as a diagnostic entity. J. Intern Med. 256, 183–194 (2004).
Stam, C. Synchronization likelihood: an unbiased measure of generalized synchronization in multivariate data sets. Physica D 163, 236–251 (2002).
Wang, B., Tang, H., Guo, C. & Xiu, Z. Entropy optimization of scale-free networks robustness to random failures. Physica A 363, 591–596 (2006).
Newman, M. E. J. Assortative mixing in networks. Phys. Rev. Lett. 89, 208701 (2002).
Latora, V. & Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 87, 198701 (2001).
Humphries, M. D. & Gurney, K. Network small-world-ness: a quantitative method for determining canonical network equivalence. PLoS ONE 3, e0002051 (2008).
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D. & Alon, U. Network motifs: simple building blocks of complex networks. Science 298, 824–827 (2002).
Cortes, C. & Vapnik, V. Support-Vector networks. Machine Learning 20, 273–297 (1995).
Meyer, D., Leisch, F. & Hornik, K. The support vector machine under test. Neurocomputing 55, 169–186 (2003).
Tan, P.-N., Steinbach, M. & Kumar, V. Introduction to Data Mining. Addison Wesley (2005).
Boser, B. E., Guyon, I. M. & Vapnik, V. N A training algorithm for optimal margin classifiers. Proc 5th Annual Workshop on Computational Learning Theory ACM Press, Pittsburg, PA 144–152 (1992).
Scholkopf, B. Support Vector Machines: A Practical Consequence of Learning Theory. IEEE Intelligent Systems 13, 18–21 (1998).
Minsky, M. & Papert, S. An Introduction to Computational Geometry. MIT Press (1969).
Domingos, P. & Pazzani, M. On the optimality of the simple Bayesian classifier under zero-one loss. Machine Learning 29, 103–137 (1997).
Acknowledgements
Work supported by Ministerio de Educación y Ciencia, Spain, through grant FIS2009-07072 and by the Community of Madrid under project URJC-CM-2010-CET-5006 and R&D Program MODELICO-CM [S2009ESP-1691]. SB acknowledges funding from the BBVA-Foundation within the Isaac-Peral program of Chairs. The authors also acknowledge the computational resources, facilities and assistance provided by the Centro computazionale di RicErca sui Sistemi COmplessi (CRESCO) of the Italian National Agency for New Technologies, Energy and Sustainable Economic Development (ENEA) and the facilities provided by CESVIMA (Spain).
Author information
Authors and Affiliations
Contributions
M.Z., P.S., R.B. and E.M. carried out the numerical experiments. M.Z., D.P., R.B., J.G.P. and S.B. analyzed the data and prepared the figures. M.Z., D.P., F.P. and S.B. wrote the Manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Zanin, M., Sousa, P., Papo, D. et al. Optimizing Functional Network Representation of Multivariate Time Series. Sci Rep 2, 630 (2012). https://doi.org/10.1038/srep00630
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00630
This article is cited by
-
The effect of the pandemic on complex socio-economic systems: community detection induced by communicability
Soft Computing (2023)
-
An evolving graph convolutional network for dynamic functional brain network
Applied Intelligence (2023)
-
Telling functional networks apart using ranked network features stability
Scientific Reports (2022)
-
A Fast Transform for Brain Connectivity Difference Evaluation
Neuroinformatics (2022)
-
Topological structures are consistently overestimated in functional complex networks
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.