Abstract
Quantum entanglement became essential in understanding the non-locality of quantum mechanics. In optics, this non-locality can be demonstrated on impressively large length scales, as photons travel with the speed of light and interact only weakly with their environment. Spontaneous parametric down-conversion (SPDC) in nonlinear crystals provides an efficient source for entangled photon pairs, so-called biphotons. However, SPDC can also be implemented in nonlinear arrays of evanescently coupled waveguides which allows the generation and the investigation of correlated quantum walks of such biphotons in an integrated device. Here, we analytically and experimentally demonstrate that the biphoton degrees of freedom are entailed in an additional dimension, therefore the SPDC and the subsequent quantum random walk in one-dimensional arrays can be simulated through classical optical beam propagation in a two-dimensional photonic lattice. Thereby, the output intensity images directly represent the biphoton correlations and exhibit a clear violation of a Bell-like inequality.
Similar content being viewed by others
Introduction
As proven by Bell1, nonlocal quantum correlations play the central role in the understanding of the famous Einstein-Podolsky-Rosen gedankenexperiment2. In the realm of optics, the most prominent source of such non-local correlations are entangled photon pairs, so-called biphotons3. They give rise to various applications such as quantum cryptography4, teleportation5,6,7,8 and quantum computation9. A particular robust approach to realize strong quantum correlations of path-entangled photons in compact settings is their propagation in optical waveguide arrays10,11 that provide a unique tool for the experimental analysis of a spatially discrete, continuous-time, quantum walks with highly controllable parameters. However, in these settings the photons are typically generated before they are launched into the array, usually via spontaneous parametric down-conversion (SPDC) in bulk optical components3. Recently, it was suggested theoretically12 that biphotons can be generated directly in a quadratically nonlinear waveguide array through SPDC and quantum walks of the generated photons can give rise to non-classical correlations at the output of this monolithic integrated optical device.
Remarkably, various quantum phenomena can be simulated via purely classical light propagation in waveguide arrays, serving as an optical test-bed of fundamental physical effects without the need of an intricate single photon setup13,14,15. In particular, the nonclassical one-dimensional (1D) evolution of correlated quantum particles can be mapped onto a classical two-dimensional (2D) evolution of a single wave packet, as was predicted recently by Longhi16,17. By increasing the dimensionality of the structure, the same dynamics is obtained as if the number of participating photon wavepackets were effectively doubled. This concept was recently applied in the context of a discrete-time random walk of coherent light18. In this article we will show that linear propagation of classical light beams can be used to simulate the nonlinear effect of SPDC leading to photon pair generation and quantum walks of the generated biphotons. Specifically, we prove theoretically and demonstrate experimentally that the quantum correlations of biphotons generated in a quadratically nonlinear 1D waveguide array with pump waveguides at the edges can be mapped onto the linear propagation in a specially designed 2D system. This analogy enables us to simulate, with classical light, the quantum coincidence counts for biphotons and the breaking of a Bell-like inequality.
Results
We first extend the theory of photon-pair generation in quadratic waveguide arrays from Ref.12 to finite waveguide arrays. This is especially important for an experimental realization, where the number of waveguides is naturally limited. We consider a type-I SPDC process with continuous-wave or narrow-band pump of frequency ωp, which converts pump photons into pairs of signal and idler photons with frequencies ωs,i. We assume spectral filtering at half of the pump frequency, such that ωs,i = ωp/2. The signal and idler photons can tunnel between the neighboring waveguides at a rate characterized by the coefficients Cs,i = C, whereas coupling of the pump can be neglected, due to the strong dispersion of the evanescent coupling10,11,12,19,20. Taking this into account and following Refs.21,22,23 one can derive the differential equations for the biphoton wave function  (see Methods)
(see Methods)

whereby ns,i label the waveguide index for signal and idler, respectively, δ denotes the Kronecker delta function and Δβ(0) is the phase mismatch in a single waveguide. The pump field is distributed over the waveguides according to An whereas deff is the effective nonlinear coefficient. This equation governs the evolution of a biphoton wave function in a quadratic nonlinear waveguide array. The term in square brackets on the right-hand side describes the quantum walks, i. e. the biphoton tunneling11,12 between the waveguides and corresponds to the model derived in Ref.17 in case of a linear waveguide array. In addition, our model also describes the nonlinear process of biphoton generation through SPDC, which is introduced by the last term. Note that both photons are always created at the same spatial location, which is expressed mathematically through δ-functions, but the biphotons subsequently spread out through correlated quantum walks.
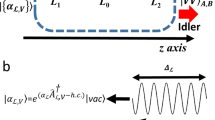
After establishing the key model Eq. (1), we now demonstrate how the biphoton wave function can be simulated classically. Note that Eq. (1) is formally equivalent to the coupled-mode equations for classical beam propagation in a square linear 2D waveguide array17,19 with additional source terms describing the pump. In the following, we demonstrate that for a pump exclusively coupled to the outermost waveguides of the 1D array, the effect of these terms can be simulated classically by introducing additional waveguides close to the corners of an equivalent 2D array, as shown in Fig. 1. We consider the case when the additional waveguide modes only weakly overlap with the modes at the array corners and the corresponding coupling coefficient Cc is very small compared to the array, Cc ≪ C. If the light is launched only into the additional waveguides, then in the undepleted pump approximation the classical field evolution in those waveguides is  exp(iβleftz) and
exp(iβleftz) and  exp(iβrightz), where
exp(iβrightz), where  and
and  are the input amplitudes, βleft and βright are the mode detunings of the additional waveguides with respect to a single waveguide in the array. Here, we consider the case where both additional waveguides are identical to the guides of the lattice (βleft = βright = 0). Then, the classical field evolution in the array follows Eq. (1) with the effective pump amplitudes in the edge waveguides
are the input amplitudes, βleft and βright are the mode detunings of the additional waveguides with respect to a single waveguide in the array. Here, we consider the case where both additional waveguides are identical to the guides of the lattice (βleft = βright = 0). Then, the classical field evolution in the array follows Eq. (1) with the effective pump amplitudes in the edge waveguides  ,
,  (there is zero effective pump, An = 0, for 1 < n < N) and the effective detuning Δβ(0) = 0. This corresponds to perfectly phase-matched SPDC in the 1D-array, which has been shown to produce the most pronounced quantum correlations12. Based on the established mathematical equivalence classical light propagation in the linear array structure shown in Fig. 1(b) can be employed to simulate the quantum properties of biphotons generated in a quadratic nonlinear array shown in Fig. 1(a). In particular the photon number correlation
(there is zero effective pump, An = 0, for 1 < n < N) and the effective detuning Δβ(0) = 0. This corresponds to perfectly phase-matched SPDC in the 1D-array, which has been shown to produce the most pronounced quantum correlations12. Based on the established mathematical equivalence classical light propagation in the linear array structure shown in Fig. 1(b) can be employed to simulate the quantum properties of biphotons generated in a quadratic nonlinear array shown in Fig. 1(a). In particular the photon number correlation  , which describes the probability of simultaneous detection of photons at the output of the waveguides with number ns and ni, is of interest. Thereby,
, which describes the probability of simultaneous detection of photons at the output of the waveguides with number ns and ni, is of interest. Thereby,  denotes the photon annihilation operator in these waveguides. In the classical simulation the output intensity distribution
denotes the photon annihilation operator in these waveguides. In the classical simulation the output intensity distribution  corresponds directly to Γ:
corresponds directly to Γ:

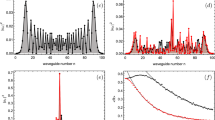
To verify the correct operation of our simulator, we first implemented a system with a single outer pump waveguide coupled to the corner of 3 × 3 waveguide array [Fig. 2(a)]. For the investigation light is launched into the device and imaged onto a CCD at the output (see Methods). The experimental output intensity distribution is shown in Fig. 2(b). We perform a simple scaling of the measured intensity according to Eq. (2) and determine the two-photon correlation function as shown in Fig. 2(c). These results closely match the theoretical predictions presented in Fig. 2(d).
Settings.
(a) Sketch of a 1D quadratic nonlinear waveguide array containing N = 3 waveguides with two pumps coupled to the edge waveguides leading to biphoton generation via SPDC and the output photon detectors. (b) Cross-section of a 2D waveguide array for the classical optical simulation of biphoton generation via SPDC consisting of 3 × 3 waveguides. The additional waveguides represent the pump beam coupled to the edge waveguides.
Results for one pump waveguide.
(a) Sketch of the linear 2D waveguide array simulating quantum correlations of biphotons generated by SPDC with one pump at the edge waveguide. (b) CCD camera image of the output light distribution when only the pump waveguide is excited. (c,d) Correlation map of the simulated 1D quantum system: (c) Extracted from intensity measurement shown in (b) and (d) calculated numerically based on Eq. (1). (e,h) Simulated non-classicality function determined with Eq. (3) for (e) experimental and (f) numerical correlations from (c) and (d), respectively.
After verifying the correct operation in the single-pump regime, we return to the initially considered case of two pump waveguides at the corners of the 2D lattice as shown in Fig. 3(a). The challenge here was to have light of the same amplitude and phase in both pump waveguides. The implementation is discussed in Methods. We likewise use the output intensity distribution [Fig. 3(b)] to calculate the photon number correlation [Fig. 3(c)] which agrees very well with the simulation shown in Fig. 3(d).
Discussion
After obtaining the correlation functions from the output intensities, we determine in accordance with Ref.11, the similarity  between the numerically calculated (
between the numerically calculated ( ) and experimentally obtained (
) and experimentally obtained ( ) distributions as S = 0.954 for the case of one pump waveguide and S = 0.972 for two pump waveguides.
) distributions as S = 0.954 for the case of one pump waveguide and S = 0.972 for two pump waveguides.
In a further step we demonstrate that our classical optical simulator can model nonclassical biphoton statistics. Following Ref.11, we calculate the non-classicality

Values of  , indicate true quantum behavior corresponding to a violation of Bell's inequality, which cannot occur in a purely classical setting. In the single pump case we plot the function
, indicate true quantum behavior corresponding to a violation of Bell's inequality, which cannot occur in a purely classical setting. In the single pump case we plot the function  for our experimental data in Fig. 2(e), which shows the presence of positive values in agreement with numerical simulations [Fig. 2(f)]. This proves that our 2D classical setting successfully simulates actual non-classical 1D statistics. Fig. 3(e) and Fig. 3(f) illustrate the experimentally and numerically calculated non-classicality for the case of two pump waveguides. Also for this setting it is evident, that the nonclassical features can be simulated with high quality. Note that the output intensities are purely classical, i.e., they do not exhibit quantum correlations themselves. Instead, the non-classical properties of the 1D system are emulated in the 2D intensity distribution.
for our experimental data in Fig. 2(e), which shows the presence of positive values in agreement with numerical simulations [Fig. 2(f)]. This proves that our 2D classical setting successfully simulates actual non-classical 1D statistics. Fig. 3(e) and Fig. 3(f) illustrate the experimentally and numerically calculated non-classicality for the case of two pump waveguides. Also for this setting it is evident, that the nonclassical features can be simulated with high quality. Note that the output intensities are purely classical, i.e., they do not exhibit quantum correlations themselves. Instead, the non-classical properties of the 1D system are emulated in the 2D intensity distribution.
As evident from the strong overexposure of the CCD at the pump waveguide in Fig. 2(b) and the fact that the majority of the light remains in the pump waveguides in Fig. 3(b), the undepleted pump approximation holds.
For both a single and double pump waveguides, the output correlation should be symmetric,  , due to the indistinguishability of two photons and we see that this feature is properly reproduced through the 2D experimental intensity distributions where
, due to the indistinguishability of two photons and we see that this feature is properly reproduced through the 2D experimental intensity distributions where  , see Figs. 2(b) and 3(b). For a double pump configuration, there appears additional symmetry due to identical pump amplitudes at the two boundaries and we have in theory
, see Figs. 2(b) and 3(b). For a double pump configuration, there appears additional symmetry due to identical pump amplitudes at the two boundaries and we have in theory  [Figs. 3(d)], whereas such symmetry is clearly broken for a single pump case [Figs. 2(d)]. In experiment we have only a slight asymmetry of the output intensity distributions due to imperfections of the three-waveguide input-coupler (see Methods). Nevertheless, for all cases we have similarity S close to unity, as well as a good agreement of the experimental and simulated non-classicality which proves excellent accuracy of the classical optical simulator.
[Figs. 3(d)], whereas such symmetry is clearly broken for a single pump case [Figs. 2(d)]. In experiment we have only a slight asymmetry of the output intensity distributions due to imperfections of the three-waveguide input-coupler (see Methods). Nevertheless, for all cases we have similarity S close to unity, as well as a good agreement of the experimental and simulated non-classicality which proves excellent accuracy of the classical optical simulator.
In conclusion, we have derived a model describing the evolution of a biphoton wave function in 1D quadratic nonlinear waveguide arrays, where the photons are generated through SPDC and undergo correlated quantum walks. We further demonstrated analytically as well as experimentally that the quantum biphoton dynamics can be simulated by a classical wave evolution in a linear 2D waveguide array with additional waveguides representing the pump. Hereby, the additional spatial dimension provides the degrees of freedom which are otherwise encoded in the two-particle dynamics. The classical measurements of the output light intensity directly simulate the quantum biphoton correlation function, in particular including the regime of the breaking of a 1D Bell-like inequality.
Additionally, our work demonstrates the practicality of using higher-dimensional photonic structures to emulate more complex quantum effects associated with structures of lower dimensionality. Since generation of many-photon states is increasingly complicated, this approach could provide significant benefits for an implementation of quantum schemes.
Methods
Derivation of the biphoton wave function
In the following a detailed derivation of the differential equation for the biphoton wave function is presented. We start from the coupled mode equations for the classical light amplitudes in waveguide n (1 ≤ n ≤ N)

with the boundary conditions E0 ≡ EN+1 ≡ 0. The eigenstates of the system are the supermodes  , where m is the mode number (1 ≤ m ≤ N), βm = 2C cos(km) is the propagation constant,
, where m is the mode number (1 ≤ m ≤ N), βm = 2C cos(km) is the propagation constant,  is the amplitude distribution and km = πm/(N + 1). For the pump, the corresponding coupling coefficient Cp would generally have a much smaller value compared to the signal and idler waves, Cp ≪ C, due to the weaker mode overlap between neighboring waveguides at higher frequencies19. Therefore, we neglect coupling effects for the pump beam (Cp ≈ 0) and assume its amplitude An to be constant along the propagation.
is the amplitude distribution and km = πm/(N + 1). For the pump, the corresponding coupling coefficient Cp would generally have a much smaller value compared to the signal and idler waves, Cp ≪ C, due to the weaker mode overlap between neighboring waveguides at higher frequencies19. Therefore, we neglect coupling effects for the pump beam (Cp ≈ 0) and assume its amplitude An to be constant along the propagation.
Subsequently, we employ the mathematical approach of Refs.21,22,23 developed for multimode waveguides and obtain the following expression for the two photon state  :
:

where

Here B is a constant,  are photon creation operators at the numbered supermode states, |0, 0〉 is the vacuum state,
are photon creation operators at the numbered supermode states, |0, 0〉 is the vacuum state,  is a two-photon wave function,
is a two-photon wave function,  is a phase mismatch between the modes and Δβ(0) is the mismatch in a single waveguide. The value
is a phase mismatch between the modes and Δβ(0) is the mismatch in a single waveguide. The value  is the normalized spatial overlap of the signal and idler distributions with the pump distribution. We note that an integration over frequency is omitted, since we consider a frequency window narrower then the phase-matching bandwidth of the SPDC.
is the normalized spatial overlap of the signal and idler distributions with the pump distribution. We note that an integration over frequency is omitted, since we consider a frequency window narrower then the phase-matching bandwidth of the SPDC.
For our analysis, it is convenient to rewrite Eq. (6) in the form of differential equations,

This allows us to change our representation to the real-space wave function, which is related to the modal formulation as  . Due to the orthogonality of the supermodes, we can invert these relations as
. Due to the orthogonality of the supermodes, we can invert these relations as  . Substituting the latter expression in Eq. (7) and again employing the orthogonality property together with the fact that by definition the supermodes satisfy Eq. (4), yields the differential equations (1) for the biphoton wave function in real-space representation.
. Substituting the latter expression in Eq. (7) and again employing the orthogonality property together with the fact that by definition the supermodes satisfy Eq. (4), yields the differential equations (1) for the biphoton wave function in real-space representation.
Experimental realization
To realize the classical light simulator of quantum biphoton statistics, we fabricate waveguide arrays in fused silica using the femtosecond direct-write technique24,25 where we used 160 fs pulses with an average power of 20 mW and a writing velocity of 60 mm/min. A sketch of the writing setup is shown in Fig. 4(a). Our optical simulator consists of a 3×3 waveguide array with outer pump waveguides coupled to the corners of the array as shown in Fig. 4(b). To ensure homogenous horizontal and vertical coupling we rotated the structure by 45° and fabricated the waveguides in a rhombic geometry. To meet the undepleted pump approximation of SPDC we made sure that the intensities in the pump waveguide do not decrease significantly by choosing a sufficiently weak coupling of Cc = 0.125 cm−1, corresponding to a distance between the pump waveguide and the array of 25 µm20. Laser light of 633 nm wavelength and a power of about 3 mW was injected into the pump waveguides and the output intensity ( ) was observed with a CCD camera. We then use the measured intensity to determine the simulated biphoton correlation.
) was observed with a CCD camera. We then use the measured intensity to determine the simulated biphoton correlation.
Fabrication setting.
(a) Sketch of the writing setup, where femtosecond laser pulses are focused into a transparent bulk material. In the focal region, the refractive index of the material is permanently increased. (b) Sketch of the setting with two edge pump waveguides, where the phase-matched symmetric amplitude distribution of the pump is achieved by a specially designed three-waveguide directional coupler. The light is launched into the central waveguide marked with an arrow. Additionally, a micrograph of the output facet is shown as inset (scale bar equals 40 µm).
In a first step we investigated a simulator having a single pump waveguide [Fig. 2(a)]. The distance between the array waveguides is 17 µm corresponding to a coupling constant of C = 0.78 cm−1.
The second step was an experiment performed with two pump waveguides at the array corners where we use a specially designed three-waveguide directional coupler that allows us to symmetrically distribute the light over the pump waveguides in a phase-matched fashion [Fig. 3(a), Fig. 4(b)]. Here we chose an inner distance of 21 µm which is best fitted by the numerical calculation with a coupling constant of C = 0.26 cm−1.
References
Bell, J. S. On the einstein rosen podolsky paradox. Physics 1, 195–200 (1964).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Shih, Y. An Introduction to Quantum Optics: Photon and Biphoton Physics (Taylor & Francis, New York, 2011).
Ekert, A. K., Rarity, J. G., Tapster, P. R. & Palma, G. M. Practical quantum cryptography based on 2-photon interferometry. Phys. Rev. Lett. 69, 1293–1295 (1992).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Boschi, D., Branca, S., De Martini, F., Hardy, L. & Popescu, S. Experimental realization of teleporting an unknown pure quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 80, 1121–1125 (1998).
Pan, J. W., Bouwmeester, D., Weinfurter, H. & Zeilinger, A. Experimental entanglement swapping: Entangling photons that never interacted. Phys. Rev. Lett. 80, 3891–3894 (1998).
Furusawa, A. et al. Unconditional quantum teleportation. .Science 282, 706–709 (1998).
Bouwmeester, D., Ekert, A. K. & Zeilinger, A. (eds.) The physics of quantum information: quantum cryptography, quantum teleportation, quantum computation (Springer, New York., 2000).
Bromberg, Y., Lahini, Y., Morandotti, R. & Silberberg, Y. Quantum and classical correlations in waveguide lattices. Phys. Rev. Lett. 102, 253904 (2009).
Peruzzo, A. et al. Quantum walks of correlated photons. .Science 329, 1500–1503 (2010).
Solntsev, A. S., Sukhorukov, A. A., Neshev, D. N. & Kivshar, Y. S. Spontaneous parametric down-conversion and quantum walks in arrays of quadratic nonlinear waveguides. Phys. Rev. Lett. 108, 023601 (2012).
Keil, R. et al. Classical analogue of displaced fock states and quantum correlations in glauberfock photonic lattices. Phys. Rev. Lett. 107, 103601 (2011).
Longhi, S. Quantum-optical analogies using photonic structures. Laser & Photon. Rev. 3, 243–261 (2009).
Szameit, A. & Nolte, S. Discrete optics in femtosecond-laserwritten photonic structures. .J. Phys. B 43, 163001 (2010).
Longhi, S. Optical bloch oscillations and zener tunneling with nonclassical light. Phys. Rev. Lett. 101, 193902 (2008).
Longhi, S. Photonic bloch oscillations of correlated particles. Opt. Lett. 36, 3248–3250 (2011).
Schreiber, A. et al. A 2d quantum walk simulation of two-particle dynamics. Science 336, 55–58 (2012).
Lederer, F. et al. Discrete solitons in optics. .Phys. Rep. 463, 1–126 (2008).
Szameit, A., Dreisow, F., Pertsch, T., Nolte, S. & Tünnermann, A. Control of directional evanescent coupling in fs laser written waveguides. Opt Express 15, 1579–1587 (2007).
Christ, A. et al. Spatial modes in waveguided parametric down-conversion. Phys. Rev. A 80, 033829 (2009).
Grice, W. P. & Walmsley, I. A. Spectral information and distinguishability in type-ii downconversion with a broadband pump. Phys. Rev. A 56, 1627–1634 (1997).
Di Giuseppe, G. et al. Entangled-photon generation from parametric down-conversion in media with inhomogeneous nonlinearity. Phys. Rev. A 66, 013801 (2002).
Itoh, K., Watanabe, W., Nolte, S. & Schaffer, C. B. Ultrafast processes for bulk modification of transparent materials. Mrs Bulletin 31, 620–625 (2006).
Szameit, A. et al. Hexagonal waveguide arrays written with fs-laser pulses. .Appl. Phys. B 82, 507–512 (2006).
Acknowledgements
The authors wish to thank the German Ministry of Education and Research (Center for Innovation Competence program, grant 03Z1HN31) and the Australian Research Council (including Future Fellowship FT100100160). R. K. is supported by the Abbe School of Photonics.
Author information
Authors and Affiliations
Contributions
A. S. S., A. A. S. and Yu. S. K. suggested the concept and did the theoretical analysis; M. G. and A. S. S. performed the numerical calculations; M. G., A. S. S., R. K. and A. S. proposed the experimental realization; M. G. fabricated the samples and performed the measurements; M. G., A. S. S., R. K., A. A. S., M. H., A. S. and Yu. S. K. discussed the results and all authors cowrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Gräfe, M., Solntsev, A., Keil, R. et al. Biphoton generation in quadratic waveguide arrays: A classical optical simulation. Sci Rep 2, 562 (2012). https://doi.org/10.1038/srep00562
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00562
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.