Abstract
In a world in which the pace of cities is increasing, prompt access to relevant information is crucial to the understanding and regulation of land use and its evolution in time. In spite of this, characterization and regulation of urban areas remains a complex process, requiring expert human intervention, analysis and judgment. Here we carry out a spatio-temporal fractal analysis of a metropolitan area, based on which we develop a model which generates a cartographic representation and classification of built-up areas, identifying (and even predicting) those areas requiring the most proximate planning and regulation. Furthermore, we show how different types of urban areas identified by the model co-evolve with the city, requiring policy regulation to be flexible and adaptive, acting just in time. The algorithmic implementation of the model is applicable to any built-up area and simple enough to pave the way for the automatic classification of urban areas worldwide.
Similar content being viewed by others
Introduction
During the eighties fractal concepts have received widespread attention, including in geography1,2,3,4,5,6,7,8,9,10. Since then, geographers, urban planners and others have investigated the relation between fractal structures and urban areas6,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26, where the calculation of the global fractal dimension (D) of cities (and surrounding areas), in Europe and the U.S.A.13,27, has been carried out. Comparison between cities worldwide lead to an average of D = 1.713,28. Growth patterns13, in turn, show a general increase of D with time for several cities. The global D for the Metropolitan Area of Lisbon (MAL), which will be used as a case study below, is in line with this trend, exhibiting the values D(1960) = 1.42, D(1990) = 1.61 and D(2004) = 1.66. In spite of these novel perspectives on geographical spatial phenomena12,13,14,18,23,25,29,30,31, characterization and regulation of urban areas remains a complex process requiring expert human intervention, study and judgment, with an inherent bias which is difficult to calibrate in space and time — a problem that also accrues to other issues in geography32 — rendering the analysis susceptible to concepts, policies and visions which are permanently evolving. As a result, not only (e.g.) Sydney and Lisbon may bear little (if any) correspondence, the classification criteria of urban areas in the 1960s may differ substantially from those of 2012, which increases even more the inherent difficulty of an automated and generalized classification scheme which can be of direct use by policy makers28.
Here we take a new approach to urban development and introduce a classification scheme which, being decoupled from human intervention, allows for a unified classification of urban areas worldwide. We resort to the spatio-temporal layout of the MAL (North side, spanning a period of nearly half a century, from 1960 to 2004), to perform a fractal analysis, based on which we devise a mathematical model which allows the automatic classification and characterization of any patch of a city or territory into one of five different types, each calling for different type of intervention and policy measures13,18,23,25,29,30.
The built-up areas of the whole of MAL (for each time snapshot corresponding to 1960, 1990 and 2004) were pixelized and subsequently arranged in a matrix of square cells of 1 km2 area (see Methods and Supplementary Information (SI) for details). We computed the fractal dimension of each cell using the standard box-counting method (see Methods). As shown below, a single (global) fractal dimension fails to provide a complete characterization of an urban area. Instead, a whole plethora of fractal dimensions is needed, showing how urban areas have heterogeneous fractal properties9. Lower fractal dimensions (D) typically represent dispersed areas, whereas fractal dimensions close to two are associated with compact built-up areas19,25. Here we explore such heterogeneous fractal properties of urban areas to develop a new tool that can be used in the context of city planning, specifically at a metropolitan scale.
Results
The top panels of Fig. 1 show the spatio-temporal evolution of these fractal structures, represented in terms of the fractal dimension D. Fig. 1 reveals that MAL is becoming increasingly compact with time, led by the growth of the Lisbon suburban areas, inter-connected by transport infrastructures (roadways and railways). The spatio-temporal fractal analysis also uncovers the non-trivial relation between the fractal dimension of each cell and its overall occupied area. Indeed, if we plot the fraction of occupied area of each cell — a = A/Ac, where A is the built-up area of each cell and Ac ( = 1 km2) the total area of the cell — as a function of the fractal dimension D, we obtain the distributions shown in the bottom panel of Fig. 1 (lin-log plot). They are bound, from above and below, at all times, by the exponential curves u(D) and l(D), depicted in green and red, respectively (see Methods for their analytic form).
Spatio-temporal fractal analysis of MAL.
Top : MAL was divided into cells of 100×100 pixels; the fractal dimension (D, 0≤D≤2) of each cell was computed. There is a progressive compactification of MAL with time. Bottom: Fraction of built-up area in each cell (a) plotted (log-scale) as a function of the associated fractal dimension D. At all times one observes a large abundance of cells satisfying 1.0≤D≤1.8, typical of an urban area. Note also that all cells are bound from above and from below by the exponential curves u(D) and l(D), respectively (see main text and Methods for details).
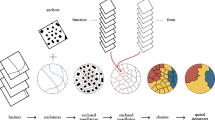
Fig. 1 shows many cells with the same D but different a and vice-versa. If, for a given cell i, ai(Di) = u(Di), there is no room for building additional area in that cell while preserving the fractal dimension and hence the only possibility is for d to increase when new constructions appear in that cell. Whenever ai(Di)<u(Di), however, growth of built-up area can still occur without necessarily increasing the fractal dimension of the cell. For a given D, we computed the number of possible configurations of built-up area satisfying l(D)≤a≤u(D) (see Methods). The logarithm of this quantity, which we call S, is plotted in Fig. 2, together with its rate of change (S') as a function of D. The quantity S can be understood as a “microcanonical” entropy, measuring the number of possible configurations compatible with a given fractal dimension. The behaviour of these curves leads to the following classification of each cell into one of five Types characterized and illustrated in Fig. 2, functions of the fractal dimension D only.
For cells of Type 1, built-up areas are isolated by definition (where land use is predominantly for agriculture or forest). At the other end of the spectrum, cells of Type 5 are already close to saturation, likely located in the most central (not only in a geographical sense) places of any metropolitan area. Here, opportunities for adding new buildings (increasing a) are highly constrained, as reflected in the rapid decline of S(D) (or the negative values of the rate S'). For regions of Type 2, the fractal dimension is still low and characterizes the transition from dispersed built-up areas towards an urban spurring along roads or railways: dispersed areas dominate, occasionally nucleating small villages. Finally, regions of Type 3 and Type 4 concentrate those situations in which opportunities to increase built-up area are not only ripe, but also there are many different ways of adding area to regions of these Types. Their difference, however, lies in the rate of change of S, which increases with D in cells of Type 3 and decreases in cells of Type 4. As Fig. 2 illustrates, growth in regions of Type 3 is mostly associated with nucleation of new areas which are essentially disconnected from previous ones, leading to the appearance of dispersed patches of built-up areas. This is what we call the metastatic phase, in analogy with metastases that occur in certain forms of cancer. Similar to metastases, these new areas may potentially constitute the first stage of urban sprawl. On the other hand, cells of Type 4 have a larger fractal dimension and already a declining rate of opportunity to incorporate new buildings into them; here, the predominant behaviour is the consolidation and compactification of existing area, forming large connected urban blocks.
Throughout the history of many urban settlements, cells started as Type 1 and evolved in time to higher and higher Types as they became more compact. Of course, there are many ways of reaching a given type of compactification and both S and S' provide useful information in this respect. Urban planning translates, in our model, in defining a general path in growing from regions of Type 1 up to Type 5. As Fig. 2 reveals explicitly, deviations from this path will most likely occur in regions of Types 3 and 4 and, consequently, these are the regions where planning must act more effectively. Indeed, such proximate planning will ensure well-designed transitions into more compact configurations.
As we discuss below (complementary analysis of empirical data is provided as SI), the correlation between the categorization made (derived purely from the functional behaviour of S(D)) and the spatio-temporal data of MAL, is extremely high. We emphasize the generality of the arguments leading to this categorization, which rely solely on the level of detail at which one carries out the decomposition of the geographical data. In SI we show how the model is calibrated whenever data to be analyzed has a different resolution. We now apply this classification scheme back into MAL.
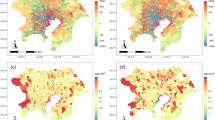
Fig. 3 shows the spatio-temporal patterns of regions of different Types in MAL. In 1960, the city of Lisbon dominated the layout of MAL. One identifies few areas exhibiting a high degree of compactness in the municipalities of Sintra and Cascais (surrounding the mountainous Sintra National Park (SNP)), which became later the main suburban areas of Lisbon, associated with the growth of regions of Type 4 in 1990.
Spatio-temporal types of regions in MAL.
We use the color codes indicated to make a longitudinal cartographic classification of MAL. Black (blue) lines stand for main roadways (railways). Between 1960 and 1990 many cells of Type 1 became cells of Type 2 (21.6% of the total of changes), whereas from 1990 to 2004 a burst of transitions from Type 2 to Type 3 occurs (11.9% of the total changes) and from Type 3 to Type 4 (10.3% of the total changes). These occurred mostly in the vicinity of administrative centers already present in 1960 (see main text and SI for details).
The road (black lines) and train (blue lines) networks connecting Lisbon to Sintra and Cascais, associated with i) a lack of affordable housing offer in the city of Lisbon and ii) an ineffective enforcement of urban policies, promoted the emergence of a continuous of built-up area in the space between. The observed burst of cells of Types 3 and 4 in 1990 can be directly correlated with those areas of MAL where an uncontrolled development of housing actually took place. Indeed, urban policies were introduced in MAL only in the late seventies and, as stated, most of them proved unsuccessful. Thus, self-organization has played a role in the urban development of MAL. However, the outcome of this unregulated growth has led to a loss of economic efficiency, given the need to build new infrastructures to serve such emergent urban patterns33. This, in turn, clearly justifies, a posteriori, the need to apply proximate regulation in regions of Types 3 and 4: simply, the odds that things go wrong are far too high. In 2004, it seems clear that the dominance of regions of Type 3 (with 30% of the total of cells) may promote the future connection between the interstitial spaces left in the agglomeration around Lisbon. Furthermore, it is noteworthy the large growth of regions of Type 3 in the northern periphery of Lisbon, nearby the black dashed line. This line indicates a road that became available only after the 2004 snapshot shown (between 2005 and 2008) showing that, already in 2004, the areas around this road have the potential, if left without regulation, to undergo undesirable growth. In fact, these cells constitute, at present, a major concern, as the trend now witnessed follows closely that observed before in southern municipalities of MAL — of suburban sprawl and surfacing of fragmented spaces.
Discussion
Our results show evidence of metropolitan areas as a dynamical, evolving organism, calling for the development of flexible yet effective planning and regulation, which must adapt to an increasing evolutionary pace of cities34,35. Such a “just in time” policy has been pointed out28,36. In this sense, our model and results provide, to the best of our knowledge, the first quantitative means for the automatic categorization and corresponding identification of different Types of areas and associated need for intervention, depending on existing plans. Hence, the present model may have a direct impact in city planning and methodologies addressing sustainability and urban regulation. In this quest, it is worth to emphasize that our model is simple enough to be applicable to any built-up area, as such opening a window of opportunity for the development of automatic and quantitative tools that are able to monitor and foresee urban growth, which may play a fundamental role in short and mid-term urban planning.
Methods
Dataset
We resort to the Metropolitan Area of Lisbon (MAL) as a convenient and mostly unstudied, example of a metropolitan area, which combines large and compact built-up areas with rapidly growing suburbs and a ring of rural regions. Built-up areas from 1960 and 1990 were extracted from the former Portuguese Geographical and Cadastral Institute at 1:50000 scale and from the military maps of the Army Geographical Institute at 1:25000 scale, respectively. Data from 2004 was obtained from photo-interpretation of orthophotomaps at a scale 1:25000. The 3 datasets were made uniform through cartographic generalization and converted to an array of pixels of 100 m2, which were combined in cells of 100×100 pixels. The fractal analysis was performed over the set of cells (see SI for an extended description of data acquisition).
Fractal dimensions and built-up areas
The fractal dimension of each cell was computed using a conventional box counting algorithm (see, e.g.37,). In each iteration k, the minimum set of Nk squares (boxes) of side  (pixels, 1 pixel = 10 m) necessary to cover all built-up area was computed. After m = 5 iterations
(pixels, 1 pixel = 10 m) necessary to cover all built-up area was computed. After m = 5 iterations  , the fractal dimension D is given by the slope of a linear regression applied to the duplets
, the fractal dimension D is given by the slope of a linear regression applied to the duplets  , given that
, given that  , where c is constant (see SI for a discussion of the quality of the fractal analysis). This expression can also be used to determine the area Ak occupied by the Nk boxes, which reads
, where c is constant (see SI for a discussion of the quality of the fractal analysis). This expression can also be used to determine the area Ak occupied by the Nk boxes, which reads  , from where we obtain the recurrence
, from where we obtain the recurrence  . Taking the limit m into account, we obtain
. Taking the limit m into account, we obtain  . This can be used to write down the expression for the upper bound of the built-up area as a function of D:
. This can be used to write down the expression for the upper bound of the built-up area as a function of D:  — where n is the length of each square cell, i.e., n = 100 pixels (or 1 km — see SI for a detailed discussion of this choice of cell size). The lower bound (L(D)) will be proportional to the upper bound U(D), such that
— where n is the length of each square cell, i.e., n = 100 pixels (or 1 km — see SI for a detailed discussion of this choice of cell size). The lower bound (L(D)) will be proportional to the upper bound U(D), such that  . Since
. Since  , we have that
, we have that  and
and  . The exponential curves u(D) and l(D) pictured in Fig. 1, where obtained from the normalized version of these expressions, with m = 5.
. The exponential curves u(D) and l(D) pictured in Fig. 1, where obtained from the normalized version of these expressions, with m = 5.
Number of configurations
Let us call  the number of possible configurations one can envisage within each cell characterized by a total built-up area A and fractal dimension D. From the expression of
the number of possible configurations one can envisage within each cell characterized by a total built-up area A and fractal dimension D. From the expression of  above, the total number of boxes covering a built-up area A at the kth stage of the box-counting algorithm reads
above, the total number of boxes covering a built-up area A at the kth stage of the box-counting algorithm reads  (assuming that c grows linearly with
(assuming that c grows linearly with  ). We may write
). We may write  , a recursive sequence in which each of the
, a recursive sequence in which each of the  boxes of side εk is divided in 4 sub-boxes of sides εk-1 and only Nk-1 of those sub-boxes are chosen to cover the built-up area at the previous stage. Denoting by
boxes of side εk is divided in 4 sub-boxes of sides εk-1 and only Nk-1 of those sub-boxes are chosen to cover the built-up area at the previous stage. Denoting by  the number of ways that this procedure can be done, one can write the total number of possible configurations as
the number of ways that this procedure can be done, one can write the total number of possible configurations as  (see SI for closed forms of f and Ω). Finally, for numerical convenience, we take the logarithm of the total number of configurations at dimension D, given by
(see SI for closed forms of f and Ω). Finally, for numerical convenience, we take the logarithm of the total number of configurations at dimension D, given by  . Thus, the quantity S offers a rough estimate of the number of possible (past, present and future) arrangements for a given fractal dimension or level of compactness. The nature of S and
. Thus, the quantity S offers a rough estimate of the number of possible (past, present and future) arrangements for a given fractal dimension or level of compactness. The nature of S and  defines different regimes (see Fig. 2) leading to the definition of 5 Types which, as shown in Fig. 3 (and SI), correlates well with empirical longitudinal analysis of MAL.
defines different regimes (see Fig. 2) leading to the definition of 5 Types which, as shown in Fig. 3 (and SI), correlates well with empirical longitudinal analysis of MAL.
References
Goodchild, M. F. Fractals and the accuracy of geographical measures. Mathematical Geology 12, 85–98 (1980).
Mark, D. M. & Aronson, P. B. Scale-dependent fractal dimensions of topographic surfaces: An empirical investigation with application in geomorphology and computer mapping. Mathematical Geology 16, 671–683 (1984).
Arlinghaus, S. L. Fractals take a Central Place. Geografiska Annaler 67B, 83–88 (1985).
Batty, M. & Longley, P. Fractal-based description of urban form. Environment and planning B: Planning and Design 14, 123–134 (1987).
Culling, W. E. H. & Datko, M. The fractal geometry of the soil-covered landscape. Earth Surface Processes and Landforms 12, 369–385 (1987).
Goodchild, M. F. & Mark, D. M. The fractal nature of geographic phenomena. Annals of the Association of American Geographers 77, 265–278 (1987).
Barnsley, M. Fractals Everywhere. (Academic Press, London, 1988).
Klinkenberg, B. University of Western Ontario, 1988.
Stanley, H. E. & Meakin, P. Multifractal phenomena in physics and chemistry. Nature 335, 405–409 (1988).
Gilbert, L. E. Are topographic data sets fractal? .Pure and Applied Geophysics 131, 241–254 (1989).
Klinkenberg, B. Fractals and morphometric measures: Is there a relationship? Geomorphology 5, 5–20 (1992).
Klinkenberg, B. & Goodchild, M. The fractal properties of topography: a comparison of methods. Earth Surface Processes and Landforms 17, 217–234 (1992).
Batty, M. & Longley, P. Fractal cities: a geometry of form and function. (Academic Press, 1994).
Bunde, A. & Havlin, S. Fractals in science. (Springer-Verlag, 1994).
Benguigui, L. A fractal analysis of the public transportation system of Paris. Environment and Planning A 27, 1147–1147 (1995).
Makse, H. A., Havlin, S. & Stanley, H. E. Modelling urban growth patterns. Nature 377, 608–612 (1995).
Batty, M. & Xie, Y. Preliminary evidence for a theory of the fractal city. Environ Plan A 28, 1,745–762 (1996).
Portugali, J. Self-organization and the City. (Springer Verlag, 2000).
Benguigui, L., Czamanski, D., Marinov, M. & Portugali, Y. When and where is a city fractal? .Environment and Planning B 27, 507–520 (2000).
Lu, Y. & Tang, J. Fractal dimension of a transportation network and its relationship with urban growth: a study of the Dallas-Fort Worth area. Environment and Planning B 31, 895–912 (2004).
Tannier, C. & Pumain, D. Fractals in urban geography: a theoretical outline and an empirical example. Cybergeo: European Journal of Geography, Systems, Modelling and Geostatistics 307 (2005).
Batty, M. Cities and complexity. (MIT Press Cambridge, MA, 2005).
Pumain, D. Hierarchy in natural and social sciences. (Springer Verlag, 2006).
Lagarias, A. Fractal analysis of the urbanization at the outskirts of the city: models, measurement and explanation. Cybergeo: European Journal of Geography, Systems, Modelling and Geostatistics 391 (2007).
Frankhauser, P. Fractal geometry for measuring and modelling urban patterns. The Dynamics of Complex Urban Systems, 213–243 (2008).
Batty, M. The size, scale and shape of cities. Science 319, 769–771 (2008).
Shen, G. Fractal dimension and fractal growth of urbanized areas. International Journal of Geographical Information Science 16, 419–437 (2002).
Alfasi, N. & Portugali, J. Planning just-in-time versus planning just-in-case. Cities 21, 29–39 (2004).
Hall, P. Cities of tomorrow: an intellectual history of urban planning and design in the twentieth century. (Blackwell, 2002).
Kibria, M. S., Zlatanova, S., Itard, L. & Dorst, M. GeoVEs as tools to communicate in Urban Projects: requirements for functionality and visualization. 3D Geo-Information Sciences, 379–395 (2009).
Rozenfeld, H. D., Rybski, D., Gabaix, X. & Makse, H. A. The area and population of cities: New insights from a different perspective on cities. American Economic Review 101, 560–580 (2011).
Goodchild, M, . F. & Gopal, S. The accuracy of spatial databases. (CRC, 1989).
Pereira, M. & Silva, F. N. Modelos de ordenamento em confronto na área metropolitana de Lisboa: cidade alargada ou recentragem metropolitana? .Cadernos Metrópole 20, 107–123 (2008).
Bettencourt, L., Lobo, J., Helbing, D., Kühnert, C. & West, G. B. Growth, innovation, scaling and the pace of life in cities. Proc Natl Acad Sci U S A 104, 7301 (2007).
Rozenfeld, H. D. et al. Laws of population growth. Proc Natl Acad Sci U S A 105, 18702 (2008).
Portugali, J. Complexity, Cognition and the City. (Springer Verlag, 2011).
Falconer, K. J. Fractal geometry: mathematical foundations and applications. (John Wiley & Sons Inc, 2003).
Acknowledgements
This research was supported by grants PTDC/FIS/101248/2008, PTDC/MAT/122897/2010, SFRH/BPD/63765/2009 and multi-annual funding of CMAF-UL, e-GEO/FCSH/UNL and INESD-ID provided by FCT Portugal through PIDDAC Program funds.
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to this work: they all designed and performed the research, analyzed the data and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Encarnação, S., Gaudiano, M., Santos, F. et al. Fractal cartography of urban areas. Sci Rep 2, 527 (2012). https://doi.org/10.1038/srep00527
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00527
This article is cited by
-
From cognitive maps to spatial schemas
Nature Reviews Neuroscience (2023)
-
Fractal dimension complexity of gravitation fractals in central place theory
Scientific Reports (2023)
-
Observing the compact trend of urban expansion patterns in global 33 megacities during 2000–2020
Journal of Geographical Sciences (2023)
-
Urban Growth Process in Greater Accra Metropolitan Area: Characterization Using Fractal Analysis
Journal of Geovisualization and Spatial Analysis (2023)
-
Emergence of urban growth patterns from human mobility behavior
Nature Computational Science (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.