Abstract
Recently, manipulating heat transport by phononic devices has received significant attention, in which phonon – a heat pulse through lattice, is used to carry energy. In addition to heat control, the thermal devices might also have broad applications in the renewable energy engineering, such as thermoelectric energy harvesting. Elementary phononic devices such as diode, transistor and logic devices have been theoretically proposed. In this work, we experimentally create a macroscopic scale thermal rectifier based on reduced graphene oxide. Obvious thermal rectification ratio up to 1.21 under 12 K temperature bias has been observed. Moreover, this ratio can be enhanced further by increasing the asymmetric ratio. Collectively, our results raise the exciting prospect that the realization of macroscopic phononic device with large-area graphene based materials is technologically feasible, which may open up important applications in thermal circuits and thermal management.
Similar content being viewed by others
Introduction
With the development of solid-state devices, the integrated circuits can be built up by diodes and transistors. The conventional diodes and transistors can realize “on” and “off” state by controlling the electrical conduction. If the thermal conduction can be well controlled, we can also realize thermal circuits by using these novel phononics devices. In addition to information processing, the thermal devices might also have broad applications for heat control/management in the future. Recent years, some theoretical proposals for thermal rectifier have been put forward, include structures based on one-dimensional nanotubes and nanowires1,2,3,4,5,6,7,8,9 and two-dimensional graphenes10,11,12,13. The first solid-state thermal rectifier has been reported experimentally by C. W. Chang et al.14 in carbon nanotubes.
However, it is still a challenge to create macroscale phononic devices based on these nanoscale architectures. Inspired by the study of thermal rectifier in nanoscale, an oxide thermal diode made of two cobalt oxides with different thermal conductivities have been experimentally demonstrated15,16. The working mechanism for this two-segment diode is that they have thermal conductivities with different temperature dependence. From a simple classical heat conduction analysis, the rectification of this two-segment diode is proportional to the difference in thermal conductivity and inversely proportional to the interface resistance17. In most bulk materials, the large interface contact resistance between the two segments limits the enhancement of the rectification ratio. Thus it is indispensable to develop single component thermal rectifier.
In this work, for the first time, we demonstrated macroscopic scale thermal rectification phenomenon in asymmetric reduced graphene oxide (rGO) materials. According to recent efforts, rGO can be used to fabricate paper-like films with large area, excellent mechanical property, high thermal conductivity and electrical conductivity18,19,20. It has been demonstrated theoretically that compared to single-layer graphene, a larger rectification ratio can be achieved in multi-layer structures, due to the presence of layer-layer interactions12. Combined with the availability of high quality, here we use a “rGO paper” material composed of stacked rGO to make thermal rectifier. Benefit from their high thermal conductivity and strong temperature dependence around room temperature, high thermal rectification ratio is achieved in both triangular and two-rectangular shaped rGO based thermal rectifier, which is in good agreement with the numerical calculation.
Results
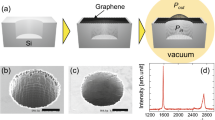
The optical photograph of the rGO paper is shown in Fig. 1(a). Figure 1(b) illustrates the surface of rGO film. Some ripples of graphene can be seen clearly. Figure 1(c) shows the cross-section of rGO. The film thickness is ∼50 μm. Figure 1(d) presents the Energy Dispersive X-ray (EDX) spectrum of rGO film. The film is mainly graphene stacked layers with little oxygen remained. The ratio of carbon and oxygen is ∼5.56. The precise chemical composition and structure of rGO film can be found as the Supplementary Fig. S1∼S3 online. Our measurement system is described as a schematic figure in Fig. 1(e). The rGO samples are suspended on two heaters. The top view of the measurement system is shown in Fig. 1(f). The distance between two heaters is 10 mm. Each side of thermocouple is placed 1 mm from its nearest heater. Triangular samples with θ = 20°, 40° and 60° are studied here.
(a) Photograph of the rGO paper. (b) Surface profile of rGO paper under SEM. (c) Cross section image of rGO paper under SEM. The thickness is ∼50 um. (d) EDX spectrum of rGO paper. There remains little oxygen atoms. (e) Schematic view of the measure system. A triangular rGO structure is tested. (f) Schematic view of the devices.
Here we denote the positive heat flux direction when the bottom of rGO paper (point 1 as shown in the inset of fig. 2(a)) is at a higher temperature and the negative heat flux direction when the top (point 2) is at a higher temperature. When the system arrives at non-equilibrium stationary state, we record the input power of the heater. Figure 2(a) and 2(b) show the monitored temperatures as a function of time at points 1 and 2 for 60° triangular sample in the positive direction and the negative direction, respectively. With increasing electrical current I, the temperature systematically increase. The heat power caused by the electrical current through the relationship of P = rI2 is controlled to keep the same stationary state temperature difference between points 1 and 2, where r is the resistance of the heater. The most striking feature is that the magnitude of the heat power in the negative direction (P-) is significantly larger than that in the positive direction (P+). This demonstrates that there exists thermal rectification phenomenon in this system. Figure 2(c) shows the experimental thermal power P+ and P- as a function of temperature difference |ΔT| = |T1−T2|. With the increase of ΔT, heat power monotonically increases. The thermal rectification coefficient R is defined as

As shown in Fig. 2(d), the rectification coefficient is 1.21 at |ΔT| = 12.7 K. The R is increased with the increasing of |ΔT|. The largest value of R is 1.28 at |ΔT| = 39.1 K. Meanwhile, the rectification coefficient in rGO based asymmetric structure is much higher than that in carbon nanotube which is just 1.02 observed experimentally14. The experimental results for 40° and 20° triangular samples can be found as Supplementary Fig. S4, S5 online. Figure 2(e) shows the heat power versus the angle of the rGO paper. The heat power P+ in the positive direction stays constant under different angle. Meanwhile, the heat power P- in the negative direction increases linearly with the angle. As shown in Fig. 2(f), the rectification coefficient increases linearly with the angle of the rGO paper. It is indicated that the rectification effect can be enhanced by tuning the asymmetricity.
Testing results of the 60° triangular shaped solid-state thermal rectifier.
Monitored temperatures (left axis) and current (right axis) as a function of time at points 1 and 2 of (a) positive direction and (b) negative direction, respectively. Measured (c) heat power and (d) rectification coefficient versus temperature difference |ΔT|. In Figure 2 (c) and (d), the first point is  (
( ,
,  in positive direction); The second point is
in positive direction); The second point is  (
( ,
,  in positive direction); The third point is
in positive direction); The third point is  (
( ,
,  in positive direction); The fourth point is
in positive direction); The fourth point is  (
( ,
,  in positive direction). Measured (e) heat power and (f) rectification coefficient versus angle
in positive direction). Measured (e) heat power and (f) rectification coefficient versus angle  under |ΔT| = 40 K. In Figure 2(f), the first point is
under |ΔT| = 40 K. In Figure 2(f), the first point is  = 20°(
= 20°( ,
,  in positive direction); The second point is
in positive direction); The second point is  = 40°(
= 40°( ,
,  in positive direction); The third point is
in positive direction); The third point is  = 60°(
= 60°( ,
,  in positive direction).
in positive direction).
In order to further study the shape effect, we also measured the rectification of the two-rectangular shaped rGO rectifier. The dimension of the two-rectangular shaped rGO (Wbot/Wtop = 9/2) and measurement system is shown in Fig. 3(a). Figure 3(b) and 3(c) show the monitored point1 (point2) temperatures as a function of time under the positive (negative) temperature bias direction, respectively. We also found that the magnitude of the heat power in the negative direction (P-) is significantly larger than that in the positive direction (P+), which corresponds to thermal rectification effect. As shown in Fig. 3(d), the rectification coefficient is 1.06 at |ΔT| = 15.3 K. The R is increased with the increasing of |ΔT|. The largest value of R is 1.10 at |ΔT| = 46.5 K. The inset shows the experimental thermal power P+ and P- as a function of temperature difference |ΔT|. With the increase of ΔT, thermal power monotonically increases. The experimental results for Wbot/Wtop = 9/5 and 9/7 samples can be found as Supplementary Fig. S6, S7 online.
Schematic structure and experimental results of the two-rectangular shaped solid-state thermal rectifier.
(a) Schematic view of the devices. Monitored temperatures (left axis) and current (right axis) as a function of time at points 1 and 2 of (b) positive direction and (c) negative direction under Wbot/Wtop = 4.5, respectively. (d) Measured rectification coefficient versus temperature difference |ΔT| under Wbot/Wtop = 4.5. Inset is heat power versus temperature difference |ΔT|. In Figure 3 (c) and (d), the first point is  (
( ,
,  in positive direction); The second point is
in positive direction); The second point is  (
( ,
,  in positive direction); The third point is
in positive direction); The third point is  (
( ,
,  in positive direction); The fourth point is
in positive direction); The fourth point is  (
( ,
,  in positive direction). Measured (e) heat power and (f) rectifying coefficient versus Wbot/Wtop under |ΔT| = 40 K. In Figure 3(f), the first point is Wbot/Wtop = 9/7 (
in positive direction). Measured (e) heat power and (f) rectifying coefficient versus Wbot/Wtop under |ΔT| = 40 K. In Figure 3(f), the first point is Wbot/Wtop = 9/7 ( ,
,  in positive direction); The second point is Wbot/Wtop = 9/5 (
in positive direction); The second point is Wbot/Wtop = 9/5 ( ,
,  in positive direction); The third point is Wbot/Wtop = 9/2 (
in positive direction); The third point is Wbot/Wtop = 9/2 ( ,
,  in positive direction).
in positive direction).
Two-rectangular shaped rGO paper with Wbot/Wtop = 9/2, 9/5 and 9/7 are used to address the impact of width ratio. Figure 3(e) shows the heat power versus the Wbot/Wtop ratio of the rGO paper. The heat power P+ in the positive direction stays constant under different width ratio. However, the heat power P- in the negative direction increases linearly with the Wbot/Wtop. As shown in Fig. 3(f), the rectification coefficient increases linearly with the width ratio of the rGO paper. It is indicated that the rectification effect can be enhanced by increasing the ratio of Wbot/Wtop.
Combining the results for both triangular and two-rectangular shaped graphene thermal rectifier, it is clear that the thermal rectification effect is more obvious in triangular shaped rGO paper. As the phonon scattering just happens at the junction of the two-rectangular shaped rGO, the rectification of heat power by shape effect is limited. Meanwhile, the phonon scattering happens along the whole bevel edge for the triangular shaped rGO, so it has larger thermal rectification coefficient. This is consistent with the idea proposed by C. Dames that interface thermal contact has negative impact on thermal rectification17.
Discussion
To understand the underlying mechanism of the rectification phenomenon, we perform finite element simulation to study the heat flux and temperature distribution in the system. For the macroscopic asymmetric shape thermal rectifier, the Fourier's law can be written as:

Where, x is the position, T(x) is the temperature at that position, k is the thermal conductivity of the rGO.
Our simulations are based on a model that the rGO paper is in contact with high and low temperature heat baths. The dimensions of rGO paper are in the range of the experimental observation. In our simulations, we only consider the steady-state case. The temperature dependent thermal conductivity of the rGO paper can be written as21:

where T is the absolute temperature and h is the thickness of rGO paper.
Natural convection and radiation as the heat transfer mechanism between the system and the surrounding air are established. The surrounding environment is assumed to be stationary air at atmospheric pressure. The finite element modeling is used to perform a steady-state thermal analysis of the system to evaluate temperature profile. Ansys Multiphysics22, a finite element analysis program, is employed.
The simulation results of the temperature distribution under positive heat flux direction and negative direction are shown in Fig. 4(a) and 4(b), respectively. Here, for the positive direction, temperatures at points 1 and 2 are set as 74°C and 27.5°C, respectively. And the temperatures at points 1 and 2 are set as 27.5°C and 74°C respectively in negative direction. It is found that the temperature shows small gradient in wide rectangular shaped rGO and large gradient in narrow rectangular shaped rGO, both in Fig. 4(a) and 4(b). As the thermal conductivity of rGO paper depends on temperature, it is indicated that the averaged total thermal conductivity kav is different in positive and negative directions. We also show the temperature profile (see Supplementary Fig. S8 online) along the two-rectangular shaped sample. In the junction, there exhibits discontinuity in the temperature profile due to the sudden structural changes. The large temperature gradient region is a result of the presence of high resistance to heat flow at the junction, which translates to a reduction in the heat flux of the structure. The asymmetric geometry may lead to different radiation heat losses to the ambient. So the thermal radiation power in positive and negative direction should be compared with the total power. Based on the Stepan-Boltzmann's law ( ), the thermal radiation power can be written as:
), the thermal radiation power can be written as:

Where,  is the Stepan constant,
is the Stepan constant,  is the absolute temperature and
is the absolute temperature and  is the surface area of the rGO paper. As the temperature is gradient from high to low, the temperature profile is simulated by finite element modeling. Then the thermal radiation power can be calculated by Eq. (4). As shown in Fig. 4(c), the thermal radiation power in positive directions is consistent with that in the negative directions. And both are much lower than the total power. It is indicated that the total power gap for positive and negative directions have little relation with the thermal radiation. So the thermal radiation of rGO paper can be neglected. The rectification effect is mainly caused by thermal conduction. As shown in Fig. 4(d), the calculated rectification coefficient versus the temperature difference |ΔT| is in a good agreement with the experimental results under Wbot/Wtop = 4.5. We also calculated the heat power and rectification coefficient versus Wbot/Wtop under |ΔT| = 40 K. As shown in Fig. 4(e) and 4(f), the theoretical results are accordance with experimental results.
is the surface area of the rGO paper. As the temperature is gradient from high to low, the temperature profile is simulated by finite element modeling. Then the thermal radiation power can be calculated by Eq. (4). As shown in Fig. 4(c), the thermal radiation power in positive directions is consistent with that in the negative directions. And both are much lower than the total power. It is indicated that the total power gap for positive and negative directions have little relation with the thermal radiation. So the thermal radiation of rGO paper can be neglected. The rectification effect is mainly caused by thermal conduction. As shown in Fig. 4(d), the calculated rectification coefficient versus the temperature difference |ΔT| is in a good agreement with the experimental results under Wbot/Wtop = 4.5. We also calculated the heat power and rectification coefficient versus Wbot/Wtop under |ΔT| = 40 K. As shown in Fig. 4(e) and 4(f), the theoretical results are accordance with experimental results.
Finite element modeling (FEM) simulation results of the two- rectangular shaped solid-state thermal rectifier.
Simulation results of the temperatures distribution in (a) positive direction and (b) negative direction, respectively. (c) The total heat power (Experiments) and the thermal radiation power (Calculation) versus temperature difference |ΔT|. (d) Calculated and measured rectification coefficient versus the temperature difference |ΔT| under Wbot/Wtop = 4.5. Calculated and measured (e) heat power and (f) rectification coefficient versus Wbot/Wtop under |ΔT| = 40 K.
As rGO paper is sensitive to humidity, we make a contrast experiment to verify the effect of humidity on our measurement. There is no obvious change before and after dry (see Supplementary Fig. S9 online). It is indicated that humidity has little impact on our experiment results.
From our simulation results, it is obvious that according to the shape effect, the temperature profile depends on the heat flux directions. In the temperature range of our experiment, the thermal conductivity of rGO paper decreases with temperature. For the positive heat flux direction, the wide segment is at high temperature contact, which corresponds to high average temperature and leads to low effective thermal conductivity. In contrary, for the negative heat flux condition, the whole system is under a “lower” average temperature, which results in higher heat flux. Thus the temperature gradient dependent averaged thermal conductivity results in the thermal rectification.
In the two-segment oxide based thermal rectifier15,16, its working mechanism is the different temperature dependence of thermal conductivity. In these two-component systems, the interface thermal contact has negative impact on thermal rectification17. However, thermal interface material is still an emerging area. In this work, we propose to create macroscopic thermal rectifier based on rGO materials. This is a single component system, thus avoiding the issue of interface thermal resistance. Here the rectification ratio depends on the change of thermal conductivity with temperature. Figure 5(a) shows the temperature dependent thermal conductivity of rGO with different thickness, which are calculated according to the empirical fitting equation (3). When temperature is higher than about 200 K, thermal conductivity decreases with temperature and the slope of the temperature dependent thermal conductivity increase with thickness, converges to a constant value when thickness is beyond 10 μm. Figure 5(b) shows the thickness dependent rectification ratio. As expected, the rectification increases with thickness and converges when thickness is larger than 10 μm, due to the impact of thickness on temperature dependent thermal conductivity.
(a) Plot of the theoretical temperature dependent thermal conductivity of rGO paper with different thickness. (b) Plot of the theoretical rectification of two-rectangular shaped rGO paper versus the film thickness under Wbot/Wtop = 9/2. (c) Comparison of temperature dependent thermal conductivity of rGO with copper and silicon.
Furthermore, it is worth to address the advantage of rGO material by comparing with other common used materials. Figure 5(c) shows the temperature dependent thermal conductivity of 50 μm rGO paper, bulk cooper, 700 nm cooper thin film23, single crystalline silicon layer and poly silicon24. It is obvious that rGO paper has a high thermal conductivity as well as cooper. Moreover, around room temperature, it has more remarkable temperature dependence than those for cooper and single crystalline silicon film. Thus it is expected to result in larger thermal rectification ratio in our proposed rGO materials than those created by cooper and single crystalline silicon films.
In summary, we demonstrated macroscopic thermal rectifier using rGO. The rectifier exhibits rectification which depends on the asymmetric shape. We analyzed the triangular and two-rectangular shaped rGO thermal rectifier experimentally. It is found that 60° triangular shaped sample has a rectification coefficient of 1.28 and the rectification coefficient is increased with the increasing of the angle. In addition, the two-rectangular shaped sample has the rectification coefficient of 1.10 which could also be enhanced by increasing the width ratio. Using finite element modeling, the rectification effect for two-rectangular shaped samples was analyzed. The simulation results were in accordance with that of the experimental results. Although asymmetric heat flux is observed in the rGO system, it is worth to mention that it is not an ideal thermal rectifier, as heat flux in the low heat flux direction is not zero. According to electrical rectifier, an ideal thermal rectifier should “stop” heat flux in one temperature bias direction. This needs further work to reduce the heat flux in the low heat flux direction to make this device for better thermal management performance. Our results shed light on macroscopic phononic device with large-area graphene based materials and may open up its important applications in thermal circuits and thermal management.
Methods
Sample preparation
Graphene oxide paper was prepared according to the Ref.25, then it was reduced by acid in one hour according to the Ref.26. The rGO detail preparation method is described in supplementary information.
Characterizations
The surface morphology and chemical composition of rGO film were observed by SEM/EDX (DI-3100). The precise chemical composition and structure of rGO film was obtained by the X-ray photoelectron spectroscopy (XPS, Physical Electronics Inc.), X-ray diffractometer (XRD, Rigaku Inc.) and Raman spectroscopy using wavelength of 532 nm (HORIBA Inc.).
Measure system setting up
First, the rGO samples were cut into triangular shape. Then rGO samples are suspended on two heaters. The two resistive heaters with R = 1245 Ω is used to apply heat current Ih into the rectifier. The silver paste (Kyocera Chemical CT285) is used to establish good thermal contact between heaters and samples. The heaters are placed on the foam to reduce the heat leakage from the substrate. Two micro thermocouples with 50 μm dimension (KRC ST-50) are attached on two sides of the rectifier to monitor the temperature in the presence of the heat current. At last, a radiation shield is covered on the whole system to protect the heat fluctuation from the environment.
Test methods
To explore the thermal rectification effect, first, the electrical current is applied to one of the heater. This establishes a temperature bias between the two sides. Here we denote the positive heat flux direction when the bottom of rGO paper (point 1 as shown in figure 2) is at a higher temperature and the negative heat flux direction when the top (point 2) is at a higher temperature. When the system arrives at non-equilibrium stationary state, we record the input power of the heater. In our measurements, we keep the same stationary state temperature difference |ΔT| for both positive and negative temperature bias direction and record the heat power in the positive direction (P+) and negative direction (P-), respectively. If the thermal rectification effect existed in the system, the value of P+ and P- should be different. The similar approach has been used by D. Sawaki et al. to study the thermal rectification in oxide materials16.
References
Terraneo, M., Peyrard, M. & Casati, G. Controlling the energy flow in nonlinear lattices: a model for a thermal rectifier. Phys. Rev. Lett. 88, 094302 (2002).
Li, B., Wang, L. & Casati, G. Thermal diode: Rectification of heat flux. Phys. Rev. Lett. 93, 184301 (2004).
Li, B., Wang, L. & Casati, G. Negative differential thermal resistance and thermal transistor. Appl. Phys. Lett. 88, 143501 (2006).
Wang, L. & Li, B. Thermal logic gates: computation with phonons. Phys. Rev. Lett. 99, 177208 (2007).
Wang, L. & Li, B. Phononics gets hot. Phys. World 21, 27–29 (2008).
Wu, G. & Li, B. Thermal rectification in carbon nanotube intramolecular junctions: Molecular dynamics calculations. Phys. Rev. B 76, 085424 (2007).
Yang, N., Zhang, G. & Li, B. Carbon nanocone: A promising thermal rectifier. Appl. Phys. Lett. 93, 243111 (2008).
Hu, M., Keblinski, P. & Li, B. Thermal rectification at silicon-amorphous polyethylene interface. Appl. Phys. Lett. 92, 211908 (2008).
Ni, X., Zhang, G. & Li, B. Thermal conductivity and thermal rectification in unzipped carbon nanotubes. .J. Phys.: Condens. Matter. 23, 215301 (2011).
Yang, N., Zhang, G. & Li, B. Thermal rectification in asymmetric graphene ribbons. Appl. Phys. Lett. 95, 033107 (2009).
Hu, J., Ruan, X. & Chen, Y. P. Thermal conductivity and thermal rectification in graphene nanoribbons: A molecular dynamics study. Nano Lett. 9, 2730–2735 (2009).
Zhang, G. & Zhang, H. Thermal conduction and rectification in few-layer graphene Y Junctions. Nanoscale 3, 4604–4607 (2011).
Yang, N., Ni, X., Jiang, Jin. & Li, B. How does folding modulate thermal conductivity of graphene? Appl. Phys. Lett. 100, 093107 (2012).
Chang, C. W., Okawa, D., Majumdar, A. & Zettl, A. Solid-state thermal rectifier. Science 314, 1121–1124 (2006).
Kobayashi, W., Teraoka, Y. & Terasaki, I. An oxide thermal rectifier. Appl. Phys. Lett. 95, 171905 (2009).
Sawaki, D., Kobayashi, W., Moritomo, Y. & Terasaki, I. Thermal rectification in bulk materials with asymmetric shape. Appl. Phys. Lett. 98, 081915 (2011).
Dames, C. Solid-state thermal rectification with existing bulk materials. J. Heat Transfer 131, 061301 (2009).
Wei, Z. Q. et al. Nanoscale tunable reduction of graphene oxide for graphene electronics. Science 328, 1173–1376 (2010).
Becerril, H. A. et al. Evaluation of solution-processed reduced graphene oxide films as transparent conductors. ACS Nano 2, 463–470 (2008).
Eda, G., Fanchini, G. & Chhowalla, M. Large-area ultrathin films of reduced graphene oxide as a transparent and flexible electronic material. Nature Nanotech. 3, 270–274 (2008).
Li, H., Zhu, Y. & Gui, J. Study of thermal conductivity of graphite films. J. Suzhou Univ. 26, 48–50 (2010).
Kraus, A. D. & Bar-Cohen, A. Hemisphere Thermal Analysis and Control of Electronic Equipment, New York, Chapter 1, 30–50(1983).
Ye, J. & Tang, Z. Molecular dynamics simulation to the thermal conductivity of copper thin film. Chin. J. Comput. Phys. 19, 321–324 (2002).
Uma, S., McConnell, A. D., Asheghi, M., Kurabayashi, K. & Goodson, K. E. Temperature-dependent thermal conductivity of undoped polycrystalline silicon layers. Int. J. Thermophys. 22, 605–616 (2001).
Dikin, D. A. et al. Preparation and characterization of graphene oxide paper. Nature 448, 457–460 (2007).
Pei, S. F., Zhao, J. P., Du, J. H., Ren, W. C. & Cheng, H. M. Direct reduction of graphene oxide films into highly conductive and fiexible graphene films by hydrohalic acids. Carbon 48, 4466–4474 (2010).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (61025021, 60936002, 51072089 and 61020106006) and the National Key Project of Science and Technology (2009ZX02023-001-3, 2011ZX02403-002).
Author information
Authors and Affiliations
Contributions
H.T. made and tested the samples, simulated the results and wrote the manuscript. T.L.R. and G.Z. oversaw all research phases, optimized the devices performance and revised the manuscript. D.X. analysed the test results and revised the manuscript. Y.Y. set up the platform. Y.F.W., C.J.Z., P.G.P. and L.G.W. participated in the preparation of samples and measurements. L.T.L. guided the experiment and revised the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Tian, H., Xie, D., Yang, Y. et al. A Novel Solid-State Thermal Rectifier Based On Reduced Graphene Oxide. Sci Rep 2, 523 (2012). https://doi.org/10.1038/srep00523
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00523
This article is cited by
-
Effect of the Filling Liquid Ratio on the Thermal Performance of a Novel Thermal Diode with Wick
Journal of Thermal Science (2024)
-
Non-Fourier heat transport in nanosystems
La Rivista del Nuovo Cimento (2023)
-
Heterogeneous irradiated-pristine polyethylene nanofiber junction as a high-performance solid-state thermal diode
Scientific Reports (2021)
-
Performance prediction of nanoscale thermal cloak by molecular dynamics
Applied Physics A (2021)
-
Thermal Rectification Film using Liquid Crystalline Asymmetric Diodes
Brazilian Journal of Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.