Abstract
How do users behave in online chatrooms, where they instantaneously read and write posts? We analyzed about 2.5 million posts covering various topics in Internet relay channels and found that user activity patterns follow known power-law and stretched exponential distributions, indicating that online chat activity is not different from other forms of communication. Analysing the emotional expressions (positive, negative, neutral) of users, we revealed a remarkable persistence both for individual users and channels. I.e. despite their anonymity, users tend to follow social norms in repeated interactions in online chats, which results in a specific emotional “tone” of the channels. We provide an agent-based model of emotional interaction, which recovers qualitatively both the activity patterns in chatrooms and the emotional persistence of users and channels. While our assumptions about agent's emotional expressions are rooted in psychology, the model allows to test different hypothesis regarding their emotional impact in online communication.
Similar content being viewed by others
Introduction
How do human communication patterns change on the Internet? Round the clock activities of Internet users put us into the comfortable situation of having massive data from various sources available at a fine time resolution. But what to look at? Which aggregated measures are most appropriate to capture how new technologies affect our communicative behavior? And then, are we able to match these findings with a dynamic model that is able to generate insights into their origin? In this paper, we provide both: a new way of analysing data from online chats and a model of interacting agents to reproduce the stylized facts of our analysis. In addition to the activity patterns of users, we also analyse and model their emotional expressions that trigger the interactions of users in online chats. Validating our agent-based model against empirical findings allows us to draw conclusions about the role of emotions in this form of communication.
Online communication can be seen as a large-scale social experiment that constantly provides us with data about user activities and interactions. Consequently, time series analyses have already revealed remarkable temporal activity patterns, e.g. in email communication. Such patterns allow conclusions how humans organize their time and give different priorities to their communication tasks1,2,3,5,6,7. One particular quantity to describe these patterns is the distribution P(τ) of the waiting time τ that elapses before a particular user answers e.g. an email. Different studies have confirmed the power-law nature of this distribution, P(τ) ~ τ−α. Its origin was attributed either to the burstiness of events2 or to circadian activity patterns3, while a recent work shows that a combination of both effects is also a plausible scenario4. However, the value of the exponent α is still debated. A stochastic priority queue model6 allows to derive α by comparing two different rates, the average rate λ of messages arriving and the average rate µ of processing messages. If µ ≤ λ, i.e. if messages arrive faster than they can be processed, α = 3/2 was found, which is compatible with most empirical findings and simulation models1,2,3,8. However, in the opposite case, µ ≥ λ, i.e. if messages can be processed upon arrival, α = 5/2 was found together with an exponential correction term. The latter regime, also denoted as the “highly attentive regime”, could be verified empirically so far only by using data about donations7. So, it is an interesting question to analyze other forms of online communication to see whether there is evidence for the second regime.
In this paper, we analyze data about instant online communication in different chatting communities, specifically Internet Relay Chat (IRC) channels, where each channel covers a particular topic. Prior to the very common social networking sites of today, IRC channels provided a safe and independent way for users to share and discuss information outside traditional media. Different from other types of online communication, such as blogs or fora where entries are posted at a given time (decided by the writer), IRC chats are instantaneous in real time, i.e. users read while the post is written and can react immediately. This type of interaction requires much higher user activity in comparison to persistent communication e.g. in fora. Further, it is more spontaneous, often leading to emotionally-rich communication between involved peers. Consequently, instant communication should require specific tools and models for analysis, that are capable of covering these predominant features.
Nowadays, IRC channels are still one of the most used platforms for collective real-time online communication and are used for various purposes, e.g. organization of open-source project development, Internet activism, dating, etc. Our dataset (described in detail in the data section), consists of 20 IRC channels covering topics as diverse as music, sports, casuals chats, business, politics, or computer related issues – which is important to ensure that there is no topical bias involved in our analysis. For each channel, we have consecutive daily recordings of the open discussion over a period of 42 days, which amounts to more than 2.5 million posts in total generated by more than 20.000 different users.
We process our analysis as follows: first, we look into the communication patterns of instant online discussions, to find out about the average response time of users and its possible dependence on the topics discussed. This shall allow us to identify differences between instantaneous chatting communities and other forms of slower, persistent communication. In a second step, we look more closely into the content of the discussions and how they depend on the emotions expressed by users. Remarkably, we find that most users are very persistent in expressing their positive or negative emotions - which is not expected given the variety of topics and the user anonymity. This leads us to the question in what respect online chats are different from offline discussions which are mostly guided by social norms. We argue that even in instantaneous, anonymous online chats users behave very much like “normal” people. Our quantitative insights into user's activity patters and their emotional expressions are eventually combined to model interacting emotional agents. We demonstrate that the stylised facts of the emotional persistence can be reproduced by our model by only calibrating a small set of agent features. This success indicates that our modeling framework can be used to test further hypothesis about emotional interaction in online communities.
Results
User activity patterns
An IRC channel is always active and enables the real time exchange of posts among users about a specific topic. User interaction is instantaneous, the post written by user u1 is immediately visible to all other users logged into this channel and user u2 may reply right away. Fig. 1 illustrates the dynamics in such a channel. As time evolves new users may enter, others may leave or stay quiet until they write follow-up posts at a later time.
Communication activity over an IRC channel.
A) Schema of the evolution of a conversation in an IRC channel. At every time step, a user enters a post expressing a positive, negative, or neutral emotion. B) Probability distribution of the user activity over all the IRC channels. The activity is expressed as the time interval τ between two consecutive posts of the same user. Inset: Probability distribution of the user activity for individual IRC channels. The time is measured in minutes. C) Scaled probability distribution of the time interval ωch between consecutive posts entered in all the 20 IRC channels. The solid line represents stretched exponential fit to the data. Inset: Probability distribution of the time interval ωch between consecutive posts entered in all the 20 IRC channels without rescaling. The time is measured in minutes.
To characterize these activity patterns, we analyzed the waiting-time, or inter-activity time distribution P(τ), where τ refers to the time interval between two consecutive posts of the same user in the same channel and ask about the average response time. We find that τ is power-law distributed P(τ) ~ τ−α with some cut-off (Fig. 1B), with an exponent α = 1.53 ± 0.02. The fit is based on the maximum likelihood approach proposed by Clauset et al.9 and the power-law nature of the distribution could not be rejected (p = 0.375).
This finding (a) is inline the power-law distribution already found for diverse human activities1,2,3,5,6,7 and (b) classifies the communication process as belonging to the regime where posts arrive faster than they can be processed. We note that for α < 2, no average response time is defined (which would have been the case, however, for the highly attentive regime). Further, we observe in the plot of Fig. 1B a slight deviation from the power-law at a time interval of about one day, which shows that some users have an additional regularity in their behavior with respect to the time of the day they enter the online discussion. Such deviations were usually treated as power-laws with an exponential cut-off and can even be explained based on simple entropic arguments10,11. However, because of the “bump” around the one day time interval, our distribution also seems to provide further evidence to the bi-modality proposed by Wu et al.12. We should note, however, that the tail is better fitted by a log-normal distribution (KS = 0.136) rather than an exponential (KS = 0.190) or a Weibull (KS = 0.188) one (again using the maximum likelihood methodology described by Clauset et al.9) as shown in Fig. 1B. Here, KS stands for the Kolmogorov-Smirnov statistical test; the smaller this number, the better the fit.
We now focus on an important difference between online chats and previously studied forms of communication, such as mail or email exchange, which mostly involve two participants. Due to the collective nature of chats, a chatroom automatically aggregates the posts of a much larger amount of users, which allows us to study their collective temporal behavior. If ω denotes the time interval between two consecutive posts in the same channel independent of any user (also denoted as inter-event time and to be distinguished from the inter-activity time characterizing a single user), we find that the distribution P(ω) is is still fat-tailed, but does not follow a power-law. Interestingly, the time interval between posts significantly depends on the topic discussed in the channel (Inset of Fig. 1C). Some “hot” topics receive posts at a shorter rate than others, which can be traced back to the different number of users involved into these discussions. Specifically, we find that the average inter-event time 〈ω〉ch depends on the amount of users in the conversation and becomes smaller for more popular channels, as one would expect.
If we rescale the channel dependent inter-event distribution Pch(ω) using the average inter-event time 〈ω〉ch per channel and plot 〈ωch〉 Pch(ωch) versus ωch/〈ωch〉, we find that all the curves collapse into one master curve (Fig. 1C). The general scaling form that we used is P(ω) = (1/<ω>)F(ω/<ω>), where F(x) is independent of the average activity level of the component and represents a universal characteristic of the particular system. Such scaling behavior was reported previously in the literature describing universal patterns in human activity13. We fit this master curve by a stretched exponential14,15,16

where the stretched exponent γ is the only fit parameter, while the other two factors aγ and βγ are dependent on γ14. A histogram of the γ values across the 20 channels is shown in Supplementary Figure S2. Using only the regression results with p < 0.001 we find that the mean value of the stretched exponents is 〈γ〉 = 0.21 ± 0.05.
We note that stretched exponentials have been reported to describe the inter-event time distribution in systems as diverse as earthquakes15 and stock markets16. These systems commonly exhibit long range correlations which seem to be the origin of the stretched exponential inter-event time distributions14. Long range correlations have also been reported in human interaction activity5,17 and we tested their presence in the temporal activity over IRC communication. As shown in the Supplementary Figure S3, we verified the existence of long range correlations in the conversation activity. We found that the decay of the autocorrelation function of the inter-event time interval between consecutive posts within a channel is described by a power-law

with exponent  . In addition, we applied the Detrended Fluctuation Analysis (DFA) technique18, described in detail in the Methods section and we found a Hurst exponent value,
. In addition, we applied the Detrended Fluctuation Analysis (DFA) technique18, described in detail in the Methods section and we found a Hurst exponent value,  , which is well in agreement with the scaling relation νω = 2 − 2Hω. For a more detailed discussion about scaling relations and memory in time series please refer to19.
, which is well in agreement with the scaling relation νω = 2 − 2Hω. For a more detailed discussion about scaling relations and memory in time series please refer to19.
In conclusion, our analysis of user activities have revealed a universal dynamics in online chatting communities which is moreover similar to other human activities. This regards (a) the temporal activity of individual users (characterized by a power-law distribution with exponent 3/2) and (b) the inter-event dynamics across different channels, if rescaled by the average inter-event time (characterized by a stretched exponential distribution with just one fit parameter). We will use these findings as a point of departure for a more in-depth analysis – because obviously the essence of online communication in chatrooms, as compared to other human activities, is not really covered. From the perspective of activity patters, there is not so much new here, which leads us to ask for other dimensions of human communication that could reveal a difference.
Emotional expression patterns
Human communication, in addition to the mere transmission of information, also serves purposes such as the reinforcement of social bonds. This could be one of the reasons why human languages are found to be biased towards using words with positive emotional charge20. Humans, from the early stages of our lives, develop an affective communication system that enables us to express and regulate emotions21. But emotions are also the mediators of our consumer responses to advertising22 and many scientists acknowledge their importance in motivating our cognition and action23. However, despite the increasing time we spend online, the way we express our emotions in online communities and its impact on possibly large amounts of people is still to be explored.
Consequently, we are interested in the role of expressed emotions in online chatting communities. Users, by posting text in chatrooms, also reveal their emotions, which in return can influence the emotional response of other users, as illustrated in Fig. 1A. To understand this emotional interaction, we carry out a sentiment analysis of each post which is described in detail in the Methods section. This automatic classification returns the valence v for each post, i.e. a discrete value {−1, 0, +1} that characterizes the emotional charge as either negative, neutral, or positive.
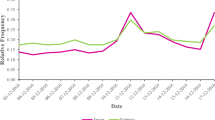
Instead of using the real time stamp of each post as in the analysis of the user activity, we now use an artificial time scale in which at each (discrete) time step one post enters the discussion, so the number of time steps equals the total number of posts. We then monitor how the total emotion expressed in a given channel evolves over time. We use a moving average approach that calculates the mean emotional polarity over different time windows. In Fig. 2A we plot the fraction of neutral, negative and positive posts as a function of time, for different sizes of the time window. While it is obvious that the emotional content largely fluctuates when using a very small time window, we find that for decreasing time resolution (i.e. increasing time window) the fractions of emotional posts settle down to an almost constant value around which they fluctuate. From this, we can make two interesting observations: (i) the emotional content in the online chats does not really change in the long run (one should notice that times of the order 103 are still large compared to the time window DT = 50 used), i.e. we observe fluctuations that depend on the time resolution, but no “evolution” towards more positive or negative sentiments. (ii) For the low resolution, the fraction of neutral posts dominates the positive and negative posts at all times. In fact there is a clear ranking where the fraction of negative posts is always the smallest. Both observations become even more pronounced when averaging over the 20 IRC channels, as Fig. 2B shows.
Our findings differ from previous observations of emotional communication in blog posts and forum comments which identified a clear tendency toward negative contributions over time, in particular for periods of intensive user activity24,25. Such findings suggest that an increased number of negative emotional posts could boost the activity and extend the lifetime of a forum discussion. However, blog communication in general evolves slower than e.g. online chats. Hence, we need to better understand the role of emotions in real time Internet communication, which obviously differs from the persistent and delayed interaction in blogs and fora.
To further approach this goal, we analyse to what extend the rather constant fraction of emotional posts in IRC channels is due to a persistence in the emotional expressions of users. For this, we apply the DFA technique18, to the time series of positive, negative and neutral posts. Since our focus is now on the user, we reconstruct for every user a time series that consists of all posts communicated in any channel, where the time stamp is given by the consecutive number at which the post enters the user's record. In order to have reliable statistics, for the further analysis only those users with more than 100 posts are considered (which are nearly 3000 users). As the examples in the Supplementary Figure S4 show, some users are very persistent in their (positive) emotional expressions (even that they occasionally switch to neutral or negative posts), whereas others are really antipersistent in the sense that their expressed emotionality rapidly changes through all three states. The persistence of these users can be characterized by a scalar value, the Hurst exponent H, (see the Material and Methods Section for details) which is 0.5 if users switch randomly between the emotional states, larger than 0.5. if users are rather persistent in their emotional expressions, or smaller than 0.5 if users have strong tendency to switch between opposite states, as the antipersistent time series of Fig. S4 shows.
If we analyse the distribution of the Hurst exponents of all users, shown in the histogram of Fig. 3A, we find (a) that the emotional expression of users is far from being random and (b) that it is clearly skewed towards H > 0.5, which means that the majority of users is quite persistent regarding their positive, negative or neutral emotions. This persistence can be also seen as a kind of memory (or inertia) in changing the emotional expression, i.e. the following post from the same user is more likely to have the same emotional value.
Hurst exponents and emotional persistence.
A) Hurst exponents (H) of the emotional expression of individual users, obtained using the DFA method. Only users contributed more than 100 posts were considered and we used the exponents obtained with fitting quality R2 > 0.98. B) Hurst exponent (H) versus the mean emotion polarity expressed by individual users, again only from users who contributed more than 100 posts. C) Hurst exponents (H) of the emotions expressed in the 20 IRC channels. The values are averages of the Hurst exponents obtained from 10 different segments of the same channel and the error bars show the standard deviation. The horizontal dashed line shows the expected value for random time series (H = 0.5) and the gray squares show the value obtained from shuffling the real time series to destroy any correlations. The difference in exponents of the real and the shuffled time series is statistically significant with p < 0.001.
The question whether persistent users express more positive or negative emotions is answered in Fig. 3B, where we show a scatter plot of H versus the mean value of the emotions expressed by each user. Again, we verify that the majority of users has H > 0.5, but we also see that the mean value of emotions expressed by the persistent users is largely positive. This corresponds to the general bias towards positive emotional expression detected in written expression20. The lower left quadrant of the scatter plot is almost empty, which means that users expressing on average negative emotions tend to be persistent as well. A possible interpretation for this could be the relation between negative personal experiences and rumination as discussed in psychology26. Antipersistent users, on the other hand, mostly switch between positive and neutral emotions.
Are the more active users also the emotionally persistent ones? In Supplementary Figure S6 we show a scatter plot of the Hurst exponent dependent on the total activity of each user. Even though the mean value of H does not show any such dependence, we observe large heterogeneity on the values of H for users with low activity. Furthermore, in Supplementary Figure S7 we show that the Hurst exponent of a very active user varies only slightly if we divide his time series into various segments and apply the DFA method to these segments. Thus we can conclude that active users tend to be emotionally persistent and, as most persistent users express positive emotions, they tend to provide some kind of positive bias to the IRC, whereas users occasionally entering the chat may just try to get rid of some negative emotions.
This leads us to the question how persistent the emotional bias of a whole discussion is. While Fig. 3A has shown the persistence with respect to the different users, Fig. 3C plots the persistence for the different channels, which each feature a very different topic. This persistence holds even even if we analyse only certain segments of the channel, as it is shown in Supplementary Figure S8. So, we conclude that the persistence of the discussion per se (which is different from the persistence of the users which can leave or enter a arbitrary times) reflects a certain narrative memory. Precisely, for each chat, we observe the emergence of a certain (emotional) ”tone” in the narration which can be positive, negative or neutral, dependent the emotional expressions of the (majority of) persistent users. If we reshuffle these time series such that the same total number of positive, negative and neutral posts is kept, but temporal correlations are destroyed, then the persistence is lost as well as Fig. 3C shows. We note that we could not find evidence of correlations using the autocorrelation function of the emotion time series, while the observed persistence in the fluctuations of user emotional expression, as captured by the Hurst exponent is very robust. This indicates that the chat community assumes an emotional memory locally encoded in the current messages (from the user perspective), while the size of the conversation is too large to detect it through averaging techniques.
An agent-based model for chatroom users
After identifying both the activity patterns and the emotional expression patterns of users in online chats, we setup an agent-based model that is able to reproduce these stylized facts. We start from a general framework27, designed to model and explain the emergence of collective emotions in online communities through the evolution of psychological variables that can be measured in experimental setups and psychological studies28,29. This framework provides a unified approach to create models that capture collective properties of different online communities and allows to compare the different emotional microdynamics present in various types of communication. The case of IRC channel communication is of particular interest because of its fast and ephemeral nature. Thus, we have designed a model for IRC chatrooms, as shown in Fig. 4A. The agents in our model are characterized by two variables, their emotionality, or valence, v which is either positive or negative and their activity, or arousal, which is represented by the time interval τ between two posts s in the chatroom. The valence of an agent i, represented by the internal variable vi, changes in time due to a superposition of stochastic and deterministic influences27,30:

The stochastic influences are modeled as a random factor Avξi normally distributed with zero mean and amplitude Av and represent all changes of the individual emotional state apart from chat communication. The deterministic influences are composed of an internal decay of parameter γv and an external influence of the conversation. The change in the valence caused by the emotionality of the field (h+ − h−) is measured in valence change per time unit through the parameter b. Previous models under the same framework27,31 had an additional saturation term in the equation of the valence dynamics. This way the positive feedback between v and h was limited when the field was very large. But, as we show in Fig. 2, chatrooms do not show the extreme cases of emotional polarization observed in other communities. Thus, we simplify the dynamics of the valence without using any saturation terms, since a large imbalance between h+ and h− is unrealistic given our analysis of real IRC data.
Modeling schema and simulation results.
A) Schematic representation of the model: The horizontal layer represents the agent, the vertical layer the communication in the chatroom where posts are aggregated. After a time lapse τ, which follows the power-law distribution of Fig. 1B, the agents writes a post s which implicitly expresses its emotions, v. Posts read in the chatroom feed back on the emotional state v of the agent. B) Hurst exponents for the individual behavior of agents in isolation with Av ∈ [0.2, 0.5] and γv ∈ [0.2, 0.5]. Only the exponents derived with fitting quality R2 > 0.9 are considered. C) Scaled probability distribution of the time interval ω′ between consecutive posts in 10 simulations of the model. Stretched exponential fit shows similar behavior to real IRC channel data.
In general, the level of activity associated with the emotion, known as arousal, can be explicitly modeled by stochastic dynamics as well31. Here, the activity of an agent is estimated by the time-delay distribution that triggers the expression of the agent, i.e. by the power-law distribution P(τ) ~ τ−1.53 shown in Fig. 1B. Assuming that an agent becomes active and expresses its emotion at time t, it will become active again after a period τ. The agent then writes a post in the online chat the emotional content of which is determined by its valence (see below). This information is stored in an external field common for all agents, which is composed of two components, h− and h+, for negative and positive information and their difference measures the emotional charge of the communication activity. Since we are interested in emotional communication, we assume that all neutral posts entered, or already present, in a chatroom do not influence the emotions of the agents participating to the conversation. Thus, the dynamics of the field is influenced only by the amount of agents expressing a particular emotion at a given time: N+(t) = Σi(1 − Θ(−1 * si)) and N−(t) = Σi(1−Θ(si)), where Θ is the Heaviside step function. Therefore, the time dynamics of the fields can be described as:

These two field components, h+ and h−, decay exponentially with a constant factor γh, i.e. their importance decays very fast as they move further down the screen (posts never disappear, but become less influential). Each field increases by a fixed amount c from every post stored in it. The values of the valence of the agents are changed by the field components, as described by Eq. 3. In contrast with traditional means of communication, online social media can aggregate much larger volumes of user-generated information. This is why h is defined without explicit bounds. Chatrooms pose a special case to this kind of communication, as they can contain large amount of posts but limited amount of users. Most IRC channels have technical limitations for the amount of users that can be connected at once, which in turn is reflected in the total amount of posts present in the general discussion. In our model, h might take any value, but the empirical activity pattern combined with the fixed size of the community dynamically constraints it to limited values.
Whenever an agent creates a new post in an ongoing conversation, the variable, si, obtain its value in the following way:

The thresholds V− and V+ represent a limit value of the valence that determines the emotional content of each post and in general can be asymmetric, as humans tend to have different thresholds for the triggering of positive and negative emotional expression. Each action contributes to the amount of information stored in the information field of the conversation, increasing h− if s = −1 or h+ if s = +1.
We emphasize that the way we model the agent behavior is very much in line with psychological research, where emotional states are represented by valence and arousal, following the dimensional representation of core affect32. The valence, v, represents the level of pleasure experienced by the emotional state, while the arousal represents the degree of activity induced by the emotional state and determines the moment when posts are created. Continuously the agent's valence relaxes to a neutral state and is subject to stochastic influences, as show empirically in33. The effect of chatroom communication on an agent's emotionality is modeled as an empathy-driven process34 that influences the valence. In the valence dynamics we propose in Eq. 3, agents perceive a positive influence when their emotional state matches the one of the community and a negative one in the opposite case. When a post is created, its emotional polarity is determined by the valence, as it was suggested by experimental studies on social sharing of emotions26,35.
All the assumptions of our model are supported by psychological theories. Parameter values and dynamical equations can be tested against experiments in psychology, providing empirical validation for the emotional microdynamics28,29. Furthermore, our model provides a consistent view of the emotional behavior in chatrooms leading to testable hypotheses that can drive future psychology research.
We performed extensive computer simulations using different parameter sets (see supplementary material for details). By exploring the parameter space, we identified which parameter sets lead to similar conversation patterns as observed in the real data. We used such set to simulate chats in 10 channels and we analysed the agent's activity and their emotional persistence. The results are shown in Fig. 4B, C. Specifically, we find that (a) the distribution of Hurst exponents for individual agents is shifted towards positive values similar to the one observed in real data, this way reproducing the emotional persistence of the conversation without assuming any time dependence between user expressions. Further, we reproduce (b) the empirically observed stretched exponential distribution for the rescaled time delays ω′ between consecutive posts, without any further assumptions.
We do note, however, that the stretched exponent, γ = 0.59 (p < 0.001), of the simulated distribution is different from real IRC channels where it was γ = 0.21, i.e. there is a faster decay in the simulations. This could be explained by the fact that in the real chat users usually write after they have read the previous post, i.e. there are additional correlations in the times users enter a chat. These, however, are not considered in the simulations, because agents post in the chat at random after a given time interval τ, i.e. there is no additional coupling in posting times. Following the same approach as we did for the real data, we calculated the Hurst exponent of the inter simulated event time-series of the discussions. We found that Hω′ = 0.75, however, we did not observe a power-law decay of the autocorrelation function (see Supplementary Figure S12). This suggests that the observed correlations are due to the power-law distributed inter-event times used as input to our model and it is inline with the above discussion about the absence of coupling that also explains the difference in the stretched exponents.
Eventually, we observe (c) the emotional persistence in the simulated conversations. The mean Hurst exponent for the 10 simulated channels is Hs = 0.567 ± 0.007, whereas for the real IRC channels Hr = 0.572 ± 0.021 was found. These results suggests that our agentbased model reproduces qualitatively the emergence of emotional persistence in the IRC conversation and thus, based on all findings, is able to capture the essence of emotional influence between users in chatrooms.
Discussion
We started with the question to what extent human communication patterns change on the Internet. To answer this, we used a unique dataset of online chatting communities with about 2.5 million posts on 20 different topics. Our analysis considered two different dimensions of the communication process: (a) activity, expressed by the time intervals τ at which users contribute to the communication and ω at which consecutive posts appear in a chat and (b) the emotional expressions of users. With respect to activity patterns we did not find considerable differences between online chatrooms and other previously studied forms on online and offline communication. Specifically, both the inter-activity distribution of users and the inter-event distribution of posts followed the known distributions. Thus, we may conclude that humans do not really change their activity patterns when they go online. Instead, these patterns seem to be quite robust across online and offline communication.
The picture differs, however, when looking at the emotional expressions of users. While we cannot directly compare our findings on emotional persistence to results about offline communication, we find differences between online chatrooms and other forms online communication, such as blogs, fora. While the latter could be heated up by negative emotional patterns, we observe that online chats, which are instantaneous in time, very much follow a balanced emotional pattern across all topics (shown in the emotional persistence of the channels), but also with respect to individual users, which are in their majority quite persistent in their emotional expressions (mostly positive ones).
This observation is indeed surprising as online chats are mostly anonymous, i.e. users do not reveal their personal identity. However, they still seem to behave according to certain social norms, i.e. there is a clear tendency to express an opinion in a neutral to positive emotional way, avoiding direct confrontations or emotional debates. One of the reasons for such behavior comes from the “repeated interaction” underlying online chats. As the daily “bump” the activity patterns also suggest, most users return to the online chats regularly, to meet other users they may already know. This puts a kind of social pressure on their behavior (even in an unconscious manner) to behave similar to offline conversations. In conclusion, we find that the online communication patters do not differ much from common offline behavior if a repeated interaction could be assumed.
Eventually, we argue that the emotional persistence found is indeed related to the nature of human conversations. After all, the correlations shown in the emotional expressions of different users indicate that there is some form of emotional sharing between participants. This suggests the presence of social bonds among users in the chatroom26 and confirms similarities between online and offline communication.
The fact that we could reveal patterns of emotional persistence both in users and in topics discussed, does not mean that we also understand their origin. One important step towards this ”microscopic” understanding is provided by our agent-based model of emotional interactions in chatrooms. By using assumptions about the agent's behavior which are rooted in research in psychology, we are able to reproduce the stylized facts of the chatroom conversation, both for the activity in channels and for the emotional persistence. Specifically, our model allows us to test hypotheses about the emotional interaction of agents against their outcome on the systemic level, i.e. for the chatroom simulation. This helps to reveal what kind of rules are underlying the online behavior of users which are hard to access otherwise.
Methods
Data collection and classification
The data used in this article is based on a large set of public channels from EFNET Internet Relay Chats (http://www.efnet.org), to which any user can connect and participate in the conversation. Based on the assessment of the initially downloaded set of recordings, 20 IRC channels were selected aiming to provide a large number of consecutive daily logs with transcripts of vivid discussions between the channel participants, measured in number of posts. The finally used data set contained consecutive recordings for 42 days spanning the period from 04-04-2006 to 15-05-2006.
The general topics of discussions from the selected channels include: music, sports, casuals chats, business, politics and topics related to computers, operating systems or specific computer programs. The IRC data set contains 2,688,760 posts. The total number of participants to all this channels is 25,166. However, because some people participate to more than one channel, the total number of unique participants is 20,441. On average, the data set provides 3055 posts per day. In the recorded period 15 users created more than 10000 posts. The distribution of the user participation i.e. the number of posts entered by every user, is shown in Supplementary Figure S1. The mean of the distribution is 97 posts per user and as we can see from Fig. S1, it is skewed with most of the users contributing only a small number of posts.
The acquired data was anonymized by substituting real user ids to random number references. The text of each post was cleaned by spam detection and substitution of URL links to avoid them from influencing the emotion classification. The emotional content was extracted by using the SentiStrength classifier36, which provides two scores for positive and negative content. Each score ranges from 1 to 5 and changes with the appearance of emotion bearing terms from a lexicon of affective word usage, specifically designed for this purpose. Each word of the lexicon has a value on the scale of −5 to 5 which determines the strength of the emotion attached to it. The classifier takes into account syntactic rules like negation, amplification and reduction and detects repetition of letters and exclamation signs as amplifiers. When one of this patterns is detected, SentiStrength applies transformation rules to the contribution of the involved terms to the sentence scores. It has been designed to analyze online data and considers Internet language by detecting emoticons and correcting spelling mistakes.
The perception of emotional expression varies largely across humans and traditional accuracy metrics are not useful when there is lack of an objective space. Human ratings of emotional texts have certain degree of disagreement that needs to be considered by sentiment analysis in order to have a valid quantification of emotions. SentiStrength scores are consistent with the level of disagreement between humans about how they perceive written emotional expressions37. This classifier combines an emotion quantization of proved validity with a high accuracy and is considered the state of the art in sentiment detection38. Due to the short length of the posts in chatrooms, we calculate a polarity measure by comparing the two different scores of SentiStrength. The sign of the difference of the positive and negative scores provides an approximation to detect positive, negative and neutral posts. The accuracy of this polarity metric was tested against texts tagged by humans and messages including emoticons from MySpace39 and Twitter40, which are of a similar length to the ones in our chatroom data. The data are freely available for research purposes and are provided as Supplementary Material. Detailed information about their structure is provided in the “Data section” of the Supplementary Information text.
Detrended Fluctuation Analysis
The method of Detrended Fluctuation Analysis (DFA)18 is a useful tool in revealing long-term memory and correlations in time series5,15,16. The method maps the system into a one-dimensional random walk and enable us to compare the properties of the real time series with the time series produced by the random case.
The DFA analysis of a time series x(t) with length T, which can be divided into N segments is performed as follows: First we integrate the time series, by calculating the profile  . Next, we divide the integrated time series into N boxes of equal length Δt. Each box has a local trend, which in a first level approximation, can be fitted by a linear function using least squares. We denote with yΔt(t) the y coordinate of the straight line segments that represent the local trend in each box and we subtract this local trend from the integrated time series Y(t). Next we use the function
. Next, we divide the integrated time series into N boxes of equal length Δt. Each box has a local trend, which in a first level approximation, can be fitted by a linear function using least squares. We denote with yΔt(t) the y coordinate of the straight line segments that represent the local trend in each box and we subtract this local trend from the integrated time series Y(t). Next we use the function

to calculate the root-mean-square fluctuation of the integrated and detrended time series and we characterize the relationship between the average fluctuation F(Δt) and the box size Δt.
Typically, F(Δt) will increase with box size as F(Δt) ~ (Δt)H, which indicates the presence of power-law (fractal) scaling. Therefore, the fluctuations can be characterized only by the scaling exponent H that is analogous to the Hurst exponent41 and it is calculated from the slope of the line relating logF(Δt) to logΔt. If only short-range correlations (or no correlations) exist in the time series, then it has the statistical properties of a random walk. Therefore F(Δt) ~ (Δt)1/2. However, in the presence of long-range power-law correlations (i.e. no characteristic length scale) H ≠ 1/2. A value H < 1/2 signals the presence of long range anti-correlations, while a value H > 1/2 signals the presence of long range correlations (persistence).
References
Oliveira, J. G. & Barabási, A. L. Human Dynamics: The Correspondence Patterns of Darwin and Einstein. Nature 437, 1251 (2005).
Barabási, A.-L. The origin of bursts and heavy tails in human dynamics. Nature 435, 207–11 (2005).
Malmgren, R. D., Stouffer, D. B., Motter, A. E. & Amaral, L. a. N. A Poissonian explanation for heavy tails in e-mail communication. Proc. Natl. Acad. Sci. U.S.A 105, 18153–8 (2008).
Jo, H.-H., Karsai, M., Kertész, J. & Kaski, K. Circardian pattern and burstiness in mobile phone communication. New J. Phys. 14, 013055 (2012).
Rybski, D., Buldyrev, S., Havlin, S., Liljeros, F. & Makse, H. Scaling laws of human interaction activity. Proc. Natl. Acad. Sci. U.S.A 106, 12640 (2009).
Grinstein, G. & Linsker, R. Power-law and exponential tails in a stochastic priority-based model queue. Phys. Rev. E 77, 012101 (2008).
Crane, R., Schweitzer, F. & Sornette, D. Power law signature of media exposure in human response waiting time distributions. Phys. Rev. E 81, 56101 (2010).
Vázquez, A. et al. Modeling bursts and heavy tails in human dynamics. Phys. Rev. E 73, 036127 (2006).
Clauset, A., Shalizi, C. R. & Newman, M. E. J. Power-law distributions in empirical data. SIAM Review 51, 661–703 (2009).
Baek, S. K., Bernhardsson, S. & Minnhagen, P. Zipf's law unzipped. New J. Phys. 13, 043004 (2011).
Adamic, L. Unzipping Zipf's law. Nature 474, 164 (2011).
Wu, Y., Zhou, C., Xiao, J., Kurths, J. & Schellnhuber, H. J. Evidence for a bimodal distribution in human communication. Proc. Natl. Acad. Sci. U.S.A 107, 18803–18808 (2010).
Candia, J. et al. Uncovering individual and collective human dynamics from mobile phone records. J. Phys. A 41, 224015 (2011).
Altmann, E. & Kantz, H. Recurrence time analysis, long-term correlations and extreme events. Phys. Rev. E 71, 56106 (2005).
Bunde, A., Eichner, J., Kantelhardt, J. & Havlin, S. Long-Term Memory: A Natural Mechanism for the Clustering of Extreme Events and Anomalous Residual Times in Climate Records. Phys. Rev. Lett. 94, 48701 (2005).
Wang, F., Yamasaki, K., Havlin, S. & Stanley, H. Scaling and memory of intraday volatility return intervals in stock markets. Phys. Rev. E 73, 026117 (2006).
Rybski, D., Buldyrev, S. V., Havlin, S., Liljeros, F., & Makse, H. A. Communication activity in social networks: growth and correlations. Eur. Phys. J. B 84, 147–159 (2011).
Peng, C.-K. et al. Mosaic organization of DNA nucleotides. Phys. Rev. E 49, 1685–1689 (1994).
Kantelhardt, J. W. Fractal and multifractal time series. Encyclopedia of Complexity and Systems Science. (Springer, 2009).
Garcia, D., Garas, A. & Schweitzer, F. Positive words carry less information than negative words. arXiv,1110.4123 (2011).
Tronick, E. Z. Emotions and emotional communication in infants. Am. Psychol. 44, 112–9 (1989).
Holbrook, M. B. & Batra, R. Assessing Mediators to of the Role of Emotions Responses as Consumer Advertising. J. Cons. Res 14, 404–420 (1987).
Izard, C. E. The Many Meanings/Aspects of Emotion: Definitions, Functions, Activation and Regulation. Emotion Rev. 2, 363–370 (2010).
Mitrović, M. & Tadić, B. Bloggers behavior and emergent communities in Blog space. Eur. Phys. J. B 73, 293–301 (2009).
Chmiel, A. et al. Negative emotions boost users activity at BBC Forum. Physica A 390, 2936 (2011).
Rime, B. Emotion Elicits the Social Sharing of Emotion: Theory and Empirical Review. Emotion Review 1, 60–85 (2009).
Schweitzer, F. & Garcia, D. An agent-based model of collective emotions in online communities. Eur. Phys. J. B 77, 533–545 (2010).
Kappas, A., Tsankova, E., Theunis, M. & Küster, D. CyberEmotions: Subjective and physiological responses elicited by contributing to online discussion forums. Poster presented at the 51st Annual Meeting of the Society for Psychophysiological Research, Boston, Massachusetts (2011).
Küster, D., Tsankova, E., Theunis, M. & Kappas, A. Measuring CyberEmotions: How do bodily responses relate to the digital world? Poster presented at the 7th Conference of the Media Psychology Division of the Deutsche Gesellschaft fuer Psychologie, Bremen, Germany (2011).
Schweitzer, F. Brownian Agents and Active Particles. Collective Dynamics in the Natural and Social Sciences, Springer Series in Synergetics. (Springer, Berlin), 1st editio edition, p. 420 (2003).
Garcia, D. & Schweitzer, F. Emotions in product reviews – Empirics and models ed. Randy Bilof. (IEEE Computer Society, Boston, Massachusetts), pp. 483–488 (2011).
Russell, J. A. A circumplex model of affect. J. Pers. Soc. Psychol. 39, 1161–1178 (1980).
Kuppens, P., Oravecz, Z. & Tuerlinckx, F. Feelings change: Accounting for individual differences in the temporal dynamics of affect. J. Pers. Soc. Psychol. 99, 1042–1060 (2010).
Preston, S. D. & de Waal, F. B. M. Empathy: Its ultimate and proximate bases. Behav. Brain Sci. 25, 1–20; discussion 20–71 (2002).
Christophe, V. & Rime, B. Exposure to the social sharing of emotion: Emotional impact, listener responses and secondary social sharing. Eur. J. Soc. Psychol. 27, 37–54 (1997).
Thelwall, M., Buckley, K., Paltoglou, G., Cai, D. & Kappas, A. Sentiment strength detection in short informal text. J. Am. Soc. Inf. Sci. Technol. 61, 2544–2558 (2010).
Thelwall, M., Buckley, K. & Paltoglou, G. Sentiment strength detection for the social web. J. Am. Soc. Inf. Sci. Technol. 63, 163–173 (2012).
Kucuktunc, O., Cambazoglu, B. B., Weber, I. & Ferhatosmanoglu, H. A Large-Scale Sentiment Analysis for Yahoo ! Answers. Proc. of the 5th ACM Int. Conf. on Web Search and Data Mining (2012).
Paltoglou, G., Gobron, S., Skowron, M., Thelwall, M. & Thalmann, D. Sentiment analysis of informal textual communication in cyberspace. (Citeseer), pp. 13–23 (2010).
Thelwall, M., Buckley, K. & Paltoglou, G. Sentiment in Twitter events. J. Am. Soc. Inf. Sci. Technol. 62, 406–418 (2011).
Hurst, H. E. Long-term storage capacity of reservoirs. Am. Soc. Civ. Eng. 116, 770–808 (1951).
Acknowledgements
This research has received funding from the European Community's Seventh Framework Programme FP7-ICT-2008-3 under grant agreement no 231323 (CYBEREMOTIONS).
Author information
Authors and Affiliations
Contributions
A.G., D.G. and F.S. designed the research, performed the research, analysed the data and wrote the manuscript. M.S. collected the data and analysed the data.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Garas, A., Garcia, D., Skowron, M. et al. Emotional persistence in online chatting communities. Sci Rep 2, 402 (2012). https://doi.org/10.1038/srep00402
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00402
This article is cited by
-
Classification of endogenous and exogenous bursts in collective emotions based on Weibo comments during COVID-19
Scientific Reports (2022)
-
Language, demographics, emotions, and the structure of online social networks
Journal of Computational Social Science (2018)
-
Generative models of online discussion threads: state of the art and research challenges
Journal of Internet Services and Applications (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.