Abstract
We prove that the theorems of TDDFT can be extended to a class of qubit Hamiltonians that are universal for quantum computation. The theorems of TDDFT applied to universal Hamiltonians imply that single-qubit expectation values can be used as the basic variables in quantum computation and information theory, rather than wavefunctions. From a practical standpoint this opens the possibility of approximating observables of interest in quantum computations directly in terms of single-qubit quantities (i.e. as density functionals). Additionally, we also demonstrate that TDDFT provides an exact prescription for simulating universal Hamiltonians with other universal Hamiltonians that have different and possibly easier-to-realize two-qubit interactions. This establishes the foundations of TDDFT for quantum computation and opens the possibility of developing density functionals for use in quantum algorithms.
Similar content being viewed by others
Introduction
The pioneering work of Hohenberg and Kohn1 in 1964 showed that the properties of a many-body system can be obtained as functionals of the simple electron density rather than the many-body wavefunction. Twenty years later, similar theorems were proven for time-dependent systems3. These developments have enabled complex simulations of physical systems at low computational cost using a very simple quantity. Can these ideas be extended to the domain of quantum computation and therefore enable similar progress in that field? In the present work, we prove analogous theorems to those of time-dependent density functional theory (TDDFT) for the domain of universal quantum computation. In a similar spirit to TDDFT for electronic Hamiltonians, the theorems of TDDFT applied to universal Hamiltonians allow us to think of single-qubit expectation values as the basic variables in quantum computation and information theory, rather than the wavefunction. From a practical standpoint this opens the possibility of approximating observables of interest in quantum computions directly in terms of single-qubit quantities (i.e. as density functionals). Additionally, we demonstrate that TDDFT provides an exact prescription for simulating universal Hamiltonians with other universal Hamiltonians which have different and possibly easier-to-realize two-qubit interactions. The theorems of TDDFT for universal Hamiltonians establish that TDDFT can in principle be used to simplify quantum computations, similar to how it has been applied in revolutionizing the simulation of atomic, molecular and condensed matter electronic structure dynamics. As we discuss below, the development of accurate approximate functionals for quantum simulation will be a necessary second step for the practical application of TDDFT to quantum computation.
We begin by briefly reviewing TDDFT for a system of N-electrons described by the Hamiltonian

where  and
and  are respectively the position and momentum operators of the ith electron,
are respectively the position and momentum operators of the ith electron,  is the electron-electron repulsion and ν(r, t) is a time-dependent one-body scalar potential which includes the potential due to nuclear charges as well as any external fields.
is the electron-electron repulsion and ν(r, t) is a time-dependent one-body scalar potential which includes the potential due to nuclear charges as well as any external fields.  is the electron density operator, whose expectation value yields the one-electron probability density. The first basic theorem of TDDFT, known as the “Runge-Gross (RG) theorem”3, establishes a one-to-one mapping between the expectation value of
is the electron density operator, whose expectation value yields the one-electron probability density. The first basic theorem of TDDFT, known as the “Runge-Gross (RG) theorem”3, establishes a one-to-one mapping between the expectation value of  and the scalar potential ν(r, t) and therefore through the time-dependent Schrödinger equation, a one-to-one mapping between the density and the wavefunction. The RG theorem implies the remarkable fact that in principle, the one-electron density contains the same information as the many-electron wavefunction. The second basic TDDFT theorem known as the “van Leeuwen (VL) theorem”4 gives a prescription for constructing an auxiliary system with a different and possibly simpler electron-electron repulsion
and the scalar potential ν(r, t) and therefore through the time-dependent Schrödinger equation, a one-to-one mapping between the density and the wavefunction. The RG theorem implies the remarkable fact that in principle, the one-electron density contains the same information as the many-electron wavefunction. The second basic TDDFT theorem known as the “van Leeuwen (VL) theorem”4 gives a prescription for constructing an auxiliary system with a different and possibly simpler electron-electron repulsion  , which simulates the density evolution of the original Hamiltonian in Eq. 1. When
, which simulates the density evolution of the original Hamiltonian in Eq. 1. When  , this auxiliary system is referred to as the “Kohn-Sham system”2 and due to it's simplicity and accuracy, is in practice used in most DFT and TDDFT calculations.
, this auxiliary system is referred to as the “Kohn-Sham system”2 and due to it's simplicity and accuracy, is in practice used in most DFT and TDDFT calculations.
It is not obvious that the RG and VL theorems extend to qubits, which are distinguishable spin 1/2 particles. In the results section, we prove analogous RG and VL theorems for a system of N qubits described by the very general universal 2-local Hamiltonian5,6,

Here,  are Pauli operators for the ith qubit, hi(t) are local applied fields arbitrarily chosen along the z-axis and
are Pauli operators for the ith qubit, hi(t) are local applied fields arbitrarily chosen along the z-axis and  and
and  are two-qubit interaction terms respectively parallel and perpendicular to the direction of the fields. The above Hamiltonian describes an open chain of N qubits arranged in a one-dimensional array, with each qubit interacting with its nearest neighbors.
are two-qubit interaction terms respectively parallel and perpendicular to the direction of the fields. The above Hamiltonian describes an open chain of N qubits arranged in a one-dimensional array, with each qubit interacting with its nearest neighbors.
More general geometries are discussed in the supplementary material. In Refs.5,6, it was shown that by appropriately tuning the local fields in Eq. 2, one can use the fixed two-qubit interaction alone to realize a set of universal two-qubit and single-qubit quantum gates, which in turn can be employed to perform universal quantum computation. In Eq. 2, the case where  yields the Heisenberg Hamiltonian which describes exchange coupled spins in solid state arrays or quantum dots in heterostructures7. The situation
yields the Heisenberg Hamiltonian which describes exchange coupled spins in solid state arrays or quantum dots in heterostructures7. The situation  and
and  yields the XXZ Hamiltonian, used to model electronic qubits on liquid Helium8 or solid-state systems with anisotropy due to spin-orbit coupling9, while the limit
yields the XXZ Hamiltonian, used to model electronic qubits on liquid Helium8 or solid-state systems with anisotropy due to spin-orbit coupling9, while the limit  yields the XY model describing superconducting Josephson junction qubits10. In the forthcoming sections, we will develop the TDDFT theorems for the Hamiltonian in Eq. 2 and discuss their implications for quantum computation and information theory.
yields the XY model describing superconducting Josephson junction qubits10. In the forthcoming sections, we will develop the TDDFT theorems for the Hamiltonian in Eq. 2 and discuss their implications for quantum computation and information theory.
Results
The qubit Runge-Gross theorem for quantum computation
We now state the equivalent RG theorem for quantum computation with the Hamiltonian in Eq. 2, the qubit Runge-Gross (qRG) theorem:
Theorem - For a given initial state |ψ(0)〉 evolving to |ψ(t)〉 under the Hamiltonian in Eq. 2 and with  and
and  fixed, there exists a one-to-one mapping between the set of expectation values
fixed, there exists a one-to-one mapping between the set of expectation values  and the set of local fields {h1, h2,…hN} up to a constant global field (see supplementary information), over a given interval [0, t].
and the set of local fields {h1, h2,…hN} up to a constant global field (see supplementary information), over a given interval [0, t].
Here, we have defined  as the expectation value of the component of the ith qubit along the field direction (z-axis). A detailed proof together with a more rigorous discussion of the conditions on the theorem are provided in the supplementary material. The qRG theorem implies that the set of local fields can be written as unique functionals of the set of expectation values
as the expectation value of the component of the ith qubit along the field direction (z-axis). A detailed proof together with a more rigorous discussion of the conditions on the theorem are provided in the supplementary material. The qRG theorem implies that the set of local fields can be written as unique functionals of the set of expectation values  , as illustrated in the first part of Figure 1. Since the solution to the time-dependent Schrödinger equation is unique and and
, as illustrated in the first part of Figure 1. Since the solution to the time-dependent Schrödinger equation is unique and and  and
and  are fixed, the wavefunction is a unique functional of the local fields. i.e. |ψ(t)〉 ≡ |ψ[h1, h2, …hN](t)〉, where the square brackets denote that ψ is a functional of the set {h1, h2, …hN} over the interval [0,t]. This fact, combined with the qRG theorem allows us to state a corollary, which is the first central result of this paper:
are fixed, the wavefunction is a unique functional of the local fields. i.e. |ψ(t)〉 ≡ |ψ[h1, h2, …hN](t)〉, where the square brackets denote that ψ is a functional of the set {h1, h2, …hN} over the interval [0,t]. This fact, combined with the qRG theorem allows us to state a corollary, which is the first central result of this paper:
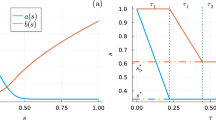
Qubit Runge-Gross theorem for a 3 qubit example.
The set of expectation values  , defined by the the Bloch vector components of each qubit along the z-axis in (a), is uniquely mapped onto the set of local fields {h1, h2, …hN} in (b) through the qRG theorem. Then, through the Schrödinger equation, the set of fields is uniquely mapped onto the wavefunction. These two mappings together imply that the N-qubit wavefunction in (c) is in fact a unique functional of the set of expectation values
, defined by the the Bloch vector components of each qubit along the z-axis in (a), is uniquely mapped onto the set of local fields {h1, h2, …hN} in (b) through the qRG theorem. Then, through the Schrödinger equation, the set of fields is uniquely mapped onto the wavefunction. These two mappings together imply that the N-qubit wavefunction in (c) is in fact a unique functional of the set of expectation values  .
.
Corollary - There exists a one-to-one mapping between the set of expectation values  over the entire interval [0,t] and the N-qubit state |ψ(t)〉.
over the entire interval [0,t] and the N-qubit state |ψ(t)〉.
The above corollary implies the counterintuitive fact that the full N-qubit wavefunction, which lives in a 2N dimensional Hilbert space, is a unique functional of only the N components of each qubit along the z-axis over the interval [0,t]. i.e.

This naturally implies that no two wavefunctions evolving under the Hamiltonian in Eq. 2 can give the same set of expectation values  for the entire time-interval [0,t]. Having established the qRG theorem, we now proceed to discuss its implications for quantum computation.
for the entire time-interval [0,t]. Having established the qRG theorem, we now proceed to discuss its implications for quantum computation.
Implications of the qubit Runge-Gross theorem for quantum computation
Although the qRG theorem does not tell us an explicit functional form for ψ, it has profound conceptual implications from a quantum information perspective. At first glance, it might appear that the set  contains much less information than the full wavefunction, since projective measurements needed to obtain
contains much less information than the full wavefunction, since projective measurements needed to obtain  would seem to imply that information about non-commuting observables, or observables depending on multi-qubit correlations is lost. However, since the wavefunction completely specifies all properties of the system, Eq. 3 implies that even properties depending on non-commuting observables or multi-qubit correlations, such as entanglement and phase information are in fact uniquely determined by the set of expectation values
would seem to imply that information about non-commuting observables, or observables depending on multi-qubit correlations is lost. However, since the wavefunction completely specifies all properties of the system, Eq. 3 implies that even properties depending on non-commuting observables or multi-qubit correlations, such as entanglement and phase information are in fact uniquely determined by the set of expectation values  .
.
From a practical standpoint, the qRG theorem implies that all observables can directly be constructed as functionals of single-qubit expectation values, without regard for the wavefunction. Although the qRG theorem proves that the set of expectation values  in principle contains all of the quantum information in ψ, extracting this information in the form of a functional of
in principle contains all of the quantum information in ψ, extracting this information in the form of a functional of  is not always straightforward. In order to do this, one must either guess the exact functional form of the observable, or try to approximate it. Borrowing an analogy from electronic TDDFT, the time-dependent dipole moment
is not always straightforward. In order to do this, one must either guess the exact functional form of the observable, or try to approximate it. Borrowing an analogy from electronic TDDFT, the time-dependent dipole moment  is a very simple density functional, while the average momentum of the system
is a very simple density functional, while the average momentum of the system  is not simple to construct as an explicit density functional, since it depends on the density very nonlocally in both space and time11. A density functional for the average momentum must therefore be approximated in practical applications.
is not simple to construct as an explicit density functional, since it depends on the density very nonlocally in both space and time11. A density functional for the average momentum must therefore be approximated in practical applications.
In quantum computation and information theory, a similar situation arises. Often, the observable of interest is simply a subset of  on designated readout qubits which encode the answer to the computation and this subset is trivially a functional of the entire set. For instance, a simple example is the Deutsch-Jozsa algorithm, where one measures a subset of
on designated readout qubits which encode the answer to the computation and this subset is trivially a functional of the entire set. For instance, a simple example is the Deutsch-Jozsa algorithm, where one measures a subset of  in a query register to determine if a function f(x) is constant or balanced12. If one finds the spin density of this subset to be zero everywhere, f(x) is constant, while if it is non-zero, f(x) is balanced. A more challenging observable functional to construct is two-qubit entanglement. We find that an exact pure state entanglement functional can in fact be constructed for a computation in which the state space is restricted to states where
in a query register to determine if a function f(x) is constant or balanced12. If one finds the spin density of this subset to be zero everywhere, f(x) is constant, while if it is non-zero, f(x) is balanced. A more challenging observable functional to construct is two-qubit entanglement. We find that an exact pure state entanglement functional can in fact be constructed for a computation in which the state space is restricted to states where  . The pure state entanglement (as measured by concurrence13) between any two qubits labeled k and l can be written as a functional of the set
. The pure state entanglement (as measured by concurrence13) between any two qubits labeled k and l can be written as a functional of the set  for this particular case as (the derivation is provided in the supplementary material)
for this particular case as (the derivation is provided in the supplementary material)

Interestingly, this particular entanglement functional is time-local, since it depends only on the set  at a given instant in time and so
at a given instant in time and so  . In the more general case, observables may be non-local in time and depend on the set
. In the more general case, observables may be non-local in time and depend on the set  over an entire interval [0,t]. Although the functional in Eq. 4 is time-local, it is “spatially” non-local, since the entanglement between qubits k and l depends on the components of all of the other N – 2 qubits. If one considers two flipped qubits instead of one, the entanglement functional becomes complicated and non-local in both space and time due to dependence on phases in the wavefunction (see supplemental material). Understanding the spatial and temporal non-locality of density functionals in electronic structure theory is a very active research topic14,15 and interestingly a similar situation arises here in TDDFT for quantum computation as well.
over an entire interval [0,t]. Although the functional in Eq. 4 is time-local, it is “spatially” non-local, since the entanglement between qubits k and l depends on the components of all of the other N – 2 qubits. If one considers two flipped qubits instead of one, the entanglement functional becomes complicated and non-local in both space and time due to dependence on phases in the wavefunction (see supplemental material). Understanding the spatial and temporal non-locality of density functionals in electronic structure theory is a very active research topic14,15 and interestingly a similar situation arises here in TDDFT for quantum computation as well.
Thus far we have proven the qRG theorem, which establishes that all observables of an N-qubit system can be obtained directly from the set of single-qubit expectation values  , without needing explicit access to the wavefunction. However, in order to make this fact useful from a practical standpoint, one would like to be able to obtain the set
, without needing explicit access to the wavefunction. However, in order to make this fact useful from a practical standpoint, one would like to be able to obtain the set  by solving an auxiliary problem that is simpler than obtaining |ψ(t)〉 itself. In the next section, we prove that there are in fact infinitely many universal Hamiltonians which can be used to simulate the same set
by solving an auxiliary problem that is simpler than obtaining |ψ(t)〉 itself. In the next section, we prove that there are in fact infinitely many universal Hamiltonians which can be used to simulate the same set  and by choosing a Hamiltonian with a simpler evolution, one can in fact make TDDFT a practical tool for quantum computation.
and by choosing a Hamiltonian with a simpler evolution, one can in fact make TDDFT a practical tool for quantum computation.
A theorem analogous to the Van Leeuwen theorem for quantum computation
We now turn to the second fundamental theorem of TDDFT for universal computation, a VL-like theorem for qubits, the qubit Van Leeuwen theorem (qVL):
Theorem - Consider a given set of spin components  obtained from the wavefunction |ψ(t)〉 evolved under the Hamiltonian in Eq. 2. One can always construct (see supplementary material for certain conditions) a Hamiltonian with different two-qubit interactions denoted
obtained from the wavefunction |ψ(t)〉 evolved under the Hamiltonian in Eq. 2. One can always construct (see supplementary material for certain conditions) a Hamiltonian with different two-qubit interactions denoted  and
and  and different local fields
and different local fields  , which evolves a possibly different initial state |ψ′(0)〉 to a different final state |ψ′(t)〉 such that the condition
, which evolves a possibly different initial state |ψ′(0)〉 to a different final state |ψ′(t)〉 such that the condition  is satisfied on the interval [0,t].
is satisfied on the interval [0,t].
Here, we have defined  . The qVL theorem allows us to obtain the set
. The qVL theorem allows us to obtain the set  by simulating the evolution with an auxiliary Hamiltonian having different two-qubit interactions and hence a different (and possibly simpler) wave-function evolution as illustrated in Figure 2. Furthermore, the qVL theorem guarantees that the auxiliary fields
by simulating the evolution with an auxiliary Hamiltonian having different two-qubit interactions and hence a different (and possibly simpler) wave-function evolution as illustrated in Figure 2. Furthermore, the qVL theorem guarantees that the auxiliary fields  , are unique functionals of the set
, are unique functionals of the set  . As we discuss in the next section, this fact opens the possibility of simplifying computations by constructing simple approximations to the auxiliary fields as functionals of single-qubit expectation values. This is a similar concept to how the exchange-correlation potential of electronic TDDFT is approximated as a functional of the one-body density in the Kohn-Sham scheme.
. As we discuss in the next section, this fact opens the possibility of simplifying computations by constructing simple approximations to the auxiliary fields as functionals of single-qubit expectation values. This is a similar concept to how the exchange-correlation potential of electronic TDDFT is approximated as a functional of the one-body density in the Kohn-Sham scheme.
Qubit Van Leeuwen theorem for a 3 qubit example.
The set  (a) obtained from evolution under Eq. 2, is uniquely mapped to a new set of fields
(a) obtained from evolution under Eq. 2, is uniquely mapped to a new set of fields  (b) for a Hamiltonian with different two-qubit interactions. Evolution under this new Hamiltonian returns the same expectation values
(b) for a Hamiltonian with different two-qubit interactions. Evolution under this new Hamiltonian returns the same expectation values  , although the wavefunction is different and hence projections of the Bloch vectors along other axes are in general different (c).
, although the wavefunction is different and hence projections of the Bloch vectors along other axes are in general different (c).
A numerical demonstration of the qubit Van Leeuwen theorem
Before discussing general approximate functionals for the auxiliary local fields  , in this section we will demonstrate the qVL theorem by constructing the exact functional for a simple example where an exact numerical solution is possible. The proof of the qVL theorem gives a mathematical procedure (see supplementary material) for engineering the exact auxiliary fields
, in this section we will demonstrate the qVL theorem by constructing the exact functional for a simple example where an exact numerical solution is possible. The proof of the qVL theorem gives a mathematical procedure (see supplementary material) for engineering the exact auxiliary fields  which reproduce a given set
which reproduce a given set  under a different two-qubit interaction. As a simple demonstration, we use this procedure to numerically simulate a 3-qubit Heisenberg Hamiltonian using an XY Hamiltonian as the auxiliary system (Figure 3). For the simulation, the system is prepared in the initial state
under a different two-qubit interaction. As a simple demonstration, we use this procedure to numerically simulate a 3-qubit Heisenberg Hamiltonian using an XY Hamiltonian as the auxiliary system (Figure 3). For the simulation, the system is prepared in the initial state  , where |1〉 and |0〉 are eigenstates of
, where |1〉 and |0〉 are eigenstates of  with eigenvalues −1 and 1 respectively. In the Heisenberg Hamiltonian,
with eigenvalues −1 and 1 respectively. In the Heisenberg Hamiltonian,  and we choose J12 = J23 = 0.5, which represents a chain with isotropic and uniform antiferromagnetic couplings. We apply a pulse of the form
and we choose J12 = J23 = 0.5, which represents a chain with isotropic and uniform antiferromagnetic couplings. We apply a pulse of the form  (odd harmonics) to the first qubit and
(odd harmonics) to the first qubit and  (even harmonics) to the third qubit. The time-dependent Schrödinger equation is solved numerically and the set
(even harmonics) to the third qubit. The time-dependent Schrödinger equation is solved numerically and the set  is read out during the evolution. Details of the simulation are provided in the supplementary material.
is read out during the evolution. Details of the simulation are provided in the supplementary material.
Simulating the Heisenberg Hamiltonain with the XY Hamiltonian.
Pulses of the form  and
and  are respectively applied to the first and third qubits of a uniform Heisenberg Hamiltonian (a). The time-dependent Schrödinger equation is then solved exactly numerically and the evolution of the set
are respectively applied to the first and third qubits of a uniform Heisenberg Hamiltonian (a). The time-dependent Schrödinger equation is then solved exactly numerically and the evolution of the set  is read out in (b). The qVL theorem gives us a prescription for constructing different auxiliary fields (c), which simulate the evolution of the set
is read out in (b). The qVL theorem gives us a prescription for constructing different auxiliary fields (c), which simulate the evolution of the set  correctly as seen in (d), but using a non-uniform XY interaction instead. (Time is measured in units of
correctly as seen in (d), but using a non-uniform XY interaction instead. (Time is measured in units of  ).
).
For the auxiliary XY Hamiltonian,  and we choose different and non-uniform couplings in which
and we choose different and non-uniform couplings in which  and
and  . Thus, we have chosen the auxiliary system to be anisotropic, with non-uniform and alternating ferromagnetic and antiferromagnetic couplings. Using the qVL theorem, we engineer the auxiliary local fields
. Thus, we have chosen the auxiliary system to be anisotropic, with non-uniform and alternating ferromagnetic and antiferromagnetic couplings. Using the qVL theorem, we engineer the auxiliary local fields  which using a this XY interaction, reproduce the set
which using a this XY interaction, reproduce the set  obtained from the original evolution under the uniform Hesienberg Hamiltonian. As seen in Figure 3, the auxiliary local fields are quite different from the original local fields applied to the Heisenberg model, but simulate the set of components
obtained from the original evolution under the uniform Hesienberg Hamiltonian. As seen in Figure 3, the auxiliary local fields are quite different from the original local fields applied to the Heisenberg model, but simulate the set of components  correctly. i.e.
correctly. i.e.  =
=  . In the language of electronic TDDFT, the XY model in our simulation is analogous to the “Kohn-Sham system” and the set
. In the language of electronic TDDFT, the XY model in our simulation is analogous to the “Kohn-Sham system” and the set  play the role of the exact Kohn-Sham potential as a density functional.
play the role of the exact Kohn-Sham potential as a density functional.
In the above example, we have constructed the exact auxiliary fields a posteriori, after having already solved the wavefunction evolution of the original system. Although such exact solutions are valuable in guiding functional development, one would ultimately like to develop accurate approximate and generic functionals for the auxiliary fields which can be used to circumvent solving the original problem. Furthermore, one would like to choose the auxiliary system so that its evolution is simpler than that of the original system. Such an approach has proven invaluable in the Kohn-Sham scheme of electronic TDDFT and we now discuss its applicability to TDDFT for quantum computation.
Discussion
The qRG and qVL theorems place TDDFT for universal quantum computation on a firm theoretical footing and open several exciting research avenues. The development of approximate density functionals has been essential for the success of electronic TDDFT and will be in quantum computation and information theory as well. In the Kohn-Sham scheme of electronic TDDFT, one simulates the correlated many-body system evolving under the Hamiltonian of Eq. 1, with an uncorrelated non-interacting system in which w′(|ri – rj|) = 0. The effective “Kohn-Sham” potential v′(r,t) of this non-interacting system must be approximated as a functional of the density. The local density approximation (LDA)2, was the first density functional to be applied to solid-state systems in the 1960s, but it was not sufficiently accurate for quantum chemistry. More than 20 years elapsed between the fundamental DFT theorem of Hohenberg and Kohn1 and the development of density functionals capable of achieving chemical accuracy in the 1980's; the so called generalized gradient approximations (GGA's)16.
In a similar vein, although we have established the fundamental theorems of TDDFT for quantum computation, the development of accurate approximate functionals will be a future challenge. Additionally, in TDDFT for quantum computation, we expect the path of functional development to be somewhat different. In the electronic Hamiltonian (Eq. 1), the kinetic and electron-electron repulsion are always the same operators and similarly the Kohn-Sham system is always non-interacting. Therefore, the Kohn-Sham potential is always the same functional for any electronic system. In contrast, in quantum computation one uses different two-qubit interaction terms depending on which universal Hamiltonian implements a given quantum circuit and therefore the functional will be different for each situation. For instance, if one wants to simulate an antiferromagnetic Heisenberg model using a ferromagnetic Heisenberg model, the functional will be different than a simulation of the same system using an XY model. Therefore, functional development will need to focus on specific implementations of quantum algorithms, rather than a single universal functional for all quantum computations. Typically, one would want to choose the auxiliary system's wavefunction to be less entangled than that of the original system, thereby making it easier to simulate using TDDFT on a classical computer. This is a similar concept to how TDDFT has been applied to electronic systems, where TDDFT provides a tool to approximately simulate quantum many-body systems efficiently on classical computers.
Naturally, there are systems that will be very hard to simulate using approximate functionals, such as those that are in the complexity class QMA and may require exponentially scaling resources on a quantum computer30. The collapse of the computational complexity class hierarchy is of course not expected and therefore finding functionals that carry out complex quantum computational tasks is extremely unlikely. Nevertheless, understanding how TDDFT functionals can approximately simulate efficient quantum algorithms on a classical computer is an open direction. Density functionals for strongly correlated lattice and spin systems have been recently proposed17,18,19,20 and could be applied to several problems of relevance in quantum computing. In Refs. 17,18,19,20 local density (LDA) and generalized gradient approximations (GGA) for one dimensional Hubbard chains and spin chains were derived from exact Bethe ansatz solutions and could readily be applied to solid-state quantum computing or perfect state transfer protocols in spin networks21. Functionals can also be parametrized from numerical simulations of one-dimensional qubit systems using time-dependent density matrix renormalization group methods (TDMRG)22, in an analogous fashion as quantum Monte Carlo simulations of the uniform electron gas have proven invaluable in electronic DFT23. In Figure 4, we summarize the analogies between electronic TDDFT and TDDFT for quantum computation, which will necessarily giude development of approximate functionals.
Analogies between electronic TDDFT and TDDFT for quantum computation.
Relevant quantities in electronic TDDFT (left column) and the corresponding quantities in TDDFT for quantum computation (right column). The current and kinetic energy of qubit TDDFT are defined in the supplementary material.
It should be noted that at present, the existing density functionals used in electronic structure calculations are far too simple to capture the entanglement and subtle correlations that play a major role in most quantum computing schemes. For instance, the adiabatic LDA and GGA functionals mentioned above are local in time and local or semi-local in space. As a result, they are poorly suited to systems that are strongly correlated and highly entangled as is typically the case in quantum computations. Whether or not it is possible to develop sufficiently non-local functionals for quantum computations remains an open question and is an essential prerequisite for making the theorems we have proven practically useful.
In a different direction, one could also imagine using the qVL theorem as an experimental tool to engineer different physical systems which perform the same computations. For instance, one could simulate an algorithm on an ion trap using a system of superconducting flux qubits, by using the qVL theorem to engineer the flux qubit Hamiltonian from knowledge of how the algorithm is performed on the ion trap. Another important research direction will be the generalization of DFT and TDDFT to other universal Hamiltonians and models of quantum computation. For instance, Ref. 24 discussed the use of TDDFT for obtaining gaps in adiabatic quantum computation. In29, groundstate DFT was used to study relationships between entanglement and quantum phase transitions, while Ref. 30 explored DFT from a complexity theory perspective.
In the supplementary material we explore connections between TDDFT for quantum computation and lattice theories of TDDFT25,26,27,28.
References
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964)
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965)
Runge, E. & Gross, E. K. U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 52, 997 (1984)
van Leeuwen, R. Mapping from densities to potentials in time-dependent densityfunctional theory. Phys. Rev. Lett. 82, 3863 (1999)
Benjamin, S. C. & Bose, S. Quantum computing with an always-on heisenberg interaction. Phys. Rev. Lett. 90, 247901 (2003)
Benjamin, S. C. & Bose, S. Quantum computing in arrays coupled by always-on interactions. Phys. Rev. A. 70, 032314 (2004)
DiVincenzo, D. P., Bacon, D., Kempe, J. Burkard, G. & Whaley, K. B. Universal quantum computation with the exchange interaction. Nature 408, 339–342 (2000)
Platzman, P. M. & Dykman, M. I. Quantum computing with electrons floating on liquid helium. Science 284, 1967 (1999)
Lidar, D. A. & Wu, L. A. Reducing constraints on quantum computer design by encoded selective recoupling. Phys. Rev. Lett. 88, 017905 (2001)
Makhlin, Y., Schön, G. & Shnirman, A. Josephson-junction qubits with controlled couplings. Nature 398, 305–307 (1999)
Rajam, A. K., Raczkowska, I. & Maitra, N. T. Semiclassical electron correlation in density-matrix time propagation. Phys. Rev. Lett. 105, 113002 (2010)
Deutsch, D. & Jozsa, R. Rapid solutions of problems by quantum computation. Proc. R. Soc. London A 439, 553 (1992)
Wooters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998)
Becke, A. D. Density functional thermochemistry. iii. the role of exact exchange. J. Chem. Phys. 98, 5648 (1993)
Maitra, N. T., Burke, K. & Woodward, C. Memory in time-dependent density functional theory. Phys. Rev. Lett. 89, 023002 (2002)
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996)
Alcaraz, F. C. & Capelle, K. Density functional formulations for quantum chains. Phys. Rev. B 76, 035109 (2007)
Verdozzi, C. Time-dependent density-functional theory and strongly correlated systems: Insight from numerical studies. Phys. Rev. Lett. 101, 166401 (2008).
Karlsson, D., Privitera, A. & Verdozzi, C. Time-dependent density-functional theory meets dynamical mean-field theory: Real-time dynamics for the 3d hubbard model. Phys. Rev. Lett. 106, 116401 (2011)
Lima, N. A., Olivera, L. N. & Capelle, K. Density-functional study of the mott gap in the hubbard model. Europhys. Lett. 60, 601–607 (2002)
Bose, S. Quantum communication through an unmodulated spin chain. Phys. Rev. Lett. 91, 207901 (2003)
White, S. R. & Feiguin, A. E. Real-time evolution using the density matrix renormalization group. Phys. Rev. Lett. 93, 076401 (2004)
Ceperley, D. M. & Alder, B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566 (1980)
Gaitan, F. & Nori, F. Density functional theory and quantum computation. Phys. Rev. B 79, 205117 (2009)
Maitra, N. T., Todorov, T. N., Woodward, C. & Burke, K. Density-potential mapping in time-dependent density-functional theory. Phys. Rev. A 81, 042525 (2010)
Baer, R. On the mapping of time-dependent densities onto potentials in quantum mechanics. J. Chem. Phys. 128, 044103 (2008)
Li, Y. & Ullrich, C. A. Time-dependent v-representability on lattice systems. J. Chem. Phys. 129, 044105 (2008)
Kurth, S. & Stefanucci, G. Time-dependent bond-current functional theory for lattice hamiltonians: Fundamental theorem and application to electron transport. Chem. Phys. 391, 164 (2011)
Wu, L. A., Sarandy, M. S., Lidar, D. A. & Sham, L. J. Linking entanglement and quantum phase transitions via density-functional theory. Phys. Rev. A. 74, 052335 (2006)
Schuch, N. & Verstraete, F. Computational complexity of interacting electrons and fundamental limitations of density functional theory. Nature Phys. 5, 732–735 (2009)
Acknowledgements
Useful discussions with S. Mostame, J. D. Whitfield, S. Boxio, M. H. Yung and J. Parkhill are greatfully acknowledged. We thank NSF award PHY-0835713 for financial support.
Author information
Authors and Affiliations
Contributions
D. G. T. and A. A. G. both developed the theory, performed the calculations and also wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Tempel, D., Aspuru-Guzik, A. Quantum Computing Without Wavefunctions: Time-Dependent Density Functional Theory for Universal Quantum Computation. Sci Rep 2, 391 (2012). https://doi.org/10.1038/srep00391
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00391
This article is cited by
-
Exact exchange-correlation potential of an ionic Hubbard model with a free surface
Scientific Reports (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.