Abstract
Unity transmittance at an interface between bulk media is quite common for polarized electromagnetic waves incident at the Brewster angle, but it is rarely observed for sound waves at any angle of incidence. In the following, we theoretically and experimentally demonstrate an acoustic metamaterial possessing a Brewster-like angle that is completely transparent to sound waves over an ultra-broadband frequency range with >100% bandwidth. The metamaterial, consisting of a hard metal with subwavelength apertures, provides a surface impedance matching mechanism that can be arbitrarily tailored to specific media. The nonresonant nature of the impedance matching effectively decouples the front and back surfaces of the metamaterial allowing one to independently tailor the acoustic impedance at each interface. On the contrary, traditional methods for acoustic impedance matching, for example in medical imaging, rely on resonant tunneling through a thin antireflection layer, which is inherently narrowband and angle specific.
Similar content being viewed by others
Introduction
The concept of metamaterials was originally introduced for electromagnetic waves and received significant attention over the last decade, due to unconventional interaction of these man-made materials with waves, as in the case of negative refraction materials1. More recently, the metamaterial concept has been extended to acoustic waves in a variety of scenarios of interest such as acoustic clocking2, superlensing3 and sound focusing and confinement4. Several challenges still hold in applying metamaterials to realistic devices, in particular when low losses and wide bandwidths of operation are desired, as most of their exotic features are based on resonant inclusions.
One particular class of metamaterials that has received special attention in recent years is an array of subwavelength apertures in an opaque screen, producing spectral bands of extraordinary transmission. In other words, more energy passes trough these subwavelength apertures than one would expect from simple geometrical considerations based on the aperture to period ratio. At first, this phenomenon has been predicted and experimentally observed in the electromagnetic domain, where it is known as extraordinary optical transmission (EOT)5,6,7,8. Lately, it has been extended to acoustic waves, as extraordinary acoustic transmission (EAT)9,10,11. Usually these phenomena are achieved under some form of resonant condition and are therefore limited in bandwidth and lossy, particularly in the case of very subwavelength apertures. In this paper, we demonstrate a different way of squeezing and tunneling acoustic waves in ultranarrow apertures, overcoming several of the conventional EAT limitations. To this goal, we show a way to manipulate the effective constitutive properties (density ρeff and sound velocity ceff) of an acoustic metamaterial mostly composed of impenetrable hard materials, in order to realize broadband impedance matching. As an example of the powerful versatility of this impedance matching technique, in the following we demonstrate acoustic matching of the metamaterial with air. Noise in the everyday environment is ubiquitous, primarily due to the large impedance mismatch between air and solid materials. Most rigid acoustic materials (glass, steel, etc.) have a large acoustic impedance compared to air, which makes them practically impenetrable to sound waves. This is related to the fact that the angle of acoustic intromission12, i.e., the angle at which the reflection is zero for an interface between air (medium 1) and a generic material (medium 2) with effective density ρeff and effective sound velocity ceff , is rarely found in conventional materials. When it exists, the intromission angle (ϑI) must satisfy the following expression12

where ρ0 and c0 are respectively the density and sound velocity in medium 1 (air in our case). The angle for unity transmittance is similar to the Brewster angle for electromagnetic waves and, although the underlying mechanisms for perfect transmittance of acoustic and electromagnetic waves are very different, they can both be understood as an impedance matching phenomenon.
It is seen in Eq. (1) that the intromission condition may be met when either ρeff/ρ0>c0/ceff>1 or ρeff/ρ0<c0/ceff<1, which cannot be satisfied by most ordinary bulk materials, due to the fact that the speed of sound generally increases with density. One instance of a naturally occurring intromission angle is in ocean acoustics at the interface of water and the sea floor13. For a muddy bottom composed of water saturated silt, the speed of sound is lower than water but the density is higher than water. This is the intromission condition that we describe below; a metamaterial having a density higher than air but a speed of sound lower than air.
In the following, we theoretically predict and experimentally demonstrate that an effective angle of intromission may be introduced at will in a metamaterial formed by an array of sub-wavelength apertures in a thick, acoustically hard screen. At this angle, nearly total transmission spanning an ultrabroad range of acoustic frequencies is obtained. Most EAT phenomena rely on resonance effects that are inherently narrow-band and for which large transmission is usually hindered by absorption losses as the aperture size becomes much smaller than the wavelength. In addition, resonant EAT frequencies strongly depend on the screen thickness and the array period, relying on the resonant coupling between entrance and exit of each aperture. Here, on the other hand, the nonresonant nature of the intromission tunneling separately arises at the entrance and exit of the screen, implying that is very robust to absorption or energy extraction for harvesting purposes within the apertures and may be tailored to impedance match dissimilar media. The impedance matching is essentially frequency independent and may be tailored by the geometry of the metamaterial, as we describe in the following.
Results
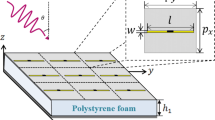
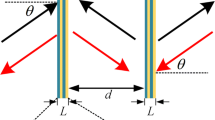
In order to provide some physical insights into this phenomenon, we refer to the geometries described in Fig. 1: an acoustic, time-harmonic e-iωt plane wave with wave-number k0 = ω/c0 is incident at an arbitrary angle (ϑ,ϕ) on an acoustically hard screen of thickness l, corrugated by slits of width w and period d; we also consider the case of 2-D apertures with periods dx and dy , area of the elementary cell S1 = dxdy and area of the apertures S2 .
Sketch of the considered geometries.
On the left a 1-D acoustic grating of period d, slit aperture w and thickness l; on the right a 2-D acoustic grating of periods dx and dy , area of the elementary cell S1 = dxdy and area of the aperture S2. Both structures are excited by an acoustic plane-wave incident at an angle ϑ with respect to the z-axis and an angleϕ in the x-y plane.
Here we suppose that the grating periodicities are smaller than the wavelength of the incident sound wave (λ>2dx, λ>2dy) so that all the diffraction orders except the zero-th are evanescent. Under this condition reflected and transmitted pressure fields may be respectively written as  for z<0 and
for z<0 and  for z>l where r and t are the reflection and transmission coefficients, respectively, kx and ky are the transverse components of the wavevector, which may be written in terms of the angles ϑ and ϕ (see Fig. 1) as: kx = k0sin(ϑ)cos(ϕ) and ky = k0sin(ϑ)sin(ϕ). Inside each aperture, only the (0,0) acoustic mode can propagate, with general expression
for z>l where r and t are the reflection and transmission coefficients, respectively, kx and ky are the transverse components of the wavevector, which may be written in terms of the angles ϑ and ϕ (see Fig. 1) as: kx = k0sin(ϑ)cos(ϕ) and ky = k0sin(ϑ)sin(ϕ). Inside each aperture, only the (0,0) acoustic mode can propagate, with general expression  . Unlike electromagnetic waveguides, there is no cutoff wavelength for a 2-D acoustic aperture. In addition, due to momentum conservation, each channel is separately excited with a phase that matches the impinging excitation at the location (x0,y0) of the aperture, implying that we may write for the pressure fields
. Unlike electromagnetic waveguides, there is no cutoff wavelength for a 2-D acoustic aperture. In addition, due to momentum conservation, each channel is separately excited with a phase that matches the impinging excitation at the location (x0,y0) of the aperture, implying that we may write for the pressure fields  for 0<z<l, where A and B are the unknown amplitudes of the forward and backward propagating modes. By imposing the continuity of the pressure field P and the normal component of the volume velocity S(iρ0ω)−1∂P/∂z at z = 0 and z = l, the transmission takes the following expression:
for 0<z<l, where A and B are the unknown amplitudes of the forward and backward propagating modes. By imposing the continuity of the pressure field P and the normal component of the volume velocity S(iρ0ω)−1∂P/∂z at z = 0 and z = l, the transmission takes the following expression:

where, according to the notation in Ref.12, we have defined the acoustic impedance of the impinging wave on the surface S1 as Zac1 = ρ0c0/(S1cosϑ) and the acoustic impedance of the guided mode inside the channels of cross section S2 as Zac2 = ρ0c0/S2. For 2-D apertures (Fig. 1 right panel) S1 = dxdy is the area of the elementary cell and S2 is the area of the aperture, while for 1-D slits (Fig. 1 left panel ) S1 = 1m·d and S2 = 1m·w are the areas normalized to 1 m along the y-axis. Resonant EAT ( ) is obtained at the FP resonances k0l = nπ, with n being an integer, consistent with the findings in Refs.9,10,11. Yet, Eq. (2) admits another peculiar condition for unitary transmission, which arises when Zac1 = Zac2.For normal incidence this condition cannot be met, due to the difference in cross sectional areas, but, by increasing the angle of incidenceϑ, Zac1 can be smoothly increased until it matches the value of Zac2 at the angle ϑI:
) is obtained at the FP resonances k0l = nπ, with n being an integer, consistent with the findings in Refs.9,10,11. Yet, Eq. (2) admits another peculiar condition for unitary transmission, which arises when Zac1 = Zac2.For normal incidence this condition cannot be met, due to the difference in cross sectional areas, but, by increasing the angle of incidenceϑ, Zac1 can be smoothly increased until it matches the value of Zac2 at the angle ϑI:

which represents the intromission angle for an acoustic metamaterial. Although rare for ordinary bulk materials12, an intromission angle can always be obtained for the metamaterial shown in Fig. 1 and the angle depends only on the geometry, i.e. the percentage of the open area of the screen. This anomalous matching phenomenon is totally independent on the grating thickness, since the effective channel impedance matches the impinging wave at each interface, producing anomalous total tunneling and energy squeezing through each channel. This strikingly simple formula captures to a large degree a novel tunneling phenomenon which may be regarded as the acoustic analog of the “plasmonic Brewster angle” introduced in Ref.14 for 1-D metallic gratings excited by electromagnetic waves. Due to the absence of modal cut-off in 2-D acoustic waveguides, this condition interestingly holds also for 2-D gratings of arbitrary cross-section in the case of acoustic waves. Eq. (2) is consistent with a rigorous homogenization of such acoustic grating as a homogeneous acoustic metamaterial with effective spatially-dispersive parameters:

Indeed, the acoustic intromission angle as defined in Eq. (1) is given by Eq. (3). We notice that in our model there is no dependence on the azimuthal angle ϕ, as one may expect given the scalar nature of the pressure fields. The advantage of the nonresonant mechanism is that acoustic energy collectors and sensors can be placed inside the apertures without harming the impedance matching and funneling at the surface. What is going on inside the apertures doesn’t affect the collection efficiency as it would for a resonant mechanism! In addition, the waveguides can reroute the acoustic energy into a single waveguide for energy collection onto one device instead of many. By tapering the cross section area of the waveguides with depth into the metamaterial it is possible to change the open area of the screen for the incident and exit surfaces independently, thereby achieving impedance matching to two acoustic media with different values of impedance.
In order to verify the basic prediction of acoustic impedance matching to air, we have fabricated 1-D and 2-D subwavelength aperture arrays in a thick aluminum plate and measured the transmission as a function of incidence angle (ϑ) and acoustic frequency.
Acoustic measurements were performed in an acoustic anechoic chamber in the frequency range 4-20 kHz: a sketch of the experimental set-up and pictures of the samples are shown in Figure 2. The sample was placed on a rotational stage and the sound pressure transmission measurements were performed from normal incidence to nearly grazing angle. In Fig. 3 we show the experimental results for the case of a 1-D structure and compare them with our theoretical homogenized model (2–4).
Transmittance for the 1-D samples.
Angular power transmission spectra for two different 1-D gratings: (upper panel) l = 25.4 mm, d = 4.275 mm and w = 1.1 mm; (lower panel) l = 25.4 mm d = 3.575 mm and w = 400 μm. Transmission bands independent of angle are due to resonant Fabry-Perot modes and transmission bands independent of frequency are due to the non-resonant intromission process. Open area of the screen for the two cases are 26% (upper) and 11% (lower).
The upper panel of Fig. 3 corresponds to the 1-D aluminum sample with dimensions l = 25.4 mm, d = 4.275 mm and w = 1.1 mm. Our analytical model captures with remarkable accuracy the fundamental physical mechanisms behind the transmission resonances of the grating: at normal incidence (ϑ = 0), typical EAT peaks based on FP resonances are visible. These resonances are the horizontal bands in the plots, since this EAT mechanism is inherently narrow-band, but weakly dependent on the incidence angle. In contrast, the intromission angle transmission arises as a vertical band, confirming weak dependence on frequency, but selectivity to the transmission angle. One may wonder how narrow can the slits be made and still realize high, ultra-broadband transmission at the intromission angle, considering that conventional EAT phenomena are very sensitive to presence of losses in the channels, in particular for large field confinements in small apertures and slits. In our homogenized model (2–4), we have neglected the finite frictional losses and field penetration in the metal, although they are inevitable in our experiments. In order to assess the robustness of the broadband intromission tunneling phenomenon against frictional losses, we have fabricated and tested a second 1-D sample (see lower panel of Fig. 3) with same thickness l = 25.4 mm, but different period and slit width d = 3.575 mm, w = 400 μm.The open area of the screen is 11% .
Our analytical model has been extended to account for small frictional losses by introducing a perturbative dissipation factor in the wave-vector, which becomes10  , where
, where  is the thickness of a viscous boundary layer. For air at 20°C, the expression for the viscous boundary layer12 is:
is the thickness of a viscous boundary layer. For air at 20°C, the expression for the viscous boundary layer12 is:  where ν is the frequency in Hz and is ~20 μm thick at these frequencies. At normal incidence, the FP transmission bands are severely affected by the presence of losses in this second scenario, both in our analytical results and in our experiment, when compared to the case with 1.1 mm slits. The intromission tunneling is however significantly more robust, providing one order of magnitude larger transmission than at the conventional FP resonances. This robustness is a symptom of the non-resonant nature of the intromission tunneling. In conventional FP tunneling, the pressure field undergoes a series of multiple reflections at the highly mismatched entrance and exit faces of the grating. This effectively forms a resonant cavity with large stored energy, thereby enhancing the frictional losses. In contrast, broadband intromission tunneling and energy squeezing is achieved due to impedance matching, for which the impinging wave, independent of the frequency of excitation, ‘feels’ the same impedance in vacuum and inside the slits, avoiding any reflection at the entrance and exit faces of the grating, regardless of the grating thickness l. As the filling ratio gets smaller, the sound squeezing increases and the corresponding angular spread of the intromission transmission band gets narrower, moving towards steeper angles. A clear vertical high transmission band at the intromission angle is seen spanning the entire frequency range, even in this extreme scenario, highlighting the robustness of this concept in terms of its practical applications.
where ν is the frequency in Hz and is ~20 μm thick at these frequencies. At normal incidence, the FP transmission bands are severely affected by the presence of losses in this second scenario, both in our analytical results and in our experiment, when compared to the case with 1.1 mm slits. The intromission tunneling is however significantly more robust, providing one order of magnitude larger transmission than at the conventional FP resonances. This robustness is a symptom of the non-resonant nature of the intromission tunneling. In conventional FP tunneling, the pressure field undergoes a series of multiple reflections at the highly mismatched entrance and exit faces of the grating. This effectively forms a resonant cavity with large stored energy, thereby enhancing the frictional losses. In contrast, broadband intromission tunneling and energy squeezing is achieved due to impedance matching, for which the impinging wave, independent of the frequency of excitation, ‘feels’ the same impedance in vacuum and inside the slits, avoiding any reflection at the entrance and exit faces of the grating, regardless of the grating thickness l. As the filling ratio gets smaller, the sound squeezing increases and the corresponding angular spread of the intromission transmission band gets narrower, moving towards steeper angles. A clear vertical high transmission band at the intromission angle is seen spanning the entire frequency range, even in this extreme scenario, highlighting the robustness of this concept in terms of its practical applications.
We now analyze the 2-D sample which may be considered even more interesting for energy concentration, harvesting and focusing purposes. In Fig. 4 we compare theory and experiments for 2-D apertures. Even in this 2-D geometry, a clear broadband intromission band is observed in our experiment (right figure of the upper panel), well captured by our analytical model (left figure of the upper panel), confirming that the grating still retains the main physical properties of a metamaterial (4). We notice a slight shift of the measured spectral position of the FP transmission bands compared to our analytical model; a corresponding small shift is also observed in the angular position of the intromission band. Both effects are attributed to having neglected in our analytical model the reactive fields associated with the evanescent higher diffraction orders excited at the grating interfaces, which may be taken into account by considering a slightly longer channel length and a slight difference in the input impedance15. Due to the large abruption in this 2-D scenario, these effects are expected to play a somewhat more relevant role than in the 1-D case. In order to further highlight the anomalous features of this tunneling phenomenon, in the lower panel we show the numerical calculation16 of the pressure wave outside and inside the channel at the frequency ν = 12.75 KHz, which represents the frequency of the second FP resonance of the grating. We compare the case of normal incidence excitation to the case of excitation at the intromission angle. It is evident how, despite both excitations ensure very high transmission levels, the field distributions inside the channels are very different. For normal incidence, total transmission is obtained by exploiting a strong FP resonance established via the large mismatch at the entrance and exit faces, which forms a typical standing wave distribution inside the channel. In contrast, at the intromission angle tunneling is based on impedance matching: the wave does not experience any change in effective impedance and it can tunnel through the channel with nearly uniform amplitude, no amplification and minimum reflections and standing-wave ratio. The normal component of the velocity (not shown here) is the one being amplified in the channel, due to the continuity of the total volume velocity, but similar differences are seen between incidence in the normal direction and at the intromission angle in terms of uniform distribution and absence of standing waves in the channel. We also note that as long as the field is tuned on a FP resonance, by increasing the incident angle it gradually passes from a resonant channeling regime to a non-resonant channeling regime with no drop in the overall transmittance.
Transmittance for the 2-D sample and localization of the pressure field inside the channels.
Angular power transmission spectra for a 2-D hole array aluminum grating with l = 25.4 mm, dx = dy = 7.94 mm and hole radius r = 2 mm. Pressure wave numerically calculated for the second FP resonance at ν = 12.75 KHz in the case of normal incidence and at the intromission angle as indicated in the figures. The open area of the screen is 20%.
Discussion
These findings may have important applications for sub-wavelength acoustic imaging, acoustic field concentration, harvesting and impedance matching for multiple applications including medical diagnostics17 and noise control18. For example, 2-D acoustic metamaterials have been explored for deep-subwavelength imaging19 by exploiting their FP resonances, also an acoustic broad-band hyperlens has been demonstrated20. Our results suggest that similar applications could be devised at the intromission angle of the grating, with exceptional broadband characteristics. We have also found that, even by reducing the slit apertures, the intromission band remains much less affected by the frictional losses with respect to the FP resonances and thus gives the possibility to funnel sound through extreme sub-wavelength apertures. This effect is, again, a symptom of the different physical mechanisms involved in classic EAT based on FP-resonances compared to the nonresonant mechanism at the intromission angle that we have elucidated in this work. Even in the extreme case in which the acoustic energy funneled into the 2-D apertures would be harvested or converted into other energy forms, for which the absence of a standing-wave resonance would suppress any form of FP tunneling, the matching phenomenon described here would be preserved. This important property suggests, for example, the application of these concepts to realize broadband acoustic to electric energy conversion through piezoelectric materials using micromechanical systems (MEMS) technology. Finally, the results presented here for impedance matching in air, indicate future possibilities for liquid and solid media.
Methods
1. Sample preparation
The 1D metallic sample was constructed using ~300 extruded aluminum flat bars 0.3175 cm by 2.54 cm. The sample size was ~0.5 m high, ~1 m wide and 2.54 cm thick, much larger than the incident beam size, in order to minimize any diffraction effects around the sample, particularly for large incidence angles. The grating was held together by metal rods through the bars at the top and bottom of the sample and the aperture width was fixed by inserting shim spacers near the rods of 1.1 mm and 400 microns. The 2D hole array structure was built by drilling 4 mm holes into a 2.54 cm thick aluminum plate with dimensions of 91 cm by 46 cm.
2. Angular acoustic transmission measurements
The acoustic angular transmission measurements were performed by building a small anechoic chamber using sound absorbing foam. The sample was placed on a rotational stage in the middle of the chamber and the distance between the driver and microphone was 190 cm. A Bruel & Kjaer pulse system was used together with a 50 kHz Crwon xTi 1000 amplifier, Bruel & Kjaer 4961 free field microphone and BMS 4512ND planar wave drive of dimensions 1’’Width ×4’’ Height. Additional sound absorbing foam was placed around the sample to ensure that no sound was leaking around the sample particularly at steeper angles. Transmission measurements through the grating were normalized with measurements without the sample in place. Each measurement was repeated several times to ensure repeatability and consistency.
3. Numerical Calculations
The numerical calculation was carried out by finite element methods, as implemented in the COMSOL Multiphysics software package. We assumed the sound wave impinging on the sample as incidence plane waves. Periodic boundary conditions were set around a unit cell, while perfectly matched layer (PML) absorbing boundary conditions were used at the top and bottom boundaries of the cell. The transmission was computed by a ratio of an integration of input and output pressure field at the top and bottom boundaries before PMLs.
References
Smith, D. R., Pendry, J. B. & Wiltshire, M. C. K. Metamaterials and Negative Refractive Index. Science 305, 788–792 (2004).
Chen, H. & Chan, C. T. Acoustic Cloaking in three dimensions using acoustic metamaterials. Appl. Phys.Lett. 91, 183518 (2007).
Ambati, M., Fang, N., Sun, C. & Zhang, X. Surface resonant states and superlensing in acoustic metamaterials. Phys. Rev. B 75, 195447 (2007).
Guenneau, S., Movchan, A., Petursson, G. & Ramakrishna, S. A. Acoustic metamaterials for sound focusing and confinement. New Journ. Phys. 9, 399 (2007).
Ebbesen, T. W. et al. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 391, 667–669 (1998).
García de Abajo, F. J. Colloquium: Light scattering by particle and hole arrays. Rev. Mod. Phys. 79, 1267–1290 (2007).
Garcia-Vidal, F. J. et al. Light passing through subwavelength apertures. Rev. Mod. Phys. 82, 729–787 (2010).
Medina, F., Mesa, F. & Marques, R. Extraordinary Transmission Through Arrays of Electrically Small Holes From a Circuit Theory Perspective. IEEE Trans. Microwave Theory Tech. 56, 3108–3120 (2008).
Mimg-Hui Lu et al. Extraordinary Acoustic Transmission through a 1D Grating with Very Narrow Apertures. Phys. Rev. Lett 99, 174301 (2007).
Wang, X. Theory of resonant sound transmission through small apertures on periodically perforated slabs. Journ. Appl. Phys. 108, 064903 (2010).
Christensen, J., Martin-Moreno, L. & Garcia-Vidal, F. J. Theory of Resonant Acoustic Transmission through Subwalength Apertures. Phys. Rev. Lett. 101, 014301 (2008).
Blackstock, D. T. Fundamentals of Physical Acoustics. John Wiley&Sons, Inc., New York (2000).
Holland, C. Geoacoustic inversion for fine-grained sediments. Journ. Acous. Soc. Am. 111, 1560–1564 (2002).
Alù, A., D’Aguanno, G., Mattiucci, N. & Bloemer, M. J. Plasmonic Brewster Angle: Broadband Extraordinary Transmission through Optical Gratings. Phys. Rev. Lett. 106,123902 (2011).
Hersh, A. S., Walker, B. E. & Celano, J. W. Helmholtz resonator impedance model, Part1: Nonlinear behavior. AIAA Journal 41, 795–808 (2003).
COMSOL MultiPhysics.
Rhee, S., Fitter, T. A., Shung, K. K., Wang, H. Cao, W. Materials for Acoustic Matching in Ultrasound Transducers. IEEE Ultrasonics Symposium 1051 (2001).
Arenas, J. P., Crocker, M. J. Recent Trends in Porous Sound Absorbing Material. Sound &Vibration 12 July (2010).
Zhu, J. et al. A holey-structured metamaterial for acoustic deep-subwavelength imaging. Nature Phys. 7, 52–55 (2011).
Li, J., Fok, L., Yin, X., Bartal, G. & Zhang, X. Experimental demonstration of an acoustic magnifying hyperlens. Nature Materials 8, 931–934 (2009).
Acknowledgements
This work has been partially supported by DARPA Phase II STTR project number W31P4Q-11-C-0098. We thank S. Horowitz for helpful discussions.
Author information
Authors and Affiliations
Contributions
G.D. has developed the analytical model, contributed to the writing of the paper and the interpretation of the experimental results, K. Q. L. has performed the numerical simulations, R.T. has performed the measurements and contributed to the experimental set-up, A.A. has contributed to the writing of the paper and the interpretation of the experimental results, N.M. has contributed to the writing of the paper, the interpretation of the experimental results and the preparation of the figures, A.D.M. has contributed to the experimental set-up, N.A. has contributed to the writing of the paper, measurements and the preparation of the samples, M.J.B. has contributed to the interpretation of the experimental results and writing the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
D’Aguanno, G., Le, K., Trimm, R. et al. Broadband metamaterial for nonresonant matching of acoustic waves. Sci Rep 2, 340 (2012). https://doi.org/10.1038/srep00340
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00340
This article is cited by
-
Acoustic transmission loss in Hilbert fractal metamaterials
Scientific Reports (2023)
-
Graphite-oxide hybrid multi-degree of freedom resonator metamaterial for broadband sound absorption
Scientific Reports (2022)
-
Hybrid fractal acoustic metamaterials for low-frequency sound absorber based on cross mixed micro-perforated panel mounted over the fractals structure cavity
Scientific Reports (2022)
-
Zero-reflection acoustic metamaterial with a negative refractive index
Scientific Reports (2019)
-
Investigation of Helmholtz resonator-based composite acoustic metamaterial
Applied Physics A (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.