Abstract
During the last few years, much research has been devoted to strategic interactions on complex networks. In this context, the Prisoner's Dilemma has become a paradigmatic model and it has been established that imitative evolutionary dynamics lead to very different outcomes depending on the details of the network. We here report that when one takes into account the real behavior of people observed in the experiments, both at the mean-field level and on utterly different networks, the observed level of cooperation is the same. We thus show that when human subjects interact in a heterogeneous mix including cooperators, defectors and moody conditional cooperators, the structure of the population does not promote or inhibit cooperation with respect to a well mixed population.
Similar content being viewed by others
Introduction
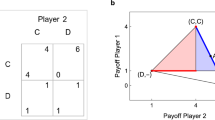
In recent years, the physics of complex systems has widened its scope by considering interacting many-particle models where the interaction goes beyond the usual concept of force. One such line of research that has proven particularly interesting is evolutionary game theory on graphs1,2, in which interaction between agents is given by a game while their own state is described by a strategy subject to an evolutionary process3,4. A game that has attracted a lot of attention in this respect is the Prisoner's Dilemma (PD)5,6, a model of a situation in which cooperative actions lead to the best outcome in social terms, but where free riders or non-cooperative individuals can benefit the most individually. In mathematical terms, this is described by a payoff matrix (entries correspond to the row player's payoffs and C and D are respectively the cooperative and non-cooperative actions)

with T > 1 (temptation to free-ride) and S < 0 (detriment in cooperating when the other does not).
In a pioneering work, Nowak and May7 showed that the behavior observed in a repeated Prisoner's Dilemma was dramatically different on a lattice than in a mean-field approach: Indeed, on a lattice the cooperative strategy was able to prevail by forming clusters of alike agents who outcompeted defection. Subsequently, the problem was considered in literally hundreds of papers1,8,9,10,11 and very many differences between structured and well-mixed (mean-field) populations were identified, although by no means they were always in favor of cooperation12,13. In fact, it has been recently realized that this problem is very sensitive to the details of the system2,14, in particular to the type of evolutionary dynamics15 considered. For this reason experimental input is needed in order to reach a sound conclusion about what has been referred to as ‘network reciprocity’.
Here, we show that using the outcome from the experimental evidence to inform theoretical models, the behavior of agents playing a PD is the same at the mean field level and in very different networks. To this end, instead of considering some ad hoc imitative dynamics7,16,17, our players will play according to the strategy recently uncovered by Grujić et al.18 in the largest experiment reported to date about the repeated spatial PD, carried out on a lattice as in Nowak and May's paper7 with parameters T = 1.43 and S = 0.
The results of the experiment were novel in several respects. First, the population of players exhibited a rather low level of cooperation (fraction of cooperative actions in every round of the game in the steady state), hereafter denoted by 〈c〉. Most important, however, was the unraveling of the structure of the strategies. The analysis of the actions taken by the players showed a heterogeneous population consisting of “mostly defectors” (defected with probability larger than 0.8), a few “mostly cooperators” (cooperated with probability larger than 0.8) and a majority of so-called moody conditional cooperators. This last group consisted of players that switched from cooperation to defection with probability  and from defection to cooperation with probability
and from defection to cooperation with probability  , ci being the fraction of cooperative actions in player i's neighborhood in the previous iteration. Conditional cooperation, i.e., the dependence of the chosen strategy on the amount of cooperation received, had been reported earlier in related experiments19 and observed also for the spatial repeated PD at a smaller scale20. The new ingredient revealed in Grujić et al.'s experiment18 was the dependence of the behavior on the own player's previous action, hence the reason to call them “moody”.
, ci being the fraction of cooperative actions in player i's neighborhood in the previous iteration. Conditional cooperation, i.e., the dependence of the chosen strategy on the amount of cooperation received, had been reported earlier in related experiments19 and observed also for the spatial repeated PD at a smaller scale20. The new ingredient revealed in Grujić et al.'s experiment18 was the dependence of the behavior on the own player's previous action, hence the reason to call them “moody”.
Results
To study how the newly unveiled rules influence the emergence of cooperation in an structured population of individuals, we first report results from numerical simulations of a system made up of N = 104 individuals who play a repeated PD game according to the experimental observations. To this end, we explored the average level of cooperation in four different network configurations: a well-mixed population in which the probability that a player interacts with any other one is the same for all players, a square lattice, an Erdös-Renyi (ER) graph and a Barabási-Albert (BA) scale-free (SF) network. It is worth mentioning that the dependence on the payoff matrix only enters through the parameters describing the players' behavior (d, γ, a, β and the fractions of the three types of players). Once these parameters are fixed the payoffs do not enter anywhere in the evolution, as this is only determined by the variables ci, the local fractions of cooperative actions within each player's neighborhood. Thus there is no possibility to explore the dependence on the payoffs because we lack a connection between them and the behavioral parameters.
In Figure 1 we present our most striking result. The figure represents, in a color-coded scale, the average level of cooperation as a function of the fraction of mostly cooperators, ρC and mostly defectors, ρD, for a BA network of contacts. The same plots but for the rest of topologies explored (lattice and ER graphs) produce indistinguishable results with respect to those shown in the figure. We therefore conclude that the average level of cooperation in the system does not depend on the underlying structure. This means that, under the assumption that the players follow the behavior of Grujić et al's experiment18, there is no network reciprocity, i.e., no matter what the network of contacts looks like, the observed level of cooperation is the same. This latter finding is in stark contrast to most previous results coming out from numerical simulations of models in which many different updating rules —all of them based upon the relative payoffs obtained by the players— have been explored.
Dependence of the average level of cooperation on the density of strategists.
Density plot of 〈c〉, as a function of the fractions of the three strategies (mostly cooperators, C, mostly defectors, D and moody conditional cooperators, X). The plot corresponds to a Barabási-Albert network of contacts (〈k〉 = 6), but the corresponding plot for an Erdös-Renyi graph or a regular lattice is indistinguishable from this one. The system is made up of N = 104 players and the rest of parameters, taken from Ref. 18, are: d = 0.38, a = 0.15, γ = 0.62, β = −0.1. The thin lines represent the mean-field estimations [c.f. Eq. (5)] for 〈c〉 = 0.32, 0.44, 0.56, 0.68. They very accurately match the contour lines of the density plot corresponding to those values of 〈c〉, thus proving that the same outcome is obtained in a complete graph (mean-field). Simulation results have been averaged over 200 realizations.
Mean-field Approach
The previous numerical findings can be recovered using a simple mean-field approach to the problem. Let the fractions of the three types of players be ρC, ρD and ρX, for mostly cooperators, mostly defectors and moody conditional cooperators, respectively, with the obvious constraint ρX = 1 − ρD − ρC. Denoting by Pt(A) the cooperation probability at time t for strategy A( = C, D, X) of the repeated PD we have

where Pt(C) = P(C) and Pt(D) = P(D) are known constants [in our case P(C) = 0.8, P(D) = 0.2]. The probability of cooperation for conditional players in the next time step can be obtained as

where the first term in the right hand side considers the probability that a conditional cooperator keeps playing as a cooperator, whereas the second terms stands for the situation in which a moody conditional cooperator switched from defection to cooperation. Asymptotically

From Eq. (3),

thus (2) implies (with the replacement ρX = 1 − ρC − ρD)

where

are functions of 〈c〉. From Eq. (5) it follows that the curves of constant 〈c〉 are straight lines in the simplex. Figure 1 clearly demonstrates this fact: The straight lines are plots of Eq. (5) for different values of 〈c〉. It can be seen that they are parallel to the color stripes and that the values of 〈c〉 they correspond to accurately fit those of the simulations. Figure 2 depicts the curve 〈c〉 vs. ρC for two different values of ρD, as obtained from Eq. (5) and compared to simulations. This figure illustrates the excellent quantitative agreement between the mean-field result and the simulation results. The match between the analytical and numerical results is remarkable, as it is the fact that this agreement does not depend on the underlying topology. This is the ultimate consequence of the lack of network reciprocity: the cooperation level on any network can be accurately modeled as if individuals were playing in a well-mixed population.
Absence of Network Reciprocity.
Average cooperation level in the stationary state, 〈c〉, as a function of the density ρC of mostly cooperators and two different values of the density ρD of mostly defectors, for two different kinds of networks: regular lattice (k = 8) and Barabási-Albert network (〈k〉 = 8). The network size is N = 104 and the rest of parameters are as in Figure 1. Lines represent the mean-field estimations. Results are averages over 200 realizations. The inset is a zoom that highlights how the different curves compare.
The steady state is reached after a rather short transient, as illustrated in Figure 3. This figure compares the approach of the cooperation level to its stationary state as obtained iterating Eq. (3) and from numerical simulations on different networks with different sizes. The initial cooperation level has been set to 〈c〉0 = 0.592, close to the value observed in Grujić et al's experiment18. The transient does exhibit a weak dependence on the underlying topology and specially on the network size, but for the largest simulated size (N = 104) the curves are all very close to the mean-field prediction.
Asymptotic level of Cooperation.
Time evolution of the cooperation level until the stationary state is reached. The results have been obtained from numerical simulations on different networks with different sizes. The Mean-Field curve is the solution of Eq. (3). P(C) = 2/3, P(D) = 1/3, P(X; t = 0) = 1, 〈k〉 = 8, ρD = 0.586, ρC = 0.053, d = 0.345, a = 0.224, γ = 0.64, β = −0.072. Averages have been taken over 103 realizations.
Distribution of Payoffs
The only observable on which the topology does have a strong effect is the payoff distribution among players. Figure 4 shows these distributions for the three studied topologies and at two different times —short and long. Smooth at short times, this distribution peaks around certain values at long times. This reflects the fact that payoffs depend on the number of neighbors of different types around a given player, which yields a finite set of values for the payoffs (the centers of the peaks). These numbers occur with different probabilities (determining the height of the peaks), according to the distribution

where p(k) is the degree distribution of the network and k = (kC, kD, kX), but it is understood that kX = k − kC − kD. The standard convention is assumed that the multinomial coefficient  whenever kC < 0, kD < 0 or kX < 0.
whenever kC < 0, kD < 0 or kX < 0.
Payoff Distributions.
Distribution of the pay-off per neighbor in the stationary state for different network topologies: regular lattice (k = 8), Erdös Rényi (〈k〉 = 8) and Barabási-Albert network (〈k〉 = 8). Black and blue lines represent the results of numerical simulations for two values of time: t = 10 (black shallow curves) and t = 104 (blue, thick line curves) while red lines represent the theoretical estimations at t = 104, as obtained from Eq. (8). N = 104, ρD = 0.586, ρC = 0.053 and other parameters are as in Figure 1. The simulation results are averages over 103 realizations.
The approach to a stationary distribution of payoffs exhibits a much longer transient. This is due to the fluctuations in the payoffs arising from the specific actions (cooperate or defect) taken by the players. These fluctuations damp out as the accumulated payoffs approach their asymptotic values. Thus, the peak widths shrink proportionally to t−1/2. In fact, one can show that the probability density for the distribution of payoffs Π for strategy Z can be approximated as

where  , the mean payoff per neighbor received by a Z strategist against a cooperator is
, the mean payoff per neighbor received by a Z strategist against a cooperator is

with k = kC + kD + kX and the average cooperation level in the neighborhood of the focal player and its variance are

The approximate total payoff distribution, W(Π) = ρCWC(Π) + ρDWD(Π) + ρXWX(Π), is compared in Figure 4 with the results of the simulations for the longest time.
Discussion
In this work we have shown both analytically and through numerical simulations that if we take into account the way in which humans are experimentally found to behave when facing social dilemmas on lattices, no evidence of network reciprocity is obtained. In particular, we have argued that if the players of a Prisoners' Dilemma adopt an update rule that only depends on what they see from their neighborhood, then cooperation drops to a low level —albeit nonzero— irrespective of the underlying network. Moreover, we have shown that the average level of cooperation obtained from simulations is very well predicted by a mean-field model and it is found to depend only on the fractions of different strategists. Additionally, we have also shown that the underlying network of contacts does manifest itself in the distribution of payoffs obtained by the players and has a slight influence on the transient behavior.
To conclude, it is worth mentioning that our results only make sense when applied to evolutionary game models aimed at mimicking human behavior in social dilemmas. The independence on the topology seems to reflect the fact that humans update their actions according to a rule that ignores relative payoffs. Interestingly, absence of network reciprocity has also been observed in numerical simulations using best response dynamics21, an update rule widely used in economics that does not take into account the neighbors's payoffs. This suggests that the result that networks do not play any role in the repeated PD may be general for any dynamics that does not take neighbors' payoffs into account. We want to stress that the same kind of models thought of in a strict biological context are ruled by completely different mechanisms which do take into account payoff (fitness) differences. Therefore, in such contexts lattice reciprocity does play its role. In any case, our results call for further experiments that uncover what rules are actually governing the behavior of players engaged in this and other social dilemmas.
References
Szabó, G. & Fáth, G. Evolutionary games on graphs. Phys. Rep. 446, 97–216 (2007).
Roca, C. P., Cuesta, J. A. & Sánchez, A. Evolutionary game theory: Temporal and spatial effects beyond replicator dynamics. Phys. Life Rev. 6, 208–249 (2009).
Hofbauer, J. & Sigmund, K. Evolutionary Games and Population Dynamics (Cambridge University Press, Cambridge, 1998).
Gintis, H. Game Theory Evolving (2nd Ed, Princeton University Press, Princeton, 2009).
Rapoport, A. & Guyer, M. A taxonomy of 2×2 games. General Systems 11, 203–214 (1966).
Axelrod, R. The Evolution of Cooperation (Basic Books, New York, 1984).
Nowak, M. A. & May, R. M. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992).
Perc, M. & Szolnoki, A. Coevolutionary games - A mini review. BioSystems 99, 109–125 (2010).
Santos, F. C. & Pacheco, J. M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 95, 98104 (2005).
Gómez-Gardeñes, J., Campillo, M., Floría, L. M. & Moreno, Y. Dynamical organization of cooperation in complex networks. Phys. Rev. Lett. 98, 108103 (2007).
Szolnoki, A. & Perc, M. Conditional strategies and the evolution of cooperation in spatial public goods games. Phys. Rev. E 85, 026104 (2012).
Hauert, C. & Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the Snowdrift game. Nature 428, 643–646 (2004).
Sysi-Aho, M., Saramäki, J., Kertész, J. & Kaski, K. Spatial snowdrift game with myopic agents. Eur. Phys. J. B 44, 129–135 (2005).
Roca, C. P., Cuesta, J. A. & Sánchez, A. The effect of spatial structure on the emergence of cooperation. Phys. Rev. E 80, 046106 (2009).
Hofbauer, J. & Sigmund, K. Evolutionary game dynamics. Bull. Amer. Math. Soc. 40, 479–519 (2003).
Helbing, D. Interrelations between stochastic equations for systems with pair interactions. Physica A 181, 29–52 (1992).
Szabó, G. & Töke, C. Evolutionary prisoners dilemma game on a square lattice. Phys. Rev. E 58, 69–73 (1998).
Grujić, J., Fosco, C., Araujo, L., Cuesta, J. A. & Sánchez, A. Social Experiments in the Mesoscale: Humans Playing a Spatial Prisoner's Dilemma. PLoS ONE 5(11), e13749 (2010).
Fischbacher, U., Gächter, S. & Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ Lett 71, 397404 (2001).
Traulsen, A., Semmann, D., Sommerfeld, R. D., Krambeck, H. J. & Milinski, M. Human strategy updating in evolutionary games. Proc. Natl. Acad. Sci. USA 107, 29622966 (2010).
Roca, C. P., Cuesta, J. A. & A. Sánchez, A. Promotion of cooperation on networks? The myopic best response case. Eur. Phys. J. B 71, 587–595 (2009).
Acknowledgements
J. A. C. and A. S. acknowledge grants MOSAICO, PRODIEVO and Complexity-NET RESINEE (Ministerio de Ciencia e Innovación, Spain) and MODELICO-CM (Comunidad de Madrid, Spain). Y. M. was partially supported by Spanish MICINN (Ministerio de Ciencia e Innovación) projects FIS2008-01240 and FIS2009-13364-C02-01, by the FET-Open project DYNANETS (grant no. 233847) funded by the European Commission and by Comunidad de Aragón (Spain) through the project FMI22/10.
Author information
Authors and Affiliations
Contributions
C.G-L, J.A.C., A. S, & Y.M designed and performed research, analyzed the data and contributed new analytical results. All authors wrote, reviewed and approved the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Gracia-Lázaro, C., Cuesta, J., Sánchez, A. et al. Human behavior in Prisoner's Dilemma experiments suppresses network reciprocity. Sci Rep 2, 325 (2012). https://doi.org/10.1038/srep00325
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00325
This article is cited by
-
Inferring strategies from observations in long iterated Prisoner’s dilemma experiments
Scientific Reports (2022)
-
Direct reciprocity and model-predictive rationality explain network reciprocity over social ties
Scientific Reports (2019)
-
Evolutionary dynamics of N-person Hawk-Dove games
Scientific Reports (2017)
-
Reputation drives cooperative behaviour and network formation in human groups
Scientific Reports (2015)
-
Aspiration dynamics in structured population acts as if in a well-mixed one
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.