Abstract
In the present study we quantify stress by measuring transient perspiratory responses on the perinasal area through thermal imaging. These responses prove to be sympathetically driven and hence, a likely indicator of stress processes in the brain. Armed with the unobtrusive measurement methodology we developed, we were able to monitor stress responses in the context of surgical training, the quintessence of human dexterity. We show that in dexterous tasking under critical conditions, novices attempt to perform a task's step equally fast with experienced individuals. We further show that while fast behavior in experienced individuals is afforded by skill, fast behavior in novices is likely instigated by high stress levels, at the expense of accuracy. Humans avoid adjusting speed to skill and rather grow their skill to a predetermined speed level, likely defined by neurophysiological latency.
Similar content being viewed by others
Introduction
Stress (defined here as physiological arousal) is an ever-present mechanism that helps humans cope with perceived or real threats or challenges. It is suspected to play a key role in the context of task execution1. There has been a lot of work on the relationship between stress and task performance, starting with the postulation of the famous Yerkes-Dodson law in 19082. According to this ‘law’, performance increases with stress up to a point and decreases past that - a relationship that proved to be true in several experimental studies. Throughout the last century researchers struggled to investigate the role of stress on performance in as realistic conditions as possible and as objectively as possible. Both aims proved difficult to attain.
Specific experimental studies focused overwhelmingly on aviation, where the effect of stress on performance deemed paramount3. There have also been some studies on the effect of stress on surgical performance4,5,6. Both the aviator and surgeon professions are critical to society and involve dexterity. Due to the introduction of new technologies, such as laparoscopy in surgery and unmanned aerial vehicles in aviation, required skills in the two professions look increasingly similar (e.g., maintaining dexterity despite loss of proprioception). Emerging professions, such as robot tele-operators and actors controlling avatars, fall under the same skilled category.
While this convergence of skilled professions takes place, the literature on addressing issues of stress versus performance in dexterous tasks remains fragmented (per profession) and lacks appropriate methods and unifying abstractions. Indeed, common threads in many published studies are the use of subjective or snapshot stress indicators and the reliance on non-orthogonal performance measures that are often culturally defined.
Key aims of our investigation are: (a) to develop an objective stress measurement method that is unobtrusive and real-time; (b) to articulate dexterous performance abstractions that can naturally link-up with neurophysiological responses and are rid of redundancies and disciplinary bias.
We monitored stress and performance patterns among surgeons during training in an inanimate laparoscopic skills lab. The selected activity locus merely serves as a sample window through which we can observe the human behaviors of interest.
To date, galvanic skin response (GSR) sensing on the fingers has been the standard method used to peripherally quantify stress in real-time7. This method is not applicable in surgical training assessment for obvious reasons; the surgeons' fingers are engaged, a limitation that would apply to all dexterous task scenarios. To solve the problem, we developed a novel stress quantification methodology where the targeted physiological response is transient perspiration on the perinasal area - a phenomenon we have shown is associated with stress8.
This perinasal response follows the transient perspiratory response on the fingers and correlates well with it, as we demonstrate in the Results-Validation Analysis section. Hence, it can be used as an alternate measure of stress with distinct advantages. The perinasal area is much more accessible than the fingers and thermal imaging can be brought to bear to quantify perspiration unobtrusively (see Methods-Thermal Imaging sections).
We have also formulated two new performance abstractions: (a) attempt pace, which unlike the standard time measure, always relates to neurophysiological latency; (b) error propensity, which includes not only standard errors but also latent errors and remains representative of accuracy across different task architectures.
Refocusing attention from the fingers to the face and replacing probes and electronics with imaging and computation empowered a field study of stress. The collected neurophysiological data were analyzed in the context of the new performance abstractions. The results brim with intriguing leads about human nature - a testament to the method's power and promise.
Results
Macroscopic Study Variables
Surgeons belonging to two skill levels (novices and experienced) engaged in training on three laparoscopic drills (Supplement-Fig. S1):
-
Task 1: A simple, ad hoc, drill where a string is manipulated from one end to the other via its colored sections.
-
Task 2: A more challenging drill that requires the cutting of a circular pattern on a piece of gauze. It is part of the Fundamentals of Laparoscopic Surgery (FLS), a widely accepted educational module in laparoscopic surgery9.
-
Task 3: A highly complex drill that requires precise suturing on a fine rubber tube. This is also part of FLS.
Training was longitudinal, with repeat sessions spread over the course of a few months; every session included multiple trials of each task. In our analysis, we studied the relation of stress indicators to surgeon performance. The stress indicators included neurophysiological (via thermal imaging) and observational (via visual imaging) trial measurements, while the performance indicators included time and error trial measurements, reflecting the grading of the surgical educator; these eventually were supplanted by better abstractions.
Neurophysiologically, stress was tracked through the perinasal response. Specifically, in every trial i of a task j in session k for a surgeon l (x ≡ (j,k,l)), we quantified the entire perinasal perspiratory signal E(x, i) and represented it via its mean intensity  . Then, we tracked stress by computing the mean signal intensity
. Then, we tracked stress by computing the mean signal intensity  over all trials i = 1,…,I of task j in session k for surgeon l.
over all trials i = 1,…,I of task j in session k for surgeon l.
Typically, the aid of an observational variable (such as facial expressions) would be necessary to disambiguate instances of negative (distress) versus positive (eustress) excitation in a sympathetic signal, such as the perinasal. This was the motivation behind gathering visual imaging data concomitantly with thermal imaging data. As it was proved at the end (see Results-Specificity Analysis section), observational annotation of the physiological signal is not absolutely necessary in the particular context. For this reason, the observational variable was dropped from consideration in the main analysis.
Regarding performance, in every trial i of a task j in session k for a surgeon l (x ≡ (j,k,l)), we defined time as the real variable Time(x, i), which represented how long (in [s]) it took a surgeon to complete the trial. We also defined error as the binary variable Err(x, i), which was 0 if the trial was flawless and 1 otherwise. Then, we tracked performance by computing the mean time  and the mean error
and the mean error  over all trials i = 1, …, I of task j in session k for surgeon l.
over all trials i = 1, …, I of task j in session k for surgeon l.
Before each session, every surgeon completed a State Anxiety Inventory (SAI) sheet10. Scoring of SAI gave an indication of the surgeon's stress level prior to the execution of the protocol.
Main Analysis
Initially we present the marginal distribution of each response variable (stress: µE(x), time: µTime(x) and error: µErr(x)) on each surgical skill level (novices and experienced), for each task (Task 1, Task 2 and Task 3) - Table 1 and Fig. 1a-c. Furthermore, we test whether the two skill groups of surgeons have equivalent mean responses or not. This is a family of n = 14 tests, including 4 tests on stress, 7 tests on time and 3 tests on error. Hence, the significance level α = 0.05 is Bonferroni adjusted11 to αB = 0.05/14 = 0.0036. Please note that for stress we include a test in the relaxation period (baseline). Please also note that regarding time, we compare mean time scores not only between groups for each task, but also between each group and the task's proficiency mark, where this is available (i.e., Task 2 and Task 3). These tests provide nuance by indicating not only if novices perform slower than experienced surgeons, but also if they meet proficiency time, a mark presumably above their level.
(a) Distribution of mean stress responses µE(x) per skill level and task. (b) Distribution of mean time performance µTime(x) per skill level and task. The competency time lines of 98 [s] and 112 [s] for FLS Task 2 and FLS Task 3 have been placed on the respective box-plot diagrams to provide comparative yardsticks of speed. (c) Distribution of mean error performance µErr(x) per skill level and task. (d) Error histograms per skill level and task. (e) Level and Task interaction plots for stress, time and error. — We used the ln (.) and  transformations to comply with analysis of variance assumptions. The ‘*’ symbols in the box-plots indicate the mean values of the distributions. n is shown at the bottom of the corresponding box-plot.
transformations to comply with analysis of variance assumptions. The ‘*’ symbols in the box-plots indicate the mean values of the distributions. n is shown at the bottom of the corresponding box-plot.
Novice surgeons arrived at each session with stress levels significantly higher than those of experienced surgeons, based on the State Anxiety Inventory (SAI) scoring (analysis of variance, P < 0.05). This anticipatory stress in novices was somewhat diffused during the baseline period, where the perinasal indicator µE(x) showed no significant stress differences between the two skill groups (analysis of variance, P > 0.0036). During task execution, stress differences between novice and experienced surgeons, as measured by µE(x), became significant again (analysis of variance, P < 0.0036 for all three tasks - Fig. 2).
(a) Novice surgeon's (subject ID: D002) thermo-physiological (perinasal) and observational (facial) images during execution of Task 3, Session 4, Trial 1. The corresponding perspiration (stress) signal is shown in the middle. There are multiple elevations in the signal due to excitations throughout the execution of the trial. The excitations are negative (distress), as the FACS-decoding [13] of facial expressions indicates along the timeline (bottom). The subject performed multiple attempts on most subtasks and committed a 2 mm deviation error from the rubber tube's mark on Subtask 1. (b) Experienced surgeon's (subject ID: D001) thermo-physiological (perinasal) and observational (facial) images during execution of Task 3, Session 4, Trial 3. The corresponding perspiration (stress) signal is shown in the middle. The signal intensity is low and remarkably flat; there is near absence of facial expressions; the subject's performance was flawless. This pattern was typical throughout the expert cohort.
Time-wise in Task 1 and Task 2 the indicator µTime(x) showed that the novice surgeons performed as fast as the experienced surgeons (analysis of variance, P > 0.0036 for both tasks). In addition, both skill levels met the FLS proficiency time in Task 2, which has been set by the American College of Surgeons (ACS) to 98 [s] (analysis of variance, P > 0.0036 for both skill levels). Task 3 was the only task where novice surgeons maintained time performance commensurate to their skill; they completed the task significantly slower than experienced surgeons and they did not meet the FLS proficiency time, which has been set by ACS to 112 [s] (analysis of variance, P < 0.0036 for both cases).
Error-wise in Task 1 and Task 3 the indicator µErr(x) showed that the novice surgeons committed significantly more errors than experienced surgeons (analysis of variance, P < 0.0036 for both cases). In Task 2, however, this significant difference in error performance between the two skill groups eroded away (analysis of variance, P > 0.0036).
Departure from the usual time and error behavior in Task 3 and Task 2 respectively, does not stand up to deeper analysis of the task architecture. Task 1 is discrete repetition of the following subtask: grab the string at the colored section s; then, proceed grabbing the colored section s+1 and repeat until the end of the string. Task 2 is nearly continuous repetition of the following subtask: cut around the circular pattern up to a point that a substantial change in direction is needed; then, transiently adjust the cutting direction and repeat until the circular pattern is fully severed. Please note that an error in a subtask of Task 1 or Task 2 has finality (cannot be corrected) and hence, the surgeon has no choice but to proceed uninterrupted to the next repetitive step. In other words, neurophysiological latency (or response speed) tracks time performance (or task speed) in the first two tasks, because there is one to one correspondence between subtasks and attempts.
Task 3 is different because there is one to many correspondence between subtasks and attempts and hence, neurophysiological latency does not track time performance. Specifically, Task 3 consists of a sequence of six different subtasks: Subtask 1: passing the needle through the marks; Subtask 2: first (double) knot; Subtask 3: second (single) knot; Subtask 4: third (single) knot; Subtask 5: grabbing the string; Subtask 6: cutting the string. In order to proceed to Subtask s + 1 one must adequately complete Subtask s. For Subtask 1 this means that the surgeon has to pass the needle as close to the marks as possible, introducing at best a small error. For the other subtasks, it means that they have to be flawlessly completed and there is little other choice. Hence, the surgeon can engage in repeated attempts in each subtask of Task 3 until it is done right (Subtask 2–6) or until further improvement is deemed counter-productive (Subtask 1). We characterize the final attempt in each subtask as the ‘settlement’. Most of the errors in Task 3 are found in settlements in Subtask 1. Barring catastrophic failure, settlements in the other subtasks are mostly successful.
Let us denote ts(y, i) the duration (in [s]) of the attempt in which surgeon l adequately completes Subtask s during trial i of Task 3 in session k (y ≡ (k, l)). Let us also denote As(y, i) the number of attempts it takes for surgeon l to adequately complete Subtask s during trial i of Task 3 in session k. Hence, As(y, i) is a random variable taking values in the positive integer range [1, 2, 3, …]. These data constitute a geometric distribution As(y, i) ∼ Geometric(Ps(y, i)), where the parameter Ps(y, i) expresses the probability of adequately completing Subtask s. For each surgeon during a session we have I data points As(y, i) (corresponding to the I trials) for the variable As. We use the As(y, i) data points of each session to obtain an estimate of the parameter of interest Ps(y), based on Maximum Likelihood Estimation (MLE):  . Hence, the higher the value of
. Hence, the higher the value of  the better the surgeon's chance to adequately complete Subtask s with fewer attempts (Fig. 3a).
the better the surgeon's chance to adequately complete Subtask s with fewer attempts (Fig. 3a).
Task 3 decomposition analysis.
(a) Distributions of the probability  of adequately completing Subtask s for novice (Level 1) and experienced (Level 2) surgeons. The ‘*’ symbols in the box-plots indicate the mean values of the distributions. (b) Scatterplot of settlement time ts(y, i) versus number of attempts As(y, i) for Subtasks 2–4 for the novice cohort.
of adequately completing Subtask s for novice (Level 1) and experienced (Level 2) surgeons. The ‘*’ symbols in the box-plots indicate the mean values of the distributions. (b) Scatterplot of settlement time ts(y, i) versus number of attempts As(y, i) for Subtasks 2–4 for the novice cohort.
Analysis reveals that novice surgeons need significantly more attempts with respect to experienced surgeons in the difficult knotting subtasks until they perform them correctly (analysis of variance, P < 0.0125 for A2 + A3 + A4 - Table 2 and Fig. 3a). This is the reason that macroscopically novices appear slow in Task 3 and do not meet time proficiency standards.
However, novices maintain fast behavior in their action attempts at the subtask level, which is similar to their behavior in Task 1 and Task 2. This is evident from two pieces of information:
-
In Settlement at Once: In the knotting subtasks, novice and experienced surgeons do not differ significantly in settlement times that correspond to immediate successes (analysis of variance, P > 0.0125 for
 ,
, 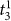 and
and 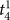 ). Please note that
). Please note that  denotes the settlement time in subtask s when the surgeon succeeds in the first attempt. We also use a Bonferroni adjusted level of significance (αB = 0.05/4 = 0.0125) to account for the 4 tests involved in the Task 3 decomposition (one for As and three for
denotes the settlement time in subtask s when the surgeon succeeds in the first attempt. We also use a Bonferroni adjusted level of significance (αB = 0.05/4 = 0.0125) to account for the 4 tests involved in the Task 3 decomposition (one for As and three for 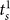 ).
). -
On an Agonizing Path to Settlement: In the knotting subtasks, there is a significant positive relationship between the number of attempts and the settlement time for novice surgeons (P < 0.05 - Fig. 3b).
Hence, when novices are lucky enough to settle at once, they are as fast as experienced surgeons. When their path is more agonizing, then their settlement represents an adjustment to slower pace.
To synopsize, time performance has been recast as an attempt pace measure rather than a task completion measure to provide a unifying abstraction across different task architectures. Error performance has been expanded to include the concept of latent errors (i.e., multiple attempts), which are not reflected in the final grade, but inform the accuracy skill of the subject. Please note that the original error performance measure µErr(x) is quite restrictive even if one excludes the possibility of latent errors in certain tasks. Due to its binary nature, it tracks apparent ‘perfection’ rather than detailed accuracy performance - a measurement philosophy that is culturally fitting to the surgical profession. For certain tasks, such as Task 1, where brief attention is needed at discrete points in time, µErr(x) tracks well detailed accuracy performance (just 4.76% of Task 1 trials have more than one errors). For other tasks, where continuous attention to accuracy is required and perfection is more difficult to attain, µErr(x) heavily undercounts errors, favoring novices. Supplement-Fig. S2 depicts how gross µErr(x) is in the case of Task 2 - a fact that explains the surprising error equivalence between the two skill groups in this task.
To investigate the role of skill versus error in the prediction of the stress differentiation between the two groups of surgeons, we ran for each task the linear regression model:

The interaction term was found insignificant and subsequently removed from Eq. (1). The simplified model showed that while the variable Level is significant (P < 0.05 for all tasks), the variable µErr(x) misses significance in all three tasks (P = 0.07 > 0.05 for Task 1, P = 0.32 > 0.05 for Task 2 and P = 0.09 > 0.05 for Task 3), mostly by a thin margin. A careful look in the error histograms of Fig. 1d reveals the reasons behind the unexpected lack of significance for µErr(x). Due to the binary nature of the error variable, the mode of the distributions is at 0 in Task 1, at 1 in Task 2 and close to 1 or at 0 in Task 3, depending on the surgeons' skill level. This bias renders the regression lines unstable and the error coefficients insignificant.
Interestingly, Fig. 1e shows the lack of interaction between level and task for stress, time and error - results that are verified by running the respective linear models. This is indication that the culturally perceived task difficulty may not be grounded to reality. Any one of the three tasks presents significant challenges to novices, while the same tasks are almost uniformly unchallenging to experienced surgeons.
Validation Analysis
The current standard in real-time measurement of peripheral sympathetic responses is GSR sensing on the fingers. The perinasal imaging method used in this study aims to become the new standard. It has two important advantages: (a) It applies on a more accessible part of the body. (b) It is contact-free and hence, has minimal imprint on stress generation. Still, it has to pass a validation check, which could be summarized as follows: “Is the perinasal imaging method equivalent to the finger GSR method?”
To provide an answer to the validation question, we conceived the following experimental design: We recruited volunteers (nV = 18, 8 males and 10 females) who underwent a controlled stress producing protocol, approved by the Institutional Review Board of the University of Houston. All subjects signed informed consent forms, including publication statements. Stress was induced using auditory startle. The experiment lasted 4 [min] per subject. After the first minute, a stimulus was delivered and after that two more were delivered, spaced about one minute apart, resulting in three events. During the experiment, the subjects focused on the simple mental task of counting circles that appeared on a monitor. This amplified their reactions to stimuli.
GSR probes were attached on the subject's left-hand index and middle fingers, a thermal imaging sensor aimed at the subject's right-hand index finger and another thermal imaging sensor aimed at the subject's perinasal area (Fig. 4a). All three measurement modalities were synchronized and recording throughout the experimental timeline. This design allows us to examine first, if the imaging method correlates with the ground-truth method (i.e., GSR) on the same part of the body (fingers). Additionally, it facilitates examination of the correlation between the perinasal and finger responses.
(a) Lab experimental setup for validation of the perinasal sympathetic measurement via thermal imaging. The insets show snapshots of the subject's thermo-physiological responses on the perinasal and index finger areas following auditory startle. The black spots in the images indicate activated perspiration pores. (b) GSR, TIMF and TIMP signals for all subjects in the validation data set.
We base our comparative analysis on a signal abstraction that is consistent with established psychophysiological views12. We reason that one can interpolate the sympathetic signal to a good approximation if s/he knows three critical points for each event: Onset (marking the start of activation), Peak and Offset (marking the end of relaxation). For the measurement methods to be in gross agreement with each other, they need to produce similar results for these three points and the trends (ascending and descending) they demarcate. Therefore, we use the time footprints of Onset, Peak and Offset and an intensity measure for the ascending and descending trends to test the relationships of GSR versus Thermal Imaging Measurement on Finger (TIMF) and GSR versus Thermal Imaging Measurement on Perinasal (TIMP).
Regarding the time axis comparisons we have 3 time points for each event, 3 events and 2 pairs of methods that we are interested to compare (GSR versus TIMF and GSR versus TIMP); this yields n = 3 × 3 × 2 = 18 tests. Therefore, the standard level of significance α = 0.05 needs to be adjusted to αB = α/n = 0.0028.
Fig. 4b depicts the signals of all three modalities for every subject in the validation data set, annotated with 3 critical points per event (Onset, Peak, Offset). Table 3 provides the P-values regarding comparisons between GSR and TIMF and between GSR and TIMP on time points critical to each event. Almost all the tests fail to reject the null hypothesis, which means that GSR reports critical event times indistinguishably from TIMF or TIMP. Table 3 also provides the r-values between GSR and TIMF and between GSR and TIMP for each critical time point across events. All r-values indicate strong linearity between methods along the event evolution pattern.
Intensity-wise, we compare the slopes of the linear ascending (Onset-Peak) and descending (Peak-Offset) trends of each event between GSR and TIMF and between GSR and TIMP. Please note that we have 2 trend slopes per event, 3 events and 2 pairs of methods; this yields n = 2 × 3 × 2 = 12 tests. Therefore, the standard level of significance α = 0.05 needs to be adjusted to αB = α/n = 0.0042.
Table 4 provides the P-values regarding comparisons between GSR and TIMF and between GSR and TIMP on trend slopes critical to each event. Almost all the tests fail to reject the null hypothesis, which means that GSR signals feature ascending and descending trends in each event that are indistinguishable from TIMF or TIMP.
To recap, GSR has a strong linear agreement with TIMF and TIMP regarding key evolution times of sympathetic events that define the activation, peak and relaxation stages. GSR also has trend agreement with TIMF and TIMP regarding the rate of change during the activation and relaxation stages of sympathetic events.
Specificity Analysis
As a sympathetic response, the perinasal response is non-specific to negative or positive excitation. One would expect then, the overall intensity of the perinasal perspiratory signal to be agnostic to the precise levels of distress versus eustress. To investigate this issue, we thought to use in parallel visual observation of facial expressions to annotate the onset of distress versus eustress bouts in the perinasal signal.
The visual imagery has been processed frame by frame by a certified expert in Facial Action Coding (FACS)13. To avoid bias, the FACS coder was not aware of the corresponding perinasal signals. The type and the duration of every facial expression was recorded on the timeline. Furthermore, facial expressions were broadly classified in three categories: positive, neutral and negative. The positive expressions indicated positive excitation (eustress), while the negative expressions negative excitation (distress).
Observational annotation of the neurophysiological response resulted in a more detailed level of stress analysis. Specifically, we quantified just the portions of the perinasal perspiratory signal where the surgeon showed facial expressions manifesting negative feelings (distress); let us denote this negative affect signal as EN (x,i) (with mean  ) and its extent (percent of total frames in the trial) as N(x,i). In this case, we tracked stress by computing the mean signal intensity
) and its extent (percent of total frames in the trial) as N(x,i). In this case, we tracked stress by computing the mean signal intensity  over all trials i = 1,…,I of task j in session k for surgeon l. We also computed the mean extent
over all trials i = 1,…,I of task j in session k for surgeon l. We also computed the mean extent  of the negative affect signal portions. Therefore, at this level of analysis distress changes were evident not only via the changes of
of the negative affect signal portions. Therefore, at this level of analysis distress changes were evident not only via the changes of  , but also via the changes of µN(x).
, but also via the changes of µN(x).
At the same time, we tracked positive excitation by quantifying the portions of the perinasal perspiratory signal where the surgeon had facial expressions manifesting positive feelings (eustress); let us denote this positive affect signal as EP(x, i) (with mean  ) and its extent (percent of total frames in the trial) as P(x,i). These positive affect signal portions were characterized by mean intensity
) and its extent (percent of total frames in the trial) as P(x,i). These positive affect signal portions were characterized by mean intensity  as well as mean extent µP (x), similarly to the negative affect signal portions. Therefore, eustress changes were evident either via the changes of
as well as mean extent µP (x), similarly to the negative affect signal portions. Therefore, eustress changes were evident either via the changes of  or µP (x).
or µP (x).
We compared this more detailed level of analysis, where physiological measurements are guided by visual observations, with the simpler, unguided physiological analysis we adopted in the main analysis. We found that both analysis styles lead to the same conclusions. To make the case, we cite an example that is related to a fundamental issue in this study: The effect of the surgeons' levels of experience on stress.
Specifically, we found that not only the unguided stress indicator E, but also the guided stress indicators EN and N pinpoint that stress levels are negatively related to experience (analysis of variance, P < 0.05 - Supplement-Fig. S3).
For this reason, after making here the case of virtual equivalence between the overall perinasal signal E(x,i) and its negative affect portion EN(x,i), we used only E(x,i) in the main distress analysis described in the Results - Main Analysis section of the article; we also prefer to use the term stress instead of distress.
Discussion
There is no rational unifying reason for novice surgeons to favor speed over accuracy. The scoring system weighs time of performance and accuracy equally, so one would expect that surgeons would be equally attentive to both performance measures. Although surgeons were informed about the FLS proficiency times for Task 2 and Task 3, they could not check time progress during tasking. Hence, in the absence of feedback it would be difficult to consistently guess the proficiency time and uniformly meet it in trial after trial (which is what happened in Task 2, where time performance tracks latency). Furthermore, there is the case of the ad-hoc Task 1, where no widely accepted proficiency time exists. There, both novice and experienced surgeons also converged to a specific time performance, in trial after trial - a point that suggests that time responses are viscerally spawned.
We theorize that a good way to apriori determine proficiency times in newly constructed dexterous tasks is by measuring latencies. In FLS, surgical educators determine proficiency times by averaging the time performance of many experienced laparoscopic surgeons. The lack of clear abstraction between time performance and latency obscures the fact that in tasks such as Task 2, these are one and the same, irrespectively of the skill level. In tasks such as Task 3, time performance aligns with latency only in the experienced cohort, who are perfect. In any case, humans appear to grow their dexterous skill to fit a mean latency level, specific to the challenge. Hence, wherever time performance does not align with latency from the start, it is the limit to which it eventually converges.
We hypothesize that the high stress levels in novice surgeons is the hidden driver of their viscerally fast behavior, which further undermines their error performance. We have two pieces of circumstantial evidence in support of this hypothesis. First, by detangling time corresponding to attempt pace from time lost in error recovery, we get a temporal measure that is close to neurophysiological latency and can be reasonably associated with arousal levels. Second, the novice's fast attempt pace clearly gets them into trouble in critical subtasks of Task 3, where they waste a lot of attempts until they get it right. Eventually they get it right only when they slow down.
To definitely prove this hypothesis one would need to perform an interventional study, where the controls will be novice surgeons following the standard training protocol, while the interventional group will be novice surgeons whom the training session stress is ameliorated via some method. Per the hypothesis, novices in the interventional group with substantially reduced stress levels would be expected to exhibit slower task attempt pace, which is more appropriate to their skill level. This reduction in speed would likely lead to reduction in errors and propensity for errors, bootstrapping confidence early on.
In the current data set all novice surgeons have relatively high stress levels and all experienced surgeons nearly identical low stress levels. Hence, it is difficult to see any direct associations of stress with performance indices within these groups.
Please note that there was no significant improvement in accuracy for the novice cohort at the end of the five session training sequence (analysis of variance, P > 0.05) - an indication that current training practices are slow in producing results. Further investigation of the hypothesis put forward in this study may lead to changes in prevailing training philosophies and practices with significant benefits.
We admit that the number of subjects in this study is relatively small (n = 17) and the null should be viewed with some caution. However, a number of ameliorating factors offer some protection: (a) This was a longitudinal rather than one shot experiment. (b) The subjects belonged to a relatively homogenized cohort of people. (c) We tested against Bonferroni corrected significance levels to further guard against Type II errors.
The outcome of this study was made possible by the introduction of a new methodology capable of unobtrusively quantifying human neurophysiological responses in natural settings and the articulation of performance measures that are orthogonal and universal. If the result of the current effort is any guide, the method and the performance abstractions are not only valuable tools for scientific discovery, but they can also be used in practice to assist in the design of dexterous training modules.
Methods
Subjects
Grouping was consistent with the standard categorization of surgical skill level14. Specifically, nTotal = 17 surgeons randomly volunteered from: (1) a pool of novices (nN = 7 ∶ 5 male/2 female) comprised of surgical residents or technicians with no surgical practice record and limited training in laparoscopic surgical skills; (2) a pool of experienced surgeons (nE = 10 ∶ 7 male/3 female) with extensive surgical practice record and at least some experience with the tested laparoscopic surgical skills.
The surgeons were controlled (analysis of variance, P > 0.05) for general psychological traits such as, anxiety10, positive affect15 and shyness16 that could bias the experimental results. All surgeons were recruited from the Methodist Hospital. All training took place in the inanimate laparoscopic skills lab of the Methodist Institute for Technology, Innovation and Education (MITIESM) in Houston, Texas. The Institutional Review Boards of the University of Houston and the Methodist Hospital approved the study and all subjects signed informed consent forms, including publication statements.
Experimental Design
The surgeons trained on three laparoscopic drills that were chosen to cover the full spectrum of difficulty according to conventional wisdom: A running string (Task 1), a pattern cut (Task 2) and an intracorporeal suture (Task 3) drill14. A supervising surgical educator scored surgeons in every trial of each task in terms of time performance and errors committed. In fact, scoring put equal emphasis on speed of execution and accuracy17.
The first task (running string) mimics the process of examination of the small intestine during laparoscopic surgery and is a simple ad-hoc drill. The surgeon uses two grasping instruments to manipulate a 1.40 m string from one end to the other, grasping the string only at colored sections marked at 12 cm intervals (Supplement-Fig. S1). The exercise is timed and errors are noted if the surgeon grasps the string outside the marked areas or drops it.
The second task (pattern cut) requires the surgeon to cut out a circle from a square piece of gauze suspended between clips (Supplement-Fig. S1). Timing starts when the gauze is grasped and ends upon completion of cutting the marked circle. A penalty is assessed for any deviation from the line demarcating the circle. There are two layers of gauze, but the error scoring is based on the marked, top layer only. This drill is part of FLS with a well-established proficiency time.
The third task (intracorporeal suture) requires the surgeon to place a suture precisely through two marks on a fine rubber tube that has been opened along its long axis (Supplement-Fig. S1). The surgeon then ties a knot using laparoscopic instruments in a box simulating the abdominal cavity. The surgeon must place three throws that include one double throw backed by two single throws in a manner that results in a square knot. A penalty is assessed for any deviation of needle placement through the marks, or for a loosely tied or insecure knot. A penalty is also assessed if a needle is dropped or if the suturing target is avulsed from the block to which it is secured by Velcro™. Timing begins when the instruments are visible on the monitor and ends when the suture material is cut. Intracorporeal suturing and knot tying is widely perceived by surgeons to be the most complex task incorporating several skills including depth perception, eye-hand coordination, ambidexterity and transferring skills. This drill is also part of FLS with a well-established proficiency time.
During the training trials the surgeons were facially imaged with a thermal and visual camera that were synchronized. The thermal imaging system included a mid-wave infrared (MWIR) camera from FLIR (model SC6000). The camera features an indium antimonite (InSb) detector operating in the range 3 – 5 µm and has a focal plane array (FPA) with maximum resolution of 640 × 512 pixels. The sensitivity is 0.025°C. The camera was outfitted with a MWIR 100 mm lens f/2.3, Si:Ge, bayonet mount from FLIR. It was calibrated with a two-point calibration at 26°C and 34°C, which are the end points of a typical thermal distribution on a human face. Thermal data has been collected at a constant frame rate of 25 fps.
The visual imaging system included a FireWire CCD monochrome zoom camera from Imaging Source with spatial resolution 1024 × 768 pixels. Visual data has been collected at a constant frame rate of 15 fps. The visual camera was mounted on top of the thermal camera to facilitate spatial co-registration (Supplement-Fig. S1). The camera system was placed at a distance of approximately 8 ft from the subject. This distance in combination with the camera optics ensured that a typical face covered a significant portion of each frame, providing maximum spatial resolution for image analysis.
This was a longitudinal study in which nTotal = 17 surgeons went through Tsession = 5 training sessions; in each training session they had Ttrial = 5 trials of Ttask = 3 tasks and each session was preceded by a baseline period, where surgeons were relaxing viewing natural landscapes. Every effort was made for the sessions to take place every two weeks, but this was not always possible due to the busy schedule of the surgeons.
Based on the protocol, the total number of thermal Cthermal and visual Cvisual clips should have been: Cthermal = Cvisual = nTotal × Tsession × (Ttrial × Ttask + 1) = 1360. However, only Cthermal = Cvisual = 977 clips have been collected and used in the statistical analysis. The missing clips either were never collected, because a couple of surgeons missed a session due to transfer to another institution, or were corrupted due to technical problems, such as disk drive malfunctioning. The missing data is a small portion of the total data set and within the range of expected loss in a realistic longitudinal study. Given their random distribution, they do not affect the statistical validity of the results.
Thermal Imaging - Tissue Tracking
Algorithmic processing of the thermal imagery yielded a signal that quantified perinasal perspiration. The algorithm included a virtual tissue tracker that kept track of the region of interest, despite the subject's small motions. This ensured that the physiological signal extractor operated on consistent and valid sets of data over the clip's timeline.
We used the tissue tracker we reported in Zhou et al.18. It is capable of handling various head poses, partial occlusions and thermal variations. On the initial frame, the user initiates the tracking algorithm by selecting the upper orbicularis oris portion of the perinasal region. The tracker estimates the best matching block in every next frame of the thermal clip via spatio-temporal smoothing (Supplement-Fig. S4a). A morphology-based algorithm is applied on the evolving region of interest to compute the perspiration signal. The signal may contain high frequency noise due to imperfections in the tracking algorithm and the effect of breathing. We use a Fast Fourier Transformation (FFT) based noise-cleaning algorithm to suppress such noise.
Thermal Imaging - Signal Extraction
A pivotal method of this study is the extraction of the perinasal perspiration signal from the thermal imagery; this is the primary indicator of stress used. Supplement-Fig. S4b1-b2 shows the thermal signature of perspiration spots on the perinasal area of a subject in a moment of excitation. In facial thermal imagery, activated perspiration pores appear as small ‘cold’ (dark) spots, amidst substantial background clutter. The latter is the thermo-physiological manifestation of the metabolic processes in the surrounding tissue. The morphological method of choice for bringing up dark (‘cold’) objects in an image is the black top-hat transformation19. However, because of the small target size and the background fuzziness, the standard black top-hat transformation does not work very well in our application. It yields inefficient background elimination and poor localization of the perspiration spots. The culprit is the structuring element; its filled nature proves to be too gross of a sculpting tool for the delicate job needed here. We opt instead to use a contour structuring element, which reportedly is a better choice for applications such as ours20.
Let f and S represent the thermal image of the perinasal region and the planar structuring element respectively. Let also ∂S be the contour of S following the connectivity of S. Then, the contour-based black top hat transformation is defined as:

where OB(f) = max{f,OCB(f)}; OCB(f) denotes contour-based opening, which is defined as:

where  denotes an erosion, while
denotes an erosion, while  a dilation operation19.
a dilation operation19.
The resultant region f ′ = BTHCB(f ) brings to the fore the cold spots (perspiration activity) - see Supplement-Fig. S4b3.
The contour-based black top-hat transformation is applied to every frame in the thermal clip to capture the evolution of the perspiration spots. This is used to compute the instantaneous energy in the perinasal region as follows:

where tz is the time at which the frame z is captured and Nc(tz) is the number of detected cold spots at that time.
Regarding the relevance of the computation, the tracker ensures that f remains in the perinasal region of interest, but cannot eliminate motion - it simply tracks it. Hence, shift and rotation invariance of E(f ′(tz)) is very important as the projection of the face on the 2D-camera plane always shifts and rotates due to motion of the head. Thankfully, due to the isotropic nature of the structuring element we use, E(f ′(tz)) is both shift and rotation invariant. For a detailed discussion on invariant properties of morphological operators, the interested reader is referred to21.
The evolution of E(f ′(tz)) produces an energy signal E(x, i), which is indicative of perspiration activity in the perinasal area for trial i of task j in session k for surgeon l (x ≡ (j, k, l)); for this reason we call it perinasal perspiration signal.
Please note that breathing has a periodic effect on the perinasal signal that cancels out over time windows longer than the breathing period. This periodic breathing effect is evident in the perinasal signals depicted in Fig. 2. The low-pass filtered versions of the original signals (depicted as blue curves in the figure) are rid of the breathing effect, which for all practical purposes can be treated as high frequency noise.
References
Lazarus, R., Deese, J. & Osler, S. The effects of psychological stress upon performance. Psychological Bulletin 49, 293–317 (1952).
Yerkes, R. & Dodson, J. The relation of strength of stimulus to rapidity of habit-formation. Journal of Comparative Neurology and Psychology 18, 459–482 (1908).
Morphew, M. The future of human performance and stress research: A new challenge. In Hancock, P. & Desmond, P. (eds.) Stress,Workload and Fatigue, 249–262 (Lawrence Erlbaum Associates, 2001).
Arora, S. et al. The impact of stress on surgical performance: A systematic review of the literature. Surgery 147, 318–330 (2010).
Arora, S. et al. Stress impairs psychomotor performance in novice laparoscopic surgeons. Surgical Endoscopy 24, 2588–2593 (2010).
Hassan, I. et al. Negative stress-coping strategies among novices in surgery correlate with poor virtual laparoscopic performance. British Journal of Surgery 93, 1554–1559 (2006).
Uncini, A., Pullman, S., Lovelace, R. & Gambi, D. The sympathetic skin response: Normal values, elucidation of efferent components and application limits. Journal of the Neurological Sciences 87, 299–306 (1988).
Shastri, D., Merla, A., Tsiamyrtzis, P. & Pavlidis, I. Imaging facial signs of neurophysiological responses. IEEE Transactions on Biomedical Engineering 56, 477–484 (2009).
Soper, N. & Fried, G. Fundamentals of laparoscopic surgery: Its time has come. Bulletin of the American College of Surgeons 93, 30–32 (2008).
Spielberger, C., Gorsuch, R. & Edward, R. Manual for the State-Trait Anxiety Inventory (Consulting Psychologists Press, 1970).
Abdi, H. Bonferroni and Sidak comparisons for multiple comparisons. Salkind, N. (ed.) Encyclopedia of Mesaurement and Statistics (Sage, 2007).
Suhodev, V. Estimation of the person psychophysiological status activation components on galvanic skin response. Psychological Journal 18, 305–328 (1997).
Ekman, P. & Rosenberg, E. What the Face Reveals: Basic and Applied Studies of Spontaneous Expression (Oxford University Press, 2005).
Tsuda, S., Scott, D., Doyle, J. & Jones, D. Surgical skills training and simulation. Current Problems in Surgery 46, 261–371 (2009).
Watson, D., Clark, L. & Tellegen, A. Development and validation of brief measures of positive and negative affect: The panas scales. Journal of Personality and Social Psychology 54, 1063–1070 (1988).
Bortnik, K., Henderson, L. & Zimbardo, P. The shy q, a measure of chronic shyness: Associations with interpersonal motives, interpersonal values and self-conceptualizations. In: 36th Annual Conference of the Association for the Advancement of Behavior Therapy (2002).
Fraser, S. et al. Evaluating laparoscopic skills. Surgical Endoscopy 17, 964–967 (2003).
Zhou, Y., Tsiamyrtzis, P. & Pavlidis, I. Tissue tracking in thermo-physiological imagery through spatio-temporal smoothing. In: Medical Image Computing and Computer Assisted Intervention - MICCAI 2009, vol. 5762 of Lecture Notes in Computer Science, 1092–1099 (2009).
Soille, P. Morphological Image Analysis: Principles and Applications (Springer, 2003).
Bai, X. & Zhou, F. Analysis of new top-hat transformation and the application for infrared dim small target detection. Pattern Recognition 43, 2145–2156 (2010).
Hendriks, C. & van Vliet, L. A rotation-invariant morphology for shape analysis of anisotropic objects and structures. Arcelli, C., Cordella, L. & di Baja, G. (eds.) Visual Form 2001, vol. 2059 of Lecture Notes in Computer Science, 378–387 (Springer Berlin/Heidelberg, 2001).
Acknowledgements
This material is based upon work supported by the National Science Foundation award IIS-0812526 entitled ‘Do Nintendo Surgeons Defy Stress?’ It was also supported in part by a grant from the Methodist Hospital entitled ‘Co-Design and Testing of Stress Quantification Experiments.’ Any opinions, findings and conclusions or recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the funding agency. We are grateful to Prof. Robert Sapolsky and Prof. Raimond Winslow for thoughtful reviews and feedback in early versions of this manuscript. We also acknowledge the help of Dr. Thirimachos Bourlai in the initial phase of the experimentation. Last but not least, we are indebted to Prof. Anthony Wagner and the anonymous reviewers for their constructive comments and suggestions.
Author information
Authors and Affiliations
Contributions
I.P. and B.B. designed research and wrote manuscript; P.T. and A.W. analyzed data; D.S. and Y.Z. developed methods; P.L., R.J. and B.D. performed experiments; P.B. developed software; A.M. processed data.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Info
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Pavlidis, I., Tsiamyrtzis, P., Shastri, D. et al. Fast by Nature - How Stress Patterns Define Human Experience and Performance in Dexterous Tasks. Sci Rep 2, 305 (2012). https://doi.org/10.1038/srep00305
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00305
This article is cited by
-
Video-based training of situation awareness enhances minimally invasive surgical performance: a randomized controlled trial
Surgical Endoscopy (2023)
-
Facial functional networks during resting state revealed by thermal infrared imaging
Physical and Engineering Sciences in Medicine (2023)
-
Stress in surgical educational environments: a systematic review
BMC Medical Education (2022)
-
Facilitating the Child–Robot Interaction by Endowing the Robot with the Capability of Understanding the Child Engagement: The Case of Mio Amico Robot
International Journal of Social Robotics (2021)
-
Functional Infrared Thermal Imaging: A Contemporary Tool in Soft Tissue Screening
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.







 ,
, 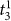 and
and 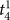 ). Please note that
). Please note that  denotes the settlement time in subtask s when the surgeon succeeds in the first attempt. We also use a Bonferroni adjusted level of significance (αB = 0.05/4 = 0.0125) to account for the 4 tests involved in the Task 3 decomposition (one for As and three for
denotes the settlement time in subtask s when the surgeon succeeds in the first attempt. We also use a Bonferroni adjusted level of significance (αB = 0.05/4 = 0.0125) to account for the 4 tests involved in the Task 3 decomposition (one for As and three for 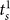 ).
). 