Abstract
The fundamental noise limit of a phase-preserving amplifier at frequency  is the standard quantum limit
is the standard quantum limit  . In the microwave range, the best candidates have been amplifiers based on superconducting quantum interference devices (reaching the noise temperature
. In the microwave range, the best candidates have been amplifiers based on superconducting quantum interference devices (reaching the noise temperature  at 700 MHz) and non-degenerate parametric amplifiers (reaching noise levels close to the quantum limit
at 700 MHz) and non-degenerate parametric amplifiers (reaching noise levels close to the quantum limit  at 8 GHz). We introduce a new type of an amplifier based on the negative resistance of a selectively damped Josephson junction. Noise performance of our amplifier is limited by mixing of quantum noise from Josephson oscillation regime down to the signal frequency. Measurements yield nearly quantum-limited operation,
at 8 GHz). We introduce a new type of an amplifier based on the negative resistance of a selectively damped Josephson junction. Noise performance of our amplifier is limited by mixing of quantum noise from Josephson oscillation regime down to the signal frequency. Measurements yield nearly quantum-limited operation,  at 2.8 GHz, owing to self-organization of the working point. Simulations describe the characteristics of our device well and indicate potential for wide bandwidth operation.
at 2.8 GHz, owing to self-organization of the working point. Simulations describe the characteristics of our device well and indicate potential for wide bandwidth operation.
Similar content being viewed by others
Introduction
The goal of quantum limited amplification at microwave frequencies has become increasingly important for superconducting qubits and nanoelectromechanical systems1. The lowest noise temperatures with respect to the quantum noise have been achieved using nondegenerate parametric amplifiers based on superconducting quantum interference devices (SQUIDs)2,3,4. They yield a noise temperature Tn of about  . Other implementations of near-quantum limited amplification have been realized by means of Josephson ring oscillators5, DC-SQUIDs6,7 and parametric amplifiers based on Josephson junction arrays2,8,9,10,11. Devices based on photon-assisted tunneling SIS-mixers yield
. Other implementations of near-quantum limited amplification have been realized by means of Josephson ring oscillators5, DC-SQUIDs6,7 and parametric amplifiers based on Josephson junction arrays2,8,9,10,11. Devices based on photon-assisted tunneling SIS-mixers yield  12. However, these devices lack power gain but they do have a large gain in photon number due to conversion from high to low frequency.
12. However, these devices lack power gain but they do have a large gain in photon number due to conversion from high to low frequency.
Negative differential resistance devices, in particular tunnel diodes, have been used in the past to construct oscillators and amplifiers for microwave frequencies. These devices are capable of very fast operation. They were among the first ones to be used at microwave frequencies because they display little or no excess noise in the negative resistance bias region13. Here, we propose a negative-resistance amplifier based on an unshunted, single Josephson junction (JJ) operating in a noise compression mode. Unshunted junctions have been analyzed and demonstrated to work in SQUID circuits at low frequencies by Seppä et al.14. We have developed analogous concepts for high frequency operation. The present device differs markedly from previous implementations using unshunted Josephson devices due to the modified impedance environment.
Unshunted junctions are attractive as low-noise devices since they minimize fluctuations by avoiding unnecessary dissipation in the junction environment. In voltage-biased (Vb) operation, these devices can be considered as mixers between the signal frequency (ωs around a few GHz) and the Josephson frequency ( ) including sidebands15. A frequency-dependent environmental impedance can be employed for controlling mixing strengths (because the Josephson junction is a phase driven current generator) and the impedance makes the conversion between these two quantities.
) including sidebands15. A frequency-dependent environmental impedance can be employed for controlling mixing strengths (because the Josephson junction is a phase driven current generator) and the impedance makes the conversion between these two quantities.
Results
The fundamental macroscopic principle of our single junction amplifier (SJA) is that the intrinsic resistance of a JJ is negative over time scales much longer than  14 (as shown in Fig. 1a). This is usually hidden in weakly damped JJs since the negative-resistance branch is unstable. On the other hand, for strongly damped junctions, the total dynamic resistance is positive. This can be seen from the current-voltage IV characteristics
14 (as shown in Fig. 1a). This is usually hidden in weakly damped JJs since the negative-resistance branch is unstable. On the other hand, for strongly damped junctions, the total dynamic resistance is positive. This can be seen from the current-voltage IV characteristics  for a Josephson junction with negligible capacitance (valid for
for a Josephson junction with negligible capacitance (valid for  ). Here
). Here  denotes the voltage scaled with critical current Ic and the shunt resistance R while
denotes the voltage scaled with critical current Ic and the shunt resistance R while  is the dimensionless current. Solving for the current through the junction alone,
is the dimensionless current. Solving for the current through the junction alone,  (illustrated by the black curve in Fig. 1a), we get for the scaled dynamic resistance
(illustrated by the black curve in Fig. 1a), we get for the scaled dynamic resistance

This yields  , negative at all bias points.
, negative at all bias points.
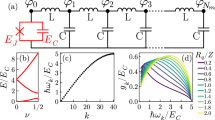
a) Typical IV of a SJA (in blue); red and black curves indicate the division of I into shunt and junction currents, respectively.b) Reflection (scattering) amplitude S11 in a Z0 = 50 Ω system as a function of the load impedance. c) Principal scheme of the SJA operation. d) Optical image of a SJA; the size of the image is approximately 270 µm × 230 µm.
The schematics of our SJA configuration is illustrated in Fig. 1c. To utilise the negative resistance of a JJ for amplification, stable operation has to be maintained by sufficient damping at all frequencies. The frequency-dependent damping is set in such a way that the external shunt damps the low ( , the signal frequency) and high (
, the signal frequency) and high ( ) frequency dynamics, which ensures both stable DC bias and overdamped Josephson dynamics. In practice, we have realised this separation by mounting the shunt resistor in series with a bandstop filter whose center frequency is at the signal frequency ωs16,17. The shunt capacitor is chosen large enough that it acts as a short at the Josephson frequency to ensure the high frequency dynamics and the IV curve are not modified. The stabilization in the stop band is provided by the postamplification circuit. The shunt circuit and the postamplification circuit together guarantee the stability of the device by generating a wide-band resistive environment for the JJ. Operated as a reflection amplifier, the power gain
) frequency dynamics, which ensures both stable DC bias and overdamped Josephson dynamics. In practice, we have realised this separation by mounting the shunt resistor in series with a bandstop filter whose center frequency is at the signal frequency ωs16,17. The shunt capacitor is chosen large enough that it acts as a short at the Josephson frequency to ensure the high frequency dynamics and the IV curve are not modified. The stabilization in the stop band is provided by the postamplification circuit. The shunt circuit and the postamplification circuit together guarantee the stability of the device by generating a wide-band resistive environment for the JJ. Operated as a reflection amplifier, the power gain  is determined by the reflection coefficient
is determined by the reflection coefficient

where  is the impedance of the JJ, the shunt and the series inductance; Z0 is the impedance of the readout circuit. As seen from the curve in Fig. 1b, there is gain (
is the impedance of the JJ, the shunt and the series inductance; Z0 is the impedance of the readout circuit. As seen from the curve in Fig. 1b, there is gain ( ) at all values of negative resistance and a strong divergence around
) at all values of negative resistance and a strong divergence around  . In the stopband of the shunt circuit, the input impedance
. In the stopband of the shunt circuit, the input impedance  consists of the JJ (and possibly of an LC impedance transformer): it is real and negative. For
consists of the JJ (and possibly of an LC impedance transformer): it is real and negative. For  , large gain with stable operation can be obtained. For operating conditions where
, large gain with stable operation can be obtained. For operating conditions where  impedance transforming circuits are employed to change the reference level impedance Z0, e.g. from 50 Ω typical for standard RF technology to a level of 1 kΩ which is a typical value of
impedance transforming circuits are employed to change the reference level impedance Z0, e.g. from 50 Ω typical for standard RF technology to a level of 1 kΩ which is a typical value of  for small Josephson junctions at high bias voltages.
for small Josephson junctions at high bias voltages.
The dynamics of SQUID circuits can be analyzed using a Langevin type of differential equation for the phase variable ϕ across the Josephson junctions18. Good agreement of such Langevin analysis with measured experimental results has been obtained in the past19,20. In the semiclassical approach, the generalized Nyquist noise formula by Callen and Welton21 with the frequency dependence  is employed as the colored noise source in the differential equation19,22,23. At the Josephson frequency, the semiclassical noise power per unit bandwidth is so large (
is employed as the colored noise source in the differential equation19,22,23. At the Josephson frequency, the semiclassical noise power per unit bandwidth is so large ( ) that, after downmixing, it will have observable effects on the phase dynamics at the signal frequency ωs. Since the noise at ωs is cut off from the Josephson junction by the bandstop filter (see Fig. 1c), direct noise from the shunt is avoided and only the down-mixed noise is present in our device. The absence of direct noise ensures good noise characteristics for our SJA and this feature is one of the basic differences when comparing SJAs with traditional microwave SQUID amplifiers.
) that, after downmixing, it will have observable effects on the phase dynamics at the signal frequency ωs. Since the noise at ωs is cut off from the Josephson junction by the bandstop filter (see Fig. 1c), direct noise from the shunt is avoided and only the down-mixed noise is present in our device. The absence of direct noise ensures good noise characteristics for our SJA and this feature is one of the basic differences when comparing SJAs with traditional microwave SQUID amplifiers.
Experimental
Fig. 2 displays noise spectra measured on the device at different bias points. At low bias currents, the magnitude of the dynamic resistance  is smaller than the environmental impedance in parallel to it, making the total damping impedance of the LC resonator in the shunt circuit negative. This leads to either spontaneous oscillations or saturation. The oscillations are highly nonlinear, which is manifested as higher harmonics in the spectra. The saturation shows up as vanishing response. As
is smaller than the environmental impedance in parallel to it, making the total damping impedance of the LC resonator in the shunt circuit negative. This leads to either spontaneous oscillations or saturation. The oscillations are highly nonlinear, which is manifested as higher harmonics in the spectra. The saturation shows up as vanishing response. As  increases at higher bias points, the system is stabilized and the harmonics disappear since the device operates as a linear amplifier generating amplified noise at the output.
increases at higher bias points, the system is stabilized and the harmonics disappear since the device operates as a linear amplifier generating amplified noise at the output.
Noise spectra of the device as function of the bias point; the reference level corresponds to 14 K k B and the power scale on the right is given in dB.
The inset displays the dependence of rd as a function of bias voltage for different values of βC. Values between 0 and  lead to unstable behaviour;
lead to unstable behaviour;  without impedance transformer (R = 1 Ω). There are no special features in the noise spectral density in the area below the inset.
without impedance transformer (R = 1 Ω). There are no special features in the noise spectral density in the area below the inset.
After finding the optimal stable bias point, the gain vs. frequency was recorded at several power levels. The maximum measured gain of the SJA was found to be 28.3 ± 0.2 dB. The measured power gain of the device is plotted in Fig. 3 at Pin = −160 dBm. The −1 dB compression point for Pin was found to be around −134 dBm; this yields a dynamic range of 70 dB as the input noise corresponds to −204 dBm. For the −3 dB bandwidth, we obtain  . However, the bandwidth depends very much on the bias voltage due to the variation of Rd along the IV-curve, indicating that fundamentally the device is capable of wideband gain. In the present experiments, we reached
. However, the bandwidth depends very much on the bias voltage due to the variation of Rd along the IV-curve, indicating that fundamentally the device is capable of wideband gain. In the present experiments, we reached  for the voltage gain - bandwidth product. The nominal parameters of the measured amplifier are given in Table I in the Methods section.
for the voltage gain - bandwidth product. The nominal parameters of the measured amplifier are given in Table I in the Methods section.
Gain of the SJA as function of frequency at the optimal point of operation (blue, noisy curve).
Results from our numerical simulation are denoted by open circles, while the smooth curve (green) illustrates the gain from a linearized electrical circuit model where the Josephson junction is replaced by a negative resistance of Rd = −1370 Ω from Eq. (1). Inset: Output noise spectra having the SJA off (lower trace) and on (at maximum gain).
The inset in Fig. 3 displays the improvement of the signal to noise ratio when the SJA is switched on and operated at its maximum gain. Based on this improvement, we find that the input-referred noise power added by the amplifier is  originating from the source has been subtracted), which corresponds to
originating from the source has been subtracted), which corresponds to  . The best noise temperature was obtained at the largest gain of the SJA.
. The best noise temperature was obtained at the largest gain of the SJA.
Theoretical
To theoretically model a single junction device with arbitrary, frequency-dependent environment with  , we simulate numerically the electrical circuit on the basis of the DC and AC Josephson relations which define a nonlinear circuit element having the properties:
, we simulate numerically the electrical circuit on the basis of the DC and AC Josephson relations which define a nonlinear circuit element having the properties:  and
and  . We have compared our numerical simulations with analytic methods using an approximate model where we have adapted the resistively and capacitively shunted junction (RCSJ) approach to the modified environmental impedance of the SJA. Our numerical and analytic models take into account the Callen and Welton quantum noise from the environment semiclassically. Down-conversion of the noise at ωJ is the main quantity to be minimized for optimum performance.
. We have compared our numerical simulations with analytic methods using an approximate model where we have adapted the resistively and capacitively shunted junction (RCSJ) approach to the modified environmental impedance of the SJA. Our numerical and analytic models take into account the Callen and Welton quantum noise from the environment semiclassically. Down-conversion of the noise at ωJ is the main quantity to be minimized for optimum performance.
The simulated power gain is included in Fig. 3 together with the experimental data. The theoretical gain curve is seen to follow the experimental behavior closely and it yields 42 MHz for the gain-bandwidth product. The simulated maximum gain amounts to 28.9 ± 0.5 dB. All these findings are in excellent agreement with the experimental data. Basically, the shape of the gain curve indicates that the amplification mechanism is based on mixing between ωs and the sidebands of ωJ. This occurs along with the conversion from down-mixed currents at ωs to voltage by the shunt impedance (see the Supplementary material). For comparison, we have also calculated a linearized response curve where the Josephson junction has been replaced by a negative resistance of Rd = −1370 Ω from Eq. (1).
Our numerical simulations yield Tn = 270 ± 30 mK which is close to the experimentally found Tn = 220 ± 70 mK. Hot-electron effects were taken into account by using the model of Ref. 24, on the basis of which we estimated the electronic temperature in the shunt to be  instead of the base temperature 70 mK. The noise temperature is not very sensitive to hot electron effects when the shunt is fully blocked by the LC resonator at the center frequency. However, when going away from the center frequency, direct noise may leak out from the shunt reducing the useful band to “a noise-temperature-limited” range. The simulated noise power spectrum and the corresponding Tn as a function of frequency are presented in Fig. 4.
instead of the base temperature 70 mK. The noise temperature is not very sensitive to hot electron effects when the shunt is fully blocked by the LC resonator at the center frequency. However, when going away from the center frequency, direct noise may leak out from the shunt reducing the useful band to “a noise-temperature-limited” range. The simulated noise power spectrum and the corresponding Tn as a function of frequency are presented in Fig. 4.
The effective output noise temperature
 (left scale) is compressed in the simulation (denoted by solid blue line) when compared with the product of the simulated gain (
G
– 1) and the uncompressed down-mixed noise of 2.4 K×
k
b
from Eq. 3 (○).
(left scale) is compressed in the simulation (denoted by solid blue line) when compared with the product of the simulated gain (
G
– 1) and the uncompressed down-mixed noise of 2.4 K×
k
b
from Eq. 3 (○).
After dividing the simulated output spectrum by the calculated gain, a clear dip is revealed in the input noise temperature (◊, right scale).
In our analytic modeling, we have generalized the semiclassical treatment of Ref. 19 to finite capacitance CJ and combined the mixing analysis with the current-voltage characteristics derived in Ref. 23. For the noise analysis, we define a noise process  , band-limited near the signal frequency. Another noise process
, band-limited near the signal frequency. Another noise process  with
with  covers the Josephson frequency and one pair of sidebands (
covers the Josephson frequency and one pair of sidebands ( ). ϕj has a small variance because of the low impedance of the junction capacitor at high Josephson frequency. We expand
). ϕj has a small variance because of the low impedance of the junction capacitor at high Josephson frequency. We expand  in order to describe the junction as a DC current generator plus two AC current noise generators: one at ωs and the other around the Josephson frequency. In the Fourier plane, the AC Josephson relation and the impedance environments at low and high frequencies establish the down-mixing noise process. We denote the variance of the phase noise over the signal band by
in order to describe the junction as a DC current generator plus two AC current noise generators: one at ωs and the other around the Josephson frequency. In the Fourier plane, the AC Josephson relation and the impedance environments at low and high frequencies establish the down-mixing noise process. We denote the variance of the phase noise over the signal band by  . In our calculations, we expand
. In our calculations, we expand  (which is a good approximation at small
(which is a good approximation at small  ) but this breaks down when additional sidebands (
) but this breaks down when additional sidebands ( and so on) become significant. These Bessel functions of the first kind have the phase noise amplitude r divided by the signal band. Ideally, r should follow the Rayleigh distribution. In our analysis, we treat separately the limit of small fluctuations,
and so on) become significant. These Bessel functions of the first kind have the phase noise amplitude r divided by the signal band. Ideally, r should follow the Rayleigh distribution. In our analysis, we treat separately the limit of small fluctuations,  and the regime with
and the regime with  , in which noise compression effects appear. With large gain and resonantly boosted current-voltage conversion, the phase fluctuations will grow so much that the non-linearities begin to limit the gain and the system is driven to a steady state where the down-mixing process becomes altered and significantly suppressed. The number of added quanta per unit band from mixed-down noise is derived in the Supplementary material:
, in which noise compression effects appear. With large gain and resonantly boosted current-voltage conversion, the phase fluctuations will grow so much that the non-linearities begin to limit the gain and the system is driven to a steady state where the down-mixing process becomes altered and significantly suppressed. The number of added quanta per unit band from mixed-down noise is derived in the Supplementary material:

where  and the factor
and the factor  can be neglected at large gain. Noise suppression is denoted by the compression factor
can be neglected at large gain. Noise suppression is denoted by the compression factor  which equals unity at
which equals unity at  and decreases towards zero with growing variance. In our model with the sidebands
and decreases towards zero with growing variance. In our model with the sidebands  , we obtain
, we obtain  . Hence, large improvement in noise performance can be achieved compared to the linear where
. Hence, large improvement in noise performance can be achieved compared to the linear where  .
.
The role of noise compression in the operation of the SJA is illustrated in Fig. 4. For reference, we plot the uncompressed noise from Eq. (3) multiplied by the simulated gain. The output noise temperature from the actual simulation differs from it (an indication of noise compression). The simulated spectrum is rounded near the gain peak, which creates a dip in the input noise temperature.
In Fig. 5, the input noise temperature at Gm is plotted as a function of the gain. Linear theories predict convergence towards Tn = 2.4 K at  (from Eq. (3) by taking ξ = 1). Above a threshold gain of ∼ 13 dB, noise suppression sets in. From our analytic model with two sidebands
(from Eq. (3) by taking ξ = 1). Above a threshold gain of ∼ 13 dB, noise suppression sets in. From our analytic model with two sidebands  , we obtain
, we obtain  for the compression factor at Gm = 28 dB and the noise temperature reduces to Tn = 1.0 K. Compared with numerical simulations, the analytic model yields nearly 3–4 times larger value for Tn.
for the compression factor at Gm = 28 dB and the noise temperature reduces to Tn = 1.0 K. Compared with numerical simulations, the analytic model yields nearly 3–4 times larger value for Tn.
Input noise temperature T n vs. maximum gain of the SJA.
The uncompressed Tn (Eq. (3) with ξ = 1, solid blue line) converges to 2.4 K at high gain. Compression suppressed Tn for the analytic model with two sidebands at  is denoted by the dashed green line. Noise temperature from the simulations is depicted using open circles and the error bars represent the statistical uncertainty in the simulated spectral density. The measurement result is marked by a filled circle (
is denoted by the dashed green line. Noise temperature from the simulations is depicted using open circles and the error bars represent the statistical uncertainty in the simulated spectral density. The measurement result is marked by a filled circle ( ), while the standard quantum limit would be
), while the standard quantum limit would be  .
.
Discussion
The compression mechanism for noise is crucial for the high bias operation of the SJA since otherwise Tn would grow directly proportional to υb (N in Eq. (3)). The operation with noise compression can be viewed as self-organization of the system. Microscopic degrees of freedom give rise to a macroscopic order which can be parametrized to describe the behavior of the system. In our device, the macroscopic ordering is dictated by the integrated noise over the amplified bandwidth. This parameter governs the macroscopic characteristics of the device (e.g. the effective critical current and the gain of the device for external signals). The actual value of the gain is set by the higher order terms present in the Josephson energy, which resembles that of the order parameter stabilization in regular phase transitions.
The bandwidth of our SJA is fundamentally limited below the Josephson and plasma frequencies,  . It can be shown that the gain-bandwidth product is
. It can be shown that the gain-bandwidth product is  in our first-order filtering scheme. In the measured amplifier, the capacitance of the bandstop filter is
in our first-order filtering scheme. In the measured amplifier, the capacitance of the bandstop filter is  and
and  . Furthermore, using
. Furthermore, using  as in our operating point of interest, the formula yields
as in our operating point of interest, the formula yields  is obtained experimentally. In general, stability of the amplifier requires that
is obtained experimentally. In general, stability of the amplifier requires that  . Reduction of the shunt capacitance facilitates improvement of the gainbandwidth product but the boundary condition
. Reduction of the shunt capacitance facilitates improvement of the gainbandwidth product but the boundary condition  must be met. High bandwidth is predicted at small Rd too, which can be obtained most effectively by increasing the critical current. Also CJ controls the value of Rd so that the optimum for gain-bandwidth product is obtained for a small junction with a high critical current density.
must be met. High bandwidth is predicted at small Rd too, which can be obtained most effectively by increasing the critical current. Also CJ controls the value of Rd so that the optimum for gain-bandwidth product is obtained for a small junction with a high critical current density.
Another possible low noise regime for the SJA is the limit of small ωJ. We analyzed a few devices at  with different βc (see the Suppl.). We obtained analytically that the down-mixed noise contribution is around
with different βc (see the Suppl.). We obtained analytically that the down-mixed noise contribution is around  at
at  without any noise compression. This was verified in numerical simulations according to which 0.9 ± 0.2 quanta were added by our SJA. Addition of one quantum indicates that the noise behaviour of the SJA is reminiscent to that of heterodyne detection where the image frequency brings an extra noise of
without any noise compression. This was verified in numerical simulations according to which 0.9 ± 0.2 quanta were added by our SJA. Addition of one quantum indicates that the noise behaviour of the SJA is reminiscent to that of heterodyne detection where the image frequency brings an extra noise of  to the detected signal25, i.e. both sidebands of the Josephson frequency add
to the detected signal25, i.e. both sidebands of the Josephson frequency add  to the noise temperature.
to the noise temperature.
The control of noise in our SJA is not fully optimized and several issues should be addressed in order to make the theoretical procedure for noise minimization more effective and transparent. Using numerical simulations, we reproduced the measured noise temperature 3.2Tq at high bias and found signs for the complex behavior of our device. Our analytical model mixes down noise only from two sidebands  , the consideration of which is sufficient at low Josephson frequency and small phase noise variance
, the consideration of which is sufficient at low Josephson frequency and small phase noise variance  . Consequently, the predictions of
. Consequently, the predictions of  from our analytical modeling are reliable at low bias voltage. In the noise compression mode,
from our analytical modeling are reliable at low bias voltage. In the noise compression mode,  , our simulations show that the analytic model fails and an extension in the number of tracked sidebands is necessary. Moreover, further work will be needed to show whether pronounced noise compression can drive the SJA into the standard quantum limit Tq. Our analysis indicates that the concept of selectively shunted junction amplifier for microwaves is sound and that it provides the best route for quantum limited operation over large bandwidths.
, our simulations show that the analytic model fails and an extension in the number of tracked sidebands is necessary. Moreover, further work will be needed to show whether pronounced noise compression can drive the SJA into the standard quantum limit Tq. Our analysis indicates that the concept of selectively shunted junction amplifier for microwaves is sound and that it provides the best route for quantum limited operation over large bandwidths.
Methods
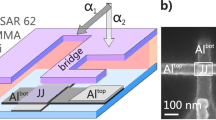
Our experimental setup for the SJA measurements is shown in Fig. 6. The device is biased with a DC current which allows the effective value of the negative resistance to be tuned over a wide range of values. The incoming signal and the reflected signal are separated by circulators and the signal postamplification is performed by high electron mobility transistor (HEMT) based amplifiers at 4 K and at the room temperature. At the optimal operating point, the dynamic resistance Rd of the Josephson junction is −1370 Ω in our amplifier. To get substantial gain according to Eq. 2, we apply impedance transformation by placing an inductor L2 in series with the junction. This converts the input impedance Zin(ωs) close to −50 Ω.
Setup for measuring the SJA characteristics.
The essential components of the SJA are located at 70 mK (indicated by the dashed black box). 60 dB of attenuation is employed to thermalize the incoming rf signal cable and two circulators eliminate the back action noise from the preamplifier. Noise temperature of the cooled preamplifier (including losses in front of the preamplifier)  at the center frequency of the SJA.
at the center frequency of the SJA.
To measure the amplifier performance, we injected a reference signal and recorded the signal-to-noise (S/N) ratio while having the SJA ON and OFF. In the OFF state, the SJA acts like a pure inductance reflecting all the incoming power (passive mirror) and the noise in the S/N ratio measurement is fully specified by the HEMT preamplifier. The largest improvement in the S/N was found at the highest bias current ∼ 140 µA (ib = 8.2). Using a source at 70 mK, the S/N ratio after the HEMT amplifier was improved by 17.2 ± 0.2 dB. Thanks to the microwave switch in the setup, the noise temperature of the HEMT amplifier could be carefully calibrated using the cold/hot load technique. The parameters of the investigated amplifier are collected into Table I.
References
Clerk, A. A., Devoret, M. H., Girvin, S. M., Marquardt, F. & Schoelkopf, R. J. Introduction to quantum noise, measurement and amplification. Rev. Mod. Phys. 81, 1155–1208 (2010).
Hatridge, M., Vijay, R., Slichter, D. H., Clarke, J. & Siddiqi, I. Dispersive magnetometry with a quantum limited SQUID parametric amplifier. Phys. Rev. B 83, 134501 (2011).
Yurke, B., Corruccini, L. R., Kaminsky, P. G. & Rupp, L. W. Observation of parametric amplification and deamplification in a Josephson parametric amplifier. Phys. Rev. A, 39, 2519–2533 (1989).
Yurke, B. et al. A low-noise series-array Josephson junction parametric amplifier. Appl. Phys. Lett. 69, 3078–3080 (1996)
Bergeal, N. et al. Phase-preserving amplification near the quantum limit with a Josephson ring modulator. Nature 465, 64–68 (2010).
Mück, M., Kycia, J. B. & Clarke, J. Superconducting quantum interference device as a near-quantum-limited amplifier at 0.5 GHz. Appl. Phys. Lett. 78, 967–969 (2001).
Asztalos, S. J. et al. SQUID-based microwave cavity search for dark-matter axions. Phys. Rev. Lett. 104, 041301 (2010).
Castellanos-Beltran, M. A., Irwin, K. D., Hilton, G. C., Vale, L. R. & Lehnert, K. W. Amplification and squeezing of quantum noise with a tunable Josephson metamaterial. Nature Physics 4, 929–931 (2008).
Teufel, J. D., Donner, T., Castellanos-Beltran, M. A., Harlow, J. W. & Lehnert, K. W. Nanomechanical motion measured with precision beyond the standard quantum limit. Nature Nanotech. 4, 820–823 (2009).
Castellanos-Beltran, M. A. & Lehnert, K. W. A widely tunable parametric amplifier based on a SQUID array resonator. Appl. Phys. Lett. 91, 083509 (2007).
Spietz, L., Irwin, K., Aumentado, K. & Aumentado, J. Input impedance and gain of a gigaherz amplifier using a dc superconducting quantum interference device in a quarter wave resonator. Appl. Phys. Lett. 93, 082506 (2008).
Mears, C. A., et al. Quantum-limited heterodyne detection of millimeter waves using superconducting tantalum tunnel junctions. Appl. Phys. Lett. 57, 2487–2489 (1990).
Tiemann, J. J. Shot noise in tunnel diode amplifiers. Proc. IRE. 8, 1418–1423 (1960).
Seppä, H., Kiviranta, M., Grönberg, L. DC SQUID based on unshunted Josephson junctions: Experimental results. IEEE Trans. Appl. Supercond. 5, 3248–3251 (1995).
Likharev, K. K. Dynamics of Josephson junctions and circuits (Gordon and Breach, New York, 1986).
Vystavkin, A., et al. One- frequency parametric amplifier using self-pumped Josephson junction. Magnetics, IEEE Trans. 13, 233–236 (1977).
Calander, N., Claeson, T. & Runder, S. Shunted Josephson tunnel junctions: High-frequency, self-pumped low noise amplifiers. J. Appl. Phys., 53, 5093–5103 (1982).
Clarke, J., & Braginsky, A. I. eds., The SQUID Handbook, volume 1 (Wiley, Weinheim, 2004).
Koch, R. H., Van Harlingen, D. J. & Clarke, J. Measurements of quantum noise in resistively shunted Josephson junctions. Phys. Rev. B, 26, 74 (1982).
Likharev, K. K. & Semenov, V. K. Fluctuation spectrum in superconducting point contacts. Zh. Eksp. Teor. Fiz. Pis'ma 15, 625 (1972) JETP Lett. 15, 442 (1972).
Callen, H. B. & Welton, T. A. Irreversibility and generalized noise. Phys. Rev. 83, 34–40 (1951).
Levinson, Y., Quantum noise in a current-biased Josephson junction. . Phys. Rev. B 67, 184504 (2003).
Brandt, F. T. Frenkel, J. & Taylor, J. C. Noise in resistively shunted Josephson junctions. Phys. Rev. B 82, 014515 (2010).
Wellstood, F. C. Urbina, C. & Clarke, J. Hot-electron effects in metals. Phys. Rev. B 49, 5942–5955 (1994).
Haus, H. A. Electromagnetic noise and quantum optical measurements, Ch. 8, (Springer, Berlin, 2000).
Acknowledgements
We thank Jari Penttilä for providing the Josephson junctions used in our experiments. We also thank Thomas Aref for his support during the writing of this article. This work was supported by Center of Excellence and Materials World Network grants of the Academy of Finland and by the European Science Foundation (ESF) under the EUROCORES Programme EuroGRAPHENE.
Author information
Authors and Affiliations
Contributions
All authors took jointly part in the planning of this experimental work and the development of its theoretical interpretation. P. L. performed the experiments and V. V. made the numerical simulations and the analytical mixing analysis. P. L. and V. V. co-operatively wrote the first versions of the main manuscript and the Supplementary material. All authors contributed to editing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Josephson junction microwave amplifier in the noise compression mode: Supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Lähteenmäki, P., Vesterinen, V., Hassel, J. et al. Josephson junction microwave amplifier in self-organized noise compression mode. Sci Rep 2, 276 (2012). https://doi.org/10.1038/srep00276
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00276
This article is cited by
-
Near-quantum-limited amplification from inelastic Cooper-pair tunnelling
Nature Electronics (2018)
-
Advanced Concepts in Josephson Junction Reflection Amplifiers
Journal of Low Temperature Physics (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.