Abstract
Quantum ground-state problems are computationally hard problems for general many-body Hamiltonians; there is no classical or quantum algorithm known to be able to solve them efficiently. Nevertheless, if a trial wavefunction approximating the ground state is available, as often happens for many problems in physics and chemistry, a quantum computer could employ this trial wavefunction to project the ground state by means of the phase estimation algorithm (PEA). We performed an experimental realization of this idea by implementing a variational-wavefunction approach to solve the ground-state problem of the Heisenberg spin model with an NMR quantum simulator. Our iterative phase estimation procedure yields a high accuracy for the eigenenergies (to the 10−5 decimal digit). The ground-state fidelity was distilled to be more than 80% and the singlet-to-triplet switching near the critical field is reliably captured. This result shows that quantum simulators can better leverage classical trial wave functions than classical computers
Similar content being viewed by others
Introduction
Quantum computers can solve many problems much more efficiently than a classical computer1. One general class of such problems is known as quantum simulation2,3. In this class of algorithms, the quantum states of physical interest are represented by the quantum state of a register of controllable qubits (or qudits), which contains the quantum information of the simulated system. In particular, one of the most challenging problems in quantum simulation is the ground-state preparation problem4 of certain Hamiltonians, H, which can be either classical or quantum mechanical. Remarkably, every quantum circuit5 and even thermal states6,7, can be encoded into the ground state of certain Hamiltonians and purely mathematical problems, such as factoring8, can also be solved by a mapping to a ground-state problem.
On the other hand, the ground-state problem has profound implications in the theory of computational complexity9. For example, finding the ground-state of a general classical Hamiltonian (e.g. the Ising model) is in the class of NP (nondeterministic polynomial time) computational problems, meaning that while finding the solution may be difficult, but verifying it is efficient when employing a classical computer. The Ising model with nonuniform couplings is an example of an NP-problem (more precisely, NP-complete)10. The quantum generalization of NP is called QMA (Quantum Merlin Arthur)5. In this class, the verification process requires a quantum computer, instead of a classical computer. An example of a problem in QMA is the determination of the ground-state energy of quantum Hamiltonians with two-body (or more) interaction terms11. So far, there is no known algorithm, classical or quantum, that can solve all problems efficiently in NP or QMA.
Most of the problems in physics and chemistry, however, exhibit special structures and symmetries, that leads to methods for approximating the ground state with trial states |ψT 〉. For example, in quantum chemistry12, the Hartree-Fock mean field solution often captures the essential information of the ground state |e0〉 for a wide range of molecular structures. However, the applicability of these trial states will break down whenever the fidelity,

quantified by the square of the overlap between the trial state |ψT 〉 and the exact state |e0〉, is vanishingly small. Specifically, if the fidelity of a certain trial state for a particular many-body problem is small, for example, about F = 0.01, it might be considered as a “poor” approximation to the exact ground state13, when used as an input state in classical computation. For quantum computing, however, the same trial state can be a “good” input, as one only needs to repeat the ground-state projection algorithm, e.g., by Abrams and Lloyd14 (see below), for about O(100) times, which is computationally efficient especially when the Hilbert space of the many-body Hamiltonian is exponentially large. This is the motivation behind our experimental work.
Several theoretical studies15,16,17,18 along this line of reasoning have been carried out for various molecular structures. Here we performed an experimental realization of this idea with one of the simplest, yet non-trivial, physical systems, namely the Heisenberg spin model in an external field. Our goals for this study are: (i) to determine the eigenvalues of the ground state and (ii) to maximize, or to distill, as much as possible the ground-state from a trial state, which contains a finite (F = 0.5) ground-state fidelity. For (i), we employed a revised version of the iterative phase estimation procedure to determine the eigenvalues of the Hamiltonian (to the 10−5 decimal digit). Subsequently, we apply a state-filtering method to extract the ground-state fidelity from the final state to achieved (ii). For this study, we specifically chose three cases corresponding to three different values of external field in the simulation, namely h = 0, h = 0.75hc and h = 1.25hc , where hc is the critical value of the external field at which the ground-state and the first excited state cross each other (see Fig. 1). This is a singlet-triplet switching and our experimental simulation captures the change of the ground state around this critical point reliably.
(Color online) (a) The energy eigenvalues versus external magnetic field of the Heisenberg Hamiltonian (defined in equation (3) ).
The optimized state |ψ *〉 ≡ |ψ(−π/4, π/2)〉 (see equation (4)) (black line) contains a linear combinations of the two eigenstates (red and blue lines) only. (b) The three-qubit NMR quantum simulator consists of a sample of 13C-labeled Diethyl-fluoromalonate dissolved in2H-labeled chloroform. The nuclear spins (circled) of13 and1H are used as the system qubits and that of19F is the probe qubit. The parameters of the NMR couplings of this molecule are listed in the table.
Finally, we note that the approach employed here is different from the method for preparing many-body ground states based on the adiabatic evolution19,20,21,22,23,24,25,26, where the initial state is usually chosen as the ground state of some simple Hamiltonian, which can be prepared efficiently, instead of the trial states, which aim to capture the essential physics of the exact ground state. The performance (complexity) of the adiabatic approach depends on the energy gap along the entire evolution path. In our approach, the performance depends on the fidelity of the initial state and the energy gap of the Hamiltonian. Furthermore, in these experiments (except Ref. 23), the eigen-energy and the ground state of the Hamiltonian are not usually determined simultaneously and therefore, cannot be considered as completely solving the ground-state problem4. In spite of the differences between these two approaches, it is possible that the adiabatic method can be incorporated in our procedure to further enhance the ground-state fidelity of the final state. However, this possible extension is not considered here.
This paper is organized as follows: first, we will provide the theoretical background for this experimental work. Then, we define the Hamiltonian to be simulated and the choice and the optimization of the initial state. Next, we outline the experimental procedures. Finally, the experimental results will be presented and analyzed by a full quantum state tomography. We conclude with a discussion of the results and the sources of errors.
Results
Theoretical background
The central idea behind this experimental work has a counterpart in the time-domain classical simulation methods27. In the context of quantum computing, the method was introduced by Abrams and Lloyd14. Specifically, it was shown that for any quantum state |ψ〉 = Σ kak |ek 〉 which has a finite overlap |ak |2 (or fidelity) with the eigenstates |ek 〉 of a simulated Hamiltonian, H, the phase estimation algorithm28 will map, with high probability, the corresponding eigenvalues to the states of an ancilla quantum register,

Consequently, a projective measurement on the register qubits will, ideally, collapse the quantum state of the system qubits into one of the eigenstates. By analyzing the measurement outcome, one can determine the ground-state eigenvalue E0 and even project the exact ground state |e0 〉.
Given any trial state |ψT 〉, the performance of the algorithm depends on the overlap |a0|2, which can be maximized using many classical methods, such as using advanced basis sets29, matrix product states (MPS) representations30, or any suitable variational method.
The Hamiltonian and the optimized input state
The method proposed here can be generalized to apply to more general Hamiltonians, but as an example, we will employ the Heisenberg Hamiltonian with an external magnetic field pointing along the z-direction:

where  and
and  is one of the Pauli matrices (α = x ,y, z) acting on the k = a, b spin. On the other hand, in general, there is no restriction to the choice of a trial state, as long as it is not orthogonal to the ground state (in this case, the ground state algorithm necessarily fails). To mimic the behavior of the commonly-employed trial states of more general systems, we require our trial state to satisfy the following conditions: (a) that it contains one or more parameters which can be adjusted to minimize the energy 〈H〉 and that this procedure usually does not lead to the exact ground state and (b) that it may capture only part of the vector space spanned by the eigenstates of the Hamiltonian H. One possible choice that fulfills the above criteria is the following variational state which contains two adjustable parameters, θ and ϕ,
is one of the Pauli matrices (α = x ,y, z) acting on the k = a, b spin. On the other hand, in general, there is no restriction to the choice of a trial state, as long as it is not orthogonal to the ground state (in this case, the ground state algorithm necessarily fails). To mimic the behavior of the commonly-employed trial states of more general systems, we require our trial state to satisfy the following conditions: (a) that it contains one or more parameters which can be adjusted to minimize the energy 〈H〉 and that this procedure usually does not lead to the exact ground state and (b) that it may capture only part of the vector space spanned by the eigenstates of the Hamiltonian H. One possible choice that fulfills the above criteria is the following variational state which contains two adjustable parameters, θ and ϕ,

Here, |θ〉 ≡ cosθ |10〉 + sinθ |01〉 and |ϕ〉 ≡ cos ϕ |00〉 + sinϕ |11〉. In general, the optimized states for each given pair of (J, h) are not necessarily the same. However, in our case, we found that the optimized state |ψ *〉 ≡ |ψ (−π/4, π/2)〉 can minimize the energy for all values of h and J > 0. Moreover, it turns out that this optimized state captured two out of the four eigen-energies (see Fig. 2a) only; therefore, a single probe qubit is sufficient to resolve them (for more general cases, see the section in Methods). We note that the fidelity F (cf. equation (1)) of the state |ψ *〉 with the exact ground state |e0〉 is exactly 50%. However, the scheme works equal well even for smaller values of the initial fidelity, as long as the peaks in the spectrum can be resolved from the background noise (cf. Fig. 3).
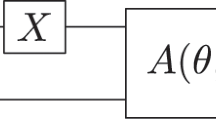
(Color online) (a) The quantum circuit diagram for the experiment.
The explicit construction of the unitary operators W and V(t) is detailed in the Appendix31. The quantum gates enclosed in a box in (a) (and pulse sequences in (b)) generate the input state |ψ *〉, which is an optimized variational state with respect to the Hamiltonian defined in equation (3). (b) The entire pulse sequence corresponds to the quantum circuit diagram for the case of zero external field, h = 0. The complexity and the lengths of the pulse sequences for the other cases, namely h = 0.75hc and h = 1.25hc , are roughly the same as this pulse sequence.
(Color online) The absolute amplitude of the eigenvalue spectra g(E) of the Heisenberg Hamiltonian as defined in equation (3) .
These are obtained for three different values of the external magnetic field h, namely h = 0, h = 0.75hc and h = 1.25hc , where hc is the critical field at which the ground state becomes degenerate. The shaded region highlights the location the the singlet state depicted in Fig. 1. The arrows indicate the direction of the peak shift when the simulated external field h is increased. The blue and red dots indicate the quantum states represented by the peak signals (cf. Fig. 1).
Outline of the method
This algorithm starts with a set of system qubits initialized in the state |ψ *〉 = Σ k ak |ek 〉 and a single “probe” qubit in the  state. For different times t, a controlled U(t) gate, where U (t) ≡ e−iHt (
state. For different times t, a controlled U(t) gate, where U (t) ≡ e−iHt ( = 1), is then applied, resulting in the following state:
= 1), is then applied, resulting in the following state:  , where ωk ≡Ek . The reduced density matrix of the probe qubit,
, where ωk ≡Ek . The reduced density matrix of the probe qubit,

contains the information about the eigenvalues in its off-diagonal matrix elements, which can be measured efficiently in an NMR setup (see Appendix31). A classical Fourier analysis on the off-diagonal matrix elements at different times yields both the eigenvalues ωk and the overlaps |ak |2. To obtain the value of ωk with high accuracy, a long time evolution of the simulated quantum state is usually needed. However, for Hamiltonians with certain symmetries, we can perform a simplified version of the iterative phase estimation algorithm (IPEA), which is similar but not identical to the ones performed previously in Ref. 23, 32. We will explain the details of this IPEA in the Method Section.
Once the ground state eigenvalue E0 of the Hamiltonian H is determined, one can, for example, employ the state-filtering method33 to isolate the corresponding ground state |e0〉 from the rest. The resulting state is of the form: a0 |e0〉 |00…0〉 + …, where the other state vectors omitted contain ancilla states that are orthogonal to |00…0〉. If we now perform a projective measurement on the ancilla qubits, the probability for projective the system qubits to the ground state is |a0|2. Therefore, this procedure solves the ground-state problem when trial wave functions are available.
Experimental procedure
The experiments were carried out at room temperature on a Bruker AV-400 spectrometer. The sample we used is the 13C-labeled Diethyl-fluoromalonate dissolved in2H-labeled chloroform. This system is a three-qubit quantum simulator using the nuclear spins of 13C and1H as the system qubits to simulate the Heisenberg spins and the19F as the probe qubit in the phase estimation algorithm (see Fig. 1b). The internal Hamiltonian HNMR of this system can be described by the following:

where νj is the resonance frequency of the jth spin and Jjk is the scalar coupling strength between spins j and k, with Jab = 160.7 Hz, Jbc = −194.4 Hz and Jac = 47.6 Hz. The relaxation time T1 and dephasing time T2 for each of the three nuclear spins are tabulated in Fig. 1a.
The experimental procedure consists of three main parts: I. State initialization (preparing the system qubits as |ψ *〉, probe qubit as |0〉), II. Eigenvalue measurement by iterative phase estimation and III. Quantum state tomography. The state initialization part is rather standard and we leave the details of it to the Appendix31. Part II is implemented with a quantum circuit as depicted in Fig. 2 (see the section in Methods for the detailed circuit construction). The probe qubit is measured at the end of the circuit (see also equation (5)).
The resulting Fourier spectra for various cases are shown in Fig. 3. The positions of the peaks indicate the eigenvalue of the Hamiltonian H. Although the peaks look sharp, the errors are in fact about 22%. However, we are able to reduce the errors to less than 0.003% (see Fig. 4) by five steps of the iterative phase estimation algorithm which is described in the Method section.
(Color online) Experimental results of the iterative phase estimation algorithm (IPEA) for improving the accuracy of the measured ground-state energy.
(a) and (b) There are five iterations performed; each of them improves one digit of accuracy in the eigenvalues. For example, consider the ground state, after the first iteration (red curve), the peak lies between −0.1 and −0.2; this means that the first digit of eigenvalue should be −0.1. After five iterations, the value of groundstate energy is determined to be −0.11936(3), with a precision of 10−5 in units of 2πJ. (c) A table listing the improvement of the numerical values (digits in red represent uncertainty). (d) Graphical visualization of the results in (c). The theoretical curve results from the improvement of the precision by a factor of 1/10 for each iteration.
Experimental Results
Once the two eigenvalues (E0 and E1) are accurately determined by the IPEA, we can identify the eigenvectors (ground state |e0) and excited state |e1〉) by the same quantum circuit as shown in Fig. 2a. The difference is that, the time τ, in the controlled rotation U (τ) ≡ e−iHτ is chosen to be τ = π/(E1 − E0). This allows us to obtain the following state,

This state is very similar to the one discussed in equation (2). The important point is that, now each eigenstate is tagged by the two orthogonal states of the ancilla qubit and can be determined separately, e.g. through quantum state tomography.
To obtain the state in equation (7), starting from the product state |ψ*〉 |0〉, we first prepared the probe state as a superposition state with a phase  “preloaded” in it, i.e.,
“preloaded” in it, i.e.,  . Next, after applying the controlled-U(τ) to the trial state |ψ*〉 = a0|e0〉 + a1|e1〉, we have,
. Next, after applying the controlled-U(τ) to the trial state |ψ*〉 = a0|e0〉 + a1|e1〉, we have,

Subsequently, we apply a single-qubit rotation gate  , which maps
, which maps  and
and  , we then obtain the final state in equation (7).
, we then obtain the final state in equation (7).
Finally, the standard procedure of quantum state tomography34 was performed on the final states (equation (7)) for the cases h = 0, h = 0.75hc and h = 1.25hc , shown respectively in Fig. 7 (b)–(d). The corresponding results of the ground state (i.e. the |e0〉 part in equation (7)) are shown in Fig. 5 (e)–(g). These density matrices allow us to obtain all information about the experimentally determined ground states. Fig. 5a shows the improvement of the magnetization M of the final states, as compared with the initial state. The inset figure shows that the magnitude of the deviations (blue bars) from the theoretical values are always smaller then that (red bars) of the trial state.
(Color online) Experimental results from the quantum state tomography procedure (real parts are shown, imaginary parts shown in the Appendix31).
(a) The initial state |ψ *〉. (b),(c) and (d) Three final states (equation (7)) for the cases, respectively, h = 0, h = 0.75hc and h = 1.25hc . (e),(f) and (g) The first 4 × 4 section of each density matrix above (after re-normalization), in the subspace where the probe qubit is projected to the |0〉 state.
(Color online) Results from quantum state tomography.
(a) Magnetization  for the initial states (red dotted line) and the final states (crossed circles) for h = 0, h = 0.75hc and h = 1.25hc . The inset shows the absolute errors of the initial state (red bars) and the three experimental values (blue bars). (b) The ground state fidelity (green) and projection (yellow) for the experimentally determined states (a)-(g) in Fig. 7. The fidelity of the initial state (blue) is included for comparison.
for the initial states (red dotted line) and the final states (crossed circles) for h = 0, h = 0.75hc and h = 1.25hc . The inset shows the absolute errors of the initial state (red bars) and the three experimental values (blue bars). (b) The ground state fidelity (green) and projection (yellow) for the experimentally determined states (a)-(g) in Fig. 7. The fidelity of the initial state (blue) is included for comparison.
The quality of the final state ρexp in the experiment is quantified by the fidelity F = 〈e0|ρexp |e0〉 (cf. equation (1)) and the projection35  , where
, where  is the purity of ρexp . The results are shown in Fig. 5b. Note that the reduced density matrices (e),(f),(g) have better fidelities than that of the original density matrices (b),(c),(d). In Fig. 6, the weights (probabilities) of the eigenstates of H in the final states are shown. Note that, as mentioned above, the trial state captures only two eigenstates. Due to experimental errors, other eigenstates also showed up in the spectral decomposition. This contributes to the deviation of the magnetization (M = 0 for the singlet state) as well. Note that the singlet-triplet switching (cf. Fig. 1), i.e., from Fig. 6c to 6d, is reliably captured.
is the purity of ρexp . The results are shown in Fig. 5b. Note that the reduced density matrices (e),(f),(g) have better fidelities than that of the original density matrices (b),(c),(d). In Fig. 6, the weights (probabilities) of the eigenstates of H in the final states are shown. Note that, as mentioned above, the trial state captures only two eigenstates. Due to experimental errors, other eigenstates also showed up in the spectral decomposition. This contributes to the deviation of the magnetization (M = 0 for the singlet state) as well. Note that the singlet-triplet switching (cf. Fig. 1), i.e., from Fig. 6c to 6d, is reliably captured.
Discussion
In this experiment, the random fluctuations of the NMR signals in this experiment are negligible. We are able to determine the eigenvalues to a very high accuracy, using the iterative phase estimation algorithm (IPEA). The major source of errors (about 10% of the fidelity) of the experiment comes from the second step of the procedure where the overall pulse sequence to construct the final state equation (7) is lengthy and therefore is dominantly a T2 error. The time spent for this operation is about 1/10 of T2 (see the Appendix31). Additional errors come from the measurement (tomography) and the inhomogeneity in the RF pulses and the external magnetic field. If these factors can be overcome, a further increase of fidelity is possible by using the final state of this experiment as the input state for another iteration of the similar distillation procedure (see the section in Methods for details).
In conclusion, we have experimentally demonstrated a method to solve the quantum ground-state problem using an NMR setup. This is achieved by distilling the exact ground state from an input state, which has 50% overlap with the ground state. The eigenvalues were determined to a precision of the 10−5 decimal digit, after five iterations of the phase estimation procedure. Then, the final states are distilled to high values of fidelity. The method we developed in this experiment is scalable to more general Hamiltonians and not limited to NMR systems. This result confirms that variational methods developed for classical computing could be a good starting point for quantum computers, opening more possibilities for the purposes of quantum computation and simulation.
Methods
State initialization
In this experiment, we used a sample of the 13C-labeled Diethyl-fluoromalonate dissolved in the 2H-labeled chloroform as a three-qubit computer, where the nuclear spins of the 13C and the1H were used as the system qubits and that of the 19F was used as the probe qubit. The structure of the molecule is shown in Fig. 1a of the main text and the physical properties are listed in the table of Fig. 1b.
Starting from the thermal equilibrium state, we first created the pseudo-pure state (PPS)

using the standard spatial average technique27. Here, ε≈10−5 quantifies the strength of the polarization of the system and II is the 8 × 8 identity matrix. Next, we prepared the probe qubit to the state  by a pseudo-Hadamard gate
by a pseudo-Hadamard gate  , where,
, where,

Here, α = x, y, z, is a rotation operation applied to the qubit j.
Finally, the system qubits are prepared to the initial state,

by applying two single-qubit rotations and one controlled-rotation.
Construction of the controlled-U(t)
The controlled-U(t) in the phase estimation algorithm (see Fig. 2a) is implemented in the following way: since all the terms in the Heisenberg Hamiltonian,

commute with each other, we decompose the time evolution operator T(t) ≡ e−iHt into three parts:

where



The quantum circuit diagram for simulating the operations controlled-Vx and controlled-Vyz is shown in the Appendix31. To simulate controlled-Vx (t), we set,

(alternatively, Iz ); to simulate controlled-Vyz (t), we set

Note that the control is “on” when the probe qubit is in the |0〉 state. In this case, the first three quantum gates cancel the last gate V(t/2), making it effectively an identity gate. When the controlling qubit is in the “off” state, this circuit executes two V(t/2) gates.
Here we exploited the symmetry of the two-spin Heisenberg Hamiltonian H (Eq. (12)), which allows us to simplify the simulation of the time evolution operator by using the decomposition in Eq. (13). To extend this method for three or more spins, we will need to simulate the full (controlled) unitary operator by breaking it up into small or simulable pieces, a procedure known as Trotterization3. This, in principle, is efficient for quantum computers3. In our setup, however, long time simulation is still limited by decoherence. Therefore, we avoid the problem by performing an iterative phase estimation algorithm (IPEA), which effectively maps long-time evolution to a process that requires a shorter evolution time. This idea follows from the special nature of the two-qubit Heisenberg Hamiltonian and will be elaborated in the IPEA section.
Measurement of the probe qubit
Here we explain the measurement method of the NMR signal of the probe qubit (see equation (5)). Denote the off-diagonal elements of ρprobe (t) as,

The phase shift φt can be obtained by using the method of quadrature detection which serves as a phase detector. By measuring the integrate value of the peak in NMR spectrum, we can obtain the value of |Mt |.
To calibrate the system, we adjust the phase of the NMR spectrum such that φ 0 becomes the reference phase and normalize its peak intensity as 1. Some of the experimental data of the spectra are shown in the Appendix31 for the case of h = 0, at t = 0.16/J and 6.4/J.
By simulating the Hamiltonian evolution for different times, a range of frequency spectrum of  can be obtained by the method of discrete Fourier transformation (DFT). The Fourier-transformed spectra are shown in Fig. 3 for the cases of h = 0, 0.75hc and 1.25hc , respectively. For each spectrum, totally 128 data points were collected.
can be obtained by the method of discrete Fourier transformation (DFT). The Fourier-transformed spectra are shown in Fig. 3 for the cases of h = 0, 0.75hc and 1.25hc , respectively. For each spectrum, totally 128 data points were collected.
Iterative phase estimation algorithm (IPEA)
To improve the resolution of the energy eigenvalues, the information stemming from long time evolution of the simulated state is needed20. Fortunately, the required resources can be significantly reduced by the IPEA approach. This is due to the symmetry of the Hamiltonian: since all the terms in the Hamiltonian (equation (3)) commute with each other, they can be simulated individually, i.e.,

for all times t. The last term  corresponds to two separate local rotations, whose implementation is straight-forward (see the Appendix31). The other terms
corresponds to two separate local rotations, whose implementation is straight-forward (see the Appendix31). The other terms  are equivalent up to some local unitary rotations and their eigenvalue spectra of
are equivalent up to some local unitary rotations and their eigenvalue spectra of  , which are 1/4 and −1/4, are the same; the eigenvalues are symmetrical about zero. This means that, in order to simulate each term for a time interval t, we can always find a shorter time τ such that
, which are 1/4 and −1/4, are the same; the eigenvalues are symmetrical about zero. This means that, in order to simulate each term for a time interval t, we can always find a shorter time τ such that  , where t = 8nπ/J + τ for some non-negative integer n which is determined by the condition: 0 ≤ Jτ ≤ 8π.
, where t = 8nπ/J + τ for some non-negative integer n which is determined by the condition: 0 ≤ Jτ ≤ 8π.
Now, denote the eigenvalue, ωk ≡ 2πJ × 0.x1x2x3…, by a string of decimal digits {x1,x2,x3…}. The first digit x1 can be determined by a short time evolution by a probe qubit described in equation (5). Once x1 is known, the second digit x2 can be iteratively determined by simulating the evolution for ten times longer than the previous ones:

Note that the first term on the right hand side is known. The second term is now amplified and can be resolved by the probe qubit. This means that the eigenvalue ωk can then be determined to two digits of precision. By repeating this scheme iteratively for x3 and so on, the eigenvalue ω k can be determined subsequently for one digit after the other (cf. Fig. 4). The accuracy of the eigenvalues is improved from about 22% to about 0.003%. The upper bounds of errors of eigenvalues are shown in Fig. 4b. We note that in the IPEA performed in Refs. 23, 32, the final unitary matrices are decomposed directly for each value of t. Therefore, one can in principle determine the eigenvalues to an arbitrary accuracy. However, the resources required for decomposing the unitary matrices grow exponentially with the system size; the methods implemented there are certainly unrealistic for larger systems. Here, we exploited the symmetry of the Hamiltonian and simulate the time evolution without performing the decomposition of the unitary matrices. The accuracy of the IPEA is limited by some natural constraints. The details about the limitation of this method are discussed in the Appendix31.
Generalization to the cases of multiple eigenvalues
In this experiment, we have chosen the case of the trial state |ψ *〉 that captures two out of four eigenstates of the two-spin Hamiltonian. Therefore, we can use a single qubit (two states) to resolve the two distinct eigenvalues and map the final state into the form defined in equation (7), which is then analyzed by a quantum state tomography to extract the information about the ground state |e0〉.
In general, a trial state may capture more than two eigenvalues. In this case, our procedure needs to be generalized. However, there is nothing fundamentally new, except for a more laborious repetition of the same procedures. This is the reason we decided to work on the specific case of the trial state being the linear combination of two eigenstates only.
To explain the details of how it works, we assume the ground-state energy of H is unique. Define the first excited state as |e1〉. Then, any trial state can be decomposed into the following form:

where |a0|2 + |a1|2 + |a2|2 = 1 and |e2〉 represents the linear combination of all higher energy states captured by |ψ *〉. Then, we perform the phase estimation algorithm, using a single probe qubit (cf. equation (5)) and obtain all of the eigenvalues. Performing the same procedure for getting equation (7), we can obtain the following state:

where |b0|2 + |b1|2 + |b20|2 + |b21|2 = 1. Now, if we perform a state tomography and extract the first part of the state, we obtain a new state

which contains no eigenstate |e1〉. If we use this new state as the new trial state for another cycle, we get one less eigen-energy. Therefore, we can in principle eliminate the higher eigenstates one after each other and obtain the ground state in the end, using a single probe qubit.
Change history
29 November 2012
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Ladd, T. D., et al. Quantum computers. Nature 464, 45 (2010).
Feynman, R. P., Simulating physics with computers.. Int. J. Theor. Phys. 21, 467 (1982).
Kassal, I., Whitfield, J. D., Perdomo-Ortiz, A., Yung, M.-H., Aspuru-Guzik, A., Simulating chemistry using quantum computers.. Annu. Rev. Phys. Chem. 62, 185 (2011).
The problem of determining the ground-state eigenvalue and other ground-state properties of a given Hamiltonian H.
Kitaev, A. Y., Shen, A. H. and Vyalyi, M. N., Classical and Quantum Computation, American Mathematical Society: Providence, RI (2002).
Somma, R. D., Batista, C. D. and Ortiz, G., Quantum approach to classical statistical mechanics.. Phys. Rev. Lett. 99, 030603 (2007).
Yung, M.-H., Aspuru-Guzik, A., A Quantum-Quantum Metropolis Algorithm. arXiv:1011.1468.
Peng, X., et at. Quantum Adiabatic Algorithm for Factorization and Its Experimental Implementation.. Phys. Rev. Lett. 101, 220405 (2008).
Papadimitriou, C., Computational Complexity, Addison-Wesley, Reading, MA (1994).
Barahona, F., On the computational complexity of Ising spin glass models., J. Phys. A: Math. Gen. 15, 3241 (1982).
Kempe, J., Kitaev, A. Y. and Regev, O., The Complexity of the Local Hamiltonian Problem. SIAM J. Comp. 35, 1070 (2006).
Helgaker, T., Jrgensen, P. and Olsen, J., Molecular Electronic-Structure Theory, Wiley, New York (2000).
Kohn, W., Nobel Lecture: Electronic structure of matterwave functions and density functionals., Rev. Mod. Phys. 71, 1253 (1999).
Abrams, D. S. and Lloyd, S., Quantum Algorithm Providing Exponential Speed Increase for Finding Eigenvalues and Eigenvectors.. Phys. Rev. Lett. 83, 5162 (1999).
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. and Head-Gordon, M., Simulated Quantum Computation of Molecular Energies.. Science 309, 1704 (2005).
Wang, H. F., Kais, S., Aspuru-Guzik, A. and Hoffmann, M. R., Quantum algorithm for obtaining the energy spectrum of molecular systems.. Phys. Chem. Chem. Phys. 10, 5388 (2008).
Veis, L. and Pittner, J., Quantum computing applied to calculations of molecular energies: CH2 benchmark.. J. Chem. Phys. 133, 194106 (2010).
Whitfield, J., Biamonte, J., Aspuru-Guzik, A., Simulation of electronic structure Hamiltonians using quantum computers.. Mol. Phys. 109, 735 (2011).
Wu, L.-A., Byrd, M. S. and Lidar, D. A., Polynomial-Time Simulation of Pairing Models on a Quantum Computer.. Phys. Rev. Lett. 89, 057904 (2002).
Brown, K. R., Clark, R. J. and Chuang, I. L., Limitations of Quantum Simulation Examined by Simulating a Pairing Hamiltonian Using Nuclear Magnetic Resonance.. Phys. Rev. Lett. 97, 050504 (2006).
Edwards, E. E., et al. Quantum simulation and phase diagram of the transverse-field Ising model with three atomic spins. Phys. Rev. B 82, 060412(R) (2010).
Kim, K., et al. Quantum simulation of frustrated Ising spins with trapped ions. Nature 465, 590 (2010).
Du, J., et al. NMR Implementation of a Molecular Hydrogen Quantum Simulation with Adiabatic State Preparation. Phys. Rev. Lett. 104, 030502 (2010).
Peng, X., Wu, S., Li, J., Suter, D. and Du, J., Observation of the Ground-State Geometric Phase in a Heisenberg XY Model.. Phys. Rev. Lett. 105, 240405 (2010).
Biamonte, J. D., Bergholm, V., Whitfield, J. D., Fitzsimons, J. and Aspuru-Guzik, A., Adiabatic Quantum Simulators.. AIP Advances 1, 022126 (2011).
Chen, H., et al. Experimental demonstration of a quantum annealing algorithm for the traveling salesman problem in a nuclear-magnetic-resonance quantum simulator. Phys. Rev. A 83, 032314 (2011).
Feit, M. D., Fleck, J. A. and Steiger, A., Solution of the Schrdinger equation by a spectral method.. J. Comput. Phys.. 47, 412 (1982).
Kaye, P., Laamme, R., Mosca, M., An Introduction to Quantum Computing (Oxford University press, Oxford, 2007).
Davidson, E. R., Feller, D., Basis set selection for molecular calculations.. Chem. Rev. 86, 681 (1986).
Verstraete, F. and Cirac, J. I., Matrix product states represent ground states faithfully.. Phys. Rev. B 73, 094423 (2006).
See the supplementary materials (Appendix).
Lanyon, B. P., et al. Towards quantum chemistry on a quantum computer. Nature Chemistry 2, 106 (2010).
Poulin, D. and Wocjan, P., Preparing Ground States of Quantum Many-Body Systems on a Quantum Computer.. Phys. Rev. Lett. 102, 130503 (2009).
Leskowitz, G. M. and Mueller, L. J., State interrogation in nuclear magnetic resonance quantum-information processing.. Phys. Rev. A 69, 052302 (2004).
Fortunato, E. M., et al. Design of strongly modulating pulses to implement precise effective Hamiltonians for quantum information processing. J. Chem. Phys. 116, 7599 (2002).
Acknowledgements
We are grateful to the following funding sources: Croucher Foundation for M.H.Y; DARPA under the Young Faculty Award N66001-09-1-2101-DOD35CAP, the Camille and Henry Dreyfus Foundation and the Sloan Foundation and the NSF Center for Quantum Information and Computation for Chemistry, Award number CHE-1037992 for A.A.G. This work is also supported by the National Nature Science Foundation of China, the CAS and the National Fundamental Research Program 2007CB925200.
Author information
Authors and Affiliations
Contributions
M.-H.Y., J.D.W. and A.A-G., contributed mainly to the experimental proposal, theoretical analysis, figures and the overall writing. Z.L., H.C. and D.L., contributed mainly to the design of the experimental procedure, data collection and analysis. X.P. and J.D. supervised the experiment. All authors contributed to the writing of the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Li, Z., Yung, MH., Chen, H. et al. Solving Quantum Ground-State Problems with Nuclear Magnetic Resonance. Sci Rep 1, 88 (2011). https://doi.org/10.1038/srep00088
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00088
This article is cited by
-
Hardware-efficient quantum principal component analysis for medical image recognition
Frontiers of Physics (2024)
-
Quantum embedding theories to simulate condensed systems on quantum computers
Nature Computational Science (2022)
-
Decoherence Control of Nitrogen-Vacancy Centers
Scientific Reports (2017)
-
Hybrid reconstruction of quantum density matrix: when low-rank meets sparsity
Quantum Information Processing (2017)
-
Adiabatic Quantum Simulation of Quantum Chemistry
Scientific Reports (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.










 , T+1 = |00〉,
, T+1 = |00〉,  and T−1 = |11〉, of the Heisenberg Hamiltonian in the initial and final states.
and T−1 = |11〉, of the Heisenberg Hamiltonian in the initial and final states.