Abstract
Recently, co-seismic seismic source characterization based on GPS measurements has been completed in near- and far-field with remarkable results. However, the accuracy of the ground displacement measurement inferred from GPS phase residuals is still depending of the distribution of satellites in the sky. We test here a method, based on the double difference (DD) computations of Line of Sight (LOS), that allows detecting 3D co-seismic ground shaking. The DD method is a quasi-analytically free of most of intrinsic errors affecting GPS measurements. The seismic waves presented in this study produced DD amplitudes 4 and 7 times stronger than the background noise. The method is benchmarked using the GEONET GPS stations recording the Hokkaido Earthquake (2003 September 25th, Mw = 8.3).
Similar content being viewed by others
Introduction
Our capability to characterize both the seismic wave propagation and the seismic sources depends on the quality (accuracy and variety) of the datasets available. Since the 1970s, seismic networks were deployed to achieve these goals at the global scale1,2. The rise of broadband and very-broadband seismometers allowed tremendous progress. These networks made many discoveries possible, amongst which anisotropy, study of the core-mantle boundary, mapping of subducting plates in the mantle, etc. Nowadays, the rising cost of operations and the difficulty of accessing best locations for new sites, make it arduous to expand these networks much further. GPS receiver, with its cheaper installation and maintenance, offers an alternative to seismic sensors when it comes to the collection data in the range of periods from 10 to 200 seconds. Other advantages of GPS receiver are 1) that it does not have instrument response, 2) that it does not clip during strong motion and 3) that it provides ground motion time-series in displacement. The challenges of integrating the acceleration or velocity records3 are thus avoided. If the GPS waveforms were demonstrated to be as reliable as seismic waveforms, they could be integrated into global Earth tomographies at long-period (T = 20 seconds or more).
Today, a few studies using GPS take advantages of GPS waveforms. Mostly, daily processing studies rather focus on the study of coseismic (first days)4 to post-seismic (first weeks to months) deformation5 in near- and far-field (distance larger than rupture length) and with remarkable results. These successes caused us to forget that the accuracy of the ground deformation measurements rely on the distribution of satellites. For positions computed over hours or days, the distribution of satellites is not an issue because the precise orbits help defining an average daily position using the satellites that are visible during the sideral day. Nevertheless, for shorter periods (minutes to hours), the lack of satellites in the sky might decrease the quality of the solutions. This effect can be seen when computing static displacement across very short sessions, but might be even more critical when GPS waveforms are computed. Yet recent studies showed that GPS receivers with high rate capabilities (e.g., 1Hz sampling rate) are sensitive to ground motion induced by seismic events including the 2002 Denali6,7,8,9, the 2003 Tokachi-Oki10,11, the 2003 San Simeon12,13, the 2004 Sumatra-Andaman14, the 2008 Iwate-Miyagi Nairiku15, the 2010Maule Earthquake16 earthquakes. In some cases, GPS observations collected were positively correlated to co-located seismic records.
The events detected by GPS stations are generally large (Mw > 6.0). This is due to the reduced GPS sensitivity to ground displacement compared to seismometers, as well as to most networks being designed to survey continental deformation (with a spacing of 40 km or more). There is no theoretical limitation to the detection of small events (Mw < 6.0). GPS phase aliasing (related to internal receiver filtering) appears to be the main parameter in reducing the sensitivity of GPS to describe ground vibrations17. To minimize this effect, operators converted their network to high sampling rate (1Hz or more). Today, a growing number of GPS receivers could be converted to 1Hz sampling rate (Figure 1) at minimal cost (change of telemetry), which encourages the support of seismic studies using long-period (Period T> 20s) GPS waveforms.
Global high-rate GPS network operating today.
Among the Global GPS network 1905 GPS sites providing data on a daily basis to SOPAC archive42, we highlight the GPS sites that belong to the NTRIP (red triangles) and IGS (black circles) networks that are recording freely available 1Hz data. For clarity reasons, the GEONET, Plate Boundary Observatory (1000+ sites) and BARD43,44,45 networks are not fully plotted on this map.
Demonstrating that the GPS is at least as reliable as seismic sensors requires 1) to calibrate successfully GPS waveforms against seismic records, 2) to address computational issue(s) that could affect the GPS accuracies and 3) to reliably detect small amplitude ground vibrations at long distance (500 km or more i.e. distance that is comparable with previous works7).
So far, some intrinsic errors have limited the reliability of records: the propagation of the GPS signal through the ionosphere and troposphere; satellite visibility; the clock delay; local site obstacles such as the multipath produced by reflection and/or diffraction of the GPS signal at the receiver site environment; and lastly, the accuracy of the displacement time-series. Because of these, GPS has failed to be integrated with seismic data into global tomographies18 yet. These issues, though, have been solved and time-series of daily solutions produced, already. Most of the effects, related to the propagation GPS signals from the satellite to the site, are now eluded by the use of adequate data analysis based on a GPS network approach19,20. These methods are based on the regional spatial filtering21 or/and the modified sidereal filtering (MSF)22.
In this study, we investigate the impact of a low number of satellites in the sky on the shape of GPS waveforms. We then test a new method to study seismic waves in 1Hz GPS time series based on the well-known computation of GPS double difference (DD) (see Methodology section). This allows for the detection of 3D ground shaking produced by surface wave propagation. The method is benchmarked using the GEONET23,24 GPS stations recording the Hokkaido Earthquake (2003 September 25th, Mw = 8.3, Figure 2). The source mechanism was favourable for surface waves generation and local static displacement at the epicentre was estimated at around 5–9 methers10,25,26.
Results
Daily processing is efficient at eliminating most of the GPS uncertainties (see Introduction). Hence, we processed the GPS data collected during the hours following the 2003 Hokkaido event (the data processing is described in detail in the Methodology section). We then extracted the residuals (LC ionosphere-free) from the daily solutions for each line-of-sight (LOS), to recover the motion of each site. The phase residuals correspond to all the phase changes that cannot be explained by the motion of satellites above the network. We use them to extract the short-lived disturbances of the phase received across the network. This methodology has already been applied to the study of volcanic atmospheric plumes in order to constrain the troposphere variations with respect to the standard atmospheric model used during the GPS processing27,28. In that case, the troposphere state changes were perturbing the GPS signals. As the GPS receivers were not moving during the explosions, the phase residuals were fully attributed to the presence of the volcanic plume. The problem we address here is similar in that the GPS phase is changed. But not by a volcanic plume; here it is the receiver's change of positions that affect the GPS phase. Each phase change is valid for a LOS (defined by the azimuth and elevation angles of one satellite from a given site).
The number of LOS residual histories equals the numbers of satellites visible at a single site. We use all the LOS residual histories available to compute the East, North and Vertical motion (E,N,U) at a given time:

where the u, v and w are the components of the unit vector of each satellite LOS and φ the phase change in the direction of LOS (e.g.17). λ is the wavelength of the residuals carrier.
Following this approach, the quality of the displacement time-series inferred from the inversion of residuals in the line-of-sight (LOS) do rely on the distribution of the satellites in the sky (Figure 3 shows these distributions of satellites for various sites) at the time of the seismic wave arrival at the site. As the GPS system is based on the time arrival of the GPS signal at the receiver, if fewer satellites are located along a North-South azimuth the accuracy of the north-south component will be affected. The quality of the ground displacement solutions will be function of a parameter that describes the geometry of the tetrahedrons defined by 3 satellites and a site. Closer to 90 degrees the angles of tetrahedron will be, better the solutions will be. We build an operator that we name K, which is the average of all the mixed products of LOS unit vectors we can create at a site:

where N is the maximal number of triplets and  are the three unit vectors of three given satellites LOS. The equation (1) says that in the best conditions (elevation angle = 0; no masks), K = 1.
are the three unit vectors of three given satellites LOS. The equation (1) says that in the best conditions (elevation angle = 0; no masks), K = 1.
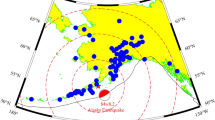
Skyview plot of the satellites above the sites 0051, 0222, 0292, MIZU and TSKB at the time of the seismic waves passage.
The satellite configuration is not optimal because the number of satellites is limited along the axis N0/N180. Although, this lack of satellites is not due to a satellite tracking issue, because the position of satellite vary little from site to site (over 300 km distance). All sites will have poor accuracy on the north component of the vibration as there are very few sites in the quadrants N135-N225 and N315-N45
However, as the satellites lower than 15 degrees elevation cut-off are usually not considered in the processing, the value of K can only be < 1. α is the maximum value for K in our computing:

The value of K ranges from 0 (all the satellites are aligned along a perfect line in the sky) to a best possible value (K ∼ 0.93 in the case of the distribution described in Table 1). At the time of the seismic wave propagation in Japan, the value of K does not exceed 0.25, one of the lowest values for that day (Figure 4).
Potential GPS constellation for three IGS (AIRA, MIZU and TSKB) sites located in Japan during the DOY 268 (25 September 2003).
The sites are respectively indicated using gray, red and black lines. We characterize this potential by plotting the number of satellites visible at each site (top panel) and the parameter K (computed every 15 min)at the site 0292 (lower panel) during the day. At the time of the earthquake (vertical red line) the number of satellites available over Japan is close to 10 satellites. Still, we stress that the orientation of these satellites is important too. The parameter K (see text for an accurate description) at the time of the seismic wave propagation is not close (K ∼ 0.2) to the theoretical value of K (∼ 0.93). We indicate the maximal theoretical value with a horizontal red line on the lower panel).
The analysis showing the frequency content of the LOS residuals showed phase residuals could be used to recover ground motion (Figure 5). In Figure 6, we compare the motion recovered for the site 0292 with the seismic records of the GEOSCOPE1 very-broadband (STS-129,30) seismometer located in INUyama, Japan (Figure 2). The seismic records have been corrected from instruments response (into displacement) and decimated to 1Hz. The distance between the two sites is ∼ 10 km. As we consider periods ranging from 30 to 50 seconds, we do not expect any difference in the motion of the two sites.
Results of the inversion computed for the 0292 site (Figure 2).
We compare the time-series of GPS displacement (in red) with the seismograms recorded at the GEOSCOPE site INU (in black). We note that while the agreement between the two sets of waveforms is reasonable for eastern and vertical components it could be more problematic for the northern one. Instrument responses have been provided by GEOSCOPE. Both datasets have been band-pass filtered between 30 and 50 seconds (20 and 35 mHz) according to the periodogram presented in Figure 5.
The agreement between both sets of horizontal records (Figure 6) is not optimal (RMSeast = 9.7310−2, RMSnorth = 5.8710−2,  with N = 400). The horizontal amplitudes are not fully recovered by the inversion of the GPS LOS. Even so, the phase of the east component is in good agreement with the phase of the east component of the seismic record. The phases and amplitudes recovered for the north component are not matching the north component of the seismic record. We note a better agreement (phase match) for east direction which is better constrained by the satellites positions in the sky (Table 2). The vertical GPS component compares well (RMSvert = 2.3210−2, N = 400) with the vertical component of the seismic sensor. We attribute the slight phase delay between the two time-series to an effect of the band-pass Butterworth filter used to produce the seismic time-series. We compare the frequency content of both seismic and GPS vertical components (Figure 7). While the agreement is good in the frequency range from 0.0125 to 0.1 Hz (10 to 80 seconds), unexpected high amplitude noise is visible for longer periods. We have not fully explained such discrepancy yet.
with N = 400). The horizontal amplitudes are not fully recovered by the inversion of the GPS LOS. Even so, the phase of the east component is in good agreement with the phase of the east component of the seismic record. The phases and amplitudes recovered for the north component are not matching the north component of the seismic record. We note a better agreement (phase match) for east direction which is better constrained by the satellites positions in the sky (Table 2). The vertical GPS component compares well (RMSvert = 2.3210−2, N = 400) with the vertical component of the seismic sensor. We attribute the slight phase delay between the two time-series to an effect of the band-pass Butterworth filter used to produce the seismic time-series. We compare the frequency content of both seismic and GPS vertical components (Figure 7). While the agreement is good in the frequency range from 0.0125 to 0.1 Hz (10 to 80 seconds), unexpected high amplitude noise is visible for longer periods. We have not fully explained such discrepancy yet.
Comparison of the time-frequency estimates of a) Seismic data and b) GPS Data.
Time-frequency amplitudes are calculated using the s-transform46 (resolution factor = 1) and are normalized using the maximum amplitude for each frequency near the event arrival time. Relative arrival times of the peak amplitudes (c) are picked from both seismic and GPS data. Good correlation is found in the 15–50 second (0.015–0.07Hz) period band.
We showed that the limitations of the GPS are due at least partially to the distribution of the satellites in the sky. We need to set up a processing strategy that enables us to estimate the ground motion whatever the number of visible satellites and their distributions in the sky are. This methodology must enable the detection of both static motions close to seismic ruptures but also of ground displacements produced by propagation of surface waves, namely Rayleigh and Love waves.
Our approach is based on the computation of the double difference (DD) from a pair of satellites and stations (Figure 8). GPS processing packages commonly use this method for computing GPS data because it allows working with few satellites. The DD allows an instantaneous quasianalytical reduction of the major errors (ionosphere, troposphere and clocks delays) assumingmost of the errors are seen by the other components of the DD (satellite or site) at the same time.
Schematic illustration of the ground shaking propagating along the surface and perturbing four ray-paths arriving at the two GPS sites i and j.
The four residuals of the four signals received at site i and j are computed using GAMIT36. Because Rayleigh waves are not arriving at the same time to both sites, the residuals of the Double Difference are not equal to zero.
Here, in order to prove the sensitivity of DD to ground motion, we employed 2 GPS stations (sites 0051 and 0222) located in the far field at ∼ 6° from the epicenter (Figure 2). We picked these two sites because they are located on a small circle and their DD residuals are expected to be minimal. Success with theses two stations will make our experiment meaningful for all the other pairs of stations.
We detected oscillations for all the stations at the expected time of seismic arrival at the sites. We focused on the two sites (0051 and 0222), 128 kilometers apart (Figure 2), along the propagation front. We show all DD residuals between the 2 sites in Figure 9. We have compared the Fourier spectra of GPS DD residuals with and without seismic transients. During the hour including the earthquake occurrence, we observe a strong peak between 20 and 35 mHz (T ∼ 30 to 50s) (Figure 10).
Examples of the residuals observed on the DD between the benchmarks 0222 and 0051 and each couple of satellite (as in the sketch of Figure 8).
The wavelength of the LC combination is ∼ 48 cm per cycle. Time is indicated in seconds. Pseudo-Range numbers (PRN) are indicated for each DD.
Frequency spectra of the residuals presented in Figure 9.
a) Amplitudes of the Fourier spectra of the GPS residuals computed for data recorded before the seismic wave arrival. Peak frequencies are located below 25mHz. b) Amplitudes of the Fourier spectra of the GPS residuals plotted in Figure 9. Peak frequencies are located around 30mHz.
Our next aim was to determine whether the GPS DD observations are related to the seismic source only, or to some other process (such as site effect, monument oscillation, etc.) as well. We thus performed a test, comparing the DD observations with synthetic DD. In order to obtain synthetic DD, we first computed the synthetic waveforms expected at the GPS sites by using a combined discrete-wave number and reflectivity method31,32,33. This is completed by combining synthetic seismograms computed using a CMT solution34 and a crustal model (Table 3) from a regional average of the global tomography35. The source parameters used in the computation are based on the seismic moment of ∼ 3 × 1021 Nm, the source depth of 13 km and the focal mechanism: strike 234°, Dip 7° and Rake 103°. The synthetic ground displacements are then converted into synthetic DD residuals ( ) by projecting the local motion (E, N and U) onto the LOS of the satellite that is defined by the unit vector (u,v,w):
) by projecting the local motion (E, N and U) onto the LOS of the satellite that is defined by the unit vector (u,v,w):

The synthetic seismic DD,  , is using four projections created at two sites k and l:
, is using four projections created at two sites k and l:

where  is the wave length of the LC signal (∼ 48cm per cycle) and
is the wave length of the LC signal (∼ 48cm per cycle) and  the seismic vibration 154 projected along the LOS between satellite x and the satellite y.
the seismic vibration 154 projected along the LOS between satellite x and the satellite y.
We compare the synthetic residuals  with the observed phase time-series (Figure 11). All seismic and GPS waveforms have been band-pass filtered between 20 and 35 mHz, coherently with the frequency signature of the transient displacement (Figure 10). The good agreement between the observed and the predicted residuals (Table 4) confirms that the DD are detecting seismic surface waves at around 700 km from the epicentre. We list the values of the RMS in Table 4.
with the observed phase time-series (Figure 11). All seismic and GPS waveforms have been band-pass filtered between 20 and 35 mHz, coherently with the frequency signature of the transient displacement (Figure 10). The good agreement between the observed and the predicted residuals (Table 4) confirms that the DD are detecting seismic surface waves at around 700 km from the epicentre. We list the values of the RMS in Table 4.
GPS Observables plotted in Figure 9 compared with synthetics.
The data and the synthetic data are filtered by using a bandpass filter 0.020 – 0.035Hz. This bandpass filter is in agreement with the spectra made using unfiltered GPS residuals data (Figure 10). There is a good matching between the residuals GPS filtered data and the filtered seismic time-series.
Discussion
We show that GPS inversion of phases in the local reference (East, North and Vertical directions) is limited by the distribution of the GPS constellation. The start of the GALILEO program, by adding more satellites in the sky, brings great hopes in the matter. Additionally, we show that the inversion of phases is meant to be limited to the local reference frame (East, North, Up) but could be expanded to the reference frame defined by the LOS of the visible satellites, using the DD method.
Whatever its capability to recover local motion histories (East, North, Vertical components), GPS can provide constraints by using LOS residuals within DD geometry. We suggest that GPS observations can provide additional constraints on the seismic moment.
This successful comparison between synthetic ground displacement and the DD GPS observations suggests that the use of GPS networks in regional or even global tomographies is possible. Our methodology also offers an opportunity to improve the GPS sensitivity to ground shaking and constitutes a powerful tool for a better understanding of long-period geophysical processes through the lithosphere.
In validating the comparison between a seismic 1D model and the GPS observations, we suggest the GPS might now be considered a supplement to broadband seismic networks. Furthermore, GPS networks could provide complementary constraints on the surface displacement by increasing the spatial resolution of the observed surface wave fronts and/or to the kinematic rupture modeling. The agreement between data and synthetics suggests that DD can be integrated in tomographic problems instead of fixed local three components, taking advantage of the higher sensitivity of DDs.
Methods
Daily Data processing
To test the sensitivity of the network to lateral motion, we select GPS receivers located approximately at 700 km radius from the epicentre (indicated by a circle in Figure 2). Working with such sub-network configuration allows for detecting both the arrival time of the surface waves and the wave polarity and amplitude variations with the site.
The local permanent GPS stations (KSMV, MIZU, TSKB, USUD, YSSK [not on Figure 2, N47.03, E142.72] in Figure 2 belonging to the International GPS Service (IGS) have been integrated in the analysis to stabilize the processing using accurate orbits.
All calculation have been completed using the GAMIT/GLOBK Tool suite36,37, following a standard procedure for large static networks (the network is not affected by co-seismic offsets) We have extracted residuals that could not be explained by tides, GPS constellation cycle slip, or tropospheric and ionospheric perturbations.
In order to minimize the noise due to the very low elevation LOS, the minimal elevation angle was fixed at 15 degrees above the horizon and the ambiguity resolution was done assuming a baseline length lower than 500 km. The troposphere delay was estimated using the standard meteorologicalmodel38 but as the weather is supposed to be constant during the wave propagation over the network, we do not expect oscillation in the computed GPS waveforms. Additionally, we have used the LC (ionosphere free) frequency, which minimizes the effect of the ionosphere on the GPS observables and assures the results are free of high frequency post-seismic perturbation taking place in the ionosphere39,40.
The double difference
A Double Difference (DD) is computed using signals from two given satellites received at two selected stations. The residuals on the DD are the difference between the residual phases of four signals received at two different stations. The DD are not oriented in the local reference frame but in a reference frame defined by the four lines of sight of the two satellites at the two GPS receivers. The DD represents the sum of displacements of two sites seen by two different satellites. For each couple of available sites, the residual on the double difference between two sites has been investigated. The final DD residuals  can be described as follows:
can be described as follows:

where  is the residual distance between the station j and the satellite l, c the speed of light and f the frequencies of the signal for the two carrier frequencies L1 and L2.
is the residual distance between the station j and the satellite l, c the speed of light and f the frequencies of the signal for the two carrier frequencies L1 and L2.  is a scalar number comprising the unmodeled processes (orbits errors, troposphere, ionosphere, noise on the measurement, etc).
is a scalar number comprising the unmodeled processes (orbits errors, troposphere, ionosphere, noise on the measurement, etc).
The residuals computed with equation 5 are free of all instrumental time stamp errors. Finally, we computed the ionosphere free residual  from L1 and L2 carrier residuals41.
from L1 and L2 carrier residuals41.

 represents the sum of all processes not modeled such as the measurement noise of the GPS receiver.
represents the sum of all processes not modeled such as the measurement noise of the GPS receiver.
References
Romanowicz, B., Cara, M., Fels, J. and Rouland, D. GEOSCOPE: A French Initiative in Long Period, Three Component, Global Seismic Networks. Eos Trans. Am. Geophys. Union 65, 753–754 (1984).
Roult, G., Lépine, J., Bonaimé, S. and Riveira, L. The GEOSCOPE program: state of the art in 2005. In AGU 2005 Fall Meet. Suppl., volume 86, (2005).
Boore, D. M. Analog-to-Digital Conversion as a Source of Drifts in Displacements Derived from Digital Recordings of Ground Acceleration. Bull. Seismol. Soc. Am. 93(5), 2017–2024 (2003).
Simons, M., Fialko, Y. and Rivera, L. Coseismic deformation from the 1999 M w 7.1 Hector Mine, California, earthquake as inferred from InSAR and GPS observations. Bull. Seismol. Soc. Am. 92(4), 1390–1402 (1999).
Marone, C. J., Scholz, C. and Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. 96, 8441–8452 (1991).
Kouba, J. Measuring seismic waves induced by large earthquakes with GPS. Stud. Geophys. Geod. 47, 741–755 (2003).
Larson, K., Bodin, P. and Gomsberg, J. Using 1-Hz GPS Data to Measure Deformations Caused by the Denali Fault Earthquake. Science 300, 1421–1424 (2003).
Bock, Y., Prawirodirdjo, L. and Melbourne, T. Detection of arbitrary large dynamic ground motions with a dense high-rate GPS network. Geophys. Res. Lett. 31(L06604) (2004).
Bilich, A., Cassidy, J. and Larson, K. GPS Seismology: Application to the 2002 Mw 7.9 Denali Fault Earthquake. Bull. Seismol. Soc. Am. 98, 593–606 (2008).
Miyazaki, S. et al. Modeling the rupture process of the 2003 September 25 Tokachi-Oki (Hokkaido) earthquake using 1-Hz GPS data. Geophys. Res. Lett. 31, L21603 (2004).
Emore, G., Haase, J., Choi, K., Larson, K. and Yamagiwa, A. Recovering absolute seismic displacements through combined use of 1-Hz GPS and strong motion accelerometers. Bull. Seismol. Soc. Am. 97, 357–378 (2007).
Ji, C., Larson, K., Tan, Y., Hudnut, K. and Choi, K. Slip history of the 2003 San Simeon earthquake constrained by combining 1-Hz GPS, strong motion and teleseismic data. Geophys. Res. Lett. 31(17) (2004).
Wang, G., Boore, D. M., Tang, G. and Zhou, X. Comparisons of ground motions from collocated and closely spaced one-sample- per-second Global Positioning System and accelerograph recordings of the 2003 M 6.5 San Simeon, California, earthquake in the Parkfield Region. Bull. Seismol. Soc. Am. 97(1B), 76–90 (2007).
Ohta, Y., Meiano, I., Sagiya, T., Kimata, F. and Hirahara, K. Large surface wave of the 2004 Sumatra-Andaman earthquake captured by the very long baseline kinematic analysis of 1-Hz GPS data. Earth Planets Space 58, 153–157 (2006).
Yokota, Y., Koketsu, K., Hikima, K. and Miyazaki, S. Ability of 1-Hz GPS data to infer the source process of a medium-sized earthquake: The case of the 2008 Iwate-Miyagi Nairiku, Japan, earthquake. Geophys. Res. Lett. 36(L12301) (2009).
Delouis, B., Nocquet, J.-M. and Vallée, M. Slip distribution of the February 27, 2010 Mw = 8.8 Maule Earthquake, central Chile, from static and high-rate GPS, InSAR and broadband teleseismic data. Geophys. Res. Lett. 37(L17305) (2010).
Houlié, N. and Allen, R. The Instantaneous Displacement (ID) Method: Application of rapid displacement estimates to earthquake early warning alerts. Eos Trans. Am. Geophys. Union 89(23) (2007).
Romanowicz, B. Global mantle tomography: Progress status in the past 10 years. Annual Review of Earth and Planetary Sciences 31(1), 303–328 (2003).
Altamimi, Z., Sillard, P. and Boucher, C. ITRF2000: A New Release of the International Terrestrial Reference Frame for Earth Science Applications. J. Geophys. Res. 107(B10), 2114 (2002).
Trota, A., Houlié, N., Sigmundsson, F. and Jònsson, S. Deformations of the Furnas and Sete Cidade Volcanoes. Velocities and furt her investigations. Geophys. J. Int. 166(2), 952 (2006).
Wdowinski, S., Bock, Y., Zhang, J., Fang, P. and Genrich, J. Southern California Permanent GPS Geodetic Array: Spatial filtering of daily solutions for estimating coseismic and postseismic displacements induced by the 1992 Landers earthquake. J. Geophys. Res. 102(B8), 18057–18070 (1997).
Choi, K., Bilich, A., Larson, K. and Axelrad, P. Modified sidereal filtering: implications for high-rate GPS positioning. Geophys. Res. Lett. 31(22) (2004).
Miyazaki, S., Hatanaka, Y., Sagiya, T. and Tada, T. The nationwide GPS array as an Earth Observation System. Bull. Geogr. Surv. Inst. 44, 11–22 (1998).
Hatanaka, Y. et al. Improvement of the Analysis Strategy of GEONET. Bull. Geol. Surv. Inst. 49 (2003).
Coffin, M. and Hirata, N. Large Earthquake Strikes Hokkaido, Japan. Eos Trans. Am. Geophys. Union 84(42) (2003).
Yagi, Y. Source rupture process of the 2003 Tokachi-oki earthquake determined by joint inversion of teleseismic body wave and strong ground motion data. Earth & Planet. Sc. Lett. 56, 311–316 (2004).
Houlié, N., Briole, P., Nercessian, A. and Murakami, M. Sounding the plume of the 18 August 2000 eruption of Miyakejima volcano (Japan) using GPS. Geophys. Res. Lett. 32(L05302) (2005).
Houlié, N., Briole, P. and Nercessian, A. 2005, March 9 th Mount St Helens explosion. Eos Trans. Am. Geophys. Union 86(30), 277–284 (2005).
Wielandt, E. and Streckeisen, G. The leaf-spring seismometer; design and performance. Bull. Seismol. Soc. Am. 72(A), 2349–2367 (1982).
Wielandt, E. and Steim, J. A digital very broadband seismograph. Ann. Geophys. 4b(227) (1986).
Bouchon, M. A simple method to calculate Green's functions for elastic layered media. Bull. Seismol. Soc. Am. 71, 959–971 (1981).
Kennett, B. L. N. Seismic Wave Propagation in Stratified Media. Cambridge University Press, Cambridge, England, (1985).
Coutant, O. Program of Numerical Simulation AXITRA. Res. Report LGIT- Grenoble, in French, (1989).
Dziewonski, A., Chou, T.-A. and Woodhouse, J. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. 86, 2825–2852 (1981).
Shapiro, N. and Ritzwoller, M. Monte-carlo inversion for a global shear velocity model of the crust and upper mantle. Geophys. J. Int. 151, 88–105 (2002).
King, R. and Bock, Y. Documentation of the GAMIT software. MIT/SIO, (2006).
Herring, T. GLOBK: Global Kalman Filter VLBI and GPS Analysis Program, version 10.2 (2005).
Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites. AGU Geophysics Monograph Series 15, 247–251 (1972).
Ducic, V., Artru, J. and Lognonné, P. Ionospheric remote sensing of the Denali Earthquake Rayleigh surface waves. Geophys. Res. Lett. 30(18), 1951, doi:10.1029/2003GL017812 (2003).
Lognonné, P. et al. Ground based GPS imaging of ionospheric post-seismic signal. Planet. Space. Science 54, 528–540 (2006).
Bender, P. L. and Larden, D. GPS carrier phase ambiguity resolution over long baselines. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Goad C., editor, volume 1, 357–361, (1985).
Jamason, P. et al. SOPAC web site (http://sopac.ucsd.edu). GPS Solutions 8(4), 272–277 (2004).
King, G. C. P., Stein, R. S. and Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 84, 835–953 (1994).
Murray, M. H., Dreger, D., Neuhauser, D., Baxter, D., Gee, L. and Romanowicz, B. Real-time geodesy. Seis. Res. Lett. 69(145) (1998).
Houlié, N. and Romanowicz, B. Asymmetric deformation across the San Francisco Bay Area faults from GPS observations in Northern California. Phys. Earth Planet. Inter. 184(3–4), 143–153 (2011).
Stockwell, R., Mansinha, L. and Lowe, R. Localization of the complex spectrum: the S transform. IEEE transactions on signal processing 44(4), 998–1001 (1996).
Acknowledgements
We thank Geographical Survey Institute for providing the 1Hz GPS data. This work was partially supported by Berkeley Seismological Laboratory (BSL) and by US Geological Survey Cooperative Agreement to BSL #G10AC00141. It is BSL Contribution #11-05
Author information
Authors and Affiliations
Contributions
N.H. and G.O. initial idea, conception and writing; T.B. calibration with seismic sensor; N.S. computed seismic synthetics presents and helped with the writing; P.L. provided the dataset and helped with the writing; and M.M. provided the dataset.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Houlié, N., Occhipinti, G., Blanchard, T. et al. New approach to detect seismic surface waves in 1Hz-sampled GPS time series. Sci Rep 1, 44 (2011). https://doi.org/10.1038/srep00044
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00044
This article is cited by
-
Surface waves magnitude estimation from ionospheric signature of Rayleigh waves measured by Doppler sounder and OTH radar
Scientific Reports (2018)
-
GPS source solution of the 2004 Parkfield earthquake
Scientific Reports (2014)
-
Observation of Earth's free oscillation by dense GPS array: After the 2011 Tohoku megathrust earthquake
Scientific Reports (2012)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.