Abstract
Fluctuation X-ray scattering (FXS) is an emerging experimental technique in which solution scattering data are collected using X-ray exposures below rotational diffusion times, resulting in angularly anisotropic X-ray snapshots that provide several orders of magnitude more information than traditional solution scattering data. Such experiments can be performed using the ultrashort X-ray pulses provided by a free-electron laser source, allowing one to collect a large number of diffraction patterns in a relatively short time. Here, we describe a test data set for FXS, obtained at the Linac Coherent Light Source, consisting of close to 100 000 multi-particle diffraction patterns originating from approximately 50 to 200 Paramecium Bursaria Chlorella virus particles per snapshot. In addition to the raw data, a selection of high-quality pre-processed diffraction patterns and a reference SAXS profile are provided.
Design Type(s) | virus particle imaging objective |
Measurement Type(s) | X-ray diffraction data |
Technology Type(s) | X-ray free electron laser |
Factor Type(s) | |
Sample Characteristic(s) | Paramecium bursaria Chlorella virus 1 |
Machine-accessible metadata file describing the reported data (ISA-Tab format)
Similar content being viewed by others
Background & Summary
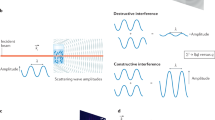
Fluctuation X-ray scattering (FXS) studies extend traditional small angle X-ray scattering (SAXS) methods by using X-ray snapshot with exposure times so short that the ensemble of illuminated particles can be well approximated as frozen in time and space. The resulting scattering patterns are no longer angularly isotropic, but instead exhibit small intensity fluctuations around the mean SAXS intensity1,2. Angular correlations of these intensity fluctuations can be directly related to the underlying molecular structure of the sample, providing much more information than traditional 1D SAXS curves3. The correlation function is defined as
where N is the total number of diffraction patterns, q and q' are the magnitudes of the scattering vectors (in inverse resolution), and ϕ and ϕ + Δϕ are the corresponding angular coordinates describing the intensity Ij(q, ϕ) of the jth scattering pattern recorded on the detector. The correlation function can be written as a Legendre series:
where Pl is the Legendre polynomial of order l and , λ is the wavelength of the incident X-rays, and ki is a scale factor equal to the number of particles in the beam for l > 0, and equal to its square for l=0. The expansion coefficients Bl(q, q′) are in turn related to the spherical harmonic expansion coefficients Ilm(q) of the 3D intensity scattering volume I(q) of the scattering particle, where q=(q, θ, ϕ):
where, in polar coordinates,
The intensity function is equal to the square of the modulus of the Fourier transform of the real-space object ρ(r) under investigation:
where ℱ denotes the Fourier transform1.
Prior work in fluctuation scattering from biological samples has demonstrated that high-quality correlation data can be obtained from single-particle diffraction data4 and can be used for ab initio structure determination using the multi-tiered iterative phasing algorithm5. Although previous work has shown that the signal to noise ratio (SNR) of such data is independent of the number of particles per shot5 when the particles are in a vacuum, the relationship between number of particles and SNR in the presence of large buffer and detector backgrounds has not yet been studied. In this communication, we describe unprocessed, experimental multi-particle scattering data from which an FXS correlation data set can be derived. The data, obtained at the Atomic, Molecular and Optical (AMO) instrument at the Linac Coherent Light Source6,7, consist of close to 60 000 high quality scattering images of the Paramecium bursaria Chlorella virus 1 (PBCV-1, ~190 nm in diameter8) and 30 000 scattering images of the sample buffer. The images presented here provide the community with experimental data on which algorithms for processing fluctuation scattering data and structure solution can be tested. The data are deposited at the CXIDB9 in the form of hdf5 and xtc files.
Methods
Sample Preparation, Sample Delivery and Data collection
A batch of Paramecium Bursaria Chlorella virus 1 sample was prepared as described previously10. Here we used 1% triton instead of Nonidet and centrifuged the virus sample at 20,000 rpm in an ultracentrifuge. The pure virus sample was dialyzed against 50 mM 4-methylmorpholine11. The quality of the FXS data was gauged by comparing the derived SAXS data against a reference Small Angle Scattering curve obtained at the cSAXS beamline at the Swiss Light Source, at an energy of 11 keV. The sample used for FXS data collection was diluted with buffer to a concentration of approximately 5 × 1011 particles per ml.
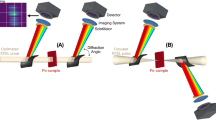
The multi-particle FXS scattering data were collected at the Atomic, Molecular and Optical (AMO) instrument at the LCLS6,7. The experiment was performed in the CFEL-ASG Multi-Purpose chamber (CAMP)12. The PBCV-1 solution described above was injected into the XFEL interaction region as a microjet of approximately 5 μm diameter, using a gas dynamic virtual nozzle (GDVN) injector13,14 at a flow rate of ~20 μl/min (Fig. 1). The diffraction data were collected in the water window, using a photon energy of 514 eV, an electron bunch length (pulse length) of 100 fs and a repetition rate of 120 Hz. The average number of photon per pulse was 1012. The focus size was approximately 25 μm2 (FWHM). Diffraction patterns were collected on two pairs of p-n junction charge-couple device (pnCCD) detectors15 read out at 120 Hz. The front and back panels of the detector consisted of two pairs of 1024 × 512 arrays of square 75 μm× 75 μm pixels. The front panels were placed 224 mm from the interaction region, separated by a horizontal gap of 23 mm. The back detector was placed 741 mm from the sample/XFEL interaction zone, with a horizontal gap of 1.73 mm (Table 1). The maximum resolution achievable under these conditions is 14.3 nm (8.9 nm) at the edge (corner) of the front and 46.8 nm (32.7 nm) at the edge (corner) of the back detector. The X-ray scattering patterns and associated metadata were stored as xtc files. These diffraction images were pre-processed using the CFEL-ASG Software Suite (CASS)16. The images were corrected for dark current; pixels systematically producing outlying intensity values were flagged. The resulting data was cast in larger arrays to include the detector gaps. The detector halves were placed roughly symmetrically around the X-ray beam. The back detector, with gaps included, is contained in an array of 1024 by 1047, with the mean beam center located at (506, 526). The front detector (with gaps included) is contained in an 1331 by 1031 array, with a mean beam center of (657, 552). The back detector was at gain mode 1, corresponding to 1250 ADU per 1keV photon. The gain mode of the front pnCCD was 4, corresponding to 78 ADU per 1keV photon. The resulting arrays are stored in an hdf5 file and are deposited in the CXIDB with accession number 79 (Data Citation 1). A Globus end-point is available for high-speed data-transfer.
(a) An FXS experiment at an XFEL can be performed by intersecting a liquid jet containing the sample particles with the XFEL pulse and recording the diffraction pattern on a multi-panel detector. The data generated by the setup described in this manuscript resulted in a maximum resolution of 14.3 nm (8.9 nm) at the edge (corner) of the front and 46.8 nm (32.7 nm) at the edge (corner) of the back detector. (b) Calculation of the intensity correlations is performed according to equation 1. The scattering patterns shown above are experimental data discussed in this report.
From the concentration, the jet diameter and the focus size the particle count per exposure is estimated to 60 particles per shot. Given that the focussed X-ray beam has extended tails beyond the focal limit, there is an uncertainty that likely places the true particle count somewhat higher. A conservative estimate of the bounds of the particle count of 50 to 200 is proposed.
Pattern Selection
Due to liquid jet and X-ray beam instabilities, not all scattering patterns collected are of sufficient quality for correlation analyses. The set of diffractions patterns of the sample collected contain, besides multi-particle hits, a set of blanks, where no virus was intersected by the XFEL beam, as well as images characterized by a very high total scattered intensity and extensive intensity streaks where the X-rays hit the edge of the jet or part of the liquid-jet nozzle, Fig. 2. Similar observations were made for the buffer run. A selection of patterns was made on the basis of the total integrated intensity on the back panel. A histogram analysis of the integrated intensity reveals a bimodal distribution, with high quality patterns occurring around the most-populated mode of the distribution.
(a). The total integrated intensities from the back panel form a bimodal distribution, for both the buffer data and the sample. In the buffer run, decent buffer-only shots (b1) dominate the low end, whereas streak dominated images (b2) and shots containing residual virus particles (b3) are found with higher integrated intensities. For the sample run, blank shots (c1) dominate the low end, and streak-dominated images (c3) are found in shots with integrated intensities residing in the extended tail (>200 AU) of the distribution. Diffraction patterns of the sample falling in the major peak (c2), with integrated intensities between 50 and 200 AU can be used to obtain experimental intensity correlations. All diffraction patterns are shown with a logarithmic colormap.
Code Availability
CASS is publicly available on github (https://gitlab.gwdg.de/p.lfoucar/cass). The reading of xtc files is supported by the psana libraries distributed by the LCLS (https://stanford.io/2lhTEwT).
Data Records
Four individual datasets have been deposited on the CXIDB website (Data Citation 1). The deposited data consists of the raw xtc file of the experimental PBCV-1 and buffer scattering data. Selected patterns, pre-processed with CASS, involving dark-current subtraction and common mode corrections, of PBCV-1 and buffer have been deposited also in separate hdf5 files for the back and front pnCCD detectors. The xtc files contain close to 100 000 scattering patterns, whereas the selected pre-processed files contain close to 60 000 patterns for PBCV-1 and 30 000 patterns for the buffer. A reference buffer subtracted SAXS data set from PBCV-1 at the same concentration, collected at 11 keV using the CSAXS beamline at the Swiss Light Source has been deposited as well. The data records are summarized in Table 2.
Technical Validation
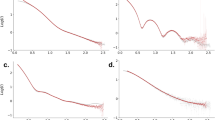
The quality of the data can be assessed by the mean intensity as a function of resolution, Fig. 3. The SAXS curve was obtained by angular integration of the images after masking out the strong jet scattering streaks seen in the diffraction patterns, Fig. 2c. A mask covering the jet streak included in the deposited hdf5 files. The experimental SAXS data were fitted in the low-q region (up to 0.015 Å−1) with the theoretical scattering curve of a hard sphere with a diameter of 174 nm. Given that the diameter of an icosahedron is 17% larger than the sphere that touches the midpoint of each vertex17, the hard sphere model derived here would correspond to a maximum particle dimension of little over 200 nm, consistent with the available model8. The analyses of the reference data collected at the Swiss Light Source can be modelled (at low q) with a hard sphere with a radius of 168 nm, corresponding to an icosahedron with diameter of 197 nm. The difference in estimated size between the reference data and the curve obtained from AMO can be ascribed to changes in relative contrast at lower X-ray energies, the effects of radiation damage on the sample at synchrotron sources, variations in sample preparations or concentration effects on the shape of the low q data.
This SAXS curve is close to a reference curve obtained from PBCV-1 at the Swiss Light Source’s CSAXS beamline at 11000 eV. Minor discrepancies between the soft X-ray and hard X-ray curve are likely due to contrast differences in the water window. A hard sphere model of the AMO data and the SLS data suggest a diameter of 174 nm and 168 nm, which would correspond to an icosahedron with diameter of 204 and 197 nm respectively.
Additional information
How to cite this article: Pande, K. et al. Free-electron laser data for multiple-particle fluctuation scattering analysis. Sci. Data. 5:180201 doi: 10.1038/sdata.2018.201 (2018).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
References
Kam, Z. Determination of Macromolecular Structure in Solution by Spatial Correlation of Scattering Fluctuations. Macromolecules 10, 927–934 (1977).
Saldin, D. K. et al. New light on disordered ensembles: ab initio structure determination of one particle from scattering fluctuations of many copies. Phys Rev Lett 106, 115501 (2011).
Malmerberg, E., Kerfeld, C. A. & Zwart, P. H. Operational properties of fluctuation X-ray scattering data. IUCrJ 2, 309–316 (2015).
Kurta, R. P. et al. Correlations in Scattered X-Ray Laser Pulses Reveal Nanoscale Structural Features of Viruses. Phys Rev Lett 119, 158102 (2017).
Kirian, R. A., Schmidt, K. E., Wang, X., Doak, R. B. & Spence, J. C. Signal, noise, and resolution in correlated fluctuations from snapshot small-angle x-ray scattering. Phys Rev E Stat Nonlin Soft Matter Phys 84, 011921 (2011).
Bozek, J. D. AMO instrumentation for the LCLS X-ray FEL. The European Physical Journal Special Topics 169, 129–132 (2009).
Ferguson, K. R. et al. The Atomic, Molecular and Optical Science instrument at the Linac Coherent Light Source. Journal of synchrotron radiation 22, 492–497 (2015).
Zhang, X. et al. Three-dimensional structure and function of the Paramecium bursaria chlorella virus capsid. Proc Natl Acad Sci USA 108, 14837–14842 (2011).
Maia, F. R. The Coherent X-ray Imaging Data Bank. Nat Methods 9, 854–855 (2012).
Van Etten, J. L., Burbank, D. E., Xia, Y. & Meints, R. H. Growth cycle of a virus, PBCV-1, that infects Chlorella-like algae. Virology 126, 117–125 (1983).
Kassemeyer, S. et al. Femtosecond free-electron laser x-ray diffraction data sets for algorithm development. Opt Express 20, 4149–4158 (2012).
Strüder, L. et al. Large-format, high-speed, X-ray pnCCDs combined with electron and ion imaging spectrometers in a multipurpose chamber for experiments at 4th generation light sources. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 614, 483–496 (2010).
DePonte, D. P. et al. Gas dynamic virtual nozzle for generation of microscopic droplet streams. Journal of Physics D - Applied Physics 41 (2008).
Weierstall, U., Spence, J. C. H. & Doak, R. B. Injector for scattering measurements on fully solvated biospecies. The Review of scientific instruments 83 (2012).
Strüder, L. High-resolution imaging X-ray spectrometers. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 454, 73–113 (2000).
Foucar, L. et al. CASS--CFEL-ASG software suite. Computer Physics Communications 183, 2207–2213 (2012).
Sloane N. J. A. editor The On-Line Encyclopedia of Integer Sequences, entries A019881 & A019863 https://oeis.org (2018).
Data Citations
Pande, K. Coherent X-ray Imaging Data Bank https://doi.org/10.11577/1437269 (2018)
Acknowledgements
This research was supported by the Max Planck society and in part, by the Advanced Scientific Computing Research and the Basic Energy Sciences programs, which are supported by the Office of Science of the US Department of Energy under Contract DE-AC02-05CH11231. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract DE-AC02-05CH11231. Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. This material is also based upon work partly supported by the National Science Foundation under Grant Nos 1240590 and 1733552. The research conducted at UWM was supported by the US Department of Energy, Office of Science, Basic Energy Sciences under award DE-SC0002164 (algorithm design and development), and by the US National Science Foundation under awards STC 1231306 (numerical trial models and data analysis) and 1551489 (underlying analytical models). Further support originates from the National Institute of General Medical Sciences of the National Institutes of Health (NIH) under Awards R01GM109019 and GM117126. The content of this manuscript is solely the responsibility of the authors and does not necessarily represent the official views of NIH.
Author information
Authors and Affiliations
Contributions
C.A.K., P.F., A.O., N.K.S., P.H.Z., I.S., C.B. arranged beamtime; P.H.Z., E.M., I.S. conceived the experiment. K.P., J.J.D., E.L.M., L.F., B.K.P., I.S. and P.H.Z. analysed the data. The manuscript was written with input from K.P., J.J.D., E.L.M., L.F., I.S., A.O., C.A.K. and P.H.Z. The experiment was performed with input from E.L.M., L.F., B.K.P., M.S., S.Bo., S.Ba., R.B.D., K.D., S.W.E., L.E., R.F., E.H., R.H., G.H., J.H., A.H., S.K., L.L., S.F.C.M., D.R., A.R., M.M.S., R.G.S., P.S., A.O., P.F., N.K.S., M.B., J.B., C.B., I.S., C.A.K. and P.H.Z. The reference SAXS data was collected by A.M.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
ISA-Tab metadata
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files made available in this article.
About this article
Cite this article
Pande, K., Donatelli, J., Malmerberg, E. et al. Free-electron laser data for multiple-particle fluctuation scattering analysis. Sci Data 5, 180201 (2018). https://doi.org/10.1038/sdata.2018.201
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/sdata.2018.201