Abstract
Efficient synthesis recipes are needed to streamline the manufacturing of complex materials and to accelerate the realization of theoretically predicted materials. Often, the solid-state synthesis of multicomponent oxides is impeded by undesired by-product phases, which can kinetically trap reactions in an incomplete non-equilibrium state. Here we report a thermodynamic strategy to navigate high-dimensional phase diagrams in search of precursors that circumvent low-energy, competing by-products, while maximizing the reaction energy to drive fast phase transformation kinetics. Using a robotic inorganic materials synthesis laboratory, we perform a large-scale experimental validation of our precursor selection principles. For a set of 35 target quaternary oxides, with chemistries representative of intercalation battery cathodes and solid-state electrolytes, our robot performs 224 reactions spanning 27 elements with 28 unique precursors, operated by 1 human experimentalist. Our predicted precursors frequently yield target materials with higher phase purity than traditional precursors. Robotic laboratories offer an exciting platform for data-driven experimental synthesis science, from which we can develop fundamental insights to guide both human and robotic chemists.

Similar content being viewed by others
Main
There is currently a poor scientific understanding of how to design effective and efficient synthesis recipes to target inorganic materials1,2,3. As a result, synthesis often becomes a bottleneck in the scalable manufacturing of functional materials4, as well as in the laboratory realization of computationally predicted materials5,6. Density functional theory (DFT)-calculated thermodynamic stability or metastability can often estimate the synthesizability of materials7,8,9, but finding an optimal synthesis recipe—including temperatures, times and precursors—still requires extensive trial-and-error experimentation. The recent emergence of robotic laboratories10,11,12,13 presents an exciting opportunity for high-throughput experiments and sequential learning algorithms to autonomously optimize materials synthesis recipes14,15,16,17,18,19,20,21,22. However, there remains a poor fundamental understanding of how changing a synthesis recipe affects the underlying thermodynamics and kinetics of a solid-state reaction. Without this scientific foundation, it is difficult to build physics-informed synthesis-planning algorithms to guide robotic laboratories13,23, meaning that parameter optimization via high-throughput experiments can end up being unnecessarily resource intensive and wasteful.
Multicomponent oxides represent an important and challenging space for targeted synthesis. These high-component materials are key to various device technologies—including battery cathodes (Li(Co,Mn,Ni)O2), oxygen evolution catalysts (Bi2Sr2Can−1CunO2n+4+x), high-temperature superconductors (HgBa2Ca2Cu3O8) and solid-oxide fuel cells (La3SrCr2Mn2O12)24. Multicomponent oxides are usually synthesized by solid-state reactions, which involves combining and firing the constituent binary oxide precursors in a furnace. However, this often yields impurity by-product phases arising from incomplete solid-state reactions. From a phase diagram perspective, precursors start at the corners of a phase diagram and combine together towards a target phase in the interior of the phase diagram. If the phase diagram is complicated, with many competing phases between the precursors and the target, undesired phases may form, consuming thermodynamic driving force and kinetically trapping the reaction in an incomplete non-equilibrium state.
High-component oxides reside in high-dimensional phase diagrams and can be synthesized from many possible precursor combinations. Here we present a thermodynamic strategy to navigate these multidimensional phase diagrams, where the primary objective is to identify precursor compositions that circumvent kinetically competitive by-products, while maximizing the thermodynamic driving force for fast reaction kinetics. We test our principles of precursor selection using a robotic inorganic materials synthesis laboratory, which automates many tedious aspects of the inorganic materials synthesis workflow such as powder precursor preparation, ball milling, oven firing and X-ray characterization of reaction products. With our robotic platform, a single human experimentalist can conduct powder inorganic materials synthesis in both a high-throughput and reproducible manner. Using a diverse target set of 35 quaternary Li-, Na- and K-based oxides, phosphates and borates, which are relevant chemistries for intercalation battery cathodes25,26 and solid-state electrolytes27, we show that precursors identified by our thermodynamic strategy frequently outperform traditional precursors in synthesizing high-purity multicomponent oxides. Our work demonstrates the utility of robotic laboratories not only for automated materials synthesis and manufacturing, but also as a platform for large-scale hypothesis validation over a broad and diverse chemical space.
Principles of precursor selection
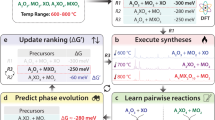
Recently, we showed that solid-state reactions between three or more precursors initiate at the interfaces between only two precursors at a time28. The first pair of precursors to react will usually form an intermediate by-product, which can consume much of the total reaction energy and leave insufficient driving force to complete a reaction29. Figure 1 illustrates this multistep reaction progression for an example target compound, LiBaBO3, whose simple oxide precursors are B2O3, BaO and Li2CO3. Because Li2CO3 decomposes to Li2O upon heating, we can examine the competing chemical reactions30 geometrically on a pseudo-ternary Li2O–B2O3–BaO convex hull. Although the overall reaction energy for Li2O + BaO + B2O3 → LiBaBO3 is large at ΔE = −336 meV per atom, there are many low-energy ternary phases along the binary slices Li2O–B2O3 (Fig. 1b, blue) and BaO–B2O3 (Fig. 1b, green). In the initial pairwise reactions between Li2O + BaO + B2O3, we anticipate that stable ternary Li–B–O and Ba–B–O oxides, such as Li3BO3, Ba3(BO3)2 or others, will form rapidly due to large thermodynamic driving forces of ΔE ≈ −300 meV per atom. Should these low-energy intermediates form, the ensuing reaction energies to the target product become miniscule, for example, Li3BO3 + Ba3(BO3)2 → LiBaBO3 has only ΔE = −22 meV per atom (Fig. 1e, orange). (Note: one advantage of analysing reactions on convex hulls is that stoichiometric reactions are automatically balanced by the barycentric coordinates of the product relative to its precursors. For brevity, we do not balance reactions explicitly in this manuscript, but we do emphasize that all reaction energies are normalized per atom of product phase.)
a–e, The traditional reaction. f–h, The predicted reaction. Schematic of the pairwise reactions process for traditional recipes (a) and our predicted recipes (f), showing the phase evolution from precursors to the target. In pseudo-ternary Li2O–B2O3–BaO convex hulls, reaction convex hulls between precursor pairs are illustrated by coloured slices, for B2O3|Li2O (blue) and B2O3|BaO (green) (b), Li3BO3|Ba3(BO3)2 (orange) (d), LiBO2|BaO (purple) (g). The corresponding two-dimensional slices of the binary reaction convex hulls are B2O3|Li2O (blue) and B2O3|BaO (green) (c), Li3BO3|Ba3(BO3)2 (orange) (e), LiBO2|BaO (purple) (h), where grey arrows show the reaction energy of the corresponding reaction. i, Free energy change in a reaction progress, where a relatively high-energy intermediate state saves more energy for the final step in forming the target. j, X-ray diffraction of the solid-state synthesis of LiBaBO3, where red and blue curves are raw X-ray diffraction data for traditional and predicted precursors, respectively, and the black curve is the fit produced by the Rietveld refinement.
Instead of allowing the reactions to proceed between the three precursors all at once, we suggest initially synthesizing LiBO2, which can serve as a high-energy starting precursor for the reaction. Figure 1g (purple) shows that LiBaBO3 can be formed directly in the pairwise reaction LiBO2 + BaO → LiBaBO3 with a substantial reaction energy of ΔE = −192 meV per atom. Moreover, along this reaction isopleth, there is a low likelihood of forming impurity phases, as the competing kink of Li6B4O9 + Ba2Li(BO2)5 has relatively small formation energy (ΔE = −55 meV per atom) compared to LiBaBO3. Finally, the inverse hull energy of LiBaBO3, which we define as the energy below the neighbouring stable phases on the convex hull31, is substantial at ΔEinv = −153 meV per atom, suggesting that the selectivity of the target LiBaBO3 phase should be much greater than any potential impurity by-products along the LiBO2–BaO slice.
Figure 1i compares the energy progression between these two precursor pathways. Although both pathways share the same total reaction energy, synthesizing LiBaBO3 from three precursors is likely to first produce low-energy ternary oxide intermediates (Fig. 1a), leaving little reaction energy to drive the reaction kinetics to the target phase28. By first synthesizing a high-energy intermediate (LiBO2), we retain a large fraction of overall reaction energy for the last step of the reaction, promoting the rapid and efficient synthesis of the target phase. We confirm this hypothesis experimentally (Fig. 1j), where we find that solid-state synthesis of LiBaBO3 from the traditional precursors Li2CO3, B2O3 and BaO does not result in strong X-ray diffraction signals of the target phase, whereas LiBO2 + BaO produces LiBaBO3 with high phase purity (Methods).
From this instructive LiBaBO3 example, we propose five principles to select effective precursors from a multicomponent convex hull. (1) Reactions should initiate between only two precursors if possible, minimizing the chances of simultaneous pairwise reactions between three or more precursors. (2) Precursors should be relatively high energy (unstable), maximizing the thermodynamic driving force and thereby the reaction kinetics to the target phase. (3) The target material should be the deepest point in the reaction convex hull, such that the thermodynamic driving force for nucleating the target phase is greater than all its competing phases. (4) The composition slice formed between the two precursors should intersect as few other competing phases as possible, minimizing the opportunity to form undesired reaction by-products. (5) If by-product phases are unavoidable, the target phase should have a relatively large inverse hull energy—in other words, the target phase should be substantially lower in energy than its neighbouring stable phases in composition space.
When there were multiple precursor pairs that could be used to synthesize the target compound, we ranked the ‘best’ precursor pair by first prioritizing principle 3, where the target compound was at the deepest point of the convex hull. This ensures that the thermodynamic driving force for nucleation of the target compound is greater than the driving forces to all other competing phases. We next prioritized principle 5, where the target compound has the largest inverse hull energy. A reaction having a large inverse hull energy supersedes principle 2, as a large reaction driving force is not a sufficient criterion for synthesis, for example, in Fig. 2b, where the magnitude of the driving force of Li2O + Zn2P2O7 → LiZnPO4 is large but selectivity may be weak compared to ZnO + Li3PO4. A large inverse hull energy also supersedes principle 4, as a large inverse hull energy means that, even if intermediate phases form, there would still be a large driving force for a secondary reaction to form the target compound.
a,c,e, The blue, red and purple slice planes correspond to Zn2P2O7 + Li2O (a), Zn3(PO4)2 + Li3PO4 (c) and LiPO3 + ZnO (e) binary reaction convex hulls, respectively. b,d,f, The corresponding two-dimensional slices of reaction convex hulls are shown for Zn2P2O7 + Li2O (b), Zn3(PO4)2 + Li3PO4 (d) and LiPO3 + ZnO (f).
In Fig. 2, we interpret these precursor design principles for an example LiZnPO4 target in the pseudo-ternary Li2O–P2O5–ZnO phase diagram. If we first synthesize Zn2P2O7 to combine with Li2O (Fig. 2a,b, blue), the deepest point in the reaction convex hull is not LiZnPO4 but rather ZnO + Li3PO4, suggesting a kinetic propensity to form these undesired by-products. If we start from Zn3(PO4)2 + Li3PO4 (Fig. 2c,d, orange), LiZnPO4 is located at the deepest point along the convex hull; however, Li3PO4 is a low-energy starting precursor, meaning that there is a small driving force (ΔE = −40 meV per atom) left to form LiZnPO4, which probably leads to slow reaction kinetics. We suggest that LiPO3 + ZnO (Fig. 2e,f, purple) are the ideal precursors for LiZnPO4. LiPO3 has a relatively high energy along the Li2O–P2O5 binary hull, resulting in a large driving force to the target phase of ΔE = −106 meV per atom. Additionally, there are no competing phases along the LiPO3 + ZnO slice, minimizing the possibility of impurity by-product phases.
In Supplementary Note 1.2, we further interpret our precursor selection principles from the dual perspective of chemical potential diagrams, and interpret the inverse hull energy with respect to the ‘chemical potential distance’, as proposed by Todd et al.32. Here, we chose a convex hull approach, since it graphically constrains stoichiometrically balanced pairwise reactions better than chemical potential diagrams. Additionally, in Supplementary Note 1.3, we show that our predicted precursors generally differ from those predicted by the algorithms of McDermott et al.30 and Aykol et al.33. Although all our works share the same goal of predicting inorganic synthesis recipes, the five principles that guide our precursor selection algorithm are based on our recent insights into the importance of pairwise reactions27,28, which was not considered in the PIRO algorithm by Aykol et al. PIRO therefore predicts the optimal precursors for BaLiBO3 to be \(\frac12\) Ba + \(\frac12\) Ba(BO2)2 + Li + \(\frac12\) O2 → BaLiBO3, which probably proceeds through intermediates in this multiprecursor reaction. Our approach of maximizing driving force also differs slightly from the cost function of McDermott et al., whose ideal predicted reaction is \(\frac13\) Ba3(BO3)2 + \(\frac13\) Li3BO3 → BaLiBO3, which, as discussed earlier, has a small driving force. As deeper fundamental understanding of solid-state reactions is achieved, we anticipate that new principles will need to be developed and included in our algorithms for the overarching ambition of predictive solid-state synthesis.
Validation with a robotic ceramic synthesis laboratory
To test our precursor selection hypotheses, we designed a large-scale experimental validation effort based on quaternary Li-, Na- and K-based oxides, phosphates and borates, which are representative chemistries for intercalation battery materials24,26. We surveyed the Materials Project34 for all known quaternary compounds in this space, and then we used our selection principles to predict optimal precursors from the DFT-calculated convex hulls. The algorithms to identify these precursors are detailed in Supplementary Note 1. We also determine the traditional precursors for these reactions, which we previously text-mined from the solid-state synthesis literature35. A full list of 3,104 reactions in this space is provided in Supplementary Data 1. To efficiently maximize the coverage of our experimental validation, we Pareto-optimized our reaction list to select the fewest number of precursors that maximize the number of candidate reactions, resulting in 28 unique precursors for 35 target materials that span 27 elements.
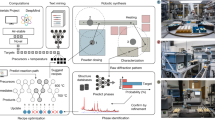
We then compare the phase purity of target materials synthesized from our predicted precursors versus that from traditional precursors. We perform this large-scale validation effort using a robotic inorganic materials synthesis laboratory named ASTRAL (Automated Synthesis Testing and Research Augmentation Lab), located at the Samsung Advanced Institute of Technology, Cambridge, Massachusetts. As shown in Fig. 3, ASTRAL uses a robotic arm to automate sample handling throughout a full ceramic synthesis workflow—from powder precursor preparation to ball milling, to oven firing and to X-ray characterization of reaction products. Videos of the robotic laboratory in action can be viewed in Supplementary Videos 1–4. Three trays of 24 samples can pass sequentially through the ASTRAL workflow every 72 hours. The throughput of ASTRAL is bottlenecked by powder dispensing and processing, as each 24-sample tray is prepared serially, whereas the firing and characterization steps can, in principle, be run in parallel.
a, A robot-enabled inorganic materials synthesis workflow—from powder precursor preparation to ball milling, to oven firing and to X-ray diffraction (XRD) characterization of reaction products. b, Photograph of the ASTRAL laboratory. c, Robotic chemists enable large-scale exploration of synthesis hypotheses over a broad chemical space, which normally would have to be undertaken by multiple experimentalist groups. d, Human experimentalists have a trade-off between throughput and reproducibility, whereas robotic chemists can achieve both high reproducibility and throughput simultaneously.
ASTRAL automates inorganic materials synthesis from powder precursors, as opposed to previous robotic laboratories that rely on solution-based precursors15,16,17,36, inkjet printing18 or combinatorial thin-film deposition14,19. Although it is easier to dose precursor concentrations using these other methods, the resulting products are typically only produced at milligram scale. Powder synthesis, on the other hand, can yield grams of material, which is needed to create ceramic pellets or electrodes for functional property characterization. Moreover, high-temperature powder synthesis is the primary synthesis method of ceramic oxides, so recipes determined from ASTRAL can be upscaled for industrial manufacturing. We overcame major practical challenges in powder precursor processing, which arise primarily from flowability differences between different powders due to varying particle sizes, hardness, hygroscopicity and compaction. In Supplementary Table 1, we summarize the challenges in working with powder precursors, as well as our solutions to these challenges. The essential task is to identify the best dosing head for each precursor, as detailed in Supplementary Table 2 for the precursors used here.
In total, we conducted 224 synthesis reactions over 35 target materials, calcined at temperatures from 600 to 1,000 °C. Each reaction was conducted for 8 hours, and then impurity by-products were assessed, without regrinding or reannealing our samples. We deliberately chose these relatively short reaction times to evaluate the intrinsic reactivity of the two competing sets of precursors.
For a target space this diverse, traditional validation of our precursor selection principles would probably have required an extensive experimental effort, consisting of multiple human experimentalists working over many years. Once the robotic laboratory is set up, we can comprehensively survey this broad crystal chemistry space in a single experimental campaign (Fig. 3c). Moreover, a large-scale human effort will inevitably require trade-offs between throughput and reproducibility. Meanwhile, a robotic laboratory produces single-source experimental data with high reproducibility, meaning we can systematically compare synthesis results while minimizing human variability and error (Fig. 3d). Altogether, the robotic laboratory offers a new platform for data-driven empirical synthesis science, where hypotheses can be investigated rapidly, reproducibly and comprehensively over diverse crystal chemistries.
Results and discussion
For the 35 materials selected, Fig. 4a shows the relative yield of the target phase starting from computationally designed versus traditional precursors. Figure 4b shows the reaction temperatures attempted and Fig. 4c shows the relative performance of the predicted versus traditional precursors. A full list of targets, precursors and reaction results is given in Supplementary Table 3. For 32 out of 35 compounds (91%), the predicted precursors successfully produced the target phase. In 15 targets, the predicted precursors achieved at least 20% higher phase purity than the traditional precursors (green), and 6 of these 15 target materials could ‘only’ be synthesized by the predicted precursors (dark green). For 16 reactions the precursors have similar target yields (light green), and only in 4 systems do the traditional precursors perform better than the predicted precursors (red). However, we note that even in these four systems, the predicted precursors also produce the target materials with moderate to high purities.
a, Table of the phase purity of 35 targets obtained from predicted precursors using the highest phase purity from various firing temperatures, compared to traditional precursors. Colour of ‘Precursor comparison’ column compares purity from predicted precursors versus traditional precursors, where green means predicted precursors achieve >10% better purity, light green means they have purities within ±10% and red means traditional precursors achieve >10% better purity. Targets with blue colour star are metastable materials. The same colour scheme is used in panels b–d. b, Heat map of phase purity of predicted precursors at different calcination temperatures. c, The target phase purity from predicted precursors versus traditional precursors. Phase purity methods in Supplementary Note 2.2.3. d, Reaction energies and inverse hull energies for all targets. The marker shape corresponds to the best phase purity of predicted precursors, where diamonds are high purity, circles are moderate and low purity, and crosses with a red outline mean that both predicted precursors and traditional precursors failed. The red box represents the low thermodynamic driving force regions where kinetic process may be rate limiting. The dashed line represents when the inverse hull energy equals the reaction energy. Inset, convex hull illustrating the reaction energy and the inverse hull energy.
We also examined the robotic solid-state synthesis of four metastable compounds with mild energies above the convex hull7—LiNbWO6 (10 meV per atom), LiZnBO3 (8 meV per atom), KTiNbO5 (1 meV per atom) and Li3Y2(BO3)3 (39 meV per atom), indicated by blue asterisks in Fig. 4. These metastable compounds formed in our solid-state reactions, although generally with low phase purity. However, we still found that our predicted precursors would yield these target metastable phases with similar or better relative purity than when starting from traditional precursors (Supplementary Note 3.2). Recent work by Zeng et al. suggests that by tuning the thermodynamic driving forces from the precursors, it may be possible to selectively form desired stable or metastable phases on the basis of their calculated nucleation barriers37. Finally, in three systems, neither sets of precursors resulted in the target material, which for NaBSiO4 was due to glass formation38, for Li3V2(PO4)3 a more reducing atmosphere was needed39 and for NaBaBO3 the published reaction temperature40 was very precise at 790 °C, suggesting that perhaps a rounded number, such as 800 °C, may be too high. As discussed further in Supplementary Note 3.4, these potential failure modes represent important considerations in future robotic laboratory design for solid-state synthesis.
Figure 4c shows that our predicted precursors tend to synthesize target materials with higher purity than traditional simple oxide precursors. Many of our predicted ternary oxide precursors are unusual, such as LiPO3, LiBO2 and LiNbO3 (see more in Supplementary Table 3), as these precursors do not appear from our previously text-mined database of 19,488 solid-state synthesis recipes41. Machine-learning algorithms for synthesis prediction trained on literature datasets would therefore be unlikely to predict our suggested precursors here. This highlights the limitations of machine-learning algorithms in predicting new opportunities in synthesis parameter space, outside the constraints of our anthropogenic biases in chemical reaction data22,42.
Our results show that the success of a reaction was not correlated to the crystal structure or chemistry of the target material; rather, it was primarily determined by the geometry of the underlying convex hull, as well as by the magnitude of the thermodynamic driving force. The success of our precursor selection principles is surprising, considering we evaluate precursor selection using only the DFT-calculated convex hull, which does not account for temperature-dependent effects, such as vibrational entropy or oxide decomposition, neglects kinetic considerations, such as diffusion rates and nucleation barriers32, and has known errors in DFT-calculated formation energies43.
Here we rationalize with order-of-magnitude energy arguments why, despite many simplifying assumptions, the DFT-calculated thermodynamic convex hull retains predictive power in identifying effective precursors. First, entropic contributions (TΔS; T is temperature and S is entropy) can generally be neglected because the free energy change ΔG of an oxide synthesis reaction is usually dominated by the change in enthalpy ΔH contribution, rather than the TΔS contribution. Supplementary Fig. 16 compiles a list of 100 experimental ternary oxide reaction energies, and shows that at 1,000 K the magnitude of |ΔG| for reactions is ~200 meV per atom, whereas the |TΔS| contribution is only ~15 meV per atom. In 60% of the reactions, |TΔS|/|ΔG| < 10%, except in cases where |ΔG| < 100 meV per atom, in which case TΔS can be comparable in magnitude to ΔH. We validate these arguments in Supplementary Fig. 17, showing that temperature-dependent free energies are negligibly different from reaction enthalpies44. The dominance of ΔH over TΔS in oxide synthesis reactions is due to the irreversible exothermic nature of reactions of the form A + B → AB; as opposed to first-order phase transitions, such as melting, or polymorphic transformations, where ΔH ≈ TΔS. This assumption relies on both the reactants and products being solid phases—for reactions that evolve gases, the reaction entropy is approximately ΔS = 1 eV per atom per 1,000 K; meaning that higher temperature largely favours the reaction direction with more moles of gas.
Second, ternary convex hulls are often skewed such that certain hull directions are much deeper than others, such as the Li2O–B2O3 and BaO–B2O3 directions illustrated on the Li2O–BaO–B2O3 convex hull in Fig. 1 (more examples can be found in Supplementary Note 3). On a high-dimensional phase diagram, there are many combinations of precursor pairs that can slice through a target phase. Even an approximate convex hull, with systematic DFT formation energy errors of 25 meV per atom (refs. 8,42), can largely capture the relative depths of the convex hull in various compositional directions, as well as the complexity of the hull arising from competing phases. Importantly, DFT is well poised to capture the very stable phases, which are low-energy thermodynamic sinks to be avoided when designing the reaction isopleths between pairs of precursors.
Although we do not explicitly calculate kinetics here, the magnitude of the thermodynamic driving force is a good proxy for phase transformation kinetics, as ΔGreaction appears in the denominator of the classical nucleation barrier, as supersaturation in the JMAK theory of crystal growth and as dμ/dx in Fick’s first law of diffusion (where μ is chemical potential and x is distance)45. Because we aim to evaluate the relative reaction kinetics of different precursors, rather than absolute kinetics, we can usually compare thermodynamic driving forces between different precursor sets without explicitly calculating diffusion barriers46 or surface energies for nucleation and growth analyses47,48.
However, there are limits to this assumption. Figure 4d shows the reaction energy and inverse hull energy for all 35 reactions using predicted precursors, among which three of the unsuccessful syntheses are marked with a cross and four red markers indicate conditions where the traditional precursors outperformed the predicted precursors. In cases where our predicted precursors were less successful (red box in Fig. 4d), the reaction energy landscapes were shallow with ΔEreaction > −70 meV per atom, and inverse hull energies of ΔEIH > −50 meV per atom. Because these driving forces are of the order of kBT at solid-state synthesis temperatures (Boltzmann’s constant × ~1,000 K ≈ 100 meV per atom), unanticipated kinetic processes may become rate limiting and disqualify our thermodynamic driving force arguments. These counter examples provide valuable ‘failed synthesis’ results49 to quantify bounds where our precursor selection principles offer less certainty of success, and can serve as soft cutoff energies for future algorithms for solid-state precursor prediction—although we note that many reactions within this energy cutoff can still be successful, as shown in our experiments.
Finally, additional opportunities to design large ΔGreaction include leveraging metathesis reactions29,31, for example, of the form 2NaCrS2 + MgCl2 → MgCr2S4 + 2NaCl (ref. 50), where reactions can be thermodynamically driven by the formation of a stable salt by-product. Because there are a wide variety of opportunities to select potential by-product phases, metathesis reactions represent a rich design space to enhance the thermodynamics, and thereby the kinetics, of solid-state reactions.
Outlook
Synthesis science is poorly understood, but new theories can be developed by examining falsifiable predictions through empirical validation. In this work, we hypothesized several principles to identify superior precursors for high-purity synthesis of multicomponent oxides. We argued that in high-dimensional phase diagrams with skewed energy landscapes, there is an opportunity to find precursors that are both high in energy and have compositions that circumvent low-energy, undesired kinetic by-products. Using a robotic synthesis laboratory, we validated this hypothesis over 35 target materials with diverse crystal chemistries, producing in this one study as many experimental results as a typical review paper might survey. This work highlights the potential of data-driven experimental synthesis science, where the high throughput and reproducibility of robotic laboratories enable a more comprehensive interrogation of synthesis science hypotheses. This exciting robotic platform can be directed to investigate further fundamental questions, such as the role of temperatures and reaction times in ceramic oxide synthesis. As we use these robotic laboratories to verify human-designed hypotheses, we will deepen our fundamental understanding of the interplay between thermodynamics and kinetics during materials formation. Simultaneously, this scientific understanding will drive the development of physically informed artificial intelligence synthesis-planning frameworks to enable truly autonomous materials processing and manufacturing.
Methods
DFT convex hulls for precursor identification
Material phases and formation energies were obtained from the Materials Project34 using its REST API51 (retrieved December 2020). Convex hulls were constructed from the phase diagram module in Pymatgen52, and reaction convex hulls were calculated from the interfacial reactions module53. Software for producing interactive reaction compound convex hulls can be found on GitHub at https://github.com/dd-debug/synthesis_planning_algorithm. Further details on the thermodynamic calculations and convex hull analysis are provided in Supplementary Note 1.
Robotic laboratory
ASTRAL transports samples between stations using two robots, a seven-axis Panda robotic arm (Franka Emika) and a linear rail (Vention). By using the rail system to extend the range of the Panda arm, the system can perform precise laboratory manipulations over an area of 1.7 m × 4 m. Surrounding the central rail system are stations that perform specialized tasks for inorganic materials synthesis, such as dispensing solid powder precursor chemicals and liquid dispersants, a mechanical ball mill, furnace to calcine and react precursors and X-ray diffraction to characterize synthesis outcomes. Precursor powders are dispensed sequentially using a Quantos powder dispenser (Mettler Toledo), with sample vials and powder dosing heads exchanged using the robotic arm. Following powder dispensing, 1 ml of ethanol is dispensed into each vial using a Freedom EVO 150 liquid handling robot (Tecan Life Sciences), followed by rotary ball milling for 15 h at 100 r.p.m. to produce a uniform fine mixture of precursor powders. Alumina crucibles (Advalue Technology) are used to hold the mixed precursors. After ball milling, samples are heated to 80 °C for 2 h under vacuum to remove ethanol and then transferred to a furnace for calcination in air atmosphere for 8 h at temperatures from 600 to 1,000 °C. Powders are then characterized via powder X-ray diffraction (Rigaku Miniflex 600). Further details on the robotic infrastructure and synthesis procedures are provided in Supplementary Note 2.
Automated X-ray diffraction refinement
Rietveld refinement of data was performed in the BGMN kernel54. The target structure is used as the sole input phase for the BMGN kernel, and the Rietveld refinement will split the X-ray diffraction signal into the target phase, background and residual. The background X-ray diffraction pattern was determined from empty sample holders. The fraction of the target phase was estimated by dividing the integrated intensity (I) of the target phase by the combined intensity of the target phase and residual phase, Itarget/(Itarget + Iresidual). Values greater than 0.5 are considered high purity, between 0.2 and 0.5 are considered moderate purity and less than 0.2 is considered low purity. Further details on the automated X-ray diffraction refinement process are provided in Supplementary Note 2.2.3.
Data availability
The data supporting the findings of this study are available within the paper and its Supplementary Information files. All thermodynamic data to reproduce our analyses can be freely obtained from the Materials Project database and its API, as discussed in Methods and Supplementary Note 1. X-ray diffraction patterns for robotic laboratory synthesis results are all provided in the Supplementary Information. All experimental protocols regarding the construction and operation of the robotic laboratory are discussed in the Supplementary Information. Candidate reactions and their energies are available via figshare at https://doi.org/10.6084/m9.figshare.22671571. Source data are provided with this paper.
Code availability
All code for evaluating precursors, as well as for producing interactive reaction compound convex hulls, can be found on GitHub at the following link: https://github.com/dd-debug/synthesis_planning_algorithm. The link includes a readme, demonstration file, installation guide, Python package requirements and instructions for use.
References
Jansen, M. A concept for synthesis planning in solid‐state chemistry. Angew. Chem. Int. Ed. Engl. 41, 3746–3766 (2002).
Kovnir, K. Predictive synthesis. Chem. Mater. 33, 4835–4841 (2021).
Cheetham, A. K., Seshadri, R. & Wudl, F. Chemical synthesis and materials discovery. Nat. Synth. 1, 514–520 (2022).
Jenks, C. et al. Basic Research Needs for Transformative Manufacturing (US DOE Office of Science, 2020).
Narayan, A. et al. Computational and experimental investigation for new transition metal selenides and sulfides: the importance of experimental verification for stability. Phys. Rev. B 94, 045105 (2016).
Acharya, M. et al. Searching for new ferroelectric materials using high-throughput databases: an experimental perspective on BiAlO3 and BiInO3. Chem. Mater. 32, 7274–7283 (2020).
Sun, W. et al. The thermodynamic scale of inorganic crystalline metastability. Sci. Adv. 2, e1600225 (2016).
Bartel, C. J. et al. The role of decomposition reactions in assessing first-principles predictions of solid stability. NPJ Comput. Mater. 5, 4 (2019).
Chen, H., Hautier, G. & Ceder, G. Synthesis, computed stability, and crystal structure of a new family of inorganic compounds: carbonophosphates. J. Am. Chem. Soc. 134, 19619–19627 (2012).
Stach, E. et al. Autonomous experimentation systems for materials development: a community perspective. Matter 4, 2702–2726 (2021).
Szymanski, N. J. et al. Toward autonomous design and synthesis of novel inorganic materials. Mater. Horiz. 8, 2169–2198 (2021).
Abolhasani, M. & Eugenia, K. The rise of self-driving labs in chemical and materials sciences. Nat. Synth. 2, 483–492 (2023).
Szymanski, N. J. et al. An autonomous laboratory for the accelerated synthesis of novel materials. Nature 624, 86–91 (2023).
Kusne, A. G. et al. On-the-fly closed-loop materials discovery via Bayesian active learning. Nat. Commun. 11, 5966 (2020).
Zakutayev, A. et al. An open experimental database for exploring inorganic materials. Sci. Data 5, 180053 (2018).
MacLeod, B. P. et al. Self-driving laboratory for accelerated discovery of thin-film materials. Sci. Adv. 6, eaaz8867 (2020).
Burger, B. et al. A mobile robotic chemist. Nature 583, 237–241 (2020).
Jonderian, A., Michelle, T. & Eric, M. C. Metastability in Li–La–Ti–O perovskite materials and its impact on ionic conductivity. Chem. Mater. 33, 4792–4804 (2021).
Yang, L. et al. Discovery of complex oxides via automated experiments and data science. Proc. Natl Acad. Sci. USA 118, e2106042118 (2021).
Ament, S. et al. Autonomous materials synthesis via hierarchical active learning of nonequilibrium phase diagrams. Sci. Adv. 7, eabg4930 (2021).
Anderson, E. et al. Combinatorial study of the Li–La–Zr–O system. Solid State Ionics 388, 116087 (2022).
Young, S. D. et al. Thermodynamic stability and anion ordering of perovskite oxynitrides. Chem. Mater. 35, 5975–5987 (2023).
David, N., Sun, W. & Coley, C. W. The promise and pitfalls of AI for molecular and materials synthesis. Nat. Comput. Sci. 3, 362–364 (2023).
Bruce, D. W., O’Hare, D. & Walton, R. I. Functional Oxides (John Wiley & Sons, 2011).
Tian, Y. et al. Promises and challenges of next-generation ‘beyond Li-ion’ batteries for electric vehicles and grid decarbonization. Chem. Rev. 121, 1623–1669 (2020).
Hautier, G. et al. Phosphates as lithium-ion battery cathodes: an evaluation based on high-throughput ab initio calculations. Chem. Mater. 23, 3495–3508 (2011).
Zhao, Q. et al. Designing solid-state electrolytes for safe, energy-dense batteries. Nat. Rev. Mater. 5, 229–252 (2020).
Miura, A. et al. Observing and modeling the sequential pairwise reactions that drive solid‐state ceramic synthesis. Adv. Mater. 33, 2100312 (2021).
Bianchini, M. et al. The interplay between thermodynamics and kinetics in the solid-state synthesis of layered oxides. Nat. Mater. 19, 1088–1095 (2020).
McDermott, M. J., Dwaraknath, S. S. & Persson, K. A. A graph-based network for predicting chemical reaction pathways in solid-state materials synthesis. Nat. Commun. 12, 3097 (2021).
Evans, D. et al. Visualizing temperature-dependent phase stability in high entropy alloys. NPJ Comput. Mater. 7, 151 (2021).
Todd, P. K. et al. Selectivity in yttrium manganese oxide synthesis via local chemical potentials in hyperdimensional phase space. J. Am. Chem. Soc. 143, 15185–15194 (2021).
Aykol, M., Montoya, J. H. & Hummelshøj, J. Rational solid-state synthesis routes for inorganic materials. J. Am. Chem. Soc. 143, 9244–9259 (2021).
Jain, A. et al. Commentary: the Materials Project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
He, T. et al. Similarity of precursors in solid-state synthesis as text-mined from scientific literature. Chem. Mater. 32, 7861–7873 (2020).
Yoshikawa, N. et al. Digital pipette: open hardware for liquid transfer in self-driving laboratories. Digit. Discov. 2, 1745–1751 (2023).
Zeng, Y. et al. Selective formation of metastable polymorphs in solid-state synthesis. Sci. Adv. 10, adj5431 (2024).
Feltz, A. & Büchner, P. Structure and ionic conduction in solids: I. Na+-ion conducting glasses in the systems NaBSiO4-Na2SiO3, NaBSiO4-Na4SiO4 and NaBSiO4-Na3PO4. J. Non-Cryst. Solids 92, 397–406 (1987).
Chen, S. et al. Kinetic studies on the synthesis of monoclinic Li3V2(PO4)3 via solid-state reaction. J. Phys. Chem. A 118, 3711–3716 (2014).
Zhong, J. et al. Understanding the blue-emitting orthoborate phosphor NaBaBO3:Ce3+ through experiment and computation. J. Mater. Chem. C 7, 654–662 (2019).
Kononova, O. et al. Text-mined dataset of inorganic materials synthesis recipes. Sci. Data 6, 203 (2019).
Jia, X. et al. Anthropogenic biases in chemical reaction data hinder exploratory inorganic synthesis. Nature 573, 251–255 (2019).
Hautier, G. et al. Accuracy of density functional theory in predicting formation energies of ternary oxides from binary oxides and its implication on phase stability. Phys. Rev. B 85, 155208 (2012).
Bartel, C. J. et al. Physical descriptor for the Gibbs energy of inorganic crystalline solids and temperature-dependent materials chemistry. Nat. Commun. 9, 4168 (2018).
Balluffi, R. W., Allen S. M. & Carter W. C. Kinetics of Materials (John Wiley & Sons, 2005).
Cosby, M. R. et al. Thermodynamic and kinetic barriers limiting solid-state reactions resolved through in situ synchrotron studies of lithium halide salts. Chem. Mater. https://doi.org/10.1021/acs.chemmater.2c02543 (2023).
Sun, W. et al. Nucleation of metastable aragonite CaCO3 in seawater. Proc. Natl Acad. Sci. USA 112, 3199–3204 (2015).
Sun, W. et al. Non-equilibrium crystallization pathways of manganese oxides in aqueous solution. Nat. Commun. 10, 573 (2019).
Raccuglia, P. et al. Machine-learning-assisted materials discovery using failed experiments. Nature 533, 73–76 (2016).
Miura, A. et al. Selective metathesis synthesis of MgCr2S4 by control of thermodynamic driving forces. Mater. Horiz. 7, 1310–1316 (2020).
Ong, S. P. et al. The materials application programming interface (API): a simple, flexible and efficient API for materials data based on REpresentational State Transfer (REST) principles. Comput. Mater. Sci. 97, 209–215 (2015).
Ong, S. P. et al. Python materials genomics (pymatgen): a robust, open-source Python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Richards, W. D. et al. Interface stability in solid-state batteries. Chem. Mater. 28, 266–273 (2016).
Doebelin, N. & Kleeberg, R. Profex: a graphical user interface for the Rietveld refinement program BGMN. J. Appl. Crystallogr. 48, 1573–1580 (2015).
Acknowledgements
This work was supported by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under award no. DE-SC0021130. We thank J. Morgan for contributions to the development of Samsung ASTRAL. W.S. thanks S. Y. Chan for important discussions and support.
Author information
Authors and Affiliations
Contributions
J.C. and W.S. developed precursor selection principles, analysed candidate synthesis reactions and predicted optimal synthesis precursors for experimental validation. S.R.C., L.J.M. and Y.W. designed the traditional synthesis precursors. S.R.C., L.J.M., J.-J.C. and Y.W. built the ASTRAL automated laboratory. S.R.C. synthesized and characterized the quaternary materials. J.C., S.R.C. and W.S. conducted phase purity analysis. J.C., S.R.C., Y.W. and W.S. wrote the manuscript and Supplementary Information, with contributions and revisions from all authors. W.S., L.J.M. and Y.W. conceived and supervised all of the main aspects of the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Synthesis thanks Milad Abolhasani and Kedar Hippalgaonkar for their contribution to the peer review of this work. Primary Handling Editor: Alexandra Groves, in collaboration with the Nature Synthesis team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–3, including Supplementary Figs. 1–52, Discussion and Tables 1–75.
Supplementary Data 1
Additional 3,104 predicted reactions.
Supplementary Video 1
ASTRAL dispensing power part 1.
Supplementary Video 2
ASTRAL dispensing power part 2.
Supplementary Video 3
ASTRAL furnace workflow.
Supplementary Video 4
ASTRAL XRD workflow.
Supplementary Data 2
Raw data for all X-ray diffraction figures in the Supplementary Information.
Source data
Source Data Fig. 1
Raw X-ray diffraction data for Fig. 1j.
Source Data Fig. 4
Statistical source data for Fig. 4c,d.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, J., Cross, S.R., Miara, L.J. et al. Navigating phase diagram complexity to guide robotic inorganic materials synthesis. Nat. Synth 3, 606–614 (2024). https://doi.org/10.1038/s44160-024-00502-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s44160-024-00502-y