Abstract
Understanding the (dis)assembly mechanisms of large metallosupramolecules is critical in their design, stability and application. The inherent complexity of these structures leads to many potential pathways for combining (or separating) the constituent building blocks, which makes this task difficult. Here we use collision-induced dissociation mass spectrometry to study the disassembly of heterometallic complexes. Collisional activation leads to the formation of a series of previously unknown smaller ring products and we characterize their geometry using ion mobility. The disassembly of both {CrxCu2} hourglass structures (x = 10, 12) and of a {Cr12Gd4} cluster shows the formation of rare closed, heptametallic species {Cr6Cu}, {Cr5Cu2} and {Cr5Gd2} as dominant products, as well as other closed ions such as {Cr5Cu}, {Cr10Cu}, {Cr12Cu}, {Cr10}, {Cr12} and {Cr6Gd2}. The collision cross-section of cyclic products and precursors has a linear correlation with ion mass—a relationship that does not hold for acyclic systems. As these rings are non-trivial to synthesize individually in solution, we propose the presented workflow to identify and characterize feasible molecules for bulk phase synthesis.

Similar content being viewed by others
Main
Tandem mass spectrometry (MS2) involves isolation of target ions in the gas phase and often their subsequent dissociation to smaller ions. The most common fragmentation method is collision-induced dissociation (CID), in which ions of interest are subjected to collisions with an inert gas at user-defined kinetic energies. The structure of newly formed products as well as non-fragmented precursor ions can be accessed when CID is combined with ion mobility mass spectrometry (IM–MS), which allows the mass as well as size and shape to be measured in the same experiment. Structural information is provided in the form of collision cross-sections (CCS), which can be compared with literature data or to theoretical values computed from candidate geometries. Due to the high energies involved in collisional activation, analytes tend to disrupt and undergo major structural change, which becomes visible in the ion mobility spectra of the precursor and/or product ions. Particularly for proteins, the term ‘collision-induced unfolding’ was coined to describe this behaviour similar to denaturation1. Although the disassembly of biomacromolecules is commonly investigated2,3,4,5, the impact of collisional activation on large synthetic molecules is not well explored.
We have been studying a family of cyclic polymetallic supramolecules proposed as qubits in quantum information processing6,7,8,9, and related compounds have also been used as resists for lithography10,11,12. As the interest in these and other metallosupramolecular complexes increases, and similarly the complexity of their structures13,14,15, the synthesis and analysis of their building blocks could aid in rationalizing the preference for certain compounds and predict the formation of others.
One prominent example where mass spectrometry was used to find a molecule stable enough to be produced in bulk phase was the discovery of the C60 buckminsterfullerene by Kroto et al. in 1985 (ref. 16), which led to the award of the Nobel Prize in Chemistry 11 years later17,18,19. More recently, Cronin and co-workers have used cryospray and IM–MS to identify polyoxometalate targets for bulk synthesis20,21,22,23 and to unravel their assembly mechanism21,23,24. We have recently applied CID and IM–MS to investigate the disassembly mechanisms and energetics of heterometallic rings and [2]-rotaxanes with the general formula [NH2RR′][Cr7MF8(O2CtBu)16] (M = MnII, FeII, CoII, NiII, CuII, ZnII and CdII), showing that both the metal M and the R,R′ groups can be used to tune the stability and conformational dynamics of these systems25.
In this Article, we investigate the disassembly dynamics of more complex heterometallic systems, two of which have hourglass structures, [NH2nPr2]2[Cr10Cu2F14(O2CtBu)22] = ‘{Cr10Cu2}’ (Fig. 1a) and [NH2iPr2]2[Cr12Cu2F16(O2CtBu)24] = ‘{Cr12Cu2}’ (Fig. 1b), and a third that involves a lanthanide tetrahedron bound to two {Cr6} chains, [NH2nPr2]2[Cr12Gd4F21(O2CtBu)29] = ‘{Cr12Gd4}’ (Fig. 1c). We demonstrate how CID, aided by IM–MS, can discriminate different disassembly pathways, which lead to the formation of closed polymetallic species that have not been made previously via solution synthesis (Fig. 1d). We suggest that this workflow could therefore inspire new synthetic targets and inform the tools available for the formation of metallosupramolecular compounds. Using information from the CID–IM–MS measurements, we also propose a workflow for the topological assignment of polymetallic systems, which applies to structures synthesized in solution as well as those formed in the gas phase.
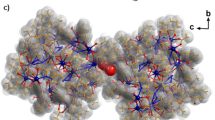
a–c, Single crystal X-ray structure of {Cr10Cu2} (a), {Cr12Cu2} (ref. 27) (b) and {Cr12Gd4} (c); Cr: dark green, Cu: brown, Gd: purple, F: yellow, O: red, N: blue, C: grey. Solvent molecules and hydrogen atoms have been removed for clarity. d, CID–IM–MS workflow following nano-electrospray of the precursor {CrxMy} from solution and m/z-selection of an appropriate precursor ion. Upon collisional activation, several fragment ions are observed with different masses, and their CCSN2 distribution can be extracted as shown for an ion of the type {Crx-aMy-b}. Different structures of {Crx-aMy-b} are possible, such as closed (low CCSN2, narrow CCSN2 distribution) or open forms (high CCSN2, wide CCSN2 distribution), of which only a closed {Crx-aMy-b} species was found in this illustrative example.
Results
{Cr10Cu2} and {Cr12Cu2} hourglasses
The hourglass structures {CrxCu2} (x = 10, 12) consist of two CuII and x CrIII centres, which are bridged via pivalate ligands (−O2CtBu = Piv−) on the outside and fluorides on the inside of the hourglass structure (Fig. 1a,b). The coordination environment of the chromium ions involves four pivalates and two cis-fluorides except for those located at the hourglass bottleneck, where three pivalates and three mer-fluorides are present. These centres are adjacent to the two copper ions, which are penta-coordinated by three pivalates and two fluorides. Additionally, one secondary ammonium cation is located in each half of the hourglass (for {Cr10Cu2}: [NH2nPr2]+ and for {Cr12Cu2}: [NH2iPr2]+), where it exhibits hydrogen bonds to the fluorides, particularly to the terminal fluorides attached to the two bottleneck chromiums26,27. Following optimization of solvent and nano-electrospray ionization (nESI) source conditions, mass spectra of {CrxCu2} (x = 10, 12) were recorded from solutions of sodium iodide in positive mode. Cations of the type [{CrxCu2} + Na]+ were obtained for both hourglasses (Supplementary Figs. 1 and 2).
Disassembly of {Cr 10 Cu 2} and {Cr 12 Cu 2}
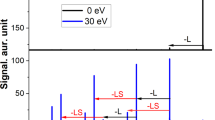
We isolated the ions [{Cr10Cu2} + Na]+ and [{Cr12Cu2} + Na]+ and ramped the energy of collisional activation with nitrogen gas, while recording the arrival time distributions (ATD) of both analytes and their products. The ATD of all ions were converted to CCS distributions in nitrogen gas (CCSN2) as a function of collision energy28,29. The MS2 spectra of both precursor ions show the loss of one secondary ammonium cation along with an anionic ligand, predominantly a pivalate, as the first dissociation step (Fig. 2). E50 values, known as a relative measure of ion stability, were determined for both precursor ions and show a slightly higher stability for [{Cr12Cu2} + Na]+ (Supplementary Fig. 3).
a,b, MS2 spectra of [{Cr10Cu2} + Na]+ (m/z = 3,365) at collision energies of 0 eV, 100 eV and 140 eV (a) and [{Cr12Cu2} + Na]+ (m/z = 3,910) at collision energies of 0 eV, 120 eV and 150 eV (b). Occurring fragmentation pathways are labelled: (i) – [NH2n/iPr2]+, – Piv−; (ii) –CuII, – 2 Piv−; (iii) – [NH2n/iPr2]+, – F− and (iv) – CuII, – Piv−, – F−. Satellite peaks (labelled with ‘s’) correspond to the labelled main peak via the exchange of one anionic ligand for another one (Piv− for F− or F− for Piv−; mass difference 82 Da). The spectra of both ions present two regions, one at lower m/z and one at higher m/z. Insets: schematics of {Cr10Cu2} and {Cr12Cu2} (Cr, green; Cu, brown).
Accurate mass and isotopic distributions were used to assign the hourglass fragments in the subsequent dissociation steps at higher collision energies. A variety of dissociation channels occur and ions are observed in two regions of the mass spectrum, one at lower m/z (x = 10, <1,800 m/z; x = 12, <2,200 m/z) and one at higher m/z (x = 10, 2,500–3,200 m/z; x = 12, 2,000–3,700 m/z). All of the observed species are singly charged cations, and between these two regions only minor ion populations were found (Fig. 2). For [{Cr12Cu2} + Na]+, more ions were found in the low mass region compared with [{Cr10Cu2} + Na]+, for which the high mass region clearly dominates. The ratio between the precursor and product ions in both regions depends both on the collision energy (Fig. 2) and the instrument used (Supplementary Fig. 4).
The dominant fragment ions of the low mass region contain seven transition metal ions. From the precursor [{Cr10Cu2} + Na]+, the dominant fragment is {Cr5Cu2} (mainly [Cr5Cu2F7Piv12Na]+ at 1,756 m/z). We also observe in minor amounts {Cr5} that probably is the other direct fragment of the {Cr10Cu2} dissociation, at least partially (Fig. 2a top and Supplementary Dataset). {Cr5Cu} was also found in low numbers (mainly [Cr5CuF7Piv10Na]+ at 1,491 m/z); however, this and other low abundance ions are presumably secondary fragments from {Cr5Cu2} as they appear at higher energies than the latter (for {Cr5Cu}: loss of CuII and two Piv−; Fig. 2a). In contrast, the precursor [{Cr12Cu2} + Na]+ dissociates to {Cr6Cu} (mainly [Cr6CuF8Piv12Na]+ at 1,764 m/z; Fig. 2b). The species in the high mass region follow fragmentation channels where CuII dissociates along with two anionic ligands, before the second ammonium cation and another ligand are lost. This in turn is followed by the dissociation of the second CuII centre, again along with two anionic ligands (Fig. 2). Overall, this yields species of the type Crx (x = 10, 12) as the product ions of the hourglass ions [{CrxCu2} + Na]+, which was confirmed by their isotopic distributions as illustrated for [Cr12F15Piv21Na]+ (m/z = 3,056; Supplementary Fig. 5).
Ion mobility allows us to probe the structure of both precursor and product ions via their CCSN2 distributions (Fig. 3). The majority of products exhibit narrow, unimodal conformations, although slightly wider distributions were found for {Cr12Cu} and {Cr12} fragment ions of [Cr12Cu2 + Na]+ (Fig. 3b) as well as for some {Cr5} species formed in the disassembly of [{Cr10Cu2} + Na]+ (Supplementary Dataset). The CCSN2 values of the hourglass precursor ions and the presented products were quantified and compared with data of similar polymetallic closed species (Table 1). The data for {Cr5Cu2} and {Cr6Cu} agree well with the CCSN2 of a seven-membered [Cr6MnF8Piv13]− ring, formed from a {Cr7Mn} ring via CID–MS25, and the small difference can be explained with the different number of bulky pivalate ligands ({Cr5Cu2}, {Cr6Cu}: 12 Piv−, {Cr6Mn}: 13 Piv−). This and their unimodal, narrow distributions clearly suggest a limited conformational flexibility and hence the presence of heptametallic {Cr5Cu2} and {Cr6Cu} species that are closed, which is distinct from other open {Cr6Mn} horseshoe fragments observed previously (Table 1)25. Other products and precursor ions cannot be directly compared with previous data; however, their similar CCSN2 values and similarly unimodal and narrow peak shapes indicate cyclic structures as well for these species (Fig. 3 and Supplementary Dataset). For the minor {Cr5} fragments, depending on the exact chemical composition of the cations, the conformational landscape is more diverse (Supplementary Dataset).
a,b, [{Cr10Cu2} + Na]+ (m/z = 3,365) including selected product ions of the types {Cr10Cu} (m/z = 2,896), {Cr10} (m/z = 2,509), {Cr5Cu2} (m/z = 1,756) (a), and [{Cr12Cu2} + Na]+ (m/z = 3,910) including selected product ions of the types {Cr12Cu} (m/z = 3,443), {Cr12} (m/z = 3,056), {Cr6Cu} (m/z = 1,764) (b). Data were recorded at collision energies of 0 eV (both precursor ions) as well as 120 eV (fragments of [{Cr10Cu2} + Na]+) and 160 eV (fragments of [{Cr12Cu2} + Na]+), respectively. Insets: schematics of {Cr10Cu2}, {Cr12Cu2} and their products (Cr, green; Cu, brown). Fragment ions that are assigned as closed, due to the ion mobility data, are presented schematically; as the IM–MS experiment informs on the stoichiometry but not on the exact connectivity between the metal centres.
{Cr12Gd4} cluster
We further investigated whether collision-induced disassembly would also lead to polymetallic rings when activating a different type of precursor. We chose the lanthanide cluster {Cr12Gd4} (Fig. 1c), which consists of a tetrahedral {Gd4F7Piv} cage, in which the fluorides and one pivalate bridge the four GdIII centres. Each of the octa-coordinated gadolinium ions is attached to a terminus of one of two {Cr6} chains, and a [NH2nPr2]+ cation is located at each {Cr6Gd2} ring centre30. The chromium atoms are each connected via two pivalate ligands and one fluoride, as in both {CrxCu2} hourglasses.
The mass spectrum of {Cr12Gd4}, sprayed from methanol in the presence of sodium iodide using nESI, yielded only a small number of largely intact analyte ions (Supplementary Fig. 6), and we assigned the dominant one to [{Cr12Gd4} – Piv]+ (m/z = 4,688; Supplementary Fig. 7 for isotopic distribution). Several other polymetallic species were observed in the mass spectrum, including {Cr6Gd} ions, which are possibly produced by decomposition reactions with the solvent. Using ion mobility, the {Cr6Gd} clusters were identified as heptametallic rings (CCSN2 values in Supplementary Table 1 including discussion of their disassembly; Supplementary Dataset), which are isostructural to a {Cr6Ce} ring reported previously, which was only synthesized in very low yield (Discussion)30. We computed the density functional theory (DFT) optimized structure of the neutral {Cr6Gd} (Supplementary Fig. 8) as well as the corresponding sodium adduct (Supplementary Dataset), supporting their stabilities in the gas phase.
Disassembly of {Cr 12 Gd 4}
We used the MS2 ion mobility workflow (Fig. 1d) to study [{Cr12Gd4} – Piv]+. Similar to the studies of [{CrxCu2 + Na]+, the tandem mass spectra show the loss of [NH2nPr2]+ along with one fluoride as the main fragmentation channel, although at higher energies (Fig. 4a). The E50 value of [{Cr12Gd4} – Piv]+ was determined and is more than 50% higher than those of the hourglass ions (Supplementary Fig. 9). Upon increasing the energy further (Fig. 4a centre), two main regions were found in the tandem mass spectra: one at 1,800–2,500 m/z and the other at 3,200–4,500 m/z; however, the separation between regions is blurred at higher collision energies (Fig. 4a top). All species also occur as singly charged cations. In the lower mass region, the cluster type {Cr6Gd2} was found as the main product (mainly [Cr6Gd2F8Piv16(NH2nPr2)]+ at m/z = 2,499; Supplementary Fig. 10 for isotopic distribution). This cluster is one half of the {Cr12Gd4} precursor, and we previously reported the solid-state structure of a cyclic {Cr6Y2} complex, albeit in low yield14. The {Cr6Gd2} ions undergo further fragmentation at even higher energies, with losses of [NH2nPr2]+ or CrIII, along with anionic ligands (mainly pivalates, Fig. 4a top). This, for example, leads to ions of the type {Cr5Gd2} (such as [Cr5Gd2F8Piv12]+ at m/z = 1,940). In contrast, the high mass region shows the stepwise disruption of the {Cr6} chains with losses of [NH2nPr2]+ along with Piv−, followed by several dissociations of {Cr(Piv)3} units (Fig. 4a centre). This infers that the {Gd4} tetrahedron remains intact.
a, MS2 spectra of [{Cr12Gd4} – Piv]+ at collision energies of 0 eV, 210 eV and 250 eV. Occurring fragmentation pathways are labelled: (i) – [NH2n/iPr2]+, – Piv−; (iii) – [NH2n/iPr2]+, – F− and (v) – CrIII, – 3 Piv−. Satellite peaks (labelled with ‘s’) correspond to the labelled main peak via the exchange of one anionic ligand for another one (Piv− for F− or F− for Piv−; mass difference 82 Da). The spectrum at 210 eV shows two regions, one at lower m/z and one at higher m/z. Minor contaminant features were observed that were m/z-selected in the quadrupole along with [{Cr12Gd4} – Piv]+, and hence produce different fragments (labelled with ‘c’). b, CCSN2 distributions of [{Cr12Gd4} – Piv]+ (m/z = 4,688) and the fragment ions {Cr6Gd2} (m/z = 2,499) and {Cr5Gd2} (m/z = 1,940). Data were recorded at collision energies of 0 eV (precursor), 130 eV for {Cr6Gd2} and 190 eV for {Cr5Gd2}, respectively. Insets: schematics of {Cr12Gd4} and the two products {CrxGd2} (x = 5, 6; Cr, green; Gd, purple). Fragment ions that are assigned as closed, due to the ion mobility data, are presented schematically; as the IM–MS experiment informs on the stoichiometry but not on the exact connectivity between the metal centres.
The structure of [{Cr12Gd4} – Piv]+ and fragment ions was investigated via their CCSN2 distributions (Fig. 4b for selected ions). The majority of the ions exhibit narrow, unimodal conformations (Supplementary Dataset). We quantified absolute CCSN2 values of the precursor [{Cr12Gd4} – Piv]+ and products of the type {Cr6Gd2} and {Cr5Gd2} (Table 1). The CCSN2 value of {Cr6Gd2} agrees well with a related {Cr7Cu} ring25, while the value for {Cr5Gd2} is similar to those of the seven-membered hourglass products {Cr5Cu2} and {Cr6Cu}, as well as to the [Cr6MnF8Piv13]− closed species25. These comparisons suggest closed, cyclic structures for the complexes of the type {Cr6Gd2} and {Cr5Gd2}.
Density functional theory and CCSN2 calculations
To assess the stability of the closed fragments formed in the disassembly of {Cr10Cu2}, {Cr12Cu2} and {Cr12Gd4}, DFT optimized structures were generated for {Cr5Cu2}, {Cr5Cu}, {Cr6Cu}, {Cr6Gd2} and {Cr5Gd2} (Supplementary Figs. 11–15). At the level of theory used, all closed cations are considerably more stable with respect to their monometallic fragments [CrFPiv2], [CrF2Piv], [CuFPiv2]−, [CuF2Piv]− and Piv−, by at least 1,400 kJ mol−1. For the heptametallic species {Cr5Cu2}, {Cr6Cu} and {Cr5Gd2}, different isomers were calculated, and the DFT energies suggest that hexametallic rings involving an additional metal bridge might even be more stable than the corresponding heptametallic rings (Supplementary Figs. 11, 13 and 15 and Supplementary Dataset). We cannot assign the observed fragments unambiguously to the computed candidate structures since the kinetics of the dissociation reaction and its mechanism are unknown; in addition, our sampling of candidate structures is not exhaustive.
Theoretical THCCSN2 values were enumerated for {Cr5Cu} and {Cr6Gd2} as well as the different isomers of {Cr5Cu2}, {Cr6Cu} and {Cr5Gd2}, using the trajectory method implemented in IMoS31. This yielded 3–8% larger values than found experimentally (Supplementary Table 2), and we previously observed this discrepancy for similar polymetallic complexes25,32, and have discussed possible explanations in detail25. An exception to this was found for the six-membered ring {Cr5Cu}, where the experimental and theoretical CCSN2 values are in good agreement. The reason for this is not known, but given that this is the most compact and dense structure (Supplementary Fig. 12), it suggests that the cavities in the larger rings are not well represented by the computational THCCSN2 methodology with the trajectory method, as previously discussed25. The THCCSN2 values of the different heptametallic isomers {Cr5Cu2}, {Cr6Cu} and {Cr5Gd2} are similar (Supplementary Table 2), and the fragment structures can hence not be resolved via comparisons of experimental and theoretical CCSN2.
We examined the high mass loss from {Cr10Cu2} in more detail. Experiment suggests that the cleavage does not occur at the hourglass bottleneck, as observed for {Cr12Cu2} and resulting in {Cr6Cu}, but counterintuitively at the adjacent Cr–Cu edge. This leads to the formation of {Cr5Cu2} instead of {Cr5Cu}, which agrees with the thermodynamic stabilities of the DFT optimized structures (Supplementary Figs. 11 and 12 and Supplementary Dataset). Here the disassembly of {Cr5Cu2} → {Cr5Cu} + [CuPiv2] is endothermic (ΔE ≈ 334 kJ mol−1), and this fragmentation channel is experimentally only observed at higher collision energies (Fig. 2a top).
Discussion
The first major finding from this work is the formation, separation and isolation of closed cyclic products in the gas phase from the CID of the {CrxCu2} hourglasses (x = 10, 12) and from {Cr12Gd4}. The observation that polymetallic rings are formed from all three precursors suggests that this workflow can produce smaller rings of varying sizes, including new types, as long as appropriate larger precursors are available. These rings form after collisions on a millisecond timescale, which suggests that both rearrangements and new bond formations occur fast. Also noteworthy is the occurrence of gaps in the tandem mass spectra of all three parent ions (Figs. 2 and 4a), which suggests that potential products in these regions are considerably less stable than those obtained at both lower and higher masses, akin to the magic numbers seen in the spectra for monatomic and molecular cluster ions16,33,34,35,36,37. For the low m/z region, the primary and kinetically most stable products from the precursor ions are {Cr5Cu2}, {Cr6Cu} and {Cr6Gd2}, whereas others such as {Cr5Cu} and {Cr5Gd2} are secondary products from these fragments.
The formation of the closed, heptametallic species {Cr5Cu2}, {Cr6Cu} and {Cr5Gd2} is striking, for which DFT optimizations indicate several plausible structures (Supplementary Figs. 11, 13 and 15). In all three cases, the lowest-energy conformer of those sampled involves a hexametallic ring with an additional metal bridge. In the family of polymetallic chromium rings38, the only closed seven-metal ring synthesized so far is {Cr6Ce}, which only forms as a very minor side product30, and this is one of three structurally characterized heptametallic rings known39,40. Given the sparsity of known heptametallic compounds it might be argued that these products are unlikely; however, in the synthesis of heterometallic chromium rings the difficulty is avoiding the formation of [Cr8F8Piv16], which is achieved by adding a cationic template that occupies the centre of the cavity and leads to an anionic heterometallic ring26. This allows formation of larger rings by choice of larger templates, but for closed seven-metal species there is insufficient space for any organic template. Applying the presented CID–MS approach on these larger complexes therefore offers a route for the formation of closed heptametallic and smaller species, and we have confirmed their gas phase stability using DFT25.
The discussed approach can inspire supramolecular chemistry outside the gas phase. In some cases, rings similar to those produced by CID–MS have been previously synthesized and characterized. For example, several {Cr10} rings have been reported by our group; however, these involved different bridging ligands41,42,43. We have also structurally characterized a {Cr6Y2} ring of the formula [Cr6Y2F8Piv17(NH2Et2)(H2O)], which is highly similar to the ion [Cr6Gd2F8Piv16(NH2nPr2)]+ observed upon fragmentation of {Cr12Gd4}. The {Cr6Y2} was formed only in low yield, which correlates with the observation that the solution synthesis leads to {Cr12Ln4} cages as the major products30.
Another aim for future endeavours is to connect gas phase experiments with bulk phase via the so-called preparative mass spectrometry (‘ion soft-landing’), in which ions produced in the mass spectrometer are transferred and gently deposited on a surface44,45,46. This surface can in turn be analysed by a range of microscopy47,48, spectroscopy49,50 or mass spectrometry techniques51, among others. As the field of soft landing is still in its infancy and rapidly evolving, we hypothesize that the presented CID–MS formation strategy will be of practical significance for synthetic chemists in the future.
Our second major observation is that ion mobility can be used to identify whether a given polymetallic complex of this family is cyclic or not, and this applies both to structures formed via CID–MS in the gas phase, and also to those synthesized in solution that are just transferred to the gas phase (such as {Cr10Cu2}, {Cr12Cu2} and {Cr12Gd4}). The two main advantages here, compared with other bulk phase methods, are small measurement times and low amounts of samples needed. When directly assigning structures using ion mobility, theoretical calculations such as DFT are commonly applied to compare theoretical CCS values to those found experimentally; however, this can be non-trivial and requires careful structural and conformational sampling. On the basis of DFT calculations, we have benchmarked the following workflow to theoretical CCSN2 values from this and previous works, yielding good agreement25,32.
We plot the CCSN2 of all species examined here and from previous work (Table 1) against their adjusted masses (Fig. 5). This correlation represents the packing density in a given ion28,52,53, which is highest for ions with small CCS and large mass. Previously, Bleiholder et al. tracked the self-assembly of peptides and, using an analogous relationship, distinguished between the formation of larger globular peptides and β-sheets relevant for amyloid fibril formation53. Later our group showed that the CCS/m slope of unfolded and intrinsically disordered proteins is significantly higher (lower density) than for native proteins28. In the case of cyclic species from this and previous works, we observe a linear correlation, which does not hold for the acyclic {Cr12Gd4} cluster and the extended {Cr6Mn} horseshoes25. These are located above the line as their estimated spherical densities (ESD) are lower than for the polymetallic cyclic structures (Fig. 5 inset). ESD were derived from CCSN2 values, following previously published calculations based on the assumption of a spherical ion52, and cannot be directly compared with the macromolecular density in the crystal structures, where available. The latter is typically higher (1.2–1.4 g cm−3) and represents the packing density of the molecules in the crystal lattice (together with solvent molecules), whereas the ESD discussed here inform on how dense the atoms are in the gas phase ion.
The cyclic complexes show a linear correlation, which does not hold for the acyclic ions ({Cr12Gd4} and {Cr6Mn} horseshoes). 1: {Cr5Cu}; 2: {Cr5Gd2}; 3: {Cr5Cu2}; 4: {Cr6Cu}; 5, 6: {Cr6Mn} rings. The mass was adjusted so that every metal centre is accounted for with the mass of chromium (52 Da). This model is reasonable as the nature of the metal in the polymetallic complex has a low overall impact on the CCSN2, although some have high masses, for example in the case of Gd. Inset: schematics of selected cyclic and acyclic complexes (Cr, green; Cu, brown; Gd, purple; Mn, black). Fragment ions that are assigned as closed, due to the ion mobility data, are presented schematically; the IM–MS experiment informs on the stoichiometry but not on the exact connectivity between the metal centres. ESD derived from CCSN2 values versus mad (black circles, cyclic; blue squares, acyclic), showing that the acyclic {Cr6Mn} horseshoes and {Cr12Gd4} have a lower ESD than the cyclic species.
Disassembly of {Cr 10 Cu 2} and {Cr 12 Cu 2}
The first dissociation step of both hourglass ions [{CrxCu2} + Na]+ (x = 10, 12) is the loss of the secondary ammonium cation, along with an anionic ligand, predominantly a pivalate. This is probably because the cation is the only non-covalently bound species in the system. As the primary fragmentation pathway is the same for both [{CrxCu2} + Na]+ ions, their E50 values are also similar. The same dissociation channel was observed for the heterometallic rotaxanes [NH2RR′][Cr7MF8Piv16], where R and R′ include bulky phenyl and tert-butyl groups25. The secondary ammonium cations are smaller here, so the relative ease of dissociation from the hourglass ions is not surprising.
The further disassembly can be rationalized by considering the sites in the hourglass structure that are most prone to CID. These are the two CuII centres and their ligands, because of the lower oxidation state (CuII versus CrIII), and hence a weaker electrostatic attraction between ligand and metal, as well as the coordination number (CuII: 5, CrIII: 6; Fig. 1a,b). It seems likely that both the initially lost ammonium cation and pivalate are adjacent to the same CuII centre. This would weaken the hourglass scaffold further in this region, which is the reason for its disruption in the second dissociation step (rather than the loss of the second ammonium cation). As discussed above, the hourglass disruption occurs via different pathways, yielding product ions either with low m/z or high m/z. It is also possible that some initial fragments at high m/z fragment further to smaller products.
Fragmentation associated with higher mass loss leads to rings of the type {Cr5Cu2} (from [{Cr10Cu2} + Na]+) and {Cr6Cu} (from [{Cr12Cu2} + Na]+; Figs. 2 and 3 and Table 1). In the disassembly of {Cr12Cu2} the dissociation occurs at the hourglass bottleneck, and this is probably the favoured site as CuII is far more reactive than CrIII, and only two bridging ligands are present. As a result, the hourglass predominantly dissociates symmetrically to {Cr6Cu}, which probably rearranges to a closed structure. For the fragmentation of {Cr10Cu2}, this same mechanism would lead to a six-membered {Cr5Cu} species, but interestingly this ring, characterized by ion mobility, is only seen at higher energies. This suggests that it is a secondary fragment (Fig. 2a and Supplementary Dataset). By contrast, we predominantly observe {Cr5Cu2} products due to an asymmetric hourglass disruption, and here three bonds need to be broken instead of two. This preference may be due to the stability given by the formation of the heptametallic species, which implies it is more stable than the alternative hexametallic {Cr5Cu}. The comparison of their energetics using DFT supports these findings, showing that {Cr5Cu2} is the thermodynamically more stable product than {Cr5Cu} (ΔE ≈ 334 kJ mol−1; Supplementary Figs. 11 and 12). Hence, the secondary and endothermic disassembly from {Cr5Cu2} to {Cr5Cu} and [CuPiv2] occurs only at higher collision energies. Notably, the lowest energy isomer found for {Cr5Cu2} is a {Cr5Cu} ring bridged by the second CuII centre, which may inspire future investigations on the stability of different bridging situations in polymetallic rings.
No ammonium cation is present in the dominant {Cr5Cu2} or {Cr6Cu} ring products, which suggests that these are formed from the part of the hourglass where the ammonium cations and Piv− are lost in the primary fragmentation step. This is possibly due to insufficient space in the central cavity of a closed seven-metal species to bind an ammonium cation. Instead, Na+ was found in the heptametallic species observed, where it is probably located in the centre of the ring as the DFT optimized structures suggest (Supplementary Figs. 11 and 13). We have previously found that Na+ is too small for a good fit for the cavity of an octametallic ring, both in the bulk and the gas phase32,54, and might hence be better suited for heptametallic species. The formation of {Cr5Cu2} from {Cr10Cu2}, probably occurring in a concerted step, implies that {Cr5} is also formed. As discussed above, we have a low number of {Cr5} ions (Fig. 2a top), which is probably due to the relatively higher stability of heptametallic rings and the preference of the charge-carrier Na+ to remain with {Cr5Cu2}, which complicates the detection of {Cr5} cations. Our data suggest that {Cr5} can occur in different conformations and/or topologies, potentially either as chains and/or rings (Supplementary Dataset).
The mechanism associated with smaller mass losses shows the stepwise disruption of the hourglasses, starting with the loss of one CuII centre along with two ligands. The formed {Cr10Cu} and {Cr12Cu} products are probably also closed due to their narrow and unimodal CCSN2 distributions (Fig. 3 and Table 1), and require the formation of new bonds on the experimental timescale. The {Cr12Cu} distribution is significantly wider than for {Cr10Cu}, indicating a higher conformational flexibility. The same qualitative trend was observed in the next fragmentation step, where the second ammonium cation is lost, predominantly along with a pivalate. After that, the second CuII centre dissociates along with two anionic ligands, leading to ions of the type {Cr10} and {Cr12}. Here both ions exhibit narrow CCSN2 distributions, once more suggesting cyclic structures.
Disassembly of {Cr 12 Gd 4}
If similar disassembly mechanisms take place for [{Cr12Gd4} – Piv]+ as for the hourglass ions, we would also expect smaller closed structures, of the type {Cr6Gd} (as discussed above and in Supplementary Table 1) or {Cr6Gd2}. For the second route involving low mass loss, we would expect the stepwise disruption of the {Cr6} chains, again followed by rearrangements to closed structures, as the {Cr6} chains are more accessible for gas collisions and less strongly bound than the {Gd4} unit.
The fragmentation of the ion [{Cr12Gd4} – Piv]+ follows similar routes as [{CrxCu2} + Na]+ (x = 10, 12) and confirms our hypothesis that the mechanisms observed for the hourglass ions can be transferred to other polymetallic complexes. Here, after the loss of one secondary ammonium cation along with a fluoride, the disassembly associated with higher mass loss leads to {Cr6Gd2} and subsequently to {Cr5Gd2} complexes, for which the comparisons with previously reported CCSN2 values clearly indicate closed structures.
The second disassembly mechanism of the {Cr12Gd4} cluster shows the loss of the second [NH2nPr2]+ and a pivalate, followed by multiple dissociation steps in which {CrPiv3} is lost. Here the loss of five {CrPiv3} units, occurring as the most abundant pathways, exceeds the number of pivalates present in a {Cr6} chain and suggests either major rearrangements, or the disruption of the second {Cr6} unit before the complete dissociation of the first. The CCSN2 distributions of the occurring products indicate more flexible structures (larger peak widths) than the precursor [{Cr12Gd4} – Piv]+; however most of the products still appear with unimodal conformations (similarly to the high mass fragments of [{Cr12Cu2} + Na]+). This suggests that no major ring perturbation takes place and both horseshoe units are possibly disrupted simultaneously. In either case, the {CrPiv3} leaving group seems to be the driving force of this disassembly route, similar to previous observations25,32.
Conclusions
For the three studied compounds, {CrxCu2} (x = 10, 12) and {Cr12Gd4}, the formation of smaller rings via rearrangements and newly established connectivities suggests a ‘self-healing’ capability upon CID, driven by the stability of closed, polymetallic species. Several of the latter were formed including {Cr6Cu}, {Cr5Cu2}, {Cr5Cu}, {Cr10Cu}, {Cr10}, {Cr12Cu}, {Cr12}, {Cr6Gd2} and {Cr5Gd2}, whose topology was identified by ion mobility. This workflow can potentially inspire applications in materials science, if these or similar complexes can be made in isolable quantities, and in general aid the design process of polymetallic complexes by identifying feasible targets. We also propose a simple method to assign whether a polymetallic complex exists as a closed or open structure, and this approach can in the future be adapted for other compound families. This workflow, with some modifications, has great promise for the structural characterization of larger metallosupramolecular compounds, and so has the diagnostic use of the tandem mass spectra to predict the precursor structure. As reliable computations and X-ray crystallography are often not feasible, IM–MS is an important expansion of the available analytical methods for these systems55.
Methods
Synthesis
{Cr12Cu2} was synthesized according to our previous work27. {Cr10Cu2} was made similarly to [NH2Et2]2[Cr10Cu2F14(O2CtBu)22] (ref. 26), but the precursor diethylamine was replaced with dipropylamine. Elemental analysis (%) calculated for {Cr10Cu2}: C 43.84, H 6.94, N 0.84, Cr 15.56, Cu 3.80; found: C 44.13, H 6.99, N 0.89, Cr 15.42, Cu 3.86. {Cr12Gd4} was synthesized similarly to [NH2Et2]2[Cr12Gd4F21(O2CtBu)29] (ref. 30), by using the previously reported56 [(NH2nPr2)3Cr6F11Piv10]2 as the reactant instead of [(NH2Et2)3Cr6F11Piv10]2. Elemental analysis (%) calculated for {Cr12Gd4}: C 39.38, H 6.17, N 0.58, Cr 13.03, Gd 13.13; found: C 39.54, H 6.21, N 0.63, Cr 12.85, Gd 13.45. All reagents and solvents were purchased from Alfa, Fisher Scientific, Fluorochem or Sigma-Aldrich and used without further purification.
Sample preparation
Samples were prepared in 4:1 toluene/methanol with 500 µM NaI. Analyte concentrations of 200–500 µM were typically used for IM–MS and MS measurements.
nESI
Samples were ionized and transferred to the gas phase with an nESI source and were sprayed from borosilicate glass capillaries (World Precision Instruments). The latter were pulled on the Flaming/Brown P-2000 laser puller (Sutter Instrument Company). The capillary voltage (typically 1.0–1.8 kV) was applied through a platinum wire (diameter 0.125 mm, Goodfellow) inserted into the nESI capillaries. Source temperatures of 23 °C (Cyclic) or 30 °C (Q Exactive UHMR) were applied.
MS2
The Q Exactive Ultra-High-Mass-Range (UHMR) Hybrid Quadrupole-Orbitrap Mass Spectrometer (Thermo Fisher) was used for the derivation of the E50 values via MS2 experiments, and more precisely CID57. Target ions were m/z-isolated in a quadrupole filter, accelerated to a user-defined kinetic energy (Elab: 0–300 eV) and injected into the higher-energy C-trap dissociation cell, which contained nitrogen gas (trapping gas pressure parameter, 2.0). Non-fragmented precursor ions and fragment ions were transferred to the Orbitrap mass analyser (maximum inject time, 100 ms; resolution, 25,000).
IM–MS experiments were performed on a Select Series Cyclic IMS (Waters)58. Following ionization (cone voltage, 20–60 V; source offset, 10–20 V; and purge gas, 0–300 l h−1), ions were transferred to the trap and activated via collisions with nitrogen gas, if appropriate (trap voltage 0–200 V and gas flow 5 ml min−1). Ions are further injected to the cyclic ion mobility drift ring (Stepwave Ion Guide RF: 300–700 V) and separated by using a non-uniform electric field under a constant nitrogen pressure with travelling waves (TW; height, 20–22 V; velocity, 375 m s−1; and gas flow, 40 ml min−1), pushing the ions through the drift ring. Ions travelled one pass in the cyclic drift ring (‘single path’, separation time: 2–60 ms) and were then transferred (transfer voltage: 4–15 V) to a time-of-flight mass analyser.
Data processing
E50 values were obtained from a method described in our previous works25,32. Mass spectra were recorded at different collision energies, and the share of the precursor ion count, relative to the total ion count (‘survival yield’), was plotted versus the collisional energy in the centre-of-mass frame (Ecom, Supplementary Figs. 3 and 9). Survival yield plots were fitted with a sigmoidal Hill function (Hill1 function in OriginPro 2020b), yielding the point (E50) at which the survival yield reaches 0.5 or 50%. This E50 value is known as a relative measure of precursor ion stability59,60,61.
Experimentally obtained ATD were converted to collisional cross-section distributions TWCCSN2 via published calibration procedures62. The Agilent tune mix was used as a calibrant63.
Density functional theory and CCS calculations
Analogous to our previous works25,32, density functional calculations were carried out using the same effective core potentials and basis sets for Cu, Cr, C, N, O, F and H, assuming high-spin ferromagnetically coupled metals. For GdIII, it was necessary to use an alternative effective core potential, including 7f electrons in core64, with the corresponding (7s6p5d)/(5s4p3d) contracted valence basis set65.
Theoretical CCS values (THCCSN2, TH: theoretical) were obtained from the software IMoS by using the trajectory method in nitrogen gas including quadrupole potential (number of orientations 3, gas molecules per orientation 300,000, temperature 298 K, and pressure 101,325 Pa = 1 atm)31.
Crystallographic data
Single crystals of {Cr10Cu2} and {Cr12Gd4} were grown by slow diffusion of acetonitrile into toluene solutions of the respective complexes. ORTEP structures of {Cr10Cu2} (Supplementary Fig. 16) and {Cr12Gd4} (Supplementary Fig. 17) can be found in Supplementary Information along with crystallographic refinement details (Supplementary Table 3). Crystal structures are also shown in Fig. 1a,c as well as in Supplementary Dataset, respectively.
X-ray diffraction data were collected using a dual wavelength Rigaku FR-X rotating anode diffractometer using MoKα (λ = 0.71073 Å) radiation, equipped with an AFC-11 4-circle goniometer, VariMAX microfocus optics, a Hypix-6000HE detector and an Oxford Cryosystems 800 plus nitrogen flow gas system, at a temperature of 100 K. Data were collected and reduced using Rigaku CrysAlisPro v42 (ref. 66), and absorption correction was performed using empirical methods (SCALE3 ABSPACK) based upon symmetry-equivalent reflections combined with measurements at different azimuthal angles. The phase problem was solved using SHELXT and the structural model refined against all F2 values using SHELXL67,68, implemented through Olex2 v1.5 (ref. 69). All non-solvent atoms were refined anisotropically. Hydrogen atoms were placed in calculated positions and refined using idealized geometries and assigned fixed isotropic displacement parameters.
Data availability
The supporting data referred to in this manuscript are contained within a supplementary information document and in a supplementary dataset available on Figshare (https://figshare.com/articles/dataset/Geue_Supplementary_Dataset_Heterocluster_Paper_zip/21751442). The latter includes the raw data of all IM–MS and mass spectrometry measurements as well as the DFT calculation outputs and crystal structures. Crystallographic data for the structures reported in this article have been deposited at the Cambridge Crystallographic Data Centre, under deposition numbers CCDC 2226287 ({Cr10Cu2}) and 2226288 ({Cr12Gd4}). Copies of the data can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/. Source data are provided with this paper.
References
Dixit, S. M., Polasky, D. A. & Ruotolo, B. T. Collision induced unfolding of isolated proteins in the gas phase: past, present, and future. Curr. Opin. Chem. Biol. 42, 93–100 (2018).
Hall, Z., Politis, A. & Robinson, C. V. Structural modeling of heteromeric protein complexes from disassembly pathways and ion mobility-mass spectrometry. Structure 20, 1596–1609 (2012).
Zhou, M. & Wysocki, V. H. Surface induced dissociation: dissecting noncovalent protein complexes in the gas phase. Acc. Chem. Res. 47, 1010–1018 (2014).
Vallejo, D. D. et al. Mass spectrometry methods for measuring protein stability. Chem. Rev. 122, 7690–7719 (2022).
Christofi, E. & Barran, P. Ion mobility mass spectrometry (IM–MS) for structural biology: insights gained by measuring mass, charge, and collision cross section. Chem. Rev. 123, 2902–2949 (2023).
Troiani, F. et al. Molecular engineering of antiferromagnetic rings for quantum computation. Phys. Rev. Lett. 94, 1–4 (2005).
Timco, G. A. et al. Engineering the coupling between molecular spin qubits by coordination chemistry. Nat. Nanotechnol. 4, 173–178 (2009).
Fernandez, A. et al. Making hybrid [n]-rotaxanes as supramolecular arrays of molecular electron spin qubits. Nat. Commun. 7, 1–6 (2016).
Lockyer, S. J. et al. Five-spin supramolecule for simulating quantum decoherence of bell states. J. Am. Chem. Soc. 144, 16086–16092 (2022).
Lewis, S. M. et al. Use of supramolecular assemblies as lithographic resists. Angew. Chem. Int. Ed. 56, 6749–6752 (2017).
Lewis, S. M. et al. Plasma-etched pattern transfer of sub-10 nm structures using a metal-organic resist and helium ion beam lithography. Nano Lett. 19, 6043–6048 (2019).
Lewis, S. M. et al. Tuning the performance of negative tone electron beam resists for the next generation lithography. Adv. Funct. Mater. 32, 2202710 (2022).
Wang, H., Li, Y., Li, N., Filosa, A. & Li, X. Increasing the size and complexity of discrete 2D metallosupramolecules. Nat. Rev. Mater. 6, 145–167 (2021).
McTernan, C. T., Davies, J. A. & Nitschke, J. R. Beyond platonic: how to build metal–organic polyhedra capable of binding low-symmetry, information-rich molecular cargoes. Chem. Rev. 122, 10393–10437 (2022).
Saha, R., Mondal, B. & Mukherjee, P. S. Molecular cavity for catalysis and formation of metal nanoparticles for use in catalysis. Chem. Rev. 122, 12244–12307 (2022).
Kroto, H. W., Heath, J. R., O’Brien, S. C., Curl, F. W. & Smalley, R. E. C60: Buckminsterfullerene. Nature 318, 162–163 (1985).
Curl, R. F. Dawn of the fullerenes: experiment and conjecture. Nobel Lecture https://www.nobelprize.org/uploads/2018/06/curl-lecture.pdf (1996).
Kroto, H. W. Symmetry, space, stars, and C60. Nobel Lecture https://www.nobelprize.org/uploads/2018/06/kroto-lecture.pdf (1996).
Smalley, R. E. Discovering the fullerenes. Nobel Lecture https://www.nobelprize.org/uploads/2018/06/smalley-lecture.pdf(1996).
Miras, H. N. et al. Solution identification and solid state characterisation of a heterometallic polyoxometalate {Mo11V7}: [MoVI11VV5VIV2O52(μ9-SO3)]7 −. Chem. Commun. 52, 4703–4705 (2008).
Wilson, E. F. et al. Probing the self-assembly of inorganic cluster architectures in solution with cryospray mass spectrometry: growth of polyoxomolybdate clusters and polymers mediated by silver(I) ions. J. Am. Chem. Soc. 130, 13876–13884 (2008).
Yan, J., Long, D.-L. Jr, Wilson, E. F. & Cronin, L. Discovery of heteroatom-‘embedded’ TeC{W18O54} nanofunctional polyoxometalates by use of cryospray mass spectrometry. Angew. Chem. Int. Ed. 48, 4376–4380 (2009).
Nadal, L. V. et al. Nucleation mechanisms of molecular oxides: a study of the assembly–dissassembly of [W6O19]2− by theory and mass spectrometry. Angew. Chem. Int. Ed. 48, 5452–5456 (2009).
Miras, H. N., Wilson, E. F. & Cronin, L. Unravelling the complexities of inorganic and supramolecular self-assembly in solution with electrospray and cryospray mass spectrometry. Chem. Commun. https://doi.org/10.1039/b819534j (2009).
Geue, N. et al. Disassembly mechanisms and energetics of polymetallic rings and rotaxanes. J. Am. Chem. Soc. 144, 22528–22539 (2022).
Larsen, F. K. et al. Horseshoes, rings, and distorted rings: studies of cyclic chromium-fluoride cages. Angew. Chem. Int. Ed. 42, 5978–5981 (2003).
Engelhardt, L. P. et al. Octa-, deca-, trideca-, and tetradecanuclear heterometallic cyclic chromium-copper cages. Angew. Chem. Int. Ed. 47, 924–927 (2008).
Beveridge, R. et al. A mass-spectrometry-based framework to define the extent of disorder in proteins. Anal. Chem. https://doi.org/10.1021/ac5027435 (2014).
France, A. P., Migas, L. G., Sinclair, E., Bellina, B. & Barran, P. E. Using collision cross section distributions to assess the distribution of collision cross section values. Anal. Chem. 92, 4340–4348 (2020).
McRobbie, A. et al. Chromium chains as polydentate fluoride ligands for lanthanides. Chem. Commun. 47, 6251–6253 (2011).
Shrivastav, V., Nahin, M., Hogan, C. J. & Larriba-Andaluz, C. Benchmark comparison for a multi-processing ion mobility calculator in the free molecular regime. J. Am. Soc. Mass. Spectrom. 28, 1540–1551 (2017).
Geue, N. et al. Adduct ions as diagnostic probes of metallosupramolecular complexes using ion mobility mass spectrometry. Inorg. Chem. 62, 2672–2679 (2023).
Echt, O., Kreisle, D., Knapp, M. & Recnagel, E. Evolution of ‘magic numbers’ in mass spectra of water clusters. Chem. Phys. Lett. 108, 401–407 (1984).
Sakurai, M., Watanabe, K., Sumiyama, K. & Suzuki, K. Magic numbers in transition metal (Fe, Ti, Zr, Nb, and Ta) clusters observed by time-of-flight mass spectrometry. J. Chem. Phys. 111, 235–238 (1999).
Tsunoyama, H. & Tsukuda, T. Magic numbers of gold clusters stabilized by PVP. J. Am. Chem. Soc. 131, 18216–18217 (2009).
Cole, H. L., Kalapothakis, J. M. D., Bennett, G., Barran, P. E. & MacPhee, C. E. Characterizing early aggregates formed by an amyloidogenic peptide by mass spectrometry. Angew. Chem. Int. Ed. 49, 9448–9451 (2010).
Ohshimo, K., Takahashi, T., Moriyama, R. & Misaizu, F. Compact non-rock-salt structures in sodium fluoride cluster ions at specific sizes revealed by ion mobility mass spectrometry. J. Phys. Chem. A 118, 9970–9975 (2014).
McInnes, E. J. L., Timco, G. A., Whitehead, G. F. S. & Winpenny, R. E. P. Heterometallic rings: their physics and use as supramolecular building blocks. Angew. Chem. Int. Ed. 54, 14244–14269 (2015).
Hoshino, N., Nakano, M., Nojiri, H., Wernsdorfer, W. & Oshio, H. Templating odd numbered magnetic rings: oxovanadium heptagons sandwiched by β-cyclodextrins. J. Am. Chem. Soc. 131, 15100–15101 (2009).
Tian, H., Bao, S. S. & Zheng, L. M. Cyclic single-molecule magnets: from the odd-numbered heptanuclear to a dimer of heptanuclear dysprosium clusters. Chem. Commun. 52, 2314–2317 (2016).
McInnes, E. J. L. et al. Solvothermal synthesis of [Cr10(μ-O2CMe)10(μ-OR)20] ‘chromic wheels’ with antiferromagnetic (R =Et) and ferromagnetic (R = Me) Cr(III)···Cr(III) interactions. Chem. Commun. 10, 89–90 (2001). .
Low, D. M. et al. A family of ferro- and antiferromagnetically coupled decametallic chromium(III) wheels. Chem. Eur. J. 12, 1385–1396 (2006).
Sun, L., Zhang, J. & Cui, S. Solvothermal synthesis, structure, and magnetic property for nano-’chromic wheels’ [Cr10(μ-O2CMe)10(μ-OMe)10(μ-OEt)10]. Polyhedron 26, 2169–2173 (2007). .
Gologan, B., Green, J. R., Alvarez, J., Laskin, J. & Cooks, R. G. Ion/surface reactions and ion soft-landing. Phys. Chem. Chem. Phys. 7, 1490–1500 (2005).
Verbeck, G., Hoffmann, W. & Walton, B. Soft-landing preparative mass spectrometry. Analyst 137, 4393–4407 (2012).
Laskin, J., Johnson, G. E., Warneke, J. & Prabhakaran, V. From isolated ions to multilayer functional materials using ion soft landing. Angew. Chem. Int. Ed. 57, 16270–16284 (2018).
Fremdling, P. et al. A preparative mass spectrometer to deposit intact large native protein complexes. ACS Nano https://doi.org/10.1021/acsnano.2c04831 (2022).
Esser, T. K. et al. Mass-selective and ice-free electron cryomicroscopy protein sample preparation via native electrospray ion-beam deposition. PNAS Nexus 1, 1–13 (2022).
Johnson, G. E., Gunaratne, K. D. D. & Laskin, J. In situ SIMS and IR spectroscopy of well-defined surfaces prepared by soft landing of mass-selected ions. J. Vis. Exp. https://doi.org/10.3791/51344 (2014).
Su, P. et al. Design and performance of a dual-polarity instrument for ion soft landing. Anal. Chem. 91, 5904–5912 (2019).
Samayoa-Oviedo, H. Y. et al. Design and performance of a soft-landing instrument for fragment ion deposition. Anal. Chem. 93, 14489–14496 (2021).
Faull, P. A. et al. Gas-phase metalloprotein complexes interrogated by ion mobility-mass spectrometry. Int. J. Mass Spectrom. 283, 140–148 (2009).
Bleiholder, C., Dupuis, N. F., Wyttenbach, T. & Bowers, M. T. Ion mobility–mass spectrometry reveals a conformational conversion from random assembly to β-sheet in amyloid fibril formation. Nat. Chem. 3, 172–177 (2011).
Sañudo, E. C. et al. Proton NMR study of Cr–Co heterometallic wheel complexes. Inorg. Chem. 48, 9811–9818 (2009).
Geue, N., Winpenny, R. E. P. & Barran, P. E. Structural characterisation methods for supramolecular chemistry that go beyond crystallography. Chem. Soc. Rev. 51, 8–27 (2022).
Ochsenbein, S. T. et al. Studies of finite molecular chains: synthesis, structural, magnetic and inelastic neutron scattering studies of hexa- and heptanuclear chromium horseshoes. Chem. Eur. J. 14, 5144–5158 (2008).
Fort, K. L. et al. Expanding the structural analysis capabilities on an Orbitrap-based mass spectrometer for large macromolecular complexes. Analyst 143, 100–105 (2018).
Giles, K. et al. A cyclic ion mobility–mass spectrometry system. Anal. Chem. 91, 8564–8573 (2019).
Kertesz, T. M., Hall, L. H., Hill, D. W. & Grant, D. F. CE50: quantifying collision induced dissociation energy for small molecule characterization and identification. J. Am. Soc. Mass Spectrom. 20, 1759–1767 (2009).
Hill, D. W. et al. Correlation of Ecom50 values between mass spectrometers: effect of collision cell radiofrequency voltage on calculated survival yield. Rapid Commun. Mass Spectrom. 26, 2303–2310 (2012).
Chakraborty, P. et al. Dissociation of gas phase ions of atomically precise silver clusters reflects their solution phase stability. J. Phys. Chem. C 121, 10971–10981 (2017).
Ruotolo, B. T., Benesch, J. L. P., Sandercock, A. M., Hyung, S.-J. & Robinson, C. V. Ion mobility–mass spectrometry analysis of large protein complexes. Nat. Protoc. 3, 1139–1152 (2008).
Stow, S. M. et al. An interlaboratory evaluation of drift tube ion mobility–mass spectrometry collision cross section measurements. Anal. Chem. 89, 9048–9055 (2017).
Dolg, M., Stoll, H. & Preuss, H. A combination of quasirelativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 85, 441–450 (1993).
Dolg, M., Stoll, H., Savin, A. & Preuss, H. Energy-adjusted pseudopotentials for the rare earth elements. Theor. Chim. Acta 75, 173–194 (1989).
CrysAlisPro Software System, Version 1.171.42.xx (Rigaku Corporation, 2022).
Sheldrick, G. M. SHELXT—integrated space-group and crystal-structure determination. Acta Crystallogr. A 71, 3–8 (2015).
Sheldrick, G. M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 71, 3–8 (2015).
Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. OLEX2: a complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 42, 339–341 (2009).
Acknowledgements
N.G. is grateful for funding through the President’s Doctoral Scholar Award by The University of Manchester. We acknowledge the support of EPSRC through the strategic equipment award EP/T019328/1 (to P.E.B.), the European Research Council for funding the MS SPIDOC H2020-FETOPEN-1-2016-2017-801406 (to P.E.B.) and Waters Corporation, particularly D. Cooper-Shepherd, for their continued support of mass spectrometry research within the Michael Barber Centre for Collaborative Mass Spectrometry. R.E.P.W. thanks the EPSRC for an Established Career Fellowship (EP/R011079/1) and the European Research Council for an Advanced Grant (ERC-2017-ADG-786734). We also thank A. Rawlinson, for support with data analysis software, T. S. Bennett, The University of Manchester, for support with the design of figures, EPSRC for funding an X-ray diffractometer (EP/K039547/1) as well as the staff in the MS and Separation Science, and the XRD Facilities in the Faculty of Science and Engineering, The University of Manchester for their assistance. We would also like to acknowledge the assistance given by Research IT and the use of the Computational Shared Facility at The University of Manchester.
Author information
Authors and Affiliations
Contributions
N.G., R.E.P.W. and P.E.B. conceived of the idea for this study. N.G. performed the mass spectrometry and IM–MS experiments as well as the data analysis and theoretical CCSN2 calculations. G.A.T. synthesized the polymetallic complexes. G.F.S.W. collected the XRD data and refined the crystal structures. N.A.B. performed the DFT calculations with input from N.G. N.G. wrote the paper with input from E.J.L.M., R.E.P.W, P.E.B. and all the other authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Synthesis thanks Xiaopeng Li, Cai-Hong Zhan and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Alexandra Groves, in collaboration with the Nature Synthesis team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–17, Tables 1–3 and crystallographic details.
Supplementary Data 1
Crystallographic details for {Cr10Cu2}.
Supplementary Data 2
Crystallographic details for {Cr12Gd4}.
Supplementary Data 3
Crystallographic details for {Cr12Cu2}.
Source data
Source Data Fig. 2
Tandem mass spectra shown in Fig. 2.
Source Data Fig. 3
CCSN2 distributions shown in Fig. 3.
Source Data Fig. 4
Tandem mass spectra and CCSN2 distributions shown in Fig. 4.
Source Data Fig. 5
Data for topology prediction plot.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Geue, N., Timco, G.A., Whitehead, G.F.S. et al. Formation and characterization of polymetallic {CrxMy} rings in vacuo. Nat. Synth 2, 926–936 (2023). https://doi.org/10.1038/s44160-023-00383-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s44160-023-00383-7