Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Discovering and forecasting extreme events via active learning in neural operators

Nature Computational Science volume 2, pages 823–833 (2022)Cite this article

Subjects

A preprint version of the article is available at arXiv.

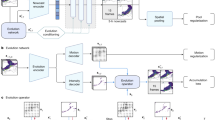
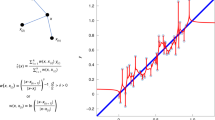
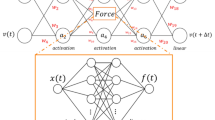
Abstract

Extreme events in society and nature, such as pandemic spikes, rogue waves or structural failures, can have catastrophic consequences. Characterizing extremes is difficult, as they occur rarely, arise from seemingly benign conditions, and belong to complex and often unknown infinite-dimensional systems. Such challenges render attempts at characterizing them moot. We address each of these difficulties by combining output-weighted training schemes in Bayesian experimental design (BED) with an ensemble of deep neural operators. This model-agnostic framework pairs a BED scheme that actively selects data for quantifying extreme events with an ensemble of deep neural operators that approximate infinite-dimensional nonlinear operators. We show that not only does this framework outperform Gaussian processes, but that (1) shallow ensembles of just two members perform best; (2) extremes are uncovered regardless of the state of the initial data (that is, with or without extremes); (3) our method eliminates ‘double-descent’ phenomena; (4) the use of batches of suboptimal acquisition samples compared to step-by-step global optima does not hinder BED performance; and (5) Monte Carlo acquisition outperforms standard optimizers in high dimensions. Together, these conclusions form a scalable artificial intelligence (AI)-assisted experimental infrastructure that can efficiently infer and pinpoint critical situations across many domains, from physical to societal systems.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Active learning of extreme events in society and nature, from pandemic spikes to rogue waves, to structural ship failures.
Fig. 2: Nailing the tail, accurate PDF and danger score convergence in 50 samples.
Fig. 3: Accelerated convergence with DNOs plus extreme acquisition functions regardless of dimensionality and parallel acquisition and shallow ensembles bring computational efficiency without performance loss.
Fig. 4: Robustness to dimensionality and initial data, with or without extremes.
Fig. 5: Efficient learning of fatigue statistics for ship design.
Fig. 6: DNOs leverage functional information for mapping to the QoI.

Data availability

All relevant data for reconstructing the results, including the LAMP dataset, are provided at dnosearch_nature_cs_data55. Additionally, all data, with exception of the LAMP data, may be computed from scratch using the code found in the dnosearch56 GitHub repository. Source data are provided with this paper.

Code availability

Code pertaining to the sequential discovery algorithm of the SIR, MMT and LAMP problems is publicly available from the GitHub repository dnosearch56. The DeepONet code framework can be found within the deepxde package on GitHub. Code pertaining to the Large Amplitude Motions Program (LAMP) v4.0.9 (May 2019) is a proprietary code developed by Leidos (formerly SAIC). Additional product information about LAMP may be found by contacting Leidos at https://www.leidos.com/contact.

References

  1. Creating a Disaster Resilient America: Grand Challenges in Science and Technology (National Academies Press, 2005).

  2. Hansteen, O. E., Jostad, H. P. & Tjelta, T. I. Observed platform response to a “monster” wave. in Field Measurements in Geomechanics 73–86 (Taylor & Francis, 2003).

  3. Gemmrich, J. & Cicon, L. Generation mechanism and prediction of an observed extreme rogue wave. Sci. Rep. 12, 1718 (2022).

    Article  Google Scholar 

  4. Sapsis, T. P. Statistics of extreme events in fluid flows and waves. Annu. Rev. Fluid Mech. 53, 85–111 (2021).

    Article  MATH  Google Scholar 

  5. Blanchard, A. & Sapsis, T. Output-weighted optimal sampling for Bayesian experimental design and uncertainty quantification. SIAM/ASA J. Uncertain. Quantif. 9, 564–592 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  6. Blanchard, A. & Sapsis, T. P. Bayesian optimization with output-weighted optimal sampling. J. Comput. Phys. 425, 109901 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  7. Lu, L., Jin, P., Pang, G., Zhang, Z. & Karniadakis, G. E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 3, 218–229 (2021).

    Article  Google Scholar 

  8. Kahn, H. & Marshall, A. W. Methods of reducing sample size in Monte Carlo computations. J. Op. Res. Soc. Am. 1, 263–278 (1953).

    MATH  Google Scholar 

  9. Shinozuka, M. Basic analysis of structural safety. J. Struct. Eng. 109, 721–740 (1983).

    Article  Google Scholar 

  10. Dematteis, G., Grafke, T. & Vanden-Eijnden, E. Extreme event quantification in dynamical systems with random components. SIAM/ASA J. Uncertain. Quantif. 7, 1029–1059 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  11. Uribe, F., Papaioannou, I., Marzouk, Y. M. & Straub, D. Cross-entropy-based importance sampling with failure-informed dimension reduction for rare event simulation. SIAM/ASA J. Uncertain. Quantif. 9, 818–847 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  12. Wahal, S. & Biros, G. BIMC: the Bayesian Inverse Monte Carlo method for goal-oriented uncertainty quantification. Part I. Preprint at https://arxiv.org/abs/1911.00619 (2019).

  13. Gal, Y., Islam, R. & Ghahramani, Z. Deep Bayesian active learning with image data. In Proc. International Conference on Machine Learning (eds Precup, D. & Teh, Y. W.) 1183–1192 (PMLR, 2017).

  14. Zhang, Y., Lease, M. & Wallace, B. Active discriminative text representation learning. In Proc. AAAI Conference on Artificial Intelligence Vol. 31, 3386–3392 (AAAI, 2017).

  15. Aghdam, H. H., Gonzalez-Garcia, A., van de Weijer, J. & López, A. M. Active learning for deep detection neural networks. In Proc. IEEE/CVF International Conference on Computer Vision 3672–3680 (IEEE, 2019).

  16. Ren, P. et al. A survey of deep active learning. ACM Comput. Surveys 54, 1–40 (2021).

    Google Scholar 

  17. Xiang, Z., Chen, J., Bao, Y. & Li, H. An active learning method combining deep neural network and weighted sampling for structural reliability analysis. Mech. Syst. Signal Process. 140, 106684 (2020).

    Article  Google Scholar 

  18. Ehre, M., Papaioannou, I., Sudret, B. & Straub, D. Sequential active learning of low-dimensional model representations for reliability analysis. SIAM J. Sci. Comput. 44, B558–B584 (2022).

    Article  MathSciNet  MATH  Google Scholar 

  19. Echard, B., Gayton, N. & Lemaire, M. AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation. Struct. Safety 33, 145–154 (2011).

    Article  Google Scholar 

  20. Snelson, E. & Ghahramani, Z. Sparse Gaussian processes using pseudo-inputs. Adv. Neural Inf. Process. Syst. 18, 1257–1264 (2006).

    Google Scholar 

  21. Titsias, M. Variational learning of inducing variables in sparse Gaussian processes. In Proc. Artificial Intelligence and Statistics (eds van Dyk, D. & Welling, M.) 567–574 (PMLR, 2009).

  22. Pickering, E. & Sapsis, T. P. Structure and distribution metric for quantifying the quality of uncertainty: assessing Gaussian processes, deep neural nets and deep neural operators for regression. Preprint at https://arxiv.org/abs/2203.04515 (2022).

  23. Wilson, A. G. & Izmailov, P. Bayesian deep learning and a probabilistic perspective of generalization. In Proc. 34th International Conference on Neural Information Processing Systems (eds Larochelle, H. et al.) 4697–4708 (Curran Associates Inc., 2020).

  24. Sapsis, T. P. Output-weighted optimal sampling for Bayesian regression and rare event statistics using few samples. Proc. R. Soc. A 476, 20190834 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  25. Mohamad, M. A. & Sapsis, T. P. Sequential sampling strategy for extreme event statistics in nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 115, 11138–11143 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  26. Sapsis, T. P. & Blanchard, A. Optimal criteria and their asymptotic form for data selection in data-driven reduced-order modelling with Gaussian process regression. Philos. Trans. R. Soc. A 380, 20210197 (2022).

    Article  MathSciNet  Google Scholar 

  27. Kermack, W. O. & McKendrick, A. G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 115, 700–721 (1927).

    Article  MATH  Google Scholar 

  28. Anderson, R. M. & May, R. M. Population biology of infectious diseases: Part I. Nature 280, 361–367 (1979).

    Article  Google Scholar 

  29. Majda, A. J., McLaughlin, D. W. & Tabak, E. G. A one-dimensional model for dispersive wave turbulence. J. Nonlinear Sci. 7, 9–44 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  30. Cai, D., Majda, A. J., McLaughlin, D. W. & Tabak, E. G. Spectral bifurcations in dispersive wave turbulence. Proc. Natl Acad. Sci. USA 96, 14216–14221 (1999).

    Article  MATH  Google Scholar 

  31. Zakharov, V. E., Guyenne, P., Pushkarev, A. N. & Dias, F. Wave turbulence in one-dimensional models. Phys. D: Nonlinear Phenom. 152-153, 573–619 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  32. Zakharov, V. E., Dias, F. & Pushkarev, A. One-dimensional wave turbulence. Phys. Rep. 398, 1–65 (2004).

    Article  MathSciNet  Google Scholar 

  33. Pushkarev, A. & Zakharov, V. E. Quasibreathers in the MMT model. Phys. D: Nonlinear Phenom. 248, 55–61 (2013).

    Article  MathSciNet  MATH  Google Scholar 

  34. Cousins, W. & Sapsis, T. P. Quantification and prediction of extreme events in a one-dimensional nonlinear dispersive wave model. Phys. D: Nonlinear Phenom. 280, 48–58 (2014).

    Article  MATH  Google Scholar 

  35. Chapelle, O. & Li, L. An empirical evaluation of Thompson sampling. In Proc. 24th International Conference on Neural Information Processing Systems (eds Shawe-Taylor, J. et al.) 2249–2257 (Curran Associates Inc., 2011).

  36. Nakkiran, P. et al. Deep double descent: where bigger models and more data hurt. J. Stat. Mech. 2021, 124003 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  37. Pickering, E. & Sapsis, T. P. Information FOMO: the unhealthy fear of missing out on information. A method for removing misleading data for healthier models. Preprint at https://arxiv.org/abs/2208.13080 (2022).

  38. Sapsis, T., Pipiras, V., Weems, K. & Belenky, V. On extreme value properties of vertical bending moment. In Proc. 33rd Symposium on Naval Hydrodynamics Osaka, Japan (Virtual) (2020).

  39. Sapsis, T. P., Belenky, V., Weems, K. & Pipiras, V. Extreme properties of impact-induced vertical bending moments. In Proc. 1st International Conference on the Stability and Safety of Ships and Ocean Vehicles (2021).

  40. Belenky, V., Weems, K., Sapsis, T. P. & Pipiras, V. Influence of deck submergence events on extreme properties of wave-induced vertical bending moment. In Proc. 1st International Conference on the Stability and Safety of Ships and Ocean Vehicles (2021).

  41. Serebrinsky, S. & Ortiz, M. A hysteretic cohesive-law model of fatigue-crack nucleation. Scripta Mater. 53, 1193–1196 (2005).

    Article  Google Scholar 

  42. Khan, R. A. & Ahmad, S. Dynamic response and fatigue reliability analysis of marine riser under random loads. In Proc. Petroleum Technology Symposium of International Conference on Offshore Mechanics and Arctic Engineering Vol. 2, 183–191 (ASME, 2007).

  43. Chasparis, F. et al. Lock-in, transient and chaotic response in riser VIV. In Proc. International Conference on Offshore Mechanics and Arctic Engineering, Vol. 5, 479–485 (ASME, 2009).

  44. Lin, W.-M., Zhang, S. & Weems, K. M. Numerical simulations of surface effect ship in waves. In Proc. 2010 Conference on Grand Challenges in Modeling and Simulation 414–421 (Society for Modeling and Simulation International, 2010).

  45. Li, Z. et al. Fourier neural operator for parametric partial differential equations. In Proc. International Conference on Learning Representations (ICLR, 2021); https://openreview.net/forum?id=c8P9NQVtmnO

  46. Yang, Y., Blanchard, A., Sapsis, T. P. & Perdikaris, P. Output-weighted sampling for multi-armed bandits with extreme payoffs. Proc. R. Soc. A 478, 20210781 (2022).

    Article  MathSciNet  Google Scholar 

  47. Hansen, L. K. & Salamon, P. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 12, 993–1001 (1990).

    Article  Google Scholar 

  48. Lakshminarayanan, B., Pritzel, A. & Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. In Proc. 31st International Conference on Neural Information Processing Systems (eds Guyon, I. et al.) 6405–6416 (Curran Associates Inc., 2017).

  49. Gustafsson, F. K., Danelljan, M. & Schon, T. B. Evaluating scalable Bayesian deep learning methods for robust computer vision. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops 318–319 (IEEE, 2020).

  50. Loshchilov, I. & Hutter, F. SGDR: stochastic gradient descent with warm restarts. In Proc. International Conference on Learning Representations (ICLR, 2017); https://openreview.net/forum?id=Skq89Scxx

  51. Huang, G. et al. Snapshot ensembles: train 1, get M for free. In Proc. International Conference on Learning Representations (ICLR, 2017); https://openreview.net/forum?id=BJYwwY9ll

  52. Smith, L. N. No more pesky learning rate guessing games. Preprint at https://arxiv.org/abs/1506.01186 (2015).

  53. Gramacy, R. B. & Lee, H. K. H. Adaptive design and analysis of supercomputer experiments. Technometrics 51, 130–145 (2009).

    Article  MathSciNet  Google Scholar 

  54. Thompson, W. R. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika 25, 285–294 (1933).

    Article  MATH  Google Scholar 

  55. Pickering, E. dnosearch_nature_cs_data (Zenodo, 2022); https://doi.org/10.5281/zenodo.7314144

  56. Pickering, E. dnosearch (Zenodo, 2022); https://doi.org/10.5281/zenodo.7312058

Download references

Acknowledgements

We acknowledge support from DARPA grant no. HR00112290029, AFOSR MURI grant no. FA9550-21-1-0058 and ONR grants nos. N00014-20-1-2366 and N00014-21-1-2357, awarded to MIT. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript. We thank V. Belenky and K. Weems from NSWC at Carderock for support regarding the LAMP code, as well as A. Blanchard for helpful and stimulating discussions around the Bayesian experimental design.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA

    Ethan Pickering, Stephen Guth & Themistoklis P. Sapsis

  2. Division of Applied Mathematics, Brown University, Providence, RI, USA

    George Em Karniadakis

Authors
  1. Ethan Pickering
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stephen Guth
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. George Em Karniadakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Themistoklis P. Sapsis
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

E.P. and T.P.S. conceived the idea and developed the neural operator–BED framework. E.P. implemented the functional search approach for neural operators. G.E.K. contributed the DNO architecture and framework. E.P. conducted the pandemic and rogue-wave simulations and numerical experiments. S.G. conducted ship simulations and numerical experiments. All authors interpreted the results. E.P. wrote the original manuscript. All authors contributed to editing the manuscript.

Corresponding authors

Correspondence to Ethan Pickering or Themistoklis P. Sapsis.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Computational Science thanks Giovanni Dematteis, Xiang Zhou and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Jie Pan, in collaboration with the Nature Computational Science team.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Eight sections of supplementary information.

Source data

Source Data Fig. 1

All data/code/information to create figure 1.

Source Data Fig. 2

All data/code/information to create figure 2.

Source Data Fig. 3

All data/code/information to create figure 3.

Source Data Fig. 4

All data/code/information to create figure 4.

Source Data Fig. 5

All data/code/information to create figure 5.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Pickering, E., Guth, S., Karniadakis, G.E. et al. Discovering and forecasting extreme events via active learning in neural operators. Nat Comput Sci 2, 823–833 (2022). https://doi.org/10.1038/s43588-022-00376-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s43588-022-00376-0

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing