Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A machine learning-based multiscale model to predict bone formation in scaffolds

Nature Computational Science volume 1, pages 532–541 (2021)Cite this article

Subjects

Abstract

Computational modeling methods combined with non-invasive imaging technologies have exhibited great potential and unique opportunities to model new bone formation in scaffold tissue engineering, offering an effective alternate and viable complement to laborious and time-consuming in vivo studies. However, existing numerical approaches are still highly demanding computationally in such multiscale problems. To tackle this challenge, we propose a machine learning (ML)-based approach to predict bone ingrowth outcomes in bulk tissue scaffolds. The proposed in silico procedure is developed by correlating with a dedicated longitudinal (12-month) animal study on scaffold treatment of a major segmental defect in sheep tibia. Comparison of the ML-based time-dependent prediction of bone ingrowth with the conventional multilevel finite element (FE2) model demonstrates satisfactory accuracy and efficiency. The ML-based modeling approach provides an effective means for predicting in vivo bone tissue regeneration in a subject-specific scaffolding system.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Statistical analysis results of predictive accuracy.
Fig. 2: Histogram errors of the ML-based model from months 1 to 12 with respect to the conventional FE2 model.
Fig. 3: Comparison between conventional FE2-based results and ML-based results.
Fig. 4: Comparison of virtual in silico X-ray and in vivo histological images of the implantation site in sheep tibia.
Fig. 5: In vivo X-ray images and the signal densities in ROIs.
Fig. 6: Equivalent von Mises strain distributions for the scaffold.

Similar content being viewed by others

Data availability

Source data are provided with this paper. Source data for Figs. 1 and 2, training data and raw/processed data required to reproduce these findings are available in a data repository in Zenodo (https://zenodo.org/record/5017032)65.

Code availability

The related code, neural networks and examples are available to academic researchers at public institutions from Zenodo (https://zenodo.org/record/5017032)65.

References

  1. Hollister, S. J. Porous scaffold design for tissue engineering. Nat. Mater. 4, 518–524 (2005).

    Article  Google Scholar 

  2. Petite, H. et al. Tissue-engineered bone regeneration. Nat. Biotechnol. 18, 959–963 (2000).

    Article  Google Scholar 

  3. Choi, N. W. et al. Microfluidic scaffolds for tissue engineering. Nat. Mater. 6, 908–915 (2007).

    Article  Google Scholar 

  4. Ringe, J. & Sittinger, M. Regenerative medicine: selecting the right biological scaffold for tissue engineering. Nat. Rev. Rheumatol. 10, 388–389 (2014).

    Article  Google Scholar 

  5. Moutos, F. T., Freed, L. E. & Guilak, F. A biomimetic three-dimensional woven composite scaffold for functional tissue engineering of cartilage. Nat. Mater. 6, 162–167 (2007).

    Article  Google Scholar 

  6. Schouman, T., Schmitt, M., Adam, C., Dubois, G. & Rouch, P. Influence of the overall stiffness of a load-bearing porous titanium implant on bone ingrowth in critical-size mandibular bone defects in sheep. J. Mech. Behav. Biomed. Mater. 59, 484–496 (2016).

    Article  Google Scholar 

  7. Pobloth, A. M. et al. Mechanobiologically optimized 3D titanium-mesh scaffolds enhance bone regeneration in critical segmental defects in sheep. Sci. Transl. Med. 10, 8828 (2018).

    Article  Google Scholar 

  8. Li, J. J. et al. A novel bone substitute with high bioactivity, strength, and porosity for repairing large and load‐bearing bone defects. Adv. Healthc. Mater. 8, 1801298 (2019).

    Article  Google Scholar 

  9. Sharma, U. et al. The development of bioresorbable composite polymeric implants with high mechanical strength. Nat. Mater. 17, 96–102 (2018).

    Article  Google Scholar 

  10. Entezari, A. et al. Architectural design of 3D printed scaffolds controls the volume and functionality of newly formed bone. Adv. Healthc. Mater. 8, 1801353 (2019).

    Article  Google Scholar 

  11. Chen, Y., Zhou, S. & Li, Q. Microstructure design of biodegradable scaffold and its effect on tissue regeneration. Biomaterials 32, 5003–5014 (2011).

    Article  Google Scholar 

  12. Chen, Y., Zhou, S. & Li, Q. Mathematical modeling of degradation for bulk-erosive polymers: applications in tissue engineering scaffolds and drug delivery systems. Acta Biomater. 7, 1140–1149 (2011).

    Article  Google Scholar 

  13. Sturm, S., Zhou, S., Mai, Y. W. & Li, Q. On stiffness of scaffolds for bone tissue engineering—a numerical study. J. Biomech. 43, 1738–1744 (2010).

    Article  Google Scholar 

  14. Adachi, T., Osako, Y., Tanaka, M., Hojo, M. & Hollister, S. J. Framework for optimal design of porous scaffold microstructure by computational simulation of bone regeneration. Biomaterials 27, 3964–3972 (2006).

    Article  Google Scholar 

  15. Sanz-Herrera, J. A., García-Aznar, J. M. & Doblaré, M. On scaffold designing for bone regeneration: a computational multiscale approach. Acta Biomater. 5, 219–229 (2009).

    Article  Google Scholar 

  16. Zhao, F., Melke, J., Ito, K., van Rietbergen, B. & Hofmann, S. A multiscale computational fluid dynamics approach to simulate the micro-fluidic environment within a tissue engineering scaffold with highly irregular pore geometry. Biomech. Model. Mechanobiol. 18, 1965–1977 (2019).

    Article  Google Scholar 

  17. Marin, A. C., Grossi, T., Bianchi, E., Dubini, G. & Lacroix, D. µ-Particle tracking velocimetry and computational fluid dynamics study of cell seeding within a 3D porous scaffold. J. Mech. Behav. Biomed. Mater. 75, 463–469 (2017).

    Article  Google Scholar 

  18. Kelly, D. J. & Prendergast, P. J. Mechano-regulation of stem cell differentiation and tissue regeneration in osteochondral defects. J. Biomech. 38, 1413–1422 (2005).

    Article  Google Scholar 

  19. Huiskes, R., Van Driel, W. D., Prendergast, P. J. & Soballe, K. A biomechanical regulatory model for periprosthetic fibrous-tissue differentiation. J. Mater. Sci. Mater. Med. 8, 785–788 (1997).

    Article  Google Scholar 

  20. Prendergast, P. J., Huiskes, R. & Søballe, K. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J. Biomech. 30, 539–548 (1997).

    Article  Google Scholar 

  21. Maslov, L. B. Mathematical model of bone regeneration in a porous implant. Mech. Compos. Mater. 53, 399–414 (2017).

    Article  Google Scholar 

  22. Shi, Q., Shui, H., Chen, Q. & Li, Z. Y. How does mechanical stimulus affect the coupling process of the scaffold degradation and bone formation: an in silico approach. Comput. Biol. Med. 117, 103588 (2020).

    Article  Google Scholar 

  23. Beaupré, G. S., Orr, T. E. & Carter, D. R. An approach for time‐dependent bone modeling and remodeling—theoretical development. J. Orthop. Res. 8, 651–661 (1990).

    Article  Google Scholar 

  24. Sanz-Herrera, J. A., García-Aznar, J. M. & Doblaré, M. Micro-macro numerical modelling of bone regeneration in tissue engineering. Comput. Methods Appl. Mech. Eng. 197, 3092–3107 (2008).

    Article  MATH  Google Scholar 

  25. Cheong, V. S., Fromme, P., Mumith, A., Coathup, M. J. & Blunn, G. W. Novel adaptive finite element algorithms to predict bone ingrowth in additive manufactured porous implants. J. Mech. Behav. Biomed. Mater. 87, 230–239 (2018).

    Article  Google Scholar 

  26. Cheong, V. S., Fromme, P., Coathup, M. J., Mumith, A. & Blunn, G. W. Partial bone formation in additive manufactured porous implants reduces predicted stress and danger of fatigue failure. Ann. Biomed. Eng. 48, 502–514 (2020).

    Article  Google Scholar 

  27. Taylor, M. & Prendergast, P. J. Four decades of finite element analysis of orthopaedic devices: where are we now and what are the opportunities? J. Biomech. 48, 767–778 (2015).

    Article  Google Scholar 

  28. Checa, S. & Prendergast, P. J. A mechanobiological model for tissue differentiation that includes angiogenesis: a lattice-based modeling approach. Ann. Biomed. Eng. 37, 129–145 (2009).

    Article  Google Scholar 

  29. Lecun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).

    Article  Google Scholar 

  30. Nguyen, A. H. et al. Cardiac tissue engineering: state-of-the-art methods and outlook. J. Biol. Eng. 13, 57 (2019).

    Article  Google Scholar 

  31. Kavakiotis, I. et al. Machine learning and data mining methods in diabetes research. Comput. Struct. Biotechnol. J. 15, 104–116 (2017).

    Article  Google Scholar 

  32. Zhang, Y. & Ye, W. Deep learning–based inverse method for layout design. Struct. Multidiscip. Optim. 60, 527–536 (2019).

    Article  MathSciNet  Google Scholar 

  33. Alber, M. et al. Integrating machine learning and multiscale modeling—perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. npj Digit. Med. 2, 115 (2019).

    Article  Google Scholar 

  34. Huang, D., Fuhg, J. N., Weißenfels, C. & Wriggers, P. A machine learning based plasticity model using proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 365, 1–33 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  35. Mozaffar, M. et al. Deep learning predicts path-dependent plasticity. Proc. Natl Acad. Sci. USA 116, 26414–26420 (2019).

    Article  Google Scholar 

  36. Freiberg, A. H. Wolff’s law and the functional pathogenesis of deformity. Am. J. Med. Sci. 124, 956–971 (1902).

    Article  Google Scholar 

  37. Lin, D., Li, Q., Li, W., Duckmanton, N. & Swain, M. Mandibular bone remodeling induced by dental implant. J. Biomech. 43, 287–293 (2010).

    Article  Google Scholar 

  38. Lin, D., Li, Q., Li, W. & Swain, M. Dental implant induced bone remodeling and associated algorithms. J. Mech. Behav. Biomed. Mater. 2, 410–432 (2009).

    Article  Google Scholar 

  39. Rungsiyakull, C. et al. Bone’s responses to different designs of implant-supported fixed partial dentures. Biomech. Model. Mechanobiol. 14, 403–411 (2015).

    Article  Google Scholar 

  40. Weinans, H., Huiskes, R. & Grootenboer, H. J. Effects of material properties of femoral hip components on bone remodeling. J. Orthop. Res. 10, 845–853 (1992).

    Article  Google Scholar 

  41. Liu, L., Shi, Q., Chen, Q. & Li, Z. Mathematical modeling of bone in-growth into undegradable porous periodic scaffolds under mechanical stimulus. J. Tissue Eng. 10, 204173141982716 (2019).

    Article  Google Scholar 

  42. Feurer, M. et al. Efficient and robust automated machine learning. in Advances in Neural Information Processing Systems 28 (eds Ghahramani, Z. et al.) 2962–2970 (NIPS, 2015).

  43. Snoek, J., Larochelle, H. & Adams, R. P. Practical Bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 4, 2951–2959 (2012).

    Google Scholar 

  44. Perier-Metz, C., Duda, G. N. & Checa, S. Initial mechanical conditions within an optimized bone scaffold do not ensure bone regeneration – an in silico analysis. Biomech. Model. Mechanobiol. https://doi.org/10.1007/s10237-021-01472-2 (2021).

  45. Cohen, D. O., Aboutaleb, S. M. G., Johnson, A. W. & Norato, J. A. Bone adaptation-driven design of periodic scaffolds. J. Mech. Des. Trans. ASME 143, 121701 (2021).

    Article  Google Scholar 

  46. Göpferich, A. Polymer bulk erosion. Macromolecules 30, 2598–2604 (1997).

    Article  Google Scholar 

  47. Shi, Q., Chen, Q., Pugno, N. & Li, Z. Y. Effect of rehabilitation exercise durations on the dynamic bone repair process by coupling polymer scaffold degradation and bone formation. Biomech. Model. Mechanobiol. 17, 763–775 (2018).

    Article  Google Scholar 

  48. Wang, L. et al. Mechanical–chemical coupled modeling of bone regeneration within a biodegradable polymer scaffold loaded with VEGF. Biomech. Model. Mechanobiol. 19, 2285–2306 (2020).

    Article  Google Scholar 

  49. Roohani-Esfahani, S.-I. I., Newman, P. & Zreiqat, H. Design and fabrication of 3D printed scaffolds with a mechanical strength comparable to cortical bone to repair large bone defects. Sci. Rep. 6, 19468 (2016).

    Article  Google Scholar 

  50. Duda, G. N. et al. Analysis of inter-fragmentary movement as a function of musculoskeletal loading conditions in sheep. J. Biomech. 31, 201–210 (1997).

    Article  Google Scholar 

  51. Guedes, J. & Kikuchi, N. Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods. Comput. Methods Appl. Mech. Eng. 83, 143–198 (1990).

    Article  MathSciNet  MATH  Google Scholar 

  52. Numerical experiments of the homogenization method. in Computing methods in applied sciences and engineering, 1977, I 330–356 (Springer, 1979).

  53. Bendsøe, M. P. & Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 71, 197–224 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  54. Wu, C., Zheng, K., Fang, J., Steven, G. P. & Li, Q. Time-dependent topology optimization of bone plates considering bone remodeling. Comput. Methods Appl. Mech. Eng. 359, 112702 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  55. Turner, C. H., Anne, V. & Pidaparti, R. M. V. A uniform strain criterion for trabecular bone adaptation: do continuum-level strain gradients drive adaptation? J. Biomech. 30, 555–563 (1997).

    Article  Google Scholar 

  56. Checa, S., Prendergast, P. J. & Duda, G. N. Inter-species investigation of the mechano-regulation of bone healing: comparison of secondary bone healing in sheep and rat. J. Biomech. 44, 1237–1245 (2011).

    Article  Google Scholar 

  57. Perier-Metz, C., Duda, G. N. & Checa, S. Mechano-Biological Computer Model of Scaffold-Supported Bone Regeneration: Effect of Bone Graft and Scaffold Structure on Large Bone Defect Tissue Patterning. Front. Bioeng. Biotechnol. 8, 585799 (2020).

    Article  Google Scholar 

  58. Chen, G. et al. A new approach for assigning bone material properties from CT images into finite element models. J. Biomech. 43, 1011–1015 (2010).

    Article  Google Scholar 

  59. Suquet, P. M. Elements of homogenization for inelastic solid mechanics, homogenization techniques for composite media. Lect. Notes Phys. 272, 193 (1985).

    Article  Google Scholar 

  60. White, D. A., Arrighi, W. J., Kudo, J. & Watts, S. E. Multiscale topology optimization using neural network surrogate models. Comput. Methods Appl. Mech. Eng. 346, 1118–1135 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  61. Funahashi, K. I. On the approximate realization of continuous mappings by neural networks. Neural Netw. 2, 183–192 (1989).

    Article  Google Scholar 

  62. Hassoun, M. H. Fundamentals of artificial neural networks (MIT press, 1995).

  63. Hogg, M. mhogg/pyvxray: an ABAQUS plug-in for the creation of virtual X-rays from 3D finite element bone/implant models (GitHub, 2013); https://github.com/mhogg/pyvxray

  64. Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 58, 240–42 (1895).

    Article  Google Scholar 

  65. Wu, C. Machine learning based multi-scale remodelling code (Zenodo, 2021); https://doi.org/10.5281/ZENODO.5017032

Download references

Acknowledgements

We acknowledge financial support from the Australian Research Council (ARC) through the Discovery (DP180104200, Q.L. and M.V.S.) and ARC Industrial Transformation Training Centre (IC170100022, Q.L. and H.Z.). The Artemis HPC provided by the Sydney Informatics Hub, a Core Research Facility of the University of Sydney, is acknowledged.

Author information

Authors and Affiliations

  1. School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, New South Wales, Australia

    Chi Wu, Keke Zheng, Grant P. Steven, Michael V. Swain & Qing Li

  2. School of Biomedical Engineering, The University of Sydney, Sydney, New South Wales, Australia

    Ali Entezari & Hala Zreiqat

  3. School of Civil and Environmental Engineering, University of Technology Sydney, Sydney, New South Wales, Australia

    Jianguang Fang

Authors
  1. Chi Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali Entezari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Keke Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jianguang Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hala Zreiqat
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Grant P. Steven
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Michael V. Swain
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Qing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

C.W. and Q.L designed the research plan. C.W. performed the simulations. C.W., A.E., K.Z. and J.F analyzed the data. C.W., A.E. and Q.L. wrote the manuscript. All authors reviewed the final manuscript.

Corresponding author

Correspondence to Qing Li.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature Computational Science thanks Jose A. Sanz-Herrera, Sara Esteban and Zhiyong Li for their contribution to the peer review of this work. Handling editor: Ananya Rastogi, in collaboration with the Nature Computational Science team.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Tables 1–3 and Figs. 1–3.

Reporting Summary

Source data

Source Data Fig. 4

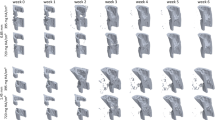
Original images for virtual X-ray images at months 3, 6, 9 and 12 and histological image at month 12.

Source Data Fig. 5

In vivo X-ray images taken at months 3, 6, 9 and 12.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, C., Entezari, A., Zheng, K. et al. A machine learning-based multiscale model to predict bone formation in scaffolds. Nat Comput Sci 1, 532–541 (2021). https://doi.org/10.1038/s43588-021-00115-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s43588-021-00115-x

This article is cited by

Search

Advanced search

Quick links

Nature Briefing: Translational Research

Sign up for the Nature Briefing: Translational Research newsletter — top stories in biotechnology, drug discovery and pharma.

Get what matters in translational research, free to your inbox weekly. Sign up for Nature Briefing: Translational Research