Abstract
Groundwater dynamics are often overlooked within historical climatology because of their complexity and the influence of multiple factors. This study presents a groundwater model for Spain, using an existing tree-ring based summer drought reconstruction to estimate the groundwater depth in Castile and León (northwestern Spain) over the 1056–2020 CE period. Spanish groundwater volume fluctuations are found to be associated with quasi-decadal variations in the North Atlantic and Pacific Oceans. The reconstructed annual groundwater depth shows significant oscillations around a mean value of 123 m. Changes in groundwater depths include a wet medieval period ( ~ 1056–1200 CE), recurring megadroughts during parts of the Little Ice Age (~1471–1600 CE), and unprecedentedly large variations during recent decades. Aligning with previous studies for the Iberian Peninsula, our new modelling approach highlights the need to enhance groundwater resilience in anticipation of potentially worsening future drought trends across the Mediterranean.
Similar content being viewed by others
Introduction
Drought poses significant threats to groundwater resources in dry regions, like the Mediterranean, and is arguably an increasing challenge as a result of global warming1. The profound effects of climate change on groundwater make it a critical global concern2,3. Despite growing awareness, the interaction between climate and groundwater is often overlooked4. This oversight persists due to the complexity of the hydrological cycle and limited data availability5,6. Historically, the French naturalist Bernard Palissy (1510–1589), demonstrated a deep understanding of water systems during the reign of Queen Catherine de’ Medicis (1519–1589). Drawing on the ideas of the ancient Roman architect Vitruvius (1st century BCE), he explained the origins of springs and rivers7. As Palissy’s biographer wrote8:
The waters, then, in caverns have been placed there by the rains engendered as well of waters that have risen from the sea as of those from the earth and from all humid things, in the drying of which their aqueous vapours are raised up on high to fall again. […] the said waters will take their course in the direction of the downward slope, provided they can find the smallest outlet: thence it most frequently happens that out of rocks and hilly places escape many beautiful springs.
Despite the constraints of his era, Palissy recognised how water moves to the ground and its connection to the whole water cycle. Understanding and safeguarding the groundwater resource remain increasingly crucial for both present and future generations. Already Palissy realised that water can be stored underground and that groundwater plays an important role for ecosystems and societies. This idea is similar to the observations made by the Italian Renaissance polymath Leonardo da Vinci (1452–1519), who also wrote about groundwater9. We should, in this light, re-think and value the importance of groundwater for both nature and people’s water needs, now as well as for the future. Within the contemporary realm of research, the Commission on Groundwater and Climate Change (CGCC), established in 2002 by the International Association of Hydrogeologists, serves as a noteworthy example (https://gwclimate.iah.org). It contributes to raising awareness regarding the environmental and economic value of groundwater systems. Groundwater depletion, exceeding recharge rates, is evident in most of the world’s aquifers10 and is linked to over-pumping and, in some regions, to the effects of climate change11.
The vulnerability of much of the Iberian Peninsula to drought12, and increasing evapotranspiration and changing precipitation patterns due to climate change13 affect its water resources, demanding a deeper understanding of climate–groundwater impacts14,15. Recognising the complexity of drought dynamics16, this study offers a unified perspective. While, for example, Tegel et al.17 shed light on historical groundwater trends in the Upper Rhine Valley (south-western Germany and north-eastern France) back to Roman times using tree-ring width data, historical climatology and palaeoclimatology has to date not studied groundwater trends in inland Spain18. This represents a crucial research gap19,20,21,22,23. Spain’s arid and semi-arid climates heighten groundwater vulnerability, compounded by over-exploitation and human impact on the water budget. Escalating demand and climate change exacerbate drought vulnerabilities24. Understanding the nexus between climate change, groundwater and sustainable development goals is important25, impacting energy, productivity, and global socio-economic structure, particularly in arid and water-scarce regions26. Land use changes, such as deforestation or reforestation of hillslopes and floodplains27, influence the hydrological cycle and groundwater recharge dynamics, linked to the groundwater reaction time (GRT). Global GRTs were mapped by integrating groundwater modelling with comprehensive datasets28. As throughout Spain, in the Castile and León (CL) region (Fig. 1a), groundwater adaptation times to climate change vary greatly, ranging from rapid to more prolonged responses. Despite prolonged groundwater residence times29, Spanish groundwater is mostly influenced by climate stresses (i.e., low precipitation and high evapotranspiration). Lower GRT systems transmit meteorological droughts to hydrological droughts faster, while higher GRT systems delay drought recovery28. This complex interplay between climate and groundwater underscores Spain’s intricate groundwater stress response. However, reconstructing and forecasting groundwater data across time poses challenges in environmental hydrogeology30,31, compounded by divergent assumptions influencing any projections made24.
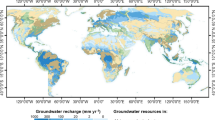
a Distribution of groundwater response times (GRT; years) in the Mediterranean region (see legend for colours). The map is adapted from Cuthbert et al.28 and can be accessed online for free at https://figshare.com/articles/dataset/Global_water_table_ratio_and_groundwater_response_time_raster_data/7393304). Black dots on the map denote the primary cities in Spain, as featured in the downloaded map from the reference website, without any reference with the study sites; b Mean annual precipitation (1981–2010) across Spain (taken from Nafría García et al.36; available at http://www.aemet.es/es/serviciosclimaticos/datosclimatologicos/valoresclimatologicos). The small black square indicates the Fuente de Piedra lagoon used for direct model validation; c Mean annual precipitation (1981–2010) pattern on the recharge area of the Castile and León region. The red dots indicate the locations of the Medina del Campo piezometer and the two sites used for indirect model validation (Valladolid, Lominchar); d The hydrological water balance for the Castile and León region, averaged for the period 1981–2010, calculated using precipitation data from GPCC-Global Precipitation Climatology Centre (https://climatedataguide.ucar.edu/climate-data/gpcc-global-precipitation-climatology-centre) and temperature data from the Climate Research Unit (CRU) of the University of East Anglia (https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.04). The plot was generated using WebWIMP 1.01, an updated version of the WebWIMP programme, as implemented at the University of Delaware (USA) in 2003 (http://cyclops.deos.udel.edu/wimp/public_html/index.html).
Comprehending groundwater–climate interactions at an aquifer scale remains limited32,33 due to the intricate task of reconstructing long-term groundwater data34. To address these challenges, and to expand understanding beyond the period of recent human influences18, the present study introduces a model bridging contemporary climate knowledge with paleoclimate data, aiming to enhance the understanding of groundwater variations back to medieval times. This lack of attention to the interplay between shifts in groundwater levels and drought occurrences35 has spurred the development of a Groundwater REsource Model for Spain (GREMS) to explain variations in GWD within the CL region. The model’s name, GREMS, emphasises its concentration on the “Inland Spain” study area, though its principles are applicable in future studies to other regions as well. The precipitation data for the period 1981–2010 from Nafría García et al.36 serve as a framework to gain insights into the climatology of the study region, particularly in comparison to the climatology of Spain (without constituting the basis for our research results). The CL region is characterised by mean annual precipitation of approximately 600 mm, with evident spatial variability (Fig. 1b, c). In CL, marked by a dry climate, summers are the driest (with a mean of around 80 mm) and certain locations receive less than 60 mm. The surrounding mountains experience higher rainfall, exceeding 100 mm, while winter, spring and autumn each receive approximately 170 mm of precipitation. Winter and spring are critical for replenishing soil water (Fig. 1d), which is essential for sustaining groundwater.
The core objectives of this study are two-fold: firstly, to address a critical gap in our understanding regarding the intricate interplay between shifts in groundwater levels and drought occurrences, and secondly to enrich our understanding of groundwater variations extending back to medieval times. To navigate the challenges imposed by data constraints, GREMS employs a set of simplified input variables. These include the self-calibrating Palmer Drought Severity Index (scPDSI37,38,39), reconstructed for the summer from tree-ring data with a 0.5° × 0.5° grid resolution for Europe40, the North Atlantic Oscillation (NAO41), the Atlantic Multidecadal Variability (AMV42) and Pacific Decadal Oscillation (PDO43) chosen over physically-based models due to data limitations. These indices collectively form the foundation for a robust analysis of the dynamic relationship between climate and groundwater. To establish the reliability of GREMS, calibration was performed using data from Medina del Campo wells (1517-4-0001 at 100 m depth and 1517-4-0002 at 140 m depth) covering the period from 1972 to 2001. Extended validation efforts included GWD data from the Fuente de Piedra lagoon in Andalusia (southern Spain) from 1960 to 1996. Additional validation proxies were used from Valladolid (in Castile and León) for the periods 1674–1711 and 1713–1764, and Lominchar (in Castile-La Mancha) for the recent period 2003 to 2020. The calibrated model was employed across distinct climatic phases: the late part of the Medieval Warm Period (LMWP, here ~1056–1299), the Little Ice Age (LIA, here ~1300–1849) and the Contemporary Warming Period (CWP, here since ~1850). Based on the tree-ring based reconstruction of the summer scPDSI spatial field and three atmospheric indices (NAO, AMV and PDO), our modelling efforts spanned the period 1056–2020 CE, providing hydrological insights specific to the CL region. In the following sections, we discuss the main results derived from the GREMS, which offer new perspectives on the hydrologic dynamics of the CL region. These findings contribute to the scientific discourse on groundwater resilience and hold broader implications for sustainable groundwater management in the face of evolving climate patterns in the wider Mediterranean region.
Results
Model calibration
The calibration of the GREMS model involved utilising GWD data obtained at the Medina del Campo piezometer station in the period from 1972 to 2001. Prior to calibration, a comprehensive analysis of the factors influencing groundwater variability was conducted. By employing a 30-year dataset, we established a significant linear relationship (y = a + b ∙ x) between the actual (y) and predicted (x) data (F-test p ~ 0.00, R2 = 0.86). The calibrated parameter values of Eq. (2) were determined as follows: B = 121.900 m represents the groundwater depth corresponding to the baseline value and A = 1.658 is a scale parameter that converts the term inside the brackets to m; η = 10 is an empirical parameter. It is noteworthy that the calibration process was designed to minimise the inclusion of parameters that lack physical significance, in order to preserve the model’s physical foundation and enable its application in different environments and periods without the need for specific measurements44. Additionally, an iterative modelling approach was employed to determine the optimal number of variables that would ensure the most feasible and accurate reconstruction. By employing the calibrated parameters, the model achieved an intercept value (a) of –0.077 ( ± 9.09 standard error) and a slope value (b) of 1.000 ( ± 0.08 standard error), with a modelling efficiency (Nash-Sutcliffe coefficient) of 0.86. The scatterplot of the actual and predicted data points (Fig. 2a) reveals minimal deviations from the 1:1 identity line, indicating a strong agreement between the model predictions and the observed data.
a Scatterplot of GWD at the calibration stage of Eq. (2) for the Medina del Campo (41° 18′ N, 04° 55′ W) piezometer station during the period 1972–200190. The inner bounds represent the 90% confidence limits (power pink coloured area), while the outer bounds show the 95% prediction limits for new observations (light pink); b Histogram of standardised residuals of the GREMS model, which exhibit an overlapped Gaussian shape (orange line); c Validation through a comparison between the GREMS model (blue line) and weighted rainfall (orange line) using a moving-window approach from four to eight years prior to the year of GWD estimation. The validation was performed for the period 1674–1764 in Valladolid (41° 39′ N, 04° 43′ W), in Castile and León, excluding the interval 1712–1725 due to anomalously high inter-annual variation in the tree-ring data and a period in Spain with limited climate documentation125. The rainfall time-series data are sourced from González Pérez et al.92 (2009); d Scatterplot at the validation stage for the period 1960–1996, comparing the GREMS model with observed groundwater depth at the Fuente de Piedra (37° 08′ N, 04° 43′ W) lagoon piezometer in Andalusia (1960 to 1996); e Validation through a comparison between the GREMS model (blue line) and water equivalent thickness (orange line) obtained from the GRACE-NASA MEaSUREs Program (available at http://grace.jpl.nasa.gov). The validation was performed for the period 2003–2020 in the site of Lominchar (40° 05′ N, 03° 57′ W), in Castile-La Mancha; f, g, h, i. Box plots illustrating the calibration in a, and the validations in c, d and e, respectively (blue: observations; orange: estimates). Each box represents the quartile range: Q3-Q1. Data features are visualised by median (horizontal line crossing each box), mean (data point inside each box), first (Q1: 25th percentile) and third (Q3: 75th percentile) quartiles (edges of each box), interquartile range (ends of the whiskers): IQR = 1.5·(Q3-Q1), outliers (data points outside the IQR).
The mean absolute error (MAE) of 2.6 m is smaller than the standard error of the estimates (3.4 m), and the mean absolute percentage error (MAPE) of 6.1%, falls below the performance target of excellence (MAPE < 10%). The Durbin-Watson statistic value of 1.14 (p ~ 0.00) suggests the presence of serial autocorrelation in the residuals of the calibration data, indicating a potential pattern or trend in the model’s performance. However, Fig. 2b illustrates that the model residuals exhibit a skew-free distribution, resembling a Gaussian distribution. Furthermore, the maximum distance between the cumulative distributions of the actual and predicted data samples is Dn = 0.12. The two-sided large sample Kolmogorov-Smirnov (SM) test results in a KS value of 0.65 and a p-value of 0.80, indicating that the two data samples are likely derived from the same distribution. This suggests that the model’s predictions closely match the observed data. In addition, standardised skewness and kurtosis of the observed and estimated time-series fall within the expected range of a Gaussian distribution (−2 to +2), as shown in Table 1. The box plots also indicate considerable overlaps between observed and modelled data samples during the calibration stage (Fig. 2f).
During the analysis to determine whether the model could be simplified, the tree-ring based scPDSI reconstruction and the teleconnection indices NAO + AMV + PDO were considered separately. It is noteworthy that the highest p-value among the independent variables is <0.05, which corresponds to PDO. Consequently, it is advisable not to eliminate any variables from the GREMS model, as all the variables contribute significantly to the model’s performance and provide valuable information for GWD estimation. Overall, the metrics used to assess the model demonstrate its accuracy and reliability in reproducing the GWD data during the calibration period. This indicates a consistent performance of the model without any observed systematic bias in its predictions.
Extended model validation
For the extended validation of the model, two distinct modalities were employed. The first modality involved an indirect, semi-qualitative approach. A historical dataset spanning the period 1674–1764 was used, which provided annual rainfall data for the same province (Valladolid) where the Medina del Campo piezometer is located. The comparison of rainfall and GWD estimate trends is presented in Fig. 2c, where the two variables are plotted against each other. Indirect validation was completed by a similar comparison between GWD estimates and water equivalent thickness at a location in Castile-La Mancha (Lominchar), outside the study region (Fig. 2e). These analyses provide insight into the relationship between patterns of water cycle components and GWD variations. The Pearson correlation coefficients (r) highlight the robust agreement in the medium and long-term patterns of the two variables: rainfall and GWD estimates (r = 0.66), and water equivalent thickness and GWD estimates (r = 0.65). This consistency becomes more relevant considering that the model’s information aligns with local-scale variables (weighted rain and water equivalent thickness) not included as predictors in GREMS. The model’s satisfactory performance in capturing historical trends, even under differing climate conditions compared to the conditions of the calibration site, indicates its robustness and adaptive capacity to changing environmental circumstances.
The second modality of extended validation involved a more direct approach. Here, we considered a location far from Medina del Campo, specifically in Andalusia, where experimental measurements of groundwater depth at the Fuente de Piedra lagoon piezometer were available for the period 1960–1996. These observed groundwater data were compared to the corresponding GREMS model data (Fig. 2d), which shows a strong linear correlation between the actual and modelled data, with statistically significant results (R2 = 0.78, F-test p ~ 0.00). However, when examining the scatter-plot, it is evident that the individual values do not align perfectly along the 1:1 bisector, indicating a bias in the data distribution. This may be linked to distinct environmental characteristics and hydrogeological settings between the calibration and validation sites. Factors such as the distance between these sites and their varying proximity to the sea could contribute to this observed bias. Further analysis or evidence may be required to substantiate the observed deviations in the data. To address this issue, further statistical analyses were performed on the standardised time-series. The results indicate the presence of serial autocorrelation in the residuals, as indicated by the Durbin-Watson (DW) statistic of 0.74 (p ~ 0.00). However, the Kolmogorov-Smirnov test does not show a statistically significant difference between the distributions, with a maximum distance between the two distributions (Dn) of 0.19 and a two-sided large sample KS statistic of 0.81 (p = 0.54). The box plots in Fig. 2g–i (all validation stages) indicate that while the distributions of observations and estimates may vary, they overlap considerably and exhibit similar general tendencies. In both the calibration and validation phases, the consistently satisfactory performance suggests that natural variability may exert a more pronounced influence on the groundwater system than anthropogenic pumping. Based on this resilience, it can be concluded that the GREMS model is suitable for operational use, even in light of observed biases and autocorrelation in the validation data.
Reconstructed groundwater depth (GWD) data and their historical patterns
Transitioning to the analysis of reconstructed GWD data, these were based on the model calibration at wells within the CL region. This analysis reveals how societal responses correspond with fluctuating changes in groundwater levels over historical periods (the reconstructed data is available in Supplementary Data 1). At least since the turn of the last millennium ( ~ 1000 CE), the hydroclimate of CL has been characterised by fluctuations in groundwater levels, alternating between periods of rise and fall, spanning climatic scales of 10–30 years and longer, with values around the median of 122.5 m (Fig. 3b). Notable peaks in these anomalies indicate both wet and dry conditions and offer insight into distinct historical periods. The first period corresponds to lower groundwater levels during a late medieval wet interval, spanning approximately 1056 to 1200 CE. The second period represents a recurring groundwater megadrought from around 1471 to 1600 CE. Lastly, the most recent period coincides with the CWP, spanning approximately from 1850 to 2020 CE. During this recent period, drought conditions have persisted, displaying more pronounced and sudden shifts compared to the past. Notable instances include a cluster of years between the late 19th century and the early 20th century, as well as the latter part of the 1980s, although it is important to note that these clusters of years occurred prior to any significant global warming, making it difficult to attribute them solely to a warming trend.
a Coefficient of variability of GWD (grey line), calculated using a moving window of 22 years. The red arrow indicates a change-point in the year 1628; b The reconstructed annual values of GWD (blue line), using Eq. (2). The green bold horizontal line represents the median value of GWD. The degraded vertical bands a, b visually illustrate hydroclimatic patterns spanning the late part of the Medieval Warm Period ( ~ 1056–1299 CE), three distinct sub-periods of the Little Ice Age (beginning: ~1301–1470 CE, central: ~1471–1600 CE and end: ~1601–1849 CE) and the Contemporary Warming Period ( ~ 1850–2020), with wet anomalies in blue and light blue, dry anomalies in straw colour, more pronounced fluctuations in orange and while white indicating values fluctuating around the mean; c. d, e. Spatial maps of the first, second and third principal components (after applying Empirical Orthogonal Function: EOF) of the tree-ring based self-calibrating Palmer Drought Severity Index (scPDSI) for the years 1520–1560 CE, respectively, across Spain (more intense orange band in a and b). The Castile and León area is indicated by black rectangles. These plots were generated using data from the Old World Drought Atlas by Cook et al.40 and arranged using Climate Explorer (https://climexp.knmi.nl; Trouet and Van Oldenborgh, 2013).
Reconstructed GWD data reveal that, except for the initial two peaks around 1140 and the final peak around 1970, the majority consistently fall within the range of approximately 90 to 140 m, aligning closely with the calibration range of 100–140 m. The wet phase observed at the beginning of the reconstruction, during the late medieval period, aligns with the findings of independent tree-ring-based reconstructions conducted by Candela Jurado et al.45, regarding extreme climatic conditions. According to these reconstructions, the 12th, 14th and 19th centuries witnessed a higher number of wet years, while the 15th century, followed by the 12th and 20th centuries, had the highest number of warm years. We acknowledge that climate conditions can indeed exhibit variability within a century and across regions and seasons. Consequently, it is important to emphasise that our research primarily concentrates on overarching interdecadal trends. In summary, our findings reveal specific historical periods marked by heightened wetness and generally warm conditions, closely aligning with the patterns observed in the reconstructions. As a result, our findings offer further substantiation for the historical patterns of increased wetness and generally warm periods observed in the climate of the Spanish region of CL.
During the 11th–12th centuries, the hydroclimate in the CL region featured relatively warm temperatures and a notable abundance of wet seasons, as reflected in the GWD data. The 25th percentile of GWD was around 124 m and the 95th percentile exceeded 160 m, indicating an ample level of groundwater variability. However, this period of favourable conditions was followed by a significant shift in temperatures, characterised by considerable increases and a succession of droughts and floods. The 25th and 95th percentiles experienced a sharp decline, reaching levels of groundwater depletion. Specifically, the 25th percentile dropped to 117 m, while the 95th percentile decreased to 136 m. By the end of the 13th century, with the onset of the LIA, a shift in climate became apparent as the region started to witness a decline in good harvests and transitioned from the first wet period to a drier one (Fig. 3b).
Discussion
Our modelling study relies entirely on the use of published data, rather than re-analysing datasets, originating from sources external to our own research team. The inherent limitation arises from our constrained means to assess uncertainties associated with the basic datasets, which are drawn from published sources. However, using published datasets provides a degree of safeguard against spurious uncertainties, given that these data have undergone previous scrutiny and validation. Considering that the primary focus of our modelling approach and model parameterisation on capturing the long-term variability of the annual GWD data within the study area and the consequent aim to ensure the generalisability of our model across the Iberian territory, some methodological limitations warrant acknowledgement.
By leveraging an understanding of the historical climate of the study area, our model demonstrates a satisfactory fit, parsimony and consistency with the climatology, though acknowledging that alternative methods, such as structural equation modelling, could be considered46. Striking a balance between computation, complexity and uncertainty, our methodology relied on ad hoc model development and the trial-and-error assignment of model parameter values using a spreadsheet utility. Despite algorithmic improvements, the common practice of using a spreadsheet solver aligns with precedents in previous studies47,48. While quantifying confidence bounds becomes challenging with increased parameter estimation steps, the model error, representing the mismatch between modelled and observed values, serves as an indicator of total model uncertainty49. In addition to the limited standard error of the slope of the observed versus predicted data in the calibration phase, a Nash-Sutcliffe efficiency value greater than 0.80 in the same phase further indicates limited model uncertainty, likely associated with narrow parameter uncertainty.
The convergence of the calibrated location parameter B, Eq. (2), representing the baseline GWD value, towards 122 m indicates that our model closely orbits the mean value of 123 m observed at Medina del Campo, with oscillations represented by the model segment excluding B. The B parameter, representing the baseline GWD, acquires a nuanced significance when considering the observed GWD at Fuente de Piedra (validation site), which stands at 142 m. Despite this difference, the estimated baseline of B = 122 m, calibrated at a location situated >600 km away, underscores the ability of the model to capture observed variability. The recalibration at Fuente de Piedra, yielding a similar value (126 m) to that obtained at Medina del Campo, confirms the limited sensitivity of the model to different site conditions. The discrepancy of about 4 m in B parameter estimation between the calibration and validation datasets, which is about 10% (Medina del Campo) and 40% (Fuente de Piedra) of their respective standard deviations ( ~ 9 m and ~ 40 m), also highlights a limited sensitivity of the model. This dual capability — precisely capturing variability around a fixed baseline and demonstrating consistent recalibration results — highlights the model’s robustness, affirming its reliability in discerning overarching patterns amid varying site-specific conditions. This is attributed to the model segment excluding B, which adeptly interprets larger-scale climatological drivers operating across diverse sub-regions.
While it is important to acknowledge certain limitations resulting from the lack of extensive sensitivity analysis and the reliance on optimised parameters, these considerations underscore the need for contextual interpretation within the broader Iberian Peninsula context. With our growing understanding of the hydrological system, in particular, in the Mediterranean region, the demonstrated robustness through model calibration and satisfactory performance comparisons with independent variables supports the effectiveness of our modelling solution with the incorporation of additional well data in future studies improving the robustness and generalisability of the model. Facilitated by optimised parameters of general validity, the reconstruction of the GWD time-series contributes to a comprehensive representation of the Iberian Peninsula, offering valuable hydrological insights into long-term variability and enhancing our understanding of regional groundwater dynamics. This, in turn, provides valuable information for understanding hydrological patterns across the wider Mediterranean region.
Resolving the uncertainties associated with estimating natural drought variability requires a thorough understanding of historical GWD variability. The challenge is particularly pronounced in regions such as north-west Spain, where, despite progress in understanding drought drivers, characterising past megadroughts and their features remains a persistent difficulty50,51. While these challenges are more pronounced in regions with sparse hydroclimatic proxy coverage (e.g., the Amazon), reliance on remote proxies (e.g., mainland Australia) or low-resolution archives with significant dating uncertainties (e.g., sub-Saharan Africa before the late 1700s), it is important to note that the CL region of Spain boasts a rich history of documenting substantial and fluctuating changes in groundwater levels. To enrich the historical context of our analysis of reconstructed GWD data, our study looked at specific cultural events such as processions. By intertwining these culturally significant practices deeply rooted in Spanish heritage with our scientific investigation of GWD, we aim to unveil a comprehensive narrative connecting societal responses to environmental challenges with the hydroclimatic changes reflected in the data.
In the CL region, cyclical patterns of water availability have been observed. Groundwater is replenished by frequent rainfall but can also face periods of drought and water shortage52. Notably, previous late-Holocene paleoclimatic research, drawing from pollen records across Iberia and Morocco on a decadal to centennial-scale, demonstrated how prolonged droughts affected economic, social and political situations in the Visigothic Kingdom and al-Andalus (in medieval times Muslim-ruled part of the Iberian Peninsula) between the 5th and 10th century CE53. In medieval and early modern times, floods and droughts were often seen as acts of God54,55, leading to the adoption of religious practices (e.g., vows, penitential processions and new devotions) to seek divine forgiveness56. Gerrard and Petley57 examined the societal impact of natural phenomena, encompassing the hydrological cycle58, while sacred processions symbolised a belief in a primordial creation narrative59, harmonising disorderly waters and dividing between heavenly (rain) and earthly waters (surface water and groundwater).
The departure from the favourable hydroclimatic conditions (warmer and wetter) of the 11th and 12th centuries highlights the impact of changing climate patterns on agricultural productivity and regional water availability. Maurice Berthe (1935–2015), a French medievalist, made significant contributions to the understanding of the 14th and 15th centuries by conducting pioneering research on periodisation of historical events. In his ground-breaking work60, he divided the years into distinct periods of crisis or recovery, shedding light on the historical context. He provides compelling evidence of the immense hardships endured by the population of northern Spain during the first half of the 14th century, thereby confirming the existence of a profound economic crisis61. This period coincided with an increasing frequency and severity of famines in parts of Europe, not least the Great Famine of 1315–1317, population stagnation and declines, a lethal cattle disease outbreak, the finally the Black Death and subsequent plague epidemics62. During the central part of the LIA, characterised by recurring megadroughts in Spain, Domínguez-Castro et al.63 found that the pro-pluvia (prayers to obtain rain from heaven) periods were consistent in central Spain. They employed a rogation series from the Toledo Cathedral Chapter, allowing for a thorough characterisation of the droughts between 1506 and 1900 CE. Our study reveals significant findings, such as the 25th and 95th percentiles of GWD, indicating a decrease of about 24 m (the lowest of the time-series) and 22 m, respectively, between 1600 and 1930. According to Gonzálvez64, the region of Toledo experienced a severe drought during the LIA. Between 1576 and 1625, there were 27 prayers pro pluvia (to request rain) and only four pro serenitate (to request that the rain stops). The most severe period was recorded between 1521 and 1581 CE. Additionally, there is documented evidence from 1557 of the procession of the Virgin of Castrotierra in Astorga, located in the northwestern part of CL. This procession, typically occurring every seven years, was held that year due to the severe drought affecting the Castile area65. The recurring megadroughts reconstructed by the GREMS model during the mid-15th to the end of the 16th century were characterised by a series of imprecations and processions in various regions, including CL and the more localised area of Medina del Campo. These historical records confirm that these droughts were serious calamities affecting both small and large scales. For instance, in the year 150066, the town of Medina del Campo and its surrounding fields desperately needed water. Similarly, in 158266 the city of Medina del Campo and its Abbey faced a prolonged water shortage, leading to the loss of its lush greenery during what should have been the vibrant month of May.
Next, we gain a deeper understanding of the impact of drought on groundwater level depletion by evaluating the Empirical Orthogonal Function (EOF)-Maps. Specifically, we focused on the 1st, 2nd and 3rd main components for the scPDSI values during the critical drought period of 1520–1560 CE. The corresponding EOF-Maps for this time period (Fig. 3c, d, e) align with the recurrent megadrought period (Fig. 3b). Within the three main hydroclimatic periods – the wet period, recurrent megadrought and shifting period – there are two interspersed intervals of equal extent. These intervals occur from 1200 to 1470 CE, marking the transition from the end-tail of the Medieval Warm Period to the beginning of the LIA, and during the latter part of the LIA from 1601 to 1849 CE. During these intervals, GWD values exhibit oscillations around the long-term mean value. The analysis reveals that these periods exhibit different time scales, ranging from 150 to 300 years, for various anomalies. This suggests the presence of scale-dependent fluctuations and/or periods of hydroclimatic polarisation. This observation was further supported by calculating the Hurst (H) exponents for the original estimated annual time-series. Using the R/S method67), the H exponent was found to be 0.95, while using the residual variance-ratio68, the H exponent was determined to be 1.00. Both values indicate a predictable time-series since H > 0.6569. Moreover, these values indicate that the time-series exhibits long-term memory, suggesting the presence of cyclical influences on rainfall and drought. Another perspective to consider is that hydrological drought, characterised by slow responses within a basin and notable groundwater memory, can actually be beneficial for drought prediction performance in Europe70.
During the later phase of the LIA, i.e., from 1601 to 1849 CE, the 25th and 95th percentiles of the GWD show a slight recovery. This implies a slight increase in GWD values between 119 and 143 m, indicating a gradual shift towards higher values during this period. However, during the Maunder Minimum of solar activity (c. 1645–1715)71, the groundwater level exhibits significant fluctuations as depicted in Fig. 3b. The Maunder Minimum was characterised in Spain by severe frosts, a mixture of humid and cold summers and autumns, long and harsh winters, and alternating periods of drought and catastrophic floods72. The influence of the Maunder Minimum of solar activity and the preceding cold (and dry) years on hydrological conditions is reflected in the inter-annual variability of GWD. This is evident from the change-point, detected using the Mann-Whitney-Pettitt test73), in the relative coefficient of variation in 1628 (Fig. 3a). Following this change-point, GWD underwent a gradual yet statistically significant increase, as confirmed by the Mann-Kendall test (S = 5340, Z = 2.16, p = 0.03). This trend persisted until the 1780s when the Iberian Peninsula faced contrasting hydrological extremes. Specifically, the region faced prolonged and severe drought conditions, along with a notable increase in unusual and excessive rainfall events, resulting in substantial societal impacts74. These episodes included heavy rains, floods and sometimes hurricanes, which led to the destruction of crops and trees, erosion of mountains, and rendered the soil unusable by removing its most fertile layers. One particular dramatic case was the agricultural crisis of 1785–1786, often referred to as the “year of hunger”, which marked the beginning of a period of instability resulting from these climatic events and their consequences75. As the LIA came to an end, the Castile area experienced a continuous deepening of water levels from 1850 to 1875 (Fig. 3b), in response to different cycles of drought. These dry phases coincided with an abrupt shift in the fire regime, creating a cascade of feedbacks between wildfire, vegetation and human use of mountain forests, shrublands and pastures during the late 19th century76. Furthermore, during the early 20th century, there was a new and more intense pulsing of groundwater deepening (Fig. 3b).
In addition to the historical periods mentioned earlier, there were minor drought events in the periods of 1981–1984 and 1991–1995, with the year 2005 being particularly dry77. However, the most severe drought period, both in terms of duration and intensity, occurred from 1991 to 1995, affecting southern Spain in particular. During this period, reduced precipitation resulted in significant decreases of over 70% in the mean annual runoff, and reservoir reserves dropped to nearly 10% of their total capacity. Although not explicitly reflected in Fig. 3b, this recent drought period stands out from previous ones due to the accompanying global warming trends and the increasing water demands. These factors have contributed to the increased vulnerability of the aquifer system29. The impacts of droughts on agriculture, water resources and ecosystems in the region have been detrimental78,79. Global trends in flash drought occurrence have been mixed in recent decades, as reported by UNODRR80. Similarly, Noguera et al.81 found mixed trends for droughts in Spain. Furthermore, Schumacher et al.82 discovered that dryland droughts are more prone to self-propagation due to the substantial response of evaporation to increased soil water stress. These factors, combined with ongoing warming and increased inter-annual variability of GWD, have created a more precarious situation for the available and manageable water resources in this region of Spain.
During this recent period, marked by extreme weather events and escalating water consumption, the GWD exhibits an anomalous trend with the 25th percentile decreasing to 110 m, while the 95th percentile continues to rise, reaching a value of 153 m. This climatic period shows the largest excursion between the maximum and minimum percentiles, confirming the high variability that characterises groundwater levels. Importantly, this period highlights the immediate consequences of ongoing climate change and anthropogenic activities, resulting in notable imbalances between water supply and demand. This situation poses significant challenges in maintaining a stable water supply and agricultural production across Spain. In fact, the reduced spring flow and increasing depletion of groundwater levels observed in the western Mediterranean region may be direct consequences of ongoing climate change, particularly attributed to hydrological drought83,84,85.
Climate change affects hydrological systems, leading to altered precipitation patterns, changes in evapotranspiration rates and shifts in recharge conditions, among other factors. These changes can have significant impacts on water resources and ecosystems in the region86. Anthropogenic activities also play a significant role in influencing water systems. Human activities such as land-use changes, water extraction for agricultural and industrial purposes, and alterations to natural hydrological regimes can exacerbate the impacts of climate change on water availability and quality87,88. Continued warming can pose challenges for dryland ecosystems, as they may respond non-linearly to climate change due to complex interactions between ecosystems, hydrology and human activities, leading to increased vulnerability to drought and heat stress89. This vulnerability puts both natural and human livelihoods at risk.
Conclusion
Our extensive exploration of millennium-long groundwater dynamics in the Iberian Peninsula unveils a profound connection between historical hydroclimatic patterns, cultural practices, and contemporary challenges. Despite facing inherent limitations in data sources and model development, our approach is a robust contribution to understanding the complex evolution of groundwater depth (GWD) over time. The calibrated model, characterised by a stable baseline parameter, consistently shows its reliability across different sub-regions, demonstrating its ability to identify overarching patterns amidst varying site-specific conditions. The historical narrative woven throughout our study transcends historical times, highlighting the socio-economic impacts of climate variability, particularly during periods such as the cold Little Ice Age. This contextual background serves as a crucial foundation for interpreting the immediate effects of modern climate change and human activity on groundwater dynamics but also underscores the paramount importance of understanding hydroclimatic forcing. The intricate relationship between hydroclimatic forcing and land-use change in this study adds complexity to the explicit separation of their effects on groundwater dynamics, highlighting that aquifer responses may be dominated by climatic shifts, with climate change in turn triggering alterations in land-use patterns79. Recognising the centrality of hydroclimatic forcing is thus pivotal in comprehending the intricate dynamics of groundwater systems, particularly in the face of contemporary challenges such as extreme weather events and the escalating demand for water, which underlines the urgency of addressing imbalances in water supply and demand.
Looking forward, research would benefit from prioritising the refinement of groundwater models, the incorporation of additional well data, and the conduct of careful sensitivity analyses. A nuanced understanding of the intricate relationships between climate change, human activities and groundwater systems is essential for formulating effective strategies to conserve water resources and ecosystems, not only in the Iberian Peninsula but also globally. At a time of various environmental challenges, our findings emphasise the need for proactive measures to ensure the resilience and sustainability of water systems for the well-being of future generations.
Methods
Environmental setting and data
Medina del Campo is centrally located in the Castile and León (CL) region (Castilla y León in Spanish), at 41° 38’ N latitude and 04° 44’ W longitude, with an elevation of 713 m a.s.l. The region experiences a continental Mediterranean climate, characterised by a mean annual temperature of 12.9 °C and an annual mean temperature range of 18.4 °C. The climate is generally dry, with a mean annual rainfall of 351 mm for the period of 1981–2020. The potential evapotranspiration is estimated to be 730 mm36. Winters in the area are relatively long and cold, while summers are comparatively short and hot, with the possibility of thunderstorms occurring particularly in spring and summer months, and hail occurring particularly in May. The landscape surrounding Medina del Campo is dominated by gentle undulations and is predominantly composed of sandy-silty soils. The region is known for its crops, such as cereals, legumes and high-quality white wines. There are also small clusters of pine forests and some streams, including the Zapardiel River, which runs through the city until it joins the left bank of the Duero River. The Zapardiel River exhibits distinct flow patterns throughout the year. It experiences two periods of maximum flow, one from November to February and the other from April to May. These periods coincide with the seasons when rainfall is typically higher. In contrast, the river experiences a minimum flow during the summer season, when rainfall is generally lower66.
Located in the Middle Duero River Basin, the aquifer comprises an upper unconfined aquifer and a deep semi-confined aquifer, and operates as a three-dimensional semi-confined system with high vertical anisotropy. Recharge comes from meteoric infiltration, with the Duero River as the main discharge outlet. Extensive groundwater pumping since the late 1960s has led to a 28-meter decline in the water table. Extraction rates (272 Mm3 yr−1) surpass natural replenishment (149 Mm3 yr−1), causing overexploitation. The aquifer, now stabilised since 2001, faces ongoing challenges in sustainable groundwater management. The calibration of the GREMS model for the Medina del Campo area (Fig. 1c) used the mean data from two piezometers, namely 1517-4-0001 with a mean depth of about 100 m and 1517-4-0002 with a mean depth of about 140 m, with two sampling dates in each year90. The calibration period spanned from 1972 to 2001 (Fig. 2a). The proximity of the two wells (3.5 km apart) limits their ability to discriminate large-scale climatological effects, which is the focus of this study. Consequently, their readings have been averaged to provide a representative measure of the Medina del Campo piezometric levels. In addition, given the redundancy of incorporating other sites within a few tens of km, we opted for Medina del Campo as the primary study site in the study of De la Hera-Portillo et al.90 because it possesses the most continuous time-series and the highest interannual variability among the considered sites.
To assess the model’s performance over an extended historical period, independent groundwater depth data from the Fuente de Piedra lagoon piezometer (direct validation) were incorporated into the analysis (Fig. 1). The validation period covered the years 1960 to 1996 (Fig. 2d), with mean groundwater depth of 142 m and standard deviation of 40.5 m. Located in Andalusia, the Fuente de Piedra lagoon relies on rainfall and underground discharge from the aquifer91. During dry years, the lagoon experiences substantial water table fluctuations, highlighting the influence of precipitation and evaporation. This mirrors groundwater dynamics affected by drought, leading to reduced aquifer recharge and increased water pumping.
Independent validation beyond the study area involved the use of two annual time-series for output variables similar to GWD. The first validation involved a historical dataset spanning the period 1674–1764, providing annual rainfall data for the province of Valladolid, where the Medina del Campo piezometer is located. This dataset, curated by González Pérez et al.92, combined diverse proxies – including tree-ring data, agricultural and historical records and historical references on climatic conditions – probabilistically combining them into a joint reconstruction that ensured consistency. To assess the concordance of rainfall trends and GWD estimates, a sliding window approach was implemented on historical rainfall data, spanning four to eight years before the GWD estimate year. It is important to note that the impacts of precipitation deficiencies on groundwater often exhibit a delay, and the effects of groundwater droughts are typically reported later than their actual occurrence93. In addition, indirect validation encompassed a comparable analysis between GWD estimates and water equivalent thickness at a location in Castile-La Mancha (Lominchar), outside the study region (Fig. 2e). In contrast to determining the piezometric level, as done for the GWD calibration site, equivalent thickness encapsulates the same concept as groundwater depletion, representing the mean rate of water height reduction. This is derived from observations of water storage changes and simulating soil-water variations through a data-integrating hydrological modelling system94.
The input variables used for both the calibration of the GREMS model and past reconstruction were derived from various sources. The self-calibrating Palmer Drought Severity Index (scPDSI38,39); used in this study derives from the Old World Drought Atlas (OWDA), a spatially resolved tree-ring based reconstruction for the summer period40, with updates until 2020 provided by CRU scPDSI 4.05 early. It has to be noted that only six tree-ring chronologies were locally available for the OWDA for Spain of which the closest to the CL study region are not extending prior to 1200 CE (a limitation that requires caution when interpreting estimates prior to this date). The North Atlantic Oscillation (NAO) data were obtained from Cook et al.95. The Atlantic Multidecadal Variation (AMV) data were derived from Wang et al.96 and the Pacific Decadal Oscillation (PDO) data were obtained from Macdonald and Case97, with updates provided by NAO-Gibraltar, AMO-HADSST and PDO-SWFSC via Climate Explorer98. All these indices are based on annual data, given the focus of our analysis at this temporal scale.
Teleconnections and drought impacts on groundwater
Drought, with its profound impacts on water availability, agriculture and society35, is closely linked to groundwater dynamics and recovery. Several studies99,100,101 have highlighted the utility of drought indices like scPDSI in understanding groundwater variability. For example, Leelaruban et al.99 demonstrated a strong correlation between drought indices and groundwater levels in the Great Plain region of the United States: positive scPDSI values indicate minimal groundwater deficiencies, while negative values during warm-season droughts are associated with groundwater decline, often occurring 1–4 years later. Teleconnection indices, such as the North Atlantic Oscillation (NAO), Atlantic Multidecadal Variability (AMV) and Pacific Decadal Oscillation (PDO), also play significant roles in influencing drought patterns. NAO has been linked to European droughts, particularly in Romania102 and groundwater behaviour in Western Europe103, given its predominant control over winter rainfall totals in the North Atlantic region. Specifically, it influences cyclone tracks, thereby affecting annual rainfall patterns in Spain, with negative NAO phases associated with reduced rainfall and positive phases with increased rainfall104. The AMV, also referred to as the Atlantic Multidecadal Oscillation (AMO), affects the Mediterranean region through its impact on temperature, precipitation and forest productivity105,106,107. In addition, the variability of the NAO-related hydrological processes in Europe, including the Iberian Peninsula, has been observed to be influenced by multi-decadal North Atlantic sea-surface temperature anomalies108. Moreover, warm PDO phases, in conjunction with El Niño–Southern Oscillation (ENSO) events, have led to severe droughts, including those in the Mediterranean basin43. Positive NAO and AMO phases can decrease forest productivity due to increased aridity109. While during periods of positive PDO conditions contrasting patterns emerge, negative PDO conditions tend to enhance rainfall over the western European Mediterranean area and result in cooler temperatures in Scandinavia110. The interplay between NAO, AMV, PDO, and groundwater is complex, and various studies have revealed multi-year relationships, such as the co-variability between NAO and piezometric levels in Portugal111, correlations between autumn precipitation, groundwater discharge and teleconnections in the northern Iberian Peninsula112, and the impact of teleconnections on temperature, persistent droughts, and groundwater recharge113. These observations underscore the intricate relationship between teleconnection indices and groundwater dynamics, highlighting the need for a comprehensive understanding of these interactions to enhance groundwater resilience in regions susceptible to droughts across the Mediterranean region.
Groundwater REsource-Model for Spain
This study develops and showcases the GREMS (Groundwater REsource Model for Spain) model, highlighting its ability to address groundwater dynamics and the impacts of climate change, and thus, aims to contribute to a comprehensive understanding of the intricate relationship between groundwater and the sub-regional water cycle within the CL region. A significant aspect of this research is the focus on unravelling the historical support and long-term sustainability of CL aquifers, tracing their origins back to medieval times. By conducting a thorough analysis of the past, this investigation seeks to provide insights into the historical management and resilience of these aquifers over several centuries. Through this historical lens, GREMS strives to gain a deeper understanding of the various factors and mechanisms that have shaped the stability and productivity of CL aquifers. The ultimate objective of this study is to facilitate informed decision-making processes and promote sustainable management practices for the future. This research recognises the importance of advancing river basin ecosystem water supply modelling, as it serves as a valuable guide for environmental conservation, water planning and decision-making processes114,115,116. Groundwater resources are not only essential for socioeconomic development but also integral components of the equilibrium within the ecological environmental system117. The harmonious relationship between climate and surface-and-subsurface water resources, facilitated by the hydrological cycle (Fig. 4a), is particularly pivotal for maintaining this equilibrium. At a global scale, the water cycles originate from the Hadley cells, which efficiently transport heat and moisture across the Earth, resulting in the redistribution of precipitation (Fig. 4b).
a Schematic representation of a typical hydrological cycle in the Castile and León region, with its components indicated by arrows. Groundwater dynamics are influenced by the atmosphere and surface water processes (adapted from an image available free from https://www.noaa.gov/education/resource-collections/freshwater/water-cycle). This illustration, offering a simplified view of the hydrological system, aims to highlight the essential components needed to establish causality between groundwater depth and the employed climatic drivers; b Global-scale hydrological cycle (source: https://en.wikipedia.org/wiki/Hadley_cell); c regional-scale hydrological cycle (https://www.shutterstock.com/it/image-vector/vector-schematic-representation-water-cycle-nature-694784353); d The transfer of these processes to local scales (adapted from https://www.arpae.it/it/temi-ambientali/clima/rapporti-e-documenti/rapporto-impatti-cambiamenti-climatici/rapporto-snpa-impatti-infografica-naturali).
On a regional scale, this intricate cycle interacts with various features of the landscape (Fig. 4c). However, it is on a local scale where the water cycle directly engages with human activities, as it provides essential water and groundwater resources in its continuous course (Fig. 4d). Cycle-controlling mechanisms within the hydrological system have the ability to influence and modulate the occurrence and duration of rainfall and drought anomalies. These mechanisms can delay, mitigate, prolong or concentrate the distribution throughout the hydrological cycle. Recognising the cumulative nature of droughts and their transmission within the water cycle118 contributes to our understanding of the complex dynamics underlying drought-related community responses. The groundwater resource model developed for the estimation of annual mean groundwater depth in CL here referred to as GREMS utilises a linear multivariate regression approach, incorporating various climatic indices as input variables. These climatic indices are supported by statistical operators to establish correlations between groundwater oscillations and climatic drivers such as teleconnection indices103 and hydrological forcing119. The derivation equation, represented by Eq. (1), takes a parsimonious approach by considering four independent variables, X, Y, Z and W (Z = A· [X + (Y, Z, W)] + B):
-
1.
X: Sub-regional climatic drought (SRCD). This variable captures local or regional climatic conditions specific to the study area, focusing on drought-related factors that can impact groundwater levels.
-
2.
Y, Z, W: Large-scale teleconnective climatic phenomena (LSCP). These variables represent broader climate patterns or oscillations that occur over large geographic regions and have the potential to influence regional climate conditions. Examples of such phenomena include teleconnections like El Niño–Southern Oscillation (ENSO), North Atlantic Oscillation (NAO), and Pacific Decadal Oscillation (PDO).
The model combines these variables as follows:
The coefficients A and B are determined through the model calibration process: A is a scale factor and B coincides with the median value of groundwater depth; then the term in square brackets, represents the GWD annual anomaly.
Equation (2) provides a more specific representation of the four main terms used to estimate the annual mean GWD for the CL region (specifically Medina del Campo) in the current year (yr = 0), GREMS(GWD)yr = 0. The model can be expressed as:
Here is the breakdown of the main terms used in the equation (Fig. 5):
-
1.
\({{Perc}}_{25}{\left({scPDSIs}\right)}_{{yr}-1}^{{yr}-4}\): The 25th percentile of the sub-regional-scale Palmer Drought Severity Index (scPDSI) calculated for the prior four years (yr-1 to yr-4). The scPDSI represents a measure of drought severity at a local or regional scale.
-
2.
\({{{Perc}}_{50}\left({NAO}+{AMV}+{PDO}\right)}_{{yr}-1}^{{yr}-8}\): The 50th percentile of the combined values of the North Atlantic Oscillation (NAO), the Atlantic Multidecadal Variation (AMV), and the Pacific Decadal Oscillation (PDO), calculated for the prior eight years (yr-1 to yr-8). These large-scale climatic indices capture broader climate patterns that can influence regional climate conditions. The 50th percentile relationship between the combined NAO, AMO and PDO index and groundwater at yr = 0 suggests their role in influencing groundwater dynamics.
The figure shows the conceptual scheme of the GREMS model, illustrating how different drivers (capital letters) are trained using annual moving windows (areas in pink). Arranged from (reference image available free): https://www.gettyimages.it/illustrazioni/idyllic.
In this way, the GREMS model comprises distinct components that jointly contribute to the reconstruction of GWD variations. The scPDSI data component operates at the sub-regional scale and focuses on characterising changes in the soil water budget. The scPDSI reconstruction is used to quantify climatological drought, capturing the combined effects of temperature and precipitation. These data provide an integrated measure of drought conditions at specific locations, considering factors such as precipitation, temperature and evapotranspiration. It is noteworthy that this component captures changes in soil water availability with a delay of five years relative to groundwater growth. In addition, the model incorporates teleconnection indices, including NAO, AMV and PDO. These indices add variability from atmospheric circulation patterns that influence local climate conditions. Notably, in our analysis, we found that AMV, when considered independently, exhibits a robust correlation with variations in GWD output (r = 0.82, based on the calibration dataset). However, examining PDO or NAO in isolation reveals negligible correlations with GWD, with r values close to zero. The significance of employing an integrated metric that combines AMV, NAO and PDO is paramount. This combined metric enhances the representation of GWD dynamics. Specifically, when we calculate the 50th percentile of the sum of these indices (AMV + NAO + PDO), we observe a substantial increase in the correlation coefficient, with the r value soaring to 0.91. This integrated approach is critical because it captures a wider spectrum of climatic influences and interconnections that impact GWD variations over an extended historical period.
In essence, this integrated approach underscores the importance of understanding the interplay between smaller-scale processes and larger-scale system behaviour (Baird, 2004). The varying responses of individual teleconnection indices in different time periods justify the use of an integrated metric to ensure response stable results over extended time frames. By combining multiple teleconnection indices into the integrated metric, GREMS effectively smooths out short-term variability associated with individual indices. Specifically, the 50th percentile of the combined indices, representing a middle ground among these indices, offers a balanced perspective of the combined influence of NAO, AMV and PDO. This balance enhances the robustness the model’s robustness, reducing its reliance on any single index to explain variations in GWD and ensuring reasonable performance across different time frames and varying climatic conditions. This approach is particularly valuable when dealing with long-term historical data, where climatic patterns and relationships between indices may evolve over time. The integrated metric provides a consistent and stable representation of GWD dynamics that can be applied over extended historical periods, mitigating the risk of overfitting to specific time periods or datasets, which can lead to model instability. By using an integrated metric, we reduce the chances of such overfitting and enhance the overall reliability of the groundwater model. This comprehensive approach enhances our ability to comprehend the complex dynamics governing GWD fluctuations, ultimately leading to a more reliable and insightful assessment of groundwater resources in the CL region.
Model parameterisation
The parameterisation of our model was based on a combination of statistical and physical evaluations120. This allowed us to optimise the model for system simulation and historical prediction purposes121. We followed a trial-and-error approach, adjusting model parameters and evaluating the goodness of fit between model outputs and the calibration dataset. This iterative process was repeated until the observed and predicted values were as close as possible, ensuring the model’s accuracy according to the following conditions:
R2 (coefficient of determination) is a statistical measure that indicates the proportion of the variance in the actual data that is explained by the model estimates. It ranges from 0 to 1, with 1 indicating a perfect fit between the actual data and the estimates.\(\,\left|{{{{{\rm{b}}}}}}-1\right|\) represents the absolute difference between the regression slope (b) of the actual data and the modelled data. A value of 0 would indicate that the regression slopes are identical, while a value greater than 0 suggests a deviation between the two. MAE (mean absolute error) is a measure of the mean magnitude of errors between the actual data and the model estimates. It quantifies the mean absolute difference between the predicted and observed values. A lower MAE indicates better accuracy and a closer fit between the model and the actual data. Our model does not directly integrate uncertainty. Instead, an assessment of its output uncertainty was conducted independently. In addition, we calculated the Nash-Sutcliffe index (ranging from -∞ to 1, with optimal performance at 1122) as an efficiency metric. This was done to verify that the model outperforms the mean of the observed time-series. A Nash-Sutcliffe index above 0.60 is indicative of limited model uncertainty123.
Exploratory and data analysis
Spreadsheet-based exploratory data and model development were carried out using various statistical tools. The online statistical programme STATGRAPHICS (http://www.statpoint.net/default.aspx) was used for data analysis and modelling. Graphical assistance was obtained from AnClim (http://www.climahom.eu/software-solution/anclim124) and CurveExpert Professional 1.6 (https://www.curveexpert.net) to visualise and further analyse the data. Box-and-whisker graphs (box plots) were generated using the free online calculator Box-and-Whisker Plot Maker (https://goodcalculators.com/box-plot-maker).
Data availability
The full set of data generated and analysed in this study is available in a data file published alongside this article in the Excel file Supplementary Data 1.
References
Dalin, C., Wada, Y., Kastner, T. & Puma, M. J. Groundwater depletion embedded in international food trade. Nature 543, 700–704 (2017).
Green, T. R. et al. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 405, 532–560 (2011).
He, X. et al. Climate-informed hydrologic modeling and policy typology to guide managed aquifer recharge. Sci. Adv. 7, eabe6025 (2021).
Ndehedehe, C. E. et al. Understanding global groundwater–climate interactions. Sci. Total Environ. 904, 166571 (2023).
Duffy, C. J. The terrestrial hydrologic cycle: an historical sense of balance. WIREs Water 4, e1216 (2017).
Fauzia, Surinaidu, L., Rahman, A. & Ahmed, S. Distributed groundwater recharge potentials assessment based on GIS model and its dynamics in the crystalline rocks of South India. Sci. Rep. 11, 11772 (2021).
Biswas, A. History of hydrology p. 265 (North-Holland Publishing Company, 1970).
Morley, H. Palissy the potter: The life of Bernard Palissy, of Saintes. Vol. 1 & 2, p. 277, 1st ed. (Ticknor, Reed and Fields, 1853).
De Lorenzo, G. Leonardo da Vinci e la geologia p. 204 (Zanichelli, 1871). (in Italian).
Rodell, M. et al. Emerging trends in global freshwater availability. Nature 557, 651–659 (2018).
Jasechko, S. & Perrone, D. Global groundwater wells at risk of running dry. Science 372, 418–421 (2021).
Pascale, S. et al. Projected changes of rainfall seasonality and dry spells in a high greenhouse, gas emissions scenario. Clim. Dyn. 46, 1331–1350 (2016).
Lorenzo, M. N., Alvarez, I. & Taboada, J. J. Drought evolution in the NW Iberian Peninsula over a 60 year period (1960–2020). J. Hydrol. 610, 127923 (2022).
Carmona, M. et al. Assessing the effectiveness of Multi-Sector Partnerships to manage droughts: The case of the Jucar River Basin. Earths Future 5, 750–770 (2017).
Vicente-Serrano, S. M. The evolution of climatic drought studies in Spain over the last few decades. Geographicalia 73, 7–34 (2021).
Zaidman, M. D., Rees, H. G. & Young, A. R. Spatio-temporal development of streamflow droughts in north-west Europe. Hydrol. Earth Syst. Sci. 6, 733–751 (2002).
Tegel, W. et al. Higher groundwater levels in western Europe characterize warm periods in the Common Era. Sci. Rep. 10, 16284 (2020).
Li, B. et al. Long-term, non-anthropogenic groundwater storage changes simulated by three global-scale hydrological models. Sci. Rep. 9, 10746 (2019).
Cramer, W. et al. Climate change and interconnected risks to sustainable development in the Mediterranean. Nat. Clim. Chang. 8, 972–980 (2018).
Baena-Ruiz, L. et al. Summarizing the impacts of future potential global change scenarios on seawater intrusion at the aquifer scale. Environ. Earth Sci. 79, 99 (2020).
Tigabu, T. B., Wagner, P. D., Hörmann, G., Kiesel, J. & Fohrer, N. Climate change impacts on the water and groundwater resources of the Lake Tana Basin, Ethiopia. J. Water Clim. Chang. 12, 1544–1563 (2020).
Tramblay, Y. et al. Challenges for drought assessment in the Mediterranean region under future climate scenarios. Earth Sci. Rev. 210, 103348 (2020).
Pulido-Velazquez, D., Collados-Lara, A. J., Pérez-Sánchez, J., Segura-Méndez, F. J. & Senent-Aparicio, J. Climate change impacts on the streamflow in Spanish basins monitored under near-natural conditions. J. Hydrol.: Reg. Stud. 38, 100937 (2021).
Wu, W. Y. et al. Divergent effects of climate change on future groundwater availability in key mid-latitude aquifers. Nat. Commun. 11, 3710 (2020).
IGRAC. Groundwater in the sustainable development goals: Position paper. 8 (International Groundwater Resources Assessment Centre, 2014).
Rubio-Aliaga, A., Molina-Garcia, A., Garcia-Cascales, M. S. & Sanchez-Lozano, J. M. Net-metering and self-consumption analysis for direct PV groundwater pumping in agriculture: A Spanish case study. Appl. Sci. 9, 1646 (2019).
Best, J. & Darby, S. E. The pace of human-induced change in large rivers: Stresses, resilience, and vulnerability to extreme events. One Earth 2, 510–514 (2020).
Cuthbert, M. O. et al. Global patterns and dynamics of climate–groundwater interactions. Nat. Clim. Change 9, 137–141 (2019).
Mediavilla, R., Santisteban, J. I., López-Cilla, I., Galán de Frutos, L. & De la Hera-Portillo, A. Climate-dependent groundwater discharge on semi-arid inland ephemeral wetlands: Lessons from Holocene sediments of lagunas reales in Central Spain. Water 12, 1911 (2020).
Manna, F. et al. Five-century record of climate and groundwater recharge variability in southern California. Sci. Rep. 9, 18215 (2019).
McCallum, J. L. et al. Assessing temporal changes in groundwater recharge using spatial variations in groundwater ages. Water Resour. Res. 56, e2020WR027240 (2020).
Qiu, J. et al. Nonlinear groundwater influence on biophysical indicators of ecosystem services. Nat. Sustain. 2, 475–483 (2019).
Saccò, M. et al. Rainfall as a trigger of ecological cascade effects in an Australian groundwater ecosystem. Sci. Rep. 11, 3694 (2021).
Zanchettin, D. et al. Atlantic origin of asynchronous European interdecadal hydroclimate variability. Sci. Rep. 9, 10998 (2019).
Pokhrel, Y. et al. Global terrestrial water storage and drought severity under climate change. Nat. Clim. Change 11, 226–233 (2021).
Nafría García, D. A. et al. Atlas agroclimatico de Castilla y León (Instituto Tecnológico Agrario de Castilla y León, Ministerio de Agricultura, Alimentación y Medio Ambiente, Agencia Estatal de Meteorología, 2013). (in Spanish)
Palmer, W. C. Meteorological drought. Research Paper No. 45, p. 58 (Office of Climatology, U.S. Weather Bureau, 1965).
Wells, N., Goddard, S. & Hayes, M. J. A self-calibrating Palmer Drought Severity Index. J. Clim. 17, 2335e2351 (2004).
van der Schrier, G., Jones, P. D. & Briffa, K. R. The sensitivity of the PDSI to the Thornthwaite and Penman-Monteith parameterizations for potential evapotranspiration. J. Geophys. Res. 116, D03106 (2011).
Cook, E. R. et al. Old World megadroughts and pluvials during the Common Era. Sci. Adv. 1, e1500561 (2015).
Hurrell, J. W. Decadal trends in the North Atlantic Oscillation: regional temperatures and precipitation. Science 269, 676–679 (1995).
McCarthy, G. D., Haigh, I. D., Hirschi, J. J. M., Grist, J. P. & Smeed, D. A. Ocean impact on decadal Atlantic climate variability revealed by sea-level observations. Nature 521, 508–510 (2015).
Wang, S. et al. Combined effects of the Pacific Decadal Oscillation and El Niño–Southern Oscillation on global land dry–wet changes. Sci. Rep. 4, 6651 (2014).
Mulligan, M. & Wainvright, J. Model and modelling building. in Environmental modelling: Finding simplicity in complexity (eds. Wainwright, J. & Mulligan, M.) 8–73 (Wiley, 2004). https://doi.org/10.1002/9781118351475
Candela Jurado, V., Manrique Menéndez, E., Fernández Cancio, A. & Genoveva Fuster, M. Análisis de la variabilidad climática de los últimos siglos en España a partir de reconstrucciones dendroclimáticas. Comparaciones con la situación actual p. 77-81 (Cuadernos De La Sociedad Española De Ciencias Forestales N. 12, 2001). (in Spanish), https://doi.org/10.31167/csef.v0i12.9264.
Hair, J. F., Anderson, R. E., Tatham, R. L. & Black, W. C. Multivariate data analysis, p. 768, 5th edition (Prentice-Hall, 1998).
Diodato, N. et al. Mixed nonlinear regression for modelling historical temperatures in Central–Southern Italy. Theor. Appl. Climatol. 113, 187–196 (2013).
Diodato, N., Bellocchi, G., Bertolin, C. & Camuffo, D. Climatic fingerprint of spring discharge. depletion in the southern Italian Apennines from 1601 to 2020 CE. Environ. Res. Commun. 4, 125011 (2022).
Shrestha, D. L. & Solomatine, D. P. Data-driven approaches for estimating uncertainty in rainfall-runoff modelling. Int. J. River Basin Manag. 6, 109–122 (2008).
Ljungqvist, F. C. et al. Northern Hemisphere hydroclimate variability over the past twelve centuries. Nature 532, 94–98 (2016).
Cook, B. I. et al. Megadroughts in the Common Era and the Anthropocene. Nat. Rev. Earth Environ. 3, 741–757 (2022).
Vicente-Serrano, S. M. et al. Global drought trends and future projections. Phil. Trans. R. Soc. A 380, 20210285 (2022).
Comuera, J. et al. Drought as a possible contributor to the Visigothic Kingdom crisis and Islamic expansion in the Iberian Peninsula. Nat. Commun. 14, 7533 (2023).
Christian, W. A. Local religion in sixteenth century Spain p. 296 (Princeton University Press, Princeton, 1982).
Pfister, C. & Wanner, H. Climate and society in Europe: The last thousand years p. 397 (Haupt, 2021).
Bossy, J. Christianity in the West: 1400–1700, p. 224 (Oxford University Press, 1985).
Gerrard, C. M. & Petley, D. N. A risk society? Environmental hazards, risk and resilience in the later Middle Ages in Europe. Nat. Hazards 69, 1051–1079 (2013).
Linton, J. What is water? The history of a modern abstraction p. 352 (UBC Press, 2010).
Grau-Satorras, M., Otero, I., Gómez-Baggethun, E. & Reyes-García, V. Long-term community responses to droughts in the early modern period: the case study of Terrassa, Spain. Ecol. Soc. 21, 33 (2016).
Berthe, M., Famines et épidémies dans les campagnes navarraises á fin du Moyen Age. Dos Tomos p. 817 (SFIED, 1984). (in French)
Ramírez Andueza, M. Conflictividad social en la Navarra bajomedieval p. 53 (Faculty of Philosophy and Letters. College of De Zaragoza, 2015). (in Spanish)
Ljungqvist, F. C., Seim, A. & Collet, D. Famines in medieval and early modern Europe – Connecting climate and society. WIREs Clim. Change 15, e859 (2024).
Domínguez-Castro, F., Santisteban, J. I., Barriendos, M. & Mediavilla, R. Reconstruction of drought episodes for central Spain from rogation ceremonies recorded at the Toledo Cathedral from 1506 to 1900: A methodological approach. Glob. Planet. Change 63, 230–242 (2008).
Gonzálvez, R. El clima toledano en los siglos XVI y XVII. Boletín. de la Real Academia de la Historia 174, 305–332 (1977). (in Spanish).
Bellido, A. Casos de continuidad en enclaves sagrados desde tiempos remotos en Castilla y León. Revista de Folklore 449, 30–43 (2019). (in Spanish).
Fornès, J. M., Sánchez del Barrio, A. & De la Hera-Portillo, A. Reconstrucción de períodos de sequías e inundaciones en Medina del Campo durante el Siglo de Oro español a partir de rogativas y otros documentos históricos. eHumanista 46, 92–105 (2020). (in Spanish).
Yin, X.-A., Yang, X. & Yang, Z.-F. Using the R/S method to determine the periodicity of time series. Chaos, Solitons & Fractals 39, 731–745 (2009).
Sheng, H. & Chen, Y. Q. Robustness analysis of the estimators for noisy long-range dependent time series p. 1157 (American Society Mechanical Engineers, 2009). https://doi.org/10.1115/DETC2009-86866
Quian, B. & Rasheed, K. Hurst exponent and financial market predictability. in Proceedings of the 2nd IASTED International Conference on Financial Engineering and Applications (ed. Hamza, M. H.) 203–209 (International Association of Science and Technology for Development, 2004).
Sutanto, S. J. & Van Lanen, H. A. J. Catchment memory explains hydrological drought forecast performance. Sci. Rep. 12, 2689 (2022).
Eddy, J. A. The Maunder Minimum. Science 192, 1189–1202 (1976).
Peribáñez Otero, J. G. Ecohistoriael medio natural de la Ribera del Duero en época medieval y moderna. Biblioteca: estudio e investigación 33, 9–30 (2018). (in Spanish).
Pettitt, A. N. A non-parametric approach to the change-point detection. Appl. Stat. 28, 126–135 (1979).
Alberol Romà, A. & Garcìa Agosta, V. Vaivenes climàticos en la penìnsula Ièrica y Nueva España en los años ochenta del siglo XVIII. Entre la”anomalia Maldà” y los”ciclos de El Niño” in Clima, riesgo, catástrofe y crisis a ambos lados del Atlántico durante la pequeña edad de hielo (eds. Alberol Romà, A. & Garcìa Agosta, V.,) 379–421 (Universidad de Alicante, 2019). (in Spanish)
Moreda, V. P. Spain. in Famine in European history (eds. Alfani, G. & Ó Gráda, C.) 48–72 (Cambridge University Press, 2017).
Camarero, J. J. et al. Historical fires induced deforestation in relict Scots pine forests during the late 19th century. Fire 4, 29 (2021).
Maia, R. & Vicente-Serrano, S. M. Drought planning and management in the iberian peninsula. in Drought and water Crises (Wilhite, D. & Pulwarty, R. S.) 481–506 (CRC Press, 2017).
Vicente-Serrano, S. M. Differences in spatial patterns of drought on different time scales: An analysis of the Iberian Peninsula. Water Resour. Manag. 20, 37–60 (2006).
López-Moreno, J. I. et al. Impact of climate and land use change on water availability and reservoir management: Scenarios in the Upper Aragón River, Spanish Pyrenees. Sci. Total Environ. 493, 1222–1231 (2014).
UNODRR. GAR Special report on drought 2021 p. 205 (United Nations Office for Disaster Risk Reduction, 2021).
Noguera, I., Domínguez‐Castro, F. & Vicente‐Serrano, S. M. Characteristics and trends of flash droughts in Spain, 1961–2018. Ann. N.Y. Acad. Sci 1472, 155–172 (2020).
Schumacher, D. L. et al. Drought self-propagation in drylands due to land–atmosphere feedbacks. Nat. Geosci. 15, 262–268 (2022).
Albiac, J., Esteban, E., Tapia, J. & Rivas, E. Water scarcity and droughts in Spain: Impacts and policy measures. in Drought in arid and semi-arid regions (eds. Schwabe, K., Albiac, J., Connor, J. D., Hassan, R. M. & González, L. M.) 323–339 (Springer, 2013).
Jiménez, L. et al. Ecosystem responses to climate-related changes in a Mediterranean alpine environment over the last ~180 years. Ecosystems 22, 563–577 (2019).
Sousa, A., García-Barrón, L., Morales, J. & García-Murillo, P. Post-Little Ice Age warming and desiccation of the continental wetlands of the aeolian sheet in the Huelva region (SW Spain). Limnetica 25, 57–70 (2006).
Calvache, M. L., Duque, C. & Pulido-Velazquez, D. Summary editorial: Impacts of global change on groundwater in Western Mediterranean countries. Environ. Earth Sci. 79, 531 (2020).
Jehanzaib, M., Shah, S. A., Yoo, J. & Kim, T.-W. Investigating the impacts of climate change and human activities on hydrological drought using non-stationary approaches. J. Hydrol. 588, 125052 (2020).
AghaKouchak, A. et al. Anthropogenic drought: Definition, challenges and opportunities. Rev. Geophys. 59, e2019RG000683 (2021).
Lian, X. et al. Multifaceted characteristics of dryland aridity changes in a warming world. Nat. Rev. Earth Environ. 2, 232–250 (2021).
De la Hera-Portillo, A. et al. Integrating current and historical water chemistry data with long-term piezometric records to develop a regional-scale conceptual flow model: Las Salinas spring, Medina del Campo, Spain. J. Hydrol.: Reg. Stud. 34, 100781 (2021).
López-Geta, J. A. & de la Orden, J. A. Drought as a catalyser of intensive groundwater use. in Intensive use of groundwater: challenges and opportunities (eds. Ramon Llamas, M. & Custodio E., eds.), 177–189 (CRC Press, 2002).
González Pérez, J., Cabrera Jerónimo, F., López Novella, M. Á., García Merino, J. M. & Gutiérrez Sanz, V. Reconstrucción multiproxy de las sequías en España. Tema B: Hidrología y gestión del agua p. 151–160 (Universidad de Castilla-La Mancha, 2009) (in Spanish)
Wilhite, D. A. Drought as a natural hazard: concepts and definitions. in A global assessment, Vol. 1 (ed. Wilhite, D. A.) 3-18 (Routledge, 2000).
Rodell, M., Velicogna, I. & Famiglietti, J. S. Satellite‐based estimates of groundwater depletion in India. Nature 460, 999–1002 (2009).
Cook, E. et al. A Euro-Mediterranean tree-ring reconstruction of the winter NAO index since 910 C.E. Clim. Dyn. 53, 1567–1580 (2019).
Wang, J. et al. Internal and external forcing of multidecadal Atlantic climate variability over the past 1,200 years. Nat. Geosci. 10, 512–517 (2017).
Macdonald, G. M. & Case, R. A. Variations in the Pacific Decadal Oscillation over the past millennium. Geo. Res. Lett. 32, L08703 (2005).
Trouet, V. & Van Oldenborgh, G. J. KNMI Climate Explorer: A web-based research tool for high-resolution paleoclimatology. Tree-Ring Res 69, 3–13 (2013).
Leelaruban, N., Padmanabhan, G. & Oduor, P. Examining the relationship between drought indices and groundwater levels. Water 9, 82 (2017).
Thomas, B. F. et al. GRACE groundwater drought index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 198, 384–392 (2017).
Hanel, M. et al. Revisiting the recent European droughts from a long-term perspective. Sci. Rep. 8, 9499 (2018).
Mares, I., Mares, C. & Mihailescu, M. NAO impact on the summer moisture variability across Europe. Phys. Chem. Earth 27, 1013–1017 (2002).
Rust, W., Bloomfield, J., Cuthbert, M., Corstanje, R. & Holman, I. The importance of non-stationary multiannual periodicities in the NAO index for forecasting water resource extremes. Hydrol. Earth Syst. Sci. 26, 2449–2467 (2022).
Muñoz-Díaz, F. & Rodrigo, S. Impacts of the North Atlantic Oscillation on the probability of dry and wet winters in Spain. Clim. Res. 27, 33–43 (2004).
Mariotti, A. & Dell’Aquila, A. Decadal climate variability in the Mediterranean region: roles of large-scale forcings and regional processes. Clim. Dyn. 38, 1129–1145 (2012).
Madrigal-González, J. et al. Forest productivity in southwestern Europe is controlled by coupled North Atlantic and Atlantic multidecadal oscillations. Nat. Commun. 8, 2222 (2017).
Deng, K.-Q. et al. Shifting of summertime weather extremes in Western Europe during 2012–2020. Adv. Clim. Change Res. 13, 218–227 (2022).
Luppichini, M., Barsanti, M., Giannecchini, R. & Bini, M. Statistical relationships between large-scale circulation patterns and local-scale effects: NAO and rainfall regime in a key area of the Mediterranean basin. Atmos. Res. 248, 105270 (2021).
Herrero, A. et al. Mediterranean pine forest distribution: Assessing vulnerability and resilience under climate change. in Pines and their mixed forest ecosystems in the Mediterranean basin, managing forest ecosystems (eds. Ne’eman, G. & Osem Y.) 251–277 (Springer Nature Switzerland AG, 2021). https://doi.org/10.1007/978-3-030-63625-8_13
Benassi, M. et al. El Niño teleconnection to the Euro-Mediterranean late-winter: the role of extratropical Pacific modulation. Clim. Dyn. 58, 2009–2029 (2022).
Neves, M. C., Jerez, S. & Trigo, R. M. The response of piezometric levels in Portugal to NAO, EA, and SCAND climate patterns. J. Hydrol. 568, 1105–1117 (2019).
Vegas-Vilarrúbia, Y. et al. Regional precipitation trends since 1500 CE reconstructed from calcite sublayers of a varved Mediterranean lake record (Central Pyrenees). Sci. Total Environ. 826, 153773 (2022).
Lenton, T. M. et al. Observed trends in the magnitude and persistence of monthly temperature variability. Sci. Rep. 7, 5940 (2017).
Diodato, N., Bellocchi, G., Fiorillo, F. & Ventafridda, G. Case study for investigating groundwater and the future of mountain spring discharges in Southern Italy. J. Mt. Sci. 14, 1791–1800 (2017).
Long, D. et al. South-to-north water diversion stabilizing Beijing’s groundwater levels. Nat. Commun. 11, 3665 (2020).
Song, K. et al. Research on drinking-groundwater source safety management based on numerical simulation. Sci. Rep. 10, 15481 (2020).
Mu, E., Yan, L., Ding, A., Deng, W. & Wang, Y. Determination of controlled limit value of groundwater level depth and management practice in Xi’an, China. Sci. Rep. 10, 15505 (2020).
McKee, T. B., Doesken, N. J. & Kleist, J. The relationship of drought frequency and duration to time scales. in Proceedings of the 8th Conference on Applied Climatology (ed.) 179–184 (American Meteorological Society, 1993). http://ccc.atmos.colostate.edu/relationshipofdroughtfrequency.pdf
Singh, N. K. & Borrok, D. M. A Granger causality analysis of groundwater patterns over a half-century. Sci. Rep. 9, 12828 (2019).
Danny Harvey, L. D. Climate and climate-system modelling. in Environmental modelling: Finding simplicity in complexity (eds. Wainwright, J. & Mulligan, M.) 77–91 (Wiley, 2004). https://doi.org/10.1002/9781118351475
Mulligan, M. & Wainwright, J. Modelling and model building in Environmental modelling: finding simplicity in complexity (eds. Wainwright, J. & Mulligan, M.) 7–73 (Wiley, 2004). https://doi.org/10.1002/9781118351475
Nash, J. E. & Sutcliffe, J. V. River flow forecasting through conceptual models part I – a discussion of principles. J. Hydrol. 10, 282–290 (1970).
Lim, K. J. et al. Effects of calibration on L-THIA GIS runoff and pollutant estimation. J. Environ. Manag. 78, 35–43 (2006).
Štěpánek, P. AnClim – software for time series analysis (Faculty of Natural Sciences, Masaryk University, 2005).
Rodrigo, F. S. The climate of Granada (southern Spain) during the first third of the 18th century (1706–1730) according to documentary sources. Clim. Past 15, 647–659 (2019).
Acknowledgements
We would like to express our gratitude to Dr. Africa De la Hera-Portillo of the Instituto Geológico y Minero de España (IGME), Geological Survey of Spain, for providing the piezometric data of Medina del Campo station. Open access publication funding for this article was provided by Stockholm University. Furthermore, we acknowledge the support from the Swedish Research Council (Vetenskapsrådet, grant no. 2018-01272) to F.C.L. and A.S. F.C.L. was also supported by Marianne and Marcus Wallenberg Foundation (grant no. MMW 2022-0114), and he conducted the work with this article as a Pro Futura Scientia XIII Fellow funded by the Swedish Collegium for Advanced Study through Riksbankens Jubileumsfond.
Funding
Open access funding provided by Stockholm University.
Author information
Authors and Affiliations
Contributions
The contributions of the authors are as follows: N.D. developed the original research design, collected and analysed the historical documentary data. N.D., A.S., F.C.L. and G.B. collaborated in writing the article and making interpretations. All authors participated in reviewing and finalising the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth and Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Carolina Ortiz Guerrero.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Diodato, N., Seim, A., Ljungqvist, F.C. et al. A millennium-long perspective on recent groundwater changes in the Iberian Peninsula. Commun Earth Environ 5, 257 (2024). https://doi.org/10.1038/s43247-024-01396-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-024-01396-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.