Abstract
The Alto Tiberina Fault system, located in Central Italy, is an active structure about 60 km long composed of a principal low-angle normal fault and several minor synthetic and antithetic splays. The system is monitored by a dense seismic network, giving us the opportunity to construct high-definition seismic catalogs with a low completeness magnitude. We analyze the clustering properties of the 2010-2015 seismicity by using a 3D stochastic declustering algorithm that also includes the earthquakes’ depth. We demonstrate that the earthquake size distribution is strongly correlated with the clustering of seismic events and their depth; in particular, the principal fault and secondary faults show an opposite behavior both in terms of earthquake size distribution and clustering properties.
Similar content being viewed by others
Introduction
Statistical seismologists usually characterize seismicity by describing two principal features: the clustering behavior, i.e. the tendency of the events to aggregate both in time and space; and the earthquake size distribution, which rules the magnitude of the events1,2,3. Both features are deeply investigated at a global, regional, and local scale. Earthquakes can occur either individually or in sequence: in the case of several events that occur individually, we have a low degree of clustering; in the other case of multiple events that occur in sequence (e.g. the aftershocks sequences after strong events4), we have a high degree of clustering.
The dependence of the clustering behavior on the physical properties of the Earth’s crust is still debated: clustering properties could change with different tectonics around the world5, or clustering is essentially similar in distinct crustal regions6. Recent studies on specific zones suggest that microseismicity clustering could be related to transient slow slip7 or background stress8. Liu et al.9 using a long earthquake catalog (about 35 years) showed that in the San Andreas fault clustering is inversely correlated with the creep rate.
The earthquake size distribution is instead dominated by a physical mechanism. Such a distribution can be well described by an exponential distribution with one parameter10, called “b-value” in the context of the Gutenberg-Richter law2. The inverse proportionality of the b-value with the differential stress was largely confirmed in laboratory events11,12 and in natural events13,14,15, showing that a physical mechanism rules this parameter.
With this study, we contribute to the investigation of a possible correlation between the clustering properties and the b-value. The detection of a common physical mechanism influencing both the clustering and the b-value would improve our general knowledge of seismicity. In particular, the understanding of the relation between these two quantities is also important for seismicity forecasting, because the large majority of the models used for short-term earthquake forecasting (ETAS-like models16,17) assume a uniform b-value for all the events.
The clustering of seismicity can be studied by using algorithms able to separate the background/independent part of the seismicity (in some methods called mainshocks) from the triggered one (in some methods called aftershocks).
The majority of the algorithms used to split independent and triggered events lead to a biased estimation of the b-value for these two subsets18. The stochastic declustering method19,20 does not suffer from this biased estimation problem for the b-value, thanks to its probabilistic approach in the identification of independent and triggered events18. Other studies already suggested a relation between the clustering and b-value7,8,9; in this work we also focus our attention on the proper (and in some cases sophisticated) statistical techniques to distinguish independent and triggered seismicity, to estimate their b-values avoiding bias, and to evaluate the possible correlation.
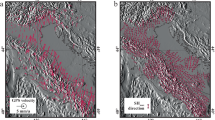
We investigate the clustering properties and the earthquake size distribution of the Alto Tiberina Fault (ATF) system, using a high-resolution earthquake catalog (Fig. 1)21 and a 3D version of a stochastic declustering algorithm able to take into account also the earthquakes’ depth22. In the case of the ATF system, composed of a principal low-angle normal fault (LANF; dip < 30°) and several minor synthetic and antithetic higher-angle normal faults23, the inclusion of depth is fundamental to properly understanding the possible connection between mechanical properties of the fault system and the characteristics of the seismicity.
a Map view of earthquakes occurred from April 2010 to December 2015. The color scale corresponds to the hypocentral depth; the red line is the surface projection of the Alto Tiberina Fault. Yellow squares are local municipalities. The dashed yellow line, AA’, indicates the trace of the vertical cross-section profile used for our analysis. Composite focal mechanism solutions for some clusters selected from Valoroso et al.30 are also shown. b Vertical cross-section of seismicity along AA’ profile. Earthquakes within +/−5.5 km from the vertical plane are shown.
The ATF case is particularly interesting for this kind of analysis. LANF have in fact been proposed as key structures for accommodating crustal extension, despite standard reactivation theory predicts that slip on these structures is extremely unlikely to happen24, consistently with the absence worldwide of large earthquakes on such low angle faults25. In detail, Anderson–Byerlee frictional fault reactivation theory, where the extending crust is characterized by vertical σ1 and faults possessing friction in the Byerlee26 range 0.6–0.85, predicts that it is easier to form a new optimally oriented fault (dip about 60°) instead of reactivating an existing one dipping less than 30°27. Thus, our study aims to better constrain the space-time-size distribution of the seismicity between mis- (e.g. low-) and well-oriented (e.g. higher-angle) normal faults.
Results and discussion
Clustering and earthquake size distribution at ATF system
We started our analysis with an accurate selection of the events in the catalog and a rigorous magnitude of completeness estimation (see Methods for details). Then we applied the stochastic declustering algorithm to identify the degree of independence of each seismic event. This algorithm associates a number between 0 and 1 to each event (i.e. the probability of being independent, PBI): values near 0 are related to the clustered/triggered seismicity, while values near 1 are related to the background/independent seismicity. Figure 2a shows the epicentral map of these probabilities. To investigate the possible relationship between the b-value and the clustering of seismicity, we estimated the b-value of the background and triggered components of the seismicity separately, using the recent weighted likelihood method21,28. We found a significantly different b-value for the two types of seismicity: a high b-value for background events, and a low b-value for triggered events (Fig. 2b). This different behavior of the b-value for background and triggered events is a key result, because until now such a difference in b-values is interpreted just as a possible bias in the estimation18,29. We underline that in this case the difference is not an artifact due to the declustering of the seismic catalog, because our stochastic declustering approach does not suffer from this biased estimation problem. The different b-values are a real property of seismicity. Therefore, to better investigate the relation of b-value and clustering properties with depth, we focused our attention on one vertical section of the catalog (11 km width). We chose this section because of the large number of events available in this part of the fault system. Figure 2c, d shows the PBI and the spatial b-value on the vertical section. From these figures, it is possible to appreciate that both high PBI and high b-values are related to the Alto Tiberina Fault, while low PBI and low b-values are related to the shallower part of the section, where the synthetic and antithetic faults are located. To give a quantitative assessment of this correspondence, we computed the correlation coefficient ρ between PBI and b-values for the events in the section, obtaining a significant positive value of ρ (Fig. 2e). Different radii are used to select the events in the section, always leading to a significant correlation (see Supplementary Information).
a Map of the events of the catalog; the color scale corresponds to the probability of being independent of each event; the section AA’ is highlighted with a black dashed line; b b-value (Y-axis) as a function of the magnitude of completeness (X-axis); yellow line for background events, blue line for triggered events, and dashed black line for all the events; b-value and their 95% confidence intervals (b+/−1.96σ) are computed using the Weighted Likelihood Method (WLM), and the weights of the computation are the probabilities of being independent of each event; non overlapping 95% confidence intervals indicate statistically significant difference in the b-values; c Section AA’, as shown in a, using a width of +/−5.5 km (in order to have a proper number of events); color scale corresponds to the probability of being independent of each event in the section; the dashed blue line represents the Alto Tiberina Fault; d b-value distribution in depth for section AA’: the sampling volumes are cylinder-shaped centered at each 1 km × 1 km grid node with a fixed radius of 3.5 km, containing at least 50 events; the b-value is estimated using the MLE approach; the dashed blue line represents the Alto Tiberina Fault; e scatter plot of the b-value (X-axis) vs the mean probability of being independent (Y-axis) for the events in the section AA’; for the i-th event the b-value and the mean probability are computed using all the events inside a circle with a radius of 3.5 km centered in the i-th event; the b-value is computed using the MLE approach for a subset of the catalog with at least 50 events; the blue ellipsis highlights the cluster of events with a low b-value and low mean probability, while the yellow ellipsis highlights the cluster of events with a high b-value and high mean probability; to quantify the strength of the correlation between these two quantities, the correlation coefficient ρ and the corresponding p-value of the significance test are computed.
Different faults, different behaviors
The results of our analysis indicate that the major Alto Tiberina Fault produces mainly background events alongside a high b-value, while the minor synthetic and antithetic faults, located in the ATF hanging wall, mainly produce clustered events with a low b-value (Fig. 3). The outcomes relative to the b-value are consistent with previous findings obtained for the same fault system23,30. Here we demonstrate that not only b-values are different in the ATF and synthetic and antithetic faults, but also the clustering behaviors are different, and strongly correlated with the b-values.
This visual representation provides a concise overview of the study’s key findings. The primary fault zone, the Alto Tiberina Fault, is depicted in red. It exhibits a high b-value and features background seismicity, indicating a high probability of being independent for seismic events. In contrast, the synthetic and antithetic faults in the hanging wall (the blue ones) exhibit a low b-value and show triggered seismicity, which implies clustered seismic events with a low probability of being independent. Notably, the most significant seismic events, indicated by the two red stars, are the ones occurring on 18/12/2013 (ML 3.62) and 22/12/2013 (ML 3.80) in the Gubbio area.
Degree of clustering of the seismic activity has been already coupled with frictional properties characterizing diverse portions of the faults system. An example is the creeping rate representing the whole spectrum of fault coupling from stable sliding to locked sectors along the San Andreas fault plane9.
Our robust statistical approach, by coupling the clustering properties of the seismicity with the earthquake size distribution, corroborates this idea. Similarly to some creeping patches of the San Andreas fault, we found a low degree of clustering and high b-values on the ATF. This is consistent with the results of the analysis of the Global Navigation Satellite System (GNSS) data suggesting creeping portions along the ATF31. Therefore, both the San Andreas and the Alto Tiberina faults show high b-values and low clustering in their creeping portions. The same GNSS data, uncovered in terms of a two-dimensional GPS velocity profile constructed through the ATF system, indicated that the low-angle normal fault has a high degree of tectonic coupling with its main antithetic fault, suggesting that creeping along the ATF may control the observed strain localization along these minor segments32.
Nowadays many observations are consistent with the occurrence of mainly aseismic deformation along the ATF plane reducing the availability of strain energy, thus somewhat lowering the seismic hazard associated to the ATF23,30,31,32,33, a fault that based on empirical relations between fault dimension and maximum magnitude, could host up to a MW 7.2 event. Such a behavior that we can call dominant, due to geometrical (e.g. misoriented fault) or mechanical (e.g. presence of velocity strengthening material along the fault plane) reasons, is not necessarily the only one. Recent studies documented that any given patch of a fault can creep, nucleate slow earthquakes, and host large earthquakes (e.g. Iquique earthquake34, Tohoku earthquake35, and Parkfield36). A seismic rupture can in fact nucleate in a small and locally well-oriented locked fault portion of the ATF and then propagate through creeping portions even if embedded within velocity-strengthening materials. During these processes, high slip velocities may favor a switch from creeping to seismic behavior, as observed for the Tohoku 2011 earthquake, which accumulated its largest seismic slip in the area that had been assumed to be creeping37,38. The reasons why a fault patch would switch from one mode of slip to another is still under investigation, together with the interaction between creep, slow, and regular earthquakes. Thus, our evidence cannot be used to evaluate the maximum expected magnitude, understood as the amount of the fault plane on the ATF that can be activated during a single strong event.
Our findings are also particularly important for the current debate on the possible b-value variations during aftershock sequences. While some works declared strong b-value variations during aftershock sequences39,40, other works show that these variations could be caused by incompleteness in the seismic catalog41,42,43. Here we demonstrate that triggered events (i.e. aftershocks) have a b-value statistically different from background events (i.e. mainshocks), adding a fundamental contribution to the controversy on b-value variations.
Moreover, it is also interesting to note that both Alto Tiberina and synthetic/antithetic faults produce seismic events with prevalent normal focal mechanisms30, but the b-values of these faults are significantly different. This observation proves that the rake of focal mechanism is just one of the features that can influence the b-value13,15: in the ATF system, also the dip of focal mechanism plays an important role. Synthetic/antithetic faults show higher dip angles and lower b-values, while the ATF shows lower dip and higher b-values.
A limitation of this work is the relatively short temporal length of the catalog (about 5 years), and the fact that it is not possible to include in the ETAS model the uncertainties of earthquake locations. A future longer catalog should be used to additionally check the findings of this study. However, although obtained using a short catalog, the results of this work are robust and statistically significant.
Conclusions
In summary, our results indicate that complex fault systems, like the Alto Tiberina zone, can have an apparently intricate behavior both in terms of clustering and earthquake size distributions. Here we have shown that these two features of seismicity are strongly correlated and correspond to different seismic behavior of the main fault and the secondary synthetic/antithetic faults: high b-value and low clustering for ATF, low b-value and high clustering for synthetic/antithetic faults. These different behaviors shed light on the relations of background and triggered seismicity with the earthquake size distributions.
Methods
Seismic catalog
The catalog we used consists of ∼50 K high-quality located earthquakes that occurred in the study region from April 2010 to December 2015, with local magnitude (ML) ranging from −2.5 to 3.8 (see details in Pastoressa et al.21).
Event selection and completeness estimation
From the starting catalog composed by ∼50 K earthquakes, we selected the events with a hypocentral depth between 0.5 and 15.0 km inside the area shown in Fig. 1, which contains most of the seismicity that occurred along the ATF system. We excluded the events in the first 500 m of the crust in order to avoid possible contamination by human-induced events (e.g. quarry blasts and explosions). We determined the completeness magnitude, Mc, by using a robust and stringent approach, i.e. the Lilliefors test method44,45, obtaining an Mc = 0.5 (and 6531 events with Mc ≥ 0.5, for details see Pastoressa et al.21). Possible Short Term Aftershock Incompleteness (STAI) periods are carefully checked, using the approach suggested by Zhuang et al.46; we found no STAI above the Mc = 0.5 threshold.
Stochastic declustering
The ETAS 3D model is described in Console et al.22. The parameters of this model are the same as in a 2D ETAS model, but in this case the distances between events are hypocentral distances (i.e. also depth is included in the computation). The goal of a stochastic declustering algorithm is to assign to each event in the catalog the probability of being independent (PBI). To compute these probabilities, we have to first fit the ETAS parameters. The calculation of the best fit ETAS parameters was carried out following these two steps:
-
1.
choice of the optimal correlation distance for the 3D spatial smoothing kernel by the maximum likelihood (ML) of half of the catalog on the grid of smoothed distribution of the other half;
-
2.
iterative search of the maximum likelihood ETAS parameters by computing (a) initial ML best fit of the ETAS parameters, (b) creation of a new catalog where a probability of being independent is associated with every earthquake, (c) creation of a new smoothed grid making use of the probability obtained in (b), (d) iteration of the process starting from (a) with the new smoothed grid and again until the optimal data set is obtained.
At the end of the above-mentioned process, we obtain an earthquake catalog where the probability of independence is associated with each event. The first events in the catalog were removed, since they all have a high PBI simply due to their temporal position at the beginning of the catalog (burn-out period, see Console et al.22 for details).
b-value estimation
We employed two methods to calculate the b-value, the classical Maximum Likelihood Estimation (MLE) for Fig. 2d, and Weighted Likelihood Method (WLM) for Fig. 2b. In the first case, the MLE10 is corrected for magnitude binning and for an unbiased estimation41:
Where \(N\) is the total number of events, \(\bar{M}\) is the mean of magnitudes, \({M}_{c}\) is the magnitude of completeness of the catalog, and \(\varDelta M\) is the binning of the magnitude.
In detail, to construct Fig. 2d, we considered a dense grid spaced 1.0 km both horizontally and in depth, and a cylinder-shaped sampling volume with a fixed radius of 3.5 km containing at least 50 events (as in Murru et al.47). The b-values estimation errors σ were computed as in Aki10, \(\hat{\sigma }=\frac{\hat{b}}{\sqrt{N}}\). Supplementary Figs. S1 and S2 display: the estimation of the b-value for different Mc values, the estimation of σ relative to the b-value of Fig. 2d, and the b-value estimation made with at least 100 events. All these results are coherent with the ones shown in Fig. 2d. For Fig. 2b, with the aim to evaluate the possible influence of changes in completeness magnitude on the b-value estimation, we computed b-values and their 95% confidence intervals as a function of completeness magnitude both for background and clustered seismicity using the WLM28. As in Pastoressa et al.21, to properly compute the b-value for the background and triggered seismicity we used as weights the probabilities of each event to be independent (\({\varphi }_{i}\)) and their complementary (\({\rho }_{i}=1-{\varphi }_{i}\)) respectively, achieved from the stochastic declustering based on the 3D ETAS model. In this way, the formulas to estimate b-values relating to background (\({\hat{b}}_{{back}}\)) and triggered seismicity (\({\hat{b}}_{{trig}}\)) are:
Supplementary Fig. S3 displays the correlation between the mean PBI and the b-values obtained with different radii for the circular search (4, 3, and 2.5 km), showing results very similar to Fig. 2e.
Data availability
The dataset used in this paper is freely available at: https://zenodo.org/records/10810647.
Code availability
The code used in this paper is freely available at: https://zenodo.org/records/10810647.
References
Utsu, T., Ogata, Y. & Matsu’ura, R. The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 43, 1–33 (1995).
Gutenberg, B. & Richter, C. F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 34, 185–188 (1944).
Kagan, Y. Y. Earthquakes: Models, Statistics, Testable Forecasts (John Wiley & Sons).
Omori, F. On the after-shocks of earthquakes (The University of Tokyo, 1895).
Kagan, Y. Y., Bird, P. & Jackson, D. D. Earthquake patterns in diverse tectonic zones of the globe. Pure Appl. Geophys. 167, 721–741 (2010).
Stallone, A. & Marzocchi, W. Features of seismic sequences are similar in different crustal tectonic regions. Bull. Seismol. Soc. Am. 109, 1594–1604 (2019).
Bocchini, G. M. et al. Direct Evidence of a Slow‐Slip Transient Modulating the Spatiotemporal and Frequency‐Magnitude Earthquake Distribution: Insights From the Armutlu Peninsula, Northwestern Turkey. Geophys. Res. Lett. 49, e2022GL099077 (2022).
Beaucé, E., van der Hilst, R. D. & Campillo, M. Microseismic constraints on the mechanical state of the North Anatolian fault zone 13 years after the 1999 M7. 4 Izmit earthquake. J. Geophys. Res. Solid Earth 127, e2022JB024416 (2022).
Liu, Y.-K., Ross, Z. E., Cochran, E. S. & Lapusta, N. A unified perspective of seismicity and fault coupling along the San Andreas Fault. Sci. Adv. 8, eabk1167 (2022).
Aki, K. Maximum likelihood estimate of b in the formula log N = a-bM and its confidence limits. Bull Earthq Res Inst Tokyo Univ 43, 237–239 (1965).
Scholz, C. H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 58, 399–415 (1968).
Amitrano, D. Brittle‐ductile transition and associated seismicity: Experimental and numerical studies and relationship with the b value. J. Geophys. Res. Solid Earth 108, 1–15 (2003).
Schorlemmer, D., Wiemer, S. & Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 437, 539–542 (2005).
Tormann, T., Wiemer, S. & Mignan, A. Systematic survey of high‐resolution b value imaging along Californian faults: Inference on asperities. J. Geophys. Res. Solid Earth 119, 2029–2054 (2014).
Petruccelli, A. et al. The influence of faulting style on the size-distribution of global earthquakes. Earth Planet. Sci. Lett. 527, 115791 (2019).
Ogata, Y. Space-Time Point-Process Models for Earthquake Occurrences. Ann. Inst. Stat. Math. 50, 379–402 (1998).
Ogata, Y. & Zhuang, J. Space–time ETAS models and an improved extension. Tectonophysics 413, 13–23 (2006).
Mizrahi, L., Nandan, S. & Wiemer, S. The Effect of Declustering on the Size Distribution of Mainshocks. Seismol. Res. Lett. 92, 2333–2342 (2021).
Zhuang, J., Ogata, Y. & Vere-Jones, D. Analyzing earthquake clustering features by using stochastic reconstruction. J. Geophys. Res. Solid Earth 109, B05301 (2004).
Console, R., Jackson, D. D. & Kagan, Y. Y. Using the ETAS Model for Catalog Declustering and Seismic Background Assessment. Pure Appl. Geophys. 167, 819–830 (2010).
Pastoressa, A. E. et al. Temporal Variations of Seismicity Rates and Gutenberg–Richter b -Values for a Stochastic Declustered Catalog: An Example in Central Italy. Seismol. Res. Lett. https://doi.org/10.1785/0220220298 (2023).
Console, R., Vannoli, P. & Falcone, G. Magnitude distribution and clustering properties of the 3-D seismicity in Central Apennines (Italy). Geophys. J. Int. 233, 2004–2020 (2023).
Chiaraluce, L., Chiarabba, C., Collettini, C., Piccinini, D. & Cocco, M. Architecture and mechanics of an active low-angle normal fault: Alto Tiberina Fault, northern Apennines, Italy. J. Geophys. Res. Solid Earth 112, B10310 (2007).
Collettini, C. The mechanical paradox of low-angle normal faults: Current understanding and open questions. Tectonophysics 510, 253–268 (2011).
Collettini, C. & Sibson, R. H. Normal faults, normal friction? Geology 29, 927 (2001).
Byerlee, J. Friction of Rocks. in Rock Friction and Earthquake Prediction (eds. Byerlee, J. D. & Wyss, M.) 615–626 (Birkhäuser, Basel, 1978). https://doi.org/10.1007/978-3-0348-7182-2_4.
Sibson, R. H. A note on fault reactivation - J. Struct. Geol. 7(6), 751–754 (1985).
Taroni, M., Zhuang, J. & Marzocchi, W. High‐Definition Mapping of the Gutenberg–Richter b‐Value and Its Relevance: A Case Study in Italy. Seismol. Res. Lett. 92, 3778–3784 (2021).
Taroni, M. & Akinci, A. Good practices in PSHA: declustering, b-value estimation, foreshocks and aftershocks inclusion; a case study in Italy. Geophys. J. Int. 224, 1174–1187 (2021).
Valoroso, L., Chiaraluce, L., Di Stefano, R. & Monachesi, G. Mixed-Mode Slip Behavior of the Altotiberina Low-Angle Normal Fault System (Northern Apennines, Italy) through High-Resolution Earthquake Locations and Repeating Events. J. Geophys. Res. Solid Earth 122, 220–10,240 (2017).
Anderlini, L., Serpelloni, E. & Belardinelli, M. E. Creep and locking of a low-angle normal fault: Insights from the Altotiberina fault in the Northern Apennines (Italy). Geophys. Res. Lett. 43, 4321–4329 (2016).
Vadacca, L., Casarotti, E., Chiaraluce, L. & Cocco, M. On the mechanical behaviour of a low-angle normal fault: the Alto Tiberina fault (Northern Apennines, Italy) system case study. Solid Earth 7, 1537–1549 (2016).
Vuan, A. et al. Intermittent Slip Along the Alto Tiberina Low‐Angle Normal Fault in Central Italy. Geophys. Res. Lett. 47, e2020GL089039 (2020).
Ruiz, S. et al. Intense foreshocks and a slow slip event preceded the 2014 Iquique Mw 8.1 earthquake. Science 345, 1165–1169 (2014).
Kato, A. et al. Propagation of Slow Slip Leading Up to the 2011 Mw 9.0 Tohoku-Oki Earthquake. Science 335, 705–708 (2012).
Veedu, D. M. & Barbot, S. The Parkfield tremors reveal slow and fast ruptures on the same asperity. Nature 532, 361–365 (2016).
Fukuda, J., Kato, A., Kato, N. & Aoki, Y. Are the frictional properties of creeping faults persistent? Evidence from rapid afterslip following the 2011 Tohoku‐oki earthquake. Geophys. Res. Lett. 40, 3613–3617 (2013).
Noda, H. & Lapusta, N. Stable creeping fault segments can become destructive as a result of dynamic weakening. Nature 493, 518–521 (2013).
Gulia, L. et al. The Effect of a Mainshock on the Size Distribution of the Aftershocks. Geophys. Res. Lett. 45, 13,277–13,287 (2018).
Gulia, L. & Wiemer, S. Real-time discrimination of earthquake foreshocks and aftershocks. Nature 574, 193–199 (2019).
Marzocchi, W., Spassiani, I., Stallone, A. & Taroni, M. How to be fooled searching for significant variations of the b-value. Geophys. J. Int. 220, 1845–1856 (2020).
Lombardi, A. M. A Normalized Distance Test for Co-Determining the Completeness Magnitude and b-Value of Earthquake Catalogs. J. Geophys. Res. Solid Earth 126, e2020JB021242 (2021).
Lombardi, A. M. Anomalies and transient variations of b -value in Italy during the major earthquake sequences: what truth is there to this? Geophys. J. Int. 232, 1545–1555 (2022).
Lilliefors, H. W. On the Kolmogorov-Smirnov Test for the Exponential Distribution with Mean Unknown. J. Am. Stat. Assoc. 64, 387–389 (1969).
Herrmann, M. & Marzocchi, W. Inconsistencies and Lurking Pitfalls in the Magnitude–Frequency Distribution of High‐Resolution Earthquake Catalogs. Seismol. Res. Lett. 92, 909–922 (2020).
Zhuang, J., Ogata, Y. & Wang, T. Data completeness of the Kumamoto earthquake sequence in the JMA catalog and its influence on the estimation of the ETAS parameters. Earth Planets Space 69, 1–12 (2017).
Murru, M., Console, R., Falcone, G., Montuori, C. & Sgroi, T. Spatial mapping of the b value at Mount Etna, Italy, using earthquake data recorded from 1999 to 2005. J. Geophys. Res. Solid Earth 112, 2006JB004791 (2007).
Acknowledgements
We thank Gian Maria Bocchini and one anonymous reviewer for providing insightful comments and suggestions which greatly improve the value of this work. This work was supported by the 2020–2024 Istituto Nazionale di Geofisica e Vulcanologia (INGV) Department Strategic Project named MUSE (Multiparametric and mUltiscale Study of Earthquake preparatory phase in the central and northern Apennines), and by the Centro di Pericolosità Sismica (CPS) of INGV.
Author information
Authors and Affiliations
Contributions
M.T., R.C., C.M., M.M., and G.F. outlined the project; M.T., R.C., M.M., and G.F. performed the statistical analyses; M.T., C.M., and A.E.P. prepared the figures; L.C. (expert of ATF system) helped interpret the results; all authors wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth and Environment thanks Gian Maria Bocchini and the other anonymous reviewer for their contribution to the peer review of this work. Primary Handling Editor: Joe Aslin. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Taroni, M., Console, R., Montuori, C. et al. Statistically significant difference between earthquake size distributions of independent and triggered seismicity. Commun Earth Environ 5, 193 (2024). https://doi.org/10.1038/s43247-024-01367-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-024-01367-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.