Multi-decadal variability controls short-term stratospheric water vapor trends

Abstract

Stratospheric water vapor increases are expected in response to greenhouse gas-forced climate warming, and these changes act as a positive feedback to surface climate. Previous efforts at inferring trends from the 3–4 decade-long observational stratospheric water vapor record have yielded conflicting results. Here we show that a robust multi-decadal variation of water vapor concentrations exists in most parts of the stratosphere based on satellite observations and atmospheric model simulations, which clearly divides the past 40 years into two wet decades (1986–1997; 2010–2020) and one dry decade (1998–2009). This multi-decadal variation, especially pronounced in the lower to middle stratosphere and in the northern hemisphere, is associated with decadal temperature anomalies (±0.2 K) at the cold point tropopause and a hemispheric asymmetry in changes of the Brewer-Dobson circulation modulating methane oxidation. Multi-decadal variability must be taken into account when evaluating stratospheric water vapor trends over recent decades.

Introduction

Stratospheric water vapor (SWV) has been the subject of intensive research due to its positive feedback on the climate system, which contributes remarkably to regulating atmospheric and surface temperature^1,2,3,4,5. In addition to its effects on temperature, SWV also influences atmospheric circulation^6,7 and stratospheric ozone chemistry^6,8, further underscoring its importance in the Earth’s climate system.

Most climate models project an increase in SWV in response to tropospheric warming⁹, which was supported by several observational datasets, including the longest SWV record at Boulder, indicating a global increase of ~1% per year before 2000^10,11. However, the significance of this increasing trend over the last 3–4 decades has been questioned^12,13,14 since HALOE satellite observations showed a sharp drop in SWV near the tropical tropopause (~0.4 ppm) around 2000, followed by persistent stratospheric drying until 2005¹⁵. Meanwhile, increasing evidence suggests that interannual to decadal variations in SWV are more complex than previous thought^16,17,18,19, potentially impacting the estimation and understanding of long-term trends^17,20.

Quantifying the long-term variations in SWV, including feature timescales, oscillations amplitudes, and global spatial patterns, remains challenging due to the limited spatial coverage of in situ measurements and the short lifetimes and time-varying drifts of satellite observation records^21,22. Recent efforts to merge satellite observations have provided homogenized globally gridded SWV records for the last 2–3 decades^12,23, which are valuable for analysis. However, the mechanism behind long-term variability and trends remains unclear. Although the relationship between mean tropical tropopause temperature and the water vapor entering the stratosphere has been proven to be robust for seasonal to interannual timescales^24,25, discontinuities in measurements of tropical tropopause temperature^26,27,28 and limitations of SWV records make it challenging to examine such relationships on longer timescales. In addition to the influence of tropopause temperature, long-term changes in SWV could be driven by structural changes in the Brewer–Dobson circulation (BDC)¹² through related modulations of methane oxidation, while growth in tropospheric methane is a minor contributor²⁹ (see also Fig. S1 and Supplementary References therein).

A comprehensive interpretation of long-term SWV variability requires model simulations. Modeling SWV represents a grand challenge for global atmospheric models due to the extreme shape gradients in water vapor around the tropopause. The current generation of free-running models exhibits limitations in this regard, though there is some improvement in capturing the quasi-biennial oscillation (QBO) signal^30,31. Recent modeling attempts using a Lagrangian framework for offline, reanalysis-driven, and climate model simulations have shown promising results, reproducing the SWV record by accurately representing the lowest temperatures and tracing the pathways of air parcels^{13,24,32,33,34}. Additionally, the age spectrum technique enables the isolation of the contributing processes³⁵, providing new insights into the mechanisms of long-term variability. Here, we reveal a key variability at multi-decadal timescales in SWV and explore its origins using satellite-observed and modeled SWV records. We also examine the influence of this variability on long-term SWV trends.

Results

Remarkable multi-decadal variation of SWV record over the past 40 years

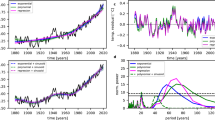
Figure 1a–e depicts the time series of deseasonalized H₂O monthly anomalies based on the Stratospheric Water and OzOne Satellite Homogenized (SWOOSH) dataset (cyan dots) and the CLaMS simulation (gray lines) in five selected regions in the stratosphere. The model simulation and observations show remarkable agreement. Despite some quantitative differences, particularly in the 1980s and early 1990s before HALOE observations were merged into the SWOOSH dataset (see also Fig. S2), both SWOOSH and CLaMS data show a similar multi-decadal variation (MDV) over the last 40 years. To isolate the MDV signal, we use the ensemble empirical mode decomposition (EEMD)³⁶ on the zonal- and monthly-averaged SWV (see “Methods” section and Fig. S3). The resulting sixth mode, with a typical period of about 27 years is extracted to estimate the MDV, shown as the dotted gray lines (regional mean) and gray shading (its variability) in Fig. 1. The MDV in SWV exhibits spatial similarity and temporal synchronization not only within the selected areas but also across different stratospheric regions (see Fig. S4). This enables us to identify two wet periods (1986–1997; 2010–2020) and one dry period (1998–2009). We notice that extreme dry events (blue/red crosses in Fig. 1) mostly occurred during the dry periods and vice versa. The well-documented H₂O drop after 2000¹⁵ precedes a persistent dry period with several consecutive extreme dry events between 2000 and 2005, marking the absolute minimum of the MDV.

Fig. 1: Multi-decadal variation signals in the H₂O records and relevant statistics.

Time series of 5-month running mean deseasonalized SWV anomalies, ∆H₂O, derived from CLaMS-ERA5 (gray lines) and SWOOSH data (cyan dots) are shown for five regions in the lower to middle stratosphere (a–e). The MDV is identified as the sixth mode using Ensemble EEMD. The gray shading indicates the range of all relevant MDVs over the region and the thick dotted gray lines represent the mean of these MDV signals. Extreme wet or dry months (larger or lower than ±1.5σ from detrended and deseasonalized SWV anomalies) are marked as red and blue triangles. Two wet decades (1986–1997 and 2010–2020) are masked by red shading and a dry decade (1998–2009) is masked by blue shading. The statistics concerning MDVs derived from the modeled SWV are summarized on the left three panels (f–h). Panel f shades the region where MDVs are significant at the 10% (p ≤ 0.1, color shaded) and 5% (p ≤ 0.05, green) level from autocorrelation-preserving bootstrapping of the original data disturbed by red noise, with the five selected regions outlined using rectangular boxes. Panel g shows the contribution of MDVs (color shades) to the interannual variability (black contours, unit in ppmv²). Panel h shows the absolute amplitudes of MDVs. The magenta thick line indicates the climatological thermal tropopause. Specifics of the EEMD and the bootstrapping methods are provided in the “Method” section.

SWV shows clear and robust MDV signals in most parts of the stratospheric overworld (above 100 hPa or 380 K), where the MDVs achieve statistical significance at the 10% and even 5% level, as shown in Fig. 1f (for details on the significance test, see “Methods” and Fig. S5). The amplitude of MDV in the modeled SWV mostly ranges from 0.08 ppmv to 0.14 ppmv, contributing 10% to 50% of the total power in interannual variability. The MDV amplitude based on SWOOSH ranges from 0.04 ppmv to 0.08 ppmv, smaller than that based on CLaMS. The largest MDV amplitude is found in the boreal middle stratosphere (NMS and NP), where MDV explains 35–50% of the total interannual variability of SWV. The southern middle stratosphere (SMS) also exhibits a remarkable MDV signal, though with an amplitude about 1/3 less than that in the boreal middle stratosphere. In the tropical lower stratosphere (TLS), the amplitude of the MDV is relatively strong (about 0.1 ppmv based on CLaMS and 0.08 ppmv based on SWOOSH), but only contributes a low percentage (about 10%) of the inter-annual variability in water vapor, and does not pass the significance test. Strong interannual variability in water vapor in this region is influenced by other natural variability, including the QBO and the El Niño-Southern Oscillation (ENSO) (see also the example in Fig. S3). MDV in the southern polar region (SP) is insignificant with relatively low amplitude and fractional contribution. A pronounced decreasing trend outweighs the MDV in this region (as shown in Fig. 1e), presumably resulting from Antarctic cooling associated with ozone losses in this region.

Simulated mean SWV anomalies are 30–50% larger than for satellite observations, as shown from composite analysis of individual wet and dry periods (Fig. 2). The overall anomaly patterns are very similar among the different data sets. Two prominent features of MDV emerge: (1) variations in each time period are statistically significant in most parts of the stratospheric overworld with relatively strong signals in the lower to middle stratosphere; and (2) the amplitude of these variations, although different in sign for the wet and dry periods, shows a clear hemispheric asymmetry with stronger variations in the northern hemisphere (NH) than in the southern hemisphere (SH).

Fig. 2: Stratospheric water vapor anomaly and its contributors averaged over three periods.

SWV anomaly (unit: ppmv) averaged over the first wet decade 1990–1997 (a and d); the dry decade 1998–2009 (b and e) and the second wet decade 2010–2020 (c and f) for SWOOSH (a–c) and CLaMS simulations (d–f). Regions with more than 50% missing values are blanked for SWOOSH. Following the procedure described in the method section and also in Hegglin et al.¹¹ (see their Eq. 2), ∆H₂O is decomposed into contributions from changes in H₂O entering the stratosphere (g–i), circulation changes (j–l), changes in methane entering the stratosphere (m–o) and the residuum (p–r). Black contours in a–f show anomalies relative to the climatological means (unit: %). The gray contours on g–i are the mean age of air (AoA) for each period (unit: year). The red and blue contours on j–l are positive and negative anomalies of AoA averaged over each period (unit: year). The magenta thick line indicates the climatological tropopause.

Contributors to the MDV of SWV

The drivers contributing to the variations in SWV are quantified using the “total water” diagnostic^11,25 (Methods). Four potential drivers are considered: the changes in H₂O entering the stratosphere controlled by the cold point tropopause (CPT) at the tropical tropopause layer (∆H₂O_[entry]), the effect of circulation changes on CH₄ oxidation ($2{{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}\Delta \alpha$), changes in methane entering the stratosphere and transformed into water vapor with a constant rate ($2\alpha \Delta {{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}$), and a residuum due to other water vapor sources or sinks (∆H₂O_[res]), such as injection from overshooting convection or removal of water vapor when PSCs form. The results for each driver within each of the three periods are shown in Fig. 2g–r, respectively.

Our analysis reveals that decadal wet and dry anomalies primarily result from a combination of changes in H₂O entering the stratosphere (∆H₂O_[entry]) and circulation changes ($2{{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}\Delta \alpha$). Contributions related to changes in methane ($2\alpha \Delta {{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}$) and the residuum (∆H₂O_[res]) are small. SWV anomalies in the lower stratosphere (±0.1 ppmv) can be attributed to the changes in the amount of water vapor entering the stratosphere (Fig. 2g–i). The resulting stratospheric distributions of ∆H₂O_[entry] are nearly hemispherically symmetric, with these anomalies decreasing with increasing age of air (see the contours in Fig. 2g–i). The hemispheric asymmetry, with more pronounced moistening and drying effects in the extratropical NH than in the SH, is mainly caused by the methane oxidation contribution associated with the hemispheric asymmetry of circulation changes on multi-decadal time scales, as shown in Fig. 2j–l. A remarkable multi-decadal oscillation of AoA with ±0.2 year amplitude corresponds to changes in the stratospheric circulation (2CH₄ ∆α_[entry]), which add up to ±0.05 ppmv in the extra-tropical NH. Particularly large variations in simulated SWV are found above the tropopause in the extratropical lowermost stratosphere and are not explained by any of the drivers but remain in the residuum (Fig. 2).

In the TLS, MDV in stratospheric entry water vapor (∆H₂O_[entry]) is closely related to variations in the CPT (∆CPT). Furthermore, we use the age of air (AoA) diagnostic to more explicitly link 2CH₄∆α with structural changes in the circulation pattern. As shown in Fig. 3a, ∆H₂O_[entry] is controlled by the CPT, with a high correlation coefficient (around 0.87) in the simulation results. The ratio between ∆H₂O_[entry] and ∆CPT is around 0.45 ppmvK⁻¹, consistent with the Clausius-Clapeyron relation for appropriate values of reference temperature (~190 K) and pressure (~90 hPa). Previous estimates of this ratio range from 0.4 ppmv per K²⁴ to 0.5 ppmv per K²⁰. MDVs in the CPT (Fig. 3b) have an amplitude of ±0.14 K, which can explain 80% (±0.08 ppmv out of ±0.1 ppmv) of the MDV in tropical lower SWV. The result agrees with previous studies^20,24,37 showing that variations in tropopause temperature dominate interannual variability in water vapor entering the stratosphere. This effect has a distinct seasonal and regional preference, with decadal anomalies in boreal winter CPT (see the triangles in Fig. 3c) having a stronger influence than those in other seasons. This boreal winter influence is contributed in large part by the “cold trap”³⁸ over the Maritime Continent (see Fig. S6).

Fig. 3: Variations in the cold point tropopause and in the strength of Brewer–Dobson circulation associated with the H₂O variability.

a Time series of deseasonalized anomalies in the cold point tropopause (∆CPT) averaged over 20°S–20°N smoothed by a 5-month running mean (solid thin line) and the range and mean of MDVs over the region (gray shade and thick dotted line). b Covariations in monthly ∆H2O[entry] averaged over 20°S–20°N at 390 K and ∆CPT (scatters). Colored diamonds show mean values for the three (wet and dry) periods. c Mean values and standard deviations over all seasons for each of the three periods are shown as diamonds and the error bars. Mean values for DJF alone are shown as triangles. Panels d–g are similar to panels a, b but for the deseasonalized age of air (∆AoA) in the NH extra-tropics and SH extra-tropics between 500 and 600 K in relation to 2CH4∆α.

As shown in Fig. 3d–g, the changes in SWV in the extratropics (30°N–90°N and 30°S–90°S) caused by the changes in the structure of the BDC (as quantified in terms of 2CH₄∆α) are well correlated with ∆AoA. Ratios between 2CH₄∆α and ∆AoA are consistent with proposed simplified AoA-α correlation functions³⁵ considering the corresponding averaged methane mixing ratio of around 1.5 ppmv. The larger MDV of AoA in the NH compared to the SH results in hemispheric asymmetry in SWV changes, primarily due to the asynchronous circulation changes between the two hemispheres after 2005, when SH stratospheric air continued to get younger while NH extratropical air aged.

A series of studies based on various observations of stratospheric tracers supports the hemispheric asymmetry of AoA changes in the mid-stratosphere^{39,40,41,42,43,44}, which is also reproduced by previous studies based on reanalysis-driven simulations^45,46 and climate model simulations⁴⁷. It is worth noting that a stronger BDC implies a colder tropical tropopause and vice versa due to the balance between radiative relaxation and wave-driven adiabatic cooling⁴⁸. Thus, ∆CPT and ∆AoA are interconnected, especially in the boreal lower to middle stratosphere.

Underlying long-term trend in SWV

The presence of multi-decadal variability may obscure any underlying long-term trend. Figure 4 shows the distribution of SWV linear trends and the statistics of 15-year trends before (top) and after (bottom) removing the MDVs (see method). The MDVs in SWV reported in this study are sufficiently robust that they substantially alter linear trends calculated over periods shorter than a single MDV cycle (~30 years). For instance, positive trends over the period 2005–2020 in both the CLaMS-simulated and SWOOSH water vapor time series (Fig. 4b, c) can be largely attributed to MDVs. Linear trends for this period after removing MDVs, as shown in Fig. 4g, h, are closer to those derived for the full 40-year period (Fig. 4a, f): a negative trend (~1–2% per decade) in the SH lower to middle stratosphere, a near-neutral trend in the NH lower to middle stratosphere and a positive trend (~1% per decade) in the upper stratosphere.

Fig. 4: Stratospheric water vapor trends with and without multi-decadal variations.

Panels a–c show linear trends with MDVs: trends estimated for the full simulation period 1980–2020 (a); trends for the period 2005–2020 from CLaMS simulation (b); trends for the period 2005–2020 from the SWOOSH dataset (c). Panels f–h show the corresponding trends without MDVs (see “Methods”). The color shading and contours show trends in ppmv per decade and percentage per decade (relative to the water vapor mixing ratio averaged over the full period), respectively. Statistically significant trends (at the 5% significance level) are dot-hatched. The thick magenta line indicates the climatological tropopause. Magnitudes of 15-year trends with (d, e) and without MDV (i, j) estimated from CLaMS (gray) and SWOOSH (cyan) are shown for the southern mid-latitudes (25–50°S, 500–600 K, d and i) and northern mid-latitudes in the mid-stratosphere (25–50°N, 500–600 K, e and j). The dots represent the means and lines depict the spread spanning from the 2.5th to the 97.5th percentile. The vertical dotted lines indicate thresholds for the trends to reach significance at the 5% level.

Further statistical analysis of 15-year SWV trends reveals that they vary greatly among selected periods (Fig. 4d, e). In particular, the 15-year trend in SWV at the northern mid-latitudes (Fig. 4e) displays greater variation across different periods than that at the southern mid-latitudes (Fig. 4d), since the multi-decadal signal is stronger in the NH than in the SH. Thus, the long-term trend in SWV in the boreal lower and middle stratosphere should be quantified with particular caution. However, these trends become more consistent after accounting for MDVs. The magnitudes of 15-year SWV trends are greatly reduced and few trends meet the significance threshold after excluding the influence of MDVs (Fig. 4I, j). These changes in the calculated trends indicate that MDVs play a dominant role in determining short-term trends in SWV.

The influence of MDVs on the trend over the full simulation period 1980–2020 is not very strong (see Fig. 4a, f, and also Fig. 5), as the period spans approximately one MDV cycle. Also, the overall simulated SWV increase associated with global warming is not significant within the 40-year period, and the magnitude of this increase is largely independent of whether MDVs are included in the trend calculation (Fig. 5a). The water vapor trends strongly differ between the stratospheric overworld and the lowermost stratosphere region (Fig. 5 and Fig. S7). In the overworld, the simulated water vapor trend is weakly negative (but does not pass the significance test), related to the cooling of the tropical tropopause and Antarctic stratosphere during 1980–2020. The net tropical tropopause cooling (about −0.1 K from ERA-5) could result from the interplay between possible BDC acceleration and tropospheric warming over this period^5,30. In the lowermost stratosphere, however, the water vapor trends are positive and significant (approximately 0.5 ppmv K⁻¹, Fig. 5). It is important to highlight that the water vapor increase in the lowermost stratosphere opposes the cooling of the CPT diagnosed from the ERA5 reanalysis. This contrast suggests that an alternative mechanism impacts the water vapor budget in the lowermost stratosphere. This mechanism might involve a positive trend in moisture transport across the extra-tropical tropopause, like convection or turbulent mixing, which could depend critically on processes that are parameterized in models. As water vapor in the lowermost stratosphere plays a pivotal role in the SWV feedback (accounting for 75% of its effect⁵), further observational efforts to detect changes in this region and in-depth investigation of the underlying mechanisms will be required.

Fig. 5: Model-based estimates for H2O trend over the period 1980–2020.

Panels a–c show WV trends with and without MDVs estimated for the full simulation period (1980–2020) over (a) the entire stratosphere (between the tropopause and 1 hPa), b the lowermost stratosphere (between the tropopause and 100 hPa) and c the stratospheric overworld (between 100 hPa and 1 hPa). The white dots indicate the mean values and the thin and thick bars denote the 95% and 50% confidence intervals, respectively. The dotted lines represent the ranges for trends to reach statistical significance at the 5% level. Annual mean SWV anomalies (∆H₂O) are plotted against the annual and global mean surface warming (∆T) calculated for each year from 1980 to 2020 for d the entire stratosphere, e the lowermost stratosphere, and f the stratospheric overworld. Linear fits are plotted when correlations are significant at the 5% level. The SWV anomalies are annual averages from the monthly H₂O record after removing seasonality and MDV. Global warming is quantified using the global surface temperature record from NASA/GISS.

Discussion and conclusions

Our combined analysis of merged satellite observations and Lagrangian transport model simulations over the last four decades shows evidence that SWV is affected by a robust and substantial MDV. Quasi-synchronous oscillations in tropical tropopause temperature and in the strength of the BDC over the past few decades are critical contributors to the MDV of SWV. In particular, MDVs in SWV are twice as large in the NH as that in SH, associated with the hemispheric asymmetry in the BDC structural changes that modulate CH₄ oxidation.

The external drivers behind alterations in the BDC and long-term variations in tropical tropopause temperatures involve factors such as low-frequency ocean variations and fluctuations in volcanic aerosol. Previous studies have suggested that low-frequency sea surface temperature (SST) variations in the Pacific sector, specifically the Pacific Decadal Oscillation (PDO)^49,50 and Interdecadal Pacific Oscillation (IPO)⁵¹, influence multi-decadal variability in the BDC and tropopause temperatures. The underlying mechanisms proposed in these studies involve increasing SSTs in the tropical central and eastern Pacific (positive IPO and PDO phases), associated with an accelerated BDC and cooler tropical tropopause temperatures. These variations likely contribute to the MDV of SWV, as also indicated in Fig. S8-9. Another external forcing derived from fluctuations in stratospheric volcanic aerosol. Increases in stratospheric volcanic aerosol due to major eruptions (e.g., El Chichon in 1982 and Pinatubo in 1991) as well as several minor NH extratropical volcanic eruptions after 2008 potentially slowed down the deep branch of the BDC^47,52,53, which could contribute to moistening the stratosphere. Note that the 40-year period considered here is not sufficient to draw definitive conclusions regarding the relative roles of fluctuations in the oceanic conditions and the volcanic aerosols in driving the MDV in SWV. Extended observational records and climate modeling studies will be needed to conduct further verification and exploration of the mechanisms involved.

The impact of MDV on the SWV trend calculated for the last four decades is weak. However, the overall SWV trend for 1980–2020 is not statistically significant. Regionally, SWV trends over this period have been negative in the SH lower to the middle stratosphere, near-neutral in the NH lower to the middle stratosphere, weakly positive in the upper stratosphere, and predominantly positive in the lowermost stratosphere. Short-term (1–2 decades) trends in SWV are diminished and typically not statistically significant when MDVs are excluded, emphasizing the necessity to account for these variations when analyzing SWV trends on time spans shorter than three decades. The presence of multi-decadal variability in SWV complicates the detection of long-term anthropogenically-forced changes that are relevant for quantifying surface climate impacts, especially in the near term.

Data and method

SWV records from CLaMS model simulation and SWOOSH merged satellite observations

CLaMS is a state-of-the-art Lagrangian chemical transport model that calculates transport and chemistry along 3D forward trajectories and includes a parameterized representation of atmospheric small-scale mixing processes^54,55,56. To drive the model, we use the newest-generation ERA5 reanalysis⁵⁷, which has been processed according to the methods outlined by Ploeger et al.⁴⁵ Notably, SWV from CLaMS is in excellent agreement with satellite observations³³. The model includes a detailed treatment of water vapor-related chemistry and microphysics, which was described by Tao et al.³²

To validate the simulation, we use the SWOOSH dataset version 2.7, which provides monthly-mean zonal-mean merged water vapor concentrations on isentropic levels at 2.5° intervals in latitude. SWOOSH is an independent long-term SWV record that covers almost 40 years, during which a series of limb profiling satellite instruments have been operated. The homogenization process and the uncertainty of SWOOSH have been described by Davis et al.²³.

We exclude the SWOOSH record during the 1980s from our study due to its relatively poor time coverage. In 1991, the HALOE and UARS MLS instruments were merged into the SWOOSH dataset, improving its coverage (see Supplementary Material for details).

In summary, we use the CLaMS model driven by ERA5 reanalysis to simulate SWV concentrations and validate the simulation results using the independent SWOOSH dataset. The combination of these two datasets provides a comprehensive understanding of the temporal and spatial variability of SWV in the stratosphere.

Decomposition of the contributions to SWV changes

To investigate the contributions to SWV changes, we decompose the amount of water vapor at a given location (r) and time (t) in the stratosphere into its various components:

$${{{\rm{{H}}}_{2}O}}(r,t)={{{\rm{{H}}}_{2}{O}}}_{[{{\rm{entry}}}]}(r,t)+2a(r,t){{{\rm{C{H}}}}}_{4[{{{\rm{entry}}}}]}(r,t)+{{{\rm{{H}}}_{2}{O}}}_{[{{\rm{res}}}]}(r,t),$$

(1)

where H₂O_[entry] is the amount of water vapor entering the stratosphere passively transported to the specified location and time, 2α(r,t)${{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}$ is the amount of water vapor chemically converted from CH₄ oxidation, and H₂O_[res] is the residual amount due to other sources or sinks, such as other troposphere-to-stratosphere transport pathways besides those that contribute to H₂O_[entry] or ${{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}$ or dehydration due to polar stratospheric cloud (PSC) formation. The chemical loss ratio of CH₄ (half of the chemical production ratio of H₂O) can be described by a fractional-release factor (α):

$$\alpha =1-{{{\rm{C{H}}}}}_{4}/{{{\rm{C{H}}}_{4}}}_{\left[{{\rm{entry}}}\right]},$$

(2)

The fractional-release factor has been used to interpret changes in the BDC^12,35. To calculate H₂O_[entry] and ${{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}$, we propagate the monthly means of H₂O and CH₄, around the tropical CPT (390–400 K, 30°S–30°N) with the (model-calculated) age spectrum to a given location (r) and time (t). To calculate the (differential) change of H₂O over a given period, Eq. (1) can be rewritten as¹²:

$$\Delta {{{{\rm{H}}}_{2}O}}=\, \Delta {{{\rm{H}}}_{2}O}_{[{{\rm{entry}}}]}+2\alpha \Delta {{{\rm{C{H}}}_{4}}}_{\left[{{\rm{entry}}}\right]}+2{{{\rm{C{H}}}_{4}}}_{[{{\rm{entry}}}]}\Delta \alpha \\ +\Delta {{{\rm{H}}}_{2}O}_{\left[{{\rm{res}}}\right]}$$

(3)

Here we accordingly disentangle four factors contributing to the variations of SWV: (a) H₂O entering the stratosphere through the CPT then passively transported within the stratosphere ($\Delta$H₂O_[entry]), (b) variations in CH₄ entering the stratosphere transformed to H₂O at a constant rate ($2\alpha \Delta {{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}$), (c) circulation changes that accelerated or decelerated CH₄ oxidation for a constant ${{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}$ ($2{{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}\Delta \alpha$), and (d) changes due to other water vapor sources or sinks (∆H₂O_[res]).

Note that the terms ∆H₂O_[entry] and $2{{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}\Delta \alpha$ both reflect responses to changes in the BDC. Specifically, ∆H₂O_[entry] represents variations in H₂O_[entry] within a time window in the past, defined by the transit time from the CPT to specific stratospheric locations. In contrast, $2{{{{\rm{CH}}}}}_{{4}_{[{{{\rm{entry}}}}]}}\Delta \alpha$ results exclusively from changes in the BDC and therefore directly reflects the changes in BDC structure. Taken together, these four factors allow us to decompose the contributions of different processes to variations in SWV.

Identification and relevant statistics of MDV

To assess the significance of MDVs, we employ bootstrapping against the corresponding red-noise spectrum. We generate a large number (N = 100,000) of surrogate red-noise timeseries with the same lag-one autocorrelation as the original timeseries. Subsequently, we compute the 90% and 95% confidence intervals for the red-noise spectrum as thresholds, i.e., p = 0.1 and p = 0.05. If any peak in the original power spectrum within the 20–30-year period exceeds the red-noise threshold, the MDV is deemed significant at that level. The power spectra and their corresponding red-noise spectra for the timeseries in Fig. 1a–e are depicted in Fig. S5.

The MDVs in our study are extracted from simulated zonal and monthly mean H₂O records as one low-frequency mode (6th mode) using Ensemble EEMD³⁶ (more details at Fig. S3 and Fig. S4). The resulting MDV time series enables us to identify wet and dry decades.

The strength of MDV is quantified using two metrics: amplitude (in ppmv) and variance contribution (in percentage). The amplitude of MDV is calculated as $(\overline{{{\rm{wet}}}}-\overline{{{\mbox{dry}}}})/2$, where $\overline{{{\mbox{wet}}}}$ and $\overline{{{\mbox{dry}}}}$ are the mean deseasonalized anomalies over the wet and dry periods, respectively. The variance contribution of MDV is calculated as the variance power of MDV divided by the total power of interannual variability (${\sigma }_{{{{\rm{MDV}}}}}^{2}/{\sigma }^{2}$).

Trends with and without the MDV and significance tests

To investigate the influence of MDVs on the water vapor trends over the past four decades, it is necessary to eliminate the MDV signal from the water vapor anomalies. For CLaMS simulation spanning 40 years, water vapor anomalies without MDV (∆H₂O^‘) are derived by removing the low-frequency mode (6th mode using EEMD) from the deseasonalized water vapor anomaly time series. For water vapor from the merged satellite-dataset SWOOSH, the length of the time series is typically less than 30 years, in which case the low-frequency mode using EEMD cannot adequately represent the MDV signals (see Fig. S10 and Supplementary Note). Therefore, we use an alternative approach for the SWOOSH dataset, applying a first-order band-pass Butterworth filter with cutoffs at 20 years and 30 years to ∆H₂O to isolate the MDV signals.

Least-squares linear trends are then calculated for the water vapor anomalies with (∆H₂O) and without MDVs (∆H₂O^‘), respectively. Student’s t-test is employed to assess the significance of all trends after accounting for autocorrelation of linear regression residuals. Potential autocorrelation reduces the number of independent degrees of freedom, thereby ensuring that the significance tests are not too liberal⁵⁸. Trends based on simulated ∆H₂O after removing MDVs estimated using a band-pass filter instead of EEMD show similar results (Fig. S11).