Abstract
Satellite remote sensing is becoming a widely used monitoring technique in coastal sciences. Yet, no benchmarking studies exist that compare the performance of popular satellite-derived shoreline mapping algorithms against standardized sets of inputs and validation data. Here we present a new benchmarking framework to evaluate the accuracy of shoreline change observations extracted from publicly available satellite imagery (Landsat and Sentinel-2). Accuracy and precision of five established shoreline mapping algorithms are evaluated at four sandy beaches with varying geologic and oceanographic conditions. Comparisons against long-term in situ beach surveys reveal that all algorithms provide horizontal accuracy on the order of 10 m at microtidal sites. However, accuracy deteriorates as the tidal range increases, to more than 20 m for a high-energy macrotidal beach (Truc Vert, France) with complex foreshore morphology. The goal of this open-source, collaborative benchmarking framework is to identify areas of improvement for present algorithms, while providing a stepping stone for testing future developments, and ensuring reproducibility of methods across various research groups and applications.
Similar content being viewed by others
Introduction
Sandy beaches are dynamic natural landscapes that undergo rapid changes in response to environmental conditions. Waves, tides, nearshore currents, and winds stir and transport the unconsolidated sediment of sandy coasts, continuously reshaping foreshore topography and bathymetry1,2. Present-day and future coastal management relies on the ability to repeatedly observe, quantify, and predict the changing position of the shoreline3. Although in situ monitoring techniques can provide highly accurate measurements of shoreline position, long-term coastal monitoring programs – which predominantly exist along developed coasts in North America, Europe, Australia, and Japan – remain scarce and limited in geographic extent4,5,6,7,8.
Earth-observing satellites have been capturing regular images of the world’s coastlines over the past four decades. Over the past five years, there has been a rapidly growing scientific interest in the development of remote sensing methods to map historical shoreline positions from satellite imagery. To illustrate this rapidly growing interest, Fig. 1a displays the number of publications and citations per year that include both “shoreline” and “satellite” as keywords (database: Web of Science). Since 2018, there has been a steep increase in the number of publications on satellite-derived shorelines as the field has started to leverage satellite imagery to analyze coastal systems at unprecedented regional to global scales9,10,11,12,13. As for other Earth Science disciplines, the use of satellite remote sensing was facilitated by the advent of Google Earth Engine (GEE)14 in 2017, a free cloud-based geospatial analysis platform. The field’s rapid progress has come in the form of approximately 40 new remote sensing algorithms that map shorelines from multispectral satellite imagery15. While these algorithms differ in their approach, they all produce similar observations in the form of time-series of shoreline change for sandy beaches. In fact, extracting satellite-derived shorelines (SDS) at sites of interest is now considered common practice in the investigation of coastal hazards by government agencies, coastal engineers/consultants, and researchers alike. As satellite remote sensing is becoming an increasingly established monitoring technique in coastal sciences16, it is now essential to benchmark the accuracy of satellite-derived shoreline observations across different methods and coastal environments.
a Number of publications and citations per year for articles that include keywords “satellite” and “shoreline.” This was retrieved from the Web of Science database with the following query: TI = (“satellite*“ AND “shoreline*“) OR AB = (“satellite*“ AND “shoreline*“) OR AK = (“satellite*“ AND “shoreline*“), where TI stands for Title, AB for Abstracts and AK for Author’s Keywords. b Present methods to automatically map shorelines on optical imagery, divided into ‘at pixel resolution’ and ‘sub-pixel resolution.’ This figure was adapted from16. The references in bold are evaluated in this study.
A variety of satellite-based shoreline detection methods are presently available. To extract shoreline observations from satellite imagery, many established SDS algorithms employ different image processing methods, including contouring of a land/water threshold12,17,18,19; maximum-gradient contouring methods20,21,22; and soft classification techniques23,24,25. These methods can also be divided into ‘at pixel resolution’ and ‘sub-pixel resolution,’, where ‘at pixel resolution’ methods tend to create a stair-cased waterline, while sub-pixel methods integrate the information of neighboring pixels to obtain a smoother contour by using, for example, the Marching Squares algorithm26. Figure 1b summarizes the breadth of SDS methods developed in previous literature. While most methods map the instantaneous shoreline on individual satellite images, some studies have used composite imagery9,12,19,27, where multiple images of the same beach taken at different times are stacked and averaged within a time window (e.g., a year). Further, many of these methods leverage advances in cloud data platforms14 to efficiently access and interrogate the archives of publicly available satellite imagery9,12,17,19.
Benchmarking consists of comparing the performance of various methods against a standard set of input data, validation data, and evaluation metrics. Benchmarking helps researchers compare the accuracy of their methods, identify areas for improvement, provide a platform for testing future developments, and promote a culture of transparency and sharing in method development and evaluation. One example of successful benchmarking in climate science is the Coupled Model Intercomparison Project (CMIP), which provides a framework for evaluating the performance and robustness of global climate models28,29. Examples in coastal science include the benchmarking of shoreline detection models using ground-based camera systems30 and the more recent Shoreshop, a blind testing of shoreline evolution models31.
In this study, a benchmarking framework was developed to test the accuracy of time-series of satellite-derived shoreline observations obtained from publicly available Landsat and Sentinel-2 imagery against in situ surveys. Four diverse, well-monitored sandy beaches, namely Narrabeen (Australia)4, Duck (USA)32, Torrey Pines (USA)7, and Truc Vert (France)6 were selected to evaluate 5 different established SDS algorithms, namely CoastSat17, SHOREX33, ShorelineMonitor9, CASSIE19, and HighTide-SDS27. The current paper and its accompanying software focus on the accuracy assessment of SDS algorithms against a set of benchmark datasets and provides an open-source, publicly available, and fully reproducible methodology to test state-of-the-art and future developments in SDS workflows. The results from this benchmarking study can help answer key research questions:
-
(i)
Establish a standard evaluation of SDS methods: how do different SDS algorithms perform across a wide range of coastal settings, from low-energy microtidal to high-energy meso/macrotidal?
-
(ii)
Identify areas for improvement based on the current limitations of SDS methods: what are the accuracy hurdles that future efforts should seek to overcome (e.g., co-registration of the satellite images, water-level corrections, shoreline-delineation methods)?
Data and methods
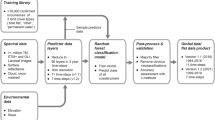
In this study, four benchmark sites are used to assess the ability of five different SDS algorithms to accurately monitor sandy beaches. The methodology developed to assess the accuracy of SDS observations is presented in the flowchart in Fig. 2. The four sandy beaches of this benchmarking study were selected based on the availability of long-term in situ coastal monitoring datasets that were publicly available. The beach characteristics and location of each site are presented in Table 1 and Fig. 3. Duck, North Carolina, United States, is a microtidal beach, mean spring tidal range (MSTR) of 1.4 m, located on a barrier island and has been monitored on a monthly to fortnightly basis since 197432. Narrabeen, New South Wales, Australia, is a microtidal beach (MSTR of 1.7 m) located on the east coast of Australia where beach surveys have been conducted monthly to fortnightly since 19764,34. Torrey Pines, located in southern California, United States, is a micro- to mesotidal (MSTR of 2.3 m) ocean beach that has been surveyed since 20017. Finally, Truc Vert, (Nouvelle-Aquitaine), France, is a meso- to macrotidal beach (MSTR of 3.2 m) located in the southwest of France which has been surveyed fortnightly since 20046. Among all the cross-shore transects that are surveyed at each of the respective sites, a subset of 4–5 shore-normal transects with the highest frequency of surveys were selected for the assessment. For each site, the required inputs for SDS detection were provided to the teams of developers: (1) a polygon defining the region of interest; (2) a set of cross-shore transects; (3) a beach-face slope value; and (4) time-series of tide levels (from the FES2014 global tide model35) and wave parameters (from the ERA5 reanalysis36). This guarantees that there is no user bias associated with the data sources or the post-processing corrections. The five SDS algorithms evaluated in this study are described in Table 2 (see Methods for a detailed description of each algorithm). All algorithms are fully automated with no manual user intervention, except for SHOREX, which pre-selects images using a manually supervised method to identify the images that are suitable for shoreline mapping and co-registration (see “Methods” section). The Mean Sea Level (MSL) contour was chosen to evaluate the SDS time-series as it is the common proxy for most of the algorithms, although we acknowledge that HighTide-SDS was optimized to match a high tide contour rather than MSL (Table 2).
A Description of the four sites with long-term shoreline change datasets used as benchmarks. B The five SDS algorithms evaluated in this study and their outputs. C The evaluation methodology; all algorithms were evaluated against the groundtruth observations of the MSL contour. CoastSat, SHOREX and CASSIE provide instantaneous shorelines from individual satellite images for which we could compare the Landsat and Sentinel-2 accuracies as well as the effect of wave setup corrections. The full methodology and benchmarking software are publicly available at https://github.com/SatelliteShorelines/SDS_Benchmark.
Results
Time-series of the Mean Sea Level contour
We compare the five SDS algorithms time-series of shoreline change derived from Landsat imagery against shorelines extracted from topographic survey data of the MSL elevation contour. The three instantaneous shoreline time-series are tidally corrected, whereas the compositing methods assume that tidal variations are averaged out over the stack of images (Fig. 2). No wave setup correction is included at this analysis stage. Figure 4 shows SDS time-series generated by each algorithm at a single transect for each site. The accuracy assessment between SDS and surveyed shorelines across all transects for each site is presented in Fig. 5a. Accuracy metrics, including standard deviation error (STD), mean bias, root mean square errors (RMSE), and coefficient of determination (R2), are reported in Table 3. At Duck and Narrabeen, all algorithms skillfully capture interannual to seasonal shoreline changes, while the accuracy of the SDS time-series decreases at Torrey Pines and drops significantly at Truc Vert. Since HighTide-SDS maps yearly shorelines, which are mainly useful for estimating long-term trends but not for estimating interannual to seasonal variability, it was excluded from this first assessment but is used later to evaluate long-term trends of coastal change along each transect (in the ‘Long-term trends’ section). Also, HighTide-SDS is optimized to map the high tide shoreline position; therefore, a landward bias is expected when benchmarking it at MSL. On the other hand, the ShorelineMonitor time-series are also derived from yearly composites but are optimized to match the MSL contour and are processed with a rolling monthly window. Consequently, the ShorelineMonitor time-series have the most data as they consistently map one shoreline per month (see number of samples in Table 3). In summary, there is a variety in performance of individual algorithms at individual sites, but no one algorithm is more accurate than all others in every situation. Further, there appears to be a greater variability between sites than between algorithms (Fig. 5).
a Duck (transect 1097), (b) Narrabeen (PF8), (c) Torrey Pines (PF525), (d) Truc Vert (transect −400). The in situ data are shown in black while the SDS time-series from each algorithm are color-coded according to the legend. Note that the y-axis limits are larger for Truc Vert to accommodate its larger variations in shoreline position.
a Boxplots showing the horizontal error distributions for each SDS algorithm at each benchmark site across the selected transects. The value of the median bias is indicated and the whiskers are set at 1.5 times the inter-quartile range. Positive (negative) errors indicate a seaward (landward) bias. The error metrics describing each distribution are presented in Table 3. Note that the y-axis limits are increased for Truc Vert to accommodate its larger errors. b Coefficient of determination (R2) for each algorithm at each site. The surveyed MSL contour was used to evaluate the SDS time-series.
At Duck, all algorithms (excluding HighTide-SDS) achieved an RMSE below 10 m, and SHOREX was the algorithm that best captured the variability in the shoreline position with a standard deviation error (STD) of 6.9 m, followed by ShorelineMonitor (STD 7.9 m), CoastSat (STD 8.2 m), and CASSIE (STD 8.9 m). The coefficient of determination (R2), depicted in Fig. 5b, is around 0.5–0.6 for all four algorithms, with a maximum of 0.58 for SHOREX and CASSIE. It is also observed that all the algorithms could resolve the step-change in shoreline position resulting from the beach nourishment that occurred at Duck in 201737 (Fig. 4a). A relatively small landward bias is present in the SHOREX (−4.8 m) and CoastSat (−4.2 m) time-series, while there is no substantial bias for CASSIE (−1.7 m) and ShorelineMonitor (−0.7 m).
At Narrabeen, all four algorithms resolved the site’s interannual variability, while CoastSat, SHOREX and CASSIE were also able to capture the strong seasonality present at PF8 between 2014–2020, as apparent in Fig. 4b. This is reflected by the relatively high R2 values for CoastSat (0.70), SHOREX (0.56), and CASSIE (0.70). At this site, the lowest STD error was achieved by CoastSat (8.3 m) followed by CASSIE (8.6 m), SHOREX (9.8 m), and ShorelineMonitor (10.2 m). The mean biases were of the same magnitude of the ones observed at Duck, with SHOREX (5.6 m), and CASSIE (6.5 m), showing a seaward bias at this site, while CoastSat maintained a slight landward bias (−3.0 m), and the ShorelineMonitor time-series were again unbiased (−0.5 m). Unbiased shoreline time-series are well suited for applications in which the absolute position of the shoreline is important (e.g., coastal hazard risk to fixed assets like roads and buildings).
The horizontal accuracy of the SDS algorithms deteriorates at Torrey Pines (MSTR of 2.3 m), with the RMSE of the various algorithms going from ~10 m at Duck and Narrabeen to 15–20 m, a notable 50–100% increase. The lowest STD error at Torrey Pines was 12.5 m for CoastSat, followed by ShorelineMonitor (13.7 m), SHOREX (15.5 m), and CASSIE (17.2 m). At this site, all the time-series show a landward (negative) bias between −2.3 m (CoastSat) and −8.2 m (ShorelineMonitor). This offset is discussed further in the section ‘Wave setup correction.’ Remarkably, the sharp retreat of the shoreline, resulting from the cluster of storms associated with the El Nino 2015/201638, is captured well by all the algorithms as shown in Fig. 4c.
At Truc Vert (MSTR 3.2 m), the horizontal accuracy of the SDS time-series (Fig. 4d) drops considerably and none of the algorithms can suitably resolve the marked seasonal signal nor the interannual shoreline variability exhibited at this site39. The lowest STD error at Truc Vert is 20.1 m for ShorelineMonitor, followed by CoastSat and SHOREX at 25.2 m and CASSIE at 48.3 m. Large landward biases are also observed, −12.0, −27.3, and −32.0 m for CoastSat, SHOREX, and ShorelineMonitor, respectively, with the exception of CASSIE, which is almost unbiased (2.9 m). It is important to note that when applying a tidal correction at Truc Vert, the shorelines mapped on images with a tidal elevation below +0.2 AMSL (based on40) were discarded, as this beach features a complex intertidal zone and instantaneous waterlines mapped on low tide images were not found to be a good proxy of the shoreline position. Additionally, the SDS produced as part of this benchmark are not comparable to the SDS time-series generated by Castelle et al.40 at this same site with CoastSat, as site-specific pre-processing (selection of images based on visual inspection) and post-processing (alongshore averaging and wave runup correction) steps were applied to achieve a much higher accuracy (RMSE of 10 m, 7 m bias and R2 of 0.78).
Long-term trends
Long-term linear trends in shoreline position estimated from each SDS algorithm were compared to long-term trends estimated using in situ data. The trends were estimated on seasonal averages of the time-series for the common period between the SDS and the surveys to make the temporal resolution uniform and avoid biases due to the varying temporal resolution in the satellite record (see Methods for more details). The comparison along the selected transects is shown in Fig. 6. At Duck (Fig. 6a), all five algorithms, including HighTide-SDS, are capable of accurately estimating the long-term trends along the cross-shore transects, clearly replicating the positive trend in the south and negative trend in the north. At Narrabeen (Fig. 6b), the beach is long-term stable, and this is correctly identified by all algorithms. At Torrey Pines (Fig. 6c), the negative trend (approx. -1m/year) observed at the northern end (PF585 and PF595) is captured by all the algorithms. However, the slightly positive trend (~0.3 m/year) observed at the southern end (PF525 and PF535) is only captured by three algorithms (CoastSat, ShorelineMonitor, and HighTide-SDS), with CASSIE significantly over-estimating the positive trend (>1 m/year) and SHOREX indicating a slightly negative trend. At Truc Vert (Fig. 6d), CASSIE is the only algorithm that could consistently estimate a positive trend, although it over- and underestimates the magnitudes, while the other algorithms fail to estimate the sign of the trend along all 4 transects.
The long-term trends estimated from the SDS time-series are compared to the trends estimated from the in situ time series over the common period at the four benchmark sites: (a) Duck; (b) Narrabeen; (c) Torrey Pines; and (d) Truc Vert. The trends were estimated on seasonal averages of the time series to ensure a homogeneous temporal resolution.
Landsat vs Sentinel-2
While the previous analysis focused on Landsat-derived shorelines, we also test the accuracy of shorelines mapped from Sentinel-2 imagery using the 7 years of available imagery (since it was first launched in 2015). This assessment provides new insights on the precision and accuracy of the two satellite missions, noting Landsat imagery has a resolution of 30 m/pixel (with a 15 m/pixel panchromatic band available since Landsat 7) while Sentinel-2 has a resolution of 10 m/pixel. Three of the five algorithms are capable of mapping shorelines from individual Sentinel-2 images, namely CoastSat, SHOREX, and CASSIE (see Table 2). The instantaneous shorelines were tidally corrected to MSL and compared to the MSL time-series extracted from the in situ topographic data. Boxplots of the horizontal errors for both satellite missions are shown in Fig. 7a, while the accuracy metrics are reported in Table 4. Note that the number of samples used to compute the error metrics is about 5 times larger for Landsat than Sentinel-2 based on the longer duration of the Landsat mission, and at Torrey Pines only 1 year of data could be compared as the publicly archived survey data ends in 2017.
a The SDS time-series for the 3 algorithms that use individual satellite images were used to compare the accuracy of the shorelines derived on Landsat and Sentinel-2 images. The full and hatched boxplots show the horizontal errors associated with the Landsat and Sentinel-2 time-series, respectively, for the 3 instantaneous shoreline algorithms (CoastSat, SHOREX, CASSIE). At Torrey Pines, as the ground truth data only spans to the end of 2016, only 1 year of Sentinel-2 data could be evaluated. The value of the median is indicated, and the whiskers are set at 1.5xIQR. Note that the y-axis was stretched for Truc Vert to accommodate for the larger errors. b A wave setup correction, based on Stockdon et al.41, was applied to the Landsat tidally corrected SDS time-series. The full and hatched boxplots show the horizontal errors associated with the tide-only and tide + wave setup time-series, respectively, for the 3 instantaneous shoreline algorithms (CoastSat, SHOREX, CASSIE). The error metrics describing the distributions in a and b are presented in Tables 4 and 5, respectively.
At Duck, the Sentinel-2 time-series show slightly lower accuracy than the Landsat time-series, with STD errors of 9.7, 6.9, and 9.4 m for CoastSat, SHOREX, and CASSIE, respectively, compared to 8.2, 6.9, and 9.0 m for Landsat, which is perhaps unexpected given the higher resolution of Sentinel-2 imagery. The biases in the time-series are similar for both satellites, apart from SHOREX, where a larger landward bias is observed in the Sentinel-2 data (−12.0 m versus −4.8 m on Landsat). At Narrabeen, the accuracy of the Sentinel-2 time-series increases considerably only for SHOREX, from an STD error of 9.8 m (Landsat) to just 5.8 m (Sentinel-2), while it remains the same for CoastSat and CASSIE (8.0 and 9.6 m, respectively). In terms of biases, both CoastSat and SHOREX display seaward shifts, of 4.7 and 8 m, in shoreline position between Landsat and Sentinel-2 time-series, respectively. While we cannot isolate the source of this seaward bias between Landsat and Sentinel-2, it could be a result of the higher resolution of Sentinel-2 images, allowing the shallow water region adjacent to the shoreline to exhibit stronger reflectance in the near-infrared band, which consequently pushes the detected waterline farther seaward. At Torrey Pines (limited Sentinel-2 data available) and Truc Vert, the overall accuracy and precision does not improve with the increased resolution provided by Sentinel-2.
Wave setup correction
One of the sources of error in satellite-derived shorelines is the effect of oscillating water levels on the position of the waterline. Time-series of shoreline position (typically based on the instantaneous waterline position) derived from imagery are affected by tide as well as wave setup and wave runup (i.e., the horizontal excursion of swash). Runup is an oscillatory motion of the waterline driven by the landward propagation of breaking waves and it generally cannot be corrected for on individual satellite images as the phase of specific waves is not known at the instant the image was taken. However, wave setup, the persistent elevation of nearshore water levels in the presence of breaking waves, can be corrected for using a method analogous to tide correction (i.e., converting a vertical offset into a horizontal one by assuming a beach slope, see Eqs. 1–2 in the Methods). Here we include wave setup correction to investigate if it improves the accuracy of the SHOREX, CASSIE, and CoastSat instantaneous shorelines. The SDS time-series at each site were corrected using the empirical parameterization of wave setup by Stockdon et al.41. Hindcasted wave data (needed to calculate wave setup in Eq. 3) were obtained from the closest offshore ERA-5 grid point. Figure 7b compares the error distributions for the SDS corrected for tide-only and tide-and-wave-setup. The accuracy metrics are reported in Table 5. The wave setup correction always shifts the satellite-derived shorelines seawards, and the calculated average correction (horizontally) is 3 m at Duck, 4.5 m at Narrabeen, 6 m at Torrey Pines, and 5 m at Truc Vert, as reported in Table 5.
The effect of wave-setup correction on the accuracy of the SDS time-series is mixed. At Duck, it greatly improved the RMSE of the time-series for CoastSat (from 9.2 to 7.6 m) and SHOREX (from 8.4 to 6.8 m), as it contributed to remove the ~5 m landward bias that was present in these time-series. At Narrabeen, however, SHOREX and CASSIE already had a seaward bias in the time-series, so adding the wave setup correction exacerbates that bias (from ~5 to ~10 m) and increases the overall RMSE for those algorithms. CoastSat, on the other hand, had a landward bias so the wave setup correction helps to remove that bias (from −3 to 1.6 m). At Torrey Pines, the wave setup correction mitigates the existing landward biases in the SDS time-series, especially for SHOREX and CASSIE, and improves the absolute accuracy of the time-series. At Truc Vert the wave-setup term also helps to reduce the existing landward bias, although a large bias remains for SHOREX (−19 m).
Discussion
State of the art of SDS
As satellites continue to revolutionize coastal science16,42, benchmarking becomes an essential tool for evaluating state-of-the-art capabilities of SDS algorithms. This collaborative benchmarking effort demonstrates that shoreline change time-series with a horizontal accuracy of approximately 10 m (1/3 of a pixel) can be automatically extracted from publicly available Landsat imagery with a variety of algorithms along microtidal wave-dominated sandy beaches like Duck and Narrabeen. However, in line with recent studies, the benchmarking reveals that the accuracy of the SDS deteriorates sharply when applied in meso- to macrotidal coastal environments. Across the SDS algorithms, the horizontal errors are observed to increase by ~50% at Torrey Pines (RMSE between 13 and 18 m) and more than 100% at Truc Vert (RMSE between 28 and 48 m). The breadth of shoreline changes that can be captured with such horizontal accuracy depends on the magnitudes of shoreline variability that are present at the site of interest. To illustrate this point, Fig. 8 compares the average SDS horizontal accuracy (reported in Table 3) to the absolute shoreline changes observed by in situ surveys at the 4 benchmark sites. While the reported SDS horizontal accuracy is the highest at Duck, the relatively small magnitudes of shoreline changes at this site mean that only a small portion of ‘actual’ shoreline changes can be captured (32%, Fig. 8a). In contrast, microtidal sites that exhibit large magnitudes of shoreline change (e.g., Narrabeen), represent an ideal environment for SDS applications as they combine a favorable SDS accuracy with a strong shoreline variability. Accordingly, 55% of shoreline changes are detectable at Narrabeen with an average SDS accuracy of 9.7 m (Fig. 8b). At Torrey Pines, 41% of shoreline variability is detectable with an accuracy of 13.4 m (Fig. 8c). In light of this, SDS time-series with 10 m accuracy along wave-dominated microtidal beaches, can be used to capture shoreline changes at a wide range of temporal scales that are of interest to coastal scientists, engineers, and managers. This includes seasonal changes37,43,44, interannual variability13,21,45,46,47, and long-term trends9,11,12,27, as identified by previous studies using individual algorithms.
a Duck; (b) Narrabeen; (c) Torrey Pines; (d) Truc Vert. The histogram shows the absolute shoreline positions based on the in situ surveys along the selected transects at each study site. The vertical lines indicate the respective standard deviation error averaged across the 5 SDS algorithms. The portion of shoreline changes that are larger than the SDS horizontal accuracy is indicated as a percentage in the text box: 32% at Duck, 55% at Narrabeen, 41% at Torrey Pines and 18% at Truc Vert.
The current benchmarking study, however, highlights that automatically extracting SDS along high-energy meso- to macrotidal coasts remains a challenge. In fact, Fig. 8d indicates that at Truc Vert only 18% of shoreline change observations fall beyond the 28 m horizontal accuracy, meaning that most of the shoreline variability at this site is drowned in the noise of the SDS time-series. As a consequence, even existing long-term trends at these meso- to macrotidal sites may not be captured by the satellite observations. The fact that long-term trends estimated from SDS can be unreliable in complex, macrotidal environments (by sometimes indicating a positive trend where there is a negative trend as shown in Fig. 6d) should warrant caution when applying today’s SDS algorithms to such environments. Global applications of SDS that are mapping long-term trends for the world’s coastlines9,10,27 might address the unreliability of long-term trend estimates along meso- to macrotidal coasts (as also pointed out by ref. 40) by flagging certain coastlines in question, citing benchmarking studies, or providing accuracy disclaimers — at least until new developments in SDS algorithms enable us to address the potential unreliability issue. It is of critical importance that coastal engineers and scientists are aware of these issues because the SDS and the long-term trends derived thereof play a key role in developing sustainable strategies for coastal management in the 21st century42,48.
Sources of SDS errors
Systematic and random errors in the SDS time-series can come from four main sources: georeferencing of the satellite images, image resolution, waterline-detection method, water-level correction.
The georeferencing accuracy of each Landsat image is calculated by the data provider49, using a database of ground-control points and the RMSE is provided in the image metadata. Hence, it is good practice to mitigate the effect of georeferencing errors by discarding the images with a RMSE larger than 10 m. This issue is more problematic for Sentinel-2 images as only a ‘pass/fail’ geometric quality flag is present in the image metadata, with ‘fail’ indicating that the RMSE is larger than 20 m50. Based on this information, it is generally not possible to exclude images with georeferencing errors of less than, but close to, 20 meters, which we consider to be a relatively high threshold when tracking shoreline changes. Out of the five SDS algorithms evaluated in this study, SHOREX is the only one that includes an image co-registration step, which seeks to enhance the absolute geolocation accuracy by fitting all images to a high-resolution orthophoto with overlapping coverage51. SHOREX also happens to be producing the most accurate Sentinel-2 time-series with an STD error of 6.9 and 5.8 m at Duck and Narrabeen, respectively (reported in Table 4), which significantly outperforms CoastSat and CASSIE. This enhanced accuracy indicates that image co-registration is an important component to mitigate georeferencing errors and improve the accuracy of shoreline time-series derived from Sentinel-2.
Image resolution determines the size of the smallest object that can be distinguished in an image. Hence, the medium resolution (10–30 m/pixel) of the Landsat and Sentinel-2 images limits the horizontal accuracy with which spatial features can be extracted. Nonetheless, the effect of image resolution can be reduced by employing sub-pixel resolution techniques, which are well suited to linear features like the shoreline. This point is evidenced by the sub-pixel accuracies, RMSE of ~10 m (1/3 of a pixel) that were obtained at Duck and Narrabeen using Landsat imagery (Table 3). While advancements in satellite technology (e.g., cubesats) in the realm of commercial satellite providers are now capable of capturing near-daily high-resolution imagery (1–5 m/pixel), it should be noted that sub-pixel accuracies may not be guaranteed at these higher resolutions. In fact, a recent study52 applied similar sub-pixel resolution shoreline mapping methods on 3 m/pixel PlanetScope imagery and obtained an RMSE of ~5 m at Narrabeen and Duck. This indicates that other sources of errors may potentially be the limiting factors and offset the realized gains in image resolution.
Another source of error in SDS algorithms is associated with the detection of the waterline position on medium-resolution satellite images. SDS algorithms vary substantially in the way they map the waterline, as described in the Methods. Firstly, the input imagery differs between algorithms, with CoastSat, SHOREX, and ShorelineMonitor using top-of-atmosphere (TOA) reflectance, while CASSIE and HighTide-SDS use surface reflectance (SR). SR images provide a higher level of processing in which TOA images are atmospherically corrected using radiative transfer models53. This correction improves the radiometric accuracy of the images; however, it comes at the cost of losing temporal depth as suitable atmospheric correction data are usually not available for all TOA images. This is reflected in the 50% reduction in the number of shorelines mapped by CASSIE compared to CoastSat and SHOREX as indicated in Table 3. Further, ShorelineMonitor and HighTide-SDS do not use the individual images but generate yearly composites using, respectively, the 15th and 10th percentile of the stacked pixel values (these low percentiles are chosen to mitigate the effect of clouds, which are bright pixels). The multispectral index selected to differentiate land from water also varies, with each algorithm using a different combination of bands. ShorelineMonitor and CASSIE use the Normalized Difference Water Index (NDWI, normalized difference between NIR and Green), CoastSat uses the modified-NDWI (normalized difference between SWIR1 and Green), HighTide-SDS uses the Automated Water Extraction Index (AWEI), while SHOREX use both the AWEI and short-wave infrared band (SWIR1). To add to that, based on the selected spectral index, different methods are employed to define the waterline, with HighTide-SDS applying a fixed 0 threshold, CASSIE using a multi-level Otsu threshold, CoastSat using a sand/water optimized Otsu threshold, ShorelineMonitor using a region growing algorithm and SHOREX using inflection points of a fitted 3D polynomial function. Clearly, the resulting waterlines will generally not represent the same visibly discernible feature3, as evidenced by the range of landward/seaward biases that are observed across the algorithms (see Table 3). For instance, at Narrabeen, the mean bias varies between −3 and 6.5 m across the algorithms. In the SHOREX time-series, a noticeable bias is even observable between sensors (Landsat and Sentinel-2) at these two sites (Fig. 7a). Since TOA reflectance values are calibrated across sensors54, this difference in bias could potentially be attributed to the distinct image resolution. The finding that distinct image processing algorithms are picking different shoreline proxies is not new, as it was also shown in another comparative study30 in which four algorithms mapping shoreline on oblique images captured by terrestrial cameras55 were evaluated at United States, Dutch, United Kingdom, and Australian sites.
The effect of instantaneous and localized water levels on the position of the waterline is currently a major obstacle to improving the accuracy of SDS time-series. Applying a tidal correction to the SDS time series has proved to be a key step, and it can now be done without any in situ information using a global tide model35 and a satellite-derived estimate of the beach slope56. Another water level adjustment that is physically justifiable is correcting for wave effects by including a wave setup term. In this assessment, the results indicate that while the wave setup correction reduced the landward bias at Duck and Torrey Pines, it introduced a seaward bias at Narrabeen for two of the algorithms (SHOREX and CASSIE). There are many plausible explanations for this, including different shoreline proxies captured by the algorithms and the fact that Narrabeen is the only fully embayed beach in this study, and as a result the offshore wave conditions may not reflect the wave heights in the surf zone or near the shoreline. Several recent studies have evaluated SDS at high-energy mesotidal beaches and found that correcting for wave setup/runup could improve the accuracy and precision of the time-series57: applied a slope-independent wave setup parametrization (\(0.016\sqrt{{H}_{0}{L}_{0}}\))41 to CoastSat SDS time-series at Ocean Beach, San Francisco58; applied a wave runup parametrization (\(0.58{H}_{0}\xi +0.46\))59 to SHOREX SDS time-series at Faro beach, Portugal; and40 used an even different slope-independent wave setup formulation (\(2.14\tanh 0.4{H}_{0}\))60 at Truc Vert, France. This shows that there is no one-size-fits-all solution and more research is needed to identify how to optimally apply wave corrections across different coastal environments and beach morphologies. The larger errors observed along high-energy meso- to macrotidal coasts have been previously identified at Truc Vert37,40 and Perranporth (UK)61 are associated with the complexity of the intertidal topography which strongly influences the position of the instantaneous waterline. Given that the shoreline proxy mapped on the images (i.e., instantaneous water line) has been identified as the main source of error in these meso- to macrotidal environments, we call for greater research on the use of alternative shoreline proxies, like the wet/dry sand interface, which may provide a more stable indicator of the shoreline position. High tide-SDS has already taken a step in that direction by using a lower percentile to create the image composites (10th percentile versus 15th percentile in the ShorelineMonitor) to shift the shoreline proxy towards a high tide mark, which has shown to be more suitable to capture shoreline changes along tropical tide-dominated coastlines (e.g., tidal flats, mangrove coastlines).
Benchmark for future developments
Three key areas of improvement are identified based on the analysis of the sources of errors:
-
(i)
the implementation of automated image (co)registration to reduce SDS errors related with the georeferencing of the images.
-
(ii)
the development of alternative shoreline proxies for meso- to macrotidal coastal environments, which are visibly discernible and can potentially be mapped automatically, like the wet/dry line or high tide mark.
-
(iii)
continue investigating the influence of tidal levels and wave runup on SDS accuracy and formulate generalized water level corrections based on available datasets at global scales.
As new algorithms and enhancements to existing algorithms are developed, this benchmarking framework provides a transparent and reproducible methodology for accuracy evaluation and algorithm inter-comparison with sets of standardized inputs and validation datasets. The open-source platform also promotes collaboration over theoretical concepts, implementation software, and supporting datasets, ensuring that research is conducted effectively and efficiently. As many fields of science are confronted with a ‘reproducibility crisis,’62 in part related to the poor metadata and data publishing practices and the rapid pace of progress in machine learning and predictive modeling63, there is a critical need for more reproducible benchmarking frameworks that enable objective assessments using transparent methodologies on standardized input data. According to a Nature survey64, 70% of researchers have tried and failed to reproduce another scientist’s published work, while 50% have failed to reproduce their own work. Given these circumstances, a standard procedure to evaluate the accuracy of satellite-derived shorelines is key to achieving improvements in shoreline mapping algorithms. Not only will it provide a testbench for new features accessible to all developers, but it will also enable researchers to have a standard set of metrics used for reporting the accuracy of SDS time-series to the coastal community and its end users (e.g., coastal scientists, managers, and engineers). For instance, there have been many new developments in this space only in the last couple of years, including the use of increasingly high-resolution satellite imagery (e.g., 3 m/pixel PlanetScope imagery52), the development of automated co-registration65 algorithms, and the use of deep learning to automatically detect the shoreline position66,67. In this context of rapid development and innovation, this benchmarking framework will help test how these new developments are improving the accuracy, precision, and reliability of satellite-derived shorelines. While the four benchmark sites presented here are a starting point, additional sites where beach surveys are available, such as Moruya, Australia68, Ocean Beach, United States69, Tairua, New Zealand70, Hasaki, Japan71, Perranporth and Slapton Sands, United Kingdom72,73, Noordwijk, the Netherlands74, Porsmilin, France8, can be added in the future to strengthen and broaden the assessment and applicability of SDS algorithms over a broad range of sites of interest.
Methods
Benchmark sites
Four sandy, wave-dominated, open-ocean beaches, namely Duck, Narrabeen, Torrey Pines, and Truc Vert (described below), where long-term beach monitoring survey data are publicly available, were selected as benchmark datasets.
The beach at Duck in North Carolina, USA, is a world-renowned coastal monitoring center, home to the U.S. Army Corps of Engineers Field Research Facility (USACE-FRF), where cross-shore transects have been surveyed monthly using a Coastal Research Amphibious Buggy (CRAB) and a military amphibious vehicle (LARC) since 198175. The site is located on the east coast of the United States, on a barrier island separating the Atlantic Ocean from mainland North Carolina. The tide regime is microtidal (MSTR of 1.4 m) with a characteristic beach face slope of \(\tan \beta =0.1\). The typical beach state is intermediate1. At this site, the relatively small shoreline variance signal is dominated by interannual variability32.
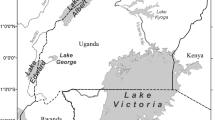
Narrabeen is a 3.6 km long embayment situated on the Northern Beaches of Sydney along the south-east coast of Australia. The tide regime is microtidal (MSTR of 1.7 m) with a characteristic beach face slope of \(\tan \beta =0.1\). Narrabeen exhibits typically intermediate beach states and varies from Reflective to Longshore Bar Trough based on the Wright and Short (1984)1 classification. The 40+ year dataset (1976 – present) of monthly profile surveys along the five cross-shore transects indicated in Fig. 3 is described in detail in Turner et al.4. The observed range of shoreline variability at Narrabeen over the 40+ year survey period varies from 80 m at transect PF1 to 55 m at transect PF6, and the observed dominant behavior in shoreline response is forced by individual and/or sequential storm events76.
Torrey Pines Beach is an 8 km-long cliff-backed sandy beach located in San Diego, California, USA. The tide regime is micro- to mesotidal (MSTR 2.3 m) with a characteristic beach-face slope of \(\tan \beta =0.04\). A 16-year topo-bathymetric dataset (sonar-mounted jetski + quandbike GNSS surveys) was collected and curated by the Scripps Institute of Oceanography7 monthly between 2001–2017. The wave climate is seasonally dominated with winter storms and calmer summers, while the shoreline position responds to the wave forcing with a 30–50 m seasonal cycle.
Truc Vert beach is situated in the southwest of France along a 100 km-long stretch of exposed sandy coastline, where the much larger tide regime is classified as meso- to macrotidal (MSTR 3.2 m). The characteristic beach face slope is gentle, \(\tan \beta =0.05\), and the beach typically exhibits a double-barred configuration: an intermediate (transverse bar and rip) inner bar and a crescentic outer bar77. Monthly to fortnightly topographic surveys using RTK-GNSS have been collected since 2005, with a 1-year interruption in 20086. Progradation and retreat of the shoreline at this site are highly seasonal and no long-term trend has been observed78. Moreover, because of the meso- to macrotidal range and gentle slope, the beach intertidal region is wide (up to 100 m) and displays a complex morphology with intertidal bars, shoals, and troughs79.
Figure 3 indicates the location of the four sandy beaches and the cross-shore transects that were used for assessing the accuracy of the SDS time-series. Four transects were selected at each site in the region with the highest survey coverage (i.e., highest temporal depth), except from Narrabeen, where all five monitored transects were used.
SDS algorithms
The same input data were provided to each group participating in the benchmarking exercise. Input data for each site included: a region-of-interest polygon, a reference shoreline and set of cross-shore transects, an estimate of the beach-face slope and time-series of tide levels and wave parameters. The beach-face slope was calculated as the linear regression between MSL and MHWS and averaged across all the available surveys. Each group downloaded the imagery for the area in the region-of-interest, pre-processed the imagery (e.g., pan-sharpening, compositing), and applied their shoreline detection algorithm to extract shoreline positions. The shoreline positions were then intersected with the cross-shore transect to obtain time-series of shoreline change. For the algorithms that produced instantaneous shorelines, mapped on individual images instead of composite images, the time-series were tidally corrected as described in Eq. 1 (‘Evaluation Methodology’). Hereafter each shoreline-detection workflow, namely CoastSat, SHOREX, ShorelineMonitor, CASSIE, and HighTide-SDS, is described.
CoastSat17 is an open-source Python toolbox that uses Landsat (5 to 9) and Sentinel-2 imagery to automatically map the position of the instantaneous waterline on each image. For each scene, the top-of-atmosphere (TOA) multispectral bands, namely Blue, Green, Red, Near-Infrared (NIR), and Short-wave infrared (SWIR1), are cropped to the region-of-interest and downloaded using Google Earth Engine’s Application Programming Interface (GEE)14. Then, the images are pre-processed locally: Landsat 5 bands (TM), which do not include a panchromatic band, are down-sampled from 30 to 15 m/pixel using bilinear-interpolation (GDAL warp function); Landsat 7 (ETM +) Green, Red, and NIR bands are pansharpened, while the Blue and SWIR1 bands are down-sampled to 15 m resolution; Landsat 8 and 9 (OLI) Blue, Green, Red bands are pansharpened, while the NIR and SWIR1 bands are down-sampled 15 m to resolution; Sentinel-2 MSI Blue, Green, Red, and NIR have a native resolution of 10 m while the SWIR1 is down-sampled from 20 to 10 m/pixel. To map the position of the sand/water interface, an image classifier is first applied to the image to label the ‘sand’ and ‘water’ pixels. The Modified Normalized Water-Index (MNDWI) is then used to select the Otsu threshold80 that maximizes the variance between classified ‘sand’ and ‘water’ pixels. The position of the waterline is then extracted using a sub-pixel resolution border segmentation method26, known as Marching Squares, to compute the iso-valued contour on the MNDWI image for a level equal to the sand/water threshold. The source code is publicly available at https://github.com/kvos/CoastSat.
SHOREX33 is a Python application that enables the automatic extraction of the shoreline position from satellite images. It follows a five-phase workflow that includes image downloading, cloud filtering, sub-pixel georeferencing, image segmentation, and shoreline sub-pixel extraction. SHOREX downloads the required bands (R, G, B, SWIR1, and AWEInsh81) from the TOA Landsat (5 to 9) and Sentinel-2 collections from GEE14. In this phase, the area of interest of each image is manually selected and cropped. During the second phase, the cloud filtering module allows the visualization of each image so a trained operator can efficiently approve or reject each image (spending about two seconds per image). This step is necessary to ensure that both the beach segment in which the shoreline will be extracted, and the area used for the sub-pixel geo-referencing process (unchanging urban areas) are cloud-free. The sub-pixel georeferencing step improves the accuracy of the image geolocation by applying a co-registration algorithm82 to align the satellite image against a very high-resolution orthophoto. This step was included at the 4 benchmark sites in this study. In the next step, an approximate pixel shoreline (APS) is obtained by applying a 0 threshold to the AWEInsh index81. The APS identifies the pixels where the kernel analysis is performed on the SWIR1 band following the method originally described in ref. 20. For each kernel analyzed, the reflectance values are fitted with a 3D polynomial function and the mathematical highest-gradient edge (where the Laplacian equals 0) is used to extract the sub-pixel location of the waterline. The source code is not publicly available.
ShorelineMonitor (http://shorelinemonitor.deltares.nl/)9 uses Landsat imagery (4 to 8) to automatically generate monthly moving average TOA reflectance composites (of 365 days) using the petabyte image catalog and parallel computing facilities of GEE14. Compared to the other algorithms previously described, ShorelineMonitor does not download the satellite images but instead uses the parallel computing capabilities of GEE to run the analysis directly in the cloud, reducing the analysis time to only several minutes per area of interest and enabling planetary scale applications. The composite images are generated by taking the 15th percentile of the NDWI pixel values as described in ref. 83. An Otsu threshold80 and region growing algorithm84 are then combined to map the position of the shoreline and a 1D Gaussian smoothing is applied to obtain shoreline vectors at sub-pixel resolution. The analysis of composite images decreases the influence of the tidal stage on the detected shoreline positions, so that the resulting shoreline approximately matches the MSL contour. Although compositing also averages out seasonal variability in wave effects, at sites with persistent swell conditions the presence of white-water due to wave breaking introduces a seaward offset in detected shorelines18. However, as this offset is likely present in all composite images, the wave effects on long-term shoreline change rates at such sites are limited. In summary, the ShorelineMonitor algorithm efficiently uses free cloud-computing resources, offering a globally applicable solution, and requires no in situ information. The source code is not publicly available.
CASSIE19 (acronym for Coastal Analyst System from Space Imagery Engine) is an open-source web tool for automatic shoreline mapping and analysis using multi-spectral satellite imagery (Landsat 5–9, and Sentinel 2). The web tool consists of a frontend user-friendly graphical interface that was built with ReactJS and JavaScript and communicates with the GEE backend. CASSIE operates entirely on the cloud and can be easily run on a PC, tablet or smartphone. In contrast with the three algorithms previously described, CASSIE uses surface reflectance (SR) instead of TOA. The images are cropped to the region of interest, mosaicked to produce a spatially continuous image and checked for cloud coverage. The automatic shoreline detection is performed by applying an Otsu threshold80 on the NDWI. The extracted shorelines are smoothed using a 1D Gaussian smoothing filter, which consists of a moving-average filter that removes the pixel-induced staircase effect from the digitized shoreline vector. The web application is publicly available at https://cassiengine.org/.
HighTide-SDS27 is an efficiency-oriented algorithm that derives annual high tide shoreline positions from Landsat archive with the entire workflow implemented on GEE. For each year in the archive, a yearly composite is created using the SR images and calculating the 10th percentile of the time-varying pixel values. The 10th percentile eliminates cloud-contaminated pixels and maximizes the water extent (darker pixels) so that the resulting composite best matches with a high tide scene. Then, a binary image is calculated by applying a 0 threshold to the Automated Water Extraction Index (AWEI)81. The binary image is then resampled with a bicubic interpolation to achieve sub-pixel resolution. Instead of extracting shoreline vectors like the previous algorithms, HighTide-SDS directly calculates the cross-shore position of the waterline along pre-defined shore-normal transects using GEE’s pixelArea function, which generates an image with the value of each pixel being the area covered by that pixel. After masking out water pixels, based on the land-water binary image, HighTide-SDS counts the number of land pixels along each transect (down-sampled to 1 m) to obtain the cross-shore position of the shoreline. The source is publicly available at https://github.com/SatelliteShorelines/SDS_Benchmark/tree/main/algorithms/UQMAO.
Evaluation methodology
The time-series of shoreline change were submitted to the Github repository (https://github.com/SatelliteShorelines/SDS_Benchmark) by each team of developers. The five algorithms at the four benchmark sites were evaluated against the in situ survey data, extracted programmatically from their respective data archives. The code for the full methodology is available in the form of Jupyter Notebooks (see ‘Data and Code Availability’). At each site, the topographic surveys or DEMs were used to extract the location of the Mean Sea Level (MSL) contour, which was then intersected with the cross-shore transects to generate the groundtruth time-series of shoreline change. Each timepoint in the groundtruth time-series was then compared to the closest satellite-derived time-series within a window of 10 days. For each site the time-series of the selected cross-shore transects were grouped and a set of error metrics were calculated, namely the root-mean-square error, standard deviation of error, mean bias and coefficient of determination (R2). The time-series were demeaned prior to calculating R2 to avoid a potential bias due to using time-series from multiple transects with different absolute values.
The long-term trends of shoreline change were computed by linear regression on the Landsat-derived MSL shoreline time-series (Fig. 4). The time-series were seasonally averaged, by computing the average of all the observations in each quarter (defined as DJF, MAM, JJA, SON), to homogenize the temporal resolution and avoid biasing the estimates towards the end of the record when more satellite observations are available (more satellites in orbit simultaneously). The same methodology was applied to the in situ time-series and the trends were estimated along each transect for the common period between the SDS time-series and the surveys.
The raw SDS time-series were tidally corrected for the algorithms that used individual images (CoastSat, SHOREX and CASSIE) using the following formula:
where \({\Delta x}_{{tide}}\) is the tidally corrected cross-shore position, \(\Delta x\) is the instantaneous cross-shore position, \({z}_{{tide}}\) is the corresponding tide level, extracted from the closest grid point in the FES2014 global tide model35, and \(\tan \beta\) is average beach-face slope derived from the topographic data (between Mean Sea Level and Mean High Water Spring).
The wave setup correction term was added on top of the tidal correction:
where \({\Delta x}_{{setup}}\) is the cross-shore position corrected for wave setup, \({\Delta x}_{{tide}}\) is the tidally corrected cross-shore position in Eq. 1 and \({z}_{{setup}}\) is the time-varying elevation of wave setup at the shoreline calculated using the generalized parametrization proposed by41:
where \({H}_{s}\) and \({L}_{p}\) are, respectively, the deepwater significant wave height and peak wavelength extracted from the closest grid point in the global ERA-5 wave hindcast36.
Data availability
The data needed to reproduce this analysis is publicly available at https://github.com/SatelliteShorelines/SDS_Benchmark and archived in a Zenodo repository at https://doi.org/10.5281/zenodo.8333435. This repository includes all the input data (regions of interest, transects, tide, and wave time-series) and the SDS time-series of shoreline change generated by each of the 5 algorithms at the 4 benchmark sites.
Code availability
The code to perform the comparison and generate the figures presented in this paper is publicly available at https://github.com/SatelliteShorelines/SDS_Benchmark and archived on Zenodo at https://doi.org/10.5281/zenodo.8333435. The in situ topographic surveys are publicly available in their respective data repositories and a Jupyter Notebook is provided to download and preprocess each dataset into time-series of shoreline change along the transects. There are 5 notebooks in the repository: - 1_preprocess_datasets.ipynb: downloads the in situ datasets from their respective source and calculates the time-series along the transects that are used as groundtruth. - 2_check_shoreline_accuracy.ipynb: checks the accuracy of your satellite-derived time-series. - 3_evaluate_submissions_Landsat_MSL.ipynb: evaluates the accuracy of the submitted SDS time-series against the in situ data and produces Figs. 4–6 and the metrics in Table 3 in this manuscript. - 4_evaluate_Landsat_vs_S2.ipynb: compares the accuracy of Landsat and Sentinel-2 SDS time-series and produces Fig. 7a and the metrics in Table 4. - 5_evaluate_wave_correction.ipynb: evaluates the addition of a wave setup term to the water level correction and produces Fig. 7b and the metrics in Table 5. Individual plots showing the comparison between the time-series produced by each algorithm and the groundtruth can be visualized in the Github repository (a total of 105 plots as there are 21 transects and 5 algorithms).
References
Wright, L. D. & Short, A. D. Morphodynamic variability of surf zones and beaches: a synthesis. Mar. Geol. 56, 93–118 (1984).
Castelle, B. & Masselink, G. Morphodynamics of wave-dominated beaches. Cambridge Prisms: Coastal Futures 1, 1–13 (2023).
Boak, E. H. & Turner, I. L. Shoreline definition and detection: a review. J. Coast. Res. 214, 688–703 (2005).
Turner, I. L. et al. A multi-decade dataset of monthly beach profile surveys and inshore wave forcing at Narrabeen, Australia. Sci. Data 3, 160024 (2016).
Barnard, P. L. et al. Coastal vulnerability across the Pacific dominated by El Niño/Southern Oscillation. Nat. Geosci. 8, 801–807 (2015).
Castelle, B., Bujan, S., Marieu, V. & Ferreira, S. 16 years of topographic surveys of rip-channelled high-energy meso-macrotidal sandy beach. Sci. Data 7, 410 (2020).
Ludka, B. C. et al. Sixteen years of bathymetry and waves at San Diego beaches. Sci. Data 6, 161 (2019).
Bertin, S. et al. A long-term dataset of topography and nearshore bathymetry at the macrotidal pocket beach of Porsmilin, France. Sci. Data 9, 79 (2022).
Luijendijk, A. et al. The State of the World’s Beaches. Sci. Rep. https://doi.org/10.1038/s41598-018-24630-6 (2018).
Mentaschi, L., Vousdoukas, M. I., Pekel, J.-F., Voukouvalas, E. & Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 8, 12876 (2018).
Castelle, B., Ritz, A., Marieu, V., Nicolae Lerma, A. & Vandenhove, M. Primary drivers of multidecadal spatial and temporal patterns of shoreline change derived from optical satellite imagery. Geomorphology 413, 108360 (2022).
Bishop-Taylor, R., Nanson, R., Sagar, S. & Lymburner, L. Mapping Australia’s dynamic coastline at mean sea level using three decades of Landsat imagery. Remote Sens. Environ. 267, 112734 (2021).
Vos, K., Harley, M. D., Turner, I. L. & Splinter, K. D. Pacific shoreline erosion and accretion patterns controlled by El Niño/Southern Oscillation. Nat. Geosci. 16, 140–146 (2023).
Gorelick, N. et al. Google Earth Engine: planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 202, 18–27 (2017).
McAllister, E., Payo, A., Novellino, A., Dolphin, T. & Medina-Lopez, E. Multispectral satellite imagery and machine learning for the extraction of shoreline indicators. Coastal Eng. 174 104102 (2022).
Vitousek, S. et al. The future of coastal monitoring through satellite remote sensing. Camb. Prisms: Coastal Futures 1, 1–18 (2023).
Vos, K., Splinter, K. D., Harley, M. D., Simmons, J. A. & Turner, I. L. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model Softw. 122, 104528 (2019).
Hagenaars, G., de Vries, S., Luijendijk, A. P., de Boer, W. P. & Reniers, A. J. H. M. On the accuracy of automated shoreline detection derived from satellite imagery: a case study of the sand motor mega-scale nourishment. Coastal Eng. 133, 113–125 (2018).
Almeida, L. P. et al. Coastal analyst system from space imagery engine (CASSIE): shoreline management module. Environ. Model. Softw. 140, 105033 (2021).
Pardo-Pascual, J. E., Almonacid-Caballer, J., Ruiz, L. A. & Palomar-Vázquez, J. Automatic extraction of shorelines from Landsat TM and ETM+ multi-temporal images with subpixel precision. Remote Sens. Environ. 123, 1–11 (2012).
Almonacid-Caballer, J., Sánchez-García, E., Pardo-Pascual, J. E., Balaguer-Beser, A. A. & Palomar-Vázquez, J. Evaluation of annual mean shoreline position deduced from Landsat imagery as a mid-term coastal evolution indicator. Mar. Geol. 372, 79–88 (2016).
Pardo-Pascual, J. E. et al. Assessing the accuracy of automatically extracted shorelines on microtidal beaches from landsat 7, landsat 8 and sentinel-2 imagery. Remote Sens. 10, 326 (2018).
Foody, G., Muslim, A. M. & Atkinson, P. M. Super-resolution mapping of the waterline from remotely sensed data. Int. J. Remote Sens. 26, 5381–5392 (2005).
Muslim, A., Foody, G. & Atkinson, P. Localized soft classification for super-resolution mapping of the shoreline. Int. J. Remote Sens. 27, 2271–2285 (2006).
Dewi, R. S., Bijker, W., Stein, A. & Marfai, M. A. Transferability and upscaling of fuzzy classification for shoreline change over 30 years. Remote Sens. (Basel) 10, 1377 (2018).
Cipolletti, M. P., Delrieux, C. A., Perillo, G. M. E. & Cintia Piccolo, M. Superresolution border segmentation and measurement in remote sensing images. Comput. Geosci. 40, 87–96 (2012).
Mao, Y., Harris, D. L., Xie, Z. & Phinn, S. Efficient measurement of large-scale decadal shoreline change with increased accuracy in tide-dominated coastal environments with Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 181, 385–399 (2021).
Covey, C. et al. An overview of results from the Coupled Model Intercomparison Project. Glob. Planet Change 37, 103–133 (2003).
Meehl, G. A., Boer, G. J., Covey, C., Latif, M. & Stouffer, R. J. Intercomparison makes for a better climate model. Eos (Washington DC) 78, 445–451 (1997).
Plant, N. G., Aarninkhof, S. G. J., Turner, I. L. & Kingston, K. S. The performance of shoreline detection models applied to video imagery. J. Coast. Res. 233, 658–670 (2007).
Montaño, J. et al. Blind testing of shoreline evolution models. Sci. Rep. 10, 2137 (2020).
Pianca, C., Holman, R. A. & Siegle, E. Shoreline variability from days to decades: results of long-term video imaging. J. Geophys. Res. Ocean. https://doi.org/10.1002/2014JC010320 (2015).
Sánchez-García, E. et al. An efficient protocol for accurate and massive shoreline definition from mid-resolution satellite imagery. Coastal Eng. 160, 103732 (2020).
Short, A. D. & Trembanis, A. C. Decadal scale patterns in beach oscillation and rotation Narrabeen Beach, Australia—Time Series, PCA and Wavelet Analysis. J. Coast. Res. 20, 523–532 (2004).
Carrere, L., Lyard, F., Cancet, M., Guillot, A. & Picot, N. FES 2014, a new tidal model—Validation results and perspectives for improvements. in Proceedings of the ESA living planet symposium. 9–13 (2016).
Hersbach, H. et al. The ERA5 global reanalysis. Quart. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Vos, K., Harley, M. D., Splinter, K. D., Simmons, J. A. & Turner, I. L. Sub-annual to multi-decadal shoreline variability from publicly available satellite imagery. Coastal Eng. 150, 160–174 (2019).
Young, A. P. et al. Southern California Coastal Response to the 2015–2016 El Niño. J. Geophys. Res. Earth Surf. 123, 3069–3083 (2018).
Castelle, B. et al. Equilibrium shoreline modelling of a high-energy meso-macrotidal. Mar. Geol. 347, 85–94 (2014).
Castelle, B. et al. Satellite-derived shoreline detection at a high-energy meso-macrotidal beach. Geomorphology 383, 107707 (2021).
Stockdon, H. F., Holman, R. A., Howd, P. A. & Sallenger, A. H. Empirical parameterization of setup, swash, and runup. Coastal Eng. 53, 573–588 (2006).
Barnard, P. L. & Vitousek, S. Earth science looks to outer space. Nat. Geosci. 16, 108–109 (2023).
Warrick, J. A., Vos, K., East, A. E. & Vitousek, S. Fire (plus) flood (equals) beach: coastal response to an exceptional river sediment discharge event. Sci. Rep. 12, 1–15 (2022).
Cabezas-Rabadán, C., Pardo-Pascual, J. E., Palomar-Vázquez, J. & Fernández-Sarría, A. Characterizing beach changes using high-frequency Sentinel-2 derived shorelines on the Valencian coast (Spanish Mediterranean). Sci. Total Environ. 691, 216–231 (2019).
Cuttler, M. V. W. et al. Interannual response of reef islands to climate-driven variations in water level and wave climate. Remote Sens. (Basel) 12, 1–18 (2020).
Ibaceta, R., Harley, M. D., Turner, I. L. & Splinter, K. D. Interannual variability in dominant shoreline behaviour at an embayed beach. Geomorphology https://doi.org/10.1016/J.GEOMORPH.2023.108706 (2023).
Warrick, J. A., Vos, K., Buscombe, D., Ritchie, A. C. & Curtis, J. A. A large sediment accretion wave along a northern california littoral cell. J. Geophys. Res. Earth Surf. https://doi.org/10.1029/2023jf007135 (2023).
Pollard, J. A., Spencer, T. & Jude, S. Big Data Approaches for coastal flood risk assessment and emergency response. Wiley Interdiscip. Rev. Clim. Change 9, e543 (2018).
USGS. Landsat Collection 1 Level 1 Product Definition. https://landsat.usgs.gov/sites/default/files/documents/LSDS-1656_Landsat_Level-1_Product_Collection_Definition.pdf (2017).
ESA. SENTINEL-2 User Handbook. https://sentinel.esa.int/documents/247904/685211/Sentinel-2_User_Handbook (2015).
Almonacid-Caballer, J., Pardo-Pascual, J. E. & Ruiz, L. A. Evaluating fourier cross-correlation sub-pixel registration in Landsat images. Remote Sens. (Basel) https://doi.org/10.3390/rs9101051 (2017).
Doherty, Y., Harley, M. D., Vos, K. & Splinter, K. D. A Python toolkit to monitor sandy shoreline change using high-resolution PlanetScope cubesats. Environ. Model. Softw. 157, 105512 (2022).
Liang, S. Quantitative remote sensing of land surfaces. Quant. Remote Sens. Land Surfaces https://doi.org/10.1002/047172372X (2003).
Chander, G., Markham, B. L. & Helder, D. L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 113, 893–903 (2009).
Holman, R. A. & Stanley, J. The history and technical capabilities of Argus. Coastal Eng. 54, 477–491 (2007).
Vos, K., Harley, M. D., Splinter, K. D., Walker, A. & Turner, I. L. Beach slopes from satellite-derived shorelines. Geophys. Res. Lett. 47, e2020GL088365 (2020).
Vitousek, S. et al. A model integrating satellite-derived shoreline observations for predicting fine-scale shoreline response to waves and sea-level rise across large coastal regions. Authorea Preprints https://doi.org/10.22541/ESSOAR.167839941.16313003/V1 (2023).
Cabezas-Rabadán, C., Pardo-Pascual, J. E., Palomar-Vázquez, J., Ferreira, Ó. & Costas, S. Satellite derived shorelines at an exposed meso-tidal beach. J. Coast. Res. 95, 1027–1031 (2020).
Ioannis, M., Dagmara, V., Luis, W. & Almeida, P. Coastal vulnerability assessment based on video wave run-up observations at a mesotidal, steep-sloped beach. Ocean Dyn. 62, 123–137 (2012).
Senechal, N., Coco, G., Bryan, K. R. & Holman, R. A. Wave runup during extreme storm conditions. J. Geophys. Res. Oceans 116, C07032 (2011).
Konstantinou, A. et al. Satellite-based shoreline detection along high-energy macrotidal coasts and influence of beach state. Mar. Geol. https://doi.org/10.1016/j.margeo.2023.107082 (2023).
Gibney, E. Is AI fuelling a reproducibility crisis in science. Nature 608, 250–251 (2022).
Kapoor, S. & Narayanan, A. Leakage and the reproducibility crisis in ML-based science. arXiv https://doi.org/10.48550/arXiv.2207.07048 (2022).
Baker, M. & Penny, D. Is there a reproducibility crisis? Nature 533, 452–454 (2016).
Scheffler, D., Hollstein, A., Diedrich, H., Segl, K. & Hostert, P. AROSICS: An automated and robust open-source image co-registration software for multi-sensor satellite data. Remote Sens. (Basel) 9, 676 (2017).
Buscombe, D. & Fitzpatrick, S. CoastSeg. Github Repository https://github.com/Doodleverse/CoastSeg (2023).
Pucino, N., Kennedy, D. M., Young, M. & Ierodiaconou, D. Assessing the accuracy of Sentinel-2 instantaneous subpixel shorelines using synchronous UAV ground truth surveys. Remote Sens. Environ. 282, 113293 (2022).
Bracs, M. A., Turner, I. L., Splinter, K. D., Short, A. D. & Mortlock, T. R. Synchronised patterns of erosion and deposition observed at two beaches. Mar. Geol. 380, 196–204 (2016).
Barnard, P. L., Hansen, J. E. & Erikson, L. H. Synthesis study of an erosion hot spot, Ocean Beach, California. J. Coast. Res. 28, 903–922 (2012).
Van de Lageweg, W. I., Bryan, K. R., Coco, G. & Ruessink, B. G. Observations of shoreline-sandbar coupling on an embayed beach. Mar. Geol. 344, 101–114 (2013).
Kuriyama, Y. Medium-term bar behavior and associated sediment transport at Hasaki, Japan. J. Geophys. Res. 107, 3132 (2002).
Valiente, N. G., McCarroll, R. J., Masselink, G., Scott, T. & Wiggins, M. Multi-annual embayment sediment dynamics involving headland bypassing and sediment exchange across the depth of closure. Geomorphology 343, 48–64 (2019).
Ruiz de Alegria-Arzaburu, A. & Masselink, G. Storm response and beach rotation on a gravel beach, Slapton Sands. U.K. Mar. Geol. 278, 77–99 (2010).
Quartel, S., Kroon, A. & Ruessink, B. G. Seasonal accretion and erosion patterns of a microtidal sandy beach. Mar. Geol. 250, 19–33 (2008).
Larson, M. & Kraus, N. C. Temporal and spatial scales of beach profile change, Duck, North Carolina. Mar. Geol. 117, 75–94 (1994).
Harley, M. D., Turner, I. L., Short, A. D. & Ranasinghe, R. Assessment and integration of conventional, RTK-GPS and image-derived beach survey methods for daily to decadal coastal monitoring. Coastal Eng. 58, 194–205 (2011).
Sénéchal, N. et al. Morphodynamic response of a meso- to macro-tidal intermediate beach based on a long-term data set. Geomorphology 107, 263–274 (2009).
Castelle, B. et al. Spatial and temporal patterns of shoreline change of a 280-km high-energy disrupted sandy coast from 1950 to 2014: SW France. Estuar. Coast. Shelf Sci. 200, 212–223 (2018).
Almar, R. et al. Video-based detection of shorelines at complex meso–macro tidal beaches. J. Coast. Res. 284, 1040–1048 (2012).
Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man. Cybern. 20, 62–66 (1979).
Feyisa, G. L., Meilby, H., Fensholt, R. & Proud, S. R. Automated Water Extraction Index: a new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 140, 23–35 (2014).
Thurman, S. T., Guizar-Sicairos, M. & Fienup, J. R. Efficient subpixel image registration algorithms. Opt. Lett. 33, 156–158 (2008). 33, 156–158.
Donchyts, G. et al. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 6, 810–813 (2016).
Kamdi, S. & Krishna, R. Image segmentation and region growing algorithm. Int. J. Comput. Technol. Electron. Eng. (IJCTEE) 2, 103–107 (2012).
Acknowledgements
K.V. is funded under a USGS Research Cooperative Agreement. K.D.S. receives funding from the Australian Research Council (FT21XX). B Castelle is supported by the Agence Nationale de la Recherche (ANR) grant number ANR-21-CE01-0015. CGAT-UPV researchers are supported MONOBESAT (PID2019−111435RB-I00) by the Spanish Ministry of Science, Innovation and Universities, C. Cabezas-Rabadán is supported by the M. Salas contract - Re-qualification program by the Spanish Ministry of Universities (NextGenerationEU), and Primeros Proyectos de Investigación (PAID-06-22) by Vicerrectorado de Investigación de la Universitat Politècnica de València (UPV). Contributions by Deltares (Arjen Luijendijk, Etienne Kras, and Floris Calkoen) are funded by the Deltares Strategic Research Programme ‘Seas and Coastal Zones’ and the H2020 project CoCliCo. D.P. acknowledges the Portuguese Fundação para a Ciência e Tecnologia (FCT) support, under the 2022.13776.BDANA Ph.D. research fellowship. L.P.A. acknowledges the European Space Agency (ESA) support, under Earth Observation Advanced science Tools for Sea level Extreme Events (EOatSEE) project. Antonio H.F. Klein and CASSIE platform development were supported by Brazilian National Council for Scientific and Technological Development (CNPq Proc no. 302238/2022-0, 406603/2022-7, 441818/2020-0, 441545/2017-3). Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. We also would like to thank Chris Leaman for developing the py-wave-runup package.
Author information
Authors and Affiliations
Contributions
K.V. designed the study, prepared the validation testbed, and invited all the participants, with input from K.D.S., B.C., D.B., and S.V. Each team ran their algorithm at the benchmark sites: SHOREX by J. P., J.E.P., J. A., and C.C., ShorelineMonitor by E.C.K., A.P.L., and F.C. CASSIE by L.P.A., D.P., A.H.F.K. HighTide-SDS by Y.M. and D.H., and CoastSat by K.V.; K.V. performed the accuracy assessment, prepared the figures, and drafted the manuscript with major contribution from S.V. All authors contributed to discussing the results and writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Eli Lazarus, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Nicole Khan, Heike Langenberg. A peer review report is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vos, K., Splinter, K.D., Palomar-Vázquez, J. et al. Benchmarking satellite-derived shoreline mapping algorithms. Commun Earth Environ 4, 345 (2023). https://doi.org/10.1038/s43247-023-01001-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-01001-2
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.