Abstract
The Gangetic Plains comprise steep gravelly river channels that transition to low gradient sandy channels 10-40 km downstream of the mountain front. This “gravel-sand transition" is characterized by an abrupt greater-than-one-order-of-magnitude drop in both gradient and sediment grain size, suggesting a degree of long-term stability. However, the stratigraphic record of the gravel-sand transition in the Miocene Siwalik Group demonstrates intermittent transport of coarse gravels tens of kilometres downstream of the transition; such events in contemporary channels would drive channel avulsion(s) and increase flood risk, devastating communities across the plains. We combine sedimentological analysis of Siwalik deposits with entrainment calculations which demonstrate that hyperconcentration is required to transport coarse bedload over low-gradient plains. Transport conditions are attainable when intense monsoon precipitation (a 200- to 1000-year event) is combined with increased suspended sediment concentrations in channels. Predicted climate change and ongoing seismicity increase the likelihood of such extreme events within this century.
Similar content being viewed by others
Introduction
The large Himalayan river system of the Gangetic Plains (Fig. 1) supports 10% of the world’s population and is home to some of the world’s poorest and most densely populated communities. Characterised by favourable climate, fertile soils, and abundant water supply, the Gangetic Plains are seen as the “bread basket" of South Asia, providing food and livelihood security for hundreds of millions of its inhabitants1,2. However, many of these rivers are also the source of devastating floods. In 2008 a single avulsion event along the Kosi River, in eastern Nepal, took the lives of almost 500 people and permanently displaced more than one million individuals3,4,5.
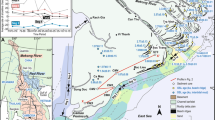
a Geology of the Himalayan Mountain range with accompanying main faults (MFT—Main Frontal Thrust, MBT—Main Boundary Thrust, MCT—Main Central Thrust, STDS—South Tibetan Detachment System, ISMZ—Indus-Tsangpo Melange Zone) and the main rivers of the Gangetic Plains digitised and placed on a 90 m Shuttle Radar Topography Mission digital elevation model71,75,76, with accompanying geological cross section. Geological cross section was adapted from ref. 77. b Geology of the Mohand anticline/Dehradun region and the main rivers (Yamuna and Ganga) which drain western Himalayas. Only Middle Siwaliks sandstone and Upper Siwalik conglomerate are exposed along the Mohand Anticline. Published Siwalik sedimentary log data used in study (MS—Mohand Section71, KS—Karnali Section63, SK—Surai Khola Section63) and Siwalik sedimentary log data collected in this study (*CS—Chakrata Section) are marked by purple lines. The red dashed line represents published data on the current position of the GST in the Gangetic Plains7,53. White stars represent the approximate location of Holocene Kosi mega-fan core8. Upper Siwalik Conglomerate paleoflow data is from ref. 71, and suggests that rivers which deposited the Siwalik stratigraphy logged in this study (*CS) flowed in the same direction as the rivers which presently occupy the Gangetic Plains (predominantly flowing south).
In the Gangetic Plains, the gravel-sand transition (GST) represents the downstream limit of coarse bedload. It is located 10–40 km downstream of the mountain front and defines an abrupt geomorphic boundary marked by a tenfold downstream reduction in channel gradient6,7. There is no evidence that historical floods (i.e. which have occurred in the past 101–102 years) have transported gravel beyond the GST, either in young terrace deposits or in modern river channels. However, coarse gravel deposits have been observed in Holocene cores from the Kosi megafan (Fig. 1), where boreholes located 30–40 km south of the modern GST record intermittent deposition of gravels8. The transport and deposition of coarse gravels in low-gradient sandy channels would cause long-term changes to the channels’ morphology and reduce conveyance capacity, increasing the risk of floodplain inundation and channel avulsion (e.g. ref. 9).
The processes that could generate extreme transport conditions over foreland basins such as the Gangetic Plains are not well understood. In the region, paleo-flood studies have been limited to the reconstruction of historic transport of coarse sediment and boulders within a confined valley setting of the High Himalaya10, with reconstructed discharges equating to 105–106 m s−1. Such discharges have been attributed to glacial lake outburst floods (GLOFs) and the collapse of landslide- dammed lakes (lakes formed via the blockage of river valleys by landslide material). In the Himalaya, catastrophic discharge from GLOFs and landslide-dammed lakes are common, although many of these floods dissipate before reaching the Gangetic Plains11,12,13,14,15.
Studies have demonstrated that increasing suspended sediment concentration promotes the entrainment of coarse bedload16,17,18. Hyperconcentrated floods occur when flood water discharge contains enhanced suspended sediment fluxes (~8–40% volume) compared to clear water flows19. Common trigger mechanisms for hyperconcentrated flows include hillslope and channel incision during intense rain storms19,20, lake-breakout floods21,22, GLOFs23, and inputs of large sediment volumes by landslides and/or floodplain recycling9,24.
Here we utilise the stratigraphic record of sediment transport processes at the GST as recorded by the boundary between the Miocene Middle and Upper Siwalik formations located along the mountain front of the Himalaya in India (Fig. 1). We analyse the sedimentary structures, grain size, bed thickness, and textural characteristics of isolated conglomerate event beds preserved in thick sandstones of the upper Middle Siwalik succession; such event beds record coarse gravel deposition into low gradient sandy plains. The data is used to constrain bedload entrainment calculations aimed at estimating paleo-river discharge, suspended sediment concentrations, and bedload flux. Reconstructed flood magnitudes are compared to modern flood return intervals for the Karnali River (Fig. 1), which is viewed as analogous to the rivers that deposited the Siwalik stratigraphy. Our results demonstrate that hyperconcentrated suspended sediment loads combined with extreme flood discharges (i.e. a one in a 200- to 1000-year event) provide the necessary conditions to transport coarse bedload beyond the GST, over the low gradient channels of the Gangetic Plains. Predicted increases in the intensity of extreme rainfall events and therefore extreme flood discharge25 combined with ongoing seismic activity in the region26 is likely to increase the future probability of sediment-laden flood waters.
Sedimentological and regional context
Since Miocene times, large trans-Himalayan rivers have dominated the landscape of the Gangetic Plains, continuously supplying the erosional products of the Himalaya to the foreland basin27. Ongoing tectonic convergence between the Gangetic Plains and the Himalaya has resulted in thin-skinned fold-and-thrust deformation that has accreted the deposits of the foreland basin into the Himalayan mountain front, forming the Siwalik foothills27,28,29,30 (Fig. 1). The Siwalik foothills are formed of a thick succession (~5–8 km) which is divided into three units that generally coarsen upwards from siltstones and sandstones to coarse conglomerates. These are termed the Lower, Middle, and Upper Siwaliks, respectively, and reflect the current depositional environments found on the Plains. The proximal gravel reaches of the present-day Himalayan rivers are represented by the Upper Siwalik conglomerate, and the sand-dominated medial and distal reaches are represented by the Lower to Middle Siwaliks31. The contact between the Middle and Upper Siwaliks exhibits an abrupt, up-section increase in grain size by a factor of ~1006 (Fig. 2). This contact is considered to represent the ancient GST and is diachronous within the stratigraphy6, as it records the progressive migration of coarse pebble- and cobble-dominated sediment over the downstream, lower gradient sand-rich regions6 (Fig. 2). This migration tracks the foreland-directed movement of the deformation front of the Himalaya at rates of 12–20 mm/yr32,33. Isolated conglomerate beds observed below the Middle to Upper Siwalik contact represent punctuated episodes of gravel transport beyond the GST into the distal sand-rich plains (Fig. 2).
Diagram illustrating how Siwalik sedimentary sequences relate to various fluvial environments from proximal to distal (relative to the mountain front) across the Gangetic Plain. Sedimentary log 3 represents the isolated conglomerate event beds which we document in this study (i.e. C1 and C2). Convergence32,33 and sediment accumulation58,59 rates were taken from published datasets, and are used in calculations estimating the Middle Siwalik conglomerate event bed transport distance (Methods).
The Mohand anticline, located in Northwest India, locally exposes Siwalik rocks, and is bounded by the Yamuna River in the west and the Ganga River in the east (Fig. 1). The anticline is separated from the Lesser Himalayan ranges by a ’dun valley’ (i.e. an intermontane sedimentary basin), known locally as Dehradun, and forms the hanging wall of the Main Frontal Thrust (MFT)34. Along the Mohand anticline the Siwalik formation is separated into Middle and Upper Siwalik units based on their dominant lithologies of sandstone and conglomerates, respectively.
Results
Conglomerate event bed descriptions
Two significant conglomerate beds (in terms of thickness) are recorded 400 m below the Middle to Upper Siwalik contact within the logged Mohand Middle Siwalik sandstones along the Mohand anticline (Fig. 3). The first deposit (C1) is characterised by an erosive base overlain by 2 m of well-rounded, well-sorted, coarse-grained (D50 = 52 mm) conglomerate, which displays little clast imbrication (Fig. 3). The conglomerate is predominately clast-supported with small matrix-supported lenses and shows little evidence of internal structure or segregation of grain sizes. The 2 m conglomerate base is overlain by 4.1 m of medium sandstone which displays faint low-angle stratification towards the top of the deposit, but is otherwise structureless. The total thickness of the event bed (conglomerate and the overlying sandstone) is 6.1 m.
a Summary sedimentary log through the Siwalik succession exposed along the Mohand anticline. The Upper Middle Siwalik to Upper Siwalik conglomerates were studied in detail to capture conglomeratic event beds below the Middle to Upper Siwalik contact. No Lower Siwalik sandstone was exposed in the study region. b Detailed sedimentary log of conglomerate beds C1 and C2. Geometries (channel depth; Fig. 5) and grain size (conglomerate beds) were taken from C2 conglomerate bed and used in bedload transport equations. Siwalik date (GPTS age 4.4 Ma) was taken from a nearby logged Siwalik section (30 km east of the logged section; Fig. 1) so can be roughly correlated to our studied section for age context71.
The second gravel bed (C2) (Fig. 3) truncates the underlying sandstone deposit of gravel bed C1. It has an undulating erosive base with individual clasts found floating within the sandstone body directly below the erosive contact (Fig. 3). The lowermost unit consists of 2 m of coarse (D50 = 45 mm) conglomerate. The conglomerate displays a weak up-section change from predominantly matrix to clast-supported and rare, weak clast imbrication. Above the conglomerate is 9.3 m of structureless medium sandstone which displays little stratification. The total thickness of the event bed (conglomerate and the associated overlying sandstone) is 11.3 m.
Seventeen thinner pebble layers are present throughout the Upper Middle Siwalik unit. Beds have a thin (~20–50 mm) erosive pebble layer at their base which is overlain by medium sandstone with differing amounts of rare, faint, low-angle stratification. Total bed thicknesses (inclusive of pebble layer base and associated overlying sandstone) range from 2 to 14.2 m. The thin Middle Siwalik gravel beds are similar to those observed in Holocene Kosi mega-fan cores8 (Fig. 4). Both the conglomerate beds (C1 and C2) and the thinner pebble layers are components of some of the thickest beds in the studied Siwalik section (Figs. 3, 5). This may suggest that there is a minimum channel height/discharge needed to transport gravels far into the distal plains.
a Photographs of conglomerate bed C2. b Close-up of coarse pebbles floating in sandstone beneath conglomerate bed C2. c Conglomerate bed C1. Photographs (d) and (e) illustrate the thin gravel layers observed in Middle Siwalik sandstone. Photographs (f) and (g) show thin gravel layers observed in Kosi megafan core (core KS4 and KS3, respectively; Fig. 1). Dashed red lines in picture (a) and (b) highlight the erosive base of the conglomerate beds (C1 and C2).
River geometries (a Slope, b Channel depth, c Channel width) of contemporary Ganga plain rivers and the river(s) which deposited the Siwaliks exposed along the Mohand Anticline (Fig. 1). Horizontal red line is the median value. Sedimentological data and empirical relationships suggest that the river that deposited the Siwalik succession in this study is comparable (in terms of geometries) to the contemporary rivers of the Ganga Plain. d–f Frequency vs bed thickness data for the Mohand, Surai Khola, and Karnali sections (Fig. 1)63 plotted in the format (d) log/linear axes, (e) log/log axes, and (f) binned data (Mohand section only). Bar colours correspond to colours used in plots (d) and (e). See methods for calculations used to determine Siwalik river geometries.
The lack of internal sorting of clasts in the 2 m conglomerate beds suggests rapid deposition, with little to no opportunity for clast imbrication to form. If the clasts in the conglomerate were transported by rolling and saltating under stream flow we would expect some grain size sorting and clast imbrication. The massive sandstones overlying the conglomerates could be indicative of suspended sediment fallout that was sufficient enough to suppress the development of laminations or structures35,36. These characteristics are typical of rapid sediment fallout from hyperconcentrated flows with a high degree of turbulence and sediment suspension distributed through the entire water column37,38,39. Sedimentological data (bedform height) and empirical relationships suggest that the river that deposited the Mohand Siwalik succession is comparable to contemporary rivers that exist in the Ganga Plain today (i.e. channel depth and slope) (Fig. 5, Methods). Here we focus on event bed C2 as it is the largest event (in terms of gravel deposition) recorded in the Mohand Middle Siwalik section.
Reconstructing flood discharge
Initially, we estimate the site of deposition of the conglomerate bed (C2) relative to the time-equivalent position of the GST. The limit of gravel deposition downstream of the GST defines the boundary at which areas in close proximity to the river will be impacted by increased inundation due to the reduction in channel capacity9. By knowing the shortening rate and the stratigraphic thickness from the conglomerate bed (C2) to the Upper Siwalik contact, and by assuming an approximately stable distance from the mountain front to the GST and a steady sediment accumulation rate in the basin, we calculate the distance downstream of the GST that the conglomerate was deposited (Methods). Based on these calculations, event bed C2 is estimated to have formed between 7 and 25 km downstream of its time-equivalent GST. These estimates are consistent with the thin gravel deposits found in the Kosi cores located between 30 and 40 km downstream of the modern GST8. The 7 to 25 km distance represents a conservative estimate of total downstream transport distance, given that the conglomerate deposit would have extended further into the basin but with decreasing thickness.
Based on bedform thickness and grain sizes, we use grain entrainment and sediment flux calculations to evaluate the flood magnitude and suspended sediment concentrations that could have transported the coarse bedload 10 km beyond the GST. Using conglomerate bed C2 (mostly structureless massive deposit), we approached our discharge calculations based on a channel that was at least 11 m deep, with a channel thalweg comprising gravels with a median diameter of 45 mm. Suspended sediment and bedload discharges (per unit width of river, m s−1/m) are estimated using established empirical approaches and assume a rectangular channel with gravel transported across the entire river width. Numerous empirical formulae exist in the literature to estimate bedload transport, and the value of bedload transport rate can vary by an order of magnitude depending on the equation used. In this study, we selected the Meyer-Peter and Müller40 approach because this widely established approach has been shown to yield the median value for the bedload transport rate from a range of empirical formulae in the literature41 (Supplementary Notes 6, Supplementary Table 2).
For the river channel described above, the threshold velocity required to mobilise 45 mm bedload particles was calculated to be approximately 3.75 m s−1(Methods). Assuming this threshold velocity for grain entrainment, bedload calculations imply that for flows with low suspended sediment concentrations (fluid density assumed—density of clear water), several months of sustained high discharge, with a magnitude more than double the average monsoon discharge, would be required to move the gravel 10 km downstream of the GST (Supplementary Notes 6, Supplementary Table 2). This duration of very high flow is improbable for monsoon-fed rivers where flood peaks of a similar magnitude, observed in the historical record, have lasted a few hours to a day. Furthermore, the studied coarse conglomerate deposits within the Middle Siwalik sandstone imply a high energy short-lived event, indicated by the erosive conglomerate base and lack of internal pebble imbrication and sorting. We explore the influence that key parameters such as flow velocity and suspended sediment concentration have on the gravel transit times.
Much of the existing suspended sediment data from Nepal was gathered during moderate floods (<8000 m s−1 and/or upstream of the GST, with maximum sediment concentrations ranging from 1 to 6 vol.% (~25 g l−1 to 150 g l−1;42,43). A concentration of 8 vol.%. is the lower limit of hyperconcentrated flow44. In certain conditions, such as during extreme discharge events and/or when there is an ample supply of fine sediment from landslide deposits or bed and bank erosion, concentrations have been observed to exceed 50 vol.% (~1600 g l−144,45). In the Gangetic Plains, high rates of recycling of the riverbed and banks below the GST43 provide a source of fine-grained sediment that could account for the large increase in suspended sediment needed for the flow to transition from dilute to hyperconcentrated sediment-laden conditions44. In hyperconcentrated flow, high concentrations of sediment are distributed through the water column and do not follow the log profile of concentration observed in dilute water flows46. As such, the density of the water-sediment mixture is higher than clear water, dampening turbulence, increasing the speed of the flood wave and resulting in more erosion44. As the concentration increases, particle settling velocity is reduced allowing sediment to be transported downstream over longer distances as wash load, even as the flow velocity attenuates44.
During a moderate monsoon (1-year return interval discharge), the thalweg depth below the GST in the Karnali was recorded as 4 m, with maximum near-bed concentration ~6 vol.%, and depth-averaged concentration ~1 vol.%43. During the passage of hyperconcentrated flows in some Chinese rivers, channels have been observed to narrow and deepen by several metres as bed sediments are eroded and carried into suspension46. Although hyperconcentrated flows in the distal plains of Nepal have not been documented previously, this phenomenon could explain the large increase in river depth during the recorded C2 event, which had a depth greater than 11 m (conglomerate bed and the overlying sandstone; Figs. 3, 4). Assuming several metres of bed are entrained into suspension to achieve this river depth, we would expect a sediment concentration much greater than the 1 to 6 vol.% previously observed during a moderate monsoon43. Using standard suspended sediment calculations41, we can approximate the depth-averaged concentration of suspended sediment (for D50 = 0.25 mm, 0.35 mm or 0.5 mm) at different bulk flow velocities, and equivalent discharge magnitude and return interval flood events (Methods). We combine these calculations with the Meyer-Peter–Müller equation40 to estimate the bedload transport rate, and the discharge required to transport enough gravel to generate a 2 m thick gravel bed 10 km downstream of the GST in less than a day, a time scale similar to large floods recorded in recent history.
In the literature, the Meyer-Peter–Müller equation40 has been revised over the last decade to account for flow regimes different to the steady state flow conditions considered in its derivation47,48,49. Cao et al.49 used a modification coefficient, φ (Eq. 16), to account for fast, turbulent flow conditions observed during a dam break, and found that a value of 3 to 6 yielded good agreement with data from laboratory studies of cascade dam breaks and landslide dam events over erodible beds, where a coefficient of 1 would represent steady-state flow and increasing coefficients represent increasingly turbulent and erosive flow conditions. Our results indicate that using the Cao et al.49 modification coefficient, combined with hyperconcentrations of suspended sediment, could reduce gravel transit time by several orders of magnitude (Fig. 6) compared to estimates obtained under low sediment-concentration assumptions. For example, the gravel could be transported 10 km downstream of the GST in under 24 h by a 200-yr to 1000-yr flood (discharge equivalent to 23,200 m s−1 to 27,500 m s−1, Fig. 6), or in under 12 hours for a 500-yr to 2000-yr flood (equivalent discharge 26,200 m s−1 to 30,500 m s−1).
a, b Time taken to transport 2 m thick gravel bed over 10 km distance vs. depth averaged concentration of suspended sediment for flow bulk velocity of (a) 7 m/s and (b) 8 m/s. The coloured lines in (a–d) represent different experimentally constrained coefficients used to modify the Meyer-Peter–Müller bedload transport equation, where φ = 1 is the standard Meyer-Peter–Müller equation (15) and φ = 6, for example, is the modified Meyer-Peter–Müller equation (16) adapted for highly turbulent and erosive flow. c, d Contour plots of suspended sediment concentration and discharge combinations required to transport sufficient gravel to deposit a 2 m thick gravel bed 10 km downstream of the GST in 12 hours (c) and 24 hours (d); dashed lines represent the concentration of suspended sediment (D50 = 0.25 mm, 0.35 mm, 0.5 mm) to discharge magnitude, estimated using standard sediment transport equations. The intersection of coloured and dashed lines are minimum estimated discharges and sediment concentrations required to transport the gravel 10 km downstream. Higher φ values (e.g. φ = 6) represent greater flow turbulance and therefore higher capacity to transport gravel at lower discharges and suspended sediment concentrations. e Estimated return interval for annual peak discharge measurements for the Karnali River, Nepal, from 1962 to 2014 at Chisapani gauging station. The Karnali River is used as a type example of a large trans-Himalayan River. Peak discharge measurements (black circles) were obtained from43). The projected return intervals were estimated using a Gumbel distribution (black dashed line). Red dashed lines represent the upper and lower 95% confidence limits. Shaded blue area represents discharges and associated return intervals to transport a 2 m thick gravel bed 10 km downstream of the GST under 24 h for φ values ranging from 3 to 6.
These calculations are conservative upper limits, bounded by the suspended sediment concentrations calculated using equivalent flow velocities for these return interval flood events, and by our assumptions on river cross sections (Fig. 6, Supplementary Notes 2, 3, 4). In the calculations We assume that the gravel is transported across the entire width of the channel. However, it is likely that the gravel was only transported in the thalweg of the river where flow depth and velocities were highest, which would allow gravel to be transported at the same rate by smaller, more frequent discharge events. Varying the median grain size of gravel by approximately 20% (±10 mm) could change the transit time by up to 6% using the modified Meyer-Peter–Müller approach.
Discussion
Our results demonstrate that the transport of coarse gravel far into the low gradient plains of Himalayan rivers could occur during an extreme monsoon event, equivalent to a 200-yr to 1000-yr flood, only when hyperconcentrated flow conditions are triggered.
Triggering mechanisms for hyperconcentrated flows could come from several sources. The region has extensive glacial cover50 and is seismically active26. Catastrophic sediment-laden floods derived from GLOFs and landslide-dammed lakes are common, but often dissipate before reaching the distal plains11,12,15. The events recorded in the Siwalik stratigraphy likely result from triggers closer to the mountain front, such as the collapse of a landslide-dammed lake located in the frontal ranges combined with the enhanced discharge mixing with recycled river bed and bank sediments (e.g. ref. 43). Similar gravel deposits are observed in Holocene Kosi megafan cores8, suggesting that similar hyperconcentrated events have occurred in more recent times during the Holocene. The rarity of such observations implies that these events are episodic over long timescales (103– 106 years).
However, predicted climate change and ongoing seismicity in the region will increase the likelihood of similarly large events over the next centuries. Using a range of general circulation models, Chapagain et al.25 showed that the intensity of extreme rainfall events in western Nepal could increase by up to 60% in the mid to far future. Predicting the likelihood of extreme floods such as those documented in the long-term record of the Siwaliks remains a major challenge for future disaster risk management, but the implications of such an event could have far-reaching consequences.
In low gradient environments such as the Gangetic Plains, coarse deposition from hyperconcentrated flows would decrease channel capacity, increasing flood risk for future moderate flow events9. Channel infilling and subsequent super-elevation of the channel could also cause avulsion44, leading to widespread inundation of the surrounding plains and causing damage to buildings and infrastructure, and loss of lives. Additionally, due to the hyperconcentrated nature of the discharge, any channel avulsion or associated inundation would deposit sand and gravel onto the surrounding fertile agricultural land. As gravel is much less mobile than sand, the effects would be long-lasting. The Kosi avulsion of 2008 deposited up to 2 m of sediment onto the surrounding floodplain51. Although the flood occurred over a decade ago, the impacts of the avulsion are still felt, with agricultural land rendered waterlogged, infertile, and the source of vector-borne disease.
Predicted climate change and ongoing seismicity in the region means that hyperconcentrated, coarse bedload transport events in low-gradient sandy rivers are likely to become more frequent in the Gangetic Plains. How to incorporate these processes into future disaster risk management strategies remains an important and major challenge.
Methods
Sedimentary logging
Detailed sedimentary logs were taken of a section of the Siwalik succession exposed along the Mohand anticline near the Chakrata River (grid references 43R 0757817; 3359903). The sequence was logged at 1:50 scale, with grain sizes, sedimentary structures, and contacts measured and recorded (Fig. 1). See ’Supplementary Notes 8’ for complete sedimentary logs.
Grain size measurements event beds (C1 and C2)
For each conglomerate bed (C1 and C2), two to three photographs were taken for use in image analysis software (Erdas). Picture resolution was 5184 × 3888 pixels. The short axis or c-axis of the pebbles were more clearly identifiable in cross-section, as noted in previous studies (e.g. refs. 52,53) (Supplementary Fig. 1). Pebble sizes were measured from each photograph by overlaying a square grid with 100 nodes and measuring the c-axis of each pebble beneath the node7,52,53,54,55. In some cases pebbles were angled slightly off c-axis, which may result in a slight over or under estimation of the c-axis. A ratio correction was applied to the conglomerate pebble measurements to convert the c-axis to b-axis, to be used in bedload entrainment calculations. The ratio of the b- and c-axis has been derived from quartzite pebble measurements from present-day gravel bars of the Karnali River (ratio of 1.5, based on 200 quartzite pebble measurements53). This method assumes that the average aspect ratios of modern and ancient samples are similar53,56. As conglomerate beds were prodominately composed of quartzite clasts (C1—95% and C2—98%) using aspect ratios derived from quartzite grains is appropriate.
Estimating event bed transport distance (C1 and C2)
The transport distance (l) of conglomerate event bed (C2) beyond the GST was estimated by using the convergent velocity (Vc) across the Himalaya (as the rate of convergence of the thrust front and stable India), sediment accumulation rate (Sa) in the basin (assuming steady state), and the thickness (t) of sediment accumulated between the gravel bed (e.g. C2) and the overlying Middle-Upper Siwalik contact, which records the ancient position of the GST (Eq. (1), Supplementary Fig. 3).
Due to the oblique convergence between the Indian and Eurasian plates, convergence velocities vary along strike of the Himalayan foreland57 with slower convergence rates reported in the western Himalayas compared to the east (18–20 mm yr−1 and 12–15 mm yr−1, respectively32,33).
Sediment accumulation rates also vary along strike of the Himalayan foreland, with higher rates observed in the east compared to the west. Sediment accumulation rates calculated from Quaternary Ganga Plain sediment cores58,59 closely match foreland subsidence rates7 and long-term sediment accumulation rates from the Miocene Siwalik Group27,60.
Median and standard deviations of both the western foreland convergence velocities (Vc) and sediment accumulation rates (Sa) were used to estimate the distance that the gravel deposits accumulated downstream of the GST (Fig. Supplementary Fig. 2).
In this calculation we assume an approximately stable distance from the mountain front to the GST. This assumption is supported by two points: the coincidence of the GST with a prominent break channel gradient7. A prominent change in slope gradient over distances of kilometres by up to an order of magnitude would require significant amounts of time. Secondly, by the long-term record of the GST observed in the Siwalik sedimentary succession. If the GST did prograde or retrograde within the basin in response to a sustained change in sediment/water discharge or subsidence rates, we would expect thick successions of conglomerate beds to exist within the Middle Siwalik sandstone (e.g.61). As there are no large conglomerate bodies observed within the Middle Siwalik succession this would suggest that the GST has been relatively stable through time.
Contemporary and Siwalik channel geometries
Channel geometries have been derived for Siwalik paleo-channels to use in bedload transport rate calculations. Contemporary channel geometries have been estimated to compare with Siwalik channel geometires to see how comparable the ancient and contemporary systems are.
Channel depth and width
Contemporary channel bankfull depths were derived from Acoustic Doppler current profiler (ADCP) channel cross-section surveys of modern Gangetic Plains rivers downstream of the GST (Karnali River43 and Ganga River62). The deepest recorded point in the channel survey was taken as the channel bankfull depth. Contemporary channel widths were also extracted from ADCP surveys of both rivers.
Ancient channel depths were estimated using the maximum thickness of preserved bedform deposits taken from Siwalik sections. Sections include the Mohand succession documented in this study and previously published detailed sections from the Surai Khola and the Karnali River section63. In literature, bankfull channel depth has been defined as the average thickness of measured barforms (e.g. bar-fill deposits, whether braid bar or point-bar dominated64,65,66). This method does not consider incomplete preservation of bedforms due to truncation, or compaction due to burial. The average bedform thickness, therefore represents an approximate, minimum bankfull height. Additionally, there may be a bias towards the preservation of bigger discharge events, and therefore larger channel depths (i.e. bedform heights), recorded in Siwalik stratigraphy67. Further details can be found in ‘Supplementary Notes 1’.
Channel slope
Contemporary channel slope profiles extending from the Himalayan mountain front to the Ganga trunk stream, were extracted from a 30 m Shuttle Radar Topography Mission Digital Elevation Model (SRTM DEM) for each of the main Ganga Plain rivers (Yamuna, Ganga, Sharda, Karnali, Gandak, and Kosi7). The slope values were averaged over a 10 km moving window7. Slope values from above and below the GST, which has been mapped and defined by noting the point at which channel deposits were exclusively sand (95%)7,53, were separated into two discrete groups (i.e. upstream and downstream of the GST).
The Mohand Siwalik paleoslope Sest for above and below the GST (i.e. above and below the Middle-Upper Siwalik contact) are calculated using two published methods. Ganti et al.68 for below the GST in the sandy reaches, and Paola and Mohrig69 for above the GST in the coarse gravel dominated reach). Both are first estimated from the simple force balance,
where τb is the bed shear stress, ρ is density of water, g is gravity, and h is median bankfull depth (m) (estimated from Mohand Siwalik logs (Fig. 3)). Given that the dimensionless particle mobility number, or Shields parameter,
where s = ρs/ρ, is the relative density of sediment to water, and D50 is the median grain size (m), we can substitute into Eq. (2) and rewrite the paleoslope as,
To estimate the range of formative Shields stress of the Middle Siwalik rivers (sand dominated, below the GST), we used the bedform stability diagram proposed by68,70, with Reynolds number, Rep, calculated by,
where v is the kinematic fluid viscosity, g is acceleration due to gravity, and D50 = 0.35 mm (measured from Siwalik sedimentary logs in this study and published data6. To allow for uncertainty, we used a range of values of D50 from 0.25 mm to 1 mm.
We included a range of the Shields parameter, θ, that corresponds to the existence of dunes and the transitional zone between dunes and upper plane beds. This is a conservative approach that represents the maximum possible range of θ for the stable existence of dunes.
Following Ganti et al.68, we carried out 10,000 Monte Carlo simulations using Eq. (4) to estimate the paleoslope of the Middle Siwalik sandstones (i.e. below the GST). For the simulations we generated random samples of θ (distributed within the bounds provided by the bedform stability diagram (0.045 - 1.1), and random samples of D50 ranging from 0.25 mm - 1 mm, and the median Siwalik Mohand bedform height of h (2.3 m), taken from the Mohand Middle Siwalik sandstone bedform thickness measurements.
For the coarse Upper Siwalik conglomerate, the paleoslope estimator for coarse-grained braied channels of Paloa and Mohrig69 was implemented by substituting θ = (1 + ε)θc into Eq. (4) such that,
Here we assume a quartz density of ρs = 2650 kg/m3. ε = 0.2 is a theoretical constant that relates the shear stress, τb, at the channel centre, to the critical shear stress, τc. θc is a constant equal to 0.047. Substituting into equation (Eq. (6))69 obtain the expression,
Again, we used 10,000 Monte-Carlo simulations using Eq. (7) to estimate the slope for the coarse-grained Upper Siwalik conglomerate channel deposits (i.e. above the GST). The median bankfull height (taken from bedform thickness) for the Upper Siwalik conglomerates, h = 3.95 m, was obtained from combined published and field data53,71. The clast grain size and D50, were chosen randomly within a realistic range (40 - 60 mm) based on published and field data from the study area53,71. Further details can be found in ‘Supplementary Notes 1’.
Estimating concentration of suspended sediment
In hyperconcentrated flows, the sediment concentration does not follow the log profile of sediment in water flows46. More detailed descriptions of the equations outlined in the following sections can be found in41,72.
In estimating the bedload transport rate, the density of the water-sediment mixture is calculated from,
where ρ is the density of the water-sediment fluid, ρw is the density of clear water (1000 kg m−3 for fresh water), c is the depth-averaged concentration of suspended sediment (% volume), and ρs is the density of the grains (2650 kg m−3 for quartzite).
The depth-averaged concentration is approximated by integrating the concentration profile as a function of height (z above the bed, through the water column such that,
where h (m) is water depth, z (m) is vertical distance above the bed, and za (m) is a reference level where the concentration is known, and the local concentration c(z) of suspended sediment at distance z (m) above the bed is estimated from the Rouse profile as
where the Rouse number, \(\hat{z}=\frac{{w}_{s}}{k{u}_{* }}\), and ca is the reference concentration at the reference elevation, z = za above the bed. In the calculation of the Rouse number, ws is the settling velocity of the sediment particles41, k = 0.4 is the von Kármán constant, and u* is the shear velocity.
73 recommend the following expressions for ca and za:
where the transport parameter, \({T}_{{{\mbox{s}}}}=\frac{{\tau }_{b}-{\tau }_{c}}{{\tau }_{c}}.\)τc is the critical shear stress, and the skin friction component of the bed shear stress is given by,
where cfs is the skin friction coefficient (Eq. (13), below), and u is the depth-averaged flow velocity, estimated using the log-law, such, that,
The coefficient of skin-friction cfs is calculated here using a logarithmic relationship, such that,
where k = 0.4 is the von Kármán constant and the bed roughness length \({z}_{0s}=\frac{2.5{D}_{50}}{30}\) for sand41, \({z}_{0s}=\frac{6.8{D}_{50}}{30}\) for gravel74.
Once we have estimated the depth-averaged concentration using Eqs. (9) and (10), we obtain the density of the water-sediment mixture using Eq. (8).
Estimating bedload discharge
Having calculated the density of the water-sediment fluid, we next estimate the rate of bedload transport under hyperconcentrated flow. Detailed descriptions of the bedload transport calculations can be found in72.
The bedload transport, qb (m s−1 per m width), can be calculated as a function of the dimensionless bedload transport rate, Φ, such that,
where g is acceleration due to gravity (9.81 m s−2), D50 is the median grain size, and the relative density, s = ρs/ρ, where ρs is the density of the grains and ρ is the density of the fluid moving above the bed, defined in equation (8).
In this study we estimate the dimensionless bedload transport rate using the40 equation:
or the modified equation,
where θ is calculated using Eq. (3), and φ is a modification coefficient introduced by49 (Supplementary Notes 2, 3, and 4).
From Eq. (15), it is clear that bedload will be mobilised only when θ > 0.047. Combining this with Eq. (3) for the Shields parameter, and the bed shear stress Eq. (11), we can estimate the threshold of motion velocity, u, for a given grain size:
Assuming a water depth of 11 m and all constant variables are the same as those defined in Supplementary Notes 5, Supplementary Table 1, the threshold of motion velocity for 45 mm grain size particles is approximately u = 3.75 m/s. Assuming the river cross sectional area, A = 0.9Bh (= 0.9 × 338 m × 11, Supplementary Notes 5), and discharge, Q = uA, this threshold velocity translates to a discharge of approximately 12,550 m s−1.
Data availability
All data used in the production of this paper and figures are listed in the text, Methods, or Supplementary Notes 1, 2, 3, 4, 5, 6, 7 and 8. Tabulated data used in the calculation of contemporary and Siwalik channel geometries and bedload transit time calculations are available from https://doi.org/10.5525/gla.researchdata.1455.
References
Aggarwal, P., Joshi, P., Ingram, J. & Gupta, R. Adapting food systems of the Indo-Gangetic plains to global environmental change: key information needs to improve policy formulation. Environ. Sci. Policy 7, 487–498 (2004).
Erenstein, O., Hellin, J. & Chandna, P. Poverty mapping based on livelihood assets: a meso-level application in the Indo-Gangetic Plains, India. Appl. Geogr. 30, 112–125 (2010).
Wells, N. A. & Dorr, J. Shifting of the Kosi River, northern India. Geology 15, 204–207 (1987).
Sinha, S., Suresh, N., Kumar, R., Dutta, S. & Arora, B. Sedimentologic and geomorphic studies on the Quaternary alluvial fan and terrace deposits along the Ganga exit. Quat. Int. 227, 87–103 (2010).
Chakraborty, T., Kar, R., Ghosh, P. & Basu, S. Kosi megafan: Historical records, geomorphology and the recent avulsion of the Kosi River. Quat. Int. 227, 143–160 (2010).
Dubille, M. & Lavé, J. Rapid grain size coarsening at sandstone/conglomerate transition: similar expression in Himalayan modern rivers and Pliocene molasse deposits. Basin Res. 27, 26–42 (2015).
Dingle, E. H., Sinclair, H. D., Attal, M., Milodowski, D. T. & Singh, V. Subsidence control on river morphology and grain size in the ganga plain. American Journal of Science 316, 778–812 (2016).
Sinha, R., Ahmad, J., Gaurav, K. & Morin, G. Shallow subsurface stratigraphy and alluvial architecture of the Kosi and Gandak megafans in the Himalayan foreland basin, India. Sediment. Geol. 301, 133–149 (2014).
Dingle, E. et al. Dynamic flood topographies in the Terai region of Nepal. Earth Surf. Process. Landforms 45, 3092 – 3102 (2020).
Huber, M. L., Lupker, M., Gallen, S. F., Christl, M. & Gajurel, A. P. Timing of exotic, far-traveled boulder emplacement and paleo-outburst flooding in the central Himalayas. Earth Surf. Dyn. 8, 769–787 (2020).
Burbank, D. W. Multiple episodes of catastrophic flooding in the Peshawar basin during the past 700,000 years. Geol. Soc. Am. Bull. 16, 43 – 49 (1983).
Goswami, D. C. Brahmaputra River, Assam, India: physiography, basin denudation, and channel aggradation. Water Resour. Res. 21, 959–978 (1985).
Keefer, D. K. Earthquake-induced landslides and their effects on alluvial fans. J. Sediment. Res. 69, 84–104 (1999).
Sinha, R., Jain, V., Babu, G. P. & Ghosh, S. Geomorphic characterization and diversity of the fluvial systems of the Gangetic Plains. Geomorphology (Amsterdam, Netherlands) 70, 207–225 (2005).
Cook, K. L., Andermann, C., Gimbert, F., Adhikari, B. R. & Hovius, N. Glacial lake outburst floods as drivers of fluvial erosion in the Himalaya. Science 362, 53–57 (2018).
Rickenmann, D. Hyperconcentrated flow and sediment transport at steep slopes. J. Hydraul. Eng. 117, 1419–1439 (1991).
Xu, J. Implication of relationships among suspended sediment size, water discharge and suspended sediment concentration: the Yellow River basin, China. Catena 49, 289–307 (2002).
An, C., Parker, G., Hassan, M. A. & Fu, X. Can magic sand cause massive degradation of a gravel-bed river at the decadal scale? Shi-ting River, China. Geomorphology (Amsterdam, Netherlands) 327, 147–158 (2019).
Beverage, J. & Culbertson, J. Hyperconcentrations of suspended sediment. J. Hydraul. Division 90, 117–128 (1964).
Major, J., Janda, R. & Daag, A. Watershed Disturbance and Lahars on the East Side of Mount Pinatubo during the Mid-june 1991 Eruptions (University of Washington Press, 1996).
Rodolfo, K. et al. Two Years of Lahars on the Western Flank of Mount Pinatubo: Initiation, Flow Processes, Deposits, and Attendant Geomorphic and Hydraulic Changes (University of Washington Press, 1996).
O’Connor, J., Hardison, J. & Costa, J. Debris flows from failures of Neoglacial-age moraine dams in the three sisters and Mount Jefferson wilderness areas, Oregon. USGS Professional Paper 1606, 93 (2002).
Maizels, J. Sedimentology, paleoflow dynamics and flood history of jokulhlaup deposits; paleohydrology of Holocene sediment sequences in southern Iceland sandur deposits. J. Sediment. Petrol. 59, 204–223 (1989).
Kostaschuk, R., Terry, J. & Raj, R. Suspended sediment transport during tropical cyclone floods in Fiji. Hydrol. Process. 17, 1149–1164 (2003).
Chapagain, D., Dhaubanjar, S. & Bharati, L. Unpacking future climate extremes and their sectoral implications in western Nepal. Clim. Change 168, 8 (2021).
Dal Zilio, L., van Dinther, Y., Gerya, T. & Avouac, J.-P. Bimodal seismicity in the Himalaya controlled by fault friction and geometry. Nat. Commun. 10, 48–11 (2019).
Burbank, D., Beck, R. & Mulder, T. The Himalayan Foreland Basin (Cambridge University Press, 1996).
Hérail, G. & Mascle, G. Les Siwalik du Népal central: Structures et géomorphologie d’un piémont en cous de déformation. Bull. Assoc. Géographique Française 431, 259–267 (1980).
Mugnier, J. et al. The Siwaliks of western Nepal: I. Geometry and kinematics. J. Asian Earth Sci. 17, 629–642 (1999).
Lavé, J. & Avouac, J. P. Active folding of fluvial terraces across the Siwaliks Hills, Himalayas of central Nepal. J. Geophys. Res.: Solid Earth 105, 5735–5770 (2000).
Jain, V. & Sinha, R. River systems in the Gangetic plains and their comparison with the Siwaliks: A review. Curr. Sci. 84, 1025–1033 (2003).
Feldl, N. & Bilham, R. Great Himalayan earthquakes and the Tibetan plateau. Nature 444, 165–170 (2006).
Stevens, V. L. & Avouac, J. P. Interseismic coupling on the main Himalayan thrust. Geophys. Res. Letters 42, 5828–5837 (2015).
Nakata, T. Geomorphic History and Crustal Movement of the Foothills of the Himalaya: Report of Tohoku University, 7th series: Geography. Tech. Rep., Sheffield (1972).
Arnott, R. W. C. & Hand, B. M. Bedforms, primary structures and grain fabric in the presence of suspended sediment rain. J. Sediment. Petrol. 59, 1062–1069 (1989).
Sumner, E. J., Amy, L. A. & Talling, P. J. Deposit structure and processes of sand deposition from decelerating sediment suspensions. J. Sediment. Res. 78, 529–547 (2008).
Lowe, D. R. Subaqueous liquefied and fluidized sediment flows and their deposits. Sedimentology 23, 285–308 (1976).
Druitt, T. Settling behaviour of concentrated dispersions and some volcanological applications. J. Volcanol. Geotherm. Res. 65, 27–39 (1995).
Xu, J. Implication of relationships among suspended sediment size, water discharge and suspended sediment concentration: the Yellow River basin, China. Catena 78 (2002).
Meyer-Peter, M. & Muller, R. Formulas for bed-load transport. In: Proc., 2nd Congress of Int. Association of Hydraulic Research. Tech. Rep., Stockholm, Sweden (1984).
Soulsby, R. Dynamics of Marine Sands: A Manual for Practical Applications (Thomas Telford, 1997).
Morin, G. P. et al. Annual sediment transport dynamics in the Narayani Basin, Central Nepal: assessing the impacts of erosion processes in the annual sediment budget. J. Geophys. Res. Earth Surf. 123, 2341–2376 (2018).
Dingle, E. H. et al. Sediment dynamics across gravel-sand transitions: Implications for river stability and floodplain recycling. Geology 48, 468–472 (2020).
Pierson, T. C. in Debris-flow Hazards and Related Phenomena Springer Praxis Books, (eds Jakob, M. & Hungr, O.) 159–202 (Springer, 2005).
Lane, E. W. Notes on limit of sediment concentration. J. Sediment. Petrol. 10, 95–96 (1940).
Wan, Z. & Wang, Z. Hyperconcentrated Flow. International Association of Hydraulic Research Monograph Series (Rotterdam, 1994).
Wong, M. & Parker, G. Reanalysis and correction of bed-load relation of Meyer-Peter and Müller using their own database. J. Hydraul. Eng. 132, 1159–1168 (2006).
Cao, Z., Hu, P. & Pender, G. Reconciled bedload sediment transport rates in ephemeral and perennial rivers. Earth Surf. Process. Landforms 35, 1655–1665 (2010).
Cao, Z., Yue, Z. & Pender, G. Landslide dam failure and flood hydraulics. Part II: coupled mathematical modelling. Natural Hazards 59, 1021–1045 (2011).
Bolch, T. et al. The state and fate of Himalayan Glaciers. Science 336, 310–314 (2012).
Mishra, S., Noor, T. & Ashrafee, S. How we coped! What we need? Perception Survey on Impact and Recovery Strategies. Tech. Rep., India (2009).
Bunte, K. & Abt, S. Sampling Surface and Subsurface Particle-size Distributions in Wadable Gravel- and Cobble-bed Streams for Analyses in Sediment Transport, Hydraulics, and Streambed Monitoring. United States Department of agriculture, Forest Service, Rocky Mountain Research. Tech. Rep. (2001).
Quick, L., Sinclair, H. D., Attal, M. & Singh, V. Conglomerate recycling in the Himalayan foreland basin; implications for grain size and provenance. Geol. Soc. Am. Bull. 132, 1639–1656 (2020).
Attal, M. & Lavé, J. in Tectonics, Climate and Landscape Evolution. Special Paper, Ch. 398 (eds. Willett, S., Hovius, N., Brandon, M. & Fisher, D.) 143–171 (Geological Society of America, 2006).
Whittaker, A. C. et al. Decoding downstream trends in stratigraphic grain size as a function of tectonic subsidence and sediment supply. Geol. Soc. Am. Bull. 123, 1363–1382 (2011).
Kellerhals, R. & Bray, D. Improved method for size distribution of stream bed gravel. Water Resour. Res. 7, 1045 – 1047 (1971).
Dewey, J. & Pitman, W. Tectonic evolution of the India/Eurasia collision zone. Eclogae Geologicae Helvetiae 82, 717 – 734 (1989).
Sinha, R., Friend, P. F. & Switsur, V. R. Radiocarbon dating and sedimentation rates in the Holocene alluvial sediments of the northern Bihar plains, India. Geol. Mag. 133, 85–90 (1996).
Singh, A. et al. Counter-intuitive influence of Himalayan river morphodynamics on Indus Civilisation urban settlements. Nat. Commun. 8, 1617–14 (2017).
Sigdel, A., Sakai, T., Ulak, P., Gajurel, A. & Upreti, B. Lithostratigraphy of the Siwalik Group, Karnali River section, far-west Nepal Himalaya. J. Nepal Geol. Soc. 43, 83 – 101 (2011).
Paola, C., Heller, P. L. & Angevine, C. L. The large scale dynamics of grain size variation in alluvial basins, 1: Theory. Basin Res. 4, 73–90 (1992).
Sonkar, G. K., Gaurav, K., Dasgupt, N., Hussain, S. A. & Sinha, R. Eco-geomorphic assessment of the varanasi turtle sanctuary and its implication for ganga river conservation. Curr. Sci. 116, 2063 (2019).
Szulc, A. G. et al. Tectonic evolution of the Himalaya constrained by detrital 40Ar-39Ar, Sm-Nd and petrographic data from the Siwalik foreland basin succession, SW Nepal. Basin Res. 18, 375–391 (2006).
Elliott, T. The morphology, magnitude and regime of a Carboniferous fluvial-distributary channel. J. Sediment. Petrol. 46, 70–76 (1976).
Moody-Stuart, M. High- and low-sinuosity stream deposits, with examples from the Devonian of Spitsbergen. J. Sediment. Petrol. 36, 1102–1117 (1996).
Wang, J. & Bhattacharya, J. P. Plan-view paleochannel reconstruction of amalgamated meander belts, Cretaceous Ferron Sandstone, Notom Delta, south-central Utah, U.S.A. J. Sediment. Res. 88, 58–74 (2018).
Sinclair, H. D. & Cowie, P. A. Basin floor topography and the scaling of turbidites. J. Geol. 111, 277–299 (2003).
Ganti, V., Whittaker, A. C., Lamb, M. P. & Fischer, W. W. Low-gradient, single-threaded rivers prior to greening of the continents. Proc. Natl Acad. Sci. 116, 11652–11657 (2019).
Paola, C. & Mohrig, D. Palaeohydraulics revisited: palaeoslope estimation in coarse-grained braided rivers. Basin Res. 8, 243–254 (1996).
Lamb, M., Grotzinger, J., Southard, J. & Tosca, N. Were Aqueous Ripples on Mars Formed by Flowing Brines? Sedimentary Geology of Mars (eds Grotzinger, J. P. & Milliken, R. E.) 139–150 (2012)
Kumar, R., Ghosh, S. K., Mazari, R. & Sangode, S. Tectonic impact on the fluvial deposits of Plio-Pleistocene Himalayan foreland basin, India. Sediment. Geol. 158, 209–234 (2003).
van Rijn, L. Sediment transport, Part I: bed load transport. J. Hydraul. Eng. 110, 1431 – 1456 (1984).
Garcia, M. & Parker, G. Entrainment of bed sediment into suspension. J. Hydraul. Eng. 117, 414–435 (1991).
Bray, D. Flow resistance in gravel-bed rivers. Can. J. Civil Eng. 14, 77–86 (1982).
Kumar, R., Sangode, S. J. & Ghosh, S. K. A multistorey sandstone complex in the Himalayan Foreland Basin, NW Himalaya, India. J. Asian Earth Sci. 23, 407–426 (2004).
Yin, A. Cenozoic tectonic evolution of the Himalayan orogen as constrained by along-strike variation of structural geometry, exhumation history, and foreland sedimentation. Earth-Sci. Rev. 76, 1–131 (2006).
Lavé, J. & Avouac, J. P. Fluvial incision and tectonic uplift across the Himalayas of central Nepal. J. Geophys. Res.: Solid Earth 106, 26561–26591 (2001).
Acknowledgements
The authors thank Prof. Vimal Singh, Prof. Rotash Kumar, Dr. Emma Graf, Parv Kasana, K.K. Sharma, and DHM (Nepal) for their help, fruitful discussions, and logistical support in the field. They are also grateful to the International Association of Sedimentologists (IAS) and The British Sedimentological Research Group (BSRG) for their financial support of the fieldwork. They also thank Dr. Laure Guerit and an anonymous reviewer for their thorough and thoughtful reviews. This study formed part of a Natural Environment Research Council (NERC) funded E3 DTP Ph.D. (NE/L002558/1).
Author information
Authors and Affiliations
Contributions
This research was conducted in collaboration with named co-authors. L.Q., M.J.C., H.D.S., M.A., and A.G.L.B designed the study and wrote the manuscript. L.Q logged the Siwalik outcrops and calculated gravel transport distance into the plains and contemporary/ancient channel geometries. M.J.C. calculated suspended sediment concentrations, bedload transport rates, transit times of conglomerate beds, and corresponding flood discharges. Figures were produced by L.Q, using ArcMap, Inkscape, and python plotting packages. R.S. gave L.Q. access to, and discussed the Kosi megafan core at the core lab facility at IIT Kanpur, India.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Laure Guerit and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Joe Aslin. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Quick, L., Creed, M.J., Sinclair, H.D. et al. Hyperconcentrated floods cause extreme gravel transport through the sandy rivers of the Gangetic Plains. Commun Earth Environ 4, 297 (2023). https://doi.org/10.1038/s43247-023-00953-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-00953-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.