Abstract
Seagrass ecosystems are important carbon dioxide sinks that can sequester carbon for centuries as organic matter in sediment. They are also a major source of methane, a potent greenhouse gas, which limits their carbon sink capacity. However, data are lacking on their methane emission dynamics. Here, we conduct a one-year survey of carbon dioxide and methane concentrations and air-sea fluxes in Red Sea seagrass, mudflat, and coral backreef ecosystems. All ecosystems were sources of methane and carbon dioxide. Methane concentrations were lowest in the reef lagoon. We suggest that lagoons may be a globally important source of greenhouse gases. Methane concentrations were lower in seagrass than mudflat ecosystems at temperatures below 29.2 °C. Seagrass had the highest annual methane air-sea fluxes but the lowest global warming potential in carbon dioxide equivalent due to a decrease in its flux. Hence, seagrasses can help climate change mitigation compared to bare sediments.
Similar content being viewed by others
Introduction
Coastal vegetated ecosystems dominated by angiosperms - seagrass meadows, mangroves forests, and saltmarshes - are recognized as significant, perennial sinks of atmospheric carbon dioxide (CO2) due to their exceptional ability to sequester organic carbon (Corg) in their sediments1,2,3. As such, they have come to be known as blue carbon ecosystems2. Although they cover less than 0.2% of the global oceanic area, these vegetated ecosystems together contribute 50% of the total Corg burial and 10% of the net primary production in the ocean environment4,5. These high rates of Corg burial are due to the combination of high sedimentation rates (the leaves or roots of the plants acting as traps for suspended particles) and important production of organic matter by the ecosystem. During the burial, part of the organic matter will be degraded through a cascade of redox processes, the last being methanogenic fermentation in anoxic sediment6.
Methane (CH4) is a highly potent greenhouse gas (GHG), although short-lived as it rapidly oxidizes into CO2 in the atmosphere. In terms of global warming potential, 1 g of CH4 produced by a constantly emitting source at the 20-year horizon is equivalent to 96 grams of CO2, and 45 g of CO2 at the 100-year horizon (i.e., CO2 equivalent, CO2eq; Sustained-flux Global Warming Potential model, GSWP)7. Recently, studies on carbon budgeting of vegetated coastal ecosystems have been calling to account for their CH4 production8,9, offsetting the greenhouse gas sink represented by the Corg burial10,11.
In recent years, blue carbon ecosystems have been proposed as hotspots of CH4 emissions. Indeed, about 6 to 11% of the global coastal and oceanic CH4 emissions come from those ecosystems despite, again, occupying only 0.2% of this global marine area (coastal and oceanic emissions being between 1.3 and 4.1%, respectively, of the total of natural and anthropogenic emissions)9. The methanogenic remineralization of organic matter in sediments follows three main pathways—acetoclastic, hydrogenotrophic, and methylotrophic—that all require permanent anoxic conditions12. High amounts of organic matter and enhanced anoxia make coastal vegetated ecosystems hotspots for carbon burial and sequestration. However, these conditions also make those ecosystems hotspots for methanogenesis13. In seagrass ecosystems, the substratum for methanogenesis might not be buried organic matter but methylated compounds released into the sediment by the plant itself, produced initially as protection against osmotic stress12. Conversely, oxygen production by seagrass primary production might enhance CH4 oxidation and reduce emissions14.
Indeed, numerous studies comparing unvegetated sediment and seagrass meadows found enhanced air-sea CH4 fluxes (FCH4 in mol or gCH4 m−2 yr−1) in seagrass, by up to 800%11,13,15,16. The emissions of CH4 in seagrass beds vary spatially and temporally, seasonally, daily, and at higher frequencies (e.g.17,18). This temporal variability is, however, poorly understood, mostly due to practical reasons10,17. Roth et al.17 highlighted that 75% of studies on CH4 fluxes in vegetated ecosystems have been conducted with discrete samples or using incubation chambers, hence with low temporal representativeness. The authors calculated that to obtain a daily mean CH4 concentration within 10% of uncertainty in vegetated and unvegetated sediments, a sampling effort of 50 samples per day is necessary. The scarcity of high-frequency and long-duration studies of FCH4 in seagrass meadows not only reduces our ability to estimate the contribution of seagrass ecosystems to the global fluxes of CH4, but also to assess the emissions due to the presence of the plants by comparing fluxes in meadows with the fluxes in adjacent unvegetated sediments.
In the present study, we investigated the temporal dynamics of CH4 production by seagrasses on a daily to monthly scale. We measured concentration and air-sea fluxes of CH4 together with CO2 and O2 in a perennial seagrass meadow (Cymodocea serrulata) of a coastal lagoon of the Red Sea and in two different types of unvegetated soft sediments: an adjacent subtidal mudflat and a coral backreef lagoon. Emissions of CH4 and CO2 were measured with underwater autonomous sensors with a frequency of 1 measurement per minute for durations of 8 to 20 days between December 2020 and December 2021. We calculated the GSWP in equivalent CO2 for these three different ecosystems and compared the global warming potential of the seagrass meadow to the two unvegetated ecosystems. We hypothesized that seagrass ecosystems could compensate for higher CH4 emission rates by lower CO2 emissions when compared to unvegetated sediment, thereby maintaining a relative benefit in terms of global warming potential.
Material and methods
Study sites
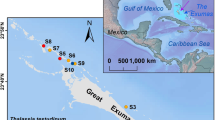
The study sites were a seagrass meadow, a nearby bare mud sediment (mudflat) of a coastal lagoon, and a coral backreef lagoon in the central-eastern Red Sea (Fig. 1).
The eastern coast of the Red Sea is dotted with coastal lagoons and semi-enclosed embayments19. These lagoons are dominated by soft sediments, ranging from sand to mud19. They generally display high turbidity, temperature, and salinity, with important seasonality20. They are a hotspot for mangrove and seagrass biomass20. The coastal lagoon site of our study (22.3292°N, 39.1005°E) is small and semi-enclosed. Three species of seagrass are present in the lagoon. Halophila ovalis and Halodule uninervis occupy nearshore areas subjected to several hours of emersion at low tide (tidal range of approximatively 10–30 cm), particularly in summer, when water levels are about 50 cm lower due to the seasonal shifts in wind regimes affecting the water exchange between Red Sea and Indian Ocean21. Meadows of the larger perennial species Cymodocea serrulata can be found in the shallow subtidal. The sediment remains unvegetated in deeper areas of the lagoon (approximatively >1 m at high tide). The coastal lagoon deployment sites were the C. serrulata meadow (22.3290°N, 39.0995°E) and soft-bottom sediment (22.3283°N, 39.1010°E).
The reef lagoon site (22.2973°N, 38.9661°E) was part of a large area of bare reef sand located on the sheltered of the Al-Fahal coral reef, a 10 km long barrier reef forming the offshore fringe of the local reef system (10–14 km offshore).
Sensor package
The sensor package was composed of a CTD-O2 (conductivity–temperature–depth–oxygen; Ocean Seven 310; Idronaut; Brugherio, Italy), a side-scanning ADCP (acoustic Doppler current profiler; Aquadopp profiler, Nortek; Rud, Norway), a Contros HydroC-CO2 and a Contros HydroC-CH4 for CO2 and CH4 partial pressures, respectively (4H-Jena GmbH; Jena; Germany). The two HydroC sensors were mounted in line and pumped with a single SBE-5T (December 2020 and January 2021 deployments) or SBE-5M pump (all other deployments) (Sea-Bird Scientific, Bellevue, USA), with the inlet at a few cm from substratum and the outlet about 30 cm above. Both inlets and outlets were protected with a copper mesh case. The two HydroC were powered with a rechargeable lithium battery pack encased in a titanium pressure housing, allowing up to 3 weeks of continuous operations.
The sensor package was deployed in the seagrass bed, mudflat, and reef sand site sequentially from December 2020 to November 2021 for 8–19 days (Table 1). For the deployment 10–26 May 2021 deployment in the seagrass bed, only the CH4 sensor was deployed.
The CTD-O2 sampling frequency was 5 min (average interval of 1 s). The ADCP sampled every 10 min (average interval of 60 s). The cell sizes were 0.5 m with a blanking distance of 0.2 m (the first cell at 0.7 m from the bottom). Only in December 2020 and January 2021 was the ADCP set-up with cell sizes of 0.1 m (first cell at 0.2 m).
Drift and response time corrections for the CH4 and CO2 sensors
The HydroC-CH4 and HydroC-CO2 sampled at a 1 min interval. The raw data from the two sensors needed to be corrected for time lag and, for the HydroC-CO2 sensor only, for drift22. The HydroC-CO2 carried a zeroing event every day (1440 min), during which the sensor measured CO2-free air. The recovery time from these events was used to correct the instrument’s drift and lag response according to the equations of Fiedler et al.22 and Miloshevich et al.23. Briefly, we retrieved the offset value (deviation from 0 µatm pCO2) from every zeroing event, applied a linear regression of the offset value versus deployment time from start, and used that equation to correct the drift value at every one-minute node of the pCO2 series. The recovery of the pCO2 to seawater values after a zeroing event follows an exponential growth model, and that recovery pattern is used to correct for the time lag of the sensor. We applied exponential fits to the recovery pCO2 and determined the time constant (t63) for each zeroing event. We interpolated the t63 linearly between events for every 1-min node of the pCO2 time series. Then, we applied the lag correction model of Fiedler et al.22 to every node of the series.
The correction of the HydroC-CH4 data was done similarly, except that this sensor does not need drift correction24. The lag correction was done using a t63-to-temperature linear relationship provided by the manufacturer during calibration for the two pump models (SBE 5M and 5T). After correction, the pCH4 data were smoothed using a centered moving average with a 15-min window. The manufacturer calibrated both CO2 and CH4 sensors prior to initial deployment in December 2020.
The accuracy of the sensors is estimated as 1% of the reading for the HydroC-CO2 and 3% (or 2 µatm, whichever is greater) for the HydroC-CH425. We found a mean difference between the pCO2 calculated from discrete samples total alkalinity and dissolved inorganic carbon (pCO2 = f(TA, DIC) or f(TA, pHT) and the pCO2 from the HydroC of −5 ± 3 % (−29 ± 17 µatm; n = 24; we removed 2 extreme outliers with differences >400 µatm) (Supplementary Material and Methods). However, this difference reflects less the accuracy and precision of the sensors than the small-scale gradients at the sediment and canopy interface and the physical disturbance caused by the sampling in extremely shallow and stratified waters in contact with fine sediment prone to resuspension. The difference in pCO2 between HydroC and discrete samples in our study is comparable to the error in pCO2 in coastal deployments of ISFET pH sensors20,26. We also note that the uncertainty in calculated pCO2 from discrete samples is 17 ± 1 µatm (mean ± SE) due to machine uncertainty and error propagation.
Current velocity
The current velocity from the ADCP was averaged over the water column. The current speed was linearly interpolated for the periods where the water column height was shallower than the first bin position. However, for the deployment in the seagrass bed in September 2021 (17 Sep–02 Oct, 2021), the water level was below the first bin for the entire deployment period. We estimated the current velocity from wind speed for that deployment. We did so to use the same k600 model combining wind speed, current velocity, and water column height for all deployments to be comparable.
We used for this estimation a wind-speed (u) to current velocity (v) relationship modeled from the next deployment at the mudflat (14–28 Oct 2021). We tested three possible models, linear, power, and exponential, and compared them using the Akaike Information Criterion (AIC). The three models presented close fits to the data, with a slight advantage for the power model, which was then chosen (v = a ub + c). The values of the parameters were a = 0.0116 ± 0.0007, b = 1.1147 ± 0.0277 and c = 0.022 ± 0.0011. All three parameters were highly significant (p < 0.001).
The salinity series from the CTD was cleaned for outliers and the missing data replaced by linear interpolation using the R function “tsclean” of the R package “forecast”27.
Wind speed data
The wind speed at 10 m, 1-min logging interval, was obtained from KAUST weather station (22.2926°N, 39.0885°E). The station’s anemometer was in maintenance between the 05 Jan and 05 Jun, 2021. For the sensor deployments outside of this period, we used hourly data on wind speed at 10 m from the ERA5 dataset of the European Centre for Medium-Range Weather Forecasts28.
Gas concentration conversions
All series from the CTD-O2, ADCP, and the wind speed were linearly interpolated to the 1-min timestamp of the pCO2 or pCH4 series and set to mean solar time (MST) (“local2Solar” function, R package “solaR”). The zeroing periods of the pCO2 series were removed and the gap filled by linear interpolation.
The pCH4 (atm) was converted to concentration xCH4 (mol kg−1), assuming it behaves as an ideal gas, using the equation:
With β the Bunsen solubility coefficient, Vm the molar volume of an ideal gas at standard temperature and pressure (STP) (m3 atm mol−1), and ρ the seawater density (kg m−3) calculated from the function “rho” of the R package “seacarb”29.
With S and T the salinity and seawater temperature (K) from the CTD; a1 = −68.8862, a2 = 101.4956, a3 = 28.7314, b1 = −0.076146, b2 = 0.04397, and b3 = 0.006867230; TSTP = 273.15 K, and R the ideal gas constant (m3 atm K−1 mol−1).
The pCO2 was converted to xCO2 (mol kg−1) using the equation31:
With fCO2 the CO2 fugacity (atm) and K0 the Henry constant (mol atm kg−1) calculated with the functions “p2fCO2” and “K0” of the R package “seacarb”29.
Flux calculations
The air-sea fluxes in (mol m−2 min−1) for CH4 and CO2 were calculated as:
With k the gas transfer velocity (m min−1), PHydroC the post-corrected pCH4 or pCO2 value from the sensor (atm), and Patm the atmospheric pCH4 and pCO2 (atm). We used as Patm the mean global atmospheric values for 2021 of 1.9 µatm CH432 and 416.4 µatm CO233.
For CO2, K0 was calculated as in Eq. 4, while for methane, K0 in (mol m−3 atm−1) was calculated from the Bunsen coefficient, assuming it behaves as an ideal gas:
The k (m min−1) was estimated for every minute using the models of Rosentreter et al.34. This choice was justified by the proximity between our ecosystems and the coastal tropical ecosystems bordered by mangroves where Rosentreter et al.34 have parametrized their equations.
k600 (cm h−1) is the gas transfer velocity normalized to a Schmidt number of 600 and Sc the Schmidt number at in-situ temperature and salinity. The Sc for CH4 and CO2 were calculated from the CTD temperature and salinity series using the fourth-order polynomials and coefficients of Wanninkhof35 at salinities 0 and 35, and assuming linearity of Sc with salinity. v (cm s−1) is the current velocity, u (m s−1) the wind speed at 10 m, and h (m) the water column height.
Data summarization and statistical analysis
The time series (Supplementary Fig. 1, 2) were summarized for statistical analysis per hour and per day. Data were averaged per hour for all series (for the fluxes, the 1-min series were integrated over 60 min) (Fig. 2). For each day of each measurement period, we excluded the first and last day as incomplete, and the minimum and maximum hourly mean were extracted. The daily amplitudes (δ) were calculated as the differences between the maximum and minimum for each day. The mean per day of the series was calculated and noted x̄. We excluded the first and last day as incomplete (for the fluxes, the one-minute series were integrated over 24 h). Those individual daily means and amplitudes were averaged per deployment and noted X̄ and Δ (Table 2, Supplementary Table 1). All means are presented ±SE; errors were propagated for X̄, Δ, x̄, and δ. Linear regressions between temperatures and gas concentrations and between concentrations themselves were done with R. The slopes between x̄[CH4] or δ[CH4] and the mean daily temperatures were compared using t-tests. The measurement periods and ecosystems were compared using one-way ANOVA after checking for normality, followed by pair-wise comparisons using Tukey Honest Significant Difference (HSD). ANOVA and HSD tests were done with the software JMP (SAS Institute, Cary, USA). All p-values were two sided.
A–C Hourly mean (±SE) of the CH4 concentration in nmol kg−1 in the seagrass, mudflat, and reef lagoon during three deployment periods (the y-scale is different for the lagoon); D–F Water CO2 partial pressure in µatm, the CO2 was not recorded in May in the seagrass; G–I. Time series of air-sea fluxes of methane in nmol m−2 h−1; K–M. Air-sea fluxes of CO2.
The yearly fluxes (mmol m−2 d−1) were calculated as the mean of the two deployments with the maximum and minimum X̄F in mmol m−2 d−1 (e.g., December and May for FCH4 in seagrass; Table 2) extended to 365 days. This calculation assumes that the fluxes have a periodic behavior at the yearly scale. The SGWP were calculated based on the sum of the yearly FCO2 and FCH4, weighted for their CO2 equivalence.
Results
Dynamics of the CH4 concentrations
We investigated the relationships between each day’s mean CH4 concentrations (x̄[CH4]) and amplitude of CH4 concentrations (δ[CH4]) with the mean temperature (as the primary marker of seasonality) (Figs. 3, 4, Supplementary Table 3). In the seagrass meadow, we found a significant increase of the x̄[CH4] with the mean daily temperatures (R2 = 0.68, p < 0.001, Supplementary Table 3) (Fig. 3A). The deployment daily mean of [CH4] (X̄[CH4]) in May (21.2 ± 0.7 nmol kg−1) was higher than in September (17.4 ± 0.7 nmol kg−1), which was itself higher than in December (11.6 ± 0.4 nmol kg−1) (Table 2; Tukey HSD, all p < 0.0003, Supplementary Table 2). The minimal and maximal hourly means ranged between 8.7 ± 0.2 and 15.5 ± 0.9 nmol kg−1 in December, and 15.2 ± 0.5 and 30.4 ± 1.5 nmol kg−1 in May (Fig. 2A, Supplementary Table 1). As with the x̄[CH4], we found a significant increase of the δ[CH4] with increasing daily mean temperatures (Fig. 3B) (R2 = 0.20, p = 0.005, Supplementary Table 3). Accordingly, we found a seasonal gradient of the mean daily amplitude (Δ[CH4]). The Δ[CH4] was higher in May (15.2 ± 1.5 nmol kg−1) than in December (6.8 ± 0.8 nmol kg−1; Tukey HSD, p < 0.002), but both periods were not different from September (10.8 ± 1.4 nmol kg−1; Tukey HSD, both p > 0.1) (Supplementary Table 1, Supplementary Table 2).
At the mudflat site, the X̄[CH4] ranged between 14.8 ± 1.3 nmol kg−1 in January and 17.7 ± 0.9 nmol kg−1 in June (Table 2). We found a significant increase of the x̄[CH4] with the mean daily temperatures in the mudflat (R2 = 0.27, p = 0.002, Supplementary Table 3) (Fig. 3A). Conversely, the Δ[CH4] decreased with increasing temperature, ranging from 15.2 ± 2.8 nmol kg-1 in January to 11.1 ± 1.5 nmol kg−1 in October (Supplementary Table 1), but the differences between the measurement periods were not significant (Tukey HSD, all p > 0.49, Supplementary Table 2) and we found no trend between δ[CH4] and mean daily temperature (R2 = 0.003, p = 0.76, Supplementary Table 3) (Fig. 3B). The mean hourly minimum concentrations were between 9.7 ± 0.6 (January) and 11.8 ± 0.3 nmol kg−1 (October) (Fig. 2B, Supplementary Table 1). The mean hourly maximum ranged from 25.0 ± 3.1 (January) to 22.9 ± 1.4 nmol kg−1 (October) (Fig. 2B, Supplementary Table 1).
Comparing the dynamics of the seagrass with the mudflat, the slope between mean daily temperature and x̄[CH4] was higher in the seagrass than in the mudflat (1.15 ± 0.13 nmol kg−1 °C, slope p < 0.001 and 0.41 ± 0.12 nmol kg−1 °C, slope p = 0.002, Supplementary Table 3; t-test comparisons of slopes p < 0.001, Supplementary Table 4). We found a higher X̄[CH4] in the seagrass in May (21.2 ± 0.7 nmol kg−1) than in the mudflat in June (17.7 ± 0.9 nmol kg−1, Table 2) (Tukey HSD, p = 0.002, Supplementary Table 2). The X̄[CH4] in May in the seagrass was also higher compared to January and October in the mudflat site (14.8 ± 1.3 and 16.5 ± 0.6 nmol kg−1, Table 2).
The X̄[CH4] in the coral reef lagoon site were comparable between April, August, and November with 7.1 ± 0.2, 6.8 ± 0.2, and 7.05 ± 0.1 nmol kg−1, respectively (Table 2). The x̄[CH4] and δ[CH4] at the reef station did not show any dependency on temperature (p = 0.68 and p = 0.28, respectively, Supplementary Table 3) (Fig. 3A, B). The mean Δ[CH4] for all three periods pooled was 0.98 ± 0.38 nmol kg−1. The x̄[CH4] in the reef (6.97 ± 0.017 nmol kg−1, all periods pooled) were lower than in the mudflat or seagrass sites at all periods (Tukey HSD, all p < 0.004, Supplementary Table 2). The δ[CH4] values in the reef were lower than the δ[CH4] in the mudflat or seagrass sites (Tukey HSD, all p < 0.0001—except for seagrass in December: Tukey HSD, all p > 0.2, Supplementary Table 2).
The daily dynamics of [CH4] varied between ecosystems and deployments and did not seem to follow a persistent day-night dynamic (Fig. 2A–C).
Dynamics of the CO2 concentrations
The X̄pCO2 in the seagrass bed was 479 ± 8 µatm in December and 533 ± 13 µatm in September (Table 2). The ΔpCO2 was 113 ± 11 µatm in December and 290 ± 48 µatm in September (Supplementary Table 1). This difference was due to higher daily maximum pCO2 in September compared to December, 704 ± 26 versus 545 ± 12 µatm (Supplementary Table 1). At the mudflat site, we found a X̄pCO2 of 491 ± 19, 602 ± 12, and 620 ± 16 µatm in January, June, and October, respectively (Table 2). The ΔpCO2 showed a similar pattern with 133 ± 21, 367 ± 27, and 318 ± 31 µatm in January, June, and October (Supplementary Table 1). In the reef lagoon, the X̄pCO2 over the deployment periods were similar in April and November with 483 ± 13 and 486 ± 9 µatm and higher in August with 541 ± 9 µatm (Table 2). Similarly, the ΔpCO2 was higher in August with 172 ± 15 µatm than in April and November with 140 ± 18 and 135 ± 15 µatm (Supplementary Table 1). All three sites displayed similar patterns of variations, with afternoon or evening maxima and morning minima, congruent with CH4 emission patterns (Fig. 2D–F).
There was no relationship between the x̄[CO2] and mean daily temperatures in any of the three ecosystems (Fig. 3C) (all R2 < 0.06, all p > 0.23, Supplementary Table 3). In January–December, we found no differences between the x̄[CO2] at the seagrass site (December X̄[CO2]: 13.2 ± 0.2 µmol kg−1) and at the mudflat site (January X̄[CO2]: 13.8 ± 0.3 µmol kg−1) (Tukey HSD, p = 0.86, Supplementary Table 2). In May–June and September–October, the x̄[CO2] in the seagrass (September, X̄[CO2]: 12.5 ± 0.3 µmol kg−1) was lower than the x̄[CO2] at the mudflat site (June X̄[CO2]: 13.6 ± 0.3 µmol kg−1, Tukey HSD, p = 0.06; October: 14.7 ± 0.3 µmol kg−1, Tukey HSD, p < 0.001, Supplementary Table 2). The δ[CO2] increased with the daily mean temperatures in all three ecosystems (seagrass: R2 = 0.23, p = 0.02; mudflat: R2 = 0.51, p < 0.001; reef: R2 = 0.12, p = 0.03, Supplementary Table 3), with slopes of 0.6 ± 0.2, 0.5 ± 0.09 and 0.3 ± 0.1 µmol kg−1 °C−1 (p = 0.02, p < 0.001 and p = 0.03, Supplementary Table 3) in seagrass, mudflat, and reef, respectively (Fig. 3D). However, the slope for the seagrass was not significantly different from the slopes for the mudflat and reef ecosystems (t-tests, p = 0.72, p = 0.15, Supplementary Table 4). On average, over the year, the Δ[CO2] was higher in the seagrass and mudflat than in the reef, with 6.2 ± 0.9, 7.5 ± 0.5 and 4 ± 0.2, µmol kg−1, respectively (t-test, both p < 0.005, Supplementary Table 4). Conversely, seagrass and mudflat were similar (t-test, p = 0.13, Supplementary Table 4). There was no difference between seagrass and mudflat δ[CO2] in January–December, April–May, and September–October (Tukey HSD, all p > 0.9, Supplementary Table 2).
Relationships between CO2, O2, and CH4 concentrations
We compared the [CH4] to the [CO2] and the [O2] in the three ecosystems (Fig. 4). We studied the relationships between their daily means, and between their daily amplitudes.
In the seagrass, the x̄[CH4] show no relationships with the x̄[O2] (R2 = 0.05, p = 0.68) or the x̄[CO2] (R2 = 0.02, p = 0.5) (Fig. 4A, C, Supplementary Table 5). In contrast, at the daily scale, the δ[CH4] relationships with the δ[CO2] and the δ[O2] were highly significant (R2 = 0.44 and 0.78, both p < 0.001) (Fig. 4B, D, Supplementary Table 5). Conversely to the seagrass, in the mudflat, the regression between x̄[CH4] and both x̄[O2] and x̄[CO2] were both significant (R2 = 0.27 and 0.36, both p < 0.003) (Fig. 4A, C, Supplementary Table 5). Still in contrast with the seagrass, the relationship between the δ[CH4] and the δ[O2] in the mudflat was only marginally significant (R2 = 0.09, p = 0.09) with a slope of opposite sign (−1.6 ± 0.9, p = 0.09) of the δ[CH4] to δ[O2] regression slope in the seagrass (3.6 ± 0.7, p < 0.001). The relationship between δ[CH4] and δ[CO2] in the mudflat station was not significant (R2 = 0.009, p = 0.59) (Fig. 4B, D, Supplementary Table 5).
At the reef sand site, there was no relationship between the x̄[CH4] and the x̄[O2] (R2 = 0.02, p = 0.4) and, between the δ[CH4] and the δ[O2] (R2 = 0.05, p = 0.19) (Fig. 4A, C, Supplementary Table 5). Conversely, x̄[CH4] and x̄[CO2] and, δ[CH4] and δ[CO2] were positively related (R2 = 0.59, p < 0.001 and R2 = 0.22, p = 0.003) (Fig. 4C, D, Supplementary Table 5).
The x̄[CO2] decreased with increasing x̄[O2] in all three ecosystems but not significantly in the seagrass (R2 = 0.07, p = 0.21) (Fig. 4E, Supplementary Table 5). The δ[CO2] increased significantly with the δ[O2] in all three ecosystems (0.62 < R2 < 0.21, all p < 0.007) (Fig. 4F, Supplementary Table 5).
Air-sea fluxes
In the seagrass, the X̄FCH4 fluxes followed the same seasonal increase as X̄[CH4] with 16.1 ± 0.9 in December, 20.4 ± 1 in September, and 25.04 ± 10.1 µmol m−2 d−1 in May (Table 2). Similarly, the ΔFCH4 followed the same pattern with 1676 ± 155, 1528 ± 90, and 691 ± 64 nmol m−2 h−1 in May, September, and December, respectively (Supplementary Table 1). In the mudflat, the X̄FCH4 were 18.8 ± 1.3 in January, 20.6 ± 0.8 in June, and 15.8 ± 0.8 in October µmol m−2 d−1 (Table 2). The ΔFCH4 was between 1537 ± 139 μmol m−2 h−1 in October and 890 ± 117 μmol m−2 h−1 in January (Supplementary Table 1). Parallel to the X̄[CH4], the X̄FCH4 in the reef lagoon site were similar in April, August, and November with 9.6 ± 0.3, 8.3 ± 0.2, and 10.2 ± 0.7 µmol m−2 d−1, respectively (Table 2). The ΔFCH4 were also very similar, ranging from 418 ± 31 in April and 446 ± 35 nmol m−2 h−1 in November. We observed a day-night dynamic in the three ecosystems, with minimal FCH4 in the evening/night and maximum in the early/mid-afternoon (Supplementary Table 1, Fig. 2G–I).
The seagrass bed was a net CO2 source to the atmosphere with X̄FCO2 of 2.6 ± 0.5 and 1.8 ± 0.3 mmol m−2 d−1 in December and September (Table 2). The mean minimum was negative in September, with −41 ± 39 µmol m−2 h−1, and positive in December, with 20.8 µmol m−2 h−1. The mean ΔFCO2 was lower in December with 199 ± 25 compared to 363 ± 54 µmol m−2 h−1 in September (Supplementary Table 1). In the mudflat, we found a progression of the mean X̄FCO2 between January, October, and June with 2.3 ± 0.6, 4.3 ± 0.4, and 4.6 ± 0.3 mmol m−2 d−1, respectively (Table 2). The ΔFCO2 also followed the progression in January, October, and June with 202 ± 24, 271 ± 26, and 408 ± 23 µmol m−2h−1, respectively (Supplementary Table 1). For each period, the mean minimum values were positive. In the reef lagoon, we found higher X̄FCO2 in August (3.8 ± 0.3 mmol m−2 d−1) than in April and November (2.4 ± 0.5 and 2.6 ± 0.3 mmol m−2 d−1, respectively) (Table 2). The mean minimum FCO2 values were −21 ± 19, 1 ± 16, and 30 ± 7 µmol m−2 h−1 in November, April, and August, respectively (Supplementary Table 1). As with the Δ[CO2], the ΔFCO2 were comparable for the three periods, ranging from 234 ± 29 to 257 ± 26 µmol m−2 h−1 (Supplementary Table 1).
Discussion
Seasonality of CH4 enhancement in the seagrass meadow
Our study shows a clear seasonal pattern of x̄[CH4] and δ[CH4] both in the seagrass (C. serrulata) meadow and the mudflat, with lesser variations in the latter. Methanogenesis peaked in May–June with a minimum in January–December. Increasing methanogenesis with increasing temperature is expected in ecosystems due to enhanced microbial activity36,37, as found in seagrass meadows and bare sediments in several studies, including in the Red Sea15,38,39,40. Although seagrass meadow and mudflat CH4 production show the same temperature/seasonal pattern, the CH4 production in the seagrass is higher than in the mudflat when seawater temperature exceeds 29.2 °C (from spring to fall). However, this pattern with temperature could be due to confounding seasonal variables, such as irradiance, photoperiod, water column height, or salinity.
We found a 13% enhancement of the CH4 fluxes in the seagrass compared to the mudflat (7.5 ± 0.2 mmol m−2 yr−1 and 6.6 ± 0.3 mmol m-2 yr−1, Table 3), which is modest compared to the 800% enhancement reported in the Red Sea C. stipulacea meadows15. Globally, the difference between vegetated and unvegetated FCH4 ranges from no differences to a 700% enhancement11,13,16,17. A lack of studies on flux data in winter has been highlighted10, and our study supports the need to conduct year-round studies to obtain a correct estimate of CH4 emissions in coastal vegetated ecosystems. We cannot affirm if the CH4 production in the meadow is modulated by the stimulation or inhibition of methane-oxidizing bacteria, through the oxygenation of the sediment or water column by the plant photosynthesis41,42. Indeed, we found no relationships at our seagrass site between mean [CH4] and [O2], or [CO2]. We did find, however, a relationship between increasing δ[O2] and δ[CH4], which we did not find at the two non-vegetated sediment sites.
Air-sea fluxes
The daily FCH4 in the C. serrulata meadow (16.1 ± 0.9 to 25.04 ± 1.33 µmol m−2 d−1) are within the low range for seagrass ecosystems globally of 1.25–401.50 µmol m−2 d−1 (mean±CI95%: 112 ± 62, median±IQR: 81 ± 87 µmol m−2 d−1)10,43 and, more specifically, for the Red Sea of 0.09–565 µmol m−2 d−1 (mean of 85.1 ± 27.8 µmol m−2 d−1)39. Previous studies in the Red Sea using 12 to 24 h ex situ incubations with sediment cores found rates 3.5 to 20 times higher than ours15,39. We cannot exclude that the difference in methodology between studies explains the disparity of observations. Incubations of seagrass in closed chambers for 24 h could affect the ecosystem’s metabolism, causing, for example, a bias toward underestimating net primary production of up to 76%44. All methods for CH4 fluxes estimates have biases (see ref. 45 for discussion) and, although less invasive and more integrative spatially and temporally than using cores, our flux estimates lack spatial replication and depends on the gas transfer equation combining wind speed, current speed, and water column height34. To our knowledge, our study is the first to use a CH4 sensor to estimate FCH4 in seagrass meadows, although, in principle, our method is not different than measures by cavity ring-down spectroscopy after air equilibration of water pumped directly from the ecosystem17,18,34,46. Both methods do not capture ebullitive fluxes (i.e., microbubbles of CH4 emitted by the sediment), in contrast with studies measuring air-sea fluxes in floating chambers. Rosentreter et al.34 compared the two methods, floating chamber, and water pumping in a mangrove-dominated estuary in Australia. They estimated that the pumping method underestimated the FCH4 by 35% due to missing the ebullitive flux.
The FCH4 in the reef lagoon (seasonal range 8.3 ± 0.2–10.2 ± 0.7 μmol m−2 d−1) is higher, although of the same order, than previous reports in the Great Barrier Reef (GBR). Studies in the GBR found a whole region mean FCH4 of 2.2 ± 0.5 μmol m−2 d−1 4646. Accordingly, surveys in Heron Island (GBR) found seasonal variations between 1.36 ± 1.03 μmol m−2 d−1 and 3.4 ± 0.1 μmol m−2 d−147,48. In comparison, we did not observe in our reef lagoon an inhibition of CH4 emissions by photosynthesis (no correlations between O2 and CH4)46,48. Our data seems to point to a co-production of CO2 and CH4, possibly due to anoxic processes in the sediment, typically dominant in permeable and carbonate-rich sediments of reef lagoons48. The FCH4 in the reef sediment was 1.5 to 2.5 times lower than in the mudflat. This could be caused by enhanced anoxia in mudflat sediments, due to a combination of higher organic carbon content from land, seagrass, and mangroves, and lesser permeability due to smaller grain size and porosity.
The FCH4 in the mudflat (Jan 15.8 ± 0.8–Oct 18.8 ± 1.3 µmol m−2 d−1) were comparable to the global values for coastal shelves (median±IQR: 12 ± 56, mean±CI95%: 754 ± 1241 µmol m−2 d−1), but one order of magnitude lower than estimates for tidal flats (median±IQR: 224 ± 3547, mean±CI95%: 5623 ± 6502 µmol m−2 d−1)9. In contrast with the reef, we did find in the mudflat a negative correlation between x̄[O2] and both x̄[CH4] and x̄[CO2], together with a positive correlation between the two greenhouse gases mean concentrations. This could point to a link between CH4 emissions and ecosystem primary production, at least at the seasonal scale, as we found no correlation at the daily scale between δ[O2] and δ[CH4].
The FCO2 were comparable in the three ecosystems and almost always positive, pointing at a domination of heterotrophy, even in the seagrass ecosystem. In the seagrass, the FCO2 (Sept: 1.8 ± 0.3–Dec: 2.6 ± 0.5 mmol m−2 d−1, Table 2) we measured were within the global range of −72 to +69 mmol m−2 d−1 (mean 3.4, median 3.0 mmol m−2 d−1)45. Globally, about a third of seagrass meadows show net heterotrophy (a quarter in the Indo-Pacific)1,49. We could not deploy our sensors in summer, due to the seasonally low water level regimes which would have exposed the sensors to emersion for up to several days. We do not exclude that the meadow could experience a peak of primary production in summer and turn autotrophic, as regularly observed in other parts of the world (e.g.50), although the combination in the Red Sea of extended emersion and seawater temperatures reaching 34–35 °C might preclude it20. The seagrass meadows of the Red Sea are net autotrophic, with primary production rates in the lower range of global meadows51. A previous study on C. serrulata primary production conducted near our site found net heterotrophy, increasing with higher seawater temperatures52,53.
Radiative balance
Expressing both FCO2 and FCH4 in terms of CO2 equivalent according to the Sustained-flux Global Warming Potential model (GSWP, 20 yr horizon: 1gCH4 = 96gCO2eq; 100 yr: 1gCH4 = 45gCO2eq7), we estimate that our three ecosystems have a GSWP20 ranging from 12.8 ± 0.1 in the seagrass to 17.7 ± 0.1 gCeq m−2 yr−1 in the mudflat (Table 3). In contrast with the two bare sediment ecosystems, the higher CH4 emission in the seagrass is compensated by lower CO2 emissions. Hence, our data shows that the presence of seagrass, although enhancing CH4 emissions, does not lead to enhanced GHG emissions (in CO2eq) due to reduced CO2 production. This makes the presence of seagrass a benefit in terms of GHG mitigation. The Red Sea seagrass ecosystems store Corg in their sediment for over 100 years, consisting of a perennial sink of atmospheric CO2 54. The average burial rates in Red Sea seagrass are modest, 6.8 ± 1.7 gC m−2 yr−1 54, compared to global estimates ranging from 138 ± 382 to 44 ± 6 gC m−2 yr−1 (arithmetic mean55). Adding the carbon burial rate to the GSWPs would bring our seagrass meadow to an estimated GSWP20 of 6.1 ± 1.7 and GSWP100 of 4.4 ± 1.7 gCeq m−2 yr−1 (Table 3). It is likely that the mudflat site also sequesters carbon from external sources, including the neighboring seagrass ecosystem. The meta-analysis conducted by Arias-Ortiz55 reported no statistical differences in carbon sequestration rates between seagrass meadows and bare sediment in studies comparing both (n = 30).
The flux estimates calculated are first-order values as ebullitive fluxes are not considered, our dataset misses spatial replication within ecosystems, and the time series do not cover the whole year 55. Moreover, these carbon budget estimates do not consider DIC export offshore. A large part of the CO2 produced or consumed by the ecosystem is exported as DIC to the neighboring ecosystems, which is dependent on the TA uptake or release occurring in the ecosystem (e.g. refs. 53,56,57). Once exported offshore, the TA anomaly will be diluted, and the excess DIC will be outgassed. In our meadow, the dissolved CO2 that could potentially be exchanged with the atmosphere on site only represented 0.8 ± 3% of the overall DIC (Supplementary Fig. 5).
Conclusion
We found a positive correlation between temperature and CH4 mean concentration and variations in the seagrass and the mudflat. Our test seagrass meadow was a source of greenhouse gas, even when considering the Corg burial in their sediment. This confirms previous studies demonstrating an enhancement of CH4 production by seagrass compared to bare sediment. However, this enhancement was observed in May–June and September–October but not in January–December, with a tipping point at 29.2 °C. This highlights the need to consider the bare sediment background in GHG accounting in seagrass for blue carbon studies. It also highlights the risk of GHG emissions enhancement with the loss of seagrass meadow and with global warming. A third of the global seagrass cover area has disappeared since 1979, with the decline reaching 7% per year in 1990–200058. Our results raise the question of the future evolution of GHG emissions by Red Sea coastal ecosystems with the potential destruction of seagrass meadows linked to ongoing intense coastal development and with global warming59. On that latter point, a recent study showed that the Red Sea might experience reduced rates of warming around the mid-21st century, due to a 70-year cycle linked to the Atlantic Multidecadal Oscilation60. Future studies should include spatial replication if more affordable technologies emerge for the high-frequency measurement of [CH4] and [CO2]. Our study also confirms the importance of the GHG emissions of reef lagoon sediments, a type of ecosystem covering a large marine area in the intertropical zone but often overlooked. Although a smaller source of CH4 than mudflats and seagrass ecosystems, reef sand lagoons need to be considered in global CH4 budgets due to the magnitude of their areal extent.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The dataset is published in the repository PANGAEA https://doi.org/10.1594/PANGAEA.948548. The authors declare no competing interests.
References
Duarte, C. M. et al. Seagrass community metabolism: assessing the carbon sink capacity of seagrass meadows. Global Biogeochem. Cycles 24, GB4032 (2010).
Mcleod, E. et al. A blueprint for blue carbon: toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2. Front. Ecol. Environ. 9, 552–560 (2011).
Bindoff, N. L. et al. Changing Ocean, Marine Ecosystems, and Dependent Communities. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate 447–588 (2019).
Duarte, C. M., Losada, I. J., Hendriks, I. E., Mazarrasa, I. & Marbà, N. The role of coastal plant communities for climate change mitigation and adaptation. Nat. Clim. Chang. 3, 961–968 (2013).
Duarte, C. M., Middelburg, J. J. & Caraco, N. Major role of marine vegetation on the oceanic carbon cycle. Biogeosciences 2, 1–8 (2005).
Arndt, S. et al. Quantifying the degradation of organic matter in marine sediments: a review and synthesis. Earth. Sci. Rev. 123, 53–86 (2013).
Neubauer, S. C. & Megonigal, J. P. Moving beyond global warming potentials to quantify the climatic role of ecosystems. Ecosystems 18, 1000–1013 (2015).
Macreadie, P. I. et al. The future of Blue Carbon science. Nat. Commun. 10, 3998 (2019).
Rosentreter, J. A. et al. Half of global methane emissions come from highly variable aquatic ecosystem sources. Nat. Geosci. 14, 225–230 (2021).
Al‐Haj, A. N. & Fulweiler, R. W. A synthesis of methane emissions from shallow vegetated coastal ecosystems. Glob. Chang. Biol. 26, 2988–3005 (2020).
Oreska, M. P. J. et al. The greenhouse gas offset potential from seagrass restoration. Sci. Rep. 10, 1–15 (2020).
Schorn, S. et al. Diverse methylotrophic methanogenic archaea cause high methane emissions from seagrass meadows. Proc Natl Acad Sci USA 119, 1–12 (2022).
Asplund, M. E. et al. Methane emissions from nordic seagrass meadow sediments. Front. Mar. Sci. 8, 1–10 (2022).
Lyimo, L. D. et al. Shading and simulated grazing increase the sulphide pool and methane emission in a tropical seagrass meadow. Mar. Pollut. Bull. 134, 89–93 (2018).
Burkholz, C., Garcias-Bonet, N. & Duarte, C. M. Warming enhances carbon dioxide and methane fluxes from Red Sea seagrass (Halophila stipulacea) sediments. Biogeosciences 17, 1717–1730 (2020).
Bahlmann, E. et al. Tidal controls on trace gas dynamics in a seagrass meadow of the Ria Formosa lagoon (southern Portugal). Biogeosciences 12, 1683–1696 (2015).
Roth, F. et al. High spatiotemporal variability of methane concentrations challenges estimates of emissions across vegetated coastal ecosystems. Glob. Chang. Biol. 1–15 https://doi.org/10.1111/gcb.16177 (2022).
Ollivier, Q. R., Maher, D. T., Pitfield, C. & Macreadie, P. I. Net drawdown of greenhouse gases (CO2, CH4 and N2O) by a Temperate Australian Seagrass Meadow. Estuaries Coasts https://doi.org/10.1007/s12237-022-01068-8 (2022).
Rasul, N. M. A. in The Red Sea 281–316 https://doi.org/10.1007/978-3-662-45201-1_17 (2015).
Saderne, V., Baldry, K., Anton, A., Agustí, S. & Duarte, C. M. Characterization of the CO2 system in a coral reef, a seagrass meadow, and a mangrove forest in the central Red Sea. J. Geophys. Res. Oceans 124, 7513–7528 (2019).
Pugh, D. T. & Abualnaja, Y. in The Red Sea 317–328 (Springer, 2015). https://doi.org/10.1007/978-3-662-45201-1_18.
Fiedler, B. et al. In situ CO2 and O2 measurements on a profiling float. J. Atmos. Ocean Technol. 30, 112–126 (2013).
Miloshevich, L. M., Paukkunen, A., Vömel, H. & Oltmans, S. J. Development and validation of a time-lag correction for vaisala radiosonde humidity measurements. J. Atmos. Ocean Technol. 21, 1305–1327 (2004).
Castro‐Morales, K. et al. Effects of reversal of water flow in an arctic floodplain river on fluvial emissions of CO2 and CH4. J. Geophys. Res. Biogeosci. 127, 1–25 (2022).
Rose Canning, A., Fietzek, P., Rehder, G. & Körtzinger, A. Technical note: seamless gas measurements across the land-ocean aquatic continuum—Corrections and evaluation of sensor data for CO2, CH4 and O2 from field deployments in contrasting environments. Biogeosciences 18, 1351–1373 (2021).
McLaughlin, K. et al. An evaluation of ISFET sensors for coastal pH monitoring applications. Reg. Stud. Mar. Sci. 12, 11–18 (2017).
Hyndman, R. J. & Khandakar, Y. Automatic time series forecasting: the ‘forecast’ package for ‘R’. J. Stat. Softw. 27, 1–22 (2008).
Hersbach, H. et al. ERA5 hourly data on single levels from 1979 to present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS). ECMWF 147 (2018).
Gattuso, J.-P. et al. seacarb: seawater carbonate chemistry with R. R package version 3.3.1. The Comprehensive R Archive Network, https://cran.r-project.org/web/packages/seacarb/index.html (last Access 28 march 2023), (2022).
Wiesenburg, D. A. & Guinasso, N. L. Equilibrium solubilities of methane, carbon monoxide, and hydrogen in water and sea water. J. Chem. Eng. Data 24, 356–360 (1979).
Weiss, R. F. Carbon dioxide in water and seawater: the solubility of a non-ideal gas. Mar. Chem. 2, 203–215 (1974).
Dlugokencky, E. Trends in Atmospheric Methane (Global Greenhouse Gas Reference Network, 2021).
Tans, P. & Keeling, R. Trends in atmospheric carbon dioxide. Dr. Pieter Tans, NOAA/GML (gml.noaa.gov/ccgg/trends/) and Dr. Ralph Keeling, Scripps Institution of Oceanography (scrippsco2.ucsd.edu/). (2022).
Rosentreter, J. A. et al. Spatial and temporal variability of CO2 and CH4 gas transfer velocities and quantification of the CH4 microbubble flux in mangrove dominated estuaries. Limnol. Oceanogr. 62, 561–578 (2017).
Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 12, 351–362 (2014).
Yvon-Durocher, G. et al. Methane fluxes show consistent temperature dependence across microbial to ecosystem scales. Nature 507, 488–491 (2014).
Wallenius, A. J., Dalcin Martins, P., Slomp, C. P. & Jetten, M. S. M. Anthropogenic and environmental constraints on the microbial methane cycle in coastal sediments. Front. Microbiol. 12, (2021).
George, R., Gullström, M., Mtolera, M. S. P., Lyimo, T. J. & Björk, M. Methane emission and sulfide levels increase in tropical seagrass sediments during temperature stress: a mesocosm experiment. Ecol. Evol. 1917–1928. https://doi.org/10.1002/ece3.6009 (2020).
Garcias-Bonet, N. & Duarte, C. M. Methane production by seagrass ecosystems in the Red Sea. Front. Mar. Sci. 4, (2017).
Borges, A. V., Speeckaert, G., Champenois, W., Scranton, M. I. & Gypens, N. Productivity and temperature as drivers of seasonal and spatial variations of dissolved methane in the Southern Bight of the North Sea. Ecosystems 21, 583–599 (2018).
Laanbroek, H. J. Methane emission from natural wetlands: Interplay between emergent macrophytes and soil microbial processes. A mini-review. Ann. Bot. 105, 141–153 (2010).
Steinle, L. et al. Effects of low oxygen concentrations on aerobic methane oxidation in seasonally hypoxic coastal waters. Biogeosciences 14, 1631–1645 (2017).
Rosentreter, J. A., Al-Haj, A. N., Fulweiler, R. W. & Williamson, P. Methane and nitrous oxide emissions complicate coastal blue carbon assessments. Global Biogeochem. Cycles 35, 1–8 (2021).
Olivé, I., Silva, J., Costa, M. M. & Santos, R. Estimating Seagrass Community Metabolism Using Benthic Chambers: the effect of incubation time. Estuaries Coasts 39, 138–144 (2016).
Rosentreter, J. A. in Carbon Mineralization in Coastal Wetlands 167–196 (Elsevier, 2022). https://doi.org/10.1016/B978-0−12-819220-7.00003-0.
Reading, M. J. et al. Spatial distribution of CO2, CH4, and N2O in the Great Barrier Reef revealed through high resolution sampling and isotopic analysis. Geophys. Res. Lett. 48, 1–13 (2021).
O’Reilly, C., Santos, I. R., Cyronak, T., McMahon, A. & Maher, D. T. Nitrous oxide and methane dynamics in a coral reef lagoon driven by pore water exchange: Insights from automated high-frequency observations. Geophys. Res. Lett. 42, 2885–2892 (2015).
Deschaseaux, E. S. M. et al. The interplay between dimethyl sulfide (DMS) and methane (CH4) in a coral reef ecosystem. Front. Mar. Sci. (in review) 9, 1–12 (2022).
Unsworth, R. K. F., Collier, C. J., Henderson, G. M. & McKenzie, L. J. Tropical seagrass meadows modify seawater carbon chemistry: Implications for coral reefs impacted by ocean acidification. Environ. Res. Lett. 7, 024026 (2012).
Fourqurean, J. W., Willsie, A., Rose, C. D. & Rutten, L. M. Spatial and temporal pattern in seagrass community composition and productivity in south Florida. Mar. Biol. 138, 341–354 (2001).
Anton, A., Baldry, K., Coker, D. J. & Duarte, C. M. Drivers of the low metabolic rates of Seagrass Meadows in the Red Sea. Front. Mar. Sci. 7, (2020).
Burkholz, C., Duarte, C. M. & Garcias-Bonet, N. Thermal dependence of seagrass ecosystem metabolism in the Red Sea. Mar. Ecol. Prog. Ser. 614, 79–90 (2019).
Akhand, A. et al. Lateral carbon fluxes and CO2 evasion from a subtropical mangrove-seagrass-coral continuum. Sci. Total Environ. 752, 142190 (2021).
Serrano, O., Almahasheer, H., Duarte, C. M. & Irigoien, X. Carbon stocks and accumulation rates in Red Sea seagrass meadows. Sci. Rep. 8, 1–13 (2018).
Arias-Ortiz, A. Carbon sequestration rates in Blue Carbon ecosystems: a perspective on climate change mitigation(Doctoral Dissertation), Universitat Autònoma de Barcelona. https://ddd.uab.cat/record/213638 (2019).
Sippo, J. Z., Maher, D. T., Tait, D. R., Holloway, C. & Santos, I. R. Are mangroves drivers or buffers of coastal acidification? Insights from alkalinity and dissolved inorganic carbon export estimates across a latitudinal transect. Global Biogeochem. Cycles 30, 753–766 (2016).
Santos, I. R. et al. The renaissance of Odum’s outwelling hypothesis in ‘Blue Carbon’ science. Estuar Coast Shelf Sci. 255, 107361 (2021).
Waycott, M. et al. Accelerating loss of seagrasses across the globe threatens coastal ecosystems. Proce. Natl Acad. Sci. 106, 12377–12381 (2009).
Chalastani, V. I. et al. Reconciling tourism development and conservation outcomes through marine spatial planning for a Saudi Giga-Project in the Red Sea (The Red Sea Project, Vision 2030). Front. Mar. Sci. 7, 1–15 (2020).
Krokos, G. et al. Natural climate oscillations may counteract Red Sea Warming over the coming decades. Geophys. Res. Lett. 46, 3454–3461 (2019).
Acknowledgements
The authors thank the personnel and skippers of the Coastal and Marine Core Laboratory of the King Abdullah University of Science and Technology (KAUST). We thank Vijayalashmi Dasari, Kaitlyn O’Toole, Darren Coker, and Ute Langner for their help in the field and the lab. This work was funded by the Baseline funds of Michael Berumen and the Academic Space, Equipment, and Planning Committee (ASEPC) at KAUST.
Author information
Authors and Affiliations
Contributions
V.S. conceptualized, designed, and supervised the study, analyzed the data, conducted the research, and wrote the original draft. A.D., W.R., S.C., J.C., and A.K. conducted the research and reviewed the MS.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Joshua Dean and Clare Davis.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saderne, V., Dunne, A.F., Rich, W.A. et al. Seasonality of methane and carbon dioxide emissions in tropical seagrass and unvegetated ecosystems. Commun Earth Environ 4, 99 (2023). https://doi.org/10.1038/s43247-023-00759-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-00759-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.