Abstract
Cordilleran arcs are built by long periods of steady-state magmatism punctuated by transient high-flux magmatic episodes or flare-ups. Such flare-ups, manifested as periods of prodigious silicic volcanism and magmatism, result from geodynamic perturbations that cause elevated rates of magma addition to the crust. Questions remain, however, about how magmatic addition rates quantitatively compare between steady-state and flare-up modes of arc magmatism, and how long after the major geodynamic perturbation the flare-up begins. Here, we compute new estimates of erupted volumes over the last 35 Myr for the 22.5–29°S segment of the Central Andes based on a new volcanic geospatial database. These yield magmatic addition rates at least an order of magnitude higher during flare-up compared to steady-state conditions. A lag time of ~8–12 Myr between ocean ridge subduction (the major geodynamic perturbation in the Central Andean arc) and the onset of flare-up conditions is estimated.
Similar content being viewed by others
Introduction
The intensity of magmatic processes in long-lived magmatic arcs varies in space and time1,2,3. Systematic studies of these variations have led to the recognition of two main magmatic stages: steady-state and flare-up4,5,6. Steady-state refers to the low eruptive/magmatic flux that characterizes the long-term evolution of the arc. Flare-ups, in contrast, are transient excursions of high eruptive/magmatic flux driven by an elevated power input from the mantle, resulting from major geodynamic changes in the subduction system7,8,9. It is during flare-ups that large-scale arc-wide explosive silicic volcanism and their intrusive equivalents (Cordilleran batholiths), are generated5,10,11. Even though the causes behind flare-ups are reasonably well understood for subduction settings5,8,12,13,14,15,16, the detailed timing between the major geodynamic perturbation and the onset of the flare-up remains elusive. Another unknown is how different the magmatic addition rates are between flare-up and steady-state stages, given detailed volumetric and space-time data for volcanism in long-lived active arcs are scarce. Resolving these issues has been challenging due to major uncertainties in both crust-mantle mass balances and plutonic-to-volcanic ratios, as well as the inherent difficulty in confidently estimating the volume of volcanic deposits.
Volumetric eruption rates determined for continental arc segments have been present in the literature since the late 1970s/early 1980s17,18. Comparisons between these values are, however, difficult, and sometimes inappropriate, due to the different methodologies and assumptions used to derive them. Approaches can either be short-term, long-term or ultra-long-term, local or regional, and can either consider flare-ups exclusively or not19,20. When only flare-ups are analyzed, mean eruption rates are obtained by simply dividing the total erupted volume by the duration of the flare-up15. These eruption rates can be used to infer intrusion rates by considering a suite of plutonic-to-volcanic ratios11,15. Sometimes the extrusive and intrusive rates are added to obtain crustal growth rates21,22, which can be useful diagnostic indicators for differentiating steady-state and flare-up stages at Myr timescales5,13,21. This, however, requires calculating volumes for all types of volcanic deposits, not only ignimbrites or other flare-up-related deposits, which can be methodologically challenging and computationally intensive. In addition, as most eruption and crustal growth rates are mean averages (i.e., volume per unit of time for long time intervals), an analysis of how these rates behave at shorter (<<1 Myr) timescales has yet to be attempted.
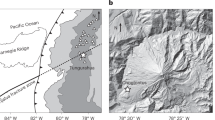
In this study, we provide a volumetric analysis for the last 35 Myr of volcanic activity in the 22.5–29°S segment of the Central Andes (Fig. 1; see Supplementary Note 1 for the tectonic setting of the study area). This arc segment records a time-transgressive Neogene flare-up that tracks the southward subduction of the Juan Fernández ocean ridge, long proposed as its major geodynamic driver (e.g., Fig. 6 in Kay and Coira23; Fig. 3 in de Silva and Kay22). In addition, this region hosts a large number of volcanoes and volcanic deposits whose diverse aspects (e.g., location, morphology, age, composition) have been compiled into a series of volcanic catalogs24,25,26,27,28,29.
a Main tectonic elements. JFR Juan Fernández, TR Taltal, CR Copiapó ridges, based on Bello-González et al.51. NVZ Northern Volcanic Zone, CVZ Central Volcanic Zone, SVZ Southern Volcanic Zone, AVZ Austral Volcanic Zone, based on Stern et al.73. b Main tectonomorphic regions. White rectangle in (b) indicates our study area. Red triangles in (a) and gray triangles in (b) correspond to the Neogene-Quaternary volcanoes according to Siebert et al.74. The black striped regions in (b) depict the Altiplano-Puna Volcanic Complex (APVC63) and the Cerro Galán56 ignimbrite provinces.
Building on this, and in light of the many new geological maps and radiometric ages available for this region and not included in previous catalogs, we collate all available geospatial information into a new volcanic database. We use this new database to examine the diversity of volcano types, volcanic deposits, eruptive volumes and eruption ages in the region. By estimating volume and age constraints for each mapped volcanic deposit, and modeling the evolution of the erupted volume at a temporal resolution of 10 kyr, we (1) provide a comprehensive evaluation of the extrusion rates, with an emphasis on how rates associated with large ignimbrite-forming episodes compare with those related to other smaller-scale volcanic products; and (2) estimate magmatic addition rates based on an ad hoc suite of plutonic-to-volcanic ratios and crustal assimilation proportions. This information is crucial to reconstruct the spatial and temporal evolution of volcanism in the region, to identify and delimit the steady-state and flare-up stages in order to compare them with each other, and to interpret the timing of the arc-segment-scale processes that drive the major variations in magmatic flux. In addition, the importance of magmatism in crustal thickening for this archetypal continental arc segment is reassessed and compared to crustal loss rates for the late Cenozoic.
Results and discussion
Volume and eruption rates estimates
Volume estimates have been made for some of the elements of the volcanic record in our study area, such as ignimbrites and lavas11,17,27,28,30,31,32, stratovolcanoes33,34,35,36,37,38, small monogenetic centers39,40, and widespread tephra deposits41. However, as these volcanic deposits are only a small fraction of the hundreds of deposits (2057) identified in our new database, we calculated a volume and age range for each mapped volcanic deposit, finding an overall good agreement with the volumes previously published in the literature (see the Methods section for information on how the database was constructed and how the volumes were calculated). All these volumes were then summed, and their evolution over time was investigated at 10 kyr intervals for the last 35 Myr. This same time interval was used to calculate eruption rates.
We obtained a total erupted volume of 28,630 ± 1070 km3 (Fig. 2a and Supplementary Fig. 1a). The evolution of the cumulative erupted volume over time shows a gradual increase: 5000 km3 at ~12 Ma; 10,000 km3 at ~8 Ma; and 20,000 km3 at ~4 Ma. The relative contribution of ignimbrites to the cumulative erupted volume has varied over time, from fairly equal proportions between ~20 and 15 Ma and at around 3.5 Ma, to lower proportions (~44%) at present (Fig. 2a).
a Cumulative erupted volume (km3) versus time (Ma). b Eruption rate (km3 per 10 kyr) versus time (Ma). Data are provided for ignimbrites (black line), other volcanic deposits (red dashed line), and these two combined (green line). Uncertainty envelopes are provided in (a). Zoom highlighting the last 10 Myr is shown as an inset in (b). The figures including the 2σ ranges for each plotted group are available in Supplementary Figs. 1–3.
The eruption rates in the past 35 Myr have varied between 0.04 and 133 km3 per 10 kyr with a mean average of ~8 km3 per 10 kyr (Fig. 2b; see Supplementary Fig. 1b for the 2σ range), the latter within the ranges reported by White et al.20 for 36 continental arc segments worldwide. Analyzing these eruption rates over time reveals a smooth increase from near zero to ~10 km3 per 10 kyr at ~16 Ma, then a steady decrease to ~2 km3 per 10 kyr at ~13.5 Ma, and an abrupt increase since then. Since ~10 Ma, nine major peaks above 20 km3 per 10 kyr are evident, with a maximum of ~133 km3 per 10 kyr attained at ~4 Ma (Fig. 2b). These peaks relate to the main pulses of ignimbrite-forming volcanism in the region during the Neogene flare-up11,42. The eruption rates for the remaining volcanic products (i.e., non-ignimbrites) have varied between ~10 and 20 km3 per 10 kyr over the last ~10 Myr (Fig. 2b).
The volume calculated for the ignimbrites is 12,760 ± 1260 km3 (Fig. 2a and Supplementary Fig. 2a). This value falls below the most recent estimates for the Altiplano-Puna Volcanic Complex (APVC) and Cerro Galán ignimbrite provinces combined (~16,500–17,300 km3 22,43), because in our study only the southern half of the APVC was analyzed (Fig. 1b; see the Methods section for information on how the study area was defined). The eruption rates calculated for the ignimbrite-forming eruptions are up to 128 km3 per 10 kyr (Fig. 2b). These rates are within the ranges reported by de Silva and Gosnold11 for the main ignimbrite pulses of the APVC (2–120 km3 per 10 kyr). Nevertheless, due to major volume and age uncertainties (Supplementary Data 1), ignimbrite-forming eruption rates may reach ~600 km3 per 10 kyr at the 2σ model range (Supplementary Fig. 3a). This latter value doubles the maximum rates reported by Salisbury et al.32 (310 km3 per 10 kyr) for the APVC ignimbrites, although Salisbury et al.32 only reported mean eruption rates and did not conduct an uncertainty assessment.
The volume of the remaining volcanic products, 15,870 ±160 km3 (Fig. 2a and Supplementary Fig. 2b), is a new estimate for the region. The mean eruption rate is ~4.5 km3 per 10 kyr (Fig. 2b), although at the 2σ model range eruption rates can be as high as 25 km3 per 10 kyr (Supplementary Fig. 3b). North of our study area, volumes between 2000 and 10,000 km3 were obtained by Francis and Rundle17, Baker and Francis30, and Francis and Hawkesworth31 for different time periods. Extrapolated to the same 10 kyr time window used in our study, Francis and Rundle17 obtained mean eruption rates between 2 and 3.3 km3 per 10 kyr (21–22°S; <10 Myr), Baker and Francis30 an average of ~5 km3 per 10 kyr (19.5–22.5°S; <20 Myr), and Francis and Hawkesworth31 between 3 and 58 km3 per 10 kyr (for different segments of latitude and time intervals). Hence, in general, our eruption rates fall within the same order of magnitude when compared to previous estimates (see Supplementary Table 1 for a comparison between our and previous results). When the eruption rates for the remaining volcanic products are plotted over time (Fig. 2b), we observe that the highest eruption rates occur at ~6 Ma and over the last 1 Myr, the former coinciding with a peak in ignimbrite-forming eruption rates.
Along-arc variations in eruption rates
In this section, in order to further scrutinize volumes and eruption rates over time, we considered the arc in three sub-segments after applying the K-means clustering algorithm to the centroids of the volcanic deposits identified in our database (Supplementary Figs. 4 and 5). The northern segment (22.5–24.5°S; Fig. 3a) groups many of the peaks observed in Fig. 2b, all related to ignimbrite-forming activity. The central segment (24.5–26°S; Fig. 3b) also contains peaks related to ignimbrite-forming eruptions, which occur during low eruption rates in the northern segment. The southern segment (26–29°S; Fig. 3c) shows few ignimbrite-forming eruptions and a steadily increasing eruption rate for smaller-scale eruption products since ~11 Ma.
a Northern segment (22.5–24.5°S). b Central segment (24.5–26°S). c Southern segment (26–29°S). In each figure, the red bracket specifies the time when the collision point of the Juan Fernández Ridge (JFR) against the continental margin moved south of each arc segment according to the two ridge models of Bello-González et al.51. For example, in the lowermost figure, the Juan Fernández Ridge moved south of ~29°S sometime between 17 and 11 Ma.
In the northern segment, the eruption rates related to non-ignimbrite-forming eruptions rise during ignimbrite peak events by almost an order of magnitude (from ~0.5 to 5 km3 per 10 kyr) (Fig. 3a), although two divergences are observed: during an ignimbrite pulse at ~4 Ma (when non-ignimbrite-forming activity remained low) and since ~1.5 Ma (apparent three-fold increase in non-ignimbrite-forming activity with no significant ignimbrite eruptions). In the central segment, there seems to be a brief correlation between ignimbrite- and non-ignimbrite-forming activity at ~2.5 Ma, and discrepancies at ~21–16 Ma and at ~5 Ma (Fig. 3b). The correspondence between ignimbrite and non-ignimbrite output in the northern segment occurred during the first half (~11–6 Ma) of the APVC flare-up. At these times, large and shallow silicic magma reservoirs were likely absent as the thermal conditioning of the upper crust was still limited, so magma generation and processing was largely in the lower to mid-crust below a deep brittle-ductile transition11,12. As the flare-up progressed, the brittle-ductile transition moved upward (~15 km at 13–10 Ma versus ~8–4 km at 5 Ma11,12). It is only when shallow crustal magmatic conditioning became pervasive, at ~6 Ma, that non-ignimbrite-forming eruption rates decrease dramatically (from 8 to 2 km3 per 10 kyr in less than 1 Myr), possibly reflecting a shallow silicic magmatic system hindering deeper, hotter, and less evolved magmas from reaching the surface for at least ~4.5 Myr. Then, at ~1.5 Ma, the removal of the crustal filter of such large and shallow silicic magma reservoirs is suggested based on the abrupt increase in non-ignimbrite-forming activity, marking the transition from flare-up to steady-state magmatism44,45,46.
Non-ignimbrite-forming eruption rates of >1 km3 per 10 kyr began later in the northern segment than in the central and southern segments (~12 Ma versus ~19 Ma and ~23 Ma, respectively) (Fig. 3). The major flare-up leading to ignimbrite emplacement began at ~11 Ma in the northern segment (Fig. 3a), and while non-ignimbrite output in the central segment began rising substantively at ~12 Ma, the flare-up did not start until ~5.5 Ma (Fig. 3b) (the long period of ignimbrite-forming eruptions observed at ~23–15 Ma will need to be further investigated to determine whether it corresponds to a flare-up event). Further south, the southern segment has shown steadily increasing activity since ~11 Ma but major ignimbrite-forming eruptions have yet to occur (Fig. 3c), resembling the activity between ~12 and 5.5 Ma in the central segment.
Temporal relations between eruptive activity and geodynamic drivers
The influence of ocean ridges on subduction settings mainly depends on ridge size, subduction obliquity, and ridge migration velocity, and can induce a transient flattening of the slab if some conditions are met47,48. In the case of the Central Andes, the southward subduction of the Juan Fernández Ridge has apparently controlled the tectono-magmatic evolution of this continental segment during the late Cenozoic22,23,26,49. Slab steepening after a transient flattening caused by the arrival and passage of the Juan Fernández Ridge has long been proposed as the major geodynamic driver to the Central Andean Neogene flare-up. Comparisons of the migration history of the Juan Fernández Ridge with the onset of large-volume volcanism at different arc segments of latitude have led to suggestions of a 5–10 Myr time lag between the two23,28,42,43,50. Based on this premise, the eruption rates shown in Fig. 3 can be compared with a new, refined timing of the migration history of the Juan Fernández Ridge51, and thus constrain the time estimates between ridge passage and the onset of large-volume volcanism for the three arc segments.
Two new kinematic reconstructions are available for the Juan Fernández Ridge starting from ~120 Ma51. Based on these two models, if we consider that the collision point of the ridge against the continental margin left the northern segment at ~19 Ma (Fig. 3a), and then left the central segment at ~17.5 Ma (Fig. 3b), a ~8–12 Myr of delay between ridge migration and flare-up onset can be estimated. This sits at the high end of the lag range of 5–10 Myr suggested by others based on the ridge migration model of Yáñez et al.52. Should this trend continue to the south, the southern segment is likely to experience a flare-up in the next few Myr. In this latter segment, some large-scale crustal anomalies detected at mid-crustal depths (15–30 km), interpreted as partial melt bodies53,54, might be an early signal of this future flare-up.
Magmatic volumes and crustal growth rates
The new volume and eruption rates estimates allow a reappraisal of the magmatic contribution to crustal growth via intrusive and extrusive processes for the last 35 Myr. With respect to ignimbrite-forming activity in our study area, estimations of plutonic-to-volcanic ratios based on geochemical and geophysical modeling can be as high as 75:155, although they usually lie between 5:1 and 35:153,54, where ~50% of that material would be mantle-derived22,42,56. There are similar broad ranges of estimates in relation to other types of volcanism in the region, with plutonic-to-volcanic ratios mostly constrained between 1:1 and 10:117,31,57,58. Likewise, estimates of crustal assimilation proportions are constrained by geochemical evidence at between 12 and 31% for andesitic compositions59,60,61, whereas more extreme values of assimilation have been estimated for large dacitic ignimbrites (~50%42) and for some isolated peraluminous silicic domes enriched in crustal isotopes (~60%62).
Using the calculated eruption rates, we estimated their corresponding intrusive contributions based on the plutonic-to-volcanic ratios outlined above (5:1 to 35:1 for ignimbrites, 1:1 to 10:1 for other volcanic products). Crust-to-mantle ratios were assumed to be 50:50 for the ignimbrites and 30:70 to 10:90 for the other diverse volcanic deposits. New volumes added to the crust from the mantle were obtained by randomly sampling the plutonic-to-volcanic and crust-to-mantle ratios for ignimbrites and other volcanic products, and by adding the calculated intrusive volumes to the extrusive volumes. This exercise was repeated 100,000 times in order to account for the statistical uncertainty (code and files required to replicate these calculations available in Supplementary Data 2). After normalizing these values by unit length of arc (~700 km for the 22.5–29°S segment), we obtained a crustal growth rate whose 1-Myr-moving average increases from ~4 × 10−4 km3 per km of arc per 10 kyr at ~35 Ma to ~0.07 km3 per km of arc per 10 kyr at ~16 Ma, and then to ~0.5 km3 per km of arc per 10 kyr at ~4 Ma, before steadily decreasing to ~one-fifth of the latter value (Fig. 4; see Supplementary Fig. 6 for the 2σ range; see Supplementary Data 3 for other moving averages). Sustained crustal growth rates above ~20 km3 per km of arc per Myr have been proposed to characterize magmatic flare-up stages in arc segments5,13,21. If we extrapolate this rate to our 10 kyr time window, crustal growth rates consistent with a magmatic flare-up are seen between ~9 and 2 Ma (Fig. 4), supporting the designation of the ~11–1 Ma flare-up22,32,42,63. However, even though the diagnostic crustal growth rate of ~20 km3 per km of arc per Myr used to discriminate between steady-state and flare-up seems to work well in our case study, it will have to be further tested in other magmatic arcs to check their viability, especially at shorter (<<1 Myr) time intervals.
Crustal growth rate is shown as a black dotted line, with respect to which a moving average of 1 Myr, shown as a blue line, is calculated. The red horizontal line is drawn at 20 km3 per km of arc per Myr (extrapolated to 10 kyr), proposed as reflecting the boundary between steady-state and flare-up magmatism5,13,21. The data including the 2σ range can be found in Supplementary Fig. 6. Moving averages for different time intervals are provided in Supplementary Data 3.
The crustal growth rates filtered through the 1-Myr-moving average have a mean value of ~0.08 km3 per km of arc per 10 kyr for the last 35 Myr. If this rate is extrapolated to a yearly time window, 0.8 × 10−5 km3 per km of arc per yr, we find that it fits well with models of Baker and Francis30 (0.6 × 10−5 km3 per km of arc per yr) and Francis and Hawkesworth31 (1.3 × 10−5 km3 per km of arc per yr), but falls below the estimates of Pritchard and Simons58 (3.5 × 10−5 to 9.6 × 10−5 km3 per km of arc per yr). The discrepancy could be due to the very different time periods used for the analyses (10 years in the Pritchard and Simons58 case versus 35 million years in our case), so Pritchard and Simons58 likely detected a very short-term pattern in the crustal growth rate that is undetectable in our approach. Our rates also fall below the mean crustal growth rates of Thorpe et al.18 (~2 × 10−5 km3 per km of arc per yr) and Reymer and Schubert19 (~3.3 × 10−5 km3 per km of arc per yr) for the whole Andes for the last 20 and 180 Myr, respectively. These discrepancies could simply be due to the different methodologies and available data used in each volume calculation, although we recognize that no matter the approach, long-term crustal growth rates in the Central Andes vary within the same order of magnitude.
Recognizing that the absolute rates are dependent on the time windows specified for the moving averages (see Supplementary Data 3), it is clear that crustal growth rates during the flare-up are at least an order of magnitude higher than the rates during the steady-state stages that preceded and followed the flare-up. The maximum crustal growth rate calculated here using a 1-Myr-moving average, ~0.5 km3 per km of arc per 10 kyr, is similar to the maximum rate calculated by Freymuth et al.43 for the Neogene ignimbrite pulses in the entire Central Andes (0.7 km3 per km of arc per 10 kyr), but it is at the low end of the range proposed for the Late Cretaceous Sierra Nevada flare-up (0.45–0.9 km3 per km of arc per 10 kyr21,22), although the latter is characterized by crustal growth rates between two and three orders of magnitude higher than during steady-state activity9. The peaks in crustal growth rate observed within the flare-up studied here are related to ignimbrite pulses at approximately 2 Myr intervals: ~8, ~6, and ~4 Ma. During this flare-up, crustal growth rates vary from 0.1–0.2 km3 per km of arc per 10 kyr in the lulls (i.e., between ignimbrite pulses) to 0.25–0.5 km3 per km of arc per 10 kyr during pulses.
When the crustal growth rates shown in Fig. 4 are integrated over time, we obtain the total volume of crust that has been created by magmatic addition (results reported considering the 2σ range in crustal growth rates shown in Supplementary Fig. 6). For the last 11 Myr, we obtain a crustal increment of 230 ± 160 km3 per km of arc. This contrasts with the ~495 km3 per km of arc obtained by de Silva and Kay22 for the 21–27°S segment, although they only considered flare-up related ignimbrites and assumed a fixed plutonic-to-volcanic ratio of 35:1. For the last 15 Myr, we calculate a crustal gain of 240 ± 170 km3 per km of arc, comparable to the ~195 km3 per km of arc obtained by Francis and Hawkesworth31 for the 21–22°S segment. Over the whole 35 Myr period, we obtain a crustal increment of 280 ± 190 km3 per km of arc. Even if the uppermost limit is considered, this accounts for only <2 km increase in the crustal thickness beneath the 22.5–29°S/66.5–69°W quadrangle. This is just ~3–5% of the current crustal thickness known in the region (40–70 km64,65). Thus, in good agreement with Francis and Hawkesworth31 and Kay et al.42 we show that, at a regional scale, late Cenozoic magmatic addition has only played a minor role in crustal thickening beneath this segment of the Central Andes (that is, crustal thickening is mostly tectonic in origin66,67). Crustal loss rates in the region (due to lithospheric foundering and forearc subduction erosion22) are, however, between 0.5 and 1.5 orders of magnitude higher than thickening rates due to magmatic addition for the last 11 Myr. Therefore, in terms of crustal balance, our new data support earlier observations of net crustal loss over the latest Cenozoic in the region22,68).
Conclusions
Our analysis suggests that average magmatic addition rates during magmatic flare-ups are at least an order of magnitude higher than during the long-term steady-state evolution of magmatic arcs. This deviation in magmatic addition rates defines the flare-up versus steady-state mode of magmatic arcs and reflects the role of higher mantle power input (i.e., thermal flux) and the growth and evolution of large, shallow silicic magma reservoirs that feed prodigious eruption rates during flare-ups. The lower rates over the long term reflect lower mantle power, less crustal processing, and smaller magma systems. Episodic flare-ups are ignited by major geodynamic changes; in the case of the Central Andes the southward subduction of the Juan Fernández Ridge seems to be the most likely cause. The Central Andean flare-up is time-transgressive, following the southward subduction of the ridge by ~8–12 Myr. Should this trend continue to the south, the 26–29°S segment of the Central Andes is likely to experience a flare-up in the next few Myr. Our study demonstrates the use of comprehensive volcanic databases as tools to unravel the tectono-magmatic history of continental arc segments.
Methods
Assembling a volcanic database of the 22.5–29°S segment of the Central Andes
The development of the new volcanic geospatial database considered both literature reviews and targeted remote sensing studies, as well as fieldwork to ground truth data in areas of poor mapping or satellite coverage. We defined our study area as the quadrangle 22.5–29°S/64.5–69.5°W (Fig. 1b). The northern limit is the Bolivian border with Chile and Argentina, which coincides approximately with the tectonomorphic boundary between the Altiplano and the Puna; the western limit is the region between the early Cenozoic magmatic arc (Precordillera) and the late Cenozoic magmatic arc (Western Cordillera); the eastern limit is the region between the foreland thrust belt (Subandean, Santa Bárbara and Sierras Pampeanas ranges) and the active foreland basin (Chaco plain); and the southern limit was defined at the latitude of the Cerro de Vidrio dome, which is the southernmost evidence of Quaternary volcanism in the Central Andes69. The study area thus encompasses the bulk of the late Cenozoic (<35 Ma) magmatic province and all known Quaternary volcanism of the southern Central Andes. It also includes the Cerro Galán ignimbrite province in its entirety56 and the southern half of the APVC63 (Fig. 1b).
At the time of this study, 53 official geological maps are available for the 22.5–29°S segment of the Central Andes (Supplementary Fig. 7). We digitized volcanic features from 22 maps of 1:100,000 scale and 21 of 1:250,000 scale, complemented by 7 maps of 1:500,000 scale and 1 map at 1:1,000,000 scale to fill gaps (Supplementary Fig. 7). In addition, two maps of active Chilean volcanoes, at 1:25,000 (Lastarria) and 1:50,000 (Láscar) scales, were included. Overall, this encompassed all late Cenozoic (<35 Ma) volcanic deposits (Supplementary Fig. 8a), volcanic vents (Supplementary Fig. 8b), radiometric ages (Supplementary Fig. 8c), and tectonic structures (Supplementary Fig. 8d). The database was housed in ArcMap 10.2, entered at a 1:20,000 scale, and is publicly available at https://doi.org/10.17608/k6.auckland.16894903.v4.
Volcanic deposits (2057 in total; Supplementary Fig. 8a) were grouped by lithotype and geological epoch. Lithotypes were defined following the Chilean Geological Survey’s 1:100,000-scale maps; that is, tephra fall deposits, lava flows, lava domes, debris flow/avalanche deposits, pyroclastic density current deposits (including ignimbrites), and undifferentiated volcanic deposits. To map volcanic features in regions of poor cartographic or satellite coverage, we drew upon geological sketches published in scientific articles or technical reports, and conducted several field trips, especially in Argentina, to crosscheck this information where possible. Geochronology data (2029 radiometric ages; Supplementary Fig. 8c) were extracted from geological maps as well as from the extensive Andean literature (217 sources in total; Supplementary Data 1). By using the age information available, volcanic deposits were classified into geological epochs by age range, with minimum and maximum ages expressed as a mean and two standard deviations. For those deposits lacking ages, we estimated these from the ages of any adjoining deposits with clear stratigraphic relationships; otherwise, age ranges were assigned by comparing them to neighboring dated deposits with similar geomorphic expression. To do the latter, we used the geological maps available to extract the geological epoch (or sub-epoch) assigned to the undated deposit, and then, we used the nearest dated deposits assigned to the same geological period as the undated deposit to estimate an age range.
Following the same methodology used for mapping and classifying the volcanic deposits, we identified 2950 volcanic vents (Supplementary Fig. 8b). Compared to earlier vent catalogs26,29, some vents were discarded due to being incorrectly sited on non-volcanic landforms (e.g., basement highs, exposed intrusions). The new vent catalog is most accurate for distinctive volcanic features (e.g., cones, isolated lava domes/flows, or craters), and least precise for eroded or partially buried volcanoes. Geomorphic data were integrated with other geological data to infer obscured volcanic vents. In the absence of additional information, we denoted volcanic topography highs, alteration zones, or summit depressions as likely vent zones, which were checked where possible in the field.
Tectonic structures, which include 5887 faults, fractures, fissures, and lineaments, were grouped based on their estimated kinematics (i.e., reverse, normal, strike-slip or unknown) reported on geologic maps (Supplementary Fig. 8d). We only mapped structures with obvious continuity across maps.
Estimating volumes of individual volcanic deposits
In order to estimate eruptive volumes for all the volcanic deposits identified in our database, we used Global Mapper v.18 (https://www.bluemarblegeo.com/global-mapper/). We intersected each digitized volcanic deposit with a global digital elevation model (DEM), using our study in 2019, 30-m resolution ASTER GDEM v.3 (https://search.earthdata.nasa.gov), which has a vertical accuracy of 7–14 m70. Two horizontal surfaces were defined at the lowest and highest elevations intersected by each volcanic deposit, so two volumes (a maximum and a minimum) were obtained by integrating the topography in excess above each horizontal surface. Generally, volume ranges are larger the older the deposit, and can be considered a sensible approach to account for any eroded or remobilized material33. Volume calculations are relatively simple for stratovolcanoes and lava domes, but more difficult for low-aspect-ratio landforms such as lava flows and debris flows. In those cases, we multiplied their surface areas by their maximum and minimum thicknesses (estimated from the DEM and crosschecked with field information where possible). For ignimbrite sheets, most volumes came from the literature (Supplementary Data 1); otherwise, they were calculated by multiplying the surface area by an estimated minimum thickness (from literature sources). Ignimbrite volumes were converted to dense rock equivalent (DRE) volumes by multiplying the bulk volume by 0.6532,71. Volumes of tephra and pyroclastic density current deposits were reported as DRE volumes as well41,72.
In general, our volume estimates fall within the ranges previously obtained for some stratovolcanoes33,34,35,36,37,38 and small monogenetic centers39,40. We identified a few inconsistencies for the youngest stratovolcanoes (e.g., Láscar, Lastarria; ~0.7% of the total number of volcanic deposits), where our volumes almost double those of Grosse et al.34. This may be due to the lower elevations of our polygon boundaries to include remobilized material, whereas those of Grosse et al.34 consider only the topographic edifice.
Volume modeling
We wrote a Matlab script to estimate an age range and a specific volume for each volcanic deposit, including ignimbrites (code and files available in Supplementary Data 2). Volumes were assumed to follow a uniform distribution between the minimum and maximum volumes estimated above. Age ranges were calculated by sampling the normal distributions of dates for each unit. The time period analyzed (last 35 Myr) was partitioned into 10 kyr intervals. Each deposit was assigned to the time interval(s) representative of its period of activity, and its volume evolution was assumed to reflect a constant eruption rate. The total eruption rate representative of each time interval was obtained by summing the eruption rates of all the deposits active at that time. Eruption rates for ignimbrite-forming events and the rest of the volcanic products were calculated separately. We ran this model 100,000 times in order to quantify the statistical uncertainty, which was reported as 2σ assuming a normal distribution.
Data availability
The volcanic geospatial database is publicly available at https://doi.org/10.17608/k6.auckland.16894903.v4. The files required to replicate the results of this study are available in Supplementary Data 2. Supplementary Data 1–3 are also available at the public repository https://doi.org/10.17608/k6.auckland.21523458.v2.
Code availability
Codes used to analyze and plot data are available in Supplementary Data 2. In this file, RecRate.m is a Matlab code that uses the data provided in RecRate.xls to calculate volumes and eruption rates over time. RecRateCrustal.m is a Matlab code that uses the results of RecRate.m to calculate crustal growth rates. These files are also available to download at the public repository https://doi.org/10.17608/k6.auckland.21523458.v2.
References
Armstrong, R. L. Cenozoic igneous history of the U.S. Cordillera from 42° to 49°N latitude. In Cenozoic Tectonics and Regional Geophysics of the Western Cordillera (eds Smith, R. B. & Eaton, G. P.) 152 (Geological Society of America Memoir); https://doi.org/10.1130/MEM152-p265 (1978).
de Silva, S. L., Riggs, N. R. & Barth, A. P. Quickening the pulse: fractal tempos in continental arc magmatism. Elements 11, 113–118 (2015).
Ducea, M. N., Paterson, S. R. & DeCelles, P. G. High-volume magmatic events in subduction systems. Elements 11, 99–104 (2015).
Noble, D. C. Some observations on the Cenozoic volcano-tectonic evolution of the Great Basin, western United States. Earth Planet. Sci. Lett. 17, 142–150 (1972).
Ducea, M. N. The California Arc: thick granitic batholiths, eclogitic residues, lithospheric-scale thrusting, and magmatic flare-ups. GSA Today 11, 4–10 (2001).
de Silva, S. L. Arc magmatism, calderas, and supervolcanoes. Geology 36, 671–672 (2008).
Lipman, P. W., Protska, H. J. & Christiansen, R. L. Evolving subduction zones in the western United States, as interpreted from igneous rocks. Science 174, 821–825 (1971).
Coney, P. J. & Reynolds, S. J. Cordilleran Benioff zones. Nature 270, 403–406 (1977).
Paterson, S. R. & Ducea, M. N. Arc magmatic tempos: gathering the evidence. Elements 11, 91–98 (2015).
Hamilton, W. The volcanic Central Andes – a modern model for the Cretaceous batholiths and tectonics of western North America. In Proceedings of the Andesite Conference (ed McBirney, A. R.) 65, 175–184 (Oregon Department of Geology and Mineral Industries Bulletin, 1969).
de Silva, S. L. & Gosnold, W. D. Episodic construction of batholiths: insights from the spatiotemporal development of an ignimbrite flare-up. J. Volcanol. Geotherm. Res. 167, 320–335 (2007).
de Silva, S. L., et al. Large ignimbrite eruptions and volcano-tectonic depressions in the Central Andes: a thermomechanical perspective. In Mechanisms of Activity and Unrest at Large Calderas (eds Troise, C., De Natale, G. & Kilburn, C. R. J.) 269, 47–63 (Special Publication of the Geological Society of London); https://doi.org/10.1144/GSL.SP.2006.269.01.04 (2006).
Ducea, M. N. & Barton, M. D. Igniting flare-up events in Cordilleran arcs. Geology 35, 1047–1050 (2007).
Best, M. G., Christiansen, E. H., de Silva, S. & Lipman, P. W. Slab-rollback ignimbrite flareups in the southern Great Basin and other Cenozoic American arc: a distinct style of arc volcanism. Geosphere 12, 1097–1135 (2016).
Gravley, D. M., Deering, C. D., Leonard, G. S. & Rowland, J. V. Ignimbrite flare-ups and their drivers: a New Zealand perspective. Earth Sci. Rev. 162, 65–82 (2016).
Chapman, J. B. et al. The causes of continental arc flare ups and drivers of episodic magmatic activity in Cordilleran orogenic systems. Lithos 398–399, 106307 (2021).
Francis, P. W. & Rundle, C. C. Rates of production of the main magma types in the central Andes. Geol. Soc. Am. Bull. 87, 474–480 (1976).
Thorpe, R. S., Francis, P. W. & Harmon, R. S. Andean andesites and crustal growth. Philos. Trans. R. Soc. A 301, 305–320 (1981).
Reymer, A. & Schubert, G. Phanerozoic addition rates to the continental crust and crustal growth. Tectonics 3, 63–77 (1984).
White, S. M., Crisp, J. A. & Spera, F. J. Long-term volumetric eruption rates and magma budgets. Geochem. Geophys. Geosyst. 7, Q03010 (2006).
Jicha, B. R. & Jagoutz, O. Magma production rates for intraoceanic arcs. Elements 11, 105–111 (2015).
de Silva, S. L. & Kay, S. M. Turning up the heat: high-flux magmatism in the Central Andes. Elements 14, 245–250 (2018).
Kay, S. M. & Coira, B. L. Shallowing and steepening subduction zones, continental lithospheric loss, magmatism, and crustal flow under the Central Andean Altiplano-Plateau. In Backbone of the Americas: Plateau Uplift, Shallow Subduction and Ridge Collision (eds Kay, S. M., Ramos, V. A. & Dickinson, W. R.) 204, 229–259 (Geological Society of America Memoir); https://doi.org/10.1130/2009.1204(11) (2009).
de Silva, S. L. & Francis, P. W. Volcanoes of the Central Andes, 216 (Spinger-Verlag, Berlin, 1991).
Coira, B., Kay, S. M. & Viramonte, J. The Argentine Puna – a model for changing subduction geometry. Int. Geol. Rev. 35, 677–720 (1993).
Trumbull, R. B. et al. The time-space distribution of Cenozoic volcanism in the South-Central Andes: a new data compilation and some tectonic implications. In The Andes: Active Subduction Orogeny (eds Oncken, O. et al.) 29–43 (Springer-Verlag, Berlin); https://doi.org/10.1007/978-3-540-48684-8_2 (2006).
Guzmán, S. et al. Spatial-temporal distribution of explosive volcanism in the 25-28˚S segment of the Andean Central Volcanic Zone. Tectonophysics 636, 170–189 (2014).
Brandmeier, M. & Wörner, G. Compositional variations of ignimbrite magmas in the Central Andes over the past 26 Ma – a multivariate statistical perspective. Lithos 262, 713–728 (2016).
Tibaldi, A., Bonali, F. L. & Corazzato, C. Structural control on volcanoes and magma paths from local- to orogen-scale: the central Andes case. Tectonophysics 699, 16–41 (2017).
Baker, M. C. W. & Francis, P. W. Upper Cenozoic volcanism in the Central Andes – ages and volumes. Earth Planet. Sci. Lett. 41, 175–187 (1978).
Francis, P. W. & Hawkesworth, C. J. Late Cenozoic rates of magmatic activity in the Central Andes and their relationships to continental crust formation and thickening. J. Geol. Soc. London 151, 845–854 (1994).
Salisbury, M. J. et al. 40Ar/39Ar chronostratigraphy of Altiplano-Puna volcanic complex ignimbrites reveals the development of a major magmatic province. Geol. Soc. Am. Bull. 123, 821–840 (2011).
Karátson, D., Telbisz, T. & Wörner, G. Erosion rates and erosion patterns of Neogene to Quaternary stratovolcanoes in the Western Cordillera of the Central Andes: an SRTM DEM based analysis. Geomorphology 139–140, 122–135 (2012).
Grosse, P., Euillades, P. A., Euillades, L. D. & van Wyk de Vries, B. A global database of composite volcano morphometry. Bull. Volcanol. 76, 784 (2014).
Grosse, P., Guzmán, S. & Petrinovic, I. A. Volcanes compuestos cenozoicos del noroeste argentino. In Ciencias de la Tierra y Recursos Naturales del NOA (eds Muruaga, C. M. & Grosse, P.) 484–517 (Relatorio del XX Congreso Geológico Argentino, 2017).
Grosse, P., Orihashi, Y., Guzmán, S. R., Sumino, H. & Nagao, K. Eruptive history of Incahuasi, Falso Azufre and El Cóndor Quaternary composite volcanoes, southern Central Andes. Bull. Volcanol. 80, 44 (2018).
Grosse, P., Guzmán, S. R., Nauret, F., Orihashi, Y. & Sumino, H. Central vs. lateral growth and evolution of the <100 ka Peinado composite volcano, southern Central Volcanic Zone of the Andes. J. Volcanol. Geotherm. Res. 425, 107532 (2022).
Naranjo, J. A., Hevia, F., Villa, V. & Ramírez, C. Miocene to Holocene geological evolution of the Lazufre segment in the Andean volcanic arc. Geosphere 15, 47–59 (2019).
Grosse, P. et al. Geomorphology, morphometry, spatial distribution and ages of mafic monogenetic volcanoes of the Peinado and Incahuasi fields, southernmost Central Volcanic Zone of the Andes. J. Volcanol. Geotherm. Res. 401, 106966 (2020).
Parra-Encalada, D. et al. Physical and chemical evolution of the largest monogenetic lava field in the Central Andes: El Negrillar Volcanic Field, Chile. J. Volcanol. Geotherm. Res. 426, 107541 (2022).
Fernández-Turiel, J. L. et al. The large eruption 4.2 ka cal BP in Cerro Blanco, Central Volcanic Zone, Andes: Insights to the Holocene eruptive deposits in the southern Puna and adjacent regions. Estud. Geol. 75, e088 (2019).
Kay, S. M., Coira, B. L., Caffe, P. J. & Chen, C.-H. Regional chemical diversity, crustal and mantle sources and evolution of central Andean Puna plateau ignimbrites. J. Volcanol. Geotherm. Res. 198, 81–111 (2010).
Freymuth, H., Brandmeier, M. & Wörner, G. The origin and crust/mantle mass balance of Central Andean ignimbrite magmatism constrained by oxygen and strontium isotopes and erupted volumes. Contrib. Mineral. Petrol. 169, 58 (2015).
Hildreth, W. Gradients in silicic magma chambers: Implications for lithospheric magmatism. J. Geophys. Res. Solid Earth 86, 10153–10192 (1981).
Burns, D. H., de Silva, S. L., Tepley, F. J., Schmitt, A. K. & Loewen, M. W. Recording the transition from flare-up to steady-state magmatism at the Purico-Chascon volcanic complex, northern Chile. Earth Planet. Sci. Lett. 422, 75–86 (2015).
Burns, D. H. & de Silva, S. L. Andesites and evolution of the continental crust: perspectives from the Central Volcanic Zone of the Andes. Front. Earth Sci. 10, 961130 (2023).
Gerya, T. V., Fossati, D., Cantieni, C. & Seward, D. Dynamic effects of aseismic ridge subduction: numerical modelling. Eur. J. Mineral. 21, 649–661 (2009).
Flórez-Rodríguez, A. G., Schellart, W. P. & Strak, V. Impact of aseismic ridges on subduction systems: insights from analog modeling. J. Geophys. Res. Solid Earth 124, 5951–5969 (2019).
Martinod, J., Gérault, M., Husson, L. & Regard, V. Widening of the Andes: an interplay between subduction dynamics and crustal wedge tectonics. Earth Sci. Rev. 204, 103170 (2020).
Beck, S. L., Zandt, G., Ward, K. M. & Scire, A. Multiple styles and scales of lithospheric foundering beneath the Puna Plateau, central Andes. In Geodynamics of a Cordilleran Orogenic System: The Central Andes of Argentina and Northern Chile (eds DeCelles, P. G., Ducea, M. N., Carrapa, B. & Kapp, P. A.) 212 (Geological Society of America Memoir); https://doi.org/10.1130/2015.1212(03) (2015).
Bello-González, J. P., Contreras-Reyes, E. & Arriagada, C. Predicted path for hotspot tracks off South America since Paleocene times: tectonic implications of ridge-trench collision along the Andean margin. Gondwana Res. 64, 216–234 (2018).
Yáñez, G. A., Ranero, C. R., Huene, R. & Díaz, J. Magnetic anomaly interpretation across the southern central Andes (32–34°S): the role of the Juan Fernández Ridge in the late Tertiary evolution of the margin. J. Geophys. Res. 106, 6325–6345 (2001).
Delph, J. R., Ward, K. M., Zandt, G., Ducea, M. N. & Beck, S. L. Imaging a magma plumbing system from MASH zone to magma reservoir. Earth Planet. Sci. Lett. 457, 313–324 (2017).
Ward, K. M., Delph, J. R., Zandt, G., Beck, S. L. & Ducea, M. N. Magmatic evolution of a Cordilleran flare-up and its role in the creation of silicic crust. Sci. Rep. 7, 9047 (2017).
Tierney, C. R., Schmitt, A. K., Lovera, O. M. & de Silva, S. L. Voluminous plutonism during quiescence revealed by thermomechanical modeling of zircon. Geology 44, 683–686 (2016).
Kay, S. M., Coira, B., Wörner, G., Kay, R. W. & Singer, B. S. Geochemical, isotopic and single crystal 40Ar/39Ar age constraints on the evolution of the Cerro Galán ignimbrites. Bull. Volcanol. 73, 1487–1511 (2011).
Haederle, M. & Atherton, M. Shape and intrusion style of the Coastal Batholith, Peru. Tectonophysics 345, 17–28 (2002).
Pritchard, M. E. & Simons, M. An InSAR-based survey of volcanic deformation in the central Andes. Geochem. Geophys. Geosyst. 5, Q02002 (2004).
Guzmán, S. et al. Petrology of the Luingo caldera (SE margin of the Puna plateau): a middle Miocene window of the arc-back arc configuration. J. Volcanol. Geotherm. Res. 200, 171–191 (2011).
Godoy, B. et al. Sr- and Nd- isotope variations along the Pleistocene San Pedro – Linzor volcanic chain, N. Chile: tracking the influence of the upper crustal Altiplano-Puna Magma Body. J. Volcanol. Geotherm. Res. 341, 172–186 (2017).
González-Maurel, O. et al. Constraining the sub-arc, parental magma composition for the giant Altiplano-Puna Volcanic Complex, northern Chile. Sci. Rep. 10, 6864 (2020).
Caffe, P. J., Trumbull, R. B., Coira, B. L. & Romer, R. L. Petrogenesis of Early Neogene magmatism in the northern Puna; implications for magma genesis and crustal processes in the Central Andean Plateau. J. Petrol. 43, 907–942 (2002).
de Silva, S. L. Altiplano-Puna volcanic complex of the Central Andes. Geology 17, 1102–1106 (1989).
Tassara, A., Götze, H. J., Schmidt, S. & Hackney, R. Three-dimensional density model of the Nazca plate and the Andean continental margin. J. Geophys. Res. 111, B09404 (2006).
Tassara, A. & Echaurren, A. Anatomy of the Andean subduction zone: three-dimensional density model upgraded and compared against global-scale models. Geophys. J. Int. 189, 161–168 (2012).
Isacks, B. Uplift of the Central Andean plateau and bending of the Bolivian orocline. J. Geophys. Res. 93, 3211–3231 (1988).
Allmendinger, R. W., Jordan, T. W., Kay, S. M. & Isacks, B. L. The evolution of the Altiplano-Puna plateau of the Central Andes. Ann. Rev. Earth Planet. Sci. 25, 139–174 (1997).
Kukowsky, N. & Oncken, O. Subduction erosion – the “normal” mode of fore-arc material transfer along the Chilean margin? In The Andes: Active Subduction Orogeny (eds Oncken, O. et al.) 217–236 (Springer-Verlag, Berlin); https://doi.org/10.1007/978-3-540-48684-8_10 (2006).
Bissig, T., Clark, A. H. & Lee, J. K. W. Cerro de Vidrio rhyolitic dome: evidence for Late Pliocene volcanism in the central Andean flat-slab region, Lama-Veladero district, 29°20’S, San Juan Province, Argentina. J. S. Am. Earth Sci. 15, 571–576 (2002).
Talchabhadel, R., Nakagawa, H., Kawaike, K., Yamanoi, K. & Raj Thapa, B. Assessment of vertical accuracy of open source 30m resolution space-borne digital elevation models. Geomat. Nat. Hazards Risk 12, 939–960 (2021).
Folkes, C. B. et al. A re-appraisal of the stratigraphy and volcanology of the Cerro Galán volcanic system, NW Argentina. Bull. Volcanol. 73, 1427–1454 (2011).
Báez, W. et al. Pulsating flow dynamics of sustained, forced pyroclastic density currents: insights from a facies analysis of the Campo de la Piedra Pómez ignimbrite, southern Puna, Argentina. Bull. Volcanol. 82, 53 (2020).
Stern, C. R. et al. Chilean volcanoes. In The Geology of Chile (eds Moreno, T. & Gibbons, W.) 149–180 (The Geological Society, London); https://doi.org/10.1144/GOCH.5 (2007).
Siebert, L., Simkin, T. & Kimberly, P. Volcanoes of the World 3rd edn, 551 (University of California Press, Berkeley, 2010).
Acknowledgements
DB acknowledges CONICYT-Becas Chile for a PhD scholarship and the University of Auckland for funding support. SLdS acknowledges the US National Science Foundation (NSF) and the National Aeronautical and Space Agency (NASA) for funding support for Central Andean work over the last three decades. SJC and JML acknowledge Transitioning Taranaki to a Volcanic Future for funding support (UOAX1913). PJC acknowledges CONICET for funding support (Grant PUE-INECOA 22920170100027CO). Discussions about Andean magmatism with F. Aguilera, D. Burns, B. Coira, S. M. Kay, G. Maro, I. Petrinovic, R. B. Trumbull, and G. Wörner are also acknowledged. We are grateful to editors Joe Aslin and Joao Duarte, as well as three reviewers (Dr White, Dr Ganade, and one anonymous), for their insightful comments and suggestions that substantially improved the quality and structure of this paper. Further information, if needed, is available by contacting the corresponding author at daniel.bertin.u@gmail.com.
Author information
Authors and Affiliations
Contributions
DB conceived the study, compiled the geospatial database, developed methods, wrote and ran all code, wrote the manuscript, and prepared all relevant figures and complements. This work was supported and supervised by SLdS, JML, SJC, PJC, and CBC, who also contributed to the interpretation and edited the manuscript with several inputs from PG, WB, EB, and RC. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Scott White, Beatriz Coira, and Carlos Ganade for their contribution to the peer review of this work. Primary Handling Editors: João Duarte and Joe Aslin. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bertin, D., de Silva, S.L., Lindsay, J.M. et al. Magmatic addition rates differentiate periods of steady-state versus flare-up magmatism in the Central Andean arc. Commun Earth Environ 4, 75 (2023). https://doi.org/10.1038/s43247-023-00744-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-00744-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.