Projected increase in carbon dioxide drawdown and acidification in large estuaries under climate change

Abstract

Most estuaries are substantial sources of carbon dioxide (CO₂) to the atmosphere. The estimated estuarine CO₂ degassing is about 17% of the total oceanic uptake, but the effect of rising atmospheric CO₂ on estuarine carbon balance remains unclear. Here we use 3D hydrodynamic-biogeochemical models of a large eutrophic estuary and a box model of two generic, but contrasting estuaries to generalize how climate change affects estuarine carbonate chemistry and CO₂ fluxes. We found that small estuaries with short flushing times remain a CO₂ source to the atmosphere, but large estuaries with long flushing times may become a greater carbon sink and acidify. In particular, climate downscaling projections for Chesapeake Bay in the mid-21st century showed a near-doubling of CO₂ uptake, a pH decline of 0.1–0.3, and >90% expansion of the acidic volume. Our findings suggest that large eutrophic estuaries will become carbon sinks and suffer from accelerated acidification in a changing climate.

Introduction

Estuaries are a major conduit of carbon and nutrients from terrestrial to marine systems and play an important role in the global carbon cycle^1,2. Many estuaries have pCO₂ values well above the atmospheric equilibrium values and are substantial sources of CO₂ to the atmosphere^3,4,5,6. Estuaries release ~0.25 Pg C y⁻¹ on a global scale, which is equivalent to 17% of the total oceanic uptake despite occupying an area that is only 0.03% of the global oceans⁷. Uncertainty in this estuarine CO₂ degassing flux, however, is rather high with the estimated total flux as high as 0.45 Pg C y⁻¹, which is on the same order of magnitude as the global riverine dissolved inorganic carbon flux to the ocean^1,4. In general, inputs from CO₂-rich riverine waters, lateral transport from coastal wetlands, and net ecosystem heterotrophy drive the emission of CO₂ to the atmosphere^8,9,10. Consequently, pH dynamics in small estuaries filled with CO₂-rich waters are thought to be relatively unaffected by rising atmospheric CO₂ level¹¹. In contrast, large eutrophic estuaries are often autotrophic and can be CO₂ sinks^{10,12,13,14,15,16}. Recent analysis of one such estuary, Chesapeake Bay, showed that this CO₂ uptake combined with high rates of bottom-water respiration of organic matter in a system with low buffering capacity leads to severe acidification and increased carbonate mineral dissolution^17,18, with potential detrimental effects on shellfish^19,20. A major open question is how estuaries, in particular large and eutrophic ones, respond to climate change with rising atmospheric CO₂, warming, sea level rise, and a changing hydrologic cycle in the 21st century.

Prior carbon budgets have shown that Chesapeake Bay is autotrophic overall, but heterotrophic in upper Bay and autotrophic in middle and lower Bay^12,21. Correspondingly, the air‐sea CO₂ flux displayed a strong along-channel gradient where the upper Bay was a strong CO₂ source, akin to small estuaries around the word, whereas the productive mid Bay was a sink, and the lower Bay was in a nearly neutral condition^22,23. This spatial variability stems from the fact that low salinity upper bay is heterotrophic and has enhanced oxidation of fluvial organic matter while seaward regions are autotrophic and allow for high rates of primary production²¹. Under the current climate Chesapeake Bay as a whole has been estimated to be a weak sink or source of CO₂, subject to natural variability and uncertainties in measurement errors and model estimates^15,23,24.

Chesapeake Bay is a poorly buffered estuarine system where eutrophication has already led to hypoxic and acidified conditions in its subsurface waters^17,19. Excessive nutrient loading stimulates primary production in the surface euphotic layer which consumes CO₂, but unassimilated organic matter sinks and decomposes in bottom waters, consuming dissolved oxygen (O₂) and producing CO₂²⁵. Cai et al.¹⁷ showed that the combined effects of river‐ocean mixing and acid production from respiration and other redox reactions lead to a low buffer capacity and severe acidification in the bottom waters of upper-middle parts of the estuary. Furthermore, Chesapeake Bay has also experienced rapid climate change in recent decades, including faster warming, rapid relative sea level rise and altered river flows^26,27,28. A 30-year (1980-2015) hindcast simulation demonstrated an acidification trend in the middle and lower Bay, although pH in the upper Bay showed an upward trend due to river basification¹⁸. It is unclear if these pH trends will continue into the future as rising atmospheric CO₂ level and global warming are expected to accelerate in the 21st century.

In this paper, we conducted climate downscaling projections by forcing coupled hydrodynamic-biogeochemical-carbonate chemistry models of Chesapeake Bay^18,20,21,22 with regional climate model projections for the mid-21st century²⁹. The model projected a near doubling of CO₂ uptake, a further pH reduction of 0.3, 90% increase in the acidic volume, and 25% increase in the under-saturated volume of the carbonate mineral aragonite. To evaluate how common these future patterns might be, we implemented a box model of two generic (large and small) estuaries to further show that these contrasting estuarine types respond differently to increasing atmospheric pCO₂, with stronger CO₂ evasion in small estuaries but large increases in CO₂ uptake in large eutrophic estuaries.

Results

Long-term changes in carbonate chemistry

We illustrate climate change effects on carbonate chemistry in Chesapeake Bay by calculating the decadal-averages of along channel distributions of summer mean salinity, Total Alkalinity (TA), Dissolved Inorganic Carbon (DIC), pH_T (in total proton concentration scale), dissolved O₂ and the aragonite saturation state (Ω_arag) for 1989–1998 (late-20th century) and 2059–2068 (mid-21st century). Distributions of TA and DIC were similar to the salinity distribution, with strong longitudinal and vertical gradients (Figs. 1a, 1d, 1g). DIC > TA in the upper Bay and bottom waters of the mid-Bay but TA > DIC in the lower Bay and surface waters of the mid-Bay (Supplementary Fig. 1a). In the late-20th century pH_T was ~7.2 in the upper Bay and ~7.8 in the lower Bay (Fig. 1j). pH_T also showed a strong vertical gradient as phytoplankton photosynthesis elevated surface pH_T to 8.0 and organic matter respiration drew down bottom pH_T. O₂ distributions showed a hypoxic zone in the bottom waters (Fig. 1m). The aragonite saturation state Ω_arag fell below 1 in the upper Bay and bottom waters of the mid-Bay (Fig. 1p). The distributions of these physical and biogeochemical properties are consistent with observations^15,30.

Fig. 1: Projected changes in carbonate chemistry parameters in Chesapeake Bay between the late-20th and mid-21st century.

Along-channel distributions of summer mean (June to August) salinity (psu, a–c), TA (Total Alkalinity, μmol kg⁻¹, d–f), DIC (Dissolved Inorganic Carbon, μmol kg⁻¹, g–i), pH_T (j–l), O₂ (mg L⁻¹, m–o) and W_arag (aragonite saturation level, p–r) in the late-20th century, mid-21st century and difference between the two periods.

In the mid-21st century, saline shelf water intrudes further into the estuary due to sea level rise (Fig. 1b), with salinity increases by ~1.5 in most of the estuary (Fig. 1c). This elevated intrusion raises TA (Fig. 1e), reaching an increase of ~70 μmol kg⁻¹ in the bottom waters of mid-Bay (Fig. 1f). A combination of sea level rise and higher shelf DIC (resulting from offshore CO₂ uptake) work in concert to elevate DIC in the intruding bottom water (Fig. 1h). Moreover, surface DIC increases due to higher atmospheric pCO₂ and a higher influx of CO₂, where DIC increases by up to 100 μmol kg⁻¹ (Fig. 1i). The isohaline at which TA = DIC shifts seaward, due to larger increases in DIC than in TA (Supplementary Figs. 1b, 1c). CO_2aq accounts for the most of DIC increases in the upper Bay and bottom waters of the mid-Bay while ${{{{\rm{C}}}}}{O}_{3}^{2-}$ accounts for the most of the DIC increases in the lower Bay and surface waters of the mid-Bay (Supplementary Figs. 1d-1i). Low pH_T bottom water expands seaward (Fig. 1k). pH_T in surface waters also decreases, with the highest pH_T area (pH_T = 8.0) shrinking substantially as the surface DIC increases. The most interesting finding is that pH_T reductions are largest (~0.3) in near-surface waters in the upper and middle part of the estuary between 38.7 and 37.8 ^°N (Fig. 1l). In contrast, pH reduction in bottom waters is considerably smaller, only ~0.1-0.15. Similarly, the hypoxic bottom water extends further seaward (Fig. 1n), with the largest O₂ reduction (−1.0 mg L⁻¹) in the near-surface waters where pH decreases are largest (Fig. 1o). The aragonite saturation horizon expands seaward and upward (Fig. 1q). The difference ΔΩ_arag can reach −0.3 in the mid-Bay, and −0.8 in the lower Bay due to the acidification in the adjacent shelf water (Fig. 1r).

Comparing the time series of hypoxic volume (in which O₂ ≤ 2 mg/L), acidic volume (pH_T ≤ 7.5), and aragonite under-saturated volume (Ω_arag ≤ 1) between the two periods shows estuary-scale impacts of climate change on hypoxia and acidification. The summer mean/peak hypoxic volume averaged over the late-20th century was 4.78/9.9 km³ (Fig. 2a), while in the mid-21st century it is projected to increase to 7.62/12.75 km³, amounting to 59%/29% increase. The hypoxic volume increases are small in some years (e.g., 31% in 2061 versus 1991) but large in other years (e.g., 127% in 2064 versus 1994). In stark contrast, summer mean acidic volume is projected to increase much more (94%), from 11.17 to 21.64 km³ (Fig. 2b). Both hypoxia and acidification will be initiated earlier in the future climate (Figs. 2a and 2b). The volume of aragonite under-saturated water also increases substantially, with its peak increasing from 30-40 km³ to over 50 km³ (or ~25%) (Fig. 2c). Relative to pH_T, warming cancels some of the acidification effect shown in Ω_arag.

Fig. 2: Projected changes in the hypoxic and acidic volumes in Chesapeake Bay.

Time series of the hypoxic (O₂ ≤ 2 mg/L) volume (a), the acidic (pH_T ≤ 7.5) volume (b), and the aragonite under-saturated (${\varOmega }_{arag}\le 1$) volume (c) during the late 20th (blue) and mid-21st century (red).

Connection between acidification and hypoxia

Model simulations show that acidification and hypoxia are tightly linked. Figure 3 explores the relationships between O₂ and carbonate chemistry variables during the summer, using the mid-Bay station CB4.3 (its location marked in Supplementary Fig. 2a) as an example. In the surface water the DIC/TA ratio decreases as pH_T increases, with no obvious differences in the slope between the two periods (Fig. 3a). pH_T and O₂ are positively correlated as phytoplankton growth removes DIC and produces O₂ while respiration results in the opposite changes (Fig. 3b). The slope of this relationship shifts downward between the two periods, with pH_T decreasing by 0.2 to 0.3 in the mid-21st century, reflecting increased CO₂ uptake from the atmosphere.

Fig. 3: Connection between acidification and hypoxia.

Changes in DIC/TA - pH_T (a,c) and pH_T - O₂ (b,d) relationships in the surface (a, b)/bottom (c, d) water at CB4.3: the late 20th (blue) and mid-21st century (red).

In the bottom water the correlation between DIC and O₂ rapidly changes as anoxia develops (Fig. 3d). pH ranges between 7.0 and 7.45 in the late-20th century but drops rapidly to 6.93 to 7.3 in the anoxic water in the mid-21st century. Non-aerobic metabolic contributions to both DIC and TA (e.g., denitrification, sulfate reduction, calcium carbonate dissolution) become more important in the expanded anaerobic environment (Fig. 1m, n). The higher production rate of TA relative to DIC by the non-aerobic metabolism enhanced the buffering capacity of bottom waters to some extent. The slope of the DIC/TA ratio as a function of pH_T is larger in the mid-21st century than the late-20th century, indicating that a larger increase in DIC/TA is needed to reduce the same amount of pH_T in the future (Fig. 3c). Though this result may appear puzzling, it is consistent with smaller pH_T reductions in the bottom water than those in the near-surface water (Fig. 1l).

Air-sea CO₂ flux, ecosystem metabolism and offshore condition

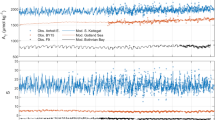
Air-sea CO₂ flux ${F}_{air-sea}$changes as a consequence of increased atmospheric pCO₂ and changes in estuarine DIC and TA. In the late-20th century the annual mean distribution showed outgassing in the upper Bay, ingassing in the mid-Bay, and near-equilibrium conditions in the lower Bay (Fig. 4a). When integrated over the main stem (excluding tributaries), the net flux into the water was −31.5 $Gg\,C\,{y}^{-1}$, indicating that Chesapeake Bay was a weak sink of CO₂. In the mid-21st century, the distribution of ${F}_{air-sea}$ looks similar, but with stronger sinks in the middle and lower Bay (Fig. 4b). The total annual CO₂ influx into the estuary increases by 88% to −59.4 $GgC/y$ (Run Fut1 in Fig. 4c), indicating that Chesapeake Bay will become a stronger sink of CO₂. It is also interesting and perhaps even unexpected that CO₂ degassing over the upper Bay does not decrease in the future. This is because that landward intrusion of higher DIC shelf water, enhanced CO₂ uptake in the middle and lower Bay, and vertical mixing in concert raise surface water pCO₂ in the upper Bay by 240-300 ppm (Supplementary Figs. 3a, b) that exceeds the atmospheric pCO₂ increase (197 ppm).

Fig. 4: Projected Changes in the air-sea CO₂ flux and ecosystem metabolism in Chesapeake Bay.

Annual averaged air-sea fluxes of CO₂ (mmol C m⁻² d⁻¹) in the late-20th (a) and mid-21st century (b). Annual integrated CO₂ flux over the mainstem of Chesapeake Bay for the two periods (c). Vertical profiles of summer mean Total Respiration (red, positive indicating DIC generation) and Gross Primary Production (green, negative indicating DIC consumption) (d), and Net Ecosystem Metabolism NEM (e) at CB4.3 during late-20th century. (f) Integrated NEM. In (c) and (f) Run Hist stands for the late-20th century and Runs Fut1—Fut4 represent four scenarios for the mid-21st century: Fut1—shelf water pCO₂ (partial pressure of carbon dioxide) increases at 50% of atmospheric pCO₂ increase; Fut2—increases in the atmospheric and shelf water pCO₂ are the same; Fut3—the shelf water pCO₂ stays constant; Fut4—riverine nutrient loading decreases by 40% and shelf water pCO₂ increases at 50% of the atmospheric pCO₂ increase.

To examine if climate change affects ecosystem metabolism (and thus DIC and TA), we compared the vertical profiles of Gross Primary Production (GPP), Total Respiration (TRESP, the sum of phytoplankton respiration, oxidation of organic matter, sulfate reduction and sediment flux) and Net Ecosystem Metabolism (NEM = GPP-TRESP) at station CB4.3. GPP (green line) caused a large uptake of DIC in the surface euphotic layer and dropped to zero below ~5 m where light became limiting to growth (Fig. 4d). TRESP (red line) also reached a maximum near the surface, but decreased more slowly with depth as organic particles settled and decomposed, including a small increase near the seabed due to the sediment flux and sulfate reduction. NEM was positive in the upper 2–3 m of surface waters but became negative below (Fig. 4e), demonstrating the effect of eutrophication-induced acidification in deeper waters. When integrated over the estuary, annual GPP increases by 3.7% and annual TRESP increases by 4.8% between the two periods, resulting in a slightly less autotrophic system with NEM decreasing by 16.89 $Gg\,C\,{y}^{-1}$ (Fig. 4f).

The projected change in the air-sea CO₂ flux is dependent on future changes in the offshore condition (Fig. 4c), namely if and how much the mid-Atlantic shelf will gain DIC and acidify³¹. In Run Fut2 the atmospheric and shelf water pCO₂ increases are in sync, and the annual ${F}_{air-sea}$ in the mid-21st century increases moderately to −42.0 $GgC\,{y}^{-1}$. In Run Fut3 where the shelf water pCO₂ stays constant and is completely decoupled to the rising atmospheric pCO₂, ${F}_{air-sea}$ increases to −93.8 $GgC\,{y}^{-1}$, which amounts to a tripling of the carbon sink, a scenario similar to a recent numerical simulation study of 1900-2000 changes³². Runs Fut2 and Fut3 represent the upper and lower limits in the projected ${F}_{air-sea}$ for the future climate and the likely result lies in-between the two limits. In Run Fut1 the shelf water pCO₂ is assumed to increase at 50% of the atmospheric pCO₂ increase, a mid-point case between Fut2 and Fut3. Nutrient management could also affect the air-sea CO₂ flux, given the sustained efforts to reduce eutrophication in Chesapeake Bay. A 40% reduction in the riverine nitrogen loading (Run Fut4), a management target set by EPA Chesapeake Bay Program, could reduce the carbon sink by 25%, resulting from lowered phytoplankton DIC uptake.

A regime diagram for estuarine response to higher atmospheric CO₂

To investigate how carbonate chemistry in a wider range of estuarine conditions responds to rising atmospheric pCO₂, we developed a box model for a generic estuary and simulated the carbonate chemistry response to elevated atmospheric CO₂ under a range of river flows and two offshore conditions (same as the 3D model Runs Fut1 and Fut3) (Fig. 5). The flushing time ${T}_{R}$ is defined as the time it takes to replace a certain water mass in an estuary and is a widely used parameter in estuarine biogeochemistry³³. The annual mean river discharge into Chesapeake Bay is about 1,150 ${m}^{3}{s}^{-1}$, corresponding to ${T}_{R}$ = 94 days. The box model predicts ${F}_{air-sea}=-1.09\,mmol\,C\,{m}^{-2}{d}^{-1}$, which compares favorably with the 3D model estimate of $-1.32\,mmol\,C\,{m}^{-2}{d}^{-1}$. As ${T}_{R}$ increases from 64 to 132 days, ${F}_{air-sea}$ changes from −6.06 (ingassing) to 1.23 (outgassing) $mmol\,C\,{m}^{-2}{d}^{-1}$, indicating that Chesapeake Bay is a weak carbon sink in wet years (shorter ${T}_{R}$) but a weak carbon source in dry years (longer ${T}_{R}$), in agreement with the observations²⁴. The change $\varDelta {F}_{air-sea}$ from a changing atmospheric pCO₂ (400 to 550 ppm, similar to the change from the late 20th and mid-21st century) in Runs Fut1 averages to −1.82 $mol\,C\,{m}^{-2}$. As pCO₂ increases from 550 to 800 ppm (from the mid- to late-21st century), $\varDelta {F}_{air-sea}$ averages to −5.95 $mmol\,C\,{m}^{-2}{d}^{-1}$. However, $\varDelta {F}_{air-sea}$in Runs Fut3 is much larger, reaching −7.57 $mol\,C\,{m}^{-2}$ as pCO₂ increases from 400 to 550 ppm and −11.87 $mol\,C\,{m}^{-2}$ as pCO₂ increases from 550 to 800 ppm, as the ocean end member maintains the same level of DIC, which is unlikely. Overall, an estuary with flushing times in the range of 2-5 months will become a substantial sink of CO₂ in the mid- to late-21st century, but the magnitude of air-sea CO₂ flux change depends on the shelf condition.

Fig. 5: A regime diagram for estuarine response to higher atmospheric CO₂ in two different types of estuaries.

Air-sea CO₂ flux versus flushing time T_R at the atmospheric pCO₂ = 400 (green), 550 (blue), and 800 (red) ppm, obtained from a box model of a generic estuary. The circles on the right half of the diagram represent large estuaries with T_R = (2–5) months and the stars on the left half represent small estuaries with T_R = (1–10) days. The black upper and low triangles represent observational estimates from Chesapeake Bay by Friedman et al.¹⁵ and Chen et al.²⁴ The black square represents the observational estimates from the Altamaha River by Cai and Wang³⁴ and Jiang et al.³⁵ The green and blue diamonds are the air-sea flux for the late-20th (Run Hist) and mid-21st century (Run Fut1) calculated from the 3D model of Chesapeake Bay. The solid blue and red lines represent model runs in which shelf water pCO₂ increases at 50% of the rate of atmospheric pCO₂ (Runs Fut1) while the dashed lines represent model runs in which shelf water pCO₂ does not change (Runs Fut3).

In contrast, estuaries with short flushing times (1–10 days) remain a source of CO₂ to the atmosphere under the future climate (Fig. 5). The Altamaha River has a flushing time of 1-2 days and a mean air-sea CO₂ efflux of ~70 $mmol\,C\,{m}^{-2}{d}^{-1}$ estimated from observations^34,35. ${F}_{air-sea}$ predicted from the box model is about the same. Interestingly, our results show that raising atmospheric pCO₂ from 400 to 550 or 800 ppm does not reduce air-sea CO₂ flux. Instead, ${F}_{air-sea}$ in Runs Fut1 increases with increasing atmospheric pCO₂ as higher DIC input from the shelf raises pCO₂ faster than the atmospheric increase inside the poorly buffered estuary (Supplementary Fig. 4a). At the short residence time of ${T}_{R}\approx 1.2$ day, appropriate for a small estuary like the Altamaha River, ${F}_{air-sea}$ increases by 24% at pCO₂ = 550 ppm and 34% at pCO₂ = 800 ppm. In Run Fut3 ${F}_{air-sea}$ decreases by 14% or 36%, but this scenario is unlikely as shelf water has been shown to uptake carbon historically albeit at a slower pace than the open ocean³¹. Our earlier 3-D simulation results for the upper part of Chesapeake Bay, which is akin to small estuaries if one would view the Bay as a mini-ocean, also support that CO₂ outgassing fluxes do not diminish as atmospheric pCO₂ increases (Fig. 4a, b). Overall small estuaries remain to be a source of CO₂ to the atmosphere in the future climate and may emit substantially more if the adjacent shelf continues to uptake CO₂.

Discussion

Our study identified that pH_T reduction was largest (−0.3) in the subsurface waters (at depths between 3 and 8 m) rather than in the lowest pH_T bottom waters (Fig. 1l, Supplementary Fig. 5). This result appears to contradict observations that show higher pH_T sensitivity in waters with higher DIC and relatively lower pH_T (e.g., in the northern Gulf of Mexico hypoxic zone²⁵). However, the pH_T response to acidification is nonlinear with its most sensitive point at roughly 7.5 and the sensitivity becomes less in the bottom waters of Chesapeake Bay where pH_T drops to 7-7.3. In seawater, the minimum buffer capacity due to the carbonate system occurs at a pH_T of about 7.5, halfway between the two dissociation constants (pK_a) of the carbonic acid³⁶. Near this pH_T, a small addition of acid or base reacting with HCO₃^- produces a substantial change in concentration of CO₂ or ${{{{\rm{C}}}}}{O}_{3}^{2-}$ and markedly changes the pH_T of the water. When pH_T < 7.5, it is less sensitive to DIC increases (i.e., CO₂ addition) than to alkalinity decreases (i.e., strong acid addition) (Supplementary Fig. 6). In addition, sulfate reduction produces more TA than DIC, at a ratio of 1.14, and the substantial previously-measured sulfate reduction rates in the mid-Bay³⁷ likely provide a buffer to pH_T changes in the bottom water.

One surprising result of our study was the strong sensitivity of estuarine air-sea CO₂ flux to the state of carbon uptake in the adjacent shelf which exchanges water with the estuaries. The annual air-sea CO₂ flux into Chesapeake Bay can vary by a factor of 2, depending on how fast the shelf water pCO₂ keeps in pace with rising atmospheric CO₂ (Fig. 4c). Analysis of global surface ocean pCO₂ data base over the past few decades suggested that pCO₂ in shelf waters might have lagged the rise in atmospheric CO₂ and, as a result, the continental shelves would become a larger carbon sink in the 21st century^31,38. Consequently, future estuarine air-sea CO₂ flux will be tightly coupled to carbon uptake on the adjacent continental shelf. Another surprising result is that the air-sea CO₂ efflux over small estuaries and the upper part of Chesapeake Bay (where pCO_{2, water} > pCO_{2, air}) does not decrease in the future climate (Figs. 4a, b, 5) though rising atmospheric CO₂ is expected to reduce the air-water pCO₂ gradient. On the contrary, the air-sea CO₂ flux could increase by 20–40% if the adjacent shelf continues to take up CO₂ and estuarine circulation transports high DIC shelf water landward, which is converted into CO₂ under low buffer capacity in low salinity water, raising pCO₂ inside the estuary more than that in the atmosphere (Supplementary Fig. 7). Even a small percentage increase in the carbon-rich low salinity water will outpace the projected atmospheric pCO₂ increase. On the other hand, pH_T and buffer capacity in small estuaries are not expected to be affected substantially by the addition of DIC except in high salinity waters in the lower reaches of the estuary (Supplementary Figs. 4b–d). In summary, global estuarine outgassing could be substantially higher in the future climate if continental shelves continue to absorb atmospheric CO₂ and return high DIC waters to the estuaries. The estuaries and continental shelves must therefore be considered as a coupled coastal system when assessing their role in the global air-sea CO₂ flux.

The box model, using the Altamaha River and Chesapeake Bay as examples of small and large estuaries, shows how the air-sea CO₂ flux varies with flushing time under the current climate and how it might respond to higher pCO₂ in the future climate. The model-predicted CO₂ flux for the Altamaha River at the current climate is about 72 $mmol\,C\,{m}^{-2}{d}^{-1}$, which compares favorably with the observational estimate of 69 $mmol\,C\,{m}^{-2}{d}^{-1}$^34,35. Similarly, the predicted CO₂ flux for Chesapeake Bay is about $-1.1\,mmol\,C\,{m}^{-2}{d}^{-1}$ under the average river flow condition, which is close to the observational estimate^15,24. These results are also broadly consistent with the observations in other estuaries^10,13,39,40. For example, Van Dam et al.⁴⁰ found that water pCO₂ decreases with the freshwater age in the Neuse River and New River, North Carolina. It exceeds the atmospheric pCO₂ by a large amount (outgassing) when the freshwater age is on the order of a few days but falls slightly below the atmospheric value (ingassing) when the age is on the order of (10–100) days. These observational results are strikingly similar to those shown in Fig. 5. However, it should be noted that estuaries around the world are highly diverse and encompass a wide range of physical and biogeochemical conditions. The simple box models developed here are not expected to capture all the processes but represent an important step towards generalizing and conceptualizing the results obtained from the 3D model of Chesapeake Bay. A quantitative comparison with the observed estimate of air-sea CO₂ flux for other estuaries would require further site-specific studies that explicitly consider nutrient loading, light field, phytoplankton production and respiration, and oxidation rate of organic matter etc. in these estuaries. An exploratory investigation using the box model suggests that the air-sea CO₂ flux is insensitive to NEM in small estuaries with short flushing times but the total carbon uptake decreases with increasing NEM in large estuaries with long flushing times (Supplementary Fig. 8). The later results may appear to be counter-intuitive since larger NEM would lead to stronger CO₂ uptake in the mid- and lower-parts of the estuary. However, estuarine circulation transports high DIC bottom water landward, resulting in considerably higher CO₂ efflux in the upper Bay which offsets the stronger carbon uptake in the mid- and lower-Bay. In this study DIC, TA, and nutrient concentration at the upstream rivers were assumed to be the same between the current and future climates. Human human-accelerated chemical weathering⁴¹, alkalinization in rivers⁴², climate-induced changes in watershed denitrification⁴³, and nutrient management⁴⁴ could alter the riverine nutrient and carbon loadings and would be interesting topics to explore in future studies.

Given the strong similarity between the 3D and box model results, however, the following conclusions could still be made (Fig. 6). Small estuaries with short flushing times (days-weeks) are currently strong sources of CO₂ to the atmosphere and will remain so or even become greater sources in the future climate. A useful future exercise would involve the reevaluation of the estuarine CO₂ fluxes from these estuaries under higher atmospheric CO₂ levels and reassess their contributions to the global carbon budget in the 21st century. On the other hand, large eutrophic estuaries with long flushing times (a few months) are projected to become substantial sinks of CO₂ in the future climate. Since the increase in the CO₂ ingassing in these large estuaries is relatively constant over a range of ${T}_{R}$, other large eutrophic estuaries will also likely become strong CO₂ sinks and experience large declines in pH and aragonite saturation state. Given the wide range of estuaries found around the world, some estuaries have a flushing time of the order O(10) days^6,10, falling between the small and large estuaries studied in this paper. Future studies of these intermediate-sized estuaries would shed lights on the carbonate chemistry in these systems, particularly the switching from a CO₂ source to a CO₂ sink as the flushing time increases⁴⁰.

Fig. 6: Schematic of how small and large estuaries respond to higher atmospheric CO₂ levels in a changing climate.

a Small estuaries with short flushing times will remain to be a CO₂ source to the atmosphere. High DIC shelf water imported to the estuaries is converted into CO₂ in low salinity water, raising pCO₂ inside the estuary more than that in the atmosphere and resulting in stronger emission of CO₂ in the future climate. b Large estuaries with long flushing times will become carbon sinks and suffer from accelerated acidification. The magnitude of air-sea CO₂ flux change depends on the shelf condition, with larger sinks if the shelf water pCO₂ stays constant and is completely decoupled to the rising atmospheric pCO₂.

To the best of our knowledge, this study provides new insights into the complex estuarine responses to climate change. Whereas many past reports have used observational data to draw inferences about the role of different estuaries in the global CO₂ budget (e.g., small and low-salinity estuaries are CO₂ sources), here we developed a relatively simple mechanistic model that can help quantify changes in CO₂ fluxes across different types of estuaries in the future climate. In particular, we quantify the effect of ocean-estuary mixing on future air-sea CO₂ flux (including the role of acidifying coastal oceans on estuarine CO₂ flux), coming to the conclusion that CO₂ fluxes in low salinity estuarine areas could actually increase in the future due to inputs of increasingly high CO₂ shelf water. Future work can identify how widespread this ocean-estuary coupling is manifested across diverse estuaries worldwide. Finally, we project a substantial increase in the acidic volume in Chesapeake Bay by the mid-21st century, and these types of volume estimates have rarely been reported in the literature.

Methods

3D coupled models of Chesapeake Bay for climate downscaling projections

To project future changes in carbonate chemistry in Chesapeake Bay, we used a coupled hydrodynamic-biogeochemical-carbonate chemistry (ROMS-RCA-CC) model, and forced it with climate downscaling projections from the North American Regional Climate Change Analysis Program (NARCCAP)²⁹. In NARCCAP, a fine resolution (50 km) regional climate model (RCM) of the North America is nested into a general circulation model (GCM) (Supplementary Fig. 9a). Simulations are available for 1971-2000 and 2041-2070 under a medium-high A2 greenhouse gas emissions scenario. The use of one emissions scenario is not a major limitation because the sensitivity of climate to emissions scenario is modest by mid-century²⁶. Given the high computational cost, we selected two decadal periods for the regional ocean model simulations: 1989-1998 (late-20th century) and 2059-2068 (mid-21st century). The intent was to model the last decade of NARCCAP’s 30-year historical period and 70 years into the future, but the simulation years were shifted 1 year earlier due to data availability.

The coupled ROMS-RCA-CC models have three sub-models. The hydrodynamic model, based on the Regional Ocean Modeling System (ROMS)^45,46, has 80 × 120 grid points (~1 km resolution) in the horizontal direction and 20 vertical sigma layers⁴⁷ (Supplementary Fig. 2b). ROMS simulates water level, currents, temperature and salinity. The biogeochemical model is based on the Row-Column Aesop (RCA) model⁴⁸, and includes a water-column component and a sediment diagenesis component⁴⁹. RCA simulates pools of organic and inorganic nutrients, two phytoplankton groups, and dissolved O₂. The carbonate chemistry (CC) model simulates dissolved inorganic carbon (DIC), total alkalinity (TA), and mineral calcium carbonate (aragonite CaCO₃)²². Other carbonate chemistry parameters such as pH_T and pCO₂ are calculated from the CC model outputs using CO2SYS program⁵⁰. The ROMS-RCA-CC models have been validated against a wide range of observational data, including sea level, currents, temperature, salinity, NO₃, NH₄, PO₃, O₂, DIC, TA, pH_T, and rates of primary production and/or respiration in the water-column and sediments, as reported in previous papers^{18,21,22,47,48,51,52}.

The ROMS hydrodynamic model is forced by river flows at 8 major tributaries, by wind stress and heat fluxes across the sea surface, and by sea level and climatology of temperature and salinity at the open boundary. Outputs from the GCM-RCM climate models are used to set the boundary conditions for ROMS. RCM’s projections for wind speeds, temperature and humidity etc. are used to calculate the air-sea fluxes of momentum and heat fluxes. RCM’s projections for precipitation over the watershed of Chesapeake Bay are used to estimate the river flows using a delta method⁵³. To correct biases in the NARCCAP RCM outputs, we used the historical data from the North American Regional Reanalysis (NARR). The NARCCAP outputs were interpolated onto the NARR grids and their biases are corrected using empirical quantile mapping method⁵⁴.

GCM projections for the northwest Atlantic were used to set the sea level and temperature at the offshore boundary of ROMS. To consider the relative sea level rise for Chesapeake Bay, we added the local factors into the GCMs sea-level projections, following Lee et al.’s ⁵⁵ methodology. To set the temperature condition at the offshore boundary, we used GCMs to calculate the differences of monthly averaged temperature between the late-20th and the mid-21st century, and added these differences to historical data. The shelf water in the southern Mid-Atlantic Bight (MAB) is affected by the competing influences of the northward shift of the Gulf Stream (along with its high salinity water) and the fresher coastal current on MAB due to melting Arctic ice, such that the net change in MAB salinity is expected to be relatively small⁵⁶. Hence we assumed that the mean salinity condition remains the same at the offshore boundary of the model.

RCA is forced by loads of dissolved inorganic and organic nutrients as well as particulate organic materials from the rivers. To simulate the years 1989-1998, the river inputs of phytoplankton, particulate and dissolved organic carbon, and organic and inorganic nutrients were obtained from Chesapeake Bay Program biweekly monitoring data (https://www.chesapeakebay.net/what/data) at stations located at the model boundary for eight major tributaries. Anthropogenic loads from point sources (e.g., wastewater treatment plants) were not considered. The ocean boundary inputs were acquired from the World Ocean Atlas 2013. Atmospheric deposition of nutrients was not considered. In this study, climate-induced changes in riverine nutrient loading were assumed to be caused by changes in river flows only and the riverine nutrient concentrations in 2059-2068 were assumed to be unchanged⁵⁷. Nutrient concentrations at the offshore boundary were also assumed to remain unchanged.

CC is forced by atmospheric CO₂, riverine loads, and offshore concentrations. Historical time series of TA measurements in riverine inputs were obtained from the USGS stations in the Susquehanna and Potomac Rivers, and the alkalinity measurements were performed with fixed endpoint and incremental titrations on filtered samples. Shen et al.²² developed an empirical relationship between the riverine TA and the river flows. This formula was used to prescribe TA concentration in years where in-situ measurements were absent. The riverine DIC concentrations were calculated through CO2SYS with the available TA and pH_T, and compared favorably with direct DIC measurements made over a limited time period¹⁸. Long-term historical carbonate chemistry data for the other tributaries in the lower bay region were not available, and the riverine TA was calculated as a function of freshwater discharge based upon limited field measurements. TA at the ocean boundary was directly estimated with the empirical equation⁵⁸ based upon salinity and temperature at the ocean boundary. DIC at the offshore boundary was calculated with the available TA, fCO₂ from SOCAT⁵⁹, salinity, and temperature using CO2SYS. DIC and TA at the riverine boundaries were assumed to be unchanged between 1989-1998 and 2059-2068. At the offshore boundary, TA is primarily a function of salinity⁵⁸ and was thus assumed to be the same. DIC in 2059-2068 was calculated using the pCO₂ and temperature output from GCM. We considered 3 possible scenarios in the shelf water’s response to increasing atmospheric pCO₂: (1) Run Fut1, the surface water pCO₂ was assumed to increase at a rate that is about 50% of the rising atmospheric pCO₂ rate; (2) Run Fut2, the surface water pCO₂ was assumed to increase at the same rate at atmospheric pCO₂; (3) Run Fut3, the surface water pCO₂ and DIC on the shelf were assumed to be unchanged. Analyses of model simulations of global continental shelf³⁰ and the historical surface water pCO₂ trends on the continental shelf in the North Atlantic suggested that Run Fut1 was the most realistic and hence was used as the configuration in the control run, but the model runs for Fut2 and Fut3 were also conducted and shown in Fig. 4. In Run Fut4 the riverine nutrient loading decreases by 40% and the shelf water pCO₂ increases at 50% of the atmospheric pCO₂ increase. The atmosphere pCO₂ was set to be 353 ppm in 1989-1998 and 550 ppm in 2049-2058.

There are a total of 12 RCM-GCM combinations in NARCCAP, 6 of which are available for the Chesapeake Bay region. Since it is computationally intensive to conduct full ensemble simulations of ROMS-RCA-CC models, we selected one RCM-GCM that was shown to be representative of the ensemble projections for hypoxia⁵⁷. RCM3-GFDL is the Regional Climate Model version 3 (RCM3⁶⁰.) driven by Geophysical Fluid Dynamics Laboratory model⁶¹. According to the RCM3-GFDL projections, the temperature will increase by an average of about 1.4 °C with strong seasonal variations (Supplementary Fig. 9b). It also projects an increase in the winter river discharge but mostly decreases in other seasons (Supplementary Fig. 9c). The relative sea level rise for Chesapeake Bay is projected to be 0.45 m by the mid-21st century⁵⁵.

A box model of a generic estuary

We developed a coupled hydrodynamic-carbonate chemistry box model for a generic estuary to study the response of carbonate system to increasing pCO₂. The estuary is divided into three regions: the upper estuary, the mid-estuary, and the lower estuary, each of which consists of an upper box and a lower box (Supplementary Fig. 10). In the box model, the vertical mixing between the upper and lower boxes is represented by a vertical mixing velocity. Water in the upper box of the upper estuary is diluted by the fresh water input from the river. We parametrize the gravitational estuarine circulation based on the horizontal density differences between the upper boxes of two adjacent estuarine regions⁶². Consideration of the salt balance leads to six differential equations for salinities in each box. This hydrodynamic model setup is based on the box model which Li et al.⁶³ developed for the Strait of Georgia and Juan de Fuca Strait (now called Salish Seas).

We extended this hydrodynamic box model by adding the state variables TA and DIC, following an approach to model plankton dynamics⁶⁴. As a simplification, TA is assumed to be conservative but receives inputs from the river (the upper box in the upper estuary) and shelf (the lower box in the lower estuary). In the DIC equation for the surface boxes, the air-sea CO₂ flux is calculated using the transfer velocity of Wannikhof et al.⁶⁵ and for simplicity, the wind speed was assumed to be 5 m s⁻¹. Additional components of the carbonate system, including pH_T and pCO2 were calculated with the CO2SYS program based upon DIC, TA, temperature, salinity etc⁵⁰. Temperature was prescribed a seasonal cycle and assumed to be the same in all boxes. The dissociation constants (K1 and K2) for carbonic acid were estimated following Millero⁶⁶, and the CO₂ solubility constant (K0) was calculated using the equations from Weiss⁶⁷. To account for phytoplankton photosynthesis and organic matter respiration in Chesapeake Bay, a sink term was added to the DIC equation in the upper boxes and a source term was added to the DIC equation in the lower boxes, using the mean values estimated from the 3D model. The box model does not directly simulate biogeochemical processes such as phytoplankton growth, phytoplankton respiration, oxidation of dissolved organic carbon, sulfate reduction, sediment flux and CaCO₃ dissolution.

We applied the coupled hydrodynamic-carbonate chemistry box model to Chesapeake Bay and the Altamaha River which have vastly different flushing times. The box model of Chesapeake Bay was prescribed according to the geometrical dimensions in Testa et al.⁶⁸, the mixing and transport estimates in Li et al.⁴⁷, and carbonate chemistry parameters in Shen et al.²² The box model of the Altamaha River was prescribed according to the geometrical dimensions in Shedon and Alber⁶⁹, the mixing and transport estimates in Di Iorio and Kang⁷⁰ and Wang et al.⁷¹, and carbonate chemistry parameters in Cai and Wang³⁴.

The flushing time in an estuary is calculated using

$${T}_{R}=\frac{1}{V}{\int }^{}\frac{{S}_{0}-S}{{S}_{0}}dv\, \left(\frac{V}{Q}\right)$$

(1)

where S₀ is the shelf salinity, S is the salinity in each box, V is the volume of the estuary, and Q is the river flow³³. ${T}_{R}$ is averaged over a year to obtain the mean residence time of an estuary.

Simulation of pH changes and buffer factors

To calculate pH_T and the buffer factors β_DIC and β_TA for Chesapeake Bay (shown in Supplementary Figs. 4 and 6), we used Cai et al.’s¹⁷ approach to simulate two river-ocean mixing scenarios: (1) late-20th century; (2) mid-21st century (with atmospheric pCO₂ = 550 ppm). DIC at the oceanic end member was calculated according to Run Fut1. Respiration effects is represented by adding 150 μmol kg⁻¹ to DIC in the estuary. The same approach was used to calculate pH_T and, pCO₂, and buffer factors in the Altamaha River but the respiration effect was not considered due to the absence of bottom water hypoxia, and the riverine DIC and TA concentration was prescribed according to Cai and Wang³⁴.