Abstract
The eruption of the submarine Hunga volcano in January 2022 was associated with a powerful blast that injected volcanic material to altitudes up to 58 km. From a combination of various types of satellite and ground-based observations supported by transport modeling, we show evidence for an unprecedented increase in the global stratospheric water mass by 13% relative to climatological levels, and a 5-fold increase of stratospheric aerosol load, the highest in the last three decades. Owing to the extreme injection altitude, the volcanic plume circumnavigated the Earth in only 1 week and dispersed nearly pole-to-pole in three months. The unique nature and magnitude of the global stratospheric perturbation by the Hunga eruption ranks it among the most remarkable climatic events in the modern observation era, with a range of potential long-lasting repercussions for stratospheric composition and climate.
Similar content being viewed by others
Introduction
The main eruption of the Hunga submarine volcano (Tonga, 20.54°S, 175.38°W) on 15 January 2022 was likely the most explosive event of the modern observational era, with an estimated Volcanic Explosivity Index (VEI) of 5.81. In the historical record, the Lamb wave triggered by the initial explosion is only comparable to that of the eruption of Mount Krakatoa in 18832,3. Stereoscopic analysis of geostationary satellite images showed that the volcanic plume reached about 58 km4, resulting in the direct injection of volcanic gases and vaporised seawater from the magmatic chamber together with tropospheric moisture entrained by the eruptive updraft.
The dryness of the stratosphere is largely set by the transit of the air masses through the cold tropical tropopause where freeze-drying usually limits the amount of water entering the stratosphere to a few ppmv5,6,7. As the atmospheric radiation budget is particularly sensitive to water vapour changes in the upper troposphere and lower stratosphere (e.g. refs. 8,9), even small changes in the stratospheric water content can lead to significant radiative forcing10 and alter stratospheric ozone chemistry11. The increase in stratospheric water vapour concentrations by a few ppmv simulated by current chemistry climate models in response to global warming may cause substantial positive climate feedbacks amplifying surface warming12. A rise in stratospheric water vapour by a few ppmv also induces important changes in atmospheric circulation, increasing the poleward and upward shift of subtropical jet streams and intensifying the stratospheric Brewer-Dobson circulation by about 30%13 with further potential implications for surface climate.
Early studies of volcanic columns (e.g. ref. 14) advocated that the major volcanic eruptions, such as those of 1815 Tambora or 1883 Krakatoa, may have led to stratospheric hydration. Water vapour constitutes about 80% in volume of the erupted gas15,16 and a few percent of the total mass of ejected material which, for Hunga, ranges from 2900 Tg17 to 13,000 Tg1. Additional moisture may also be entrained from the troposphere14,18. Ref. 19 proposed that the 1991 eruption of Mount Pinatubo injected about 37 Tg of water but this estimate was based solely on modeling considerations.
The January 2022 Hunga eruption provided first observational evidence for substantial volcano-driven stratospheric hydration20,21,22, supposedly due to the submarine location of the volcano. Without efficient sinks of moisture in the stratosphere, the ample hydration of this atmospheric layer is expected to persist for years, affecting various climatic variables such as stratospheric ozone23, radiative balance24,25 and dynamics26. The global impact of the Hunga eruption on the stratospheric aerosol loading is another outstanding question required to assess the magnitude of climatic effects of this event.
With this study, we describe and quantify the stratospheric repercussions of the unique natural experiment in the middle atmosphere provided by the Hunga eruption. We investigate the formation and evolution of the stratospheric moisture and sulfate aerosol plume at a wide range of scales—from minutes and kilometres to monthly and planetary scales using a synergy of satellite and ground-based observations supported by transport modeling. Spanning 9 months, the Hunga observations available to-date enable the first accurate assessment of the annual-scale stratospheric aftermath of this eruption, uncovering its climate-altering capacity.
Results
Eruptive column and water phase transition
While the Hunga eruptive sequence on January 15 (D0) started around 04:05 UTC27, the paroxysmal blast occurred at 04:16 UTC1,2. At 04:25, the main volcanic plume reached its top recorded altitude of 58 km (Fig. 1a) with an ascent speed of at least 40 m/s over the previous 10 min, as shown by stereoscopic analysis of high-resolution imaging by GOES-17 and Himawari-8 geostationary satellites. The time evolution of the cloud top height reveals three successive updrafts (Fig. 1a, Supplementary Movie S1), in agreement with observations of infrasound waves suggesting three eruptive events28.
a CTH time evolution from stereoscopic retrieval using Himawary-8 and GOES-17 geostationary imagers. b Hovmoller diagram of the maximum CTH (note the inverted time axis). Superimposed lines are color-coded by altitude and represent linear trajectories released from the volcano location at different heights indicated in the panel. The circles color-coded by altitude indicate the detections of water vapour and aerosol plumes respectively by MLS and CALIOP (see panel e). The black-encountered circles indicate the detection of hydrated layers by COSMIC-2 (see panel d). Note the color correspondence between the trajectories and downwind detections of the plume confirming the CTH retrieval. c Temperature and zonal wind profiles averaged over 5° × 5° box centered at the volcano location from European Center of Medium-range Weather Forecasts (ECMWF). d water vapour profiles inside the volcanic plume (locations shown in panel b) retrieved from COSMIC-2 radio occultations (using ECMWF temperature) and the corresponding saturation mixing ratio profiles (black dashed lines) from ECMWF analysis. The dashed black curves provide an approximate range of uncertainty from the median of the retrievals ±3 standard deviations on the day before the eruption (January 14). e Latitude-altitude cross section of water vapour from MLS (color map) and depolarization ratio from CALIOP (contours, first contour is 0.05, interval is 0.05, last contour is 0.25). The time and longitude of MLS and CALIOP plume measurements are given in panel b.
Figure 1b shows the motion and lifetime of the volcanic ice cloud at different heights, which can readily be explained by the easterly-sheared background flow and sublimation of ice due to dilution within a warmer and drier environment. At higher levels, the plume was subject to faster westward advection, but also to warmer temperatures towards the stratopause (Fig. 1c), leading to a quicker sublimation—within an hour at 40 km. The lower umbrella, topping at around 35 km altitude, persisted longer and, carried by fast stratospheric easterlies, expanded 500 km to the West and grew to 320,000 km2 in 3 h, nearly the size of Germany (Supplementary Notes S.1, Fig. SI). We note that vertical motions, including sedimenting ice, also likely contribute to this evolution. The ice plume persisted the longest (about 20 h) in the lower stratosphere, near the cold tropopause. Below the tropopause (~17 km), the cloud drifted in the opposite direction (Fig. 1b) due to prevailing upper-tropospheric westerlies (Fig. 1c).
The persistence of ice in the upper stratosphere, although foreseen by modelling studies14,29, implies near ice-saturation and humidity more than three orders of magnitude above the background stratospheric level. Such near-saturation conditions are confirmed by Global Navigation Satellite System (GNSS) COSMIC-2 radio occultation soundings (hereafter GNSS-RO) on D0 downwind of the eruption (marked as circles in Fig. 1b). Extreme anomalies in refractivity at altitudes between 30–40 km in about an hour after the eruption translate into strikingly-high stratospheric water vapour anomalies up to >14,000 ppmv at ~33 km (Fig. 1d). Near saturation conditions are also revealed in later soundings and even persisted for 3–4 days at 20–30 km (Fig. S2).
Extrapolating the two early GNSS-RO profiles to the whole area of the young umbrella cloud (150,000 km2) and assuming all water is found as vapour at the time of the profiles (neglecting the contribution of remaining ice) leads to a stratospheric total water injection lying between 70–150 Tg (Supplementary notes SI). This estimate is consistent with estimates of the mass of injected water from Microwave Limb Sounder (MLS) provided hereinafter and those by refs. 20,21. It is noteworthy that the volume of water injected into the stratosphere corresponds to the average amount of water discharged by the Amazon river (2.1 × 105 m3 s−1) over about 10 min (cf. the peak volumetric discharge of the plume of ∼9 × 105 m3 s−117).
The young outflow of the eruption was also sampled by MLS at 14:20 UT, revealing a ~12 km-thick layer of strongly enhanced water vapour with a top at around 52 km (Fig. 1e) as well as by the Cloud-Aerosol LIdar with Orthogonal Polarization (CALIOP) satellite sensor reporting a strongly depolarizing layer of particles between 35–40 km, just beneath the moist plume (Fig. 1e). The high depolarization ratio of the plume suggests the presence of non-spherical particles such as ash and/or ice.
Early evolution of volcanic cloud
The explosive eruptive transport together with sedimentation and sublimation of ice produced a multitude of moist and aerosol-rich layers throughout the depth of the stratosphere. Their spatiotemporal evolution during the first days after eruption (D + 2 to D + 4), as observed by MLS (Fig. 2a–c), reveals a wind shear-shaped slant column of moisture extending throughout the stratospheric layer and spanning from Australia to Africa already on D + 2. This is consistent with the MLS data analysis by ref. 20. The strongly hydrated patches were accompanied by aerosol layers detected by the Ozone Monitoring and Profiling Suite (OMPS) Limb Profiler (LP) satellite instrument at all altitudes between the tropopause (~17 km) and 42.5 km30. The presence of aerosols up to 37 km is confirmed by lidar measurements at La Reunion island downwind of Hunga on D + 4 (Figs. 2c and 3), which is the highest-level aerosol plume ever observed by ground-based lidars.
a–c Longitude-altitude section of MLS V4 maximum water vapour mixing ratio (WVMR) between 30° S–10° S on the respective day. Black points indicate the ice cloud top height on the day of eruption (D0). The white curve represents zonally-averaged ECMWF zonal wind profile. Black contours mark the areas where OMPS-LP detected aerosol layers with extinction ratio above 5. Diamonds and circles mark the detection of WVMR enhancements above 50 ppmv respectively by SAGE III and meteorological Vaisala RS41 radiosoundings. d–f Geographical extent of the hydrated plume within the 20–35 km layer reconstructed from MLS detections of WVMR > 50 ppmv (black circles) and COSMIC-2 refractivity anomalies indicative of hydrated layers (squares). The magenta color map shows the cumulative number of MLS and COSMIC-2 detections per million km2 (computed using 3°×3° cells) on the given day. Locations of the Australian radiosounding stations are shown as green circles, the stations marked red represent the radiosonde detections of WVMR enhancements. g–i Radiosonde profiles bearing WVMR enhancements above 50 ppmv on the respective day (from 00:00 to 24:00 UTC) and corresponding saturation mixing ratio profiles in black.
The figure includes the scattering ratio (SR) profiles corresponding to the earliest detections of volcanic plume (blue and red profiles) as well as to the most intense aerosol layers in terms of their peak scattering ratio (violet and orange profiles). The Mauna Loa lidar measurements at 694 nm were converted to 532 nm using the color exponent of 0.9 (Jager and Deshler, 2022). Note that the El Chichon plume obtains its maximum SR much later than the Hunga plume.
The primary cloud of moisture at lower altitudes ~25–30 km, (Fig. 2d–f) reconstructed using MLS detections of hydrated layers with mixing ratios above 50 ppmv and COSMIC-2 detections of refractivity anomalies (see Methods), was extensively sampled by the Australian upper-air meteorological network. The radiosondes showed numerous moist layers between 20–30 km with peak water vapour mixing ratios increasing with altitude from around 100 ppmv at 21 km to 2900 ppmv at 28 km following the physical limit of ice saturation at the given level (Fig. 2g–i). This is consistent with the analysis of radiosounding data by ref. 22.
The presence of large amounts of water in the volcanic plume has probably led to very fast oxidation of volcanic sulfur dioxide emissions to sulfuric acid—the main component of stratospheric aerosol droplets31,32. Another potential factor of expedited SO2 conversion to aerosols could be heterogeneous oxidation of SO2 on the surface of ash31,33. We note though that according to CALIOP depolarization measurements, the aerosol particles were mostly spherical since D + 1 and could therefore be characterized as sulfate aerosol droplets34.
The primary aerosol plume at 27–30 km altitude, overpassing La Reunion island (21° S) on D + 6—D + 7, was marked by a remarkably high aerosol optical depth (AOD) of 0.6 and scattering ratio (532 nm) reaching 28035, which to our knowledge represents the most intense stratospheric aerosol plume ever observed by ground-based lidars. Figure 3 compares early lidar detections of the Hunga and El Chichon plumes at La Reunion and Mauna Loa observatories, both located downwind of the respective volcanic eruptions36. While the maximum scattering ratio and AOD of the Hunga plume is observed already on D + 4, the El Chichon plume reaches its maximum scattering of 181 and AOD of 0.81 much later, on D + 40. This corroborates the hypothesis on the expedited conversion of SO2 to sulfate aerosols due to abundance of water in the Hunga plume31.
Fast circumglobal transport and vertical motion of moisture and aerosols
The altitude reach of the Hunga eruption has led to an unusually fast circumglobal transport of volcanic material entrained by strong zonal winds in the upper stratosphere, up to 60 m/s at 47 km altitude (Fig. 2a). Consequently, the uppermost plume of moisture circumnavigated the Earth in only 1 week—as already noted by ref. 20 — and made three full circles in 25 days whilst ascending through the Brewer-Dobson circulation from ~43 km to ~49 km (Fig. 4a), that is ~200 m per day. The aerosol plume above 40 km has travelled around the globe in 9 days and only made a single round as was also noted by ref. 30. The limited lifetime of aerosols at this level could be due to sedimentation and/or evaporation of sulfate particles in the warm upper stratospheric environment37. We note though that the nature of the upper-stratospheric aerosols is unknown due to the absence of CALIOP depolarization measurements above 40 km.
a Evolution of the water vapour mixing ratio (WVMR) peak altitude for the hydrated layers (WVMR > 10 ppmv) in the upper stratosphere (40–50 km) as a function of time and longitude. The black squares with altitude-dependent color meshing indicate the detections of aerosol layers with extinction ratio (ER > 0.25) by OMPS-LP within the respective altitude range. Note that the uppermost plume at around 45 km circumnavigates the globe in only 1 week. b Same as A but for the hydrated layers (WVMR > 10 ppmv) and aerosol layers (ER > 2.5) in the middle stratosphere (30–40 km). c Same as panel b but for the lower stratosphere (20–30 km) and with detection threshold of 30 ppmv. The black circles with altitude-dependent color meshing indicate the radiosonde detections of WVMR enhancements above 50 ppmv. The horizontal dashed lines in c indicate the dates shown in Fig. 5a, b.
In the middle layer, between 30–40 km (Fig. 4b), the aerosol and moisture plumes travelled in close tandem for about a month, and their leading edges circumnavigated the globe in 9 days, covering entirely the Southern tropical band by 29 January, that is in 2 weeks20,21. Ref. 20 showed the consistency of the plume’s vertical shear with reanalysis winds. Such a fast circumnavigation of the tropical stratosphere by a volcanic plume is remarkable compared to other major eruptions: the stratospheric plumes produced by 1982 El Chichon38 and 1991 Pinatubo39 eruptions had circled the globe in 3 weeks, although their plumes were mostly confined to lower altitudes.
The zonal progression of the bulk of the plume contained within the 20–30 km layer is found to be fully consistent between MLS and radiosoundings, both showing a complete circumnavigation in 2 weeks (Fig. 4c). During its first circumnavigation, the plume undergoes considerable subsidence, as seen from MLS and radiosounding data (Fig. 4c). We estimate an average descent rate around 200 m/day with maximum plume top altitudes decreasing from near 30 km during the first overpass over Australia (January 16–19) to ~26 km during the second overpass (February 1–10). Ref. 24 proposed that this vertical motion be driven by radiative cooling induced by the large water vapor anomaly.
Further insight into the morphological evolution of the volcanic moist plumes is provided by simulations with the Chemical Lagrangian Model of the Stratosphere (CLaMS)40 initialised with MLS water vapour observations (Supplementary Notes S.II, Fig. S3). The simulation reveals a relatively compact bulk plume during its first Australian overpass on D + 4 (Fig. 5a), whereas during the second overpass on 2nd February the plume appears as a dragon-shaped structure with a head emerging around 10° S, where the easterlies are strongest, and a tail at around 20° S extending all across the Pacific (Fig. 5b and Supplementary Movie S2). The model-simulated plume location, extent and circumglobal transport is in good agreement with MLS satellite observations (pink circles in Fig. 5). The cross-Pacific extent of the bulk plume by the time of the second Australian overpass is also largely consistent with radiosonde detections of hydrated layers (Fig. 5b). By the time of the third Australian overpass, the head of the plume catches up with its tail thereby gaining complete zonal coverage (Fig. 5c).
The panels show the geographical extent of the hydrated plume at 21 hPa during its first (a), second (b) and third (c) overpass above Australia. The values represent the WVMR difference between the control (pre-eruption initialization) and perturbed (post-eruption) simulations exceeding 3 ppmv at 21 hPa level (see Methods). The magenta open circles indicate the locations of MLS hydrated layers at 21 hPa with WVMR > 30 ppmv. The green open circles show the locations of radiosounding stations involved in the analysis. The red-filled circles indicate the radiosonde detections of hydrated layers on the respective day. ECMWF wind field at 21 hPa is shown in grey arrows. See Supplementary Movie S2 for the complete sequence.
Meridional dispersion of volcanic plumes
After being injected into the southern tropical stratosphere, the volcanic material was subsequently transported in the meridional plane into Northern and Southern hemispheres by the stratospheric circulation on a timescale of weeks to months (Fig. 6). The CLaMS simulation vividly shows the transport towards the North pole along the deep branch of the Brewer-Dobson circulation on a timescale of 1–2 months as well as a fast isentropic transport towards the South pole in the lowermost stratosphere (Fig. 6a). These pathways are consistent with the known seasonality of the stratospheric BDC, with the deep branch circulation maximising in hemispheric winter and the shallow branch circulation maximising in hemispheric summer (e.g. ref. 41).
a Poleward dispersion of hydrated plumes detected by MLS V5 with WVMR climatological anomalies exceeding 3 ppmv. The pixels are colour-coded by the age of hydrated layers since 15 January 2022. The contours (age colour-coding) represent the results of CLaMS model simulation of hydrated plumes transport (WVMR anomalies above 3 ppmv). The initial extent of the wet anomaly in the CLaMS simulation (initialised with MLS V5 data on 18 January) is represented by the inner isoline. Thick solid curves mark the tropopause and the stratopause, thin dashed curves indicate isentropic levels. b Same as A but for OMPS-LP detections of aerosol layers with extinction ratios exceeding 3. The black rectangles with age-dependent colour meshing indicate the first aerosol layer detections by ground-based lidars (Fig. S4 and Supplementary notes S.III).
The MLS observations show that within 5 months of the eruption, the hydrated plumes have spread in both directions from 65° S to 35° N but mostly within the bulk plume layer (20–30 km). The deep Brewer-Dobson transport is not captured by MLS, whereas the CLaMS simulation lacks the lower-branch northbound transport. The differences between the simulation and observations regarding meridional transport could be due to various factors, such as the broad vertical resolution of MLS complicating the detection of thin layers; uncertainty in the model heating rates, which were altered due to radiative cooling in the stratosphere induced by excessive moisture24 as well as due to errors in the ECMWF meridional winds in the tropics (e.g. ref. 42). The meridional dispersion of aerosol plumes (Fig. 6b), as inferred from OMPS-LP measurements, exhibits prominently the various transport pathways: the fast transport in the lowermost stratosphere towards the South pole (3–4 weeks), the transport along the BDC between 500 K–700 K isentropes into both hemispheres (1–2 months), which is followed by subsequent dispersion from the Northern tropics towards the North pole (3–4 months). The observed meridional transport pattern and timescale is very similar to that reported after the Pinatubo eruption with the faster lower-stratospheric and slower mid-stratospheric branches43. In both Pinatubo and Hunga cases, the transport into the opposite hemisphere was slower at all levels, with the lower stratospheric branch showing vertical separation in the northern subtropics, likely due to confinement by the Summer monsoon anticyclones. The eventual occurrence of aerosols below the zonally-averaged tropopause level in the Northern and Southern subtropics suggests sedimentation of large sulfate particles out of the stratosphere.
The satellite-derived meridional transport timescale is confirmed by ground-based lidar detections of aerosol layers (Fig. S4, Supplementary notes SIII) shown as black squares in Fig. 6b. The fast transport towards the South pole within the lowermost stratosphere is captured by lidars at Lauder station, New Zealand (45° S) and Dumont d’Urville French Antarctic station (67° S) respectively 3 and 4 weeks after the eruption. The northbound dispersion of aerosols is captured by lidar detections in the northern tropics (Mauna Loa, Hawaii), subtropics (Tsukuba, Japan), mid-latitudes (OHP, France and Kuhlungsborn, Germany) as well as high-latitudes (Alomar, Norway) (Fig. 6b). Overall, in about 3 months since the eruption, the Hunga sulfates have spread nearly pole-to-pole, although the aerosol layers detected in the Northern extratropics are less intense, with scattering ratios below 1.8 (Fig. S4).
Three-dimensional structure and evolution of stratospheric water and aerosol perturbation
The extreme explosiveness of the Hunga eruption along with the submarine nature of the source has led to in-depth perturbations of stratospheric water vapour and aerosol amounts. Figure 7a shows the broad-range positive post-eruption water vapour anomaly (colours) that extends throughout the depth of the tropical stratosphere—from the tropopause to nearly the stratopause. The region of highest anomalies, exceeding 100% on a zonal-mean scale and averaged over 5 months after the eruption, is found in the southern tropics within the 23–27 km altitude layer. The anomaly in aerosol extinction (contours) exceeding 100% extends across most of the tropical lower and middle stratosphere and reaches 1000% at 24-–25 km altitude in the southern tropics. The latitudinal pattern of the aerosol extinction anomaly is well correlated with that of water vapour, except for the downward shift of aerosol anomalies. Indeed, while the bulk layer of gaseous water and the upper boundary of the positive water anomaly are both gradually rising in the tropical upwelling branch of the Brewer-Dobson circulation, the bulk of aerosols is sedimenting with a vertical rate estimated as 0.26 mm/s (Fig. 7b, Fig. S6f). The subsidence and meridional dispersion of the bulk aerosol layer is well captured by Aeolus ALADIN satellite lidar (Fig. S8). Despite the vertical decoupling of bulk water vapour and aerosol layers in the stratosphere, their meridional dispersion reveals a very similar pattern with a more efficient transport towards the Southern pole (Fig. 7c).
a MLS V5 zonal-mean WVMR anomaly above 5% averaged over 5 months following the eruption with respect to MLS 17-yr climatology (%, color map) and OMPS-LP extinction ratio anomaly with respect to pre-eruption conditions (%, contours). b Same as A but as a function of time for the latitude band 30° S–10° N. c Time-latitude variation of WVMR anomaly within 20–27 km altitude layer (color map) and change in OMPS-LP AOD with respect to the pre-eruption levels within the same layer (contours).
Perturbation of stratospheric water isotopic composition
The underwater blast associated with Hunga eruption and subsequent ice-vapour phase transition in the stratosphere led to a substantial increase in heavy water isotopologues as inferred from Atmospheric Chemistry Experiment Fourier Transform Spectrometer (ACE-FTS) satellite observations. Figure 8 shows the perturbation in the HDO/H2O ratio (δD), which represents the negative deviation from the Standard Mean Ocean Water (SMOW). The δD enhancement is found between 30° S–10° N, extends over 23–29 km layer (Fig. 8c), and amounts to about 275‰ over typical values found in the previous years (Fig. 8a). Above 30 km, the increase of δD is associated with oxidization of methane heavy isotopologues.
The extreme excursion of water isotopic ratio towards the Standard Mean Ocean Water (SMOW) levels strongly suggests seawater as the main source of injected moisture. The deviations of δD from typical lower stratospheric values are generally associated with convective cross-tropopause lofting of ice44,45. In this case, however, the signal is much stronger and comes from the direct injection of evaporated seawater into the stratosphere. This moisture condensed during the rise of the eruptive column, and the subsequent sublimation in the stratosphere has led to its strong isotopic enhancement. It is worth noting that the 2019/2020 Australian wildfires, which caused a substantial hydration of the stratosphere46, did not lead to a measurable large-scale increase of water isotopic ratio in the stratosphere (Fig. 8b), which is another indication for the sea water as the main source of stratospheric hydration by Hunga.
Evolution of sulphate particles
Of particular interest is the post-eruption evolution of stratospheric aerosol size. Figure 9 shows the effective radius retrieved from the Stratospheric Aerosol and Gas Experiment (SAGE) III for the months following the Hunga eruption using different assumptions on the aerosol composition. The effective radius parameter is not measured directly, but calculated from fitted lognormal distributions to the SAGE III extinction spectra (Supplementary notes S.V). While the retrieved particle size is dependent on composition assumptions, there is insufficient information in the SAGE spectra to determine both size and if the relative fraction of water in the droplet makeup may be changing. Background conditions, shown in dashed lines, typically have an effective radius of ~230 nm. After the eruption, particle size increases from the background values to over 400–500 nm, depending on composition; larger than at any other point in the SAGE III/ISS record. This growth is contained primarily between 22 and 26 km, which contains the bulk of the enhanced aerosol. By mid-March the particles have reached their maximum size and this layer begins settling. A more detailed analysis of retrieved size parameters suggests a complex interplay between the sedimentation, condensation and coagulation processes (Supplementary notes S.V, Fig. S7).
The A–G show monthly averaged effective radius retrieved from SAGE III/ISS (January through July 2022, month indicated in each panel) assuming background (red) and pure-water (blue) aerosol composition. Dashed lines indicate the average effective radius pre-eruption, computed from October and November 2021 profiles.
The sedimentation rate of aerosol was estimated from OMPS-LP tomographic retrieval of extinction profiles by tracking the peak altitude of the plume (Supplementary notes S.V, Fig. S6). A linear fit to the peak beginning March 10th suggests a settling rate of 0.26 mm/s, which is in agreement with CALIOP-derived estimates34. Taking into account the monthly averaged ERA5 vertical wind speed we obtain the fall speed, based on which the particle size can be estimated using the method proposed by ref. 47. Depending on the assumption on the particles’ relative fraction of H2O/H2SO4, we obtain a radius of 350–540 nm in April-May, which is fully consistent with the SAGE III-derived particle sizes, providing confidence in these estimates. Somewhat larger particles with effective radius between 500–700 nm are reported by ref. 34.
Global perturbation of stratospheric water vapour and aerosol burden
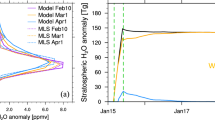
Figure 10a shows the annual cycle of stratospheric water vapour mass (between 100 hPa–1 hPa pressure levels), which is characterised by a minimum in boreal spring and a maximum in Austral spring with a peak-to-peak amplitude of 60 Tg. The Hunga eruption occurred at the midpoint of the decay phase and boosted the stratospheric water burden by 119 ± 6 Tg, which is nearly twice the annual amplitude. This figure is consistent with the GNSS-RO-based mass estimate of 70 − 150 Tg. Using an older V4 version of MLS data we obtain the mass of water transported across the 100 hPa level of 137 ± 7 Tg (Supplementary Fig. S6), which is consistent with earlier estimates of 146 ± 5 Tg20 and 139 ± 8 Tg21 using the same data version. The stratospheric water burden perturbation by the Hunga eruption is about a factor of 5 larger than the previous record-breaking perturbation of stratospheric water vapour (27 Mt) by the Australian “Black Summer” wildfires in 2019/202046. The other volcanic or wildfire events during the MLS period did not lead to a measurable increase in the global stratospheric water budget, although local enhancements in water vapour were observed by MLS following the 2017 Canadian wildfires eruption20.
a Evolution of the global MLS V5 stratospheric water vapour mass (3-day averages) between 100 hPa–1 hPa pressure levels (solid black curve) and climatological (2004-2021 period) annual cycle (dashed curve), the positive and negative anomalies are shown respectively as red and blue shading. b Deseasonalized stratospheric water vapour mass anomaly (per cent 3-day averages) for both hemispheres and the whole globe from MLS. The embedded panel shows the evolution of global anomaly in 2022. c Stratospheric aerosol optical depth (SAOD) anomalies for the 60° S–60° N latitude band (monthly averages) from GloSSAC merged satellite record extended using OMPS-LP measurements at 675 nm scaled to 525 nm wavelength using GloSSAC data and SAGE III/ISS measurements at 521 nm converted to 525 nm using SAGEIII-derived Angstrom exponent. The SAOD anomalies are computed with respect to the background level estimated as GloSSAC SAOD average over volcanically-quiescent 1995–2003 period. The embedded panel shows the full time span of SAOD series. The cyan and pink letters indicate the most significant volcanic eruptions and wildfire events respectively (EC El Chichon, Pi Pinatubo, Sa Sarychev, Na Nabro, Ke Kelud, Ca Calbuco, PNE Pacific Northwest wildfire event, Ra Raikoke, ANY Australian New Year wildfire event, HT Hunga Tonga).
Figure 10b shows that the stratospheric water vapour mass anomaly has reached ~24% in the Southern and ~11% in the Northern hemisphere, whereas the global anomaly has reached ~16% after the eruption. Note that over the 17-yr time span of MLS data, the global and hemispheric anomalies do not exceed 5%, which renders the Hunga-induced perturbation of stratospheric water load unique in the record. Indeed, the Stratospheric Water and OzOne Satellite Homogenized data set (SWOOSH)48 including satellite measurements of stratospheric water vapour since 1985, clearly shows that the perturbation is unprecedented in the satellite record of stratospheric water vapour. The same conclusion is reached by on the basis of GROZCARDS merged satellite data20.
In order to place the stratospheric aerosol load perturbation by Hunga into historical perspective, we combined the GloSSAC merged satellite dataset spanning 1979–202049 with the recent aerosol extinction measurements by OMPS-LP and SAGE III satellite sensors. Figure 10c provides evidence that the Hunga eruption led to a 4-5-fold increase in the stratospheric aerosol optical depth (SAOD), exceeding by far any volcanic or wildfire event in the last three decades. With that, the absolute magnitude of SAOD perturbation (embedded panel in Fig. 10c) by Hunga is at least a factor of 6 smaller than that of the previous major eruption of Pinatubo in 1991 and factor of 3 smaller than that of El Chichon in 1982.
Discussion
The extreme explosiveness of the Hunga eruption and the submarine location of the volcano add up to the unprecedented character, magnitude and the propagation timescale of the global stratospheric perturbation20,22,24,31,32,34,50. The eruption provided a unique natural testbed, lending itself to studies of climate sensitivity to strong change in both stratospheric gaseous and particulate composition. The nine-month aftermath of the Hunga eruption in terms of stratospheric water vapour and aerosol burden, provided with this study, sheds light on the further evolution of this perturbation and its longevity.
The stratospheric aerosol perturbation by the Hunga eruption has reached its peak in early June and exceeded in magnitude the strongest volcanic or wildfire events in the last three decades, including 2009 Sarychev eruption51, 2015 Calbuco eruption33, 2019 Raikoke52 and 2019/2020 Australian Black Summer wildfires46. Since June, the post-Hunga stratospheric optical depth anomaly has been decreasing and, assuming its further exponential decay, the extrapolation projects the return of SAOD anomaly to pre-eruption levels in 14–17 months, that is by mid-2023. We note that the gravitational settling of sulphate aerosols from the stratosphere may be expedited by their fast growth in the humid environment.
The perturbation of stratospheric water vapour burden by 13% is tremendous and has no frame of comparison in the entire observation record dating back to 1985. As there are no efficient sinks of water vapour in the stratosphere, this perturbation is expected to last over several years. Indeed, in 9 months since the eruption, the water vapour mass anomaly has gradually decreased only by 2.5% (4.3 ± 0.1% annual rate), which should lead to the perturbation timescale of over 3 years, assuming the further linear decay trend. The persistent stratospheric moist anomaly may lead to changes in atmospheric radiative balance;20,24,25,53,54 stratospheric dynamics26 as well as amplification of the polar ozone depletion through wider occurrence of polar stratospheric clouds31. The ability to assess the longer-term impacts of the HT eruption on stratospheric chemistry will depend strongly on the quality and availability of global satellite observations such as MLS in the coming years.
Given the magnitude, the depth and the expected longevity of the stratospheric perturbation, the Hunga eruption can be said to have initiated a new era in stratospheric gaseous chemistry and particle microphysics with a wide range of potential long-lasting repercussions for the global stratospheric composition and dynamics. It is essential to note that the effect is expected to be much stronger in the Southern stratosphere, which contained the bulk of the eruptive material after 9 months since the event.
While the longer-term aftermath of the Hunga effects is yet to be known, the available data provide enough evidence to rank this eruption among the most remarkable climatic events in the modern observational era and strongest in the last three decades. As remote sensing techniques and satellite coverage of the stratosphere have been substantially improved in the XXI century, the wealth of observational data on the Hunga event together with various modelling approaches should provide a major advance in understanding the impacts of stratospheric composition change on global climate.
Methods
Supplementary Table S1 lists all the datasets involved in this study.
Stereoscopic cloud top height (CTH) retrieval
Two primary steps were used in the derivation of cloud top height for the Hunga Tonga-Hunga Ha’apai eruption cloud based on GOES-17 and Himawari-8 geostationary satellite observations: (1) spatially matching simultaneous observations from the two satellites, and (2) using the stereoscopy principle to construct a 3D profile of the cloud. Because the two satellites have sufficiently different viewing angles, it is possible to derive a cloud top height with accuracy equal to or better than the spatial resolution of the imagery being used. Level 1B infrared (IR) brightness temperature (BT) data in the 10.3 μm is collected at 2 km/pixel nadir resolution every 10 min and nearly simultaneously from GOES-17 and Himawari-8 because the imagers on these satellites, the Advanced Baseline Imager (ABI) and Advanced Himawari Imager (AHI) respectively, are nearly identical and have the same scan initiation times and scan rate. Although IR imagery is of lower resolution than the visible, it has its own advantages as it is free of shadows, is nearly isotropic, and is available at nighttime. Pixel geolocation in Level 1B data is obtained by intersecting the instant view axis of the imager instrument with the Earth reference ellipsoid, and thus the nominal image registration is accomplished assuming a zero elevation of observed scenes. Once these Level 1B data are reprojected from the satellite’s pixel/line space to a geographical projection, any elevated scene exhibits a parallax displacement, which is different for images recorded at different viewing angles. With simple geometric transformations, the two parallax displacements from the two satellites can be directly related to the height.
An algorithm developed at NASA Langley Research Center uses image subsets (chips) ranging from 8 × 8 to 20 × 20 pixel sizes to obtain a cross correlation between chips from the two image sources. Trying different relative displacements between the chips consecutively yields the highest correlation at the position of optimal displacement, which corresponds to the actual height for that image subset. Analyses indicate that we were able to achieve a subpixel accuracy when calculating the position of the highest correlation. This translates to a typical accuracy of the derived height on the order of 0.2–0.4 km. When the analyzed image chips have little texture, the correlation matching may fail for smaller chip sizes. In that case, a larger chip can be used to obtain a reliable peak in the correlation profile, but that lowers the effective resolution of the resulting map of retrieved heights. More than 90% of image chips, however, were reliably matched using the 8 × 8 chip size, which helps to resolve smaller features and details within the eruption cloud, like the small peaks of cloud extending above 50 km altitude. Overall, we estimate the spatial resolution of the cloud top height retrieval product to be ~4–6 km/pixel. This algorithm was applied to satellite data from 0400 to 2350 UTC on 15 January 2022 to quantify heights reached by the eruption cloud and document its temporal evolution.
COSMIC-2 water vapour retrieval
Constellation Observing System for Meteorology Ionosphere and Climate (FORMOSAT-7/COSMIC-2)55 is a recently launched equatorial constellation of six satellites carrying advanced GNSS (Global Navigation Satellite System) radio occultation (RO) receivers, providing high vertical resolution profiles of bending angles and refractivity, which contain information on temperature and water vapor. A few RO soundings occurred inside the Hunga plume on January 15th, depicting extremely unusual large refractivity anomalies. While refractivity N in the neutral atmosphere depends on temperature T (K), pressure P (hPa), water vapor partial pressure e (hPa) and liquid water W (g m−3) (ref. 56 equations 7 and 11):
we expect negligible liquid water amounts and the magnitude of the anomalies of the profiles in the early plume would result in temperature anomalies with unphysically low values near the plume. On the contrary volcanic plume studies suggest that the temperature within the plume relaxes to that of the background atmosphere within a few tens of minutes, with differences (e.g., associated with waves) typically below 10 K amplitude in the stratosphere. Hence, we assume that the temperature and pressure are at environmental values, as given by the high resolution operational analysis of the European Center for Medium Range Weather Forecast (ECMWF), and attribute the refractivity anomaly signal solely to water vapor, in agreement with expectations regarding the adjustment of a volcanic plume14,57, which can be retrieved from ref. 56, equation 11:
There are large uncertainties associated with this retrieval procedure, in particular in the ECMWF temperature and pressure profile. This can lead to unphysical e retrievals, e.g. negative or largely above ice saturation in the lower stratosphere. In order to roughly quantify the associated error, we applied the same retrieval to refractivity profiles obtained on January 14, the day before the eruption. The median ±3 standard deviations of those retrievals provide an estimate of the bias and uncertainty associated with the approach, and are shown in Fig. 1d (dashed black lines). In the lower stratosphere, the typical uncertainty and detection limits are orders of magnitude larger than the saturation mixing ratio, preventing any meaningful retrieval in that altitude range.
The RO-based estimates of the injected water mass were obtained as described below. First, water vapor columns from 20 km to 50 km ASL are computed for the two early water mixing ratio profiles (Fig. 1d) through vertical integration. Before performing that step, unphysical values in the profiles are replaced as follows: mixing ratio values corresponding to relative humidities over ice >100% are replaced by the saturation value (computed with ECMWF temperature), negative values and values >5 ppmv (arising due to uncertainties in the procedure, e.g. in ECMWF T) by a background of 5 ppmv. The two estimates of the water vapor column are then multiplied by the area occupied by the plume at that time (150,000 km2 according to the geostationary satellite), which leads to two estimates of the injected mass (75 and 140 Tg, respectively). Obviously, this calculation only takes into account the water vapor, to which GPS-RO is sensitive, neglecting the effect of the later sublimation in the stratosphere of the ice still present at the measurement time (i.e. assuming most of it will fall out). This approach also relies on the assumption that the profiles are representative of the whole area covered by the plume (neglecting heterogeneities), which should be realistic if, as suggested by the profiles, the whole plume seen from the geostationary satellites is at ice saturation.
Aura MLS
The MLS (Microwave Limb Sounder)58 instrument on the NASA Aura satellite has been measuring the thermal microwave emission from Earth’s atmospheric limb since July 2004. With ~15 orbits per day, MLS provides day and night near-global (82° S–82° N) measurement of vertical profiles of various atmospheric gaseous compounds, geopotential height and temperature of the atmosphere. The measurements yield around to 3500 profiles per day for each species with a vertical resolution of ~3–5 km.
For this study we use MLS version 5.01 water vapour and geopotential height product59 except for the analysis of the early evolution of the hydrated plume and its vertical structure (Figs. 1 and 2), where we use the older v4.32 product60. The reason is that v5 data suffers from pointing issues in the presence of extreme humidities, which can lead to low height anomalies as large as 2.5 km20. The MLS data are accompanied by indicators about data quality and the status of the retrieval convergence. As stated by ref. 20 most of the early MLS measurements of the Hunga hydrated plume did not pass the MLS quality screening. Therefore, here we use MLS water vapour data without accounting for the quality flag as in ref. 20.
The stratospheric mass load of H2O was derived from MLS volume mixing ratio measurements (using both v4 and v5 products) of water vapour in log pressure space, molecular mass of the compound and the air number density derived from MLS temperature profile on pressure levels between 100 hPa–1 hPa levels. The error bars on the mass of injection are estimated by combining accuracies on the measurements and the mean standard deviations over 20-day periods before and after the sharp increase. See Supplementary notes S.IV for further detail on the mass estimation method.
OMPS-LP
The Ozone Mapping and Profiler Suite Limb Profiler (OMPS-LP) on the Suomi National Polar-orbiting Partnership (Suomi-NPP) satellite, which has been in operation since April 2012, measures vertical images of limb scattered sunlight in the 290–1000 nm spectral range61. The sensor employs three vertical slits separated horizontally to provide near-global coverage in 3–4 days and >7000 profiles a day. Here we use OMPS-LP V2.0 aerosol extinction data62 at 675 nm for analysis of long-term stratospheric AOD evolution (Fig. 10) and a special time period-limited V2.1 data version extended to 45 km altitude30 for the rest of the analysis. Extinction ratio is computed as the ratio between aerosol and molecular extinction. For estimating the sedimentation rate of aerosol particles, we use OMPS-LP data retrieved using a tomographic algorithm63, which provides extinction profiles at 755 nm with 1–2 km resolution throughout the stratosphere.
CALIPSO CALIOP
The Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP) is a two-wavelength polarization lidar on board the CALIPSO mission that performs global profiling of aerosols and clouds in the troposphere and lower stratosphere64. We use the total attenuated 532 nm backscatter level 1 product V3.40. The depolarization ratio is computed as the ratio between the perpendicular and parallel components of the attenuated backscatter.
SCISAT ACE-FTS
The ACE-FTS (Atmospheric Chemistry Experiment Fourier Transform Spectrometer)65 is the primary instrument aboard SCISAT. It has been observing about 30 solar occultations per day since 2004, recording spectra between 750 cm-1 to 4400 cm-1 at a spectral resolution of 0.02 cm-1 and an altitude resolution of 1–2 km. Volumetric mixing ratio profiles of >30 trace gases can be inferred from these spectra, including those of H2O and HDO. In this study we use the Version 4.1/4.2 Level 2 VMR retrievals of H2O and HDO. Vapor-phase deltaD is derived from these quantities at altitude levels between 12 and 40 km. DeltaD is a measure of the HDO/H2O ratio in a sample relative to ratio found in Standard Mean Ocean Water (SMOW). Flags from both species are used to assess retrieval quality and determine at which altitude ranges retrievals were actually performed.
ISS SAGE III
The Stratospheric Aerosol and Gas Experiment (SAGE) III provides stratospheric aerosol extinction coefficient profiles using solar occultation observations from the International Space Station (ISS)66. These measurements, available since February 2017, are provided for nine wavelength bands from 385 to 1550 nm and have a vertical resolution of ~0.7 km. The SAGE III/ISS instrument and the data products have characteristics nearly identical to those from the SAGE III Meteor mission. We use version V5.2 of SAGE III solar occultation species data. Particle size is retrieved from SAGE III/ISS by fitting the extinction spectrum from 384 to 1540 nm using a unimodal lognormal particle size distribution. Typically, particles in the stratosphere are composed primarily of sulfuric acid and water with a 75/25 mix of H2SO4/H2O. This assumption impacts the particle size retrieval through the index of refraction, which for background conditions is typically between 1.40 and 1.44, depending on wavelength. If particles are more hydrated this may reduce the index of refraction. To estimate the upper bound of the error due to the assumed index of refraction the retrieval is also performed assuming droplets of pure-water, which leads to retrieved effective radii consistently 100 nm larger than when particles have a H2SO4/H2O mix.
ALADIN/Aeolus
The European Space Agency’s Aeolus satellite carries a Doppler wind lidar called ALADIN (Atmospheric Laser Doppler INstrument), which operates at 355 nm wavelength and which can separate the molecular (Rayleigh) and particular (Mie) backscattered photons (high spectral resolution lidar, HSRL). The lidar observes the atmosphere at 35° from nadir and perpendicular to the satellite track, its orbit is inclined at 96.97°, and the instrument overpasses the equator at 6 h and 18 h of local solar time (LST). We use its L2A Aerosol/Cloud optical product (baseline 12 and above) retrieved with the help of Standard Correct Algorithm67 and available at 87 km horizontal resolution.
Meteorological radiosoundings
We use the data of meteorological radiosoundings conducted with high-accuracy Väisälä RS41 sondes in the Southern tropics (Australia, Saint Helena island, Seychelles, Chile and Argentina). Under normal circumstances, stratospheric humidity is particularly difficult to measure due to low ambient relative humidity and large outgassing from the balloon (~100 ppmv at 30 km) overwhelming the small stratospheric water signal (e.g. ref. 68). However, this contamination is outweighed by the ultra-moist plume HT plume which clearly stands out from background variability and exceeds uncertainties of Vaisala RS41 during its first round-the-globe tour. The humid plume (RH > 20%) within the relatively warm upper stratosphere (T > 220 K) constitutes a favorable environment for RS41 humidity measurements69. While only RS41 data are included in this survey, other lower resolution sondes detected the plume during its first overpass (Vaisala RS92) whereas others did not exhibit notable enhancements (M10, iMET).
Later on during the plume dispersion, the raw water vapor signal is diluted and becomes difficult to isolate from the effect of altitude-dependent outgassing. It is nevertheless possible to track the plume as an anomaly from a typical contamination profile defined as the 90% quantile profile over 1 month for each station. This simple approach is sufficient for the second overpass over continental stations but fails over tropical islands where outgassing exhibits large variability related to low level moisture and cloudiness profile.
Ground-based lidars
We use aerosol backscatter measurements at 532 nm provided by ground-based lidars at various locations to characterize the time scale of the meridional dispersion of Hunga aerosol plumes. The aerosol plumes are detected as local maxima in scattering ratio exceeding 1.2. The lidar stations involved in this study (sorted by latitude) are Dumont d’Urville (67° S), Lauder (45° S), Reunion (21° S), Mauna Loa (20° N), Tsukuba (36° N), Haute Provence (44° N), Kuhlungsborn (54° N) and Alomar (69° N). The description of the measurement stations and lidar instruments is provided in Supplementary Methods.
GloSSAC merged satellite aerosol climatology
The Global Space-based Stratospheric Aerosol Climatology (GloSSAC) is a 38-year climatology of stratospheric aerosol extinction coefficient measurements by various satellite instruments such as SAGE, OSIRIS, CALIOP49. Data from other space instruments and from ground-based, aircraft and balloon-borne instruments are used to fill in key gaps in the data set. Here we use GloSSAC V2.1 data on aerosol extinction at 525 nm.
CLaMS chemistry-transport model simulation
The evolution of the Hunga Tonga water vapour plume through the stratosphere has been simulated with the Chemical Lagrangian Model of the Stratosphere, CLaMS (e.g. ref. 40). CLaMS is a 3d Lagrangian chemistry transport model with transport and chemistry offline driven by wind and temperature data from meteorological (re)analysis or climate models. Lagrangian model transport is based on the computation of forward trajectories with an additional parameterization of small-scale turbulent mixing processes, depending on the shear in the large-scale flow. The calculation of stratospheric water vapour in CLaMS is based on a freeze-drying parameterization depending on local saturation mixing ratios along the air parcel trajectories and a mean sedimentation velocity for ice, and additional chemistry for representing methane oxidation (e.g. ref. 70). This model representation of relevant de- and re-hydration processes together with CLaMS’ Lagrangian transport scheme has been shown advantageous for reliably simulating the stratospheric water vapour distribution (e.g. ref. 71) and its trend72. Also the transport of volcanic plumes has recently been simulated realistically with CLaMS52.
For this study we used the operational analysis from the European Centre of Medium-range Weather Forecasts (ECMWF) for driving model simulations. Model transport in the stratosphere is formulated using a diabatic coordinate in the vertical (potential temperature) and the required diabatic heating rates have been calculated via a Morcrette scheme assuming clear-sky conditions (e.g. ref. 73). We carried out a control simulation for unperturbed conditions, with stratospheric water vapour initialised with mixing ratios observed by MLS just before the Tonga eruption on 13 January 2022, and a perturbed simulation with water vapour initialised just after the eruption on 18 January 2022. For preparing 3D water vapour initialisation fields, MLS measurements (data version 5) have been mapped onto the closest synoptic time (12 UTC) using forward/backward trajectories, and have subsequently been binned to a regular 1 × 3 degree latitude-longitude grid on the respective MLS pressure levels (see above). Data gaps in these regularly gridded MLS water vapour distributions related to the coarse satellite sampling have been filled by interpolation from values around, before using these distributions for initialising the CLaMS irregularly spaced Lagrangian model grid on 13 and 18 January 2022 via interpolation.
Data availability
MLS water vapour data are available at https://acdisc.gesdisc.eosdis.nasa.gov/data/Aura_MLS_Level2/ML2T.005/2022/. CALIOP data v3.41 are available at: https://doi.org/10.5067/CALIOP/CALIPSO/CAL_LID_L1-VALSTAGE1-V3-41. OMPS V2.0 data is available at https://snpp-omps.gesdisc.eosdis.nasa.gov/data/SNPP_OMPS_Level2/OMPS_NPP_LP_L2_AER_DAILY.2/2022/; COSMIC-2 data are available at https://data.cosmic.ucar.edu/gnss-ro/cosmic2/nrt/level2/; OMPS-LP V2.1 data is available at https://avdc.gsfc.nasa.gov/pub/data/satellite/Suomi_NPP/L2/LP-L2-AER-45km/LP-L2-AER-DAILY/2022/; OMPS-LP tomographic retrieval data are available at ftp://odin-osiris.usask.ca/ with login/password osirislevel2user/hugin; SAGE III data at https://doi.org/10.5067/ISS/SAGEIII/SOLAR_BINARY_L2-V5.2; Aeolus data are available at https://aeolus-ds.eo.esa.int/oads/access/collection/Level_2A_aerosol_cloud_optical_products/; ACE-FTS data are available upon registration at https://databace.scisat.ca/l2signup.php; GloSSAC data are available at https://asdc.larc.nasa.gov/project/GloSSAC/GloSSAC_2.1; Eruptive column cloud top height data are available at https://clouds.larc.nasa.gov/prod/OT/15January2022_tonga_CTH.tar; Meteorological radiosounding data are available at http://www.weather.uwyo.edu/upperair/bufrraob.shtml; Ground-based lidar data are available at https://ndacc.larc.nasa.gov/; ECMWF data are available at https://doi.org/10.21957/open-data.
Code availability
The scripts and notebooks used in this study as well as intermediate datasets are available from Zenodo https://doi.org/10.5281/zenodo.7347758.
References
Poli, P. & Shapiro, N. M. Rapid characterization of large volcanic eruptions: Measuring the impulse of the Hunga Tonga Ha’apai explosion from teleseismic waves. Geophys. Res. Lett. 49, e2022GL098123 (2022).
Matoza, R. S. et al. Atmospheric waves and global seismoacoustic observations of the January 2022 Hunga eruption, Tonga. Science https://doi.org/10.1126/science.abo7063 (2022).
Wright, C. J. et al. Surface-to-space atmospheric waves from Hunga Tonga–Hunga Ha’apai eruption. Nature 609, 741–746 (2022).
Carr, J. L., Horváth, Á., Wu, D. L. & Friberg, M. D. Stereo plume height and motion retrievals for the record-setting Hunga Tonga-Hunga Ha’apai eruption of 15 January 2022. Geophys. Res. Lett. 49, e2022GL098131 (2022).
Brewer, A. W. Evidence for a world circulation provided by the measurements of helium and water vapour distribution in the stratosphere. Q. J. Roy. Meteor. Soc. 75, 351–363 (1949).
Mote, P. W. et al. An atmospheric tape recorder: the imprint of tropical tropopause temperatures on stratospheric water vapor. J. Geophys. Res. 101, 3989– 4006 (1996).
Bonazzola, M. & Haynes, P. H. A trajectory-based study of the tropical tropopause region, J. Geophys. Res. 109, D20112 (2004).
Forster, P. M. de F. & Shine, K. P. Assessing the climate impact of trends in stratospheric water vapor. Geophys. Res. Lett. https://doi.org/10.1029/2001GL013909 (2002).
Riese, M. et al. Impact of uncertainties in atmospheric mixing on simulated UTLS composition and related radiative effects, J. Geophys. Res. 117, D16305 (2012).
Solomon, S. et al. Contributions of stratospheric water vapor to decadal changes in the rate of global warming. Science 327, 1219–1223 (2010).
Anderson, J. G., Wilmouth, D. M., Smith, J. B. & Sayres, D. S. UV dosage levels in summer: increased risk of ozone loss from convectively Injected Water Vapor. Science 337, 835–839 (2012).
Dessler, A. E., Schoeberl, M. R., Wang, T., Davis, S. M. & Rosenlof, K. H. Stratospheric water vapor feedback. Proc. Natl. Acad. Sci. USA 110, 18087–18091 (2013).
Li, F. & Newman, P. Stratospheric water vapor feedback and its climate impacts in the coupled atmosphere–ocean Goddard Earth Observing System Chemistry-Climate Model. Clim Dyn 55, 1585–1595 (2020).
Glaze, L. S., Baloga, S. M. & Wilson, L. Transport of atmospheric water vapor by volcanic eruption columns. J. Geophys. Res. 102, 6099–6108 (1997).
Holland, H. D. The Chemistry of the Atmosphere and Oceans (Wiley-Interscience, New York, 1978).
Pinto, J. P., Turco, R. P. & Toon, O. B. Self-limiting physical and chemical effects in volcanic eruption clouds. J. Geophys. Res. 94, 11165–11174 (1989).
Yuen, D.A. et al. Under the Surface: Pressure-Induced Planetary-Scale Waves, Volcanic Lightning, and Gaseous Clouds Caused by the Submarine Eruption of Hunga Tonga-Hunga Ha’apai Volcano (Earthquake Research Advances, 2022).
Joshi, M. M. & Jones, G. S. The climatic effects of the direct injection of water vapour into the stratosphere by large volcanic eruptions. Atmos. Chem. Phys. 9, 6109–6118 (2009).
Pitari, G. & Mancini, E. Short-term climatic impact of the 1991 volcanic eruption of Mt. Pinatubo and effects on atmospheric tracers. Nat. Hazards Earth Syst. Sci. https://doi.org/10.5194/nhess-2-91-2002 (2002).
Millán, L. et al. The Hunga Tonga-Hunga Ha’apai Hydration of the stratosphere. Geophys. Res. Lett. 49, e2022GL099381 (2022).
Xu, J., Li, D., Bai, Z., Tao, M. & Bian, J. Large amounts of water VaporWere injected into the stratosphere by the Hunga Tonga–Hunga Ha’apai volcano eruption. Atmosphere 13, 912 (2022).
Vömel, H., Evan, S. & Tully, M. Water vapor injection into the stratosphere by Hunga Tonga-Hunga Ha’apai. Science. 377, 1444–1447 (2022).
Dvortsov, V. L. & Solomon, S. Response of the stratospheric temperatures and ozone to past and future increases in stratospheric humidity. J. Geophys. Res. 106, 7505–7514 (2001).
Sellitto, P. et al. The unexpected radiative impact of the Hunga Tonga eruption of 15th January 2022. Commun Earth Environ 3, 288 (2022).
Zhang, H. et al. Potential impact of Tonga volcano eruption on global mean surface air temperature. J. Meteorol. Res. 36, 1–5 (2022).
Maycock, A. C., Joshi, M. M., Shine, K. P. & Scaife, A. A. The circulation response to idealized changes in stratospheric water vapor. J. Clim. 26, 545–561 (2013).
Astafyeva, E. et al. The 15 January 2022 Hunga Tonga eruption history as inferred from ionospheric observations. Geophysical Research Letters 49, e2022GL098827 (2022).
Podglajen, A. et al. Balloon-Borne Observations of Acoustic-Gravity Waves From the 2022 Hunga Tonga Eruption in the Stratosphere, Earth and Space Science Open Archive. https://doi.org/10.1002/essoar.10511570.1 (2022).
Textor, C., Graf, H.-F., Herzog, M. & Oberhuber, J. M. Injection of gases into the stratosphere by explosive volcanic eruptions, J. Geophys. Res. 108, 4606 (2003). D19.
Taha, G. et al. Tracking the 2022 Hunga Tonga-Hunga Ha’apai aerosol cloud in the upper and middle stratosphere using space-based observations. Geophys. Res. Lett. 49, e2022GL100091 (2022).
Zhu, Y. et al. Perturbations in stratospheric aerosol evolution due to the water-rich plume of the 2022 Hunga-Tonga eruption. Commun. Earth Environ 3, 248 (2022).
Carn, S., Krotkov, N., Fisher, B. & Li, C. Out of the blue: volcanic SO2 emissions during the 2021-2022 eruptions of Hunga Tonga—Hunga Ha’apai (Tonga). Front. Earth Sci. https://doi.org/10.3389/feart.2022.976962 (2022).
Zhu, Y. et al. Stratospheric aerosols, polar stratospheric clouds, and polar ozone depletion after the Mount Calbuco eruption in 2015. Journal of Geophysical Research: Atmospheres 123, 308–312 (2018).
Legras, B. et al. The evolution and dynamics of the Hunga Tonga plume in the stratosphere. EGUsphere https://doi.org/10.5194/egusphere-2022-517 (2022).
Baron, A. et al. Early evolution of the Hunga-Tonga aerosol stratospheric plume from lidar observations at La Réunion. Geophys. Res. Lett. https://doi.org/10.1002/essoar.10512319.1 (2022).
Barnes, J. E. & Hofmann D. J. “Lidar measurements of stratospheric aerosol over Mauna Loa Observatory.” Geophys. Res. Lett. 24, 15 (1997): 1923-1926.
Kremser, S. et al. Stratospheric aerosol—observations, processes, and impact on climate. Rev. Geophys. https://doi.org/10.1002/2015RG000511 (2016).
Robock, A. & Matson, M. Circumglobal transport of the El Chichón volcanic dust cloud. Science 221, 195–197 (1983).
Bluth, G. J. S., Doiron, S. D., Krueger, A. J., Walter, L. S. & Schnetzler, C. C. Global tracking of the SO2 clouds from the June 1991 Mount Pinatubo eruptions. Geophys. Res. Lett. 19, 151–154 (1992).
McKenna, D. S. et al. A new Chemical Lagrangian Model of the Stratosphere (ClaMS), 1, Formulation of advection and mixing. J. Geophys. Res. https://doi.org/10.1029/2000JD000114 (2002).
Konopka, P., Ploeger, F., Tao, M., Birner, T. & Riese, M. Hemispheric asymmetries and seasonality of mean age of air in the lower stratosphere: Deep versus shallow branch of the Brewer-Dobson circulation. J. Geophys. Res. Atmos. 120, 2053–2066 (2015).
Podglajen, A., Hertzog, A., Plougonven, R. & Žagar, N. Assessment of the accuracy of(re)analyses in the equatorial lower stratosphere, J. Geophys. Res. Atmos 119, 11166–11188 (2014).
Aquila, V., Oman, L. D., Stolarski, R. S., Colarco, P. R. & Newman, P. A. Dispersion of the volcanic sulfate cloud from a Mount Pinatubo–like. eruption, J. Geophys. Res. 117, D06216 (2012).
Moyer, E. J., Irion, F. W., Yung, Y. L. & Gunson, M. R. ATMOS stratospheric deuterated water and implications for troposphere-stratosphere transport, Geophys. Res. Lett. 23, 2385–2388 (1996).
Khaykin, S. M. et al. Persistence of moist plumes from overshooting convection in the Asian monsoon anticyclone, Atmos. Chem. Phys. 22, 3169–3189 (2022).
Khaykin, S. et al. The 2019/20 Australian wildfires generated a persistent smoke-charged vortex rising up to 35 km altitude. Commun Earth Environ 1, 22 (2020).
Kasten, F. Falling speed of aerosol particles. J. Appl. Meteorol. 7, 944–947 (1968).
Davis, S. M. et al. The Stratospheric Water and Ozone Satellite Homogenized (SWOOSH) database: a long-term database for climate studies. Earth Syst. Sci. Data https://doi.org/10.5194/essd-8-461-2016 (2016).
Kovilakam, M. et al. The Global space-based Stratospheric Aerosol Climatology (version 2.0): 1979–2018. Earth Syst. Sci. Data 12, 2607–2634 (2020).
Schoeberl, M. R. et al. Analysis and impact of the Hunga Tonga-Hunga Ha’apai stratospheric water vapor plume. Geophysical Research Letters 49, e2022GL100248 (2022).
Jégou, F. et al. Stratospheric aerosols from the Sarychev volcano eruption in the 2009 Arctic summer, Atmos. Chem. Phys. 13, 6533–6552 (2013).
Kloss, C. et al. Stratospheric aerosol layer perturbation caused by the 2019 Raikoke and Ulawun eruptions and their radiative forcing, Atmos. Chem. Phys. 21, 535–560 (2021).
Santer, B. et al. Volcanic contribution to decadal changes in tropospheric temperature. Nat. Geosci. 7, 185–189 (2014).
Santer, B. D. et al. Observed multivariable signals of late 20th and early 21st century volcanic activity. Geophys. Res. Lett. 42, 500–509 (2015).
Schreiner, W., Rocken, C., Sokolovskiy, S., Syndergaard, S. & Hunt, D. Estimates of the precision of GPS radio occultations from the COSMIC/FORMOSAT-3 mission. Geophys. Res. Lett. 34, L04808 (2007).
Kursinski, E. R., Hajj, G. A., Schofield, J. T., Linfield, R. P. & Hardy, K. R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System, J. Geophys. Res. 102, 23429–23465 (1997).
Woods, A. W. The fluid dynamics and thermodynamics of eruption columns. Bull Volcanol 50, 169–193 (1988).
Waters, J. W. et al. The earth observing system microwave limb sounder (EOS MLS) on the Aura satellite. IEEE Trans. Geosci. Remote Sens. 44, 1106–1121 (2006).
Livesey, N. J. et al. EOS MLS Version 5.0× level 2 and 3 Data Quality and Description Document, Tech. Rep., Jet Propulsion Laboratory D-105336 Rev. B. http://disc.sci.gsfc.nasa.gov/Aura/data-holdings/MLS (2022).
Livesey, N. J. et al. Version 4.2x Level 2 and 3 Data Quality and Description Document (Tech. Rep. No. JPL D-33509 Rev. E). Jet Propulsion Laboratory. http://disc.sci.gsfc.nasa.gov/Aura/data-holdings/MLS (2020).
Jaross, G. et al. OMPS Limb Profiler instrument performance assessment. J. Geophys. Res. Atmos. 119, 4399–4412 (2014).
Taha, G. et al. OMPS LP Version 2.0 multi-wavelength aerosol extinction coefficient retrieval algorithm. Atmos. Meas. Tech. 14, 1015–1036 (2021).
Zawada, D. J., Rieger, L. A., Bourassa, A. E. & Degenstein, D. A. Tomographic retrievals of ozone with the OMPS Limb Profiler: algorithm description and preliminary results. Atmos. Meas. Tech. 11, 2375–2393 (2018).
Winker, D. M. et al. The CALIPSO mission: a global 3D view of aerosols and clouds. Bull. Am. Meteorol. Soc. 91, 1211–1230 (2010).
Boone, C. D., Bernath, P. F., Cok, D., Jones, S. C. & Steffen, J. Version 4 retrievals for the atmospheric chemistry experiment Fourier transform spectrometer (ACE-FTS) and imagers. J. Quant. Spectrosc. Radiat. Transf. 247, 106939 (2020).
Cisewski, M. et al. The stratospheric aerosol and gas experiment (SAGE III) on the International Space Station (ISS) Mission. Proc. SPIE 9241, Sensors, Systems, and Next-Generation Satellites XVIII, 924107 (2014).
Flament, T. et al. Aeolus L2A aerosol optical properties product: standard correct algorithm and Mie correct algorithm. Atmos. Meas. Tech. 14, 7851–7871 (2021).
Vömel, H., David, D. E. & Smith, K. Accuracy of tropospheric and stratospheric water vapor measurements by the cryogenic frost point hygrometer: Instrumental details and observations, J. Geophys. Res. 112, D08305 (2007).
Survo, P., Leblanc, T., Kivi, R., Jauhiainen, H., & Lehtinen, R. Comparison of selected in-situ and remote sensing technologies for atmospheric humidity measurement. In Proc. 19th Conference on Integrated Observing and Assimilation Systems for the Atmosphere, Ocean and Land Surface (American Meteorological Society, 2015).
Poshyvailo, L. et al. Sensitivities of modelled water vapour in the lower stratosphere: temperature uncertainty, effects of horizontal transport and small-scale mixing. Atmos. Chem. Phys. 18, 8505–8527 (2018).
Ploeger, F. et al. Horizontal water vapor transport in the lower stratosphere from subtropics to high latitudes during boreal summer, J. Geophys. Res. Atmos. 118, 8111–8127 (2013).
Konopka, P. et al. Stratospheric moistening after 2000. Geophys. Res. Lett. 49, e2021GL097609 (2022).
Konopka, P. et al. Contribution of mixing to upward transport across the tropical tropopause layer (TTL). Atmos. Chem. Phys. 7, 3285–3308 (2007).
Acknowledgements
This research has been supported by the Agence Nationale de la Recherche (grants no: 21-CE01-0028-01, PyroStrat; 21-CE01- 335 0007-01, ASTuS; 21-CE01-0016-01, TuRTLES; 15-CE04-0003- 336 01, VolcPlume) as well as the Centre National d’Études Spatiales (CNES) via TOSCA/EECLAT project. Felix Ploeger has been funded by the Helmholtz Association (grant no. VH-NG-1128, Helmholtz Young Investigators Group A–SPECi). We gratefully acknowledge the computing time for the CLaMS simulations, which was granted on the supercomputer JUWELS at the Jülich Supercomputing Centre (JSC) under the VSR project ID CLAMS-ESM. Ghassan Taha, NASA, is gratefully acknowledged for the help with OMPS V2.1 data. We thank the personnel of lidar stations (OPAR, Lauder, DDU, Mauna Loa, Tsukuba, OHP, Kuhlungsborn and Alomar for conducting the lidar measurement). MLS data are provided by the NASA Goddard Space Flight Center Earth Sciences (GES) Data and Information Services Center (DISC). FORMOSAT-7/COSMIC-2 is a partnership between the National Space Organization in Taiwan and NOAA, the U.S. Air Force, and the University Corporation for Atmospheric Research (UCAR) in the United States. We thank NASA Langley for public availability of the SAGE III/ISS Level 2 data products. GloSSAC data were obtained from the NASA Langley Research Center Atmospheric Science Data Center. The Atmospheric Chemistry Experiment (ACE), also known as SCISAT, is a Canadian-led mission mainly supported by the Canadian Space Agency. We thank Michelle Santee and Nathaniel Livesey from the NASA MLS team for helpful discussions. We thank the discussions at the SSiRC volcano forum led by Jean-Paul Vernier. The suggestions for improvements from the three anonymous reviewers are gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
S.K. conceived the study and performed analysis of MLS, OMPS-LP, CALIOP, SAGEIII, GLoSSAC and CLaMS data; A.P. performed analysis of radiosoundings and COSMIC-2 data, F.P. and JUG performed CLaMS simulation and analysis of MLS data, K.K. and K.B. performed stereoscopic CTH retrieval; F.T. and S.B. computed stratospheric water vapour masses; B.Le. provided Ash RGB data; L.R. computed particle radius from SAGEIII and OMPS-LP data; T.S., J.B., O.U., I.M., T.N., R.W., G.B., M.G., A.B., V.D., G.P., J.J., R.Q., B.Li., A.H. provided processed lidar data; A.F. performed analysis of Aeolus data; B.C. performed analysis of ACE-FTS data; B.Le., A.P., P.S., S.B., S.G.-B., F.R., A.B. were involved in discussions of the results and their interpretation. All authors contributed to the final manuscript. The paper was written by S.K., A.P., F.P., S.B., L.R., S.G.-B., J.-U.G.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Kerstin Schepanski, Clare Davis. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Khaykin, S., Podglajen, A., Ploeger, F. et al. Global perturbation of stratospheric water and aerosol burden by Hunga eruption. Commun Earth Environ 3, 316 (2022). https://doi.org/10.1038/s43247-022-00652-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00652-x
This article is cited by
-
Strong persistent cooling of the stratosphere after the Hunga eruption
Communications Earth & Environment (2024)
-
Indirect stratospheric moisture increase after a Pinatubo-magnitude eruption can be comparable to direct increase after 2022 Hunga
Communications Earth & Environment (2024)
-
Unexpected self-lofting and dynamical confinement of volcanic plumes: the Raikoke 2019 case
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.