Abstract
Supraglacial debris strongly modulates glacier melt rates and can be decisive for ice dynamics and mountain hydrology. It is ubiquitous in High-Mountain Asia, yet because its thickness and supply rate from local topography are poorly known, our ability to forecast regional glacier change and streamflow is limited. Here we combined remote sensing and numerical modelling to resolve supraglacial debris thickness by altitude for 4689 glaciers in High-Mountain Asia, and debris-supply rate to 4141 of those glaciers. Our results reveal extensively thin supraglacial debris and high spatial variability in both debris thickness and supply rate. Debris-supply rate increases with the temperature and slope of debris-supply slopes regionally, and debris thickness increases as ice flow decreases locally. Our centennial-scale estimates of debris-supply rate are typically an order of magnitude or more lower than millennial-scale estimates of headwall-erosion rate from Beryllium-10 cosmogenic nuclides, potentially reflecting episodic debris supply to the region’s glaciers.
Similar content being viewed by others
Introduction
Supraglacial debris exists on 7.3% of Earth’s mountain glacier surfaces1 and is increasing in areal extent in many mountain ranges due to recent climatic warming2,3,4,5,6,7,8,9. It can strongly modify the glacier–surface energy balance, enhancing or reducing the melt rate of the ice it overlies depending on its thickness10,11. As such, the dynamic and hydrological responses of debris-covered glaciers can be strikingly different from those of debris-free glaciers to similar climatic forcing12,13,14. Debris-covered glaciers tend to have long, low-gradient tongues with low surface velocity and stable termini15,16, and inefficient drainage systems which cause runoff to be delayed17,18.
In High-Mountain Asia, where large populations and unique mountain ecosystems are dependent on glacier-derived runoff19,20,21,22 and 8.3–12% of glacier area is debris covered1,23,24, it is essential to be able to accurately predict glacier change. However, models of the region’s glaciers have either ignored the effects of supraglacial debris or dealt with them in a simplified manner23,25. This is because two key model inputs, supraglacial debris thickness and supply rate, the second of which is likely to be an important control on debris thickness and extent, are either lacking or poorly constrained at the regional scale.
In-situ measurements of debris thickness have been made at only ~28 of the largely inaccessible 95000 glaciers of High-Mountain Asia (Supplementary Table 1), often with sparse and biased spatial coverage, while remote-sensing estimates have been made at a range of spatial scales23,26,27,28,29,30,31,32 but at larger scales using empirical approaches23,32 or physical models run at relatively coarse spatial resolution31. Headwall-erosion rate has been measured at point locations for ~19 glaciers (Supplementary Table 2), mostly in the northwestern Himalaya e.g.33,34, while debris-supply rate, which we distinguish from headwall-erosion rate as the rate at which debris is eroded from a glacier’s debris-supply slopes and reaches its surface, has been estimated at only eight glaciers using debris mass-balance models, so is mostly unknown35,36,37.
To secure widespread, systematic coverage of supraglacial debris thickness and supply rate in High-Mountain Asia, and thus facilitate advances in our understanding of the role of debris in the evolution of the region’s glaciers, we used a combination of remote sensing and modelling techniques. We generated regionally consistent datasets of both variables comprising 4689 and 4141 individual glaciers respectively, deriving debris thickness from specific mass balance, with which it is strongly correlated e.g.38. In the process, we calculated englacial debris content, which has only been measured at three glaciers in High-Mountain Asia37,39,40,41, supraglacial debris volume and debris-supply-slope area. We carried out a thorough uncertainty assessment and validated our datasets using all available in-situ data, primarily from existing literature. Finally, we used our datasets to disentangle the factors that regulate supraglacial debris supply, occurrence and distribution.
Our results indicate high spatial variability in debris thickness and supply rate, with more than 50% of debris thinner than 0.1 m. We observe an exponential increase in debris-supply rate with the slope and mean annual temperature of debris-supply slopes across High-Mountain Asia, and a tendency towards increasing debris thickness with decreasing ice flow on individual glaciers. The debris-supply rates we calculate are typically an order of magnitude or more lower than measurements of headwall-erosion rate from 10Be cosmogenic nuclides, potentially because debris supply is episodic and our debris-supply rates integrate erosive episodes on centennial rather than millennial timescales.
Results and discussion
Supraglacial debris thickness and volume
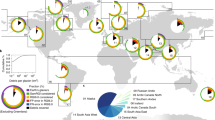
We resolved supraglacial debris thickness by altitude for the 4689 study glaciers for the period 2000–2016 (Fig. 1a), via a specific mass balance-inversion approach. Forcing an energy-balance model of the debris surface with downscaled ERA5-Land reanalysis data, we derived the physical relationship between debris thickness and specific mass balance independently for each 100 m of elevation of each glacier, then inverted those relationships leveraging a recent dataset of altitudinally resolved specific mass balance42,43. Using Monte Carlo simulations, we propagated source uncertainties to our results (Methods). Our modelled debris thickness data are consistent with in-situ data within 0.1 m 79% of the time at 14 validation sites, and agree closely in terms of altitudinal pattern and central value per glacier (Supplementary Note 1; Supplementary Figs, 1–16 and 35). The performance of our approach declines as debris thickness increases however (Supplementary Fig. 35), and biases are apparent for some glaciers.
a top panel, Glacier-mean debris thickness across High-Mountain Asia, with points scaled by debris-covered area (DCA) and base map from Natural Earth; small panels, distributed debris thickness for selected glaciers. b Median debris thickness (red) and debris-covered area (blue) with respect to normalised glacier elevation. c Debris thickness frequency distribution. d Glacier-mean debris thickness binned by debris-covered area. e Glacier-mean debris thickness binned by debris-cover stage from1. f Debris volume by mountain region relative to the total volume of debris on the 4689 study glaciers. Plots with bins show median and interquartile range, where each bin contains one tenth of the data. μ is mean value. Spearman’s ρ is calculated for bin centres. Validation sites are Pensilungpa (PEN), Koxkar (KOX), Batal (BAT), Hamtah (HAM), Panchi Nala (PNA), Dokriani (DOK), Satopanth (SAT), Ngozumpa (NGO), Langtang (LAN), Khumbu (KHU), Imja-Lhotse Shar (IMJ), 24K (24K), Hailuogou (HAI), Chorabari (CHO).
There is strong spatial variability in debris thickness both regionally and locally (Fig. 1a; Supplementary Fig. 29), a strong overall skew towards thin debris (61% < 0.1 m), and relatively little thick debris (10% ≥ 0.5 m, 3% ≥ 1 m). Thinner debris is concentrated at higher elevations up-glacier due to recent exhumation from the ice, where fractionally little debris cover exists (Fig. 1b; Fig. 1a subplots), while thicker debris is concentrated at lower elevations down-glacier due to a slowing conveyor-belt effect44, where there tend to be large moraines, and where debris cover is more extensive. Mean debris thickness for the study glaciers (representing 58% of total debris-covered glacier area) is 0.20+0.29−0.1 m (Fig. 1c; 1σ uncertainties), which corresponds to a debris volume of 0.98+1.43−0.49 km3, given an observed debris-covered glacier area of 48,000 km2. Median debris thickness is much lower, reaching the lower limit of the inversion procedure, 0.03 m. Interestingly, our debris thickness values are considerably thinner on average than those of31, likely due to methodological differences (Supplementary Fig. 33).
Importantly, we found that glaciers in an advanced stage of their debris-cover evolution1, where stage is the fraction of the ablation zone that is debris covered, and whose surfaces are fractionally more debris covered overall, have higher mean debris thickness (Fig. 1d, e) and therefore carry more debris per area. This is consistent with the notion that supraglacial debris thickens as glaciers lose mass, exhuming more debris to their surfaces from within45,46, and implies that supraglacial debris will thicken further in High-Mountain Asia in response to the warming climate indicated by current scenarios47.
It is surprising then, that our results suggest debris thickness is greatest in the Kunlun Shan and Inner Tibetan Plateau (Table 1), as the debris-covered fractions of glacier areas in these subregions are low. We hypothesise that this is because i) the minimal debris cover in these subregions (6.1 and 5.8% respectively) occurs close to the glacier margins where debris tends to be thick, and (ii) temporal inconsistencies between glacier and debris-cover outlines (we used data from48 and24,49) mean some non- or formerly-glacierised areas, which exhibit no specific mass balance signal, which would normally be indicative of thick debris, are identified as glacierised42. That is, there are artefacts in some of the input data. Otherwise debris thickness is greatest in the Everest and Bhutan subregions of the southeastern Himalaya, where debris stage is advanced and fractional debris-covered area is high. Considering total glacier area, supraglacial debris is most concentrated in the Everest and Bhutan subregions and least concentrated in the Tien Shan, the Pamir and the Karakoram (Supplementary Fig. 18).
Debris-supply rate and englacial debris content
We estimated debris-supply rate as a mean terrain-perpendicular value for the debris-supply slopes of 4141 study glaciers by calculating the volume flux of englacial debris to the glacier surface using our supraglacial debris thickness results and observed glacier surface velocities50,51, then calculating debris-supply-slope area and solving a mass-balance equation such that the mass of debris being eroded from the debris-supply slopes was equal to the mass of debris emerging at the glacier surface35,36 (Methods). In doing this we calculated volume fluxes of surface debris and englacial debris content (Methods), and assumed that material eroded by each glacier from its bed52 stays there33.
Our results show that debris-supply rate is strongly skewed towards lower values and varies over orders of magnitude between glaciers (16–84th percentile = 0.0012–0.10 mm yr −1, median = 0.018 mm yr−1; Fig. 2a, c; Supplementary Fig. 30), the latter of which we attribute to the high climatic, topographic and geologic variability of the High-Mountain Asia region. Mean debris-supply rate for the study glaciers is 0.07+0.15−0.03 mm yr−1 (Fig. 2c; Table 2) which, given an observed terrain-perpendicular debris-supply-slope area of 29000 km2, corresponds to a volume rate of eroded rock of approximately 210,000 m3 yr−1.
a top panel, Debris-supply-slope (DSS) mean debris-supply rate in High-Mountain Asia, with points scaled by debris-supply slope area and base map from Natural Earth, showing the Main Central Thrust (MCT); small panels, debris-supply rate for selected glaciers. b Median supraglacial debris flux (red), median glacier–surface velocity (blue) and debris-supply slope area (black) with respect to normalised glacier elevation. c Frequency distribution of debris-supply rate. d Debris-supply slope mean debris-supply rate binned by distance north (N) of the MCT, where Spearman’s ρ is calculated for bin centres, where each bin contains one tenth of the data. e Frequency distribution of debris-supply slope area. f Frequency distribution of EDC. μ is mean value. Validation sites are Panchi (PAN), Urgos (URG), Hamtah (HAM), Chhota Shigri (CHO), Batal (BAT), Gangotri (GAN), Khumbu (KHU), Rongbuk (RON).
Interestingly, our modelled debris-supply rates are typically an order of magnitude or more lower than headwall-erosion rates estimated using 10Be cosmogenic nuclides33,34,53,54,55 (Supplementary Fig. 20). This could be because erosion in the region is episodic, and because cosmogenic nuclides capture erosive processes on a timescale of ~10,000 years years56, while our debris mass-balance model captures glacier mass-turnover on centennial timescales57. Debris-supply episodes would have to be to some extent correlated with each other in space and time to explain the low mean debris-supply rate of our relatively large sample of glaciers. If erosional episodicity is in fact the cause of the discrepancy between our debris-supply rates and the 10Be erosion rates, our short-term estimates of debris-supply rate may be more appropriate than the longer-term estimates for modelling glacier change on human timescales. Despite the magnitudinal differences, we observe a weak correlation (r = 0.12) between our debris-supply rates and the 10Be erosion rates for the small subset of glaciers in our dataset at which 10Be measurements have been made (Supplementary Fig. 20). Our debris-supply rate estimates are comparable to previous estimates for six glaciers in High-Mountain Asia which were also made using a debris mass-balance model but based on in-situ data36 (mean bias = 0.026 mm yr−1; Supplementary Fig. 19).
Further, our results show that debris-supply rate decreases with distance northwards of the Main Central Thrust, by approximately an order of magnitude over ~100 km, corroborating at mountain-range scale the observation of34 for the headwall-erosion rate of 15 glaciers in the northwestern Himalaya. However, we cannot rule out the possibility that this decrease is due to topoclimatic rather than geological factors, as the slope and temperature of the debris-supply slopes also decrease towards the Tibetan Plateau (Supplementary Fig. 34), and debris-supply rate decreases with decreasing debris-supply slope slope and temperature (Fig. 3).
Debris-supply-slope mean DSR binned by (a) mean annual air temperature (MAAT), (b) annual precipitation, (c) slope, (d) aspect and (e) rock type: sedimentary (Sed), plutonic (Plu), metamorphic (Met) and volcanic (Vol). f Supraglacial debris thickness (SDT) with respect to glacier surface velocity (blue) and inverse surface velocity (red) for Khumbu Glacier, where marker size indicates the number of data points. g Frequency distributions of Spearman’s ρ for debris thickness and glacier–surface velocity (blue) and debris thickness and inverse surface velocity (red) for glaciers with debris-covered area larger than 1 km2. h Glacier-mean debris thickness binned by englacial debris content (EDC). i Debris-cover stage binned by EDC. Plots with bins show median and interquartile range, where each bin contains one tenth of the data. Spearman’s ρ is calculated for bin centres. Boxplots show the median, 25th and 75th percentiles, and outliers, where outliers are data points that fall outside approximately ± 2.7 times the standard deviation.
We found that englacial debris content has a mean value of 0.05+0.09−0.03% by ice volume over High-Mountain Asia but is also highly variable between glaciers and skewed low (median = 0.007%). Our model estimates are within the reported range of literature values for bulk glacier ice globally (Fig. 2f; Supplementary Table 3), in the few places it has been measured in situ, but are considerably smaller than for basal ice, where englacial debris tends to be concentrated. We estimated a bulk value for Khumbu Glacier, Nepal, of 0.017+0.090−0.0032%, the upper uncertainty bound of which is the same as the lower uncertainty bound of the valuable but localised measurements of39 (Fig. 2a), who derived bulk values of 0.1-0.7% in active areas of the debris-covered part of Khumbu Glacier, Nepal, but 6.4% in ice near the terminus, which should be expected to show values that are similar to basal ice.
Mean terrain-perpendicular debris-supply-slope area is 7 km2 (Fig. 2e; Table 2), compared to a mean glacier area of 7.9 km2, and interestingly the debris-supply slopes of most glaciers exist largely within their own elevation ranges (Fig. 2b). Volume fluxes of supraglacial debris down-glacier (Fig. 2b) increase to a point near the terminus as debris thickness increases, before decreasing to the terminus after ice flow becomes negligible. Despite the fact that we define debris-supply slopes in a different way, our debris-supply-slope areas deviate only slightly from those in the literature and show good agreement overall (mean bias = −2.1 km2; Supplementary Fig. 21).
Subregionally, debris-supply rate is highest around Nyainqentangla and in Bhutan, while englacial debris content is highest in the Kunlun Shan and Hindu Kush (Table 2). The Hindu Kush has the largest debris-supply slopes compared to glacier area.
Controls on the glacier-debris system
Exploiting the 1-km WorldClim 2 climatologies for 1970–200058, we found that debris-supply rate increases exponentially with debris-supply-slope mean annual air temperature (MAAT) and stepwise with annual precipitation (Fig. 3a, b). In the case of MAAT, our results show that the main result of36, that erosion rates decline with elevation for six glaciers in the Himalaya, holds over the whole of High-Mountain Asia. In both cases the relationship is likely causal. We found that debris-supply rate is highest at MAAT > −7 ∘C, within the range −8 to −3 ∘C in which frost cracking–the dominant process by which physical erosion occurs in cold environments–is particularly efficient59,60. We suggest that increasing precipitation primarily increases DSR by increasing water availability for the ice growth that occurs as part of the frost-cracking process61. However, in some places this effect may be overridden by increased snow cover, which can act to insulate underlying rock surfaces62.
Debris-supply rate increases additionally with the slope of the debris-supply slopes and is weakly higher from slopes of south-facing aspect (Fig. 3c, d). Slope will affect debris-supply rate via gravitational redistribution and landsliding in particular, which is more frequent on steeper slopes63. Indeed, landsliding is particularly prevalent on slopes steeper than 30∘64, around which we found strong increases in debris-supply rate. Aspect, meanwhile, may exert a control on debris-supply rate via incoming shortwave radiation. South-facing slopes are likely to experience larger diurnal temperature variations due to high incoming shortwave radiation receipts during the day and therefore (i) pass more often through the frost-cracking window65, and (ii) undergo increased cyclic thermal stressing due to rock expansion and contraction66.
We found no clear relationship between debris-supply rate and major rock types as given by the global lithological map GLiM67 (Fig. 3e), which is likely a reflection of the fact that at large spatial scales, rock-mass strength is governed rather by the spatial frequency of structural geological discontinuities such as joints and faults68. Indeed, as discussed above, we found that debris-supply rate is higher near the Main Central Thrust–the major fault at the interface of the Indian and Eurasian tectonic plates (Fig. 2d), to which debris-supply rate could be linked.
Over long timescales, the englacial debris content of a glacier should closely correspond to its debris-ice supply ratio, which is the debris supply to the glacier via erosion divided by the ice supply to the glacier via snowfall. The debris mass-balance model we used to calculate englacial debris content leads to an increase in englacial debris content with glacier-mean debris thickness and debris-cover stage1 (Fig. 3h, i), in-line with the idea that debris-ice supply ratio is a control on the extent to which a glacier becomes debris covered69. A high (low) debris-ice supply ratio or englacial debris content will tend to produce an extensively (minimally) debris-covered glacier with thick (thin) debris, although this will depend also on the efficiency of debris transport from the glacier by the glacifluvial system. This complements the finding of a previous study that glaciers with large debris-supply slopes tend to have large debris-covered areas70.
Finally, for glaciers in High-Mountain Asia with a debris-covered area larger than 1 km2, we found that debris thickness is typically positively correlated with the inverse of the surface velocity (Fig. 3f, g). Where surface velocity is low (high), debris thickness tends to be great (small). This is in agreement with the theory for glaciers whose debris is in steady state44 and indicates that, while debris-ice supply ratio via englacial debris content governs supraglacial debris thickness and volume at the glacier scale, ice flow modulates the spatial distribution of these variables locally.
Conclusions
We have quantified supraglacial debris thickness, debris-supply rate and englacial debris content across High-Mountain Asia, showing that each is highly spatially variable, and that supraglacial debris is extensively thin. We have shown that debris-supply rate increases with debris-supply-slope MAAT, annual precipitation, slope, aspect from north, and proximity to the Main Central Thrust, while debris thickness increases with the inverse of glacier surface velocity, and further, we have demonstrated the character of the relationship between englacial debris content and debris thickness, given our physical understanding of the glacier-debris system. This is valuable information because the amount, location and movement of debris within a glacier-debris system can strongly influence both the evolutionary trajectory of the glacier(s) in that system14,16,33,71, and the downstream transport of sediment from it69. Crucially, while previous studies have produced vital data for spatial representation of supraglacial debris in glacier models1,24,31,32, our data and findings pave the way additionally to more sophisticated temporal representation of debris in combined glacier-landscape evolution models33,71.
Given the importance of characterising future water supply in High-Mountain Asia–a highly-populated mountain region with rapidly increasing water demand20–and the recent boom in the region’s hydropower sector72, the development of such models for application at large spatial scales should be a key direction for future research–an endeavour for which the episodicity of debris supply will be a particular challenge. In a warming climate, documented increases in debris thickness and debris-covered glacier area in High-Mountain Asia2,3,4,5,6,7,8,9,73 could intensify in a highly localised and non-linear way due to increased melt-out of englacial debris and debris supply, substantially impacting glacier specific mass balance and runoff. Combined with likely increases in moraine collapse and rockwall debuttressing due to glacier retreat74, and increases in subglacial erosion due to increases in basal sliding52, these processes could in turn boost proglacial sedimentation and suspended sediment concentration in rivers.
Methods
Supraglacial debris thickness and volume
We calculated supraglacial debris thickness by generating a series of Østrem curves10 for each glacier using a debris-surface energy-balance model, then inverting these Østrem curves using observed specific mass balance data from42. This process is described by the flow chart in Supplementary Fig. 22, and builds on the work of28,75,76. We generated the Østrem curves in a Monte Carlo simulation setup with 100 simulations for each 100 m of glacier elevation. In each simulation, we assigned a debris thickness value, along with values of key model parameters and variables (Supplementary Table 4), to a random point on the glacier surface. We then ran the model, forcing it with the forcing dataset described below, and recorded the resulting modelled specific mass balance value. After all the simulations had finished, we fitted, to the assigned debris thickness and modelled specific mass balance values, Østrem curves of a rational form14:
where b is yearly specific mass balance, c1 and c2 are free parameters and hsd is debris thickness (Supplementary Fig. 23). To prevent unrealistic Østrem curves, we imposed c1 > − 12 and < 0 and c2 > 0, and discarded curves with r2 < 0.4, filling any resulting gaps by linear interpolation. Because the physics of debris-surface energy-balance models is often poor when debris thickness is very small77, and ice melt is negligible when debris thickness is great, we imposed debris thickness ≥ 0.03 m and ≤ 5 m, and an uncertainty of ± 0.02 m at the thin debris limit. Further, we filtered debris thickness values that were simultaneously > 0.3 m and > 3x the mean value on an altitudinal basis, using a moving window of 100 m, considering these to be outliers, and those for which specific mass balance was within uncertainty of neutrality or above the equilibrium line altitude. The units of all variables in this section are provided in Supplementary Table 5.
Because we generated our debris thickness dataset from the specific mass balance dataset of42, it shares that dataset’s spatial resolution, i.e. each glacier is segmented i) by elevation, such that each segment covers an elevation range of roughly 25 m (based on a smoothed DEM), ii) by tributary, in the case that a glacier has multiple tributaries. We call this altitudinally resolved. Further, because39 separated debris-covered and debris-free glacier surfaces using the dataset of24, our debris thickness data are not affected by the melt rates of debris-free ice that might exist at the same elevation as debris-covered ice. However, it is important to note that we neglected to account for supraglacial ponds and ice cliffs, which can exhibit relatively high melt rates on debris-covered glaciers78,79. As a result, our calculated debris thickness values are effective rather than absolute, and may underestimate true debris thickness in absolute terms. While such an underestimation is not obvious in the comparisons we have made of our results with in-situ data (Supplementary Figs. 3-16), we estimate its magnitude could be up to 10% on average over High-Mountain Asia, and could vary considerably in space, likely affecting areas with thick debris more than those with thin debris (Supplementary Note 2).
The debris-surface energy-balance model we used bears similarities to those of80,81,82. We calculated ice melt below debris M on an hourly basis (Eq. 2), the negative yearly sum of which is equal to yearly specific mass balance b if there is no net mass gain, by simultaneously solving the heat equation (Eq. 3) and the debris-surface energy balance (Eq. 4):
where Δt is the time step of the model, ρw is the density of water, Lf is the latent heat of fusion of water, kd is the bulk thermal conductivity of debris, Tsd is supraglacial debris temperature, z is depth, ρd is debris density, cd is the specific heat capacity of debris, t is time, S is the shortwave radiation flux at the debris surface, L is the longwave radiation flux, H is the sensible heat flux, LE is the latent heat flux, P is the heat flux due to precipitation, and the subscripts s and i indicate evaluation at the debris surface (the interface between the debris and the atmosphere above) and the ice surface (the interface between the debris and the ice below) respectively. We solved these equations by iteratively varying Tsd,s using Newton’s method and calculating debris internal temperatures using the Crank-Nicolson method, assuming Tsd,i is the melting temperature of ice. If there was snow on the debris surface we set Tsd,s to the melting temperature of ice, which shortly resulted in negligible ice melt below the debris if the snow persisted. We calculated the shortwave radiation flux broadly following83:
where S↓dif is the diffuse incoming shortwave radiation of the grid cell of the chosen point on the glacier surface, αd is debris albedo and S↓dir is direct incoming shortwave radiation at the grid cell, which we calculated as:
where Z is solar zenith angle, A is solar azimuth angle, \(Z^{\prime}\) is the surface slope of the grid cell and \(A^{\prime}\) is the surface azimuth of the grid cell. S↓b,dir is direct incoming shortwave radiation normal to the solar beam, which we calculated as:
where S↓r,dir is the direct part of the incoming shortwave radiation of the nearest grid cell of the forcing dataset S↓r:
where we calculated the diffuse part S↓r,dif as:
and where we set fdif, the fraction of incoming shortwave radiation that is diffuse, to 0.15 following84. We calculated diffuse incoming shortwave radiation at the grid cell as:
where fsv is the sky-view factor of the grid cell and S↓ter is the shortwave radiation reflected to the grid cell from the surrounding terrain, which we calculated as:
where we assumed the albedo of the surrounding terrain αter to be 0.25 and
where θ is the horizon angle at azimuth ϕ and Δϕ is the azimuth step at which horizon angles are calculated, which we set to 12∘. We determined whether the grid cell was in the shade or in the sun using the algorithm of85, and calculated solar azimuth angle and solar elevation angle E following86, then calculated solar zenith angle as Z = 90 − E. We calculated the longwave radiation flux L, also following83, as:
where L↓sky is incoming longwave radiation from the sky that is visible at the grid cell, L↓ter is longwave radiation emitted from nearby terrain, and L↑ is outgoing longwave radiation from the debris surface. We calculated L↓sky as:
where L↓r is the incoming longwave radiation of the nearest forcing-dataset grid cell. We calculated L↓ter as
where σ is the Stefan-Boltzmann constant, εter is the emissivity of the surrounding terrain, and Tter is the temperature of the surrounding terrain, which we set to the air temperature of the grid cell Ta, which we lapsed from the nearest forcing-dataset grid cell according to Ta = Ta,r − Γ(z − zr), where Ta,r is the temperature of the forcing-dataset grid cell, zr is the elevation of the forcing-dataset grid cell, z is the elevation of the grid cell, and Γ is the lapse rate. We calculated L↑ according to:
where εsd is the emissivity of the debris. We calculated the sensible and latent heat fluxes following e.g.87:
where ρa is the density of air, ca,dry is the specific heat capacity of dry air, u is the wind speed of the grid cell, corrected to the air-temperature reference height (zref, 2 m) from the wind speed ur of the nearest forcing-dataset grid cell using the logarithmic wind-profile law, and Lv is the latent heat of vaporisation of water. Cbt is a bulk transfer coefficient, which we calculated assuming neutral atmospheric stability from the reference height and the surface roughness length of the debris z0,d:
where kvk is the von Kármán constant. We calculated ρa as:
where pa is atmospheric pressure, which we calculated using the barometric formula, ma is the molecular weight of dry air, and R is the gas constant. We calculated the specific humidity at the debris surface qs, assuming that water vapour in the atmospheric surface layer is well-mixed88, as
where qa is the specific humidity of the atmosphere above the debris surface, and ca,dry is the specific heat capacity of dry air:
We calculated the specific humidity of the atmosphere above the debris:
where ea is the vapour pressure of the atmosphere above the debris, which we calculated as:
from the saturated vapour pressure of the atmosphere above the debris surface89:
and the relative humidity RH of the grid cell, which we calculated from forcing-dataset air and dew-point temperatures using the Clausius–Clapeyron equation. Finally we calculated the heat flux due to precipitation following90 as:
where cw is the specific heat capacity of water, r is the precipitation rate, and Tr is the temperature of the precipitation, which we set to the air temperature of the grid cell.
The forcing dataset we developed comprises hourly climatologies (multi-year hourly means) of the meteorological variables needed to force the energy-balance model for the period of the observed specific mass balance data of42, 2000–2016. We used these climatologies rather than complete time series for computational efficiency over such a large study area, having found that ice melt modelled using the former was a close approximation of the latter (Supplementary Fig. 25). For all variables except snow cover, we developed the climatologies using the ERA5-Land reanalysis product91 at 0.1∘ spatial resolution. An example is shown for air temperature for a location on Langtang Glacier, Nepal, in Supplementary Fig. 24. For snow cover, we used the dataset of92, for the period 2003–2016, because of its higher 500-m spatial resolution, at the cost of its only 8-day temporal resolution. We adjusted the precipitation climatology to avoid constant drizzle by allocating the mean yearly precipitation of the complete time series proportionally to the hours of the year in which, on average, most precipitation fell, such that the mean yearly number of precipitation hours of the complete time series was maintained. Likewise we adjusted the snow cover climatology to avoid constant snow cover by allocating snow cover to the periods of the year in which there was, on average, most snow cover, such that mean yearly snow cover duration was maintained. We used the ERA5-Land product to develop the forcing dataset because its high spatial resolution, and therefore explicit accommodation of glacierised elevations, along with its accommodation of cryospheric surface types, means it should resolve well glacier–surface boundary-layer conditions, and be suitable for use directly in glacier energy-balance models with minimal additional downscaling93,94.
We calculated supraglacial debris volumes Vsd as the product of debris thickness and debris-covered glacier area Asd, where we computed Asd from the the debris-cover masks of42, which were modified from24.
We did not analyse all glaciers in High-Mountain Asia because (i) the specific mass balance data of42 are limited to 5527 glaciers larger than 2 km2 and (ii) we had to discard some, which exhibited erratic or unusual debris thickness profiles, which we took to be indicative of poor-quality input data or surging that was not identified by42.
Uncertainty in supraglacial debris thickness and volume
We assessed supraglacial debris thickness uncertainty at the point scale by combining uncertainties in modelled and observed specific mass balance using the fitted Østrem curves (Supplementary Fig. 23). We considered uncertainty in modelled SMB to be dominated by uncertainty in (i) air temperature forcing, (ii) surface albedo, (iii) air temperature lapse rate, iv) debris thermal conductivity, and v) debris surface roughness length28,95,96. We did this through the Monte Carlo simulations described above. We did not consider uncertainty in precipitation because we dealt with snow cover using observations, and the energy flux due to precipitation is typically relatively small90. Based on the finding of95 that uncertainty in modelled specific mass balance is dominated by systematic rather than random error, we assigned systematic errors to these variables and parameters in the Monte Carlo simulations, i.e. for each simulation we did not vary the assigned errors in time. The distributions from which we drew errors and variable or parameter values are given in Supplementary Table 4. We took uncertainty in observed specific mass balance directly from42, and assumed this too to be systematic at the point scale. Because the fitted Østrem curves are nonlinear, debris thickness uncertainty is asymmetric and increases with debris thickness (Supplementary Fig. 23; Supplementary Fig. 32). We calculated uncertainties in mean debris thickness at the glacier scale as the means of the point-scale uncertainties, both positive and negative.
We assessed uncertainty in mean debris thickness at the regional and subregional scale by assuming no uncertainty in observed specific mass balance and by running the Monte Carlo simulations again but without assigning errors to the air temperature forcing, then taking the means of the region’s or subregion’s point-scale debris thickness uncertainties. We did this on the basis that air temperature forcing and observed specific mass balance errors are likely to be random and therefore negligible, rather than systematic, at such large spatial scales.
We assessed debris volume uncertainty \({\sigma }_{{V}_{{{{{{{{\rm{sd}}}}}}}}}}\) at the regional, subregional and glacier scales according to:
where \(\bar{{h}_{{{{{{{{\rm{sd}}}}}}}}}}\) is regional-, subregional- or glacier-scale mean debris thickness with uncertainty \({\sigma }_{\bar{{h}_{{{{{{{{\rm{sd}}}}}}}}}}}\), and where Asd is the debris-covered area of the study glacier(s) with an estimated relative uncertainty, for the dataset of24, of 10%1.
Debris-supply rate and englacial debris content
We calculated debris-supply rate, qds, as a mean value for each glacier’s debris-supply slopes by assuming conservation of mass of debris to the glacier’s surface by ice melt, from its debris-supply slopes, via its interior (Supplementary Fig. 26a). That is, we assume a balanced sediment budget between the debris-supply slopes and the debris-covered area of each glacier (Supplementary Note 3). This can be expressed as such:
where ρd is debris density, Ads is debris-supply-slope area calculated as described below then converted from planimetric to terrain-perpendicular, ρr is rock density, qed is the rate of emergence of englacial debris at the glacier surface, and Asd is the area of the glacier that is debris covered35,36. We used values of 1842 kg m−3 and 2700 kg m−3 for debris and rock density respectively30,97. The units of all variables are provided in Supplementary Table 5.
To account for non-steady-state debris cover, and in order that calculated debris-supply rates represent recent debris supply36,98 (Supplementary Fig. 26a), we calculated the volume flux of englacial debris to each glacier’s surface qedAsd by splitting each glacier’s debris-covered part into two: an active part and an inactive part (Supplementary Fig. 26b):
where qed,a and qed,ia are the emergence rates of englacial debris to the surfaces of the active and inactive parts respectively, and where Asd,a and Asd,ia are the areas of the active and inactive parts respectively. The volume flux of debris from the upper, active part of the glacier should be a reasonable approximation of the steady-state debris flux36, so we calculated the emergence rate of englacial debris to the surface of the active part first, according to:
(Supplementary Fig. 26c) then used it to calculate the emergence rate to the inactive part. Here, Qsd,a↓ and Qsd,a↑ are the volume fluxes of surface debris into and out of the active part respectively where Qsd,a↓ is zero. We calculated the volume fluxes of the surface debris at flux gates along each glacier according to:
where usd is the the down-glacier component of the surface-velocity field of the debris at the flux gate (taken from the velocity fields of42), Ω is the glacier boundary, and y is the across-glacier direction. We considered the active part of the glacier to be that which is up-glacier of the gate of maximum volume flux of surface debris, and, in order to avoid very high debris fluxes, we applied a moving-mean filter to the volume fluxes of surface debris, such that each smoothed volume flux data point comprised 10% of all the volume flux data points (Supplementary Fig. 27).
From qed,a, we calculated englacial debris content in the ablation area of the glacier ced,abl such that:
where Ma is the melt rate of the active part of the debris-covered part of each glacier, converted to ice equivalent from the specific mass balance data of42 using a density of 915 kg m−3, leaving the emergence rate of englacial debris to the surface of the inactive part qed,ia to be calculated as:
where Mia is the melt rate of the inactive part.
To calculate the englacial debris content of the whole of each glacier, we performed a density conversion using a bulk glacier density of 850 kg m−399:
We delineated each glacier’s debris-supply slopes, the areas above the glacier that are able to contribute debris to it through erosion, by (i) identifying the upslope areas of the glacier’s debris-covered parts and (ii) identifying and subtracting from these upslope areas overlapping glacierised areas, where there is no erodable rock surface. Example debris-supply slopes can be seen in Fig. 2. We identified each glacier’s upslope areas by (i) filling sinks in an elevation model of the area surrounding the glacier, (ii) placing pour points at the at the 75th percentile elevation of the glacier’s debris elevation range, or anywhere there was a debris-ice transition below the 75th percentile elevation, (iii) downsampling these pour points so that there was a maximum of one every 100 m, (iv) refining the locations of the downsampled pour points by searching locally for those with the highest topographic index, (v) calculating the upslope areas of the refined pour points, (vi) merging these upslope areas. We identified the glacierised areas by modifying Randolph Glacier Inventory (RGI) v6.0 glacier areas48, which sometimes incorrectly identify snow as glacier area, by (i) deriving Normalised-Difference Snow Index (NDSI) for each glacier for the duration of the42 specific mass balance data from Landsat 5–8 imagery in Google Earth Engine, (ii) thresholding the NDSI images to identify rock outcrops within the RGI glacier areas using Otsu’s method, and (iii) subtracting these rock outcrops from the RGI glacier areas.
To calculate mean debris-supply rate and englacial debris content at the regional (subregional) scale, we normalised glacier-scale means by calculated debris-supply-slope area and and glacier volume100, respectively.
We were only able to calculate debris-supply rate and englacial debris content for 4141 of the 4689 glaciers for which we calculated debris thickness because some glaciers did not carry any debris and so could not produce a meaningful calculation of the rate of emergence of englacial debris to their surfaces.
We note that we calculate debris-supply rate rather than headwall-erosion rate because some of the debris that is eroded from a glacier’s headwall or debris-supply slopes may go straight to the bed of the glacier and never reach its surface, and Eq. 28 does not account for debris that is lost in this way. A flow chart of our approach to calculating debris-supply rate and englacial debris content is provided in Supplementary Fig. 31.
Uncertainty in debris-supply rate and englacial debris content
We assessed the uncertainty in each glacier’s debris-supply rate as the sum in quadrature of the uncertainties in Eq. (28)’s constituent variables and parameters:
where we estimated \({\sigma }_{{\rho }_{{{{{{{{\rm{d}}}}}}}}}}\) and \({\sigma }_{{\rho }_{{{{{{{{\rm{r}}}}}}}}}}\), the uncertainties in debris and rock density respectively, to be 100 kg m−2, and where we estimated the relative uncertainty in Ads to be 10%. We calculated \({\sigma }_{{q}_{{{{{{{{\rm{ed}}}}}}}}}{A}_{{{{{{{{\rm{sd}}}}}}}}}}\) by propagating uncertainties through Eq. (29), as:
where we estimated the relative uncertainties of Asd,a and Asd,ia to be 10%, where:
where we assumed \({\sigma }_{{Q}_{{{{{{{{\rm{sd,a\uparrow }}}}}}}}}}\) is dominated by \({\sigma }_{{h}_{{{{{{{{\rm{sd}}}}}}}}}}\), and, for simplicity, where:
We assessed ablation zone englacial debris content uncertainty, also at the glacier scale, according to Eq. (32) as:
where we took \({\sigma }_{{M}_{{{{{{{{\rm{a}}}}}}}}}}\) from the specific mass balance uncertainties of42, and where \({\sigma }_{{M}_{{{{{{{{\rm{a}}}}}}}}}{q}_{{{{{{{{\rm{ed,a}}}}}}}}}}\) is the covariance of \({\sigma }_{{M}_{{{{{{{{\rm{a}}}}}}}}}}\) and \({\sigma }_{{q}_{{{{{{{{\rm{ed,a}}}}}}}}}}\), which we calculated using the Cauchy-Schwarz inequality, and which arises because the debris thickness uncertainties include the specific mass balance uncertainties of42. To get whole-glacier englacial debris content uncertainty, we propagated the uncertainties of Eq. (34):
where \({\sigma }_{{\rho }_{{{{{{{{\rm{i,glac}}}}}}}}}}\) and ρi,glac were assumed to be 60 and 850 kg m−3 following99, and the relative uncertainty of the density of ablation-zone ice was assumed to be negligible.
Because debris thickness uncertainty is asymmetric, so is uncertainty in the rate of debris emergence at the glacier surface, and therefore debris-supply rate and englacial debris content. As such, we assessed positive and negative debris-supply rate and englacial debris content uncertainties separately.
We assessed uncertainty in mean debris-supply rate and englacial debris content at the regional (subregional) scale in a similar way as for debris thickness, as described above. We produced a second set of glacier-scale debris-supply rate and englacial debris content uncertainties, using the debris thickness uncertainties of the second set of Monte Carlo simulations (also described above––those that are exclusive of uncertainty in air temperature and observed specific mass balance) and assuming no uncertainty in Ma in Eq. (39), and took the means of the upper and lower bounds of these uncertainties, normalising by debris-supply-slope area and glacier volume, for debris-supply rate and englacial debris content, respectively. In this way, uncertainties in mean debris-supply rate and englacial debris content at the regional (subregional) scale, as do uncertainties in debris thickness, account for the likely random nature of the uncertainty in air-temperature forcing and observed specific mass balance at such large scales, and the likely systematic nature of the uncertainty in other key input variables and parameters.
Data availability
The supraglacial debris thicknesss, englacial debris content, debris-supply slope and debris-supply rate data generated in this study are available from Zenodo via https://doi.org/10.5281/zenodo.7070657. The specific mass balance data of42 are available from Zenodo via https://doi.org/10.5281/zenodo.3843292. The ice surface velocity data of50 are available from NASA MEaSUREs via https://its-live.jpl.nasa.gov/. The glacier outlines of48 are available from the NSIDC via https://doi.org/10.7265/4m1f-gd79. The debris cover outlines of24 are available from GFZ Data Services via https://doi.org/10.5880/GFZ.3.3.2018.005. The WorldClim 2 climatologies of58 are available from WorldClim via http://www.worldclim.com/version2. The lithological maps of67 are available from Universität Hamburg via https://www.geo.uni-hamburg.de/en/geologie/forschung/aquatische-geochemie/glim.html.
Code availability
An implementation of the code we used to calculate supraglacial debris thickness, englacial debris content and debris-supply rate is available from GitHub via https://github.com/mchl-mccrthy/sdt-dsr-hma.
References
Herreid, S. & Pellicciotti, F. The state of rock debris covering Earth’s glaciers. Nat. Geosci. 13, 621–627 (2020).
Kirkbride, M. P. & Warren, C. R. Tasman Glacier, New Zealand: 20th-century thinning and predicted calving retreat. Glob. Planet. Change 22, 11–28 (1999).
Deline, P. & Orombelli, G. Glacier fluctuations in the western Alps during the Neoglacial, as indicated by the Miage morainic amphitheatre (Mont Blanc massif, Italy). Boreas 34, 456–467 (2005).
Kellerer-Pirklbauer, A. The supraglacial debris system at the Pasterze Glacier, Austria: spatial distribution, characteristics and transport of debris. Zeitschrift für Geomorphologie, Supplementary Issues 3-25 (2008).
Thakuri, S. et al. Tracing glacier changes since the 1960s on the south slope of Mt. Everest (central Southern Himalaya) using optical satellite imagery. Cryosphere 8, 1297–1315 (2014).
Xie, F. et al. Upward expansion of supra-glacial debris cover in the Hunza Valley, Karakoram, during 1990 2019. Front. Earth Sci. 8, 308 (2020).
Jiang, S. et al. Glacier change, supraglacial debris expansion and glacial lake evolution in the Gyirong river basin, central Himalayas, between 1988 and 2015. Remote Sens. 10, 986 (2018).
Glasser, N. F. et al. Recent spatial and temporal variations in debris cover on Patagonian glaciers. Geomorphology 273, 202–216 (2016).
Tielidze, L. G. et al. Supra-glacial debris cover changes in the Greater Caucasus from 1986 to 2014. Cryosphere 14, 585–598 (2020).
Østrem, G. Ice melting under a thin layer of moraine, and the existence of ice cores in moraine ridges. Geografiska Annaler 41, 228–230 (1959).
Mattson, L. Ablation on debris covered glaciers: an example from the Rakhiot Glacier, Punjab, Himalaya. Intern. Assoc. Hydrol. Sci. 218, 289–296 (1993).
Scherler, D., Bookhagen, B. & Strecker, M. R. Spatially variable response of Himalayan glaciers to climate change affected by debris cover. Nat. Geosci. 4, 156–159 (2011).
Ragettli, S., Immerzeel, W. W. & Pellicciotti, F. Contrasting climate change impact on river flows from high-altitude catchments in the Himalayan and Andes mountains. Proc. Natl Acad. Sci. 113, 9222–9227 (2016).
Anderson, L. S. & Anderson, R. S. Modeling debris-covered glaciers: response to steady debris deposition. Cryosphere 10, 1105–1124 (2016).
Quincey, D., Luckman, A. & Benn, D. Quantification of Everest region glacier velocities between 1992 and 2002, using satellite radar interferometry and feature tracking. J. Glaciology 55, 596–606 (2009).
Benn, D. et al. Response of debris-covered glaciers in the Mount Everest region to recent warming, and implications for outburst flood hazards. Earth- Sci. Rev. 114, 156–174 (2012).
Fyffe, C. et al. Do debris-covered glaciers demonstrate distinctive hydrological behaviour compared to clean glaciers? J. Hydrol. 570, 584–597 (2019).
Miles, K. E. et al. Hydrology of debris-covered glaciers in High Mountain Asia. Earth-Science Rev. 207, 103212 (2020).
Immerzeel, W. W., Van Beek, L. P. & Bierkens, M. F. Climate change will affect the Asian water towers. Science 328, 1382–1385 (2010).
Pritchard, H. D. Asia’s shrinking glaciers protect large populations from drought stress. Nature 569, 649–654 (2019).
Immerzeel, W. W. et al. Importance and vulnerability of the world’s water towers. Nature 577, 364–369 (2020).
Cauvy-Fraunié, S. & Dangles, O. A global synthesis of biodiversity responses to glacier retreat. Nat. Ecol. Evolution 3, 1675–1685 (2019).
Kraaijenbrink, P. D., Bierkens, M., Lutz, A. & Immerzeel, W. Impact of a global temperature rise of 1.5 degrees Celsius on Asia’s glaciers. Nature 549, 257–260 (2017).
Scherler, D., Wulf, H. & Gorelick, N. Global assessment of supraglacial debriscover extents. Geophys. Res. Lett. 45, 11–798 (2018).
Rounce, D. R., Hock, R. & Shean, D. E. Glacier mass change in High Mountain Asia through 2100 using the open-source python glacier evolution model (PyGEM). Front. Earth Sci. 7, 331 (2020).
Schauwecker, S. et al. Remotely sensed debris thickness mapping of Bara Shigri Glacier, Indian Himalaya. J. Glaciology 61, 675–688 (2015).
Rounce, D. & McKinney, D. Debris thickness of glaciers in the Everest area (Nepal Himalaya) derived from satellite imagery using a nonlinear energy balance model. Cryosphere 8, 1317–1329 (2014).
Rounce, D. R., King, O., McCarthy, M., Shean, D. E. & Salerno, F. Quantifying debris thickness of debris-covered glaciers in the Everest region of Nepal through inversion of a subdebris melt model. J. Geophys. Research: Earth Surf. 123, 1094–1115 (2018).
Huang, L. et al. Estimation of supraglacial debris thickness using a novel target decomposition on L-band polarimetric SAR images in the Tianshan mountains. J. Geophys. Research: Earth Surf. 122, 925–940 (2017).
McCarthy, M. J. Quantifying supraglacial debris thickness at local to regional scales. Ph.D. thesis, University of Cambridge (2018).
Rounce, D. et al. Distributed global debris thickness estimates reveal debris significantly impacts glacier mass balance. Geophys. Res. Lett. 48, 1–12 (2021).
Boxall, K., Willis, I., Giese, A. & Liu, Q. Quantifying patterns of supraglacial debris thickness and their glaciological controls in High Mountain Asia. Front. Earth Sci. 9, 504 (2021).
Scherler, D. & Egholm, D. Production and transport of supraglacial debris: Insights from cosmogenic 10Be and numerical modeling, Chhota Shigri Glacier, Indian Himalaya. J. Geophys. Research: Earth Surf. 125, e2020JF005586 (2020).
Orr, E. N., Owen, L. A., Saha, S., Hammer, S. J. & Caffee, M. W. Rockwall slope erosion in the northwestern Himalaya. J. Geophys. Research: Earth Surf. 126, e2020JF005619 (2021).
Heimsath, A. M. & McGlynn, R. Quantifying periglacial erosion in the Nepal High Himalaya. Geomorphology 97, 5–23 (2008).
Banerjee, A. & Wani, B. A. Exponentially decreasing erosion rates protect the high-elevation crests of the Himalaya. Earth Planet. Sci. Lett. 497, 22–28 (2018).
Barker, A. Glaciers, erosion and climate change in the Himalaya and St. Elias Range, SE Alaska. Ph.D. thesis (2016).
Shah, S. S., Banerjee, A., Nainwal, H. C. & Shankar, R. Estimation of the total sub-debris ablation from point-scale ablation data on a debris-covered glacier. J. Glaciology 65, 759–769 (2019).
Miles, K. E. et al. Continuous borehole optical televiewing reveals variable englacial debris concentrations at Khumbu Glacier, Nepal. Commun. Earth Environ. 2, 1–9 (2021).
Nakawo, M. Supraglacial debris of G2 Glacier in Hidden Valley, Mukut Himal, Nepal. J. Glaciology 22, 273–283 (1979).
Shroder Jr, J. F. Sediment transport and yield at the Raikot Glacier, Nanga Parbat, Punjab Himalaya. In Himalaya to the Sea (eds. Gardner, J. S. & Jones, N. K.) 134–141 (Routledge, 2002).
Miles, E. et al. Health and sustainability of glaciers in High Mountain Asia. Nat. Commun. 12, 2868 (2021).
Miles, E. et al. Results for ’Health and sustainability of glaciers in High Mountain Asia’. Zenodo. Accessed on 01-06-2021 (2021).
Anderson, L. S. & Anderson, R. S. Debris thickness patterns on debris-covered glaciers. Geomorphology 311, 1–12 (2018).
Kirkbride, M. P. & Deline, P. The formation of supraglacial debris covers by primary dispersal from transverse englacial debris bands. Earth Surf. Process. Landf. 38, 1779–1792 (2013).
Anderson, R. S. A model of ablation-dominated medial moraines and the generation of debris-mantled glacier snouts. J. Glaciology 46, 459–469 (2000).
Hock, R. et al. High mountain areas: In: IPCC special report on the ocean and cryosphere in a changing climate. Tech. Rep., IPCC (2019).
RGI Consortium. Randolph Glacier Inventory - a dataset of global glacier outlines: Version 6.0. National Snow and Ice Data Center. Boulder, Colorado, USA. (2017).
Scherler, D., Wulf, H. & Gorelick, N. Supraglacial debris cover. v. 1.0. GFZ Data Services. Accessed on 01-01-2020 (2018).
Dehecq, A. et al. Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 12, 22–27 (2019).
Gardner, A. S., Fahnestock, M. A. & Scambos, T. A. ITS_LIVE regional glacier and ice sheet surface velocities: Version 1. Data archived at National Snow and Ice Data Center. Accessed on 01-01-2020 (2019).
Cook, S. J., Swift, D. A., Kirkbride, M. P., Knight, P. G. & Waller, R. I. The empirical basis for modelling glacial erosion rates. Nat. Commun. 11, 1–7 (2020).
Streule, M. J., Searle, M. P., Waters, D. J. & Horstwood, M. S. Metamorphism, melting, and channel flow in the greater himalayan sequence and makalu leucogranite: Constraints from thermobarometry, metamorphic modeling, and u-pb geochronology. Tectonics 29, 1–28 (2010).
Orr, E. N., Owen, L. A., Saha, S. & Caffee, M. W. Rates of rockwall slope erosion in the upper Bhagirathi catchment, Garhwal Himalaya. Earth Surf. Process. Landf. 44, 3108–3127 (2019).
Owen, L. A. et al. Quaternary glaciation of Mount Everest. Quaternary Sci. Rev. 28, 1412–1433 (2009).
Kirchner, J. W. et al. Mountain erosion over 10 yr, 10 ky, and 10 my time scales. Geology 29, 591–594 (2001).
Chen, J. & Ohmura, A. Estimation of alpine glacier water resources and their change since the 1870s. IAHS Publication 193, 127–135 (1990).
Fick, S. E. & Hijmans, R. J. Worldclim 2: new 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37, 4302–4315 (2017).
Hales, T. & Roering, J. J. Climatic controls on frost cracking and implications for the evolution of bedrock landscapes. J. Geophys. Research: Earth Surf. 112, 1–14 (2007).
Scherler, D. Climatic limits to headwall retreat in the Khumbu Himalaya, eastern Nepal. Geology 42, 1019–1022 (2014).
Eppes, M.-C. & Keanini, R. Mechanical weathering and rock erosion by climate-dependent subcritical cracking. Rev. Geophysics 55, 470–508 (2017).
Hirschberg, J. et al. Climate change impacts on sediment yield and debris-flow activity in an alpine catchment. J. Geophys. Research: Earth Surf. 126, 1–26 (2020).
Montgomery, D. R. & Brandon, M. T. Topographic controls on erosion rates in tectonically active mountain ranges. Earth Planet. Sci. Lett. 201, 481–489 (2002).
Larsen, I. J. & Montgomery, D. R. Landslide erosion coupled to tectonics and river incision. Nat. Geosci. 5, 468–473 (2012).
Nagai, H., Fujita, K., Nuimura, T. & Sakai, A. Southwest-facing slopes control the formation of debris-covered glaciers in the Bhutan Himalaya. Cryosphere 7, 1303–1314 (2013).
Collins, B. D. & Stock, G. M. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 9, 395–400 (2016).
Hartmann, J. & Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochemistry, Geophysics, Geosystems 13, 1–37 (2012).
Schmidt, K. M. & Montgomery, D. R. Limits to relief. Science 270, 617–620 (1995).
Benn, D. I., Kirkbride, M. P., Owen, L. A. & Brazier, V. Glaciated valley landsystems. Glacial landsystems 372-406 (2003).
Brun, F. et al. Heterogeneous influence of glacier morphology on the mass balance variability in High Mountain Asia. J. Geophys. Research: Earth Surf. 124, 1331–1345 (2019).
Rowan, A. V., Egholm, D. L., Quincey, D. J. & Glasser, N. F. Modelling the feedbacks between mass balance, ice flow and debris transport to predict the response to climate change of debris-covered glaciers in the Himalaya. Earth Planet. Sci. Lett. 430, 427–438 (2015).
Zarfl, C., Lumsdon, A. E., Berlekamp, J., Tydecks, L. & Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 77, 161–170 (2015).
Gibson, M. J. et al. Temporal variations in supraglacial debris distribution on Baltoro Glacier, Karakoram between 2001 and 2012. Geomorphology 295, 572–585 (2017).
Woerkom, T.v., Steiner, J. F., Kraaijenbrink, P. D., Miles, E. S. & Immerzeel, W. W. Sediment supply from lateral moraines to a debris-covered glacier in the Himalaya. Earth Surf. Dynamics 7, 411–427 (2019).
Ragettli, S. et al. Unraveling the hydrology of a Himalayan catchment through integration of high resolution in situ data and remote sensing with an advanced simulation model. Adv. Water Resour. 78, 94–111 (2015).
Westoby, M. J. et al. Geomorphological evolution of a debris-covered glacier surface. Earth Surf. Process. Landf. 45, 3431–3448 (2020).
Evatt, G. W. et al. Glacial melt under a porous debris layer. J. Glaciology 61, 825–836 (2015).
Buri, P., Miles, E. S., Steiner, J. F., Ragettli, S. & Pellicciotti, F. Supraglacial ice cliffs can substantially increase the mass loss of debris-covered glaciers. Geophys. Res. Lett. 48, e2020GL092150 (2021).
Miles, E. S. et al. Surface pond energy absorption across four Himalayan glaciers accounts for 1/8 of total catchment ice loss. Geophys. Res. Lett. 45, 10–464 (2018).
Reid, T. D. & Brock, B. W. An energy-balance model for debris-coveredglaciers including heat conduction through the debris layer. J. Glaciology 56, 903–916 (2010).
Reid, T., Carenzo, M., Pellicciotti, F. & Brock, B. Including debris cover effects in a distributed model of glacier ablation. J. Geophys. Research: Atmospheres 117, 1–15 (2012).
Rounce, D., Quincey, D. & McKinney, D. Debris-covered energy balance model for Imja-Lhotse Shar Glacier in the Everest region of Nepal. Cryosphere 9, 3503–3540 (2015).
Arnold, N. S., Rees, W. G., Hodson, A. J. & Kohler, J. Topographic controls on the surface energy balance of a high Arctic valley glacier. J. Geophys. Research: Earth Surf. 111, 1–15 (2006).
Konzelmann, T. & Ohmura, A. Radiative fluxes and their impact on the energy balance of the Greenland Ice Sheet. J. Glaciology 41, 490–502 (1995).
Arnold, N., Willis, I., Sharp, M., Richards, K. & Lawson, W. A distributed surface energy-balance model for a small valley glacier. i. development and testing for Haut Glacier d'Arolla, Valais, Switzerland. J. Glaciology 42, 77–89 (1996).
Walraven, R. Calculating the position of the sun. Sol. Energy 20, 393–397 (1978).
Paterson, W. S. B. Physics of glaciers (Butterworth-Heinemann, 1994).
Collier, E. et al. Representing moisture fluxes and phase changes in glacier debris cover using a reservoir approach. Cryosphere 8, 1429–1444 (2014).
Murray, F. W. On the computation of saturation vapor pressure. J. Appl. Meteorol. 6, 203–204 (1967).
Hay, J. & Fitzharris, B. A comparison of the energy-balance and bulkaerodynamic approaches for estimating glacier melt. J. Glaciology 34, 145–153 (1988).
2019). ERA5-Land hourly data from 1981 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). Accessed on 01-01-2020.
Muhammad, S. & Thapa, A. An improved Terra–Aqua MODIS snow cover and Randolph Glacier Inventory 6.0 combined product (MOYDGL06*) for High-Mountain Asia between 2002 and 2018. Earth Syst. Sci. Data 12, 345–356 (2020).
Mölg, T. & Kaser, G. A new approach to resolving climate-cryosphere relations: Downscaling climate dynamics to glacier-scale mass and energy balance without statistical scale linking. J. Geophys. Research: Atmospheres 116, (2011).
Mölg, T., Maussion, F. & Scherer, D. Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia. Nat. Clim. Change 4, 68–73 (2014).
Machguth, H., Purves, R. S., Oerlemans, J., Hoelzle, M. & Paul, F. Exploring uncertainty in glacier mass balance modelling with Monte Carlo simulation. Cryosphere 2, 191–204 (2008).
Miles, E. S., Steiner, J. F. & Brun, F. Highly variable aerodynamic roughness length (z0) for a hummocky debris-covered glacier. J. Geophys. Research: Atmospheres 122, 8447–8466 (2017).
Clark, S. P. Handbook of physical constants, vol. 97 (Geological society of America, 1966).
Wirbel, A., Jarosch, A. H. & Nicholson, L. Modelling debris transport within glaciers by advection in a full-stokes ice flow model. Cryosphere 12, 189–204 (2018).
Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 7, 877–887 (2013).
Farinotti, D. et al. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 12, 168–173 (2019).
Acknowledgements
This study would not have been possible without the in-situ supraglacial debris thickness data we used for validation, from colleagues including Bhanu Pratap, Lavkush Patel, and from the Zenodo Community of the IACS Working Group on Debris Covered Glaciers. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement No 772751, RAVEN, "Rapid mass losses of debris-covered glaciers in High Mountain Asia”. We thank Argha Banerjee and two anonymous reviewers for their comments and suggestions, which helped to improve this study.
Author information
Authors and Affiliations
Contributions
M.M., E.M. and F.P. designed the study and developed the methods for calculating supraglacial debris thickness and debris-supply rate. M.K., P.B. and E.M. mapped and developed the methods for mapping the debris-supply slopes. M.M. performed the calculations and led the writing of the paper. E.M., F.P., S.F., M.K. and P.B. helped interpret the results and write the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Argha Banerjee, David Rounce and Arjun Heimsath for their contribution to the peer review of this work. Primary Handling Editors: Jan Lenaerts, Joseph Aslin, Clare Davis and Heike Langenberg. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
McCarthy, M., Miles, E., Kneib, M. et al. Supraglacial debris thickness and supply rate in High-Mountain Asia. Commun Earth Environ 3, 269 (2022). https://doi.org/10.1038/s43247-022-00588-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00588-2
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.