Abstract
The basin and plateau regions of the Central Andes have undergone phases of rapid subsidence and uplift during the last ~20 Myr in addition to internal tectonic deformation. Paleoelevation data and the presence of high seismic wave speed anomalies beneath the Puna Plateau suggest that these tectonic events may be related to lithospheric foundering. Here, we study the geodynamic processes in the region using three dimensional, scaled, analogue models and high-resolution optical image correlation techniques. The analogue experiments show how a gravitational instability of the mantle lithosphere developing into a lithospheric drip may form a circular sedimentary basin in the crust that undergoes subsidence and subsequently reverses to uplift, while simultaneously undergoing internal crustal shortening. The model results reveal that drips may be “symptomatic” where the crust is well coupled to the sinking mantle lithosphere and manifests tectonic deformation at the surface, or poorly coupled “asymptomatic” drips with weak crustal surface manifestations. Overall, the physical models suggest that the formation of the Arizaro Basin and nearby Central Andean basins are caused by symptomatic lithospheric dripping events and highlight the significant role of non-subduction geodynamic mechanisms in driving surface tectonics.
Similar content being viewed by others
Introduction
Rapid and short-lived phases of crustal shortening and extension, topographic perturbations, and exhumation processes are interpreted as the geological manifestations of lithospheric foundering in which gravitationally unstable (thickened) lithosphere sinks/drips into the underlying sub-lithospheric (asthenospheric) mantle1,2,3,4. In addition to conceptual tectonic models, seismic tomography provides robust examples of drip-like high wave speed anomalies beneath the Colorado Plateau5,6, Great basin7, Sierra Nevada region of California8,9,10, Altiplano Plateau11, Tibetan Plateau12, Carpathians13, and Anatolia14. This type of “drip tectonics” has been associated with magmatism beneath continental interiors, such as the Mongolian plateau15, and the Siberian16, North China17,18,19, and Wyoming Cratons20. Among these many examples, however, the surface tectonic response of the lithospheric foundering process is not well resolved since, apart from a few studies21,22,23,24, geodynamic model predictions have not been tested in the context of direct regional geological or geophysical observations. Here, using analogue (laboratory) models with geological and geophysical constraints, we test a hypothesis that the topographic and tectonic evolution of hinterland basins of the Central Andes are caused by lithospheric drip processes.
The Central Andean Plateau is defined by the Puna and Altiplano high plateaus (>3 km elevation; Fig. 1) and was formed by subduction of the Nazca plate beneath the South American plate25,26,27,28. Paleoaltimetric studies suggest that the rise of Central Andean topography has not been uniform in time but rather was built during the Cenozoic through pulses of uplift29,30,31. Further, geological and paleoelevation estimates indicate that the relative timing and mechanism of topographic uplift and the styles of tectonic deformation are different between the Puna and Altiplano plateaus32,33. The Puna Plateau is characterised by higher average elevation including local isolated hinterland basins (e.g., Salar de Arizaro, Salar de Atacama) and distinct volcanic centres (Fig. 1). Various studies invoke lithospheric removal--and the associated mantle dynamics--to account conceptually for the widespread (non subduction related) magmatism, surface deformation, and time-dependent topographic evolution of the plateaus3,34,35,36,37.
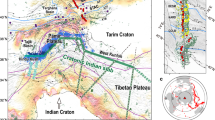
a 3-D view of the lithospheric and upper mantle structure of the region, and b Map view of the same area showing tomography slices at 55 km depth. The locations of the Atacama (AT), Arizaro (AZ), and Salinas Grandes (SG) basins are marked. A, B, C and D represent major high speed P-wave anomalies. Diagram modified from ref. 64.
Figure 1 shows a P-wave seismic tomography model beneath the Puna Plateau surface. The locations of basins within the plateau have been marked on the map (viz., Atacama (AT), Arizaro (AZ) and Salinas Grandes (SG)). Higher wave speed, colder anomalies (A, B, C and D) at ~200 km depth have been interpreted as foundered lithosphere, formed following plate shortening during Andean orogenesis3. Based on stratigraphic and structural work, DeCelles et al. (2015) suggests that the Miocene Arizaro Basin (Fig. 1), an internally drained, 3.5 km deep oval shaped hinterland basin, represents a geological manifestation of dripping lithosphere33. Their study determines that an event of rapid subsidence changing to uplift is documented in the basin’s sedimentary record, and these motions are not consistent with characteristics of tectonic flexural response and local stretching. Further, crustal shortening in the Arizaro Basin interior is well documented by folding and local thrust faults, but the basin is not bounded by known plate boundary scale fault systems33. Overall, this suggests that more regional geodynamic processes are required to account for the geological evolution of the Arizaro Basin since the Miocene. Geological studies have also inferred lithospheric dripping beneath other parts of the Puna Plateau, for instance the southern part of the Arizaro and Salar de Atacama basins38,39. Such studies advance evidence for lithospheric drips in the region, but the dynamical process(es) of lithospheric dripping and their role in driving local tectonics in these purported geological cases are uncertain.
Here we use three-dimensional (3D), scaled, analogue experiments to investigate the complex deformational response of the brittle (upper crust) to descending mantle lithosphere. The experiments build on a suite of analogue models from Pysklywec and Cruden (2004) that explored lithospheric instabilities and surface tectonics40. We use techniques that permit a detailed investigation of the evolution of topography and strain in the models so that the model findings can be interpreted in the context of active foundering in the Central Andes region (Fig. 1). As such, our work aims to clarify the link between mantle processes and crustal tectonics, and how such geodynamic processes may be interpreted with observed or inferred episodes of lithospheric removal.
Results
We conducted a series of ten scaled experiments in a plexiglass box, and three of these are representative of tectonic evolution of the Central Andes. These models contained sub-lithospheric mantle made of Polydimethylsiloxane (PDMS), a mantle lithosphere made of a modelling clay and PDMS mixture with varied density and viscosity, two different brittle upper crust materials (e-spheres & silica spheres or sand), and one case with a viscous lower crust made of modelling clay and PDMS. We investigated two different methods (Method 1 and Method 2) of initiating the lithospheric perturbation that evolved into distinct styles of removal. The main objective of this study was to understand the different styles of instability of the mantle lithosphere, and the resulting deformation in the brittle upper crust. This builds upon previous analyses in which variable rheological properties of the upper and lower crust were investigated40.
Using Particle Image Velocimetry (PIV), Stereo Digital Image Correlation (SDIC), and digital photogrammetry techniques, we have tracked crustal strain and evolution of topography and drip descent throughout the experiments. Details regarding materials, scaling, and experimental setup are given in the Methods section below.
EXP-1
The experiment begins when the initial density perturbation (12.5 mm radius) in the centre of the model box develops as a Rayleigh-Taylor (gravitational) instability, attached using Method 1 of drip initiation. In Method 1 (EXP-1 and EXP-3), the mantle lithosphere was placed onto the sub-lithospheric mantle (PDMS) and then a 2.5 cm diameter hemisphere of clay+PDMS was pushed into the mantle lithosphere from the top of the layer and left to settle until a flat surface was reformed (see Methods section).
Figure 2a, b shows the plan view evolution of surface topography overlain with cumulative surface strain (Exx) components and the sideview (photograph) evolution of the experiment from 0–40 h, which scales to 25.2 Myr total time in nature. By 10 h, a cylindrical shape drip has developed and is actively descending (green vectors). In response to the downwelling, upward return flow (red vectors) have evolved around the drip as a small-scale mantle circulation process (Fig. 2b). By 20 h, the drip undergoes necking (thinning) while its rate of descent has decelerated (Fig. 2c). Note that the downward pointing green vectors have greater magnitude around the base of the drip where the drip volume and the viscous tractions are larger than the sides and the neck. This suggests rapid descent at the base (drip head) compared to the neck. The red vectors in the mantle (PDMS) surrounding the drip demonstrate upward motion as the drip displaces adjacent material. After 30 h, the descent has terminated, and the drip head reaches the bottom of the tank. Figure 2c demonstrates that the descent rate is steady from 0–18 h, with a hiatus for a few hours, and then a slower descent from approximately 23 h to the end of the experiment.
a Plan view showing the evolution of topography from 0 to 40 h for EXP-1 with arrows depicting cumulative surface strain. Convergence towards the centre occurs between 0 h to 40 h. Convergence stuctures are shown in the photograph at 40 h with a possible extensional feature in the bottom right corner. Note the presence of an air bubble in the top right corner of the images. b Below surface (sideview) evolution of the drip from 0 to 40 h. Green vectors track downward motion of the drip and red vectors the upward motion of the PDMS. c Progression of the drip through the mantle starting at the base of the mantle lithosphere (Position = 0) with corresponding scaled Earth time values. The drip touched the bottom of the box at ~35 h. Drip descent appears to cease at ~18 h before sinking again at ~23 h.
The map of surface elevation shows that an approximately circular surface basin develops as a response to the pull of the dripping lithosphere on the overlying crust (Fig. 2a). The centre of the basin shows ~ −1.5 mm of subsidence (approximately 6 km in nature). We interpret that the downward force exerted by the drip on the overlying crust is maximum at the start and decreases as the experiment continues owing to progressive down-dip extension and necking. As the experiment progresses, the radius of the circular basin is ~6 cm at its widest points and decreases to ~1.5 cm (~75%) with progressive shortening of the surface crust and loss of dynamic support. Topographic uplift (>1 mm) occurs around the periphery of the circular basin and more significantly the right side of the box as lower density mantle material replaces higher density mantle lithosphere. These results show a more distinct circular basin formation than the point instability (P) experiments of Pysklywec and Cruden (2004).
Crustal strain on the top surface is 0% at 0 h (Fig. 2a). By 10 h the strain is increasing as the surface is pulled downward and inwards by the drip as indicated by the cumulative strain magnitude and directions. By 30 h, we observe the highest accumulation of strain (approaching 15%) immediately above the drip with minor change in magnitude and direction of strain between 30 h and 40 h despite further increase in surface elevation. The high crustal strain manifests as wrinkle-like linear features that developed in the central section of the model during shortening and folding of the upper crust (see Fig. 2, 40 h frame). This deformation is akin to the results of other 3-D analogue drip experiments40,41.
EXP-2
In EXP-2 an alternative method (Method 2) was used to initiate a drip with a perturbation less well coupled to the overlying mantle lithosphere (while all other model parameters remain the same as EXP-1). In Method 2, the same size hemisphere as EXP-1 was inserted into the PDMS rather than the mantle lithosphere and then the mantle lithosphere was placed on top akin to the method described in Pysklywec and Cruden (2004)40.
The lack of horizontal crustal convergence and accumulation of strain in the crust indicates that the mantle lithospheric drip was not well coupled to the upper mantle lithosphere compared to EXP-1 (Fig. 3a). Figure 3b shows overall evolution of the drip in EXP-2 that is similar to EXP-1, although the volume of mantle lithosphere involved in the drip is significantly reduced. By 20 h the drip has travelled approximately two thirds the depth of the box and we see strong downward motion (green vectors) with the greatest velocity occurring at the bottom of the drip. The red vectors show outward and upward motion of the PDMS away from the drip as it displaces surrounding mantle material. Like the previous experiment, the drip descends rapidly at the beginning (until ~15 h) (Fig. 3c). It reaches the bottom of the tank by approximately 25 h (Fig. 3c) but the downwelling of mantle lithosphere persists down the neck of the drip until the end of the experiment. The width of the neck (stretched portion) of the drip is approximately one third of the neck in EXP-1. There is less lithospheric removal from beneath the crust in comparison to EXP-1, which further supports the interpretation that the drip is not well coupled to the mantle lithosphere.
a Plan view evolution of topography and cumulative strain over 40 h. Red strain arrows indicate some accumulation of strain at 0 h. Photograph of the surface at 40 h depicts no convergence in the crust. A basin ~0.5 mm deep is illustrated at 40 h. b Evolution of drip (sideview) beneath the surface with downward green displacement vectors. Red vectors indicate upward displacement of the PDMS. c Progression of drip beneath the base of the mantle lithosphere. The drip sank in a continuous path and touched the bottom of the box at ~25 h.
Figure 3a shows that a circular depression initially develops in the central part of the box as a topographic expression above the incipient downwelling. This depression forms very rapidly–over a few minutes in the time between model construction and before the imaging system could be started. The horizontal strain vectors at 0 h indicate low (<2%) strain inward, and this does not change over the span of the 40 h experiment. There is no appreciable surface strain measured in the crust (40 h frame) despite the active mantle dynamics below, showing that this perturbation and resulting drip does not induce crustal deformation42. These results with essentially no surface deformation are consistent with findings from Pysklywec and Cruden (2004) describing a non-published experiment (P4). As the drip moves downward and the neck thins, there is relative uplift as the surface rebounds back from its initial rapid subsidence, and the planform of the basin narrows (Fig. 3a) The topography measurements show that a small depression remains in the centre of the experiment throughout (~0.5 mm deep).
EXP-3 (addition of a lower crust)
In this experiment, we kept all model parameters the same as EXP-1 but included a viscous lower crust (see Methods section) between the brittle upper crust and mantle lithosphere. A drip was initiated using Method 1 with the same 12.5 mm radius instability as EXP-1 and EXP-2. The overall dynamic evolution of the drip in EXP-3 is like EXP-1, which is evident in Fig. 4c where the drip is shown to descend in two stages. However, it evolves at a slower rate than EXP-1 (Fig. 4c). For instance, by 20 h the drip has only travelled ~85 mm compared to EXP-1 where the drip had descended ~125 mm. At 30 h (Fig. 4b) the drip starts to grow slowly, and the rate of descent increases rapidly at ~32 h (Fig. 4c). The neck of the drip is wider in the side view than that of EXP-1 and EXP-2, being approximately two times the width of that in EXP-1. The weak and buoyant lower crust that is included in EXP-3 is entrained downward by the descending drip. This is not visible in the sideview images but was discovered during the post-experiment dissection of the model. Compared to the results of Pysklywec and Cruden (2004; Fig. 5) a smaller amount of crustal material is entrained with the sinking mantle lithosphere.
a Plan view evolution of topography over 40 h with cumulative surface strain. Full extension of the lithosphere was visible in the crust at 45 h (top left of photograph). b Below surface (sideview) evolution of the drip. The cloud surrounding the drip is visible discoloration of the (polydimethylsiloxane) PDMS from the clay in the mantle lithosphere. Green vectors show downwward motion of drip while red vectors illustrate out and upward movement of the PDMS (mantle). c Progression of the drip beneath the base of the mantle lithosphere. Drip progression temporarily ceases at ~25 h before sinking again at ~32 h. The drip touched the bottom of the box at ~37 h.
a Relative surface elevation of EXP-1, EXP-2, and EXP-3, with elevation of Arizaro Basin from ref. 33. The dotted red line in EXP-2 depicts rapid subsidence before the recording began. This occurred in a short span of time between setting up the experiment and starting the camera recording (minutes). b Geological map of the Arizaro Basin, demonstrating folding and thrust faults within the basin, modified from ref. 33. Sierra de Macon ridge (SdM). c Surface view of EXP-1 above the drip, demonstrating folding and direction of shortening depicted with red arrows.
Figure 4a shows that a large, well-defined depression develops in response to the lithospheric instability. Strain arrows indicate inward convergence of surface crust throughout the experiment. The buildup of strain in the crust as it converges yields similar wrinkle-like linear features to EXP-1 (Fig. 4; 45 h frame), with the highest cumulative strain reaching 20%. Zones of the crust are extended (beginning at ~10 h) on the margins of the basin as material is pulled inwards in the finite volume model box.
Symptomatic vs. asymptomatic drips
In all the experiments, the lithospheric drips are associated with vertical surface displacements (e.g., some subsidence and/or uplift), however, not all drips caused appreciable shortening and accumulation of strain in the upper crust. This behaviour stems from differing initial conditions and allows for classification of a drip as either symptomatic or asymptomatic. A symptomatic drip is well coupled to the entire mantle lithosphere (and partially the crust): It sinks through the mantle and pulls the upper part of the mantle lithosphere inward and horizontally, producing an accumulation of strain (shortening) and the formation of structures like fold-and-thrust ridges in the upper crust. These drips tend to generally remove more material from the lithosphere. EXP-1 and EXP-3 can be classified as symptomatic drips (Figs. 2a and 4a). There may be other factors controlling these symptoms in the crust (such as thermal and compositional), but we did not explore these variables in this study.
In contrast, an asymptomatic drip responds with initial subsidence, but is less developed throughout the entire mantle lithosphere and consequently is not as efficiently coupled to the crust. Accordingly, crustal strain is subdued and there may be little to no evidence of horizontal deformation in the crust despite the active mantle dynamics below. EXP-2 is an asymptomatic drip where lithospheric removal produced transient subsidence and topographic recovery but no tectonic deformation in the crust.
Discussion
Our findings from the analogue experiments are reconciled with the unique lithospheric and mantle structure, and key features of the tectonic evolution of hinterland basins in the Southern Puna Plateau over the last 20 Myrs36,37 (Fig. 5). Below, we describe how our primary experimental results may explain several geological and geophysical features pertaining to the geodynamic evolution of the region.
Our experiments found that lithospheric downwellings are characterised by a sinking bulbous drip head attached to a thin neck, formed by the stretching of a viscous lithospheric instability. A seismic tomography model (Fig. 1) shows that, there are four higher seismic wave speed anomalies (~25°S and 65.5°W), labelled A,B,C and D surrounded by a lower seismic wave speed upper mantle domain below the southern Puna Plateau region. The current positions of the inferred anomalies may have been offset due to the mantle flow generated by the subduction of the Nazca plate beneath the South American plate43. Their surface projections suggest that they are approximately located beneath the Arizaro Basin, the Salar de Atacama (basin) and the Salinas Grandes, and as such they may be interpreted as lithospheric drips that have controlled the tectonic evolution of these basins. Note that these basins and high seismic wave speed anomalies are similar in size and geometry (viz., oval shaped). Götze and Krause (2002) suggests that the Central Andean gravity high is associated with dense lithosphere (400 km long and 100–140 km wide; 10–38 km depth), which stretches across the Arizaro and Atacama Basins44. Further, our experiments showed continuous removal of the lithosphere, including portions of the (lower) crust. This crustal removal is consistent with the Arizaro region where the Moho depth is much shallower (42 km), inferred from receiver function and wide-angle seismic studies45.
Figure 5a compares the subsidence curve of the Arizaro Basin33 against the experiment results (EXP-1, 2 and 3). For the experiments, the plot represents the relative surface elevation change of a point (approximately the centre of the experiment) above the dripping lithosphere as a function of time. The results of EXP-1 and EXP-3 agree with the three-stage evolution of the relative elevation of the Arizaro Basin. The stages are characterised by deflection of surface topography from negative (subsidence) to positive (uplift). In EXP-1 and EXP-3, Stage 1 corresponds to ~1 mm (~4 km) of accelerated surface subsidence that develops as a response to the initial (strong) downwelling effect of the drip (0 h-15 h in EXP-1 and 0 h-32 h in EXP-3) in which a substantial amount of lithospheric material is removed. This stage also includes the initial growth of the lithospheric instability. In Stage 2, the surface topography is recovered since there is a release of drip-pull forces related to the thinning and stretching of the drip (15 h-27 h in EXP-1 and 32 h-44 h in EXP-3). Stage 3 of topographic development is associated with additional isostatic surface uplift likely due to further removal of mantle lithosphere along the neck of the drip. During these stages, we observe surface contraction where linear wrinkle fold-and-thrust belt like features develop (Fig. 5c). In EXP-3, with the addition of a lower crust, the rate of surface uplift is greater, and the rate of subsidence is slower, compared to basin development in the previous experiments. The Arizaro Basin similarly shows the stages of subsidence and uplift (Fig. 5a). DeCelles et al. (2015) estimates that the basin underwent an initial, ~2–3 Myr period of subsidence followed by an accelerated phase with a higher rate of sedimentation inferred from deposition of deep-water lacustrine facies (6–9 Myr). Evaporates and mudflats were subsequently deposited which can be ascribed to a decrease in basin subsidence and termination of deepening in the basin centre. Late stages of the model evolution may correspond to the reactivation of the Sierra de Macon ridge (Fig. 5b) and basin inversion that occurred ~10 Ma33. In terms of width of the basin, our results scale to 60–240 km, within the range of the 75–100 km diameter of the Arizaro Basin33.
Compared to EXP-1, EXP-3 exhibits a longer period of subsidence followed by a rapid rate of uplift. The conditions that control the growth rate of the instability clearly influence the related history of basin subsidence and uplift. The surface topography in EXP-2 behaves quite differently from EXP-1, EXP-3, and the Arizaro Basin. EXP-2 shows gradually increasing surface elevation (0–10 h) from initial depression (induced by the perturbation). Notably, in EXP-2 the instability related subsidence is limited and rapid; only present during the very early phase of the experiment, before any downwelling was recorded at 0 h. Further, the topography progressively increases although there is no shortening or accumulation of strain in the upper crust. EXP-2 suggests that lithospheric drips can create a basin without internal shortening and that topography may fully recover over the lifetime of the drip.
The results of EXP-1 and EXP-3, in which surface deformation is localised both by shortening above the drip and extension on the periphery, are consistent with the observed crustal tectonics in the Puna Plateau region. This is especially true for the Arizaro Basin, and the internal shortening inferred from thrust faulting that develops in conjunction with basin subsidence (see Fig. 5b and c for comparison). Based on our classification, the tectonic manifestation of the underlying mantle lithospheric dynamics suggests the drip beneath the Arizaro Basin is symptomatic. In both EXP-1 and EXP-3, saucer shaped basins and ridge-type structures were formed like the Sierra de Macon in the central Arizaro Basin (Figs. 2a 40 h and 4a 45 h, 5b). Previous studies also show geological evidence for normal faulting in the Pasto Ventura region (in the southern part of the Arizaro basin) that occurred by lithospheric removal38. Further, the tectonic effect of a drip may extend over the fore-arc of the Andean subduction system in which normal faulting has been documented by the computed earthquake focal mechanism (e.g., Salar de Atacama)39.
These analogue models support geological and geophysical findings in the Puna Plateau region of South America, indicating that the formation and tectonic evolution of hinterland basins are driven by lithospheric dripping46. The results also suggest that asymptomatic lithospheric dripping may occur in some cases (not in the Central Andes) without inducing crustal shortening, in which the resulting basin may be shallower or fully recover its topography leaving little to no trace in the crust that this mantle lithosphere removal process occurred.
Methods
Experimental setup
A plexiglass box with dimensions 25 cm × 25 cm × 21.5 cm was filled with polydimethylsiloxane (PDMS), an analogue for the mantle, and was left to rest until it was free of air bubbles (approximately 14 days). A homogenous mixture of Plasticine™ modelling clay and PDMS represented a 2 cm thick layer of mantle lithosphere. Plasticine™ was used to increase the density of the PDMS to create a higher density mantle lithosphere than the underlying mantle. Overlying the mantle lithosphere in EXP-3 was a 0.5 cm thick lower crust, made of a different ratio of PDMS and modelling clay with a lower viscosity than the mantle lithosphere. All three experiments had a 2 mm thick brittle upper crust. Material properties are outlined in Table 1.
Lithospheric downwellings in the form of viscous drips developed naturally during experiments owing to the density contrast between the mantle lithosphere and underlying sub-lithospheric mantle (asthenosphere) and minor undulations of the thickness of the mantle lithosphere. We hypothesised that in nature a perturbation may correspond to localised high density lower crustal eclogites within or resting above the mantle lithosphere, formed by the gabbro-eclogite phase transformation. Lower crustal eclogitization has been previously interpreted as the cause of lithospheric removal in the Central Andes while adding to the net negative buoyancy of the lithosphere47. Therefore, to control the location and size of a drip and to initiate the sinking process, a localised perturbation was implemented in the centre of the box. We introduced a 2.5 cm diameter hemisphere with the same density as the mantle lithosphere to trigger a lithospheric instability (Fig. 6a).
a Analogue model dimensions and materials. Modified from ref. 40. b Experimental setup and camera positioning.
Specifically, two different methods were used to initiate a point instability at the centre of the mantle lithosphere (Method 1 & 2):
-
1.
In Method 1 (EXP-1 and EXP-3), the mantle lithosphere layer was placed onto the sub-lithospheric mantle (PDMS). Then, a 2.5 cm diameter hemisphere was pushed into the top of the mantle lithosphere layer and left to settle until a flat surface reformed. This created a perturbation at the base of the mantle lithosphere into the PDMS sub-lithospheric mantle.
-
2.
In Method 2 (EXP-2), the same size hemisphere was inserted directly into the sub-lithospheric mantle (PDMS) and left to settle until a flat surface reformed. Then the mantle lithosphere was placed/attached on top of the instability, akin to the method described in Pysklywec and Cruden (2004).
In both methods of model setup, the addition of the crust (upper and lower) was the last step.
Petroleum Jelly was used to lubricate the edges of the Plexiglass box and reduce the drag forces on the mantle lithosphere when inserting this layer on top of the PDMS during model setup. These edges were fixed during the experiment and produced drag at the sidewalls. However, the box was large enough that this drag did not prevent flow in the centre where the experiment was focused, so an additional lubricant such as a mixture of petroleum jelly and paraffin oil was not neccessary48. The upper crustal material was sieved on top of the mantle lithosphere (or lower crust in EXP-3) to a thickness of ~2 mm in all experiments. Black sand particles were used as tracers to track movement in the crust. The plexiglass box was open, so the model had a free surface.
The monitoring equipment consisted of three digital cameras (CCD, 11 MPx, 16 bit): two from above (Imager ProX by LaVision GMbH, Göttingen, Germany) and one from the side (Imager Pro by LaVision GMbH, Göttingen, Germany) (Fig. 6b). The recording of all cameras was synchronised and connected to a computer where the imaging software DaVis 7.2 for the top cameras and DaVis 7.1 for the side camera by LaVision GMbH recorded the evolution of the model at a frequency of 0.017 Hz (or one image every 58 s). The model was illuminated from above and from the side against a black background to create a strong contrast, so the camera only recorded motion from the model. We used recycled PDMS that had small particles of clay dispersed throughout that functioned as particles whose relative displacement were detected by the camera, which was subsequently used to calculate velocity vectors in the analogue mantle. The contrast between the black background and the instability allowed us to track the motion of the drip and the flow in the mantle, however, this means that the results show flow velocities integrated throughout the volume of the box.
We employed two similar optical image correlation techniques in the models: Stereo Digital Image Correlation (SDIC) and Particle Image Velocimetry (PIV). Previous studies have used these techniques or similar imaging techniques to compute mantle flow and crustal velocity fields49,50,51. SDIC was used to compute cumulative strain (Exx) in the granular crust. The black sand particles in the crust functioned as markers. As the crust deformed, the markers were displaced, and the cameras recorded this change in pattern. The DaVis software computes displacement fields by cross-correlating the translation and distortion of the sand particle pattern in successive images52. The software computes further derivative calculations to determine strain tensor components. To compute height and vertical displacement of the surface, the DaVis software uses digital photogrammetry. The two top cameras were calibrated so the relationship between the raw images and real-world space was known by creating a calibration model. This model was used in conjunction with matching the pattern between the two cameras above the model to calculate vertical displacement and height to a precision of ±0.0945 mm. PIV was used on the images from the side camera to visualise viscous mantle flow in response to the movement of the drip. This technique also uses optical image correlation to visualise flow and deformation and has been shown in previous sandbox experiments to be a useful analytical tool52,53,54. In these experiments, we used 2D PIV where the displacement field was created by cross-correlation of translated marker particles in the mantle, in successive images at the given time interval52.
Materials and rheology
The dimensions and materials used in the experiments were scaled for length (L), effective dynamic viscosity (ηeff), and density (ρ) compared to natural estimated Earth values. Following other analogue modelling studies, we used a granular material as an analogue for the brittle upper crust55,56. This material was composed of 37% fine grained (500 μm dry, solid) silica spheres and 63% (300 μm, dry, hollow) ceramic E-spheres (Envirospheres®). We assumed the upper crust had negligible cohesion57. The angle of internal friction (φ) was measured to be ~40° based on the angle of repose of the material in a conical pile and equating it to the angle of internal friction58. This assumption is reasonable for granular materials that are uniform in size, density and moisture content59.
The sub-lithospheric mantle was comprised of the silicon polymer polydimethylsiloxane (PDMS). The mantle lithosphere and lower crust were mixtures of PDMS and modelling clay. These materials are non- Newtonian viscous, and their rheology is defined by the power law:
where σ is stress, \(\dot{\epsilon }\) is strain rate, η is consistency and n a stress exponent40,60. The effective dynamic viscosity (ηeff) and n values for each viscous material were measured over a range of values using a strain-controlled rheometer (Discovery HR-3 Hybrid). For these materials, we recorded the effective dynamic viscosity at a strain rate of 10−5 s−1, which approximated the rate of deformation of the experiments. The n value for all viscous materials was 1.01.
In nature, both thermal and metamorphic processes may change the composition of the mantle lithosphere by changing its density or viscosity. This can play a significant role in mantle dynamic processes; however, thermal effects are not easily incorporated into analogue models. Viscosity decreases with increasing temperature, therefore as an approximation to the Earth like rheological structure, we used discrete layers of differing materials as an analogue to temperature
Scaling
Scaling relationships were derived for time, length, gravity, density, and dynamic viscosity. The length scale (L) was defined based on a model mantle lithosphere thickness lm = 20 mm. A teleseismic study by Heit et al. (2014) suggests a thin lithosphere beneath the Southern Puna Plateau with the lithosphere asthenosphere boundary (LAB) at 70 km – 90 km depth61 (Fig. 1). The upper crust in these models represented the purely brittle part of the upper crust in nature, where geophysical studies have determined an elastic thickness of <10 km for the Central Andes62. In two of three experiments we assumed that the viscous lower crust was part of the mantle lithosphere. Seismic studies interpret that there is no evidence for the presence of mafic (high speed) lower crust beneath the Central Andes, suggesting that this layer has been removed63. This interpretation is in accord with our model design in which the dense (possibly eclogitized) lower crustal material is part of the underlying mantle lithosphere that will be removed.
Based on a mantle lithosphere thickness of ln = 80 km in nature, the length scale ratio is L = lm/ln = 2.50 × 10−7. The density of the PDMS used for the mantle in the experiments was ρm = 1010 kg m−3. Assuming an average density of the upper mantle in nature of ρn = 3060 kg m−3, this yields a density scaling factor of P = ρm/ρp = 0.33. The experiments are gravity driven and the scaling ratio for gravity is G = gm/gn = 1. The measured effective dynamic viscosity of the PDMS (ηm) was 1.9 × 104 Pa s, and scaling with an approximate viscosity of the asthenosphere (ηp) of 1021 Pa s gives a viscosity scale ratio M = ηm/ηn = 1.50 × 10−17. Using M, P, L and G; the time scaling factor (T) can be defined as T = M/PLG = tm/tn = 1.82 × 10−10. Using this scaling factor, 1.59 h in the model is 1 Myr in nature. Table 1 lists the material properties for materials used in each experiment and the dimensionless scaling factors. The upper crust material in EXP-2 had a higher density (ρ) and a lower angle of internal friction (φ) than EXP-1 and EXP-3. This change was made to a few experiments from the full model set of ten experiments due to a lack of crustal deformation in some models. Further experiments revealed that the primary controlling parameter of deformation of the crust in the model was not the density of the crust, but the method used to initiate a drip (Method 1 vs. Method 2).
Data availability
The data that support the findings of this study are available at the University of Toronto Dataverse repository and can be accessed at this address: https://doi.org/10.5683/SP3/Q6T9BE.
References
Platt, J. P. & Vissers, R. L. M. Extensional collapse of thickened continental lithosphere: a working hypothesis for the Alboran Sea and Gibraltar arc. Geology 17, 540–543 (1989).
Saleeby, J. & Foster, Z. Topographic response to mantle lithosphere removal in the southern Sierra Nevada region, California. Geology 32, 245–248 (2004).
Decelles, P. G., Ducea, M. N., Kapp, P. & Zandt, G. Cyclicity in Cordilleran orogenic systems. Nat. Geosci. 469, 1–7 (2009).
Garzione, C. N. et al. Tectonic evolution of the Central Andean Plateau and implications for the growth of plateaus. Annu. Rev. Earth Planet. Sci. 45, 529–559 (2017).
Schmandt, B. & Humphreys, E. Seismic heterogeneity and small ‐ scale convection in the southern California upper mantle. Geochemistry, Geophys. Geosystems 11, 1–19 (2010).
Levander, A. et al. Continuing Colorado plateau uplift by delamination-style convective lithospheric downwelling. Nature 472, 461–466 (2011).
West, J. D., Fouch, M. J., Roth, J. B. & Elkins-Tanton, L. T. Vertical mantle flow associated with a lithospheric drip beneath the Great Basin. Nat. Geosci. 2, 439–444 (2009).
Jones, C. H., Kanamori, H. & Roecker, S. W. Missing roots and mantle ‘drips’: Regional Pn.and teleseismic arrival times in the southern Sierra Nevada and vicinity, California. J. Geophys. Res. 99, 4567–4601 (1994).
Jones, C. H. et al. P-wave tomography of potential convective downwellings and their source regions, Sierra Nevada, California. Geosphere 10, 505–533 (2014).
Jiang, C., Schmandt, B. & Clayton, R. W. An anisotropic contrast in the lithosphere across the Central San Andreas fault. Geophys. Res. Lett. 45, 3967–3975 (2018).
Ward, K. M., Zandt, G., Beck, S. L., Wagner, L. S. & Tavera, H. Lithospheric structure beneath the northen Centreal Andean Plateau from the joint inversion of ambient noise and earthquake-generated surface waves. J. Geophys. Res. Solid Earth 121, 8217–8238 (2016).
Chen, M. et al. Lithospheric foundering and underthrusting imaged beneath Tibet. Nat. Commun. 8, 1–10 (2017).
Ren, Y. et al. Upper mantle structures beneath the Carpathian-Pannonian region: Implications for the geodynamics of continental collision. Earth Planet. Sci. Lett. 349, 139–152 (2012).
Fichtner, A. et al. Multi-scale full waveform inversion. Geophys. J. Int 194, 534–556 (2013).
Ancuta, L. D., Zeitler, P. K., Idleman, B. D. & Jordan, B. T. Whole-rock 40Ar/39Ar geochronology, geochemistry, and stratigraphy of intraplate Cenozoic volcanic rocks, central Mongolia. GSA Bull. 130, 1397–1408 (2018).
Elkins-tanton, L. T. & Hager, B. H. Melt intrusion as a trigger for lithospheric foundering and the eruption of the Siberian flood basalt. Geophys. Res. Lett. 27, 3937–3940 (2000).
Gao, S., Rudnick, R. L., Carlson, R. W., Mcdonough, W. F. & Liu, Y. S. Re-Os evidence for replacement of the original mantle lithosphere beneath the North China craton. Earth Planet. Sci. Lett. 198, 307–322 (2002).
Windley, B. F., Maruyama, S. & Xiao, W. J. Delamination/thinning of sub-continental lithospheric mantle under Eastern China: The role water and multiple subduction. Am. J. Sci. 310, 1250–1293 (2010).
Wu, F., Yang, J., Xu, Y., Wilde, S. A. & Walker, R. J. Destruction of the North China Craton in the mesozoic. Annu. Rev. Earth Planet. Sci. 47, 173–195 (2019).
Dave, R. & Li, A. Destruction of the Wyoming craton: Seismic evidence and geodynamic processes. Geology 44, 883–886 (2016).
Göğüş, O. & Pysklywec, R. N. Near-surface diagnostics of dripping or delaminating lithosphere. J Geophys Res 113, B11404 (2008).
Wang, H., Currie, C.A., & DeCelles, P.G., Hinterland basin formation and gravitational instabilities in the central Andes: Constraints from gravity dataand geodynamic models. In Geodynamics of a cordilleran orogenic system: the central andesof argentina and northern chile: geological society of america memoir (eds. DeCelles, P. G., Ducea, M. N., Carrapa, B., & Kapp, P. A.) 212, p. 387–406 (2015).
Göğüş, O. H. et al. Drip tectonics and the enigmatic uplift of the Central Anatolian Plateau. Nat Commun. 8, 1538 (2017).
Bodur, Ö. et al. Mantle Lithosphere Rheology, Vertical Tectonics, and the Exhumation of (U)HP Rocks. J. Geophys. Res.: Solid Earth 123, 1824–1839 (2018).
Jordan, T. E., Isacks, B. L., Ramos, V. A. & Allmendinger, R. W. Mountain building in the Central Andes. Episodes 3, 20–26 (1983).
Isacks, B. L. Uplift of the central Andean Plateau and bending of the Bolivian Orocline. J. Geophys. Res. 93, 3211–3231 (1988).
Oncken, O. et al. The Andes - active subduction orogeny. Frontiers in Earth Sciences. (Springer, 2006).
Martinod, J., Gérault, M., Husson, L. & Regard, V. Widening of the Andes: an interplay between subduction dynamics and crustal wedge tectonics. Earth-Science Rev. 204, 103170 (2020).
Garzione, C. N., Molnar, P., Libarkin, J. C. & MacFadden, B. J. Rapid late Miocene rise of the Bolivian Altiplano: evidence for removal of mantle lithosphere. Earth Planet. Sci. Lett. 241, 543–556 (2006).
Saylor, J. E. & Horton, B. K. Nonuniform surface uplift of the Andean plateau revealed by deuterium isotopes in Miocene volcanic glass from southern Peru. Earth Planet. Sci. Lett. 387, 120–131 (2014).
Sundell, K. E., Saylor, J. E., Lapen, T. J. & Horton, B. K. Implications of variable late Cenozoic surface uplift across the Peruvian central Andes. Sci. Rep. 9, 1–12 (2019).
Canavan, R. R. et al. Early cenozoic uplift of the Puna plateau, central andes, based on stable isotope paleoaltimetry of hydrated volcanic glass. Geology 42, 447–450 (2014).
DeCelles, P. G. et al. The Miocene Arizaro Basin, central Andean hinterland: response to partial lithosphere removal? Geol. Soc. Am. Mem 212, 359–386 (2015).
Kay, R. W. & Kay, S. M. Delamination and delamination magmatism. Tectonophysics 219, 177–189 (1993).
Allmendinger, R. W., Jordan, T. E., Kay, S. M. & Isacks, B. L. The evolution of the Altiplano-Puna plateau of the Central Andes. Annu. Rev. Earth Planet. Sci. 25, 139–174 (1997).
Ducea, M. N., Seclaman, A. C., Murray, K. E., Jianu, D. & Schoenbohm, L. M. Mantle-drip magmatism beneath the Altiplano-Puna plateau, central Andes. Geology 41, 915–918 (2013).
Murray, K. E., Ducea, M. N. & Schoenbohm, L. Foundering-driven lithospheric melting: the source of central Andean mafic lavas on the Puna Plateau (22°S–27°S). in Geodynamics of a Cordilleran Orogenic System: The Central Andes of Argentina and Northern Chile (eds. DeCelles, P. G., Ducea, M. N., Carrapa, B. & Kapp, P. A.) 212, (Geological Society of America, 2015).
Schoenbohm, L. M. & Carrapa, B. Miocene-Pliocene shortening, extension, and mafic magmatism support small-scale lithospheric foundering in the Central Andes, NW Argentina. Geol. Soc. Am. Mem. 212, 167–180 (2014).
Metcalf, K. & Kapp, P. Along-strike variations in crustal seismicity and modern lithospheric structure of the central Andean forearc. Mem. Geol. Soc. Am 212, 61–78 (2015).
Pysklywec, R. N. & Cruden, A. R. Coupled crust-mantle dynamics and intraplate tectonics: two-dimensional numerical and three-dimensional analogue modeling. Geochem. Geophys. Geosystems 5, Q10003 (2004).
Pysklywec, R. N., Gogus, O., Percival, J., Cruden, A. R. & Beaumont, C. Insights from geodynamical modeling on possible fates of continental mantle lithosphere: collision, removal, and overturn. Can. J. Earth Sci. 47, 541–563 (2010).
Hoogenboom, T. & Houseman, G. A. Rayleigh – Taylor instability as a mechanism for corona formation on Venus. Icarus 180, 292–307 (2006).
Strak, V. & Schellart, W. P. Thermo-mechanical numerical modeling of the South American subduction zone: a multi-parametric investigation. J. Geophys. Res. Solid Earth 126, e2020JB021527 (2021).
Gotze, H. J. & Krause, S. The Central Andean gravity high, a relic of an old subduction complex? J. South Am. Earth Sci. 14, 799–811 (2002).
Yuan, X., Sobolev, S. V. & Kind, R. Moho topography in the central Andes and its geodynamic implications. Earth Planet. Sci. Lett. 199, 389–402 (2002).
Göğüş, O. H. et al. Rapid surface uplift and crustal flow in the Central Andes (southern Peru) controlled by lithospheric drip dynamics. Sci Rep 12, 5500 (2022).
Leech, M. L. Arrested orogenic development: eclogitization, delamination, and tectonic collapse. Earth Planet. Sci. Lett. 185, 149–159 (2001).
Duarte, J. C., Schellart, W. P. & Cruden, A. R. Rheology of petrolatum-paraffin oil mixtures: applications to analogue modelling of geological processes. J. Struct. Geol. 63, 1–11 (2014).
Funiciello, F. et al. Mapping mantle flow during retreating subduction: laboratory models analyzed by feature tracking. J. Geophys. Res. Solid Earth 111, B03402 (2006).
Boutelier, D. & Cruden, A. Slab rollback rate and trench curvature controlled by arc deformation. Geology 41, 911–914 (2013).
Strak, V. & Schellart, W. P. Evolution of 3-D subduction-induced mantle flow around lateral slab edges in analogue models of free subduction analysed by stereoscopic particle image velocimetry technique. Earth Planet. Sci. Lett. 403, 368–379 (2014).
Adam, J. et al. Shear localisation and strain distribution during tectonic faulting - New insights from granular-flow experiments and high-resolution optical image correlation techniques. J. Struct. Geol. 27, 299–301 (2005).
White, D., Take, A. & Bolton, M. Measuring soil deformation in geotechnical models using digital images and PIV analysis. In 10th International Conference on Computer Methods and Advances in Geomechanics 997–1002 (2001).
Wolf, H., König, D. & Triantafyllidis, T. Experimental investigation of shear band patterns in granular material. J. Struct. Geol. 25, 1229–1240 (2003).
Davy, P. & Cobbold, P. R. Experiments on shortening of a 4-layer model of the continental lithosphere. Tectonophysics 188, 1–25 (1991).
Rossi, D. & Storti, F. New artificial granular materials for analogue laboratory experiments: aluminium and siliceous microspheres. J. Struct. Geol. 25, 1893–1899 (2003).
Keaton, J. R. Noncohesive Soils BT. Encyclopedia of Engineering Geology (Springer International Publishing, 2018). https://doi.org/10.1007/978-3-319-73568-9_212
Miura, K., Maeda, K. & Toki, S. Method of measurement for the angle of repose of sands. Soils Found. Japanese Geotech. Soc 37, 89–96 (1998).
Nelson, B. E. Measurement of the repose angle of a tablet granulation. J. Am. Pharm. Assoc. 44, 435–437 (1955).
Molnar, N. E., Cruden, A. R. & Betts, P. G. Interactions between propagating rotational rifts and linear rheological heterogeneities: Insights from three-dimensional laboratory experiments. Tectonics 36, 420–443 (2017).
Heit, B. et al. Structure of the crust and the lithosphere beneath the southern Puna plateau from teleseismic receiver functions. Earth Planet. Sci. Lett. 385, 1–11 (2014).
García, H. P. A. et al. Effective elastic thickness in the Central Andes. Correlation to orogenic deformation styles and lower crust high-gravity anomaly. J. South Am. Earth Sci 87, 232–246 (2018).
Beck, S. L. & Zandt, G. The nature of orogenic crust in the central Andes. J. Geophys. Res. Solid Earth 107, 1–16 (2002).
Scire, A., Biryol, C. B., Zandt, G. & Beck, S. L. Imaging the Nazca slab and surrounding mantle to 700 km depth beneath the central Andes (18°S to 28°S). Geol. Soc. Am. Mem 212, 23–41 (2015).
Acknowledgements
J.A. and R.N.P. were supported by an NSERC Discovery Grant (RGPIN-2019-06803)-RNP. O.H.G. acknowledges ANATEC (ILP/International Lithosphere Programme) and the 2232 International Fellowship for Outstanding Researchers Programme of the Scientific and Technological Research Council of Turkey (118C329). The collaborative research was enabled by a TUBITAK Fellowship for Visiting Scientists 2221 Programme to R.N.P. This research was enabled in part by support provided by Compute Ontario (computeontario.ca) and the Digital Research Alliance of Canada (alliancecan.ca).
Author information
Authors and Affiliations
Contributions
J.A., O.H.G. and R.N.P. conceived the ideas and interpretations. J.A. and T.S. conducted analogue experiments and data analysis at the University of Toronto with data analysis contributed by E.Ş.U. The depiction of seismic subsurface data was generated by E.Ş.U. The manuscript was written and prepared by J.A., O.H.G. and R.N.P., with comments and input included from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Vincent Strak, Alexander Cruden and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: João Duarte, Joe Aslin. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Andersen, J., Göğüş, O.H., Pysklywec, R.N. et al. Symptomatic lithospheric drips triggering fast topographic rise and crustal deformation in the Central Andes. Commun Earth Environ 3, 150 (2022). https://doi.org/10.1038/s43247-022-00470-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00470-1
This article is cited by
-
Seismically imaged lithospheric delamination and its controls on the Mesozoic Magmatic Province in South China
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.