Abstract
Accurate representation of the viscous flow of ice is fundamental to understanding glacier dynamics and projecting sea-level rise. Ice viscosity is often described by a simple but largely untested and uncalibrated constitutive relation, Glen’s Flow Law, wherein the rate of deformation is proportional to stress raised to the power n. The value n = 3 is commonly prescribed in ice-flow models, though observations and experiments support a range of values across stresses and temperatures found on Earth. Here, we leverage recent remotely-sensed observations of Antarctic ice shelves to show that Glen’s Flow Law approximates the viscous flow of ice with n = 4.1 ± 0.4 in fast-flowing areas. The viscosity and flow rate of ice are therefore more sensitive to changes in stress than most ice-flow models allow. By calibrating the governing equation of ice deformation, our result is a pathway towards improving projections of future glacier change.
Similar content being viewed by others
Introduction
Mass loss from ice sheets presents both the greatest potential contribution to future sea-level rise and the largest source of uncertainty in such estimates1,2. In Antarctica, mass loss occurs principally through fast-flowing glaciers that flow into floating ice shelves, which provide resistive buttressing stresses that impede the seaward flow of ice and stabilize marine grounding zones3,4,5. The rate at which glaciers flow is controlled by the shear-thinning viscous deformation of ice6. The most commonly adopted constitutive relation, known as Glen’s Flow Law, is often employed to quantify the viscous deformation of glacier ice by relating the rate of deformation, hereafter called strain rate, to the deviatoric stress7. Glen’s Flow Law is most simply expressed as
where \({\dot{\epsilon }}_{e}\) is the effective strain rate, τe the effective deviatoric stress, n the stress exponent, and A the rate factor or flow-law coefficient. Variation in parameter A can be used to represent the effects of temperature, grain size, grain orientation (fabric), impurities, and interstitial water content8.
Glen’s Flow Law is routinely implemented in large-scale ice-flow models with the prescribed value n = 3 assumed to be constant in space and time9,10. Glen’s laboratory experiments pinpointed the power-law rheology and extrapolated his findings to flows of natural ice7,8,11. Shortly thereafter, Glen’s findings and supporting evidence were widely adopted in the glaciological literature, with the field converging on the canonical value of n = 312,13,14. However, multiple mechanisms influence the viscous deformation of ice, each with a suggested value of n: dislocation creeps (n = 4), grain-boundary sliding (n ≈ 2, with slight variance dictated by the direction of motion of dislocations), and diffusion creep (n = 1) all accommodate creep at the individual grain level and, in aggregate, describe the flow of glacier ice15. These mechanisms are not treated independently in Glen’s Flow Law (Eq. (1)). Rather, it serves as a lumped parameterization representing the combined effect of all mechanisms. Generalized forms of the flow law have been proposed to account for multiple creep mechanisms, fabric, and grain size, but these have not been widely tested, calibrated, nor implemented10,15,16.
The simplicity of Glen’s Flow Law has proven useful and, subject to suitable calibration under different conditions, has the potential to provide a reasonably accurate general description of the flow of glacier ice7,8,14,17. Glen’s Flow Law (Eq. (1)) with n = 3 shows consistency with sparse observations of natural ice flows such as borehole deformation measurements and ice-flow velocities, as well as laboratory experiments on polycrystalline ice aggregates under conditions relevant for ice sheets7,15,18,19,20,21,22,23,24,25. However, the broad range of conditions over which the rheological behavior of ice has been examined reveals the way in which variations in stress can influence the stress exponent and, in turn, the mechanisms of creep10,26,27,28. Nearly 70 years after its introduction, the need remains to test and rigorously calibrate the parameters n and A in the natural environment.
We infer the stress exponent of Glen’s Flow Law across wide areas of Antarctic ice shelves, the floating extensions of the ice sheet. Using satellite observations, we are able to address the long-standing problem of benchmarking a flow law that can be used in ice-flow models. The abundance and extent of the data allow us to investigate the creep of glacial ice on a continental scale, assembling inferences to reveal spatial coherence and patterns with statistical constraints. To do so, we require independent estimates of strain rates and (deviatoric) stresses (Eq. 1). The schematic in Fig. 1 graphically illustrates the methodology, showing how we begin with independent observations of surface velocities and ice thicknesses, apply these to evaluate strain-rates \({\dot{\epsilon }}_{e}\) and stresses τe, and then conduct a regression analysis to infer the parameters in Glen’s Flow Law. This method is comparable to previously published work21,22,26,29, but applied to Antarctic ice shelves using continental-scale remote sensing observations. Our results reveal that a value of n = 4.1 ± 0.4 is the most representative flow-law exponent in fast-flowing, extensional regions, where the magnitude of deviatoric stresses are comparable to those expected in other dynamic regions of the ice sheet. Making use of continent-scale remote sensing observations on Antarctic ice shelves, we demonstrate how the viability of power-law rheology can be constrained directly using observations.
Visual summary of our methodology. The schematic shows how we begin with publicly available satellite observations of surface velocity vector ui and ice thickness H. Using the strain-rate tensor, \({\dot{\epsilon }}_{ij}\), we calculate the effective strain-rate \({\dot{\epsilon }}_{e}=\sqrt{{\dot{\epsilon }}_{ij}{\dot{\epsilon }}_{ij}/2}\) and along-flow strain-rate \({\dot{\epsilon }}_{xx}\). In our areas of interest, where \({\dot{\epsilon }}_{xx}\approx {\dot{\epsilon }}_{e}\), we estimate the effective deviatoric stress \({\tau }_{e}=\sqrt{{\tau }_{ij}{\tau }_{ij}/2}\approx {\tau }_{xx}\) using the force balance detailed in the Methods, which gives τxx ∝ H (Eq. (2)). The values of \({\dot{\epsilon }}_{e}\) and τe are then correlated through a flow law, indicated by the horizontal dashed arrow labeled with Glen’s Flow Law (Eq. (1)).
We focus on ice shelves because the underlying ocean provides negligible shear resistance to ice flow, allowing for two important simplifications in our analysis. First, we can neglect drag at the base of the ice and thus consider a stress regime that is simpler for our purposes than would be expected for grounded ice, where basal drag presents a further unknown that must be constrained. Second, the lack of drag at the base means that strain rates are approximately constant with depth. For this reason, the horizontal strain rates we calculate from observations of the surface velocity fields approximate the strain rates at all depths.
Ice shelves cover areas that are large compared with the sub-kilometer resolution of observations, providing ample opportunities to comprehensively observe broad regions of flow undergoing relatively simple one-dimensional deformation. As a result, we can focus on regions that are close to being in pure extension, where the ice spreads under its own weight in one direction and the governing equations of flow reduce to a simple two-term balance, detailed further in this report. This basic premise has been employed for decades to study the rheology of glacier ice22,24,30 but has not been systematically applied on continental scales before now.
We use measurements of ice thickness provided through the BedMachine project31, and surface velocity data from the NASA Inter-mission Time Series of Land Ice Velocity and Elevation (ITS_LIVE) project32. The surface velocity data, which encompass most of the Antarctic Ice Sheet at a grid spacing of 120 m × 120 m, are derived from Landsat 4, 5, 7, and 8 imagery using the auto-RIFT feature tracking processing chain, providing reliable constraints on the two horizontal components of ice velocity32. We use these to calculate the horizontal strain-rates \({\dot{\epsilon }}_{ij}\) (for i, j = x, y the two horizontal coordinates) across all Antarctic ice shelves, as defined by \(2{\dot{\epsilon }}_{ij}=\big(\partial {u}_{i}/\partial {x}_{j}+\partial {u}_{j}/\partial {x}_{i}\big)\), where ui represents the horizontal components of the ice velocity vector and xi the horizontal coordinates. To calculate the components of the velocity gradient, we apply a two-dimensional Savitzky-Golay filter with a polynomial order of one and a square window of 3720 m (31 pixels)33. More detail on the strain-rate calculations is found in the Supplementary Methods.
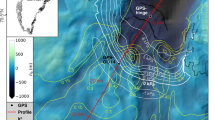
After deriving strain rates from the surface velocity fields, we determine regions flowing in approximately pure extension, with a view to simplifying the force balance governing the local ice flow. The two-dimensional strain-rate tensor \({\dot{\epsilon }}_{ij}\) has three unique components (the off-diagonal terms are equal by definition) and a scalar invariant representing the effective horizontal strain-rate \(\dot{\epsilon }=\sqrt{{\dot{\epsilon }}_{ij}{\dot{\epsilon }}_{ij}/2}\), where the summation is implied for repeated indices. Note that the effective strain-rate \({\dot{\epsilon }}_{e}\) in Eq. 1 follows the same definition as for \(\dot{\epsilon }\) but is applied to the three-dimensional strain-rate tensor. We focus on areas of the ice shelves that are solely confined by seaward pressure in the along-flow, or x, direction, and analyze areas in which the along-flow component of the strain-rate tensor \({\dot{\epsilon }}_{xx}\) is much larger than both lateral normal and shear strain rates (\({\dot{\epsilon }}_{xx}\gg {\dot{\epsilon }}_{yy},{\dot{\epsilon }}_{xy}\)). We combine these into a single criterion \({\dot{\epsilon }}_{xx}\approx \sqrt{2}\dot{\epsilon }\), corresponding to areas of the ice shelves where longitudinal extension is dominant. The more specific criterion \({\dot{\epsilon }}_{xx} \, > \,\dot{\epsilon }\) is used to define large, spatially coherent regions where the extensional component of deformation dominates the flow (Fig. 2 and Supplementary Figs. S1 and S2). Approximately 20% of the total surface area of all Antarctic ice shelves satisfies this criterion. In these areas it follows from the incompressibility of ice and the absence of drag at the base of ice shelves that \({\dot{\epsilon }}_{xx}\approx {\dot{\epsilon }}_{e}\), the three-dimensional effective strain rate in Eq. (1).
Estimates of effective deviatoric stress τe plotted against effective strain-rate \({\dot{\epsilon }}_{e}\) shown as log–log plots in panels a–h, corresponding to geographic regions on Filchner-Ronne Ice Shelf (FRIS) and Ross Ice Shelf (RIS). The results of each regression substantiate a power-law rheology in the form of Glen’s Flow Law, where the value of n is the slope of the plotted solid line and \({\log }_{10}(A)\) is given by the value of the y − intercept. The color map corresponds to the value of the ratio \({\dot{\epsilon }}_{xx}/\dot{\epsilon }\) where a maximum value of \(\sqrt{2}\) signifies a purely extensional flow regime. The range of stresses used in this plot span 65–165 kPa, and the range of strain-rates spans 0.001–0.004 yr−1. The dashed line corresponds to a slope n = 3 with an unrealistic value of A in order to visually match the starting point of the line segment for n = 4. For a comparison with existing flow laws (n = 3) see Supplementary Fig. S3.
To estimate the effective deviatoric stress from remote sensing observations, we utilize a well-established reduced form of the Stokes equations that govern the viscous flow of glacier ice. Over the ice shelves, where negligible shear stress applies at both the upper (atmosphere) and lower (ocean) surfaces of the ice, we can adopt the depth-integrated form of the Stokes equations commonly referred to as the Shallow-Shelf Approximation (SSA), which contains only body forces and the horizontal gradients of the stress tensor elements. Based on the conditions described above, we can further reduce the SSA equations to a simple expression relating the (depth-averaged) along-flow deviatoric stress τxx to local ice thickness H as:
where \(g^{\prime} =g(1-\rho /{\rho }_{w})\) is the reduced gravity, representing the balance between the resistive longitudinal stress and the driving buoyancy force (the full derivation is provided in the Methods). Here, we take ρ = 910 kg/m3 as the mass density of glacier ice and ρw = 1026 kg/m3 as the mass density of seawater. Where the criteria for predominantly extensional flow is met (\({\dot{\epsilon }}_{xx}\approx {\dot{\epsilon }}_{e}\)), we expect τxx ≈ τe. Thus, the criteria we apply to the strain-rate fields to identify areas in primarily extensional flow allows us to calculate effective stress τe (Eq. (1)) from observations of ice thickness and independently of the surface velocity fields used to calculate \({\dot{\epsilon }}_{e}\). Before fitting a model to the data, we ensure that the gradients of horizontal shear stress transverse to flow are small compared to the gradients of longitudinal stress from the position of the ice parcel all the way to the ice shelf calving front. This supports the suitability of the derivation for effective stress over the fast-flowing, extensional regions of Antarctic ice shelves of interest.
Critically, this study neither takes into account firn or marine ice, which are characteristic of all ice shelves, nor do we need to explicitly account for viscous anisotropy (fabric). Complexities caused by firn and marine ice are partially subsumed by the uniform density profile but remain a source of uncertainty in our analysis. Given that the mass densities of firn and ice are within a factor of two and firn typically comprises a thin upper layer of ice shelves, we expect the uncertainties due to firn and marine ice are small enough to not meaningfully impact our results. Our focus on a single flow regime and parcels of ice defined along and parallel to flow lines allow us to avoid the complexities that arise from viscous anisotropy in ice, which would require a non-scalar form of A to represent deformation in multiple directions, and spatial variations in characteristics like ice temperature and liquid water content.
Results
Linear regressions fitted to the values for \(\log ({\dot{\epsilon }}_{e})\) and \(\log ({\tau }_{e})\) constrain n through the slope and A in the y − intercept, divulging values of the flow-law parameters across viable regions of Antarctic ice shelves. To determine 95% confidence intervals on the regression of strain rate on stress, we implement a non-parametric bootstrap, which allows us to estimate constraints on the determined value of n without making assumptions on the underlying structure of the distribution34. Our analysis encompasses regions of both large ice shelves, such as those shown in Fig. 2, and smaller ice shelves that line the continent. We focus first on highlighted areas on the Ross and Filchner-Ronne Ice Shelves in Fig. 2, which we extracted from areas along flow lines, with probable consistency between values of temperature, grain size, and fabric, and therefore A and n.
The log–log plots between strain rate and deviatoric stress shown in Fig. 2 exhibit linear trends that are consistent with a power-law relation. These results provide strong evidence that, for a suitable choice of n, Glen’s Flow Law is a viable approximation of the viscous flow of Antarctic ice shelves and, as discussed later, likely other dynamic regions of Antarctica. Critically, we find n ≈ 4 in the fast-flowing, extensional regions of Antarctic ice shelves. This result is consistent with other evidence for a higher value of the flow-law exponent7,24,26,30,35,36, and demonstrates that this higher value is applicable to natural ice flow at the continental scale. Additional comparison with the value n = 3 and other typical values of the existing flow law can be found in Supplementary Fig. S3; it is worth noting that n = 3 provides a poor fit to the data used in this study as shown in Fig. 2. Additionally, the residuals from the linear regressions in subplots a-h of Fig. 2 are shown in Supplementary Fig. S4 and demonstrate the suitability of the linear fit in these areas.
The results of our full analysis covering all viable regions of Antarctic ice shelves are shown in Fig. 3, which includes regions of both large and small ice shelves (mapped in Supplementary Figs. S1 and S2). The normalized kernel density estimates of the bootstrapped values of the flow-law exponent (Fig. 3) indicate that n = 4.1 ± 0.4 in extensional regions of Antarctic ice shelves. Figure 3 shows the confidence with which our estimate stands across geographic areas of different sizes and represents a range of stresses. Large areas extracted for analysis, > 1000 km2, have less spread in the error estimation and are centered closer to n = 4.1, whereas smaller areas exhibit a greater spread in the distribution. This is likely because the broader ranges of stresses and the greater number of observations in the larger ice shelves provide more accurate inferred trends across the data. Notably, geographic regions from West Antarctica have slightly higher values of n than regions sampled from East Antarctica. This observation could be attributed to higher sub-ice-shelf melt rates in West Antarctic ice shelves, where the bulk of ice is created on the ice shelf by compaction of snow as opposed to being inherited from the grounded glacier37. Additionally, there is a possible grain size dependence wherein warmer conditions would contribute to larger grains38,39. In such regions, larger grains, strain rate, and values of the stress exponent validate a hypothesis that ice deformation is facilitated primarily by dislocation creep15,29. Our results highlight further spatial variability in the precise values of the flow-law exponent and rate factor across different ice shelves, and even different regions within single ice shelves (see Fig. 3). We reserve for future work detailed analysis and modeling of these variations.
Normalized kernel density estimation of the value of the stress exponent n obtained over viable regions of Antarctic ice shelves from bootstrap error estimation. The probability density shows that the value of n is concentrated at 4.1 ± 0.4. The estimates here represent stress estimates of 50–180 kPa and effective strain-rate estimates of 0.001–0.006 yr−1 (Supplement Fig. S6). Larger areas sampled from Ross Ice Shelf and Filchner-Ronne Ice Shelves show a greater range of stresses (and strain rates) and smaller spread of inferred n values in comparison to smaller geographic areas which have a narrower range of stresses and produce a greater spread in the possible values of n.
We find values of the flow-law rate factor, A, spanning 10−35–10−27 Pa−n s−1 for the range of inferred n values (see Supplement Fig. S5). Inferred values of A depend on the inferred values of n. Here, we do not attempt to provide newly calibrated values for A because proper constraints on the physical properties of the ice, like temperature and grain size, are not currently available in these areas and require work that is beyond the scope of this study. Rather, we note that the smaller values of A found here to validate our method for deriving Glen’s Flow Law and we recommend that future efforts using a value n ≈ 4 utilize standard tabulated sources for A40 and scale these values accordingly for the new value of n. A comparison of our results to the more commonly used n = 3 can be seen in Supplement Fig. S3, highlighting the incompatible values of A in these results, and the generally poor fit of n = 3 to the data.
Conclusion
The result that n ≈ 4 challenges the long-held practice of assuming the flow-law exponent is n = 3 everywhere, and at all times, in large-scale ice-sheet flow models. While our observations focus on specific regions in extensional flow regimes on ice shelves that experience stresses of order 100 kPa (Supplement Fig. S6), complementary laboratory work showing that n = 4 is suitable at higher stresses15 supports extending our conclusion that n ≈ 4 to other dynamic regions in Antarctica. Additionally, our conclusion complements a growing body of work advocating for the use of n > 3 in other areas of the cryosphere19,26. Taken together, this work calls for a broader community effort to quantify the uncertainties in the flow-law parameters and the consequences of these uncertainties on models of glacier dynamics. A higher value of n increases the sensitivity of viscosity to changes in stress but the impact of n = 4 on large-scale ice-flow models used for projections of sea-level rise and ice-sheet evolution remains unclear as few sensitivity analyses have been conducted10 and n is not a parameter explored in current ensemble-model analyses1,2. The value n = 4 has the potential to increase the sensitivity of ice-sheet mass loss to ongoing climate change considerably relative to n = 3 due to the stronger dependence of flow rates to changes in resistive stresses.
By applying continental-scale satellite observations to standard models in glacier dynamics, we have validated Glen’s Flow Law, a constitutive relationship that helps form the foundation of modern glaciology, and calibrated the stress exponent in Antarctic ice shelves. This work serves as a pathway towards a standard calibration framework for the community using publicly available remote sensing data. Our conclusion that n ≈ 4 across much of Antarctica’s ice shelves is a step towards reassessing the governing equations of ice flow in the satellite age, and reveals an increased sensitivity of flow rates to applied stresses relative to the commonly used n = 3. As a consequence, future sea-level rise is likely more sensitive to climate forcings than predicted by present models using common assumptions of the flow law.
Methods
Solving for effective stress
Conservation of momentum (Stokes equations) describes all forces acting on the volume of glacier ice such that
where p is the pressure, ρgi is the driving gravitational force (with \({{{{{{{\boldsymbol{g}}}}}}}}=g{{{\hat{{{{{\boldsymbol{z}}}}}}}}}\)), and summation is implied for repeated indices. For a layer of ice floating on top of an ocean, we can derive depth-integrated equations to describe the balance of forces in such a system, given that the ice shelf is much larger in horizontal extent than in thickness41. At scales of order the ice thickness, bending (and bridging) stresses are negligible, allowing us to simplify the equilibrium equations42. As a result, we take the vertical normal stress to be equivalent to the overburden stress (weight of the ice per unit area). This can be expressed as
where H is the ice thickness, \(g^{\prime} =g({\rho }_{w}-\rho )/{\rho }_{w}\) is the reduced gravity, and the second equality arises from the fact that the deviatoric stress tensor is traceless. Eq. (4) is derived by integrating the vertical component of Eq. (3) and applying the condition of continuous normal stress at the top and bottom of the layer.
Then, neglecting basal drag (due to our focus on ice shelves) and depth integrating the x-component of Eq. (3), we can obtain
where all deviatoric stresses are now depth-averaged. A complete derivation can be found in ref. 43, which uses different notation but reveals the same outcome. A comparable derivation is found in ref. 30 with the notable distinction here being our omission of α = τyy/τxx because we only consider areas where α ≪ 1. In this way, we are able to look at large areas without potential complications arising from multiple stress components (e.g., viscous anisotropy).
We can simplify Eq. (5) in two steps. First, we assume that the lateral normal stresses (τyy) are negligibly small compared with the longitudinal normal stresses (τxx) due to our emphasis on areas with \({\dot{\epsilon }}_{xx}\gg {\dot{\epsilon }}_{yy}\)44. Then, we apply the constitutive relation in Supplementary Eq. 6 and recall that in our areas of interest, we require that \({\dot{\epsilon }}_{xx}\approx {\dot{\epsilon }}_{e}\). Thus, Eq. (5) becomes
where \(\phi =h{\dot{\epsilon }}_{xx}^{1/n}{A}^{-1/n}\) and \(\beta ={\dot{\epsilon }}_{xy}/{\dot{\epsilon }}_{xx}\). The derived strain-rate data indicate that in our areas of interest, the lateral (∂/∂y) and longitudinal (∂/∂x) gradients in \(h{\dot{\epsilon }}_{xx}\) have the same order of magnitude. Assuming A and n vary slowly in space in our areas of interest, then ∂ϕ/∂y is of order ∂ϕ/∂x, placing the emphasis on the term β. Our criteria that \({\dot{\epsilon }}_{xx}\approx {\dot{\epsilon }}_{e}\) requires that β ≪ 1 everywhere in our areas of interest, which are wide enough that ∂β/∂y is negligibly small. This means that within the error in currently available data, we can assume that the lateral shear term (second on the left-hand side of Eqs. (5) and (6)) is negligible.
Vastly reduced, what began as four components—extension, lateral shear, basal drag, and buoyancy—now only requires terms for extension and buoyancy to illustrate the force balance of an unconfined ice shelf44. Equation (5) is now
We can now rearrange the right-hand side of Eq. (7) to an equivalent form
Integrating this equation subject to the free stress condition at the front of the ice shelf and simplifying the resulting equation results in
which we use as the basis for our analysis of extensional deviatoric stress in floating ice shelves. This derivation shows how we can use the extensional deviatoric stress as the total effective stress in our regions of interest, allowing us to use a dataset of ice thickness to determine the stress in the system parameter.
Data availability
No new data were generated in this analysis; the strain-rate fields were generated using velocity data from NASA ITS_LIVE (https://its-live.jpl.nasa.gov/). The MEaSUREs ice thickness data are available at the NSIDC.
Code availability
The Python codes used to analyze the remote sensing datasets and prepare figures are available on Github (https://github.com/jdmillstein/n_equals_4).
References
DeConto, R. M. et al. The paris climate agreement and future sea-level rise from antarctica. Nature 593, 83–89 (2021).
Edwards, T. L. et al. Projected land ice contributions to twenty-first-century sea level rise. Nature 593, 74–82 (2021).
Gudmundsson, G., Krug, J., Durand, G., Favier, L. & Gagliardini, O. The stability of grounding lines on retrograde slopes. Cryosphere 6, 1497–1505 (2012).
Haseloff, M. & Sergienko, O. V. The effect of buttressing on grounding line dynamics. J. Glaciol. 64, 417–431 (2018).
Pegler, S. S. Marine ice sheet dynamics: the impacts of ice-shelf buttressing. J. Fluid Mech. 857, 605–647 (2018).
Nye, J. F. The flow law of ice from measurements in glacier tunnels, laboratory experiments and the jungfraufirn borehole experiment. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 219, 477–489 (1953).
Glen, J. W. The creep of polycrystalline ice. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 228, 519–538 (1955).
Glen, J. W. The flow law of ice: a discussion of the assumptions made in glacier theory, their experimental foundations and consequences. IASH Publ. 47, e183 (1958).
Larour, E., Seroussi, H., Morlighem, M. & Rignot, E. Continental scale, high order, high spatial resolution, ice sheet modeling using the ice sheet system model (issm). J. Geophys. Re. Earth Surface 117, https://doi.org/10.1029/2011JF002140 (2012).
Zeitz, M., Levermann, A. & Winkelmann, R. Sensitivity of ice loss to uncertainty in flow law parameters in an idealized one-dimensional geometry. Cryosphere 14, 3537–3550 (2020).
Glen, J. Experiments on the deformation of ice. J. Glaciol. 2, 111–114 (1952).
Nye, J. F. The distribution of stress and velocity in glaciers and ice-sheets. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 239, 113–133 (1957).
Haefeli, R. Contribution to the movement and the form of ice sheets in the arctic and antarctic. J. Glaciol. 3, 1133–1151 (1961).
Lliboutry, L. General theory of subglacial cavitation and sliding of temperate glaciers. J. Glaciol. 7, 21–58 (1968).
Goldsby, D. & Kohlstedt, D. L. Superplastic deformation of ice: Experimental observations. J. Geophys. Res. Solid Earth 106, 11017–11030 (2001).
Ma, Y. et al. Enhancement factors for grounded ice and ice shelves inferred from an anisotropic ice-flow model. J. Glaciol. 56, 805–812 (2010).
Steinemann, S. Results of preliminary experiments on the plasticity of ice crystals. J. Glaciol. 2, 404–416 (1954).
Alley, R. B. Flow-law hypotheses for ice-sheet modeling. J. Glaciol. 38, 245–256 (1992).
Cuffey, K. & Kavanaugh, J. How nonlinear is the creep deformation of polar ice? a new field assessment. Geology 39, 1027–1030 (2011).
Hooke, R. Flow law for polycrystalline ice in glaciers: comparison of theoretical predictions, laboratory data, and field measurements. Rev. Geophys. 19, 664–672 (1981).
Jezek, K. C., Alley, R. B. & Thomas, R. H. Rheology of glacier ice. Science 227, 1335–1337 (1985).
Thomas, R. H. The creep of ice shelves: interpretation of observed behaviour. J. Glaciol. 12, 55–70 (1973).
Treverrow, A., Budd, W. F., Jacka, T. H. & Warner, R. C. The tertiary creep of polycrystalline ice: experimental evidence for stress-dependent levels of strain-rate enhancement. J. Glaciol. 58, 301–314 (2012).
Weertman, J. Deformation of floating ice shelves. J. Glaciol. 3, 38–42 (1957).
Weertman, J. Creep deformation of ice. Ann. Rev. Earth Planet. Sci. 11, 215–240 (1983).
Bons, P. D. et al. Greenland ice sheet: higher nonlinearity of ice flow significantly reduces estimated basal motion. Geophys. Res. Lett. 45, 6542–6548 (2018).
Durham, W., Heard, H. & Kirby, S. H. Experimental deformation of polycrystalline h2o ice at high pressure and low temperature: preliminary results. J. Geophys. Res. Solid Earth 88, B377–B392 (1983).
Qi, C. & Goldsby, D. L. An experimental investigation of the effect of grain size on “dislocation creep” of ice. J. Geophys. Res. Solid Earth 126, e2021JB021824 (2021).
Budd, W. & Jacka, T. A review of ice rheology for ice sheet modelling. Cold Reg. Sci. Technol. 16, 107–144 (1989).
Thomas, R. H. The creep of ice shelves theory. J. Glaciol. 12, 45–53 (1973).
Morlighem, M. et al. Deep glacial troughs and stabilizing ridges unveiled beneath the margins of the antarctic ice sheet. Nat. Geosci. 13, 132–137 (2020).
Gardner, A. S. et al. Increased west antarctic and unchanged east antarctic ice discharge over the last 7 years. Cryosphere 12, 521–547 (2018).
Savitzky, A. & Golay, M. J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 36, 1627–1639 (1964).
Diaconis, P. & Efron, B. Computer-intensive methods in statistics. Sci. Am. 248, 116–131 (1983).
Goldsby, D. L. Superplastic flow of ice relevant to glacier and ice-sheet mechanics. Glacier science and environmental change. 308–314 (Harvard, 2006).
Gillet-Chaulet, F., Hindmarsh, R. C. A., Corr, H. F. J., King, E. C. & Jenkins, A. In-situ quantification of ice rheology and direct measurement of the Raymond Effect at Summit, Greenland using a phase-sensitive radar. Geophys. Res. Lett. 38, https://doi.org/10.1029/2011GL049843 (2011).
Pritchard, H. et al. Antarctic ice-sheet loss driven by basal melting of ice shelves. Nature 484, 502–505 (2012).
Baker, R. W. The influence of ice-crystal size on creep. J. Glaciol. 21, 485–500 (1978).
Ranganathan, M., Minchew, B. M., Meyer, C. R. & Pec, M. Recrystallization of ice enhances creep and the vulnerability to fracture of ice shelves. Earth Planet. Sci. Lett. 576, 117219 (2021).
Cuffey, K. M. & Paterson, W. S. B. The Physics of Glaciers (Academic Press, 2010).
Pegler, S. S. & Worster, M. G. Dynamics of a viscous layer flowing radially over an inviscid ocean. J. Fluid Mech. 696, 152–174 (2012).
Budd, W. Ice flow over bedrock perturbations. J. Glaciol. 9, 29–48 (1970).
MacAyeal, D. R. in Dynamics of the West Antarctic ice sheet, 141–160 (Springer, 1987).
Pegler, S. S. The dynamics of confined extensional flows. J. Fluid Mech. 804, 24–57 (2016).
Acknowledgements
We benefited from discussions with Jerome Neufeld, Colin Meyer, and Andrew Ashton. We appreciate insightful reviews from Jeremy Bassis and Paul Bons. J.D.M. was partially funded through an NSF Graduate Research Fellowship. J.D.M. and B.M.M. where partially funded through NSF-NERC award 1853918. B.M.M. received additional funding through NSF-NERC award 1739031.
Author information
Authors and Affiliations
Contributions
The authors worked together to conceive and design the project. J.D.M. undertook the analysis, generated the figures, and wrote the initial version of the manuscript. B.M.M. and S.S.P. helped revise the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Jeremy Bassis and Paul Bons for their contribution to the peer review of this work. Primary Handling Editors: Jan Lenaerts and Clare Davis. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Millstein, J.D., Minchew, B.M. & Pegler, S.S. Ice viscosity is more sensitive to stress than commonly assumed. Commun Earth Environ 3, 57 (2022). https://doi.org/10.1038/s43247-022-00385-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00385-x
This article is cited by
-
A framework for estimating the anthropogenic part of Antarctica’s sea level contribution in a synthetic setting
Communications Earth & Environment (2024)
-
Development and Benchmarking of the Shallow Shelf Approximation Ice Sheet Dynamics Module
Ocean Science Journal (2023)
-
Ice thickness distribution of Himalayan glaciers inferred from DInSAR-based glacier surface velocity
Environmental Monitoring and Assessment (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.