Abstract
Subduction zones have recurrently formed on Earth. Previous studies have, however, suggested that they are unlikely to start in the interior of a pristine ocean. Instead, they seem to be more likely to form from another pre-existing subduction zone. One widely cited conceptual model to start new subduction zones is polarity reversal, resulting from the shutdown of a pre-existent subduction zone due to the arrival of a buoyant block at the trench. However, the dynamic conditions by which this process occurs remain elusive. Here, we present 3D numerical models of subduction zone initiation by polarity reversal resulting from the arrival of an oceanic plateau at the trench. Our results show that this process is more likely to occur for old subducting plates and narrow plateaus, and that new subduction zones can form from previous ones in a self-replicating manner, without requiring any other external tectonic forcing.
Similar content being viewed by others
Introduction
Subduction zone initiation (SZI) constitutes one of the main unsolved problems in geodynamics. Multiple mechanisms have been previously proposed to explain SZI, differing on their assumed geometries, kinematics and driving forces1,2,3,4. These include the formation of subduction zones by mantle plumes5,6, or by the reactivation of lithospheric scale weaknesses, such as transform faults7,8, old subduction zone interfaces9 and passive margins10,11. One commonly proposed mechanism for SZI is subduction polarity reversal1,2,3. This assumes that the arrival of a buoyant terrane12,13,14 at the trench of an active intraoceanic subduction zone is capable of causing the local termination of the subduction system, and to force the overriding plate to subduct in the opposite direction. This type of SZI has been proposed to have occurred in several different natural instances15,16,17,18. For example, it has been suggested19,20 that polarity reversal SZI represents one of the modes by which subduction zones can be transferred from Pacific-type into Atlantic-type oceanic basins (a process generally referred to as subduction infection19 or invasion21). However, the dynamic factors that govern the switch in the subduction polarity are still poorly understood. A reversal of subduction polarity must arise from the balance between driving forces22 (e.g., slab pull force), resisting forces22 (e.g., positive buoyancy of plate segments, and viscous resistance of plates and mantle), and facilitating/weakening mechanisms6,23,24,25 (e.g., grain size reduction, presence of fluids or shear heating).
Here, we investigate the dynamics of subduction initiation by polarity reversal using 3D self-consistent visco-elasto-plastic geodynamic models that include a free surface (see Methods). In these models, an oceanic plateau is incorporated into the subducting plate (Supplementary Fig. 1), eventually colliding with an oceanic overriding plate. Model plate velocities are never externally imposed in any of the experiments, arising instead from the evolving dynamic balance between internal driving and resisting forces. The only relevant driving force in our system is the slab pull (Fsp), which results from the negative buoyancy of the subducting plates. This driving force is opposed by the viscous resistance forces of the plates/mantle and by the deformation of the overriding plate during plateau collision.
We show that polarity reversal subduction initiation by plateau collision is geodynamically viable in the absence of external driving forces, but that it is limited by the along-trench width of the oceanic plateau. Also, the duration of the polarity reversal event is strongly controlled by the along-trench plateau width and by the age of the subducting plate.
Modelling rationale
The objective of this work is to understand the dynamics of the processes governing subduction initiation by polarity reversal. Specifically, we aim to understand the time-evolving force balance between the slab pull and the resisting forces that are implied in the deformation of the overriding plate during the collision with an oceanic plateau. Hence, we varied the following parameters/conditions to better understand how these influence the force balance as to trigger polarity reversal SZI:
-
1.
Along-trench width of the oceanic plateau (WSP). Wider plateaus imply not only a higher volume of material that resists subduction when arriving at the trench, but also a smaller active subducting trench after collision (increasing effective slab pull FSP/WSP). Consequently, varying the width of the plateau along the subduction trench allows us to simultaneously assess the impact of a narrower active subduction zone on the triggering of a new one by polarity reversal.
-
2.
Age of the overriding and subducting plates. While Fsp is the main driving force of a subduction zone, its effects are balanced by the relative strength of the intervening plates, which is directly correlated to the plate’s thermal age. Thus, to understand how the relative plate strength influences the evolution of the subduction system, we used different combinations of initial overriding and subducting plate ages. In our simulations, the oceanic plateau has the same age as the subducting plate, which means that a change in plate age directly (and proportionally) affects the implied Fsp.
-
3.
Presence or absence of a positively buoyant magmatic arc along the tip of the overriding plate. These alternative conditions were considered to assess the potential role of the volcanic arc in the development of a new subduction zone by polarity reversal.
A total of eleven model runs were conducted (see Supplementary Table 1). All models were run considering half of a symmetrical domain (see detailed explanation in “Methods”). In all but one model, a new subduction zone is initiated on the overriding plate by polarity reversal, after the arrival of an oceanic plateau at the trench (plateau collision).
We monitored several parameters in each of the different models: the evolution of the emerging trench-normal subducting plate velocity (VSP), as a proxy for the subduction dynamics; the migration of the original and the newly formed subduction zones, to track the plate organization of the model; and the ratio (WR) between the length of the newly formed subduction zone (LNSZ) and the width of the oceanic plateau (WP; Supplementary Fig. 1B), to measure the efficiency of the plateau in triggering a new subduction zone.
Results and discussion
Geodynamics of subduction polarity reversal
The evolution of the reference model, comprising 70 Myr old overriding and subducting plates, a 600 km wide plateau (Wp = 600 km) and a buoyant magmatic arc, is shown in Fig. 1 (and Supplementary Movie 1). In this model, we distinguish four different phases recognized in most numerical simulations: (I) evolution of the original subduction zone (Fig. 1a); (II) arrival of the plateau at the trench (i.e., plateau collision—Fig. 1b); (III) polarity reversal and subduction initiation of the former overriding plate (Fig. 1c); (IV) development of an opposite verging subduction system (Figs. 1d and 2).
The mantle flow is illustrated with arrows: trench-normal mantle flow is shown in white arrows; along-trench flow is marked by blue arrows. Subduction trenches are marked by dashed lines: initial subduction in black, newly formed opposite dipping subduction in white. a Phase I—Early evolution of the original subduction. During this stage, the plateau is still moving towards the active subduction trench and a mantle-wide trench-normal flow is observed. b Phase II—Initial plateau collision. During this stage, the plateau arrives at the subduction trench and, due to its positive buoyancy, blocks it. Laterally, the initial subduction is still active and continues to steadily rollback. c Phase III—Subduction polarity reversal. Driven by the slab pull exerted by the laterally ongoing original subduction, the plateau is forced onto the overriding plate. Consequently, the overriding plate is underthrusted and, eventually forced to subduct in the opposite direction. The original slab is broken-off below the plateau. d Phase IV—Opposite polarity double subduction system. At this stage, both subduction zones are dynamically maintained by the slab pull of each of their sinking slabs. As the newly formed subduction undergoes trench rollback and migrates laterally, a mantle upwelling forms below the plateau (see Fig. 2).
To better visualize the sub-lithospheric mantle flow in the area marked by a square in Fig. 1d, the plateau was made semi-transparent in the depicted evolutionary stages, which comprise: a Initial opposite verging double subduction system (same stage as in Fig. 1d). b Early lateral migration of the newly formed SZ, aided by mantle flow funnelling beneath the arc. The arc itself is strongly strained, showing signs of necking. c Evolving lateral migration with mantle upwelling. d Bifurcation of mantle flow enhances incipient propagation of the original subduction zone behind the oceanic plateau. This is similar to what has been previously described for plateau-continent collisions27,28.
During Phase I, the initial subduction zone develops as the original slab progressively sinks into the upper mantle resulting in an increase of the subduction velocity (Figs. 1a and 3a). At around 4.7 Myr, the slab reaches the upper-lower mantle discontinuity, at 660 km depth (Fig. 1a, b). This causes a deceleration in the subducting plate velocity (VSP, Fig. 3a), which is followed by a new period of slight acceleration as a consequence of slab draping (backwards bending and accumulation along the upper-lower mantle transition26). Shortly after, at around 6 Myr, the plateau arrives at the trench and resists subduction (Phase II in Fig. 1; diamonds in Fig. 3a, b). This happens not only because of the plateau’s positive buoyancy, but also because of its relatively higher viscosity which makes it harder to bend (see Supplementary Fig. 2). This obstruction eventually leads to the termination of the original subduction zone in this domain (Fig. 1b, c) and to the tearing of the initial slab beneath the oceanic plateau (Fig. 1c, d). Driven by the slab pull implied by the ongoing initial subduction, the oceanic plateau and buoyant arc are pushed against and above the overriding plate forcing it to bend downwards and to start subducting in the opposite direction (Phase III in Fig. 1; triangles in Fig. 3 and Supplementary Fig. 3). Plateau collision causes a shift in trench migration from pre-collision rollback to post-collision motion towards the overriding plate (Fig. 3b). From ca. 8.8 Myr onwards, there are two fully developed opposite verging subduction zones (Phase IV; Fig. 1d and Fig. 2). The newly formed opposite dipping slab initially accelerates quickly into the upper mantle (Fig. 3a) before entering a steady roll-back stage (Fig. 3b).
The coloured diamonds indicate the moment at which collision with the plateau is initiated, while the coloured triangles indicate the time at which full polarity reversal is achieved. The subducting plate velocity (VSP) is measured at the trailing edge of the subducting plate, along longitudinal sections both near the mirror symmetry boundary that cuts through the plateau (c.f. section A-A’ in Supplementary Fig. 1), and along the opposite model boundary that crosses only the initial intra-oceanic subduction zone. a Evolution of subduction plate velocity (VSP) over time (subduction plate acceleration), for the original subduction zone (full lines), and for the newly formed opposite dipping one (dashed lines). Note that narrower plateaus imply a smaller indentation area and accompanying lower energy dissipation, resulting in both higher VSP values and plate accelerations. Narrower plateaus also lead to an early trigger of polarity reversal events, expressed by the diminishing distance between diamonds and triangles in the graph. b Subduction trench migration as a function of time (trench velocity), for the original subduction zone (full lines) and for the newly formed subduction trench (dashed lines). The plateau collision event causes an abrupt migration of the newly forming trench towards the overriding plate (OP), even before the new opposite dipping subduction zoned is fully formed. c Plateau indentation efficiency, expressed by the time evolution of the WR ratio (see Supplementary Fig. 1B) between the growing length of the new subduction zone (LNSZ) and the original along-trench width of the plateau (WP). As no new subduction zones are formed before the collision of the plateau with the overriding plate, WR values prior to this event are always zero. Narrower plateaus create notably longer subduction zone trenches relative to their initial widths. The WP = 2400 km line was not included in (c) due to the lack of a polarity reversal event. SZ subduction zone, OP overriding plate, SP subducting plate, LNSZ length of new subduction zone.
As the (initial) overriding plate sinks into the mantle, it is deformed and bent around the oceanic plateau (Figs. 1d and 2a, b). This causes the mantle flow to be laterally funnelled beneath the curved (and necked) magmatic arc (Fig. 2b–d), assisting the trench retreat lateral propagation of the newly formed subduction zone (Fig. 2b). Such a propagation occurs simultaneously with local mantle upwelling, which in nature could correspond to the formation of an oceanic basin (see example discussed below). The implied trench retreat and slab rollback (compare Fig. 2b–d), further enhances the flow of mantle material in a positive feedback loop. Bifurcation of the laterally funnelled mantle flow also drives incipient propagation of the original subduction zone to the back of the oceanic plateau (Fig. 2d). Given sufficient time, it is likely that this would aid in fully propagating the original subduction zone behind the plateau, leading to the development of two bordering side by side, opposite verging subduction zones.
This general model evolution shows that upon arrival of the plateau at the trench its viscous resistance to bending, and its positive buoyancy eventually determine the local shutdown of the original subduction zone. The initial main subduction zone, however, remains active laterally away from the collision zone, and its implied slab pull is enough to initiate thrusting of the plateau above the overriding plate, eventually causing this plate to subduct into the mantle. This is enabled by an initially strong dynamic coupling between the pre-existent and the emerging subduction systems, which allows the first to work as the source of the stress that drives the initial underthrusting and sinking of the overriding plate. However, such a dynamic coupling wanes as the original overriding plate progressively sinks into the mantle, and a new dynamically self-sustained subduction system is formed, driven by the slab pull force of the new subducting slab.
A similar evolution has previously been described in the context of a plateau-continent collision setting27,28. In these cases, the continental nature of the overriding plate prevents it from subducting. However, under the modelling conditions addressed by Moresi26, plateau-continent collision can trigger the lateral formation of an extensional basin on the continental overriding plate, by favouring trench-rollback to the side of the collisional domain, in the lateral active segment of the subduction zone. Continued convergence subsequently forces the subduction zone to migrate to the back of the plateau, accreting it to the overriding continental plate. While our results show comparable lateral extensional basin formation, we infer that the new opposite dipping subduction zone dissipates part of the energy that would otherwise assist a consistent rollback of the original subduction zone.
The role of the plateau’s along-trench width
To understand the influence of the effective slab pull force of the original subduction zone (FSP/WSP) in the formation of a new opposite dipping one, four different initial along-trench widths of the plateau were tested (between 300 and 2400 km, see Supplementary Table 1 and Supplementary Fig. 1). Note that a wider plateau implies a narrower active lateral subduction zone after plateau collision, which in turn leads to a stronger slab pull (higher effective slab pull FSP/WSP, see Supplementary Table 2). The evolution of these models can be seen in Supplementary Movies 1–4.
The evolution of the initial subduction zone is identical for all models until the arrival of the plateau at the trench (Fig. 3a). However, from the plateau collision onwards, the subducting plate velocity (VSP), and its variation along time, is consistently higher/steeper in models with narrower plateaus (i.e., with lower WP widths and correspondingly higher, trench parallel, subduction zone lengths—Fig. 3a). It has been previously shown26,29 that for the same volume of subducted slab, a narrowing of the subduction zone (i.e., the decrease of its trench-parallel length—WSP) causes an increase in both VSP and trench migration velocity, due to a resulting higher effective slab pull force at the surface. However, this is strikingly contrary to what we observe in Fig. 3a. In the present case, the decrease of the subduction trench length in the models comprising wider plateaus is proportionally compensated by an increase in the width of the collision zone. This yields higher levels of horizontal resisting forces/stresses at the front of the plateau (see Supplementary Fig. 4), which are capable of blocking the system, resulting in lower values of VSP and trench velocity in these cases. In Supplementary Table 2, we list the buoyancy force and the effective slab pull force available to drive the polarity reversal. These show that higher effective slab pull forces are implied by wider plateaus as expected. However, the new subduction zone to be initiated is also much longer in these cases, since it will extend along the wider collisional front of the plateau, thus requiring even higher forces to nucleate along the whole of its width (WP). This is readily illustrated when considering the available buoyancy force divided by the length of the new subduction zone (Supplementary Table 2), which unambiguously shows that the resulting driving force available to initiate the new subduction zone is lower for cases comprising wider plateaus. For plateaus with the highest considered width (WP = 2400 km) the collision area corresponds to ca. 80% of the whole model width, which renders only 25% of the slab pull force (per collision zone length) available to initiate the new subduction system. As a result, no new subduction zones are formed in this case, and instead, a complete termination of the whole subduction system occurs (as shown in Supplementary Movie 4).
Furthermore, the duration of the polarity reversal event—i.e., the time interval between the initial stages of collision (diamonds in Fig. 3) and the full achievement of polarity reversal (triangles)—is consistently longer for wider plateaus. Slower trench migrations (Fig. 3b) and lower indentation ratios (expressed by the time variation of WR in Fig. 3c) are also observed for collisions with wider plateaus, in compliance with a more efficient dissipation of Fsp in these cases.
The role of plate age contrast
We have also investigated the effect of changing the age contrast between the overriding and subducting plates, by testing different initial age combinations for the same plateau width (WP = 600 km, see Supplementary Table 1, and Supplementary Movies 1 and 9 to 11). Changing the thermal age of the subducting plate directly affects the negative buoyancy of the slab, thus allowing to modify Fsp without changing the width of the plateau or the implied indentation area.
Similar to the reference model, triggering a polarity reversal event requires the contribution of the driving slab pull force of a pre-existing subduction zone to bend the overriding plate. Therefore, a weaker and thinner overriding plate would, in principle, be easier to subduct22,30,31,32 and hence favour polarity reversal subduction initiation. Our results confirm this assumption by showing that in models with relatively weaker/thinner overriding plates, but identical subducting plate ages, polarity reversal occurs earlier (Fig. 4).
Coloured diamonds and triangles, as well as VSP measurements, with the same meaning, and obtained in the same way, as explained in the caption of Fig. 3. a Evolution of subduction plate velocity (VSP) over time (subduction plate acceleration), for the original subduction zone (full lines), and for the newly formed opposite dipping one (dashed lines). Note that older subducting plates show faster evolutions, expressed by the steeper variations over time, derived from their higher negative buoyancy and effective slab pull (see Supplementary Table 4). b Subduction trench migration as a function of time (trench velocity), for the original subduction zone (full lines) and for the newly formed subduction trench (dashed lines). The plateau collision event causes an abrupt migration of the trench towards the overriding plate (OP). Younger subducting plates show longer time gaps between plateau collision and the polarity reversal event. c Plateau indentation efficiency, expressed by the time evolution of the WR ratio (see Supplementary Fig. 1B and caption of Fig. 3c). As no new subduction zones are formed before the collision of the plateau with the overriding plate, WR values prior to this event are always zero. Despite the fact that older subducting plates trigger polarity reversal at earlier stages, plate age appears to have no relevant influence on the effectiveness of plateau indentation (expressed by a similar steepness of all the curves). SZ subduction zone, OP overriding plate, SP subducting plate, LNSZ length of the new subduction zone.
For the same considered width of the plateau (WP = 600 km) and for equal initial ages of the subducting plate, the resulting driving forces should also be similar. However, in models with younger overriding plate thermal ages their corresponding lower strength and lower thickness facilitate, not only a more efficient indentation by the plateau, but also an earlier development of polarity reversal SZI (Fig. 4). In accordance, the models with younger overriding plates also show an overall higher VSP (Fig. 4a). This higher velocity of the subduction plate cannot be ascribed to an increase in the available driving forces, but can instead be easily explained by a relatively weaker and thinner overriding plate, and therefore an implied lower dissipation of Fsp during and after the collision.
By contrast, models with younger, and therefore weaker, less negatively buoyant subducting plates, but identical overriding plate ages, show an overall slower evolution (Fig. 4). At the start of the model, the younger subducting plates have a lower density contrast with the underlying mantle and, consequently, a lower FSP (ca. 17% lower, see Supplementary Table 4). Therefore, there is a delay in the initial sinking phases of the original subduction (see Fig. 4b, and Supplementary Movie 11), resulting in an overall slower evolution of the system.
The role of a mature volcanic arc
Lastly, we ran a set of models with the same variation of plateau widths (WP), but without the buoyant magmatic arc on the overriding plate. This allowed for a straightforward comparison between the two sets of experiments (with and without arc), in which any observed difference must derive from the missing arc. Regardless of the considered (WP) width of the plateau, models without an arc developed convergent double-sided subduction systems, in which both the overriding and the subducting plates sink into the ambient mantle (see Supplementary Fig. 5 and Supplementary Movies 5–8). Different nuances of this same conspicuous double-sided subduction mode have been previously reported in several other numerical studies, although this type of subduction was never recorded in the Earth’s lithosphere33.
In the present models, during the formation of the original subduction zone, the lithospheric mantle at the tip of the overriding plate is dragged downwards by the slab, forming a slab-dominated asymmetric double-sided subduction (i.e., the direction of subduction is controlled by the slab, see Supplementary Movies 5–8). During collision, the original subduction zone is terminated in front of the oceanic plateau and, as in previous models, the overriding plate begins subducting. However, unlike in the previous models, no extensional basin is formed on the overriding plate in this case. Rather, the polarity reversal event is triggered along the entire width of the plate, resulting in a nearly model-wide symmetrical double-sided subduction zone (see Supplementary Fig. 5 and Supplementary Movies 5–8). Thus, under the assumed model conditions, we argue that the buoyant magmatic arc on the tip of the overriding plate plays a fundamental role, not only in stabilizing this plate by avoiding it being initially dragged into the mantle by the original subducting plate, but also in preventing the immediate plate-wide propagation of the newly formed subduction after the collision with the plateau, and the consequent formation of a double-sided subduction zone also at this later stage.
Natural systems and tectonic implications
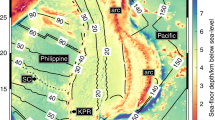
The objective of the present generic numerical modelling study was not to explore the specific geodynamic constraints of a natural case, but rather to gain new insight on the main underlying dynamics governing the occurrence of polarity reversal SZI. Nevertheless, we consider our results to be comparable to one of the most well-studied cases of subduction initiation by polarity reversal, the Vanuatu subduction zone in the southwest Pacific16,17,34,35 (Fig. 5).
a Incipient formation of the Vanuatu subduction zone. During the late Miocene, the Ontong-Java plateau (OJP) begins to dock along the Pacific trench triggering the initiation of the subduction of the Australian plate with opposite polarity. The currently observed cross-section along the Solomon Islands arc (inset), still allows the recognition of the incipient new subduction zone corresponding to the initial development of the Vanuatu SZ. This configuration is also coherently observed in the shown model (Model 1, 70 Myr overriding and subducting plate and WP = 600 km). b Formation of an extensional basin in the Pacific plate after the termination of the original subduction zone. The trench rollback/lateral migration of the newly formed Vanuatu subduction zone triggers extension in the new overriding plate area, forming an extensional basin ridge between this subduction zone and the Ontong-Java plateau45. This is consistent with our models, along the A-A’ cross-section, where a newly formed basin is found between two subduction zones of opposite polarity. The proposed mantle inflow at that time46 as well as the end of the Pacific subduction zone in front of the Ontong-Java plateau are also mirrored by the model results.
Here, a new subduction system was initiated as a consequence of the Late Miocene arrival of the Ontong-Java plateau at the trench. This oceanic plateau, carried by the 150–120 Myr old Pacific plate, was driven to collide with the 49–25 Myr old overriding Australian plate16,34,35. While these ages are not in accordance with the modelled conditions, the event sequence in our models generically agrees with this natural example. The collision of the oceanic plateau triggered the initiation of the Vanuatu subduction zone with an opposite (northwards) polarity in front of the Ontong-Java plateau16,35. As this system continues to propagate across the front of the plateau, we argue that the present-day Solomon arc setting (west side) is likely to closely mimic what was observed in the Late Miocene along the eastern side of the plateau. Under this assumption, during the collision, the Ontong-Java plateau would have been forced to overthrust the Australian plate. Consequently, this plate would have been wedged between the plateau and the Pacific plate (see cross-section in Fig. 5a). This geometric configuration is coherently observed in equivalent frontal-plateau sections in our models (see model inset in Fig. 5a).
The collision of the Ontong-Java plateau with the ancient Solomon subduction zone, and consequent reversal of the subduction polarity, is a good example of the transmission of a subduction zone from one plate to another, in this case, from the Pacific plate to the Australian plate. Our modelling results support the geodynamic viability of such transmission and show that this is possible to occur in the absence of any external forcing mechanism, just due to the interplay between the driving and resisting forces that govern a subduction system. This bears fundamental implications for the understanding of the elusive process of subduction initiation throughout the history of our planet. It has been shown that subduction zones require unrealistic forces to initiate along Atlantic-type or passive oceanic margins22, i.e., ocean-continent transitions without a subduction zone. Our work shows that once a subduction system has initiated, it has all the ingredients to dynamically self-replicate and to transfer subduction zones from one plate to another, and ultimately from ocean to ocean, without the need for external forces. Another example may be the Lesser Antilles in the Atlantic. Here, SZI by polarity reversal may have resulted from the collision of an oceanic plateau with the East Pacific subduction system, leading to the local shut down of the subduction zone and initiation of a new one in the Atlantic. This mechanism, by which a subduction zone is forced to start in a pristine ocean by the action of a nearby subduction zone, has been dubbed as subduction infection19 or invasion21, and polarity reversal provides an efficient mechanism for the introduction of new subduction zones in pristine Atlantic-type oceans.
New subduction zones can be born from the interplay between slab pull of a subduction zone and resistive forces implied by an oceanic plateau collision. Oceanic plateaus are common features on the Earth’s oceans and may arrive frequently at intra-oceanic trenches, leading to the formation of new subduction zones. If one assumes that subduction initiation was easier in the past because the Earth was hotter and plates were weaker6,36, subduction may have persisted on Earth by self-sustaining and self-replicating mechanisms such as subduction initiation by polarity reversal induced by plateau collision.
Methods
Numerical approach
All numerical models were run using the LaMEM code37, with no artificially imposed forcing. The models are visco-elasto-plastic and self-consistent (i.e., internally driven), in which the only driving force is the slab pull exerted by the subducting slab.
LaMEM employs a finite difference staggered grid discretization coupled with a particle-in-cell approach37 to solve the equations of conservation of mass, momentum, and energy (Eqs. 1–3), assuming conditions of incompressibility.
Here vi is the velocity, xi the cartesian coordinates, P the pressure, τij the shear stress, ρ the density, g the gravitational acceleration, Cp the specific heat, T the temperature, t the time, κ the thermal conductivity, and HR and Hs represent the radiogenic and shear heating components, respectively. The shear heating component is defined as:
Here \({\dot{{{{{{\boldsymbol{\varepsilon }}}}}}}}_{{{{{{\rm{i}}}}}}{{{{{\rm{j}}}}}}}\) is the total strain rate tensor and \({\dot{{{{{{\boldsymbol{\varepsilon }}}}}}}}_{{{{{{\rm{i}}}}}}{{{{{\rm{j}}}}}}}^{{{{{{\rm{elastic}}}}}}}\) is the strain rate imposed by the elastic deformation. Our models were run using non-linear visco-elasto-plastic rheology constitutive equations37,38.
Here ηeff is the effective viscosity, \({\mathop{{{{{{\boldsymbol{\tau }}}}}}}\limits^{\diamond }}_{{{{{{\boldsymbol{ij}}}}}}}\) is the Jaumann objective stress rate, ωij is the spin tensor, G is the elastic modulus and Q is the plastic flow potential.
The effective viscosity, ηeff, is calculated according to the following model:
Here A is the diffusive or dislocation pre-exponential factor, n is the stress exponent, \({\dot{\varepsilon }}_{II}\) is the second invariant of the strain rate tensor (Eq. 5), Ea is the activation energy, Va is the activation volume and R is the gas constant. For phases where both dislocation and diffusive creep laws are defined (see Supplementary Table 5), the viscosity is calculated using the two sets of values at each timestep. The lowest value is defined as the effective viscosity after a simple comparison.
Plastic flow is ensured by employing a Drucker-Prager yield criterion39:
Here σII is the second invariant of the stress tensor, ϕ is the internal friction angle and C is the cohesion. Plastic weakening occurs when mantle materials accumulate at least 10% of total plastic strain and stop once at least 60% of total plastic strain has been accumulated. During softening, the materials’ cohesion and internal friction angles are linearly reduced to 1% of their initial values. The weakening is not applied to crustal materials as they are defined as being frictionless, allowing them to act as subduction interface layers (see Supplementary Table 5).
The age dependence of the thermal profiles of the plates follows the half-space cooling model:
Here Tsurface is the temperature at the surface of the model (273 K), Tmantle is the temperature at the lithosphere-asthenosphere boundary (1523 K), y is the depth, κ the diffusivity, and t is the age of the plate. The effective (rheological) lithosphere thickness throughout the model is set by the 1523 K (1250 °C) isotherm. The upper mantle thermal profile follows the mantle adiabat, with a gradient of 0.5 K/km.
All material densities are temperature and pressure dependent:
Here ρ0 is the density of the material at the reference temperature T0, α is the thermal expansibility and β is the compressibility.
Experimental setup
Models were run in 3D conditions, simulating the arrival of an oceanic plateau to an active subduction system. The prescribed model domain was 4000 km long, 3000 km wide and 710 km thick (see Supplementary Fig. 1A, B) discretized along a 256 × 96 × 192 resolution grid. The model includes a 50 km thick sticky-air layer that acts as a free surface. The top boundary is open, ensuring a free movement of this layer. All other boundaries are free slip, allowing for motion along the direction of the boundary but not across it.
The initial subduction was prescribed from the start in all numerical runs by always considering that the slab was already present at a depth of 300 km (initial slab configuration in Supplementary Fig. 1c), along the entire width of the model. Such an initial setting allowed for a gravity driven, fully dynamic, model as the weight of the slab is enough to create a self-sustained steady-state subduction40,41,42, as required for any model of induced subduction initiation2,3. The original interface between the two plates was prescribed as a thin, weak layer with very low viscosity and denser than the surrounding oceanic plate crust (see Supplementary Table 5). This initial weak layer is subducted during the onset of the run and does not interfere with the original subduction zone. The sticky-air free surface is an insulating layer with a low density (1000 kg/m3) and constant low viscosity (1019 Pa.s).
Both overriding and subducting plates are oceanic and assumed to be composed of olivine. The crust and lithospheric mantle have maximum thicknesses of 15 and 90 km, respectively (see inset of Supplementary Fig. 1C). The base density (ρ0) of both layers is 3300 kg/m3. Their initial thermal profiles (i.e., vertical temperature distribution) were defined following the half-space cooling model (Eq. 10). The oceanic plate crustal materials follow a plagioclase viscous creep law but, due to their low cohesion and lack of friction coefficient (see Supplementary Table 5), they are controlled by plastic flow. This allows crustal materials to act as subduction interfaces once the initial weak layer is subducted.
All lithospheric and sub-lithospheric mantle materials follow a dry olivine creep law (Supplementary Table 5), standard for the depleted upper mantle. On the trailing edges of both plates, the isotherms are tapered, allowing for ascension of material, defining a pair of corresponding initial ridge centres (see Supplementary Fig. 1C). This allows for free plate migration and prevents the otherwise strong downwelling of cold material formed at the edges of the model, which would perturb the mantellic flow42,43. Note that these correspond to initial geometric conditions and that no continuous spreading rates were prescribed. Any spreading observed is entirely caused by the adjacent subduction zone and the respective slab pull force.
The modelled oceanic plateau was defined with a parallelepipedal geometry, with four different along-trench widths (WP in Supplementary Fig. 1A and Supplementary Table 1). The plateau is located along a free slip mirror symmetry plane boundary, which divides the model into two halves along its middle length, with the modelled domain corresponding only to one of them. As such, calculations are performed in just half of the whole conceptual domain41. As an example, a 600 km wide plateau in the model would correspond to a 1200 km wide plateau in nature. The plateau crust and the plateau lithospheric mantle have thicknesses of 20 and 90 km and base densities of 2800 kg/m3 and 3220 kg/m3, respectively (see inset in Supplementary Fig. 1C). The crust follows a quartzite law viscous creep law (see Supplementary Table 5), with a higher cohesion and friction angle than the surrounding oceanic plate crust. This setup allows for our oceanic plateau to be both less dense than the underlying asthenosphere (i.e., positively buoyant—see inset on Supplementary Fig. 1C) and simultaneously stronger than the surrounding oceanic plate crust.
The arc was modelled using a trapezoidal geometry that spans the entire length of the model, has a trench-normal width of 200 km, with a maximum crustal thickness of 9 km and a maximum lithospheric mantle thickness of 90 km (see Supplementary Fig. 1A, C). It represents a mature volcanic arc and is less dense than the underlying asthenosphere (see inset in Supplementary Fig. 1C and Supplementary Table 5).
The initial strength depth and thermal profiles for the different model phases can be seen in Supplementary Fig. 2.
The slab pull force44 is estimated using:
where FSP represents the slab pull force, g is the gravity acceleration, ρslab is the average density of the subducted slab, ρastenosphere is the density of the underlying asthenosphere, and VS represents the volume of subducted slab. The effective slab pull force is only c.a. 10% of the calculated value44. The calculated values for the effective slab pull forces in all models can be found in Supplementary Tables 2 and 3.
Data availability
The raw model outputs relative to this article can be found at https://doi.org/10.17605/OSF.IO/XSVZ3.
Code availability
The source for the LaMEM modelling code can be accessed at https://bitbucket.org/bkaus/lamem/src/master/.
References
Crameri, F. et al. A transdisciplinary and community-driven database to unravel subduction zone initiation. Nat. Commun. 11, 1–14 (2020).
Stern, R. J. Subduction initiation: spontaneous and induced. Earth Planet. Sci. Lett. 226, 275–292 (2004).
Stern, R. J. & Gerya, T. Subduction initiation in nature and models: a review. Tectonophysics https://doi.org/10.1016/j.tecto.2017.10.014 (2018).
Lallemand, S. & Arcay, D. Subduction initiation from the earliest stages to self-sustained subduction: insights from the analysis of 70 Cenozoic sites. Earth-Sci. Rev. 221, 103779 (2021).
Whattam, S. A. & Stern, R. J. Late Cretaceous plume-induced subduction initiation along the southern margin of the Caribbean and NW South America: the first documented example with implications for the onset of plate tectonics. Gondwana Res. 27, 38–63 (2015).
Gerya, T. V., Stern, R. J., Baes, M., Sobolev, S. V. & Whattam, S. A. Plate tectonics on the Earth triggered by plume-induced subduction initiation. Nature 527, 221–225 (2015).
Arcay, D., Lallemand, S., Abecassis, S. & Garel, F. Can subduction initiation at a transform fault be spontaneous? Solid Earth Discuss. https://doi.org/10.5194/se-2019-63 (2019).
Zhou, X. et al. Subduction initiation dynamics along a transform fault control trench curvature and ophiolite ages. Geology 46, 607–610 (2018).
Faccenna, C., Holt, A. F., Becker, T. W., Lallemand, S. & Royden, L. H. Dynamics of the Ryukyu/Izu-Bonin-Marianas double subduction system. Tectonophysics 746, 229–238 (2018).
Marques, F. O. et al. Testing the influence of far-field topographic forcing on subduction initiation at a passive margin. Tectonophysics 608, 517–524 (2013).
Cloetingh, S., Wortel, R. & Vlaar, N. J. On the initiation of subduction zones. Pure Appl. Geophys. PAGEOPH 129, 7–25 (1989).
Harris, P. T., Macmillan-Lawler, M., Rupp, J. & Baker, E. K. Geomorphology of the oceans. Mar. Geol. 352, 4–24 (2014).
Tetreault, J. L. & Buiter, S. J. H. Future accreted terranes: a compilation of island arcs, oceanic plateaus, submarine ridges, seamounts, and continental fragments. Solid Earth 5, 1243–1275 (2014).
Mortimer, N. et al. Zealandia: Earth’s hidden Continent. GSA Today 27, 27–35 (2017).
Cooper, P. A. & Taylor, B. Polarity reversal in the Solomon Islands arc. Nature 314, 428–430 (1985).
Mann, P. & Taira, A. Global tectonic significance of the Solomon Islands and Ontong Java Plateau convergent zone. Tectonophysics 389, 137–190 (2004).
Miura, S. et al. Seismological structure and implications of collision between the Ontong Java Plateau and Solomon Island Arc from ocean bottom seismometer–airgun data. Tectonophysics 389, 191–220 (2004).
Konstantinovskaya, E. Early Eocene Arc–Continent Collision in Kamchatka, Russia: Structural Evolution and Geodynamic Model. Front. Earth Sci. 4, 247–277 (2011).
Mueller, S. & Phillips, R. J. On The initiation of subduction. J. Geophys. Res. 96, 651 (1991).
Duarte, J. et al. Are subduction zones invading the atlantic? Evidence from the southwest iberia margin. Geology 41, 839–842 (2013).
Duarte, J. C., Schellart, W. P. & Rosas, F. M. The future of Earth’s oceans: consequences of subduction initiation in the Atlantic and implications for supercontinent formation. Geol. Mag. 155, 45–58 (2018).
Gurnis, M., Hall, C. & Lavier, L. Evolving force balance during incipient subduction. Geochem. Geophys. Geosyst. 5, (2004).
Dymkova, D. & Gerya, T. Porous fluid flow enables oceanic subduction initiation on Earth. Geophys. Res. Lett. 40, 5671–5676 (2013).
Korenaga, J. Thermal cracking and the deep hydration of oceanic lithosphere: a key to the generation of plate tectonics? J. Geophys. Res. Solid Earth 112, 1–20 (2007).
Thielmann, M. & Kaus, B. J. P. Shear heating induced lithospheric-scale localization: does it result in subduction? Earth Planet. Sci. Lett. 359–360, 1–13 (2012).
Schellart, W. P., Freeman, J., Stegman, D. R., Moresi, L. & May, D. Evolution and diversity of subduction zones controlled by slab width. Nature 446, 308–311 (2007).
Moresi, L., Betts, P. G., Miller, M. S. & Cayley, R. A. Dynamics of continental accretion. Nature 508, 245–248 (2014).
Betts, P. G., Moresi, L., Miller, M. S. & Willis, D. Geodynamics of oceanic plateau and plume head accretion and their role in Phanerozoic orogenic systems of China. Geosci. Front. 6, 49–59 (2015).
Guillaume, B., Funiciello, F., Faccenna, C., Martinod, J. & Olivetti, V. Spreading pulses of the Tyrrhenian Sea during the narrowing of the Calabrian slab. Geology 38, 819–822 (2010).
Ulvrova, M. M., Coltice, N., Williams, S. & Tackley, P. J. Where does subduction initiate and cease? A global scale perspective. Earth Planet. Sci. Lett. 528, 115836 (2019).
Irvine, D. N. & Schellart, W. P. Effect of plate thickness on bending radius and energy dissipation at the subduction zone hinge. J. Geophys. Res. Solid Earth 117, 1–14 (2012).
Kemp, D. V. & Stevenson, D. J. A tensile, flexural model for the initiation of subduction. Geophys. J. Int 125, 73–94 (1996).
Gerya, T. V., Connolly, J. A. D. & Yuen, D. A. Why is terrestrial subduction one-sided? Geology 36, 43 (2008).
Schellart, W. P., Lister, G. S. & Jessell, M. W. Analogue modelling of asymmetrical back-arc extension. J. Virtual Explor. 7, https://doi.org/10.3809/jvirtex.2002.00046 (2002).
Schellart, W. P., Lister, G. S. & Toy, V. G. A Late Cretaceous and Cenozoic reconstruction of the Southwest Pacific region: tectonics controlled by subduction and slab rollback processes. Earth-Sci. Rev. 76, 191–233 (2006).
Rey, P. F., Coltice, N. & Flament, N. Spreading continents kick-started plate tectonics. Nature 513, 405–408 (2014).
Kaus, B. J. P. et al. Forward and inverse modelling of lithospheric deformation on geological timescales. NIC Ser. 48, 978–3 (2016).
Piccolo, A., Kaus, B. J. P., White, R. W., Palin, R. M. & Reuber, G. S. Plume — Lid interactions during the Archean and implications for the generation of early continental terranes. Gondwana Res. 88, 150–168 (2020).
Drucker, D. C. & Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 10, 157–165 (1952).
Stegman, D. R., Freeman, J., Schellart, W. P., Moresi, L. & May, D. Influence of trench width on subduction hinge retreat rates in 3-D models of slab rollback. Geochem. Geophys. Geosyst. 7, n/a-n/a (2006).
Stegman, D. R., Farrington, R. & Capitanio, F. A. A regime diagram for subduction styles from 3-D numerical models of free subduction. Tectonophysics 483, 29–45 (2010).
Riel, N., Capitanio, F. A. & Velic, M. Numerical modeling of stress and topography coupling during subduction: inferences on global vs. regional observables interpretation. Tectonophysics https://doi.org/10.1016/j.tecto.2017.07.023 (2017).
Capitanio, F. A., Morra, G., Goes, S., Weinberg, R. F. & Moresi, L. India-Asia convergence driven by the subduction of the Greater Indian continent. Nat. Geosci. 3, 136–139 (2010).
Schellart, W. P. Kinematics of subduction and subduction-induced flow in the upper mantle. J. Geophys. Res. B Solid Earth 109, 1–19 (2004).
Schellart, W. P. & Lister, G. S. The role of the East Asian active margin in widespread extensional and strike-slip deformation in East Asia. J. Geol. Soc. London. 162, 959–972 (2005).
Heyworth, Z., Knesel, K. M., Turner, S. P. & Arculus, R. J. Pb-isotopic evidence for rapid trench-parallel mantle flow beneath Vanuatu. J. Geol. Soc. London. 168, 265–271 (2011).
Acknowledgements
J.A., F.M.R. and J.C.D. acknowledge financial support by FCT through project UIDB/50019/2020 – IDL. J.A. also acknowledges FCT PhD grant no. PD/BD/135067/2017 – Earthsystems - IDL. N.R. and B.K. were funded by the European Research Council through the MAGMA project, ERC Consolidator Grant # 771143. The authors would like to thank Wouter Schellart for the insightful discussion on the dynamics of subduction and subduction initiation. The authors would also like to thank José G. Almeida for the editing of the Supplementary Movies. The authors also would like to thank Taras Gerya and two anonymous reviewers for their insightful and constructive reviews which substantially improved the manuscript.
Author information
Authors and Affiliations
Contributions
J.A. and N.R. designed and carried out the numerical models. J.A. conducted the post-processing analysis. B.K. contributed to the development of the numerical code. J.A., N.R., F.M.R. and J.C.D. discussed the implications for subduction initiation dynamics. All authors contributed equally to writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests. J.C.D. is an Editorial Board Member for Communications Earth & Environment, but was not involved in the editorial review of, nor the decision to publish this article.
Peer review
Peer review information
Communications Earth & Environment thanks Taras Gerya, Louis Moresi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Joe Aslin. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Almeida, J., Riel, N., Rosas, F.M. et al. Self-replicating subduction zone initiation by polarity reversal. Commun Earth Environ 3, 55 (2022). https://doi.org/10.1038/s43247-022-00380-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00380-2
This article is cited by
-
Onset of double subduction controls plate motion reorganisation
Nature Communications (2024)
-
Subduction initiation triggered the Caribbean large igneous province
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.