Abstract
Symmetric instability is a mechanism that can transfer geostrophic kinetic energy to overturning and dissipation. To date, symmetric instability has only been recognized to occur at the ocean surface or near topographic boundary layers. Analyses of direct microstructure measurements reveal enhanced dissipation caused by symmetric instability in the northwestern equatorial Pacific thermocline, which provides the first observational evidence of subsurface symmetric instability away from boundaries. Enhanced subsurface cross-equatorial exchange provides the negative potential vorticity needed to drive the symmetric instability, which is well reproduced by numerical modeling. These results suggest a new route to energy dissipation for large scale currents, and hence a new ocean turbulent mixing process in the ocean interior. Given the importance of vertical mixing in the evolution of equatorial thermocline, models may need to account for this mechanism to produce more reliable climate projections.
Similar content being viewed by others
Introduction
The northwestern equatorial Pacific Ocean (NWEPO) is the meeting point of the equatorward western boundary currents, namely the Mindanao Current and the New Guinea Coastal Current and the New Guinea Coastal Undercurrent (NGCUC), forming water mass crossroads1,2 (Fig. 1a). The Indonesian Throughflow (ITF) and the north and south equatorial Pacific are connected via the regional currents. Thus, the state of the NWEPO plays an important role in setting global climate3,4,5. A key factor that regulates the state of the NWEPO is the vertical mixing of water properties and momentum6,7. However, direct observations of microscale turbulence in the NWEPO are quite limited, consisting primarily of those by Liu et al. 20178 and the present study. As we show below, an added complication is that these two sets of results differ dramatically in their character. Consequently, regional mixing is poorly observed and, therefore, poorly constrained in climate models9,10,11,12.
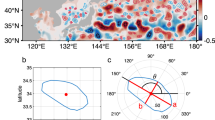
a Schematic of major currents in the tropical western Pacific Ocean. NEC, North Equatorial Current; KC, Kuroshio Current; MC, Mindanao Current; NECC, North Equatorial Counter Current; NGCC, New Guinea Coastal Current; SEC, South Equatorial Current; ME, Mindanao Eddy; HE, Halmahera Eddy; ITF, Indonesian Throughflow; NGCUC, New Guinea Coastal Undercurrent. The black dots indicate locations of microstructure profiles, and color shading shows the absolute dynamic topography (ADT) with the surface absolute geostrophic velocity (arrows) averaged between October 27 to November 6 in 2017 from altimetry (Supplementary Notes (2)). b, c Latitude-depth sections of temperature (T;°C)/salinity (S;PSU) measured by the microstructure profiler (MSP) along 130°E section, thick gray lines are isopycnals; thick purple lines mark the upper and lower boundary of the thermocline (see Methods); black dots in the top axis are locations of MSP measurements. d, e Latitude-depth sections of zonal (U)/meridional (V) velocities (cm s−1) measured by Shipboard Acoustic Doppler Current Profiler (SADCP) along 130°E section. f Zonal geostrophic velocity (GU) calculated from the synchronous full-depth CTD measurements.
Most of the ocean kinetic energy is contained in large-scale currents and the vigorous geostrophic eddy field. To achieve equilibrium, the geostrophic currents must lose kinetic energy, which in turn must be viscously dissipated at much smaller scales. Submesoscale instabilities have been implicated as mediators in this transfer13. Among the participant processes, symmetric instability (SI) has been identified as effective at removing kinetic energy from geostrophic currents and initiating a forward energy cascade leading to dissipation14,15,16,17. The necessary condition for SI is the presence of Ertel’s potential vorticity (PV\(;q=(f\hat{{{{{{\bf{k}}}}}}}+\nabla \times {{{{{\bf{u}}}}}})\cdot \nabla b\), in which f is the Coriolis parameter, \(\hat{{{{{{\bf{k}}}}}}}\) a vertical unit vector, u velocity, \(b=-g(\rho -{\rho }_{0})/{\rho }_{0}\) buoyancy, g gravity, ρ density, and \({\rho }_{0}\) a reference density) with a sign opposite to that of f17. Given that such PV patches are strongly unstable, Hoskins (1974)18 concluded that their appearance could only result from an external force.
At the sea surface, atmospheric forcing can extract PV through cooling or down-front winds, and the latter can promote the onset of SI15. Observations in the Japan/East Sea, Gulf Stream, and Kuroshio have documented SI in the near-surface ocean15,16,19,20. Numerical simulations and observations have also suggested subsurface SI near topography, where viscous boundary effects can generate opposite signed PV21,22,23,24. D’Asaro et al. (2011)16 argue that direct conversion from geostrophic energy to turbulence was required to sustain observed Kuroshio dissipation levels. Further, SI provides the pathway by which the near-surface ocean mesoscale processes can lose energy to mixing. These results suggest that SI is likely confined to ocean boundaries, i.e., at the surface or near topography.
In contrast, we present evidence in this paper for SI-driven turbulent mixing in the NWEPO at depths away from atmospheric or topographic contact. The requisite opposite signed PV is provided by cross-equatorial exchange. The observations supporting this interpretation show elevated turbulence levels relative to data obtained in the same region from a few years earlier8 (supplementary Table 1). The two sets of observations are differentiated strongly by the associated El Niño-Southern Oscillation (ENSO) state: the present data was obtained under a La Niña condition, in contrast to the earlier observations under an El Niño (Supplementary Note (1)). We are not aware of any previous measurements of SI in the open ocean interior. We suggest that the enhanced subsurface cross-equatorial exchange during the late fall in the 2017 La Niña promotes the negative PV needed for the onset of SI. Additionally, we support this mechanism using nested ocean model simulations based on the Massachusetts Institute of Technology general circulation model (MITgcm)25.
Results and discussion
Upper-ocean vertical structure
From October 27 to November 7, 2017, 33 measurements of turbulent dissipation rate were carried out by a quasi-free-falling microstructure profiler (MSP) along 130°E every 1° between 9°N–13°N and 0.25° between 2°N and 9°N (Fig. 1a; Supplementary Note (2); Supplementary Tables 1 and 2). A series of two to three consecutive MSP casts were launched at each site to obtain profiling measurements of temperature, conductivity, and microscale velocity shear from the sea surface down to nominal depths of 500 m (Supplementary Data 1), depending on weather and oceanographic conditions.
The temperature and salinity profiles clearly show the typical dome-like structure centered around 7.5°N associated with the Mindanao eddy (Fig. 1b, c). South of the Mindanao eddy, both temperature and isopycnals show a bowl-shaped structure centered around 4°N associated with the Halmahera eddy (HE), especially below 200 m. Two patches of high salinity water with maxima exceeding 35.0 PSU occupy isopycnals between 23.5 and 25.5 \({\sigma }_{\theta }\) (1.0 \({\sigma }_{\theta }\)= density-1000 kg m−3) south of 6°N and north of 9°N. These clearly indicate the South Tropical Pacific Water (SPTW) and North Tropical Pacific Water. The SPTW identified here is transported by the HE, as shown by the absolute geostrophic currents (Fig. 1a). The northwestward flow appears in vertical profiles of zonal and meridional velocity from the Shipboard Acoustic Doppler Current Profiler (SADCP; Fig. 1d, e; Supplementary Data 1), and the much thicker layer of SPTW between 3°N and 5.5°N also confirm the existence of the HE. Located around (4.5°N, 129.5°E), the HE has apparently shifted northwestward during the cold phase of ENSO26. There is another patch of high salinity water (>35.0 PSU) between 250 m and 350 m south of 3.5°N, where westward/northwestward flow dominates (Fig. 1d, e). This subsurface flow corresponds to the lower part of the NGCUC27,28, which can be verified by the synchronous Acoustic Doppler Current Profiler measurements upstream by the mooring deployed at (1.7°S, 141.4°E)28 (Supplementary Fig. 2). The westward North Equatorial Subsurface Current29,30 can also be identified under the North Equatorial Counter Current. Its core speed exceeds 10 cm s−1 below 200 m around 5°N–6°N in both SADCP measurements and the zonal geostrophic velocity (Fig. 1d, f). These observations suggest energetic alternating undercurrents and intense convergence of North and South Pacific water masses during our observational campaign in the NWEPO.
Enhanced thermocline turbulent mixing in NWEPO
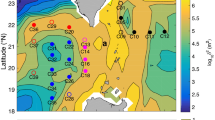
The turbulent kinetic energy dissipation rate, ε, in the surface mixed layer is relatively high with the maximum amplitude exceeding 10−7 W kg−1 (Fig. 2a). In contrast, the averaged ε decreases to about 10−8.5 W kg−1 in the thermocline and 10−9 W kg−1 below the thermocline. However, patches of intensive dissipation with ε ranging from 10−7.5 to 10−8 W kg−1 in the thermocline appear associated with the elevated vertical shears (Fig. 2d). These shears reflect the geostrophic shear in this region (Fig. 2e), corresponding to the energetic alternating undercurrents revealed from the SADCP measurements (Fig. 1d–f).
a Observed turbulence kinetic energy dissipation rate ε (unit in W kg−1), b diapycnal diffusivity κρ (m2 s−1), c squared buoyancy frequency \({N}^{2}\) (s−2), d the total vertical shear squared \({S}^{2}\) (s−2), e the geostrophic vertical shear squared \({S}_{g}^{2}\)(s−2), f the gradient Richardson number \({R}_{i}\), g the balanced Richardson number RiB, and h the Turner angle (Tu). Thick purple lines are the upper and lower boundary of the thermocline, respectively. Gray lines are the isopycnals, and red dots in the top axis are locations of the microstructure profiler measurements.
The diapycnal diffusivity κρ below the mixed layer was estimated using the Osborn (1980)31 formula (Fig. 2b), \({\kappa }_{\rho }=\varepsilon \varGamma /{N}^{2}\) (with \({N}^{2}\) the squared buoyancy frequency and \(\varGamma =0.2\) a constant mixing efficiency). The buoyancy frequency shows quite strong density stratification between the mixed layer and 150 m (Fig. 2c), and thus weak mixing with κρ generally O (10−6 to 10−5.5) m2 s−1 (Fig. 2 d). By contrast, in the thermocline below 150 m, the diapycnal diffusivity is increased significantly, and the density stratification is reduced, with some patches of κρ reaching 10−4 to 10−3 m2 s−1. These patches are consistent with those of high ε and strong vertical shears at these depths (Fig. 2a, d, e) and exhibit low gradient Richardson numbers (\({R}_{i}={N}^{2}/{S}^{2}\) with \({S}^{2}\) being the shear squared) as calculated from the SADCP measurements (Fig. 2f). Very low \({R}_{i}\) (<1) south of 6°N can be identified in patches of high ε and κρ (Fig. 2a, b), although the coarse resolution of the SADCP measurements may underestimate the vertical shear32.
Generally, our observations suggest that turbulent dissipation is unusually strong in the thermocline south of 6°N with dissipation reaching O (10−7 to 10−8.5) W kg−1. From this, we infer strong mixing, with diapycnal diffusivity reaching O (10−3 to 10−5) m2 s−1. These are one to three orders of magnitude higher than in Liu et al. (2017)8, which conducted the same turbulence microstructure measurements in 2014 during the development of the 2014–16 El Niño event (Supplementary Note (1)). A previous study suggests that the level of mixing within the thermocline is strongly modulated by ENSO events in the western equatorial Pacific based on measurements near the equator6. The more vigorous dissipations observed during our cruise relative to those of Liu et al. (2017)8 suggest modulation by ENSO of turbulent mixing in the NWEPO (see Supplementary Discussion).
We emphasize the correspondence of negative PV patches with the regions of elevated dissipation (Fig. 3a), strongly suggesting the presence of SI. Negative PV may extract energy from the available potential energy, lateral shear, or vertical shear of the background flow to induce an overturnings, termed gravitational, centrifugal, or symmetric instability, respectively17. We further estimate the energy sources of the three types of instability (see Methods), as shown in Fig. 3b. The vertical integral of \(\varepsilon\) in the thermocline for stations between 5.5°N and 6°N ranges from 2.5 × 10−7 to 3.1 × 10−7 Wkg−1, and is broadly consistent with the value of 2.6–3.6 × 10−7 Wkg−1 for the vertical shear production rate (Fig. 3b). This consistency suggests that the observed overturning principally extracts energy from the vertical shear of the background flow. Further inspection indicates that the geostrophic shear of the zonal component dominates the total shear (Fig. 2d, e) and results in the balanced Richardson numbers (Fig. 2g), \({{Ri}}_{B}=\frac{{N}^{2}}{{u}_{z}^{2}}=\frac{{N}^{2}}{{b}_{y}^{2}}{f}^{2}\), to satisfy the instability criterion for SI (see “Methods”). These supercritical areas overlay the enhanced patches of elevated dissipation (Fig. 2a, b), arguing for SI-driven turbulence in these patches.
a The Latitude-depth section of PV (in s−3) calculated from the MSP measurements between 150 and 350 m along the 130°E section between 2°N and 8°N. Areas of negative and zero pv are marked in red and green to indicate the overturning instabilities. b The 150–350 m vertically integrated turbulent kinetic energy dissipation rates, ε (yellow bars) and the turbulent kinetic energy production associated with gravitational instability (\({F}_{b}\), gray line), symmetric instability (\({P}_{{{{{{\rm{vrt}}}}}}}\), blue line), and centrifugal instability (\({P}_{{{{{{\rm{lat}}}}}}}\), black line). Unit is W kg−1.
Observational evidence of subsurface SI in the ocean interior
Liu et al. (2017)8 attributed their observed weak thermocline mixing in the NWEPO to weak internal wave breaking at low latitudes. However, our observations suggest much higher turbulent mixing in this region, especially in the convergence regions of the North Equatorial Counter Current, the New Gunie Coastal Current, the NGCUC, and the HE, where very strong vertical shear exists in the subsurface. Moreover, the lower part of the NGCUC crosses the equator and joins into the HE with Southern Hemisphere water during the MSP observation period (Fig. 1 and Supplementary Fig. 2). In the thermocline, geostrophic zonal shear contributes most of the shear, especially in those patches of enhanced turbulence accompanied by negative PV (Fig. 3). All these conditions are favorable for the development of subsurface SI.
Since turbulence in the thermocline is extraordinarily patchy and intermittent, we choose the MSP cast taken at (5.75°N, 130°E) to illustrate the evidence of the SI-driven turbulence. The ε profile reaches a maximum of almost 10−8 W kg−1 around 200 m (Fig. 4a). Corresponding to the high ε, the κρ also peaks at this depth with its 1 m- and 10 m-averaged magnitudes reaching 10−3 m2 s−1 and 10−4 m2 s−1, respectively (Fig. 4b). Meanwhile, the \({N}^{2}\) shows a relatively weak density stratification (~10−6 s−2, Fig. 4c), which requires much weaker vertical shear to promote turbulent mixing. The total vertical shears at these depths are quite large, as expected from the minimal values of the gradient Richardson number, \({R}_{i}\) (roughly 0.1–1.0, Fig. 4e), meeting the criterion for turbulent mixing33,34.
a Turbulent kinetic energy dissipation rate ε (W kg−1), b diapycnal diffusivity (κρ), c squared buoyancy frequency (\({N}^{2}\)), d vertical shear squared calculated from shipboard ADCP measured zonal currents (\({{S}}_{u({{{{{\rm{SADCP}}}}}})}^{2}\)), zonal and meridional currents \({{S}}_{{uv}({{{{{\rm{SADCP}}}}}})}^{2}\), and from geostrophic current based on MSP observations (\({{S}}_{g({{{{{\rm{MSP}}}}}})}^{2}\)), and e gradient Richardson number, Ri, based on shipboard ADCP measurements, and balanced Richardson number, \({{{{{{\rm{Ri}}}}}}}_{{{{{\rm{B}}}}}}\), as a function of depth with blue dots indicating those \({{{{{{\rm{Ri}}}}}}}_{{{{{\rm{B}}}}}}\) values meeting the criterion for the SI. Red and cyan curves in a–c and e represent data with a 1 m interval, and black and blue curves are 10 m average.
The next question pertains to the source of the mixing. We exploit the observation that the shear at this station is almost entirely due to the zonal geostrophic shear between 120 and 270 m (Fig. 4d). Low latitudes are locations where geostrophy might be suspect. Yet, in this area north of 5°N, comparisons between the total velocity and geostrophic velocity from GOFS 3.1 data support the accuracy of geostrophy (Supplementary Note (3).
The Ertel’s PV can be written in the form of \({\zeta }_{g}{N}^{2}-{{fu}}_{z}^{2}\), with \({\zeta }_{g}=f-{u}_{y}\), indicating the zonal geostrophic shear plays a role in PV. Thus, any anticyclonic shear can reduce the PV value. Large vertical geostrophic shear combined with weak stratification and a small Coriolis parameter creates conditions favorable for SI. A variety of instabilities can develop when the PV is negative in the Northern Hemisphere. According to the linear instability analysis from the energetics perspective given by Thomas et al. (2013)17, for anticyclonic vorticity (i.e.,\(\,\frac{{\zeta }_{g}}{f} < 1\)) and stable stratification, both the lateral shear production and geostrophic shear production contribute to the energetics of the instabilities in varying degrees depending on the angle, \({\varnothing}_{{{{{{\rm{Ri}}}}}}_{{{{{\rm{B}}}}}}}={{\tan }}^{-1}\left(-\frac{{\left|\nabla {h}_{b}\right|}^{2}}{{f}^{2}{N}^{2}}\right)\). This angle can be used to distinguish the type of instability that can result. When −90°< \({\varnothing}_{{{{{{\rm{Ri}}}}}}_{{{{{\rm{B}}}}}}}\) <−45°, or equivalently when expressed by the balanced Richardson number, \(0 \, < \, {{{{{{\rm{Ri}}}}}}}_{{{{{\rm{B}}}}}} \, < \, 1\), the ratio geostrophic shear production/lateral shear production >1, so SI is the dominant mode of instability. We calculate the vertical \({{{{{{\rm{Ri}}}}}}}_{{{{{\rm{B}}}}}}\) profile using the vertical geostrophic shear and buoyancy frequency derived from the MSP observations, which lead to RiB values from 0.25 to 1.0 and thus that the needed criterion for SI-driven turbulent mixing is well met around 200 m (Fig. 4e). This is where the observed high dissipation rates occur and provides observational evidence of the subsurface SI-driven turbulence at this location.
Usually, shear-driven overturning indicated by low gradient Richardson numbers in the interior ocean thermocline is attributed to internal gravity wave activity. To determine whether internal gravity waves are the mechanism in our observations, we compare the diapycnal diffusivity κρ below 200 m at all our observation sites between direct microstructure measurements and fine-scale estimates. The standard formulas relating 10 m-shear to mixing based on internal wave theory is applied in the diffusivity calculation (see “Methods”). The comparisons shown in Fig. 5 suggest that the agreement between the two estimates is within a factor of 5 (medium gray) at most sites with κρ more often underestimated than overestimated by the fine-scale parameterization (10 sites of underestimation versus 2 sites of overestimation within a factor of 5). The underestimation by the fine-scale estimates is more than a factor of 10 in the light gray regions. It appears the application of standard formulas relating internal wave shear to mixing below 200 m, based on internal wave theory, tends to underestimate the turbulent intensity levels in this region, and the largest underestimates correspond to the latitudes where the MSP observes the SI. This also supports our argument of SI-driven turbulence in the thermocline in the NWEPO.
Modeling of subsurface SI in the ocean interior
Since SI tends to homogenize PV towards zero by mixing with waters of the opposite sign, it is a self-limiting process. For the SI to be sustained, there must be a negative PV supply, which has traditionally been thought to happen near the surface or topographic boundaries, where frictional or diabatic PV fluxes can occur. However, our observations suggest SI-driven turbulence in the ocean interior away from the surface or any topographic boundaries in the Northern Hemisphere. What process then supplies the negative PV?
To answer this question, a hierarchy of MITgcm model simulations with horizontal resolution of 0.08o, 0.025o, 0.008o, 0.0025o and 0.0008o are conducted. The model reproduces consistent basic dynamical features with those obtained from the observations (Supplementary Note (4)). Figure 6a shows the salinity and velocity at the depth of 197.5 m from the 0.008o-resolution simulation on November 7, 2017. High salinity waters (> 35.1 PSU), namely the SPTW, occupy the region south of 2°N and east of 130°E. They spread northwestward by the NGCUC along the New Guinea coast from the South Pacific, consistent with the synchronous Acoustic Doppler Current Profiler observed northwestward velocity between 150 and 200 m (Supplementary Fig. 2). Around 130°E, some of the SPTW is advected northeastward by the HE and reaches about 4°N (Supplementary Movie 1), in which the strong vertical shear associated with the North Equatorial Counter Current and the HE exists. These South Pacific waters with negative planetary vorticity supply the negative PV needed for the SI to develop.
a The distribution of salinity (color shading) and velocity (vectors) at 197.5 m on November 7, 2017, from the 0.008°-resolution MITgcm simulation. The two black boxes are downscaling nested domains with horizontal resolutions of 0.0025° and 0.0008°, respectively. The profile of b potential vorticity (PV), c the angle \({\varnothing}_{{{{{{{\rm{Ri}}}}}}}_{{{{{\rm{B}}}}}}}\) distinguishing various overturning instabilities along the transect (the red line in (a)) from the 0.0008°-resolution simulation, respectively.
To examine this, Fig. 6b shows the PV profile around 4°N from the 0.0008°-resolution simulation (the magenta line in Fig. 6a). Many patches of negative PV exist between 150 and 250 m, and the angle \({\varnothing}_{{{{{{\rm{Ri}}}}}}_{{{{{\rm{B}}}}}}}\) satisfying −90°< \({\varnothing}_{{{{{{{\rm{Ri}}}}}}}_{{{{{\rm{B}}}}}}}\) <−45° around those negative PV patches further argues that SI is the dominant mode of instability (Fig. 6c). This also excludes inertial instability (when \({f\zeta }_{g} < \, 0\)), which is suggested to play an important role in turbulent mixing in the equatorial thermocline35.
Moreover, the intrusion of South Pacific water north of 4°N is also supported by the observed relations of potential temperature versus salinity (T–S), potential temperature versus dissolved oxygen concentration (DO; T-DO), and salinity versus DO (S-DO) from the hydrographic data obtained simultaneously during the MSP observations (Fig. 7a–c). The T–S diagram shows that waters between 4 and 8°N are characterized by a mixture of South and North Pacific waters, especially below 25.5 \({\sigma }_{\theta }\) (corresponding to depths of 150–250 m). The salinity minima (34.3 PSU) along 26.5 σθ for waters North of 8°N clearly mark the North Pacific Intermediate Water originating from the North Pacific Ocean, and the salinity maxima (35.0 PSU) on this isopycnal South of 4°N demonstrates their origin in the South Pacific carried by the lower NGCUC (Fig. 1d, e and Supplementary Fig. 2). The salinity of waters between 4 and 8°N shows intermediate values between the North and South Pacific waters suggesting the enhanced mixing in this region (Fig. 7a). Dissolved oxygen offers further information about the origin of these waters. The T-DO and S-DO diagrams show that the SPTW and North Tropical Pacific Water are distinct in their DO structure (Fig. 7b, c). The North Tropical Pacific Water is thought to be formed due to excessive evaporation in the subtropical gyre with high DO (>4.0 mg/l)1,36,37, while the SPTW is characterized by much lower DO compared to the North Tropical Pacific Water37. In the upper salinity maxima layers, the DO of waters south of 8°N is obviously much lower than those north of 8°N, with the former ranging from 4.5 to 5 mg/l and the latter 6–6.5 mg/l, suggesting that the origin of waters south of 8°N is the South Pacific Ocean. In summary, water mass analyses based on hydrographic data support the intrusion of negative PV water north of 4°N. This observed information, along with the 0.0008°-resolution numerical simulation, indicate subsurface SI is sustained by a supply of South Pacific negative PV water. To our knowledge, this shows for the first time a new direct pathway from geostrophic flow to mixing in the ocean interior.
Relations of a potential temperature versus salinity (T–S), b potential temperature versus dissolved oxygen concentration (T-DO), and c salinity versus dissolved oxygen concentration (S-DO) from the hydrographic data collected during the cruise. Light gray lines represent stations south of 4°N, black lines represent stations north of 8°N, and colored lines represent stations between 4°N and 8°N.
Conculsions
Observations obtained during the Northern Hemisphere fall, 2017 in the NWEPO are consistent with strong subsurface mixing driven by SI away from any boundaries. The evidence favoring this interpretation includes the strong geostrophic vertical shear in regions of intense turbulence dissipation isolated from surface or topography. The geostrophic shear is sufficient to achieve the necessary condition for SI. Negative Ertel’s PV, itself a requirement for SI, is supplied by a Southern Hemisphere source. Evidence backing this claim comes from the observed regional velocity fields, salinity, dissolved oxygen hydrographic characteristics, and successful simulation of the SI by a hierarchy of high-resolution MITgcm simulations.
The observations of high turbulent dissipation and mixing are at odds with those obtained three years earlier. The difference in the mixing levels can possibly be ascribed to the cross-equatorial water exchanges associated with different phases of the 2014–2017 ENSO event (Supplementary Text). The 2014 observations were obtained during the development of an El Niño event and the 2017 observations during the following La Niña. The regional circulations are thus quite distinct, with the latter promoting a much stronger cross-equatorial subsurface exchange due to both the deepening of the NGCUC and the northwestward shift of an enhanced HE. This idea is confirmed by the results of high-resolution MITgcm model simulations, which reproduce the enhanced subsurface cross-equatorial transport of negative PV reaching north of 4°N from the South Pacific Ocean.
In addition to the favorable preconditions for SI during our observations, the observed zonal current has an anticyclonic curvature associated with the HE. In this case, the angular velocity and the curvature associated with this anticyclonic front increase the likelihood of instability38,39. Also, the non-traditional meridional Coriolis component near the equator tends to expand the range of Ri where SI might be present40. All these conditions increase the likelihood of SI in this region.
The energy provided to the NWEPO thermocline turbulence comes directly from the large scale, balanced flow, thus illustrating a novel mechanism by which the mesoscale field can drive mixing. As the NWEPO provides the source water for the ITF, the appearance of SI questions the use of the island rule to link ENSO to the ITF in low-resolution models, where the amount of water that flows through the ITF is constrained by the conservation of PV41. Besides the shear-driven instabilities, salt finger double diffusion also plays a role in vertical mixing in the NWEPO (Fig. 2h; Supplementary Note (5)).
The generation mechanisms accounting for the subsurface SI-induced turbulent mixing are schematically summarized in Fig. 8. The opposite direction of surface and subsurface geostrophic currents manifest the strong shear, and the cross-equatorial undercurrent provides the negative PV water north of the equator, hence satisfying the necessary condition for SI. While the mechanism described here, that of subsurface SI whose requisite PV field is provided by the cross-equatorial exchange, has only been observed in northwestern equatorial Pacific, we suggest that this mechanism might well apply generally to the equatorial zones of all the world’s oceans where both opposite PV water exchanges and strong geostrophic shear exist. Given the importance of equatorial thermocline structure to global climate, models may need to take account of this mechanism in order to produce more reliable climate projections.
The opposite directions of surface and subsurface currents provide the strong shear, and the cross-equatorial undercurrent provides the negative potential vorticity water, satisfying the necessary condition of overturns associated with symmetric instability. The axis W means westward, N means northward, S means southward, and Z means downward.
Methods
Energy source estimation
The rate of extraction of available potential energy along the 130°E transect was estimated as \({F}_{b}=\overline{{w}^{{\,\prime} }{b}^{{\prime}}}\) based on measurements of the vertical velocity (w) derived from the SADCP and buoyancy. The overbar in the formula denotes a spatial average over the area of the instability, and primes represent the deviation from that average following Naveira Garabato et al. (2017)42. Here, the spatial average was computed horizontally at each depth level along the entire transect, to capture the buoyancy flux induced by the substantial up- and downwelling flows associated with the instability. The rates of vertical and lateral shear production were estimated from velocity measurements as \({P}_{{{{{{\rm{vrt}}}}}}}=-\overline{{{{{{{\boldsymbol{u}}}}}}}_{h}^{{\prime} }{w}^{{\prime} }}\cdot \left(\partial \overline{{{{{{{\boldsymbol{u}}}}}}}_{h}}/\partial z\right)\) and \({P}_{{lat}}=-\overline{{{{{{{\boldsymbol{u}}}}}}}_{h}^{{\prime} }{v}_{s}^{{\prime} }}\cdot \left(\partial \overline{{{{{{{\boldsymbol{u}}}}}}}_{h}}/\partial s\right)\), respectively with \({{{{{{\boldsymbol{u}}}}}}}_{h}=\left(u,v\right)\). Here ‘s’ is the horizontal coordinate perpendicular to the depth-integrated flow, and vs is the component of uh in that direction. The spatial average was calculated vertically at each horizontal location between 150 and 350 m of the transect.
Instability criterion of symmetric instability for a zonal geostrophic flow at low latitudes
For a zonal geostrophic flow, the Ertel’s PV, q, can be expressed as17:
where \({\zeta }_{g}=f-{u}_{y}\), is the vertical component of the absolute vorticity of the zonal geostrophic flow, \(f\) is the Coriolis parameter, \({N}^{2}=-(g/\rho )\frac{{{{{{\rm{d}}}}}}\rho }{{{{{{{\rm{d}}}}}}z}}\) is the squared Brunt–Vaisala frequency, g gravity, ρ density, u zonal geostrophic velocity. The first and second terms in the right hand are the vertical component, \({q}_{{{{{{\rm{vert}}}}}}}={\xi }_{a}{N}^{2}\), and the baroclinic component,\({q}_{{bc}}={u}_{z}{b}_{y}\), respectively. Using the thermal wind relation,
where \(b=-g\rho /{\rho }_{0}\) is the buoyancy, and ρ0 a reference density, Eq. 1 is reduced to
By defining the balanced Richardson number
So the condition of the negative PV of the zonal geostrophic flow can equivalently be expressed in terms of the balanced Richardson number meeting the following criterion:
When the vertical component of the absolute vorticity of the zonal geostrophic flow \({\zeta }_{g} < \, f\), the instability criterion will be enlarged (\({R}_{{ib}}\ge 1\)). This is the case in our study (see Supplementary Fig. 3), the \({u}_{y}\) is about 2.0 × 10−6 s−1 around 200 m at the station where the SI-induced dissipation was observed, and the \(\frac{f}{{\zeta }_{g}}=1.15\), which enlarges the zone over which we infer the presence of SI. Although the \({u}_{y}\) is negative below 227 m, its absolute value is about one order of magnitude smaller than the Coriolis parameter at this latitude (\(f\)= 1.5 × 10−5 s−1), so the \(\frac{f}{{\zeta }_{g}} \sim 1\).
The mixed layer and thermocline
Here the mixed layer depth is calculated as the depth where the vertical temperature gradient is larger than 0.5 °C. The thermocline is bounded by the lower boundary of the mixed layer and the depth with the maximum vertical gradient of temperature.
Geostrophic vertical shear
The geostrophic vertical shear is calculated from temperature and salinity data obtained from the MSP observations. The reference level is 400 m, and since the vertical shear is determined by the relative velocity between two neighboring levels, the shallow depth of the zero velocity assumption doesn’t influence the shear.
Numerical simulation
The MITgcm25 is used to conduct numerical simulations in the western equatorial Pacific for this study (Supplementary Fig. 5). The highest-resolution model setup is aimed at resolving non-hydrostatic processes and instabilities. Four intermediate grids are used to provide reasonable initial and boundary conditions from coarse runs to finer ones to ensure the accuracy of the innermost nested highest-resolution simulation. The horizontal resolution of the simulations from coarse to fine are 0.08°, 0.025°, 0.008°, 0.0025°, and 0.0008°, and the depth of vertical layers is illustrated in Supplementary Table 3. The original initial and boundary conditions of the coarsest simulation are extracted from the HYCOM GLBa0.08 data (HYCOM + NCODA Global 1/12° Analysis). Both the 0.08°-resolution and 0.025°-resolution simulations initiated from April 1, 2017, and ran for 10 months to provide stable initial and boundary conditions for the higher-resolution nested runs. The first day of 0.008°-, 0.0025°-, and 0.0008°-resolution runs are July 1, September 15, and September 25, respectively. All of them ended after November 19 to ensure the temporal coverage of the entire observation period. The coarsest simulation’s horizontal resolution is set the same as the HYCOM data to ensure consistency. The number of vertical layers increased from 33 to 88 are configured in the simulations. The value of the interface depths at which vertical velocity locate is shown in Supplementary Table 3. Layers with tracer points are centered between the interface depths. The non-hydrostatic module is only switched on in the 0.0008°-resolution simulation. Surface forcing fields are provided hourly from the NCEP CFSR data (https://www.ncdc.noaa.gov/data-access/model-data/model-datasets).
Fine-scale parameterization
The strain-based fine-scale parameterization has been widely used to estimate the diapycnal diffusivity from the vertical thermohaline structure of the ocean. We compared the diapycnal diffusivity κρ below 200 m at all our observation sites between direct microstructure measurements and fine-scale estimates. At each site, the κρ is estimated for each 200 m segment based on the strain-based fine-scale parameterization of Kunze et al. (2006)43. Strain variance within the surface 200 m layer is discarded because it is caused by the sharper pycnocline rather than internal waves. Microstructure measurements in the same depth range were then averaged to get the microstructure-based κρ.
Salt finger
Usually, the density ratio is used to classify the double diffusion contribution to the vertical mixing44, Rρ =α\(\frac{\partial \theta }{\partial z}\)/β\(\frac{\partial S}{\partial z}\), where α =−\({\rho }_{w}\)−1 is the thermal expansion coefficient, β = −\({\rho }_{w}\)−1\(\frac{\partial {\rho }_{w}}{\partial S}\) is the haline contraction coefficient, the vertical coordinate is taken to be positive upward. Here to avoid extremely large Rρ values that alternate in sign, we use the Turner angle, \({T}_{u}={{{{{\rm{arctan }}}}}}(\alpha \bar{\frac{\partial \theta }{\partial z}}-\beta \bar{\frac{\partial S}{\partial z}})/(\alpha \bar{\frac{\partial \theta }{\partial z}}+\beta \bar{\frac{\partial S}{\partial z}})\), to discuss different types of double diffusion45,46. Rρ and \({T}_{u}\) are related by Rρ = −tan (\({T}_{u}\)+45). The water column is doubly stable for −45°< Tu < 45° (or 0 < Rρ < ±∞), “diffusive” double-diffusion when −90°< Tu < −45° (or 0 < Rρ < 1), and “salt-fingering” double-diffusion when 45° < Tu < 90° (or 1 < Rρ < ± ∞).
The buoyancy Reynolds number (\({R}_{{eb}}\)) is calculated by \({R}_{{eb}}=\varepsilon /(\nu {N}^{2})\)47,48, where \(\nu\) is the kinematic viscosity, and \(\nu =1.0{\times 10}^{-6}{{{{{\rm{m}}}}}}^{2}/{{{{{\rm{s}}}}}}\). The temperature \(({K}_{T}^{f})\) and salinity \(({K}_{S}^{f})\) diffusivity caused by salt-fingering is calculated according to Schmitt (1981)49 and Merryfield et al. (1999)50:
\({K}_{S}^{f}=0\) otherwise;
Where \({K}^{* }=1\times {10}^{-4}\,{{{{{\rm{m}}}}}}^{-2}{{{{{\rm{s}}}}}}^{-1}\), Rc = 1.6 and n = 6.
Data availability
The daily gridded products of merged absolute dynamic topography heights (MADT-H) and absolute geostrophic velocities (MADT-UV) can be obtained by Aviso+ (http://www.aviso.altimetry.fr) and Copernicus Marine Environment Monitoring Service (CMEMS http://marine.copernicus.eu/). The Niño3.4 index is available by NOAA/ESRL (https://stateoftheocean.osmc.noaa.gov/sur/pac/nino34.php). Underlying data for the main manuscript figures is included as Supplementary Data 1 and can be accessed from http://www.casodc.com/data/metadata-detail?id=1397806118125707266.
References
Fine, R. A., Lukas, R., Bingham, F. M., Warner, M. J. & Gammon, R. H. The Western Equatorial Pacific—a water mass crossroads. J. Geophys. Res. 99, 25063–25080 (1994).
Hu, D. X. et al. Pacific western boundary currents and their roles in climate. Nature 522, 299–308 (2015).
Gordon, A. L. The age of water and ventilation time-scales in a global ocean model. J. Geophys. Res. 91, 5037–5046 (1986).
Godfrey, J. S. A Sverdrup model of the depth-integrated flow for the World Ocean allowing for island circulations. Geophys. Astrophys. Fluid Dyn. 45, 89–112 (1989).
Sprintall J. et al. Detecting change in the Indonesian Seas. Front. Mar. Sci. https://doi.org/10.3389/fmars.2019.00257 (2019).
Richards, K. J., Kashino, Y., Natarov, A. & Firing, E. Mixing in the Western Equatorial Pacific and its modulation by Enso. Geophys. Res. Lett. 39, L02604 (2012).
Furue, R. et al. Impacts of regional mixing on the temperature structure of the equatorial Pacific Ocean. Part 1: Vertically uniform vertical diffusion. Ocean Modelling 91, 91–111 (2015).
Liu, Z. et al. Weak thermocline mixing in the North Pacific low-latitude western boundary current system. Geophys. Res. Lett. 44, 10530–10539 (2017).
Richards, K. J., Xie, S.-P. & Miyama, T. Vertical mixing in the ocean and its impact on the coupled ocean-atmosphere system in the eastern tropical Pacific. J. Climate 22, 3703–3719 (2009).
Zhang, Z., Qiu, B., Tian, J., Zhao, W. & Huang, X. Latitude-dependent finescale turbulent shear generations in the pacific tropical-extratropical upper ocean. Nat. Commun. 9, 4086 (2018).
Zhu, Y. & Zhang, R.-H. An Argo-derived background diffusivity parameterization for improved ocean simulations in the tropical Pacific. Geophys. Res. Lett. 45, 1509–1517 (2018).
Liu, C., Armin, K., Liu, Z., Wang, F. & Stammer, D. Deep-reaching thermocline mixing in the equatorial Pacific cold tongue. Nat. Commun. 7, 0–11576 (2016).
Molemaker, M. J., McWilliams, J. C. & Capet, X. Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 654, 35–63 (2010).
Taylor, J. R. & Ferrari, R. On the equilibration of a symmetrically unstable front via a secondary shear instability. J. Fluid Mech. 622, 103–113 (2009).
Thomas, L. N. & Taylor, J. R. Reduction of the usable wind-work on the general circulation by forced symmetric instability. Geophys. Res. Lett. 37, L18606 (2010).
D’Asaro, E., Lee, C., Rainville, L., Harcourt, R. & Thomas, L. Enhanced turbulence and energy dissipation at ocean fronts. Science 332, 318–322 (2011).
Thomas, L. N., Taylor, J. R., Ferrari, R. & Joyce, T. M. Symmetric instability in the Gulf stream. Deep Sea Res. II 91, 96–110 (2013).
Hoskins, B. J. Role of potential vorticity in symmetric stability and instability. Q. J. Roy. Met. Soc. 100, 480–482 (1974).
Thomas, L. N. & Lee, C. M. Intensification of ocean fronts by down-front winds. J. Phys. Oceanogr. 35, 1086–1102 (2005).
Joyce, T. M., Thomas, L. N. & Bahr, F. Wintertime observations of subtropical mode water formation within the Gulf stream. Geophys. Res. Lett. 36, L02607 (2009).
Molemaker, M. J., McWilliams, J. C. & Dewar, W. K. Submesoscale instability and generation of mesoscale anticyclones near a separation of the California undercurrent. J. Phys. Oceanogr. 45, 613–629 (2015).
Ruan, X., Thompson, A., Flexas, M. & Sprintall, J. “Contribution of topographically generated submesoscale turbulence to Southern Ocean overturning.” Nat. Geosci. https://doi.org/10.1038/ngeo3053 (2017).
Naveira Garabato, A. C. et al. Rapid mixing and exchange of deep-ocean waters in an abyssal boundary current. Proc. Natl Acad. Sci. USA 116, 13233–13238 (2019).
Gula, J., Molemaker, M. J. & McWilliams, J. C. Topographic generation of submesoscale centrifugal instability and energy dissipation. Nat. Commun. 7, 12811 (2016).
Marshall, J., Hill, C., Perelman, L. & Adcroft, A. Hydrostatic, quasi-hydrostatic, and nonhydrostatic ocean modeling. J. Geophys. Res. 102, 5733–5752 (1997).
Kashino, Y., Atmadipoera, A., Kuroda, Y. & Lukijanto. Observed features of the Halmahera and Mindanao Eddies. J. Geophys. Res. 118, 6543–6560 (2013).
Kashino, Y. et al. The water masses between Mindanao and New Guinea. J. Geophys. Res. 101, 12391–12400 (1996).
Zhang, L. L. et al. Seasonal and interannual variability of the currents off the New Guinea coast from mooring measurements. JGR Oceans https://doi.org/10.1029/2020JC016242 (2020).
Yuan, D., Zhang, Z., Chu, P. C. & Dewar, W. K. Geostrophic circulation in the tropical north Pacific Ocean based on Argo profiles. J. Phys. Oceanogr. 44, 558–575 (2014).
Wang, F., Wang, J., Guan, C., Ma, Q. & Zhang, D. Mooring observations of equatorial currents in the upper 1000 M of the western Pacific Ocean during 2014. J. Geophys. Res. 121, 3730–3740 (2016).
Osborn, T. R. Estimates of the local-rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89 (1980).
Richards, K. J. et al. Shear-generated turbulence in the equatorial Pacific produced by small vertical scale flow features. J. Geophys. Res.-Oceans 120, 3777–3791 (2015).
Miles, J. W. On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508 (1961).
Thorpe, S. A. The Turbulent Ocean (Cambridge University Press, 2005).
Richards, K. J. & Edwards, N. R. Lateral mixing in the equatorial Pacific: The importance of inertial instability. Geophys. Res. Lett. 30, 1888 (2003).
Tsuchiya, M. Upper Waters of the Intertropical Pacific Ocean. Johns Hopkins Oceanographic Studies 4 50p (The Johns Hopkins University Press, 1968).
Qu, T. D., Mitsudera, H. & Yamagata, T. On the western boundary currents in the Philippine sea. J. Geophys. Res. 103, 7537–7548 (1998).
Shakespeare, CallumJ. “Curved density fronts: Cyclogeostrophic adjustment and frontogenesis. J. Phys. Oceanogr. 46, 3193–3207 (2016).
Jeffery, N. & Wingate, B. The effect of tilted rotation on shear instabilities at low stratifications. J. Phys. Oceanogr. 39, 3147–3161 (2009).
Buckingham, C. E., Gula, J. & Carton, X. The role of curvature in modifying frontal instabilities. J. Phys. Oceanogr. 51, 299–315 (2021).
Jochum, M., Fox-Kemper, B., Molnar, P. H. & Shields, C. Differences in the Indonesian seaway in a coupled climate model and their relevance to Pliocene climate and El Niño. Paleoceanography https://doi.org/10.1029/2008PA001678 (2009).
Naveira Garabato, A. C. et al. Vigorous lateral export of the meltwater outflow from beneath an Antarctic ice shelf. Nature 542, 219–222 (2017).
Kunze, E. Limits on growing, finite-length salt fingers: A Richardson number constraint. J. Marine Res. 45, 533–556 (1987).
Turner, J. S. Buoyancy Effects in Fluids (Cambridge University Press, 1973).
Ruddick, B. R. A practical indicator of the stability of the water column to double-diffusive activity. Deep-Sea Res. 30, 1105–1107 (1983).
Mcdougall, T. J., Thorpe, S. A. & Gibson, C. H. Small‐scale turbulence and mixing in the ocean: A glossary, in Small‐scale turbulence and mixing in the ocean. Vol. 46, (Elsevier, 1988).
Gregg, M. C. Mixing in the thermohaline staircase east of Barbados. Elsevier Oceanography Series, Vol. 46, 453–470 (Elsevier, 1988).
Inoue, R., Yamazaki, H., Wolk, F., Kono, T. & Yoshida, J. An estimation of buoyancy flux for a mixture of turbulence and double diffusion. J. Phys. Oceanogr. 37, 611–624 (2007).
Schmitt, R. W. Form of the temperature–salinity relationship in the central water: Evidence for double-diffusive mixing. J. Phys. Oceanogr. 11, 1015–1026 (1981).
Merryfield, W. J., Holloway, G. & Gargett, A. E. A global ocean model with double-diffusive mixing. J. Phys. Oceanogr. 29, 1124–1142 (1999).
Acknowledgements
H.Z. is supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB42000000), the National Natural Science Foundation of China (NSFC) projects (41876009,41376032), and grant XDA11010205. WKD is supported by the National Science Foundation through grants OCE-1829856, OCE-1941963, OCE-2023585 and a CNRS/ANR grant in support of the ‘Make Our Planet Great Again’ initiative started by E. Macron. Special thanks to the crew of the R/V KEXUE on the NSFC Open Research Cruise (Cruise No. NORC2017-09) for their expertize and help in collecting the data. We thank Dr. Ya Yang for providing the real-time SSHA map during the cruise, Dr. Yuchao Zhu for sharing the code of fine-scale parameterizations, Dr. Xiang Li for his help in the coding, and Dr. Chuanyu Liu for his kind suggestion. We thank Yuhuan Xue for his instruction of the instrument operation. Special thanks to Dr. Kelvin Richards for the valuable discussion to improve the manuscript. We thank NSFC Shiptime Sharing Project (41649909) and Dr. Dongliang Yuan for the coordination of this project. We appreciate Dr. Baylor Fox-Kemper and another two anonymous reviewers for their valuable comments.
Author information
Authors and Affiliations
Contributions
H.Z. obtained funding to support the direct microstructure Profiler (MSP)measurements and research, designed and implemented the cruise experiments, served as the chief scientist for the cruise, conducted the MSP observations, and oversaw the data analyses. She leads the drafting of the manuscript. W.D. contributed to the manuscript writing, interpretations, and discussions that led to the final figure design. W.Y. attended the MSP measurements and did the hydrographic and MSP data analyses. H.L. attended the MSP measurements and did the data analyses. X.C. did the MITgcm model simulation and related analyses and writing. R.L. was responsible for the configuration of the MSP and attended the MSP measurements. C.L. prepared the installation of the MSP. G.G. helped with the coding of the model simulation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Baylor Fox‐Kemper and the other, anonymous, reviewers for their contribution to the peer review of this work. Primary Handling Editors: Regina Rodrigues and Clare Davis.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhou, H., Dewar, W., Yang, W. et al. Observations and modeling of symmetric instability in the ocean interior in the Northwestern Equatorial Pacific. Commun Earth Environ 3, 28 (2022). https://doi.org/10.1038/s43247-022-00362-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00362-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.