Abstract
Mountainous topography reflects an interplay between tectonic uplift, crustal strength, and climate-conditioned erosion cycles. During glaciations, glacial erosion increases bedrock relief, whereas during interglacials relief is lowered by rockwall erosion. Here, we show that paraglacial, frost cracking and permafrost processes jointly drive postglacial rockwall erosion in our research area. Field observations and modelling experiments demonstrate that all three processes are strongly conditioned by elevation. Our findings on catchment scale provide a potential multi-process explanation for the increase of rockwall erosion rates with elevation across the European Alps. As alpine basins warm during deglaciation, changing intensities and elevation-dependent interactions between periglacial and paraglacial processes result in elevational shifts in rockwall erosion patterns. Future climate warming will shift the intensity and elevation distribution of these processes, resulting in overall lower erosion rates across the Alps, but with more intensified erosion at the highest topography most sensitive to climate change.
Similar content being viewed by others
Introduction
The topography of glaciated mountains reflects an interplay between tectonic uplift, crustal strength, and climate1,2. During glaciations, the glacial buzzsaw3,4 can limit summit elevations, but glacial erosion mostly increases relief by carving deep valleys5,6. During and after deglaciation, non-glacial hillslope erosion processes, that tend to limit relief, takeover. Glacier retreat typically exposes steep, unsupported rockwalls that erode via paraglacial slope failure4,7,8. Paraglacial slope failures are directly conditioned by glacial activity9,10,11, and are prepared and triggered by glacial debuttressing12,13,14, internal stress redistribution15,16 and seismic activity17,18 following deglaciation. Periglacial processes operate on the same rockwalls, and include frost cracking and permafrost dynamics3,4,7,8. Frost cracking is a climate-driven19 mechanical weathering process that breaks down rock20. Permafrost is a state of frozen ground, which can stabilise rock by increasing shear resistance21, but can also amplify frost cracking processes22 and cryogenic stresses, which can, along with permafrost degradation, weaken rock masses23. These periglacial processes prime and trigger rockfalls24, contributing to rockwall erosion, and have been conceptualised as a relief-limiting frost buzzsaw25.
As paraglacial and periglacial processes cohabit similar topography, postglacial erosion of most alpine rockwalls is likely to be driven by a combination4,7,8 of glacier retreat26,27,28,29, frost cracking30,31,32 and permafrost processes33,34,35. Climate warming will modify the intensity and overlapping distribution of all three processes, and so anticipating trajectories of alpine topography evolution and rockfall hazard requires holistic quantification of these drivers. Investigation of these processes has tended to be in isolation and seldom at a landscape-scale, such that the relative contributions of these processes and their spatial distribution has hitherto never been quantified.
Here we provide a systematic analysis of postglacial rockwall erosion drivers by the integration of field and modelling experiments. We use empirically-validated models to evaluate the contributions of permafrost, frost cracking, and glacier retreat to rockwall erosion within an alpine basin. Our data indicate that paraglacial and periglacial processes combine to control climate-driven rockwall erosion in our research area and that both are elevation dependent, contributing to increased erosion rates at higher elevations. Our findings provide a potential explanation of rockwall erosion rate pattern that we compiled for the European Alps that is characterised by increasing erosion with increasing elevations. This relationship is amplified at catchments with mean rockwall elevations above 2500 m (all elevations refer to m above sea level). As these processes are linked to climate, climate warming will reduce periglacial and paraglacial erosion at lower elevations but intensify it at higher elevations. As a consequence, we propose that periglacial and paraglacial processes jointly exert a limit on postglacial summit heights, extending the existing frost buzzsaw hypothesis25.
Results and discussion
Rockwall erosion in the European Alps
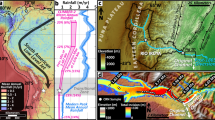
The most unstable alpine rockwalls exist within environments of climate extremes and climate sensitivity. An analysis of the glacier inventory36 for the European Alps reveals that 85% of extant glaciers are located above 2500 m, and the majority (82.4%) are very small (<0.5 km2) (Fig. 1c). Smaller glaciers are particularly sensitive to climatic changes37, so future climate warming will drive disproportionate retreat of small glaciers. Permafrost affects 6220 km2 (index ≥ 0.5) of the European Alps38, existing at elevations of 2200–4400 m such that most glaciers in the Alps are embedded within permafrost terrain. Consequently, high-elevation rockwalls are exposed to both paraglacial and periglacial process dynamics39. To explore the impact of these processes on erosion, we compiled rockwall erosion rates across the European Alps, which we classified into short-term (<10 a)40,41,42,43,44,45,46,47, mid-term (10–2500 a)43,48,49,50 and long-term (>2500 a) rates31,40,51,52,53,54,55,56,57,58. The compilation exhibits no clear spatial pattern (Fig. 1a) but reveals an increase of erosion with increasing elevation (Fig. 1b; r2 0.46, p < 0.001). This relationship is stronger for areas with mean rockwall elevations above 2500 m (r2 = 0.64, p < 0.001).
a Compiled short-term, mid-term and long-term erosion rates in the European Alps along with the extent of LGM glaciation144, current glaciers36 and permafrost distribution38,114(DEM source: European Digital Elevation Model). b Relationship between erosion rates and elevation. The linear relationship increases from r2=0.46 for all erosion rates to r2=0.63 (p < 0.001) when limited to catchment areas with mean elevation >2500 m. c Inset histogram: frequency of very small glaciers (<0.5 km2; light blue), small glaciers (0.5 to 5 km2, blue), medium-sized glaciers (5 to 10 km2, turquoise) and large glaciers (>10 km2, dark blue) in the Alps. Main graph: Elevation of the terminus36 of different sized glaciers (using same colours as for inset histogram) and permafrost distribution (purple line)38,114. d Comparison of short-, mid- and long-term erosion rates, to evaluate influence of integration period (i.e. time-scale) on calculated erosion rates. Error bars indicate the minimum and maximum range of rockwall elevation and erosion rates. For detailed erosion rates including used methods, see Supplementary Table 1.
At locations with mean rockwall elevations below 2500 m, the long-term erosion rates range from \({0.252}_{-0.142}^{+0.148}\) mm a−1 to \({0.5}_{-0.15}^{+0.5}\) mm a−1 40,51,52,54,55 and are higher than the short-term erosion rates of \({0.05}_{-0.02}^{+0.03}\) to \({0.225}_{-0.075}^{+0.075}\) mm a−1 40,41 from equivalent elevations. An explanation for this may be that long-term erosion rates reflect a period of more intense periglacial processes and paraglacial adjustment59 (consistent with conceptual paraglacial exhaustion curves) that would have existed immediately following cool Last Glacial Maximum (LGM) conditions60. Long-term erosion rates may also integrate a period of elevated post-glacial seismic activity, suggested to have increased mass movements in some locations18. In contrast, the short-term rates below 2500 m represent areas that are presently glacier- and permafrost-free and with relatively mild frost cracking32.
For rockwall elevations above 2500 m, which are potentially affected by permafrost (Fig. 1c), long-term erosion rates range from \({0.252}_{-0.142}^{+0.148}\) to \({3.2}_{-1.8}^{+1.3}\) mm a−1 31,51,52,53,56,57,58, and mid-term rates are between \({0.83}_{-0.416}^{+0.629}\) and 2.9 mm a−1 43,48,50. The short-term erosion rates are generally greater, ranging from \({0.4}_{-0.3}^{+0.3}\) to 14.4 mm a−1 41,42,43,44,45,46,47. The greatest erosion rates are from glacier headwalls, ranging from \({1.9}_{-1.55}^{+8.40}\) to 8.4 mm a−1 44,45,46, or high-elevation permafrost-affected rockwalls with rates of up to 14.4 mm a−1 43. More intense modern erosion rates at high elevations, compared to low elevations, have previously been hypothesised to reflect permafrost degradation and active-layer thaw43,45,46 or increased frost weathering within bergschrunds47, but such hypotheses have not been robustly tested and have tended to ignore paraglacial effects.
The time-scale dependant contrast in erosion rates above and below 2500 m suggests that elevation, though its influence on local climate, is a fundamental control on erosion processes. The patterns we observe are unlikely due to data preservation bias or the Sadler effect61 (like has previously been observed in glaciated landscapes with short term rates exceeding long-term rates, interpreted as bias62). The data we compiled reveal no consistent pattern of short-term erosion rates being greater than long-term rates (Fig. 1d), with instead long-term rates exceeding short-term rates at lower elevations. Sedimentary incompleteness can introduce bias61, but the long-term rockwall erosion rate data are largely from coarse-grained sedimentary archives such as talus slopes40,49,50,51,52,53,54,58 or rock glaciers48,57 that are unlikely to have major sediment depletion gaps. There is limited opportunity for reworking and erosion of such coarse-grained deposits, which are located mostly within low-connectivity systems, such as disconnected glacial hanging valleys, and are net stores of postglacial sediment63. Furthermore, as our data compilation is from a single orogen we can exclude bias arising from comparing sites that experience markedly different tectonic regimes. In the following section, we evaluate the hypothesis that elevation is a first-order control on rockwall erosion rate patterns through its influence on periglacial and paraglacial processes.
Rockfall processes and potential influencing factors
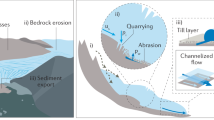
To explore the relationship between elevation and rockwall erosion rate for the European Alps, we quantified and modelled periglacial and paraglacial processes and compared these to patterns of contemporary and post-LGM rockfall activity in an alpine valley. We chose the Hungerli Valley (Fig. 2), a hanging valley of the Turtmann Valley, itself a tributary of the Rhône Valley, Valais, in the southern Swiss Alps. The Hungerli Valley hosts a very small (0.045 km2 in 201764) cirque glacier (Rothorn Glacier), steep rockwalls, and sedimentary landforms (moraine, rock glaciers65 and talus slopes63) disconnected from the Turtmann Valley63 (Supplementary Fig. 1). The rockwalls have been glacially eroded and experienced phases of glacial advance and retreat since the LGM. With periglacial conditions and a glacier terminus above 2850 m, the Hungerli Valley is representative of many alpine valleys in the European Alps (Fig. 1c). The rockwalls studied occur on the north and north-east facing slopes of Hungerlihorli peak and Rothorn cirque, respectively, with elevations from 2500 to 3277 m.
a Scanned rockwalls of the Hungerli Valley with highlighted glacier history (coloured lines). Instrumented rockwalls (red point), investigated talus slopes (brown polygons) and scan positions (red stars) are highlighted (source: swissALTI3d from swissTopo). b 3D representation of scanned rockwall area (red rectangle), modelled permafrost distribution and quantified rockfall volumes for 2016 to 2019 (source: swissALTI3d and swissIMAGE25 from swissTopo).
We detected 263 rockfall events in the valley between 2016 and 2019 using annually repeated terrestrial laser scanning. Rockfall volumes ranged from 0.1 to 159.4 m3 (Fig. 3a), with a median of 0.26 m3, and 96% being smaller than 10 m3 (Fig. 4e). The rockfall magnitude-frequency data exhibit a typical inverse relationship (N2016-19 = 17.59 V−0.68; Fig. 3a), with a power law exponent, within the range (−0.48 to −0.77) of those previously published for alpine rockwalls40,43,47,66, that differs little between the three years (N2016-17 = 19.08 V−0.57, N2017-18 = 17.97 V−0.76, N2018-19 = 18.01 V−0.65). Studied rockwalls possess a modal elevation of 2900–3000 m (using 100 m elevation bands; Fig. 4a). The median rockfall volume scales positively with increasing elevation below the 3000–3100 m elevation band and negatively above this band (Fig. 4e), rather than following the distribution of available rockwall area proportionally (Fig. 4a). Most high-magnitude (> 10 m3) events occurred between 2900 and 3200 m, which encompasses most of the elevation range of the present-day glacier (Fig. 2).
a Rockfall frequency-magnitude distribution for individual periods (2016–17 in yellow, 2017–18 in red, 2018–19 in green) and for the entire 2016–2019 period (in grey) in the Hungerli Valley. Linear correlation r2 of power laws is between 0.98 and 0.99 with p < 0.001. b PCA of rockfall variance between five variables: deglaciation age (i.e. proxy for paraglacial condition, elevation (proxy for frost cracking), MARST (proxy for permafrost), slope angle, and rockfall volume.
a Rockwall area distribution per 100 m elevation band. The presence of scree and glacial cover reduces the area of exposed rockwall within the 2800–2900 m and 3000–3100 m elevation bands (Fig. 2). b Modelled frost cracking intensities for different rock types, plotted against elevation. For detailed mean and annual frost cracking, see Supplementary Fig. 7. c The elevation distributions of newly deglaciated areas from the LGM to 2017 with mean elevation as diamonds. d MARST plotted against elevation; permafrost is shown in violet and permafrost-free areas are light blue with mean elevation as diamonds. e Rockfall volumes at different elevation bands with solid bars indicating median values and points are statistical outliers. Short-term erosion rates plotted against (f) elevation, (g) deglaciation age and h MARST. Error bars indicate the minimum and maximum range of rockwall elevation or erosion rate. Colours in g and h refer to applied colour schemes in c and d.
As a preliminary exploration of rockfall patterns in the Hungerli Valley, we used a principal component analysis (PCA) to examine statistical relationships between modelled or inferred periglacial and paraglacial conditions, and topography. For each rockfall we related the deglaciation age (i.e. a paraglacial proxy; from historical aerial photos, moraine positions, and ice surface reconstructions), mean annual rock surface temperature (MARST; from a rock surface temperature driven permafrost model67), elevation (i.e. a frost cracking proxy), slope angle (i.e. shear stress proxy), and the rockfall volume. The results show that the first two PCA dimensions explain 74.0% of the data variation (Fig. 3b), with a strong relationship found for deglaciation age (Eigenvalue 0.84) and MARST (0.72), and an inverse relationship with elevation (-0.85) on dimension 1 (PC1). The results suggest that all three elevation-dependent processes (deglaciation history, permafrost, and frost cracking) correlate, and are therefore potentially involved in explaining the modern rockfall activity at Hungerli Valley. The slope angle of the rockfall (low eigenvalue of −0.04) has low correlation to the other variables. We suggest this is due to the steep nature of the rockwalls, such that threshold slope conditions and sensitivity to triggers exist over much of the rockwall68,69. Consequently, at the scale of individual rockwalls, the external drivers (paraglacial stress release and debuttressing, and periglacial processes), all of which are elevation dependent, may be more important than slope form (i.e. slope oversteepening from glacial erosion) at explaining the local distribution of rockfall5,70,71. Rockfall volume (−0.20) relates to PC2. Rockfall volume is likely to be influenced by differences in the fractures spacings and patterns of the rock masses present in the valley, which while not explicitly included in the PCA, are captured by variation in elevation and possibly slope angle.
Spatial distribution of rockfall driving processes
Here we refine and analyse the spatial distribution of the three most correlated PCA variables; frost cracking, MARST (permafrost) and deglaciation age (paraglacial adjustment). Whereas for the PCA we treated elevation as a proxy for frost cracking, here we modelled frost cracking by applying a thermo-mechanical model72 to measured rock surface temperatures32. Modelled frost cracking affects all rockwall locations in the Hungerli Valley, but is most intense within the three highest permafrost-affected rockwalls (RW1-3; Supplementary Fig. 5), and varies by rock type/strength within each elevation band (Supplementary Fig. 7). Rock type ranges from weaker schisty quartz slate with aplite inclusions in the Rothorn cirque to stronger schisty quartz slate with inclusions of amphibolite and aplite in the Hungerlihorli (Supplementary Figs. 1 and 2)73. Regardless of the influence of lithological variations (Fig. 4b), a strong (non-monotonic) relationship was persistent between frost cracking and elevation. Our model results suggest frost cracking increases with elevation up until 3000 m, thereafter reducing at higher elevations (Fig. 4b). The modelled penetration depth of frost cracking is mostly shallower than 0.5 to 2 m, and exhibits increasing depth at higher elevations, up until ~3000 m (Supplementary Fig. 6). The modelled frost cracking pattern corresponds to the measured fracture spacing32, with more intense frost cracking generating more near-surface fracturing. As potential rockfall size is limited by the spacing of fractures, areas of more intense frost cracking will likely produce more numerous but smaller rockfalls, and be unlikely to trigger large events (>10 m3).
Modelled MARST (a proxy for permafrost) is inversely related to elevation in the Hungerli Valley (Fig. 4d), such that colder MARST and permafrost likelihood increase at higher elevations. Rockwall with MARST below −3 °C is located at a mean elevation of 3113 m (1st Q. = 2989 m; 3rd Q. = 3190 m), whereas rockwall with MARST between −1 to 0 °C is located at a mean of 2901 m (1st Q. = 2765 m; 3rd Q. = 3034 m) (Fig. 2d). Permafrost-free areas (taken to have positive MARST) exist mostly below 2760 m, whereas above 2800 m, 75% of the rockwall area is frozen, and above 3100 m nearly the entire rockwall is affected by permafrost (Fig. 2). While MARST provides an indication of permafrost presence66,74, it cannot be used to assess the depth of seasonal warming and thaw, which influence rockfalls by decreasing shear resistance21,75,76,77 or increasing hydrostatic pressure21. The depth of warming and thaw depend additionally on seasonal temperature fluctuations and insulating snow cover78, which are challenging to model at a landscape scale. Consequently, we use MARST only as a proxy for permafrost presence, which we in turn use to identify rockwalls that are likely to have permafrost-related instability processes present (without modelling the processes themselves).
The deglaciation history since the LGM has resulted in a general trend for newly exposed rockwalls to occur at higher elevations over time (Fig. 4c). The general trend deviates because glacier retreat can involve thinning (vertical retreat) and terminus recession (planform retreat), both of which expose new rockwall but at different elevations (as evidenced by historic photos; Supplementary Fig. 3 and Fig. 2a). Between the LGM and Egesen, the thickness of the valley glacier decreased, and newly-exposed rockwalls (mean = 2653 m; 1st Q. = 2631 m; 3rd Q. = 2680 m; Fig. 4c) were restricted to the Hungerlihorli (Fig. 2). Between the Egesen and Little Ice Age (LIA), retreat of the valley glacier involved thinning and lateral retreat of the Rothorn cirque glacier, exposing new rockwall across a large elevation range (1st Q. = 2886 m; 3rd Q. = 3162 m; Fig. 4c). Since the 19th century (i.e. LIA), new rockwall exposure in Hungerli Valley has been occurring generally at higher elevations over time (Fig. 4c); between 1882 and 1929 the mean elevation of newly exposed rockwall was 2958 m (1st Q. = 2909 m; 3rd Q = 2982 m), which increased to 3059 m (1st Q. = 2986 m; 3rd Q = 3127 m) between 1964 and 2019. For context, the present-day Rothorn Glacier is located between 2850 and 3100 m (Fig. 2a).
Short-term rockwall erosion rates
To quantify short-term rockwall erosion in the Hungerli Valley, we converted our contemporary rockfall data (volumes, m3) into annual rockwall erosion rates (mm a−1) by dividing by the area of scanned rockwall. We then explored how erosion rate varies with the patterns of frost cracking, permafrost and paraglacial processes described above. The mean rockwall erosion rate of the entire scanned area was 0.86 mm a−1 between 2016 and 2019, but varies with elevation (assessed for 100 m elevation bands; Fig. 4f). Between 2600 and 3000 m the mean rockwall erosion rates increased with elevation, from 0.02 mm a−1 at the 2600–2700 m elevation band to 2.04 mm a−1 at the 2900–3000 m band. At higher elevations, the rates became smaller (1.52 mm a−1 at 3000–3100 m; 1.73 mm a−1 at 3100–3200 m, and 0.02 mm a−1 above 3200 m). The elevation bands with the greatest erosion rates, between 2900 and 3200 m (Fig. 4f), correspond to elevations with the most intense frost cracking (Fig. 4b). While frost-cracking rates are known to vary with elevation32,72,79, hitherto frost-cracking rates had not been quantitatively and directly linked to rockwall erosion rates. Previous research suggested that frost cracking is positively related to catchment-wide erosion but inversely related to elevation80. This contrasts with our observed positive relationship between rockwall erosion rates and elevation. Catchment-wide erosion rates are measured from stream sediments that integrate multiple erosion processes throughout a catchment81. Moreover, rockwall erosion products (i.e. coarse rockfall debris) tend to be stored (e.g. in talus) with poor downstream connectivity. Consequently, and especially because rockwalls are underrepresented according to hypsometric curves3,7, the contribution of rockwall erosion to catchment-wide erosion and the relationships between rockwall erosion and its drivers are poorly captured by catchment-wide erosion rate measurement approaches.
Rockwall erosion rates in the Hungerli Valley also vary with deglaciation age, generally increasing from the oldest to the most recently deglaciated rockwalls. Ice-free rockwalls (on the Hungerlihorli) and rockwalls deglaciated between the LGM and Egesen had erosion rates of \({0.25}_{-0.10}^{+0.14}\) and \({0.04}_{-0.01}^{+0.01}\) mm a−1, respectively. Allowing for the possibility of a cold-based glacier occupying the Hungerlihorli (i.e. reducing the area of exposed rockwall) between LGM and Egesen, the erosion rate increases to \({0.13}_{-0.0}^{+0.06}\) mm a−1. Between the Egesen and 1882, a large part of the cirque became glacier-free and 30% of all recorded rockfalls, including the largest (159 m3), occurred within this area. These rockfalls contributed to an erosion rate of \({0.79}_{-0.20}^{+0.13}\) mm a−1. For rockwalls deglaciated between 1882 and 1929 there was an erosion rate of \({0.24}_{-0.13}^{+0.13}\) mm a−1, which increases to a rate of \({0.92}_{-0.88}^{+0.88}\) mm a−1 for those deglaciated between 1929 and 1964. The greatest rate, of \({5.69}_{-0.44}^{+0.44}\) mm a−1, was for rockwalls deglaciated between 1964 and 2019 (Fig. 4g). In general, rockfalls were prevalent in proximity to the extant glacier, with 77 rockfalls or 29% of all measured events, including four >10 m3 sourced from rockwalls deglaciated between 1964 and 2019. Enhanced rockfall erosion in proximity to a retreating cirque glacier margin has been observed elsewhere44 for which paraglacial processes such as thermo-mechanical stresses13, unloading stresses amplified by cirque glacier erosion12,82, or increased frost cracking within a bergschrund83 may play a role. While we do not know which processes operate at the Hungerli Valley, the rockwall erosion rate patterns, at least partly, appear to reflect paraglacial adjustment9,84. Moreover, while some studies have suggested paraglacial rockwall adjustment (i.e. stress release and fracture propagation) operates at a millennial timescale12,15, our data show that adjustment can be more rapid (i.e. over decadal timescales). The older rockwalls in the Hungerli Valley may still be experiencing gradual paraglacial adjustment, but the rates of adjustment have slowed over time, as predicted by paraglacial exhaustion curves9,84.
We also find a relationship between modelled permafrost and rockfall erosion rates. Permafrost-affected rockwalls revealed higher erosion rates ranging from \({0.27}_{-0.01}^{+0.01}\) to \({1.90}_{-0.04}^{+0.04}\) mm a−1 than permafrost-free rockwalls (\({0.14}_{-0.01}^{+0.00}\) mm a−1; Fig. 4h). Erosion rates decrease with increasing MARST. While MARST gives information about potential presence of permafrost, it does not reflect the magnitude of active-layer thaw21,85 or cryostatic pressures from refreezing23, which drive rockfall generation. However, 92% of all rockfall events (and 97% by volume) were released from permafrost-affected rockwalls, producing an overall erosion rate of \({1.01}_{-0.02}^{+0.02}\) mm a−1, suggesting the importance of permafrost presence in rockwall erosion.
Long-term rockwall erosion rates
To evaluate rockwall erosion rates within a longer temporal framework, we used geophysics to measure the volume of three talus accumulations in the Hungerli Valley. Talus slope-1 (TS1)—within the cirque and below a rockwall source area with elevation of 2900–3000 m (Fig. 2a)—integrates 55 years of rockfall accumulation, giving a rate of \({50.7}_{-10.3}^{+10.9}\,\)mm a–1. This erosion rate is one order of magnitude higher than those measured using the contemporary (i.e. 2016–2019) rockfall data from the same (2900–3000 m) elevation band (2.04 mm a−1; Figs. 4f and 5f) or from rockwalls of equal deglaciation age (\({5.69}_{-0.44}^{+0.44}\) mm a–1; Fig. 4g).
a Compiled mean short-term, mid-term and long-term erosion rates from the European Alps, complemented by short-term, mid-term and long-term erosion rates from the Hungerli Valley. Error bars indicate the range in elevation and erosion rate. b The same data as plot (a), but for elevations of 2500 m and above only. c Short-term erosion rates only, for the Hungerli Valley. d Mean short-term erosion rates of the Hungerli Valley versus the mean elevation of each deglaciation age class. Error bars show range of erosion rates and 1st and 3rd quartile of elevation of deglaciation age class (see Fig. 4c). e Short-term erosion rates of the Hungerli Valley versus mean elevation of MARST class. Error bars show 1st and 3rd quartile of elevation of MARST class (see Fig. 4d). f Data from plots (c-e) plotted together with mid-term and long-term erosion rates determined from talus slopes. For colour scheme of (c–f) see Fig. 4.
Talus slope-2 (TS2) and Talus slope-3 (TS3) are located at the base of Hungerlihorli peak, an area last glacierized during the Egesen stage (Younger Dryas), and integrate 10 to 12 ka of rockfall activity. The contributing rockwalls are located between 2600 and 2891 m for TS3 and between 2620 and 2891 m for TS2, and their talus accumulations suggest rockwall erosion rates of \({1.0}_{-0.4}^{+0.6}\) mm a−1 (TS3) to \({1.2}_{-0.5}^{+0.6}\) mm a−1 (TS2). The erosion rates are one to two orders of magnitude higher than those measured using the contemporary rockfall (i.e. laser scanning) data from the equivalent elevation bands (0.02 to 0.31 mm a−1; Figs. 4f and 5f). It is probable that the rates from long-term measurements exceed those of the short-term measurements due to integrating an aggressive period of paraglacial adjustment (expected soon after glacier retreat), and more intense permafrost thaw and frost cracking during colder phases (e.g. LIA) of the Holocene. The long-term measurements possibly also integrate episodic co-seismic rockfall activity, with more than 36 Mw 4.0 and larger events recorded in Switzerland since 250 AD86 and possibly increased seismic activity following deglaciation like found elsewhere17,18.
Elevation-dependent paraglacial and periglacial processes and their implications for rockwall erosion patterns in the European Alps
The short-term and long-term erosion rates in the Hungerli Valley both share the same positive relationship between elevation and erosion rates that was found for data compiled for the entire European Alps (Fig. 5a), especially at elevations above 2500 m (Fig. 5b). Our analyses from the Hungerli Valley suggest that this relationship is driven by frost cracking, permafrost occurrence and deglaciation age, all of which vary with elevation. Our modelled frost cracking magnitudes are elevation-dependent (Fig. 4b) and correspond to erosion rates increasing with elevation (Fig. 5c) up until a threshold elevation. Above this threshold, frost cracking decreases with increasing elevation72,79 due to a decreasing availability of water (essential for frost cracking) at higher elevations72,87. This decreasing pattern is reflected in our frost cracking results, with reduced frost cracking at 3150 m (Fig. 4b), but the decrease will be more apparent for rockwalls that reach elevations higher than those of the Hungerli Valley. It is likely that frost cracking will be relatively minor on the highest summits of the Alps in the present climate, but will increase with further warming.
When we substitute elevation for MARST (i.e. permafrost), we see that permafrost presence contributes to greater erosion rates at higher elevations at our research area (Fig. 5e). Based on the European Alps permafrost model, most rockwalls above ~2800 m are potentially affected by permafrost38, and therefore are likely to be experiencing elevated rockwall erosion rates, as presumed by previous high-elevation studies41,42,43,45,46. The development of regional scale models that can quantify the magnitude of active-layer thaw and permafrost warming effects (in addition to permafrost presence) will help to further evaluate the patterns we observe.
Substituting elevation for deglaciation age (Fig. 4c) reveals that short-term erosion rates increase with elevation in the Hungerli Valley (Fig. 5d), suggesting an elevation dependency to paraglacial adjustment. Over 80% of glaciers in the Alps are very small and located above 2500 m. These glaciers are very sensitive to climatic changes37 and are retreating rapidly (in length but also laterally, especially within cirques), as observed for the Rothorn Glacier (Fig. 2). Consequently, our catchment scale study suggests that paraglacial processes will be responsible for a short-term increase (i.e. rapid adjustment) in rockwall erosion, especially at elevations above 2500 m.
Permafrost, frost cracking, and glacier retreat do not operate in isolation, but overlap and interact. Like for most alpine valleys, rockwalls deglaciated since the LIA in our research area (Fig. 4c) are located at elevations with permafrost (Fig. 4d). When warm-based glaciers retreat within permafrost terrain, rockwalls lose the insulating effect of the ice88,89, allowing permafrost to encroach into the newly exposed rockwall89, potentially increasing rockwall erosion23 until the climate has sufficiently warmed to degrade all permafrost at those elevations. In a similar way, glacier retreat can introduce new thermo-mechanical stresses by exposing rockwalls to ambient temperature fluctuations13. Glacier retreat can also expose large bedrock fractures lengthened by glacier stresses12,14,15. As frost cracking is sensitive to crack length32,72,87 and larger cracks freeze first90, the exposure of large cracks can facilitate more efficient frost cracking32. Permafrost presence can also amplify frost cracking, through bidirectional freezing22, which produces the highest rates in frost cracking models32. As a consequence of these interactions, climate warming has a profound, but non-uniform, effect on the breakdown of rockwalls by shifting the distribution and intensity of multiple paraglacial and periglacial processes. Climate warming in the European Alps is causing the retreat, and eventual disappearance, of very small glaciers37, which will drive paraglacial rockwall adjustment and the temporary growth—but long-term warming and degradation—of permafrost33. That warming and retreat will intensify frost cracking at higher elevations and in proximity to retreating glaciers, respectively, whereas at lower elevations the warming will reduce frost cracking32. Although lower elevations will experience a reduction of periglacial and paraglacial processes, other climate-dependent weathering processes19 such as chemical and thermal weathering91,92,93 may replace them as the main drivers of rockwall erosion94. Over time, the areas of most intense periglacial and paraglacial processes and resulting erosion will shift to higher elevations, in locations where higher topography exists.
Methods
Rockwall erosion rates in the European Alps
We compiled existing rockwall erosion rate data for the European Alps (Supplementary Table 1) and classified them into short-term (≤10 years), mid-term (>10 to ≤2500 years) and long-term (>2500 years) erosion rates. Short-term erosion rates were derived from rockfall collectors41 or terrestrial laserscanning campaigns40,42,43,45,46,47 and integrate several years of rockfall activity (Fig. 1d). Due to the short integration time, these erosion rates are unlikely to include low-frequency high-magnitude events; however, if they do then the rates can be grossly over-estimated. Mid-term erosion rates (integrating 10 to 2500 years) were derived from lichenometric measurements50, averaged rates from talus-derived rock glacier deposits48 or up-scaled rates using rockfall frequency-magnitude relationships43,49. Long-term rockwall erosion rates (integrating > 2500 years) were provided from geophysical imaging51,52,53,54 or morphological estimation40,58 of talus slope accumulations or rock glacier deposits57, and from cosmogenic nuclide exposure age dating31,55,56. Mid- to long-term rates potentially capture paraglacial and periglacial processes from pre-historical glacier recession and associated climate conditions (e.g. LIA or Younger Dryas; Fig. 1d). We compiled the mean, and the lower and upper range of the erosion rates to reflect the variability of erosion within catchments, and evaluated the relationship between erosion rate and elevation (Fig. 1b). If rockwall elevations were not reported in the original studies, they were derived from topographic maps or Google Earth.
Reconstruction of glacier retreat history of the Hungerli Valley
We used an orthophoto from 2017, historical photos, moraine locations and a regional study on LGM glacier thickness95 to reconstruct the deglaciation history of the Hungerli Valley. To assess the locations and elevations of newly exposed rockwall as a result of glacier retreat since the LGM96, we used a regional study that suggests an ice surface elevation of 2800 m95 for the main trunk glacier in proximity to Hungerli Valley at the LGM. Based on the ice surface isoline, the glaciated areas at the LGM were coherently enlarged to the cirque and firn basin headwalls97. For pre-historical rockwall exposure, we reconstructed the Egesen glaciation from mapped moraines (Supplementary Fig. 3e), previously correlated to Egesen age (11 ± 1 ka96; equivalent to Younger Dryas)63,98. We projected the moraine height to the rockwall (Fig. 2a) to approximate the ice surface at the rockwalls.
These approximate ice surface reconstructions suggest that the Rothorn cirque was fully glacierized during LGM and Egesen, while the upper Hungerlihorli peak (>2800 m) remained ice-free. While our reconstruction approach provides only a crude approximation, we consider it acceptable for the purpose intended, and we account for uncertainty by applying a ± 50 m vertical buffer to our Egesen and LGM glacier extents, which is propagated into the calculated erosion rates. Reconstructions based on trimlines ignore small, cold-based glaciers that might have been present on higher parts of the rockwalls, and to examine the impact of this we included a scenario with a cold-based glacier on the Rothorn during the LGM.
Historical photos were used to reconstruct the exposure of new rockwall from the 19th century onwards. Historic photos were available for 196499, 1929 and 1882 (Supplementary Fig. 3a–c), and swissTopo provided a georeferenced orthophoto from summer 2017 (Fig. 2b). We reconstructed the glaciated area of the Rothorn cirque by using distinct landforms, ridges and mountain peaks, with an estimated vertical error of ±5%.
Rock temperature measurements
To model frost cracking and mean annual rock surface temperature (MARST), we measured rock surface temperature (RST) at five rockwalls along a topographic gradient from 2580 to 3148 m (Fig. 2) using Maxim iButton DS1922L temperature loggers installed in 0.1 m deep boreholes, similar to previous studies32,78,91,100. The loggers recorded RST at 3 h intervals (Supplementary Fig. 4) between 1 September 2016 and 31 August 2019 at RW2 and RW5, and between 29 August 2017 and 28 August 2019 at RW1. MARST was calculated to compare temperature logger locations and for permafrost modelling (Supplementary Table 2). The rockwall thermal regime is affected by snow cover, with a significant influence on permafrost distribution78,100,101,102 and frost cracking32,103. We examined the daily standard deviation in RST as a measure of snow cover, and applied a uniform threshold of <0.5 °C for positive and negative RST following established practice78,100 (Supplementary Note 1).
Rock temperature modelling
We propagated measured rock surface temperature into the rockwalls by conductive heat transfer with latent heat effects at the phase transition between water and ice32,103. Rock temperatures T over depth z and time t in one dimension were calculated by conservation of heat and Fourier´s Law104:
where Qh is vertical heat flux, ρr is rock density, c is specific heat capacity, and κ is thermal conductivity. Following the approach of previous studies32,103,105, we used a temperature-dependent volumetric specific heat capacity C and thermal conductivity κ to consider latent heat L effects for the phase changing envelope DT, which was set between −1 and 0 °C:
where the subscripts f and u stand for frozen and unfrozen, ρb is bulk (rock, water, ice) density, W reflects the total water content of the substrate as a fraction of mass, and Wu is the remaining unfrozen water content below Tf = −1 °C. W equals the porosity for unfrozen rock. We set W to 3% following previous rock temperature models32,78,89,106 and assumed a fully saturated rockwall, consistent with previous investigations of rock moisture measurements107,108. For unfrozen water content Wu, we set a value 5%32,103. Thermal conductivity κ and specific heat capacity c were geometrically weighted in the frozen and unfrozen region of the rock mass:
where i, w, r are the subscripts for ice, water, rock, and ν is the fractional content. The geology of the Hungerli Valley is predominantly paragneiss from the Mischabel nappe, consisting of schisty quartz slate with thin bands of aplite at the Rothorn cirque and intersections of amphibolite and aplite at the Hungerlihorli109 (Supplementary Figs. 1 and 2). For the calculations, we used previously measured rock density data (Supplementary Table 3) and took published thermal conductivity λ and heat capacity c110 values for these rock types. To determine the temperature depth profile in each rockwall, we used our logged temperatures as rock surface temperatures, and applied Eqs. 1–4 with a spatial resolution ∆z of 0.1 m. To evaluate the start conditions, we used a spin-up of 4 years on each temperature logger until steady-state rock temperature conditions were achieved32,78,105. Rock temperature modelling revealed permafrost occurrence with 2 to 3 m active layer thawing at RW1-3, while seasonal freezing penetrated 2 to 4 m at RW4-5 (Supplementary Fig. 5).
Frost cracking modelling
To model frost cracking, we used our modelled rock temperature profiles to drive a frost cracking model (Supplementary Note 2). We applied a model that incorporates rock strength (Supplementary Table 3) and which assumes a porosity change to occur alongside frost cracking72. The model determines an upper temperature limit ∆Tc for segregation ice growth depending on rock strength:
where Tm is the bulk melting temperature, ρi ice density, L latent heat, Pc the critical ice pressure, KC the critical fracture toughness, and xi the crack radius. We incorporated rock strength by using critical fracture toughness previously determined for each lithology73. The lower limit of ice segregation is controlled by water availability, which is determined by permeability:
where kpf is the frozen and kp0 the unfrozen permeability, ∆Tf is the pore freezing point, α is a power law exponent, and ∆T is the temperature below the bulk freezing point. Water migration in the frozen fringe was calculated based on the unfrozen permeability of the rock mass, with a value of 10−18 m2 adopted for all rockwalls (based on the permeability of schisty quartz slate111). While permeability is likely heterogeneous within a single rockwall, and will vary slightly between the amphibolite and aplite lithologies, we consider it reasonable to assume a uniform value, consistent with existing model approaches72,83. Sensitivity tests on permeability, initial crack length and fracture toughness demonstrated that while these factors affect the magnitude of frost cracking, they do not change the pattern of affected rock mass depth32.
To analyse the dependence of frost cracking on elevation, we calculated the total amount of permanent rock expansion (λ) induced by frost cracking at each rockwall72. Total rock expansion is a sum of the frost cracking intensity at different depths within the rockwall and is calculated here as:
The diffusivity D is
where α is a power law exponent and μ is the water viscosity72. Diffusivity is used as a measure of the propensity for frost-induced porosity changes. We calculated the total expansion separately for each year and lithology, to calculate a minimum, mean and maximum annual rock expansion total over the monitoring period (Supplementary Fig. 7). We consider the total rock expansion to represent the amount of (depth-integrated) frost cracking taking place at each rockwall.
Rockwall permafrost model
We used a multiple linear regression model fitted with multi-annual rock surface temperature (RST) measurements67 to model rock permafrost distribution in the Hungerli Valley, taking into account the effects of snow cover limiting incoming solar radiation32. We simulated the potential incoming solar radiation (PISR) for each 2 m digital elevation model (DEM) raster cell using the area solar calculator of ESRI ArcGIS 10.7.1 for a snow-free period74,112,113 from June to October in hourly steps assuming an atmosphere with no diffusivity67,105,114,115. The ‘long-term’ average length of the snow-free period was derived from a 20-year meteo station dataset116, located at Oberer Stelli Glacier in the Matter Valley. The station is 2–3 km SE of our study site at 2910 m elevation, and the snow duration at the meteo station corresponded well to snow cover in the Hungerli Valley for the 3-year period observed by our rock surface temperature measurements (Supplementary Fig. 8). To develop a statistical relationship between mean annual rock surface temperature (MARST) and the mean annual air temperature (MAAT) and PISR, we used temperature loggers at north and south facing slope aspects in the Hungerli Valley (two south facing loggers, RW1-S and RW2-S, and five north-facing loggers, RW1-5; Supplementary Table 4). We calculated MARST for each raster cell as:
with a, b and c representing calculated coefficients. For every logger location, we calculated the MAAT for the respective elevation using a temperature lapse rate of 6 °C km−1 derived from a comparison of daily air temperature between meteo station Oberer Stelligletscher at 2910 m and a near-by meteo station, Grächen at 1605 m117. We tested the quality of the relationship using r2, mean absolute error (MSE) and root mean square error (RMS) (Supplementary Table 5). Similar to previous approaches, we applied a 30-year MAAT for the period 1990 to 2019 (Supplementary Table 4) to Eq. (9) for the rockwall area to incorporate the slow response time of rock permafrost67,114. We interpret a MARST ≤ 0 °C as permafrost74.
Laserscanning and rockfall detection
We scanned the rock faces in our study area from the opposing side of the valley floor, with a total of six positions (Fig. 2a), providing comprehensive coverage of all rockwalls. Due to the steep nature of the rockwalls, the oblique look-angle of our terrestrial laser scanning resulted in negligible scan shadowing (overcoming a limitation of aerial LiDAR scanning of steep rockwalls118). Only minor, gently sloping ledges, of little importance for rockfall generation119, were missed (confirmed by aerial LiDAR inspection). Laserscanning took place over four consecutive summers from 2016 to 2019 using Riegl VZ400 or Riegl VZ2000i scanners with identical accuracy (Supplementary Table 6). To produce a reference point cloud, we registered the 2017 scan positions by manually selecting several pairs of pseudo-homologous points. The point clouds were then aligned using an iterative-closest-point (ICP) algorithm120,121 implemented as the Multi Station Adjustment (MSA) in RiScan Pro 2.9. The basic assumption for this registration approach is that topographic change (i.e. rockfall) between scan epochs is negligibly small compared to the total scanned surface area used for point cloud alignment. To minimise registration errors, we excluded any non-rockwall surfaces (e.g. debris slopes). We applied the MSA algorithm to every subsequent scan from 2016, and 2018 to 2019 and registered each point cloud to our reference scan from 2017. The registration error lies between 2.7 and 5.0 cm, similar to that reported by others43,46,47,122,123. An octree filter implemented in RiScan Pro was used to adapt all point clouds to a spatially continuous resolution of 0.1 m. We assumed that a rockfall event produces a distance difference between two point clouds, which we identified using the Multiscale Model to Model Cloud Comparison (M3C2) algorithm124 implemented in Cloud Compare 2.9.1, similar to previous studies47,125,126. The algorithm parameterizes surface roughness and alignment uncertainty to estimate a confidence interval, with a rockfall or movement recognised when the confidence interval is exceeded127,128. In our analyses, we used the significant change option for determining rockfall with a projection scale of 1 m and a maximum depth of 15 m. Every identified potential rockfall event was analysed manually and visually, with its volume estimated using the cut-fill volume tool in RiScan Pro. Due to the annual resolution of our data collection (i.e. long time between scans), it is likely that many ‘events’ assumed to be single rockfalls could have been multiple smaller rockfalls129, which would affect our magnitude-frequency analyses. However, this issue has little bearing on the overall spatial patterns of our annual rockwall erosion rates, for which an annual scanning frequency is deemed suitable126.
Statistical analysis of influencing factors
Environmental variables are often auto-correlated and a principal component analysis (PCA) can be used to find an axis or dimension that summarizes this redundancy130. We applied a PCA using R software packages FactoMineR and ggplot to evaluate the relationships between rockfall variables similar to previous approaches131,132. For each rockfall event, we extracted (i) elevation as a proxy for frost cracking, (ii) MARST as a proxy for permafrost, (iii) deglaciation age as a proxy for paraglacial adjustment, (iv) slope angle as a proxy for shear stress, and (v) rockfall volume. In using deglaciation age as a proxy for paraglacial process intensity we assumed that paraglacial processes were most intense at the start of deglaciation and decreased thereafter in the form of an exhaustion curve9,84. We used the rockfall elevation as a proxy for frost cracking, which at the Hungerli Valley has been shown to strongly scale with elevation32 despite variability in lithology and other local influences73,87. For each rockfall event, we extracted slope angle and rockfall volume from our laserscanning-derived DEM. All parameters were standardised using
where \(\bar{x}\) is the mean and σ is the standard deviation130. To standardise slope angle, we converted degree angles to radians. We kept principal components with values >1 (PC1) or close to 1 (PC2; Supplementary Table 7 and Fig. 3b).
Derivation of short-term rockwall erosion rates
For evaluating the influence of elevation on rockwall erosion rates, we derived rockwall area within 100 m elevation bands (Supplementary Table 8). Based on our reconstructed glacier distribution, we calculated rockwall erosion rates for every deglaciation step (i.e. successively exposed rock wall area) incorporating a glacier extent uncertainty of ±5% for 2017, 1964, 1929 and 1882 glacier extents and an uncertainty of ±50 m for Egesen and LGM glacier extents (Supplementary Table 9). We classified MARST into <−3 °C, −3 to −2 °C, −2 to −1 °C, −1 to 0 °C and >0 °C classes, similar to previous permafrost model approaches74, and calculated the area and rockwall erosion rate for every MARST class (Supplementary Table 10). Area was calculated in Cloud Compare using the Poisson Surface Reconstruction tool133,134 to produce a mesh (with a relatively high octree depth of 10 to 12). The mesh was adjusted using the output density to optimise it for the input cloud, to capture the full complexity of the surface area, without over-smoothing data gaps and patchy areas of the point cloud.
Mid- and long-term rockwall erosion calculation using talus slopes
We selected only talus slopes that have not been reworked by rock glaciers for our analysis in the Hungerli Valley. We applied electric resistivity tomography (ERT) and seismic refraction tomography (SRT) in longitudinal transects from the rockwall to the toe of three talus slopes (Supplementary Note 3) to quantify the sediment thickness. For topographic corrections, we extracted elevations along each transect from the swissTopo Alti3D digital elevation model. ERT data were acquired using a Wenner-Schlummberger approach and were processed using Res2DInv with a resolution of half of the electrode spacing (Supplementary Table 11). The root mean square error (RMS) was used to provide an estimation of model quality, and the values were within the ranges found in previous talus slope studies51,135,136,137,138. Seismic refraction signals were triggered by sledgehammer shots, recorded using a Geometrics Geode with 24 Geophones, and processed using ReflexW 9.1.3 (Supplementary Table 11). First-arrivals were picked manually139,140 to derive the travel-time of the refracted seismic waves, which were analysed to identify seismic layers139,140,141. Layer properties were used to adjust initial starting models and gradients. Sediment thickness was interpreted from one-dimensional profiles of electrical resistivity and seismic velocity every 12.5 m (Supplementary Fig. 9). Talus slopes 2 and 3 indicated the possible presence of a basal moraine, which would result in smaller talus volumes. We accounted for this uncertainty by using two different basal talus surfaces in the volume calculations (with and without moraine). Talus slope volume (Vt) was calculated by subtracting the lower subsurface boundary from the talus ground surface using Golden Software Surfer 17. The rockwall erosion rate Er was calculated as:
where ρr is the density of the rockwall (2800 kg m−3, Supplementary Table 3), ρt is talus density, Ar is the rockwall surface area providing rockfall material, and t is the time period of talus accumulation. Talus density varies vertically from 2000 kg m−3 near the surface to 2500 kg m−3 at the base142. We incorporated the entire range of talus density into our erosion rate calculation to avoid bias from densification61 if using only a single value. Talus age was derived from glacier reconstruction and ranged from 55 a (Talus slope-1) to 11 ± 1 ka (Talus slope-2 and -3). Rockwall surface area and talus slope surface area were both determined from the DEM with an assumed mapping uncertainty of ±5%, which we included, along with potential moraine presence, in our erosion rate calculation (Supplementary Table 12). Mid- to long-term erosion rates integrate changes in seismic activity86 or climatic phases60 and the influence should be similar in a single mountain range as the European Alps.
Data availability
The data that support the findings of this study are available at figshare (https://doi.org/10.6084/m9.figshare.17152481.v1)143. For the regional analysis, we used freely available data including a 25 m digital elevation model of the European Alps provided by Copernicus (https://land.copernicus.eu/imagery-in-situ/eu-dem/eu-dem-v1.1), LGM extent (https://booksite.elsevier.com/9780444534477/DCW_Europe_WGS84.php) and permafrost extent (https://www.geo.uzh.ch/microsite/cryodata/PF_map_explanation.html). Digital elevation data (swissALTI3D; https://www.swisstopo.admin.ch/de/geodata/height/alti3d.html) and orthophoto (swissIMAGE25; https://www.swisstopo.admin.ch/de/geodata/images/ortho/swissimage25.html) is available from swissTopo. Meteo data used in this study is free available from MeteoSwiss (https://gate.meteoswiss.ch/idaweb).
Code availability
The authors declare that the code used to obtain the main results of this study can be made available from the corresponding author upon request.
References
Whipple, K. X. The influence of climate on the tectonic evolution of mountain belts. Nat. Geosci. 2, 97–104 (2009).
Whipple, K. X., Kirby, E. & Brocklehurst, S. H. Geomorphic limits to climate-induced increases in topographic relief. Nature 401, 39–43 (1999).
Egholm, D. L., Nielsen, S. B., Pedersen, V. K. & Lesemann, J. E. Glacial effects limiting mountain height. Nature 460, 884–887 (2009).
Brozovic, N., Burbank, D. W. & Meigs, A. J. Climatic limits on landscape development in the northwestern Himalaya. Science 276, 571–574 (1997).
Harbor, J. M., Hallet, B. & Raymond, C. F. A numerical model of landform development by glacial erosion. Nature 333, 347 (1988).
Hallet, B., Hunter, L. & Bogen, J. Rates of erosion and sediment evacuation by glaciers: a review of field data and their implications. Glob. Planet. Change 12, 213–235 (1996).
Pedersen, V. K., Egholm, D. L. & Nielsen, S. B. Alpine glacial topography and the rate of rock column uplift: a global perspective. Geomorphology 122, 129–139 (2010).
Mitchell, S. G. & Montgomery, D. R. Influence of a glacial buzzsaw on the height and morphology of the Cascade Range in central Washington State, USA. Quat. Res. 65, 96–107 (2006).
Ballantyne, C. K. Paraglacial geomorphology. Quat. Sci. Rev. 21, 1935–2017 (2002).
McColl, S. T. Paraglacial rock-slope stability. Geomorphology 153–154, 1–16 (2012).
McColl, S. T. & Draebing, D. in Geomorphology of proglacial systems—Landform and sediment dynamics in recently deglaciated alpine landscapes (eds Tobias Heckmann & D. Morche) 119–141 (Springer, 2019).
Grämiger, L. M., Moore, J. R., Gischig, V. S., Ivy-Ochs, S. & Loew, S. Beyond debuttressing: mechanics of paraglacial rock slope damage during repeat glacial cycles. J. Geophys. Res. Earth 122, 1004–1036 (2017).
Grämiger, L. M., Moore, J. R., Gischig, V. S. & Loew, S. Thermo-mechanical stresses drive damage of Alpine valley rock walls during repeat glacial cycles. J. Geophys. Res. Earth 123, 2620–2646 (2018).
Grämiger, L. M. et al. Hydromechanical rock slope damage during Late Pleistocene and Holocene glacial cycles in an Alpine valley. J. Geophys. Res. Earth 125, e2019JF005494 (2020).
Leith, K., Moore, J. R., Amann, F. & Loew, S. Subglacial extensional fracture development and implications for Alpine Valley evolution. J. Geophys. Res. Earth 119, 62–81 (2014).
Leith, K., Moore, J. R., Amann, F. & Loew, S. In situ stress control on microcrack generation and macroscopic extensional fracture in exhuming bedrock. J. Geophys. Res. Sol. Earth 119, 594–615 (2014).
Köpfli, P., Grämiger, L. M., Moore, J. R., Vockenhuber, C. & Ivy-Ochs, S. The Oeschinensee rock avalanche, Bernese Alps, Switzerland: a co-seismic failure 2300 years ago? Swiss J. Geosci. 111, 205–219 (2018).
Oswald, P., Strasser, M., Hammerl, C. & Moernaut, J. Seismic control of large prehistoric rockslides in the Eastern Alps. Nat. Commun. 12, 1059 (2021).
Eppes, M.-C. & Keanini, R. Mechanical weathering and rock erosion by climate-dependent subcritical cracking. Rev. Geophys. 55, 470–508 (2017).
Matsuoka, N. & Murton, J. Frost weathering: Recent advances and future directions. Permafrost Periglac 19, 195–210 (2008).
Krautblatter, M., Funk, D. & Günzel, F. K. Why permafrost rocks become unstable: a rock–ice-mechanical model in time and space. Earth Surf. Proc. Land. 38, 876–887 (2013).
Murton, J. B., Peterson, R. & Ozouf, J. C. Bedrock fracture by ice segregation in cold regions. Science 314, 1127–1129 (2006).
Draebing, D., Krautblatter, M. & Hoffmann, T. Thermo-cryogenic controls of fracture kinematics in permafrost rockwalls. Geophys. Res. Lett. 44, 3535–3544 (2017).
Krautblatter, M. & Dikau, R. Towards a uniform concept for the comparison and extrapolation of rockwall retreat and rockfall supply. Geogr. Ann. A 89, 21–40 (2007).
Hales, T. C. & Roering, J. J. A frost “buzzsaw” mechanism for erosion of the eastern Southern Alps, New Zealand. Geomorphology 107, 241–253 (2009).
Vargo, L. J. et al. Anthropogenic warming forces extreme annual glacier mass loss. Nat. Clim. Change 10, 856–861 (2020).
Sommer, C. et al. Rapid glacier retreat and downwasting throughout the European Alps in the early 21st century. Nat. Commun. 11, 3209 (2020).
Farinotti, D. et al. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 12, 168–173 (2019).
Roe, G. H., Baker, M. B. & Herla, F. Centennial glacier retreat as categorical evidence of regional climate change. Nat. Geosci. 10, 95–99 (2017).
Girard, L., Gruber, S., Weber, S. & Beutel, J. Environmental controls of frost cracking revealed through in situ acoustic emission measurements in steep bedrock. Geophys. Res. Lett. 40, 1748–1753 (2013).
Mair, D. et al. The role of frost cracking in local denudation of steep Alpine rockwalls over millennia (Eiger, Switzerland). Earth Surf. Dynam 8, 637–659 (2020).
Draebing, D. & Mayer, T. Topographic and geologic controls on frost cracking in Alpine rockwalls. J. Geophys. Res. Earth 126, e2021JF006163 (2021).
Biskaborn, B. K. et al. Permafrost is warming at a global scale. Nat. Commun. 10, 264 (2019).
Scandroglio, R., Draebing, D., Offer, M. & Krautblatter, M. 4D-Quantification of alpine permafrost degradation in steep rock walls using a laboratory-calibrated ERT approach. Near Surf. Geophys. 19, 241–260 (2021).
Harris, C. et al. Permafrost and climate in Europe: Monitoring and modelling thermal, geomorphological and geotechnical responses. Earth-Sci. Rev. 92, 117–171 (2009).
RGI Consortium. Randolph Glacier Inventory – A Dataset of Global Glacier Outlines: Version 6.0: Technical Report, Global Land Ice Measurements from Space, Colorado, USA. Digital Media (2017).
Huss, M. & Fischer, M. Sensitivity of very small glaciers in the Swiss Alps to future climate change. Front. Earth Sci 4, 34 (2016).
Boeckli, L., Brenning, A., Gruber, S. & Noetzli, J. Permafrost distribution in the European Alps: calculation and evaluation of an index map and summary statistics. Cryosphere 6, 807–820 (2012).
Haeberli, W. In Cryospheric Systems: Glaciers and Permafrost Vol. 242 Special Publications (eds C. Harris & J. B. Murton) 29−37 (Geological Society, 2005).
Mohadjer, S. et al. Temporal variations in rockfall and rock-wall retreat rates in a deglaciated valley over the past 11 k.y. Geology 48, 594–598 (2020).
Sass, O. Spatial patterns of rockfall intensity in the northern Alps. Z. Geomorphol. Supp 138, 51–65 (2005).
Kenner, R. Mass wasting processes affecting the surface of an alpine talus slope: annual sediment budgets 2009–2018 at Flüelapass, eastern Swiss Alps. Land Degrad. Dev. 31, 451–462 (2020).
Guerin, A., Ravanel, L., Matasci, B., Jaboyedoff, M. & Deline, P. The three-stage rock failure dynamics of the Drus (Mont Blanc massif, France) since the June 2005 large event. Sci. Rep. 10, 17330 (2020).
Hartmeyer, I. et al. Current glacier recession causes significant rockfall increase: the immediate paraglacial response of deglaciating cirque walls. Earth Surf. Dynam 8, 729–751 (2020).
Kenner, R. et al. Investigation of rock and ice loss in a recently deglaciated mountain rock wall using terrestrial laser scanning: Gemsstock, Swiss Alps. Cold Reg. Sci. Technol. 67, 157–164 (2011).
Rabatel, A., Deline, P., Jaillet, S. & Ravanel, L. Rock falls in high-alpine rock walls quantified by terrestrial lidar measurements: a case study in the Mont Blanc area. Geophys. Res. Lett. 35, L10502 (2008).
Hartmeyer, I. et al. A 6-year lidar survey reveals enhanced rockwall retreat and modified rockfall magnitudes/frequencies in deglaciating cirques. Earth Surf. Dynam 8, 753–768 (2020).
Haeberli, W. et al. Pollen analysis and 14C age of moss remains in a permafrost core recovered from the active rock glacier Murtèl-Corvatsch, Swiss Alps: geomorphological and glaciological implications. J. Glaciol. 45, 1–8 (1999).
Krautblatter, M., Moser, M., Schrott, L., Wolf, J. & Morche, D. Significance of rockfall magnitude and carbonate dissolution for rock slope erosion and geomorphic work on Alpine limestone cliffs (Reintal, German Alps). Geomorphology 167, 21–34 (2012).
Sass, O. Spatial and temporal patterns of talus activity – a lichenometric approach in the stubaier alps, austria. Geogr. Ann. A 92, 375–391 (2010).
Sass, O. Bedrock detection and talus thickness assessment in the European Alps using geophysical methods. J. Appl. Geophys. 62, 254–269 (2007).
Sass, O. & Wollny, K. Investigations regarding Alpine talus slopes using ground-penetrating radar (GPR) in the Bavarian Alps, Germany. Earth Surf. Proc. Land. 26, 1071–1086 (2001).
Goetz, J., Otto, J. C. & Schrott, L. Postglacial sediment storage and rockwall retreat in a semi-closed inner-Alpine sedimentary basin (Gradenmoos, Hohe Tauern, Austria). Geogr. Fis. Din. Quat. 36, 63–80 (2013).
Hoffmann, T. & Schrott, L. Modelling sediment thickness and rockwall retreat in an Alpine valley using 2D seismic refraction (Reintal, Bavarian Alps). Z. Geomorphol. Supp 127, 153–173 (2002).
Lehmann, B. et al. Postglacial erosion of bedrock surfaces and deglaciation timing: new insights from the Mont Blanc massif (western Alps). Geology 48, 139–144 (2019).
Mair, D. et al. Fast long-term denudation rate of steep alpine headwalls inferred from cosmogenic 36Cl depth profiles. Sci. Rep.-UK 9, 11023 (2019).
Barsch, D. Rockglaciers. Indicators for the present and former geoecology in high mountain environments. (Springer, 1996).
Kaiser, B. Variations spatiales et temporelles dans les rythmes d'évolution des versants alpins (Variability in time and space concerning alpine slope evolution). Bull. Assoc. Geogr. Fr. 69, 265–270 (1992).
Matthews, J. A. et al. Small rock-slope failures conditioned by Holocene permafrost degradation: a new approach and conceptual model based on Schmidt-hammer exposure-age dating, Jotunheimen, southern Norway. Boreas 47, 1144–1169 (2018).
Affolter, S. et al. Central Europe temperature constrained by speleothem fluid inclusion water isotopes over the past 14,000 years. Sci. Adv. 5, eaav3809 (2019).
Sadler, P. M. Sediment accumulation rates and the completeness of stratigraphic sections. J. Geol. 89, 569–584 (1981).
Ganti, V. et al. Time scale bias in erosion rates of glaciated landscapes. Sci. Adv. 2, e1600204 (2016).
Otto, J. C., Schrott, L., Jaboyedoff, M. & Dikau, R. Quantifying sediment storage in a high alpine valley (Turtmanntal, Switzerland). Earth Surf. Proc. Land. 34, 1726–1742 (2009).
Linsbauer, A. et al. The New Swiss Glacier Inventory SGI2016: from a topographical to a glaciological dataset. Front. Earth Sci 9, 774 (2021).
Nyenhuis, M., Hoelzle, M. & Dikau, R. Rock glacier mapping and permafrost distribution modelling in the Turtmanntal, Valais, Switzerland. Z. Geomorphol. 49, 275–292 (2005).
Ravanel, L., Magnin, F. & Deline, P. Impacts of the 2003 and 2015 summer heatwaves on permafrost-affected rock-walls in the Mont Blanc massif. Sci. Total Environ. 609, 132–143 (2017).
Magnin, F. et al. Permafrost distribution in steep rock slopes in Norway: measurements, statistical modelling and implications for geomorphological processes. Earth Surf. Dynam 7, 1019–1040 (2019).
Montgomery, D. R. & Brandon, M. T. Topographic controls on erosion rates in tectonically active mountain ranges. Earth Planet. Sc. Lett 201, 481–489 (2002).
Schmidt, K. M. & Montgomery, D. R. Limits to relief. Science 270, 617–620 (1995).
MacGregor, K. R., Anderson, R. S. & Waddington, E. D. Numerical modeling of glacial erosion and headwall processes in alpine valleys. Geomorphology 103, 189–204 (2009).
Alley, R. B., Cuffey, K. M. & Zoet, L. K. Glacial erosion: status and outlook. Ann. Glaciol. 60, 1–13 (2019).
Rempel, A. W., Marshall, J. A. & Roering, J. J. Modeling relative frost weathering rates at geomorphic scales. Earth Planet. Sc. Lett 453, 87–95 (2016).
Draebing, D. & Krautblatter, M. The efficacy of frost weathering processes in Alpine rockwalls. Geophys. Res. Lett. 46, 6516–6524 (2019).
Kenner, R., Noetzli, J., Hoelzle, M., Raetzo, H. & Phillips, M. Distinguishing ice-rich and ice-poor permafrost to map ground temperatures and ground ice occurrence in the Swiss Alps. Cryosphere 13, 1925–1941 (2019).
Mamot, P., Weber, S., Lanz, M. & Krautblatter, M. Brief communication: The influence of mica-rich rocks on the shear strength of ice-filled discontinuities. Cryosphere 14, 1849–1855 (2020).
Mamot, P., Weber, S., Schröder, T. & Krautblatter, M. A temperature- and stress-controlled failure criterion for ice-filled permafrost rock joints. Cryosphere 12, 3333–3353 (2018).
Davies, M. C. R., Hamza, O. & Harris, C. The effect of rise in mean annual temperature on the stability of rock slopes containing ice-filled discontinuities. Permafrost Periglac 12, 137–144 (2001).
Draebing, D., Haberkorn, A., Krautblatter, M., Kenner, R. & Phillips, M. Thermal and mechanical responses resulting from spatial and temporal snow cover variability in permafrost Rock Slopes, Steintaelli, Swiss Alps. Permafrost Periglac 28, 140–157 (2017).
Scherler, D. Climatic limits to headwall retreat in the Khumbu Himalaya, eastern Nepal. Geology 42, 1019–1022 (2014).
Delunel, R., van der Beek, P. A., Carcaillet, J., Bourles, D. L. & Valla, P. G. Frost-cracking control on catchment denudation rates: Insights from in situ produced Be-10 concentrations in stream sediments (Ecrins-Pelvoux massif, French Western Alps). Earth Planet. Sci. Lett 293, 72–83 (2010).
von Blanckenburg, F. The control mechanisms of erosion and weathering at basin scale from cosmogenic nuclides in river sediment. Earth Planet. Sc. Lett 237, 462–479 (2005).
Nishiyama, R. et al. Bedrock sculpting under an active alpine glacier revealed from cosmic-ray muon radiography. Sci. Rep 9, 6970 (2019).
Sanders, J. W., Cuffey, K. M., Moore, J. R., MacGregor, K. R. & Kavanaugh, J. L. Periglacial weathering and headwall erosion in cirque glacier bergschrunds. Geology 40, 779–782 (2012).
Church, M. & Ryder, J. M. Paraglacial sedimentation: a consideration of fluvial processes conditioned by glaciation. Geol. Soc. Am. Bull. 83, 3059–3071 (1972).
Draebing, D., Krautblatter, M. & Dikau, R. Interaction of thermal and mechanical processes in steep permafrost rock walls: A conceptual approach. Geomorphology 226, 226–235 (2014).
Schweizerischer Erdbebendienst: ECOS. Earthquake Catalogue of Switzerland (2019).
Walder, J. & Hallet, B. A theoretical-model of the fracture of rock during freezing. Geol. Soc. Am. Bull. 96, 336–346 (1985).
Myhra, K. S., Westermann, S. & Etzelmüller, B. Modelled distribution and temporal evolution of permafrost in steep rock walls along a latitudinal transect in Norway by CryoGrid 2D. Permafrost Periglac 28, 172–182 (2017).
Wegmann, M., Gudmundsson, G. H. & Haeberli, W. Permafrost Changes in Rock Walls and the retreat of alpine glaciers: a Thermal Modelling Approach. Permafrost Periglac 9, 23–33 (1998).
Deprez, M., De Kock, T., De Schutter, G. & Cnudde, V. A review on freeze-thaw action and weathering of rocks. Earth-Sci. Rev. 203, 103143 (2020).
Draebing, D. Identification of rock and fracture kinematics in high Alpine rockwalls under the influence of elevation. Earth Surf. Dynam 9, 977–994 (2021).
Eppes, M. C. et al. Deciphering the role of solar-induced thermal stresses in rock weathering. Geol. Soc. Am. Bull. 128, 1315–1338 (2016).
Eppes, M. C. et al. Warmer, wetter climates accelerate mechanical weathering in field data, independent of stress-loading. Geophys. Res. Lett. 47, 2020GL089062 (2020).
Collins, B. D. & Stock, G. M. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 9, 395–400 (2016).
Kelly, M. A., Buoncristiani, J. F. & Schlüchter, C. A reconstruction of the last glacial maximum (LGM) ice-surface geometry in the western Swiss Alps and contiguous Alpine regions in Italy and France. Eclogae Geol. Helv. 97, 57–75 (2004).
Ivy-Ochs, S. et al. Chronology of the last glacial cycle in the European Alps. J. Quat. Sci 23, 559–573 (2008).
Wirsig, C. et al. A deglaciation model of the Oberhasli, Switzerland. J. Quaternary Sci. 31, 46–59 (2016).
Otto, J. C. & Sass, O. Comparing geophysical methods for talus slope investigations in the Turtmann valley (Swiss Alps). Geomorphology 76, 257–272 (2006).
Swissair Photo AG. Turtmanntal, Barrhorn (1964).
Haberkorn, A. et al. Thermal regime of rock and its relation to snow cover in steep alpine rock walls: Gemsstock. Central Swiss Alps. Geogr. Ann. A 97, 579–597 (2015).
Haberkorn, A., Hoelzle, M., Phillips, M. & Kenner, R. Snow as a driving factor of rock surface temperatures in steep rough rock walls. Cold Reg. Sci. Technol. 118, 64–75 (2015).
Phillips, M., Haberkorn, A. & Rhyner, H. Snowpack characteristics on steep frozen rock slopes. Cold Reg. Sci. Technol. 141, 54–65 (2017).
Anderson, R. S., Anderson, S. P. & Tucker, G. E. Rock damage and regolith transport by frost: an example of climate modulation of the geomorphology of the critical zone. Earth Surf. Proc. Land. 38, 299–316 (2013).
Carslaw, H. S. & Jaeger, J. C. Conduction of heat in solids. 2nd edn, (Clarendon Press, 1986).
Hipp, T., Etzelmüller, B. & Westermann, S. Permafrost in Alpine Rock Faces from Jotunheimen and Hurrungane. Southern Norway. Permafrost Periglac 25, 1–13 (2014).
Noetzli, J., Gruber, S., Kohl, T., Salzmann, N. & Haeberli, W. Three-dimensional distribution and evolution of permafrost temperatures in idealized high-mountain topography. J. Geophys. Res.-Earth 112, F02S13 (2007).
Rode, M., Schnepfleitner, H. & Sass, O. Simulation of moisture content in alpine rockwalls during freeze–thaw events. Earth Surf. Proc. Land. 41, 1937–1950 (2016).
Sass, O. Rock moisture measurements: techniques, results, and implications for weathering. Earth Surf. Proc. Land. 30, 359–374 (2005).
Bearth, P. Geologischer Atlas der Schweiz 1:25000. Erläuterungen zum Atlasblatt 71 (1308 St. Niklaus). (Schweizer Geologische Kommission, 1980).
Cermák, V. & Rybach, L. In Landolt–Börnstein Zahlenwerte and Funktionen aus Naturwissenschaften und Technik, Neue Serie, Physikalische Eigenschaften der Gesteine (V/1a) (ed. G. Angeneister) 305–343 (Springer, 1982).
Krautblatter, M. Detection and quantification of permafrost change in alpine rock walls and implications for rock instability PhD Thesis thesis, Universität Bonn, (2009).
Hoelzle, M. Mapping and modelling of mountain permafrost distribution in the Alps. Norsk Geogr. Tidsskr. 50, 11–15 (1996).
Hoelzle, M. & Haeberli, W. Simulating the effects of mean annual air-temperature changes on permafrost distribution and glacier size: an example from the Upper Engadin, Swiss Alps. Ann. Glaciol. 21, 399–405 (1995).
Boeckli, L., Brenning, A., Gruber, S. & Noetzli, J. A statistical approach to modelling permafrost distribution in the European Alps or similar mountain ranges. Cryosphere 6, 125–140 (2012).
Magnin, F., Brenning, A., Bodin, X., Deline, P. & Ravanel, L. Statistical modelling of rock wall permafrost distribution: application to the Mont Blanc massif. Geomorphologie 21, 145–162 (2015).
MeteoSwiss. Climate data station Oberer Stelligletscher 2000-2019. Provided by MeteoSwiss, the Swiss Federal Office of Meteorology and Climatology (2019).
MeteoSwiss. Climate data station Grächen, 2000-2019. Provided by MeteoSwiss, the Swiss Federal Office of Meteorology and Climatology (2019).
Abellan, A. et al. Terrestrial laser scanning of rock slope instabilities. Earth Surf Proc Land 39, 80–97 (2014).
Matasci, B. et al. Assessing rockfall susceptibility in steep and overhanging slopes using three-dimensional analysis of failure mechanisms. Landslides 15, 859–878 (2017).
Chen, Y. & Medioni, G. Object modelling by registration of multiple range images. Image Vision Comput 10, 145–155 (1992).
Besl, P. & McKay, N. Method for registration of 3-D shapes. Vol. 1611 (Proceedings Volume 1611, Sensor Fusion IV: Control Paradigms and Data Structures, 1992).
Rosser, N., Lim, M., Petley, D., Dunning, S. & Allison, R. Patterns of precursory rockfall prior to slope failure. J. Geophys. Res.-Earth 112, F04014 (2007).
Abellán, A., Vilaplana, J. M., Calvet, J., García-Sellés, D. & Asensio, E. Rockfall monitoring by Terrestrial Laser Scanning – case study of the basaltic rock face at Castellfollit de la Roca (Catalonia, Spain). Nat. Hazard. Earth Syst 11, 829–841 (2011).
Lague, D., Brodu, N. & Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogram 82, 10–26 (2013).
James, M. R., Robson, S. & Smith, M. W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: precision maps for ground control and directly georeferenced surveys. Earth Surf. Proc. Land. 42, 1769–1788 (2017).
Williams, J. G., Rosser, N. J., Hardy, R. J., Brain, M. J. & Afana, A. A. Optimising 4-D surface change detection: an approach for capturing rockfall magnitude–frequency. Earth Surf. Dynam 6, 101–119 (2018).
Soudarissanane, S., Lindenbergh, R., Menenti, M. & Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogram 66, 389–399 (2011).
Hodge, R. A. Using simulated Terrestrial Laser Scanning to analyse errors in high-resolution scan data of irregular surfaces. ISPRS J. Photogram 65, 227–240 (2010).
Williams, J. G., Rosser, N. J., Hardy, R. J. & Brain, M. J. The importance of monitoring interval for rockfall magnitude-frequency estimation. J. Geophys. Res.-Earth 124, 2841–2853 (2019).
Leyer, I. & Wesche, K. Multivariate Statistik in der Ökologie. (Springer, 2007).
Crippa, C. et al. Semi-automated regional classification of the style of activity of slow rock-slope deformations using PS InSAR and SqueeSAR velocity data. Landslides 18, 2445–2463 (2021).
Messenzehl, K., Viles, H., Otto, J.-C., Ewald, A. & Dikau, R. Linking rock weathering, rockwall instability and rockfall supply on talus slopes in glaciated hanging valleys (Swiss Alps). Permafrost Periglac 29, 135–151 (2018).
Kazhdan, M., Bolitho, M. & Hoppe, H. Poisson surface reconstruction. In Proceedings of the fourth Eurographics symposium on Geometry processing. (2006).
Kazhdan, M. & Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 32, Article 29 (2013).
Kneisel, C. The nature and dynamics of frozen ground in alpine and subarctic periglacial environments. Holocene 20, 423–445 (2010).
Kneisel, C. Assessment of subsurface lithology in mountain environments using 2D resistivity imaging. Geomorphology 80, 32–44 (2006).
Kenner, R. et al. New insights on permafrost genesis and conservation in talus slopes based on observations at Flüelapass, Eastern Switzerland. Geomorphology 290, 101–113 (2017).
Brody, A. G., Pluhar, C. J., Stock, G. M. & Greenwood, W. J. Near-surface geophysical imaging of a talus deposit in Yosemite Valley, California. Environ. Eng. Geosci. 21, 111–127 (2015).
Krautblatter, M. & Draebing, D. Pseudo 3D - P-wave refraction seismic monitoring of permafrost in steep unstable bedrock. J. Geophys. Res. Earth 119, 287–299 (2014).
Cody, E., Draebing, D., McColl, S., Cook, S. & Brideau, M.-A. Geomorphology and geological controls of an active paraglacial rockslide in the New Zealand Southern Alps. Landslides 17, 755–776 (2020).
Hilbich, C. Time-lapse refraction seismic tomography for the detection of ground ice degradation. Cryosphere 4, 243–259 (2010).
Scapozza, C., Baron, L. & Lambiel, C. Borehole Logging in Alpine Periglacial Talus Slopes (Valais, Swiss Alps). Permafrost Periglac 26, 67–83 (2015).
Draebing, D., Mayer, T., Jacobs, B. & McColl, S. T. Alpine rockwall erosion patterns follow elevation-dependent climate trajectories. Data set. Figshare (2021).
Ehlers, J., Gibbard, P. L. & Hughes, P. D. Quaternary Glaciations - Extent and Chronology. Vol. 15 (Elsevier, 2011).
Acknowledgements
This study was funded by the German Research Foundation (DR1070/1‐1). S.M. acknowledges additional funding by the Technical University of Munich and its August-Wilhelm Scheer Visiting Professor programme. We thank all students involved in fieldwork for their support. The authors acknowledge the valuable comments by five anonymous reviewers that helped to improve the manuscript. D.D. thanks Michael Krautblatter and Maarten Kleinhans for hospitality.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
All authors contributed to field data collection. T.M. and B.J. processed the laserscanning data. T.M. and D.D. performed the frost cracking modelling. D.D. designed the research set up, the study, modelled the permafrost distribution, and analysed the data and D.D. and S.M. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Arjun Heimsath, Ludovic Ravanel and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Clare Davis. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Draebing, D., Mayer, T., Jacobs, B. et al. Alpine rockwall erosion patterns follow elevation-dependent climate trajectories. Commun Earth Environ 3, 21 (2022). https://doi.org/10.1038/s43247-022-00348-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00348-2
This article is cited by
-
Hyperconcentrated flows shape bedrock channels
Communications Earth & Environment (2024)
-
The evolution of “riskscapes”: 100 years of climate change and mountaineering activity in the Lake Louise area of the Canadian Rockies
Climatic Change (2024)
-
The development of terrestrial ecosystems emerging after glacier retreat
Nature (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.