Abstract
Carbon dragged at sub-arc depths and sequestered in the asthenospheric upper mantle during cold subduction is potentially released after millions of years during the breakup of continental plates. However, it is unclear whether these deep-carbon reservoirs can be locally remobilized on shorter-term timescales. Here we reveal the fate of carbon released during cold subduction by analyzing an anomalously deep earthquake in December 2020 in the lithospheric mantle beneath Milan (Italy), above a deep-carbon reservoir previously imaged in the mantle wedge by geophysical methods. We show that the earthquake source moment tensor includes a major explosive component that we ascribe to carbon-rich melt/fluid migration along upper-mantle shear zones and rapid release of about 17,000 tons of carbon dioxide when ascending melts exit the carbonate stability field. Our results underline the importance of carbon-rich melts at active continental margins for emission budgets and suggest their potential episodic contributions to atmospheric carbon dioxide.
Similar content being viewed by others

Introduction
Recent studies integrating petrological modeling and geophysical imaging of the Earth mantle1,2,3 have revealed the importance of long-term carbon sequestration into the mantle wedge of cooler subduction zones4,5. Low paleogeothermal gradients allow for the preservation of carbonates and hydrous minerals in the downgoing slab to asthenospheric depths6,7. Their breakdown8,9 produces carbonate-rich hydrous melts that infiltrate the overlying mantle wedge inducing peridotite partial melting10,11. The resulting melt network, revealed under favorable conditions by shear-wave low-velocity anomalies in seismic tomography models12,13, is frozen when the mantle geotherm crosses the carbonated hydrous peridotite solidus10,11. The attainment of subsolidus conditions leads to extensive peridotite carbonation and the formation of a long-term carbon reservoir in the asthenospheric and/or lithospheric upper mantle.
These processes are documented in the mantle wedge of the European Alps3,14, where a prominent shear-wave low-velocity anomaly, located at depths as shallow as ~180 km beneath the Po Plain, provides evidence of active carbon sequestration in the asthenospheric mantle above the European slab (Fig. 1). This vast carbon reservoir, detected over an area of ~105 km2, could be remobilized during episodes of continental breakup by increasing temperature, adiabatic decompression, or redox melting5,15,16, thus determining future peaks of carbon dioxide (CO2) outgassing due to massive recycled-carbon release3. Notwithstanding the impact of these processes on timescales typical of plate-tectonic cycles17,18,19, we explore the possibility that deep carbon could be variably mobilized on much shorter timescales relevant to anthropogenic processes. Melt and fluid migration within the Earth can be revealed by the volumetric components of earthquake moment tensors20,21. Here, we combine seismological analysis and petrological modeling with the results of recent geophysical studies of the deep structure of the Alpine region3,14 to reveal the evolution of deep carbon in the mantle beneath the Po Plain.
a Tectonic sketch map of the Alpine region (modified after ref. 48). The blue star marks the location of the 4.6 ± 0.3 moment magnitude seismic event recorded in the lithospheric mantle beneath the city of Milan, at 66 ± 20 km depth. The earthquake-felt area is shown in magenta. The dashed green lines indicate the cells of the surface-wave absolute tomography model shown in (b). b Cross-section of the cellular surface-wave tomography model of the Alpine upper mantle3,23. Shaded areas indicate the variability range of layer thickness. The prominent shear-wave low-velocity anomaly beneath the Adriatic plate (light blue colors) is ascribed to carbon-rich melts generated after the breakdown of carbonates and hydrous minerals subducted with the European slab. These melts would be responsible for extensive peridotite carbonation and the formation of a carbon reservoir in the overlying asthenospheric mantle3. The white horizontal dashed line indicates the lithosphere-asthenosphere boundary, the east-dipping dashed line indicates the top of the European slab. Image generated using Inkscape 1.0 (https://inkscape.org).
The seismic event that occurred beneath Milan on the 17th of December 2020 at 15:59:22 UTC (Fig. 1a) provides an invaluable opportunity to investigate the possibility that carbon sequestered beneath the Po Plain is released to the atmosphere. The region around Milan is almost aseismic and experienced few earthquakes in the last century22. The hypocenter of the analyzed 4.6 ± 0.3 moment magnitude earthquake is located in the lithospheric mantle of the Adriatic plate at depths of 66 ± 20 km (latitude 9.03 ± 0.17°E, longitude 45.53 ± 0.12°N). According to the cellular surface-wave absolute tomography model of the Alpine upper mantle shown in Fig. 13,23, the seismic event originated in a region with shear-wave velocities that are slightly lower than those generally observed in the lithospheric mantle of the Adriatic plate (4.25–4.55 km s−1 vs 4.50–4.80 km s−1). This may suggest the presence of minor amounts of melt, possibly sourced from deeper regions in the asthenosphere where shear-wave velocities are as low as 4.00–4.30 km s−1 (Fig. 1b).
Here we show that the source moment tensor of the Milan earthquake includes a major explosive component. This is interpreted as the effect of rapid CO2 release when carbon-rich melts migrating along upper-mantle shear zones exit the carbonate stability field. Melting of carbonated peridotite occurs in the asthenosphere at depths around 180–100 km. Carbon-rich melts ascend to depths less than 100 km due to buoyancy and very low viscosity. The associated CO2 output towards Earth’s surface is greater than the daily CO2 emissions of top-ranking most actively degassing volcanoes, which underlines the importance of carbon-rich melts for the emission budget of active continental margins.
Results and discussion
Explosive earthquake moment tensor and estimated volume change
Seismic moment tensors can be decomposed into a deviatoric part and an isotropic (volumetric) part24. Although isotropic components are generally negligible in most tectonic earthquakes, relevant explosive volumetric components are sometimes observed in volcanic zones due to magma injection or magma degassing20,25,26. In order to detect a potential volumetric component of the moment tensor during the Milan earthquake, we performed inversion of the full source moment tensor using the INPAR method, a non-linear inversion method that adopts a point-source approximation27,28, fairly adequate to the available data. As the Po Plain is a noisy area for seismic signals, we used the dominant part of the complete waveforms recorded from events at regional distances to maximize the signal-to-noise ratio (see Methods and Supplementary Fig. 1 for details).
The INPAR inversion of the Milan earthquake returned a double-couple component associated with a major explosive component (Fig. 2 and Supplementary Table 1). The confidence level of the moment tensor solution is given in Fig. 2b. The confidence area of the vector L describing the total mechanism denotes the robustness of the solution and the reliability of the volumetric component. The deviatoric part of the tensor points to a strike-slip mechanism with near-vertical N-S and E-W nodal planes, which are common to most anomalously deep earthquakes sourced in the Adriatic mantle and previously described in the western Po Plain29. The explosive volumetric component of the moment tensor encompasses one-third of the total tensor and consistently masks part of the negative polarities that would be expected for a pure double-couple mechanism, especially for those seismic stations located away from the maximum radiation of the double-couple component. The volumetric component of the analyzed earthquake has a longer duration than the deviatoric one. These results are consistent with potential fluid migration within a framework likely controlled by tectonics during Adria-Europe convergence22,30.
a Fault plane solution and source time functions of the deviatoric and volumetric components of the source moment tensor after INPAR inversion27. The volumetric component encompasses one-third of the total tensor and has a longer duration than the deviatoric component. b Genetic algorithm inversion results with confidence error areas28. T, P, and B are the tensional, compression, and null axes, respectively. L is the vector describing the total mechanism; d is the double-couple (DC) vector; l and l’ are the compensated linear vector dipole (CLVD) components along the tensional and pressure axes; i represents the volumetric (V) component. The distance of L from vectors i, d, l, and l’ indicates the share of the V, DC, and CLVD components (35, 64, and 1%, respectively). The small confidence area of vector L denotes the robustness of the solution and the reliability of the volumetric component. Downward-pointing triangles are vectors in the lower hemisphere, upward-pointing triangles are vectors in the upper hemisphere. The source time function is normalized to the maximum source time function of the population for a unitary tensor. The scalar moment is normalized to the value given in Supplementary Table 2. Image generated using Inkscape 1.0 (https://inkscape.org).
The volume change associated with the Milan earthquake can be inferred from the measured isotropic seismic moment and the Lamé parameters of the ambient rocks of the earthquake source (see Methods for details). Different assumptions allow for the definition of a range of possible volume-change values21, which are higher under the hypothesis of a cracklike rupture with partly tensile components (ΔV ≈ 2.2 104 m3), and lower for a compact form of volume change that may be expected in case of concentrated phase transformations (ΔV ≈ 1.3 104 m3). The latter value provides a lower bound for volume-change estimates based on earthquake source moment-tensor analysis21 (see Supplementary Tables 2 and 3).
Carbon-rich melts along upper-mantle shear zones
Assessment of a potential linkage between the explosive Milan earthquake and processes reactivating the deep-carbon reservoir in the underlying asthenospheric mantle requires a complete understanding of the petrological evolution of the upper mantle in the framework of Alpine tectonics14. Essential are the relationships between the mantle geotherm and the carbonated hydrous peridotite solidus, which are illustrated in the pressure–temperature diagram of Fig. 3. Firstly, buoyant carbonate-rich melts are released from the subducting slab3 into the overlying asthenospheric wedge at supersolidus peridotite conditions (i in Fig. 3). The resulting melt network infiltrates the asthenospheric upper mantle at depths as shallow as the intersection of the peridotite solidus with the mantle geotherm curve (ii in Fig. 3). The occurrence of subsolidus conditions at depths less than ~180 km suggests that relevant amounts of carbon can potentially be accumulated in this part of the mantle wedge over time. However, in the uppermost part of the asthenospheric mantle, the experimental CO2-bearing hydrous peridotite solidus13 runs near-parallel and very close to the mantle geotherm. This implies that minor thermal perturbations—on the order of a few tens of degrees—may induce carbonated peridotite incipient melting, generating low fractions of carbonate-rich mobile melts even at depths shallower than ~180 km (iii in Fig. 3). Large thermal perturbations, such as those associated with a mantle plume, would determine melt remobilization over hundreds of kilometers in map view, unlike observed in the tomography model of Fig. 1b. More localized thermal perturbations could be associated with the activity of upper mantle shear zones, which may also increase permeability, thus favoring the ascent of carbonate-rich mobile melts towards the lithosphere (iv in Fig. 3).
The gray arrow indicates the European lithosphere cold subduction path to asthenospheric depths3. Progressive thermal re-equilibration of the slab (horizontal arrow segment) to mantle geotherm49 (black line) induces partial melting of subducted carbonated hydrous metasediments (GS9) and carbonated meta basics (D048). Generated carbon-rich hydrous melts determine supersolidus conditions (thick magenta line FB10,11) in the mantle-wedge peridotite. The temperature difference between the CO2-bearing hydrous peridotite solidus and the mantle geotherm decreases with decreasing pressures and the two curves intersect at ~180 km. At shallower depths, carbon-rich melts are frozen on reaction with peridotites3. In the uppermost asthenospheric mantle, the CO2-bearing hydrous peridotite solidus segment (G1913) runs near-parallel to the mantle geotherm, and minor thermal perturbations may induce partial melting generating carbon-rich melts (magenta field)50. Additional heating would be required for melting at the base of the lithosphere, where the CO2-bearing hydrous peridotite solidus diverges sharply from the mantle geotherm. The CO2-bearing hydrous peridotite solidus loop at ~2 GPa, in the depth range of the explosive earthquake recorded beneath Milan, reflects carbonate destabilization with the consequent shift of the solidus towards higher temperatures. In the diagram, the uppermost part of the mantle geotherm is constrained by earthquake depth; the dotted part is inferred. Roman numbers i–v indicate steps described in Fig. 4. Image generated using Inkscape 1.0 (https://inkscape.org).
Faults in the lithospheric mantle of the Adriatic plate are extensively documented by near-vertical alignments of earthquake hypocenters that define N-S trending belts down to ~75 km depth14,22,29. The focal solutions of these mantle earthquakes are invariably strike-slip. These observations are supportive of N-S-trending lithospheric faults that accommodate differential Adria-Europe convergence by sinistral strike-slip motion22,29, in agreement with the double-couple component returned by the Milan earthquake. At greater depths and temperatures higher than ∼600 °C, the onset of olivine crystal plasticity precludes frictional instability and earthquake occurrence in mantle rocks31,32. Differential convergence is thus accommodated by strike-slip motion along ductile shear zones33 that remain undetected by seismotectonic methods. These shear zones likely extend to the uppermost part of the asthenospheric mantle (Fig. 4). Deformation related to differential Adria-Europe convergence, which is much faster in the east than in the west30, is in fact necessarily transmitted to the underlying asthenosphere because the Adriatic plate has a reverted-U shape due to the presence of two opposite-dipping slabs attached to its northeastern and southwestern edges14,34. Deformation of the asthenospheric mantle produces lattice-preferred-orientation of olivine crystals, which is revealed by the birefringence of core-refracted shear waves (SKS phase) and associated transverse anisotropy of seismic velocities35. SKS splitting measurements beneath the Po Plain systematically show NNE-SSW fast-axis directions14, which are consistent with the orientation of nodal planes retrieved for the Milan earthquake (Fig. 2). This provides further support to the hypothesis that the lithospheric faults underlined by earthquake alignments also affect the uppermost part of the asthenospheric mantle and may interact with the carbonated mantle revealed beneath the Po Plain.
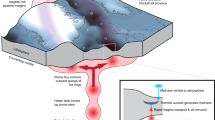
i) Carbon-rich hydrous-silicate melts, generated by the breakdown of subducted carbonates and hydrous minerals along the slab interface, infiltrate the mantle wedge inducing peridotite partial melting. ii) The carbon-rich melts lead to extensive peridotite carbonation and the formation of a carbon reservoir in the asthenospheric upper mantle at depths less than ~180 km3. iii) Minor thermal perturbations along upper-mantle shear zones allow remobilization of carbon-rich melts. iv) Melts ascend along the shear zone owing to their low viscosity until they exit the carbonate stability field. v) Explosive earthquakes reveal consequent rapid CO2 release in the lithospheric mantle. In the lithospheric mantle outside the shear zone, melts are not generated. The gray spheres compare the CO2 output towards Earth’s surface calculated for the Milan earthquake (~17,000 tons) with the daily CO2 emissions of the top-ranking most actively degassing volcanoes Nyiragongo and Etna41. Image generated using Inkscape 1.0 (https://inkscape.org).
Rapid CO2 release and emission to the atmosphere
Viscous dissipation during deformation is a potential source of heat36. The duration of heat dissipation via conduction increases as the square of the width of a shear zone37. Therefore, the cumulative effects of viscous heating produced by sequential deformation within km-thick shear zones in the upper mantle cannot dissipate over millions of years and contribute to a progressive temperature increase36. Albeit small, we postulate that this localized temperature increase is sufficient to locally remobilize carbon-rich melts in the uppermost part of the asthenosphere (iii in Fig. 4). Melts migrate along the shear zone towards the base of the lithosphere, where the CO2-bearing hydrous peridotite solidus diverges sharply from the mantle geotherm (Fig. 3). Although numerical models suggest that a periodic shear-heating mechanism may account for the required temperature increase in the lithospheric mantle38, mobile melts may continue their ascent along the shear zone owing to their low viscosity39. At pressure conditions below the carbonate stability field (Fig. 4), decarbonation reactions release CO2 fluids in the lithosphere40.
In pressure–temperature diagrams, the carbonate stability limit is reflected by a loop in the CO2-bearing hydrous peridotite solidus at pressures ~2 GPa, consistent with the hypocentral depth of the explosive earthquake analyzed in this work (v in Fig. 3). We suggest a causal relationship between the inferred CO2 release and the volume increase revealed by earthquake source moment-tensor analysis. Carbonate-melt outgassing determines a shift of the peridotite solidus towards higher temperatures and consequent melt freezing inside the shear zone, and an increase in shear-wave seismic velocity.
The quantity of CO2 possibly released during faulting has been evaluated based on the measured volume change and the pressure conditions at the hypocentral depth (see Methods for details). The lower-bound amount of degassed CO2 inferred for the Milan earthquake is ~17,000 tons (cf., Methods), exceeding CO2 emitted daily by the most actively degassing volcanoes in the world (Fig. 4), such as the top-ranking Nyiragongo–Nyamuragira (~15,790 tons/day) and Mt. Etna (9083 tons/day)41. Direct measurements of CO2 emissions associated with mantle earthquakes are not available yet. They may be hindered by diffusion in aquifers and soils42,43 and hardly resolvable from anthropogenic emissions, especially in industrial areas as the Po Plain. Nevertheless, our findings demonstrate that asthenospheric-mantle carbon reservoirs formed during cold subduction can experience nearly “instantaneous” remobilization driven by tectonics, episodically contributing to atmospheric CO2. We conclude that diffuse carbon outgassing through faults and shear zones is a relevant process, not only in continental rifts and transform faults44,45 but also in active continental margins where emissions away from arc volcanoes are primarily controlled by the interplay between the evolution of deep carbon in the upper mantle and active tectonics.
Methods
INPAR moment tensor inversion
The INPAR non-linear method for the moment tensor inversion of the earthquake source, which is particularly suited in sparse station coverage settings, adopts a point-source approximation and consists of two main steps. In the first linear step, the time functions describing the time behavior of the components of the moment tensor, namely the moment tensor rate functions (MTRFs) are obtained independently from each other by deconvolution from the data of the raypath Green’s function. Using the modal-summation technique46,47, the synthetic Green’s functions are computed at each grid point of a model space defined by a preassigned range of possible hypocentral coordinates and, by interpolation, at the intermediate points. The hypocentral location is perturbed until the difference between synthetic and observed seismograms is minimized with respect to a preassigned threshold. Since the MTRFs are treated as independent functions, this step leads to an over-parameterization of the problem that is advantageous for absorbing poor modeling of the structure. In the second non-linear step, the mechanism and the source time function are obtained after factorization of the MTRFs in a time constant moment tensor mij and a common source time function f(t), which implies considering the geometry of the source stable in time. The predicted MTRFs are then matched to the observed MTRFs obtained as the output of the first step26. The preferred solution is obtained through a genetic algorithm that allows for the estimate of the confidence areas for the different source parameters, consistent with clear-cut P-wave polarities when available.
Volume change at the source
Volume change was estimated through the isotropic seismic moment (M0iso) and Lamé parameters (λ, μ) of the source structure. Three different cases have been considered. (1) a volumetric change in a fluid: ΔV = M0iso/λ; (2) a cracklike rupture with partly tensile components: ΔV = M0iso/(λ + 2μ/3); and (3) a compact source: ΔV = M0iso/(λ + 2μ). The equivalent sphere radius is given for each case. Cases 1 and 3 provide upper- and lower-bound values, respectively (see Supplementary Tables 2 and 3).
Volume change to CO2 conversion
The amount of CO2 fluids inferred by volume change has been calculated based on the equivalent sphere volume (radius 15 m), assuming a compact source (Supplementary Table 3). Assuming a density of 1100 kg m−3 for CO2 fluids in equilibrium with lithostatic pressure conditions at the considered mantle temperatures (2–2.5 GPa – 800–900 °C), the corresponding mass is 1,683,000 kg or 16,830 tons. This amount of CO2 should be considered a minimum possible value. Were the fluids in overpressure conditions, the mass should increase considerably.
Data availability
All seismic data used in this study can be accessed and downloaded through the IRIS Wilber 3 system (https://ds.iris.edu/wilber3/find_stations/11354649) from the Italian Seismic Network (https://doi.org/10.13127/SD/X0FXnH7QfY) and the Mediterranean Very Broadband Seismographic Network (https://doi.org/10.13127/SD/fBBBtDtd6q).
References
Abers, G. A., van Keken, P. E. & Hacker, B. R. The cold and relatively dry nature of mantle forearcs in subduction zones. Nat. Geosci. 10, 333–337 (2017).
Syracuse, E. M., Van Keken, P. E. & Abers, G. A. The global range of subduction zone thermal models. Phys. Earth Planet. Inter. 183, 73–90 (2010).
Malusà, M. G. et al. Active carbon sequestration in the Alpine mantle wedge and implications for long-term climate trends. Scientific Reports 8, 1–8 (2018).
Dasgupta, R. & Hirschmann, M. M. The deep carbon cycle and melting in Earth’s interior. Earth Planet. Sci. Lett. 298, 1–13 (2010).
Dasgupta, R. Ingassing, storage, and outgassing of terrestrial carbon through geologic time. Rev. Mineral. Geochem. 75, 183–229 (2013).
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted marine sediments and the transport of volatiles into the Earth’s mantle. Nature 411, 293–296 (2001).
Poli, S. & Schmidt, M. W. Petrology of subducted slabs. Annu. Rev. Earth Planet. Sci. 30, 207–235 (2002).
Dasgupta, R., Hirschmann, M. M. & Withers, A. C. Deep global cycling of carbon constrained by the solidus of anhydrous, carbonated eclogite under upper mantle conditions. Earth Planet. Sci. Lett. 227, 73–85 (2004).
Grassi, D. & Schmidt, M. W. The melting of carbonated pelites from 70 to 700 km depth. J. Petrol. 52, 765–789 (2011).
Foley, S. F. et al. The composition of near-solidus melts of peridotite in the presence of CO2 and H2O between 40 and 60 kbar. Lithos 112, 274–283 (2009).
Brey, G. P., Bulatov, V. K. & Girnis, A. V. Influence of water and fluorine on melting of carbonated peridotite at 6 and 10 GPa. Lithos 112, 249–259 (2009).
Yoshino, T., Nishihara, Y. & Karato, S. I. Complete wetting of olivine grain boundaries by a hydrous melt near the mantle transition zone. Earth Planet. Sci. Lett. 256, 466–472 (2007).
Gaillard, F. et al. in Deep Carbon: Past to Present Ch. 7 (Cambridge Univ. Press, 2019).
Malusà, M. G. et al. The deep structure of the Alps based on the CIFALPS seismic experiment: a synthesis. Geochem. Geophys. Geosyst. 22, e2020GC009466 (2021).
Rohrbach, A. & Schmidt, M. W. Redox freezing and melting in the Earth’s deep mantle resulting from carbon–iron redox coupling. Nature 472, 209–212 (2011).
Muirhead, J. D. et al. Displaced cratonic mantle concentrates deep carbon during continental rifting. Nature 582, 67–72 (2020).
Kelemen, P. B. & Manning, C. E. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc. Natl. Acad. Sci. USA 112, E3997–E4006 (2015).
Lee, H. et al. Massive and prolonged deep carbon emissions associated with continental rifting. Nat. Geosci. 9, 145 (2016).
Brune, S., Williams, S. E. & Müller, R. D. Potential links between continental rifting, CO2 degassing and climate change through time. Nat. Geosci. 10, 941 (2017).
Dreger, D. S., Tkalčić, H. & Johnston, M. Dilational processes accompanying earthquakes in the Long Valley Caldera. Science 288, 122–125 (2000).
Müller, G. Volume change of seismic sources from moment tensors. Bull. Seism. Soc. Am. 91, 880–884 (2001).
Eva, E., Malusà, M. G. & Solarino, S. Seismotectonics at the transition between opposite‐dipping slabs (western Alpine region). Tectonics 39, e2020TC006086 (2020).
Brandmayr, E. et al. The lithosphere in Italy: structure and seismicity. J. V. Expl. 36, 1–73 (2010).
Vavryčuk, V. Moment tensor decompositions revisited. J. Seism. 19, 231–252 (2015).
Hrubcová, P., Doubravová, J. & Vavryčuk, V. Non-double-couple earthquakes in 2017 swarm in Reykjanes Peninsula, SW Iceland: sensitive indicator of volcano-tectonic movements at slow-spreading rift. Earth Planet. Sci. Lett. 563, 116875 (2021).
Panza, G. F. & Saraò, A. Monitoring volcanic and geothermal areas by full seismic moment tensor inversion: are non‐double‐couple components always artefacts of modelling? Geophys. J. Int. 143, 353–364 (2000).
Šílený, J., Panza, G. F. & Campus, P. Waveform inversion for point source moment tensor retrieval with variable hypocentral depth and structural model. Geophys. J. Int. 109, 259–274 (1992).
Šílený, J. Earthquake source parameters and their confidence regions by a genetic algorithm with a ‘memory’. Geophys. J. Int. 134, 228–242 (1998).
Malusà, M. G. et al. Earthquakes in the western Alpine mantle wedge. Gondwana Res. 44, 89–95 (2017).
Nocquet, J. M. Present‐day kinematics of the Mediterranean: a comprehensive overview of GPS results. Tectonophysics 579, 220–242 (2012).
Raterron, P., Wu, Y., Weidner, D. J. & Chen, J. Low-temperature olivine rheology at high pressure. Phys. Earth Planet. Int. 145, 149–159 (2004).
Chen, W. P. et al. Moho, seismogenesis, and rheology of the lithosphere. Tectonophysics 609, 491–503 (2013).
Vauchez, A., Tommasi, A. & Mainprice, D. Faults (shear zones) in the Earth’s mantle. Tectonophysics 558-559, 1–27 (2012).
Brandmayr, E., Marson, I., Romanelli, F. & Panza, G. F. Lithosphere density model in Italy: no hint for slab pull. Terra Nova 23, 292–299 (2011).
Mainprice, D., Barruol, G. & Ismail, W. B. The seismic anisotropy of the Earth’s mantle: from single crystal to polycrystal. AGU Geophys. Monograph 117, 237–264 (2000).
Burg, J. P. & Gerya, T. V. The role of viscous heating in Barrovian metamorphism of collisional orogens: thermomechanical models and application to the Lepontine Dome in the Central Alps. J. Metam. Geol. 23, 75–95 (2005).
Stüwe, K. Geodynamics of the Lithosphere (Springer, 2002).
Kelemen, P. B. & Hirth, G. A periodic shear-heating mechanism for intermediate-depth earthquakes in the mantle. Nature 446, 787–790 (2007).
Kono, Y. et al. Ultralow viscosity of carbonate melts at high pressures. Nat. Commun. 5, 5091 (2014).
Wallace, M. E. & Green, D. H. An experimental determination of primary carbonatite magma composition. Nature 335, 343–346 (1988).
Aiuppa, A., Fischer, T. P., Plank, T. & Bani, P. CO2 flux emissions from the Earth’s most actively degassing volcanoes, 2005–2015. Sci. Rep. 9, 1–17 (2019).
Chiodini, G. et al. Quantification of deep CO2 fluxes from Central Italy. Examples of carbon balance for regional aquifers and of soil diffuse degassing. Chem. Geol. 159, 205–222 (1999).
Chiodini, G. et al. Correlation between tectonic CO2 Earth degassing and seismicity is revealed by a 10-year record in the Apennines, Italy. Sci. Adv. 6, 2938 (2020).
Tamburello, G., Pondrelli, S., Chiodini, G. & Rouwet, D. Global-scale control of extensional tectonics on CO2 Earth degassing. Nat. Comm. 9, 1–9 (2018).
Wong, K. et al. Deep carbon cycling over the past 200 million years: a review of fluxes in different tectonic settings. Front. Earth Sci. 7, 263 (2019).
Panza, G. F. Synthetic seismograms-the Rayleigh waves modal summation. J. Geophys. 58, 125–145 (1985).
Panza, G. F., Romanelli, F. & Vaccari, F. Realistic modelling of waveforms in laterally heterogeneous anelastic media by modal summation. Geophys. J. Int. 143, 340–352 (2000).
Malusà, M. G. et al. Contrasting styles of (U)HP rock exhumation along the Cenozoic Adria-Europe plate boundary (Western Alps, Calabria, Corsica). Geochem. Geophys. Geosyst. 16, 1786–1824 (2015).
Akaogi, M., Ito, E. & Navrotsky, A. Olivine-modified spinel-spinel transitions in the system MgSiO4–FeSiO4-calorimetric measurements, thermochemical calculation, and geophysical application. J. Geophys. Res. 94, 15671–15685 (1989).
Foley, S. F. & Fischer, T. P. An essential role for continental rifts and lithosphere in the deep carbon cycle. Nat. Geosci. 10, 897 (2017).
Acknowledgements
Funding was provided by National MIUR (n.2017LMNLAW) and Milano-Bicocca University to M.L.F. and M.G.M. This article is an outcome of Project MIUR – Dipartimenti di Eccellenza 2018-2022. E.B. acknowledges the “Beniamino Segre” 2019 grant by Accademia Nazionale dei Lincei.
Author information
Authors and Affiliations
Contributions
M.G.M. reconstructed the geodynamic framework, interpreted carbon processes in the upper mantle, and wrote the manuscript; E.B. and G.F.P. performed earthquake location and INPAR inversion and contributed to manuscript writing; F.R. contributed to manuscript writing; S.F. interpreted carbon processes in the upper mantle and contributed to manuscript writing; M.L.F. interpreted carbon processes in the upper mantle and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests. Maria Luce Frezzotti is an Editorial Board Member for Communications Earth & Environment but was not involved in the editorial review of, nor the decision to publish this article.
Peer review information
Communications Earth & Environment Materials thanks Jiří Zahradník, Jan Sileny, and Giovanni Chiodini for their contribution to the peer review of this work. Primary Handling Editor: Joe Aslin. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Malusà, M.G., Brandmayr, E., Panza, G.F. et al. An explosive component in a December 2020 Milan earthquake suggests outgassing of deeply recycled carbon. Commun Earth Environ 3, 5 (2022). https://doi.org/10.1038/s43247-021-00336-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00336-y
This article is cited by
-
Dynamic modeling of tectonic carbon processes: State of the art and conceptual workflow
Science China Earth Sciences (2023)
-
Modelling of Moment Tensors and Source Parameters of the 25 July 2021 Rare Lower Crustal Hyderabad (India) Earthquake of Mw 3.9
Pure and Applied Geophysics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.