Abstract
The hadal zone at trenches is a unique region where forearc mantle rocks are directly exposed at the ocean floor owing to tectonic erosion. Circulation of seawater in the mantle rock induces carbonate precipitation within the deep-sea forearc mantle, but the timescale and rates of the circulation are unclear. Here we investigated a peculiar occurrence of calcium carbonate (aragonite) in forearc mantle rocks recovered from ~6400 m water depth in the Izu–Ogasawara Trench. On the basis of microtextures, strontium–carbon–oxygen isotope geochemistry, and radiocarbon analysis, we found that the aragonite is sourced from seawater that accumulated for more than 42,000 years. Aragonite precipitation is triggered by episodic rupture events that expel the accumulated fluids at 10−2–10−1 m s−1 and which continue for a few decades at most. We suggest that the recycling of subducted seawater from the shallowest forearc mantle influences carbon transport from the surface to Earth’s interior.
Similar content being viewed by others
Introduction
The hadal zone is one of the least explored territories on Earth’s surface and is characterized by high hydrostatic pressures, geological instability, and low nutrient supply. In particular, as the depth of a trench is greater than the thickness of arc crust, fresh mantle rocks are continuously exposed at erosive trenches1. Chemical reactions between mantle rocks and seawater exert an influence on global elemental transport and energy production for life2,3,4,5,6,7. Life in the hadal zone is potentially fed by the energy released during the alteration of mantle rocks (i.e., serpentinization)8, which produces an alkaline (pH = 9–11), reducing, and hydrogen- and methane-rich fluid derived from circulating seawater2,3. Understanding the mechanism and dynamics of coupled fluid flow, mass transport, and reaction provides a quantitative understanding of the link between the lithosphere and biosphere.
Carbonate minerals provide a unique opportunity to investigate the effects of fluids on the carbon cycle9,10,11,12,13, which occurs actively in subduction zones14,15,16,17,18. Carbon is released from the subducting slab via metamorphic devolatilization and melting, and is returned to Earth’s surface via plumes emitted from volcanoes and through diffuse degassing from the flanks of volcanoes. The deep carbon cycle (>70 km depth) occurs on timescales of around 10 Myr;15,17,19 however, carbon cycling also occurs in the shallow forearc (<20 km). Investigation of upwelling fluids and serpentinite from the Mariana forearc has revealed that carbon is released from the subducting slab at shallow forearc depths20,21,22. However, in contrast to the deep carbon cycle, little is known about the timescale and rates of carbon and fluid cycling in shallower forearc regions.
Aragonite (CaCO3), a polymorph of calcite, has been identified in samples of serpentinized peridotite recovered from the seafloor13,23,24,25,26. In the ocean, the chemical environments for inorganic aragonite precipitation are limited by the aragonite saturation depth (ASD), which is defined by the thermodynamic equilibrium between aragonite and seawater. The ASD varies substantially with latitude and longitude and is estimated to be ~2500 and 0–1000 m below sea level (mbsl) in the North Atlantic and North Pacific oceans, respectively27. In hydrothermal vents along the Mid Atlantic Ridge (MAR), aragonite precipitation occurs at depths of 2000–2500 mbsl, which is slightly shallower than the ASD28,29. Aragonite precipitation can also occur at depths greater than the ASD23,24,26,30,31, where it is induced by the interaction between ultramafic rocks and circulating seawater13,23. Here we report a new occurrence of aragonite in serpentinized peridotite recovered from a depth of >6400 mbsl from the inner wall of the Izu–Ogasawara Trench (IOT; Fig. 1a, b). This aragonite is from the hadal zone (>6000 mbsl), which is far deeper than the ASD (1000 mbsl)27, aragonite compensation depth (ACD; 500–1500 mbsl)32, and carbonate (calcite) compensation depth (CCD; 4500 mbsl;33 Fig. 1c), suggesting that the aragonite was formed by fluid–rock reactions. Therefore, the hadal aragonite potentially records fluid flow and chemical reactions during the circulation of seawater within the shallowest parts of the forearc mantle, and its investigation should provide insights into the transport of carbon from the surface to Earth’s interior. For this study, we used major- and trace-element compositions, C–O–Sr isotopes, and microstructural characteristics of hadal aragonite to determine the origin of carbonic fluids and mechanisms of aragonite formation. Moreover, we used radiocarbon dating to estimate fluid residence time in the hydrothermal system34,35. Combining the results of these analyses provides important and unique clues into the dynamics of fluid circulation and the influence of fluid–rock interaction on the carbon cycle within the forearc mantle in the hadal zone.
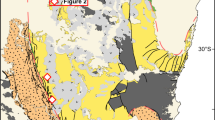
a Bathymetric map of Izu–Ogasawara trench, with inset map showing the location of Japan and of the study area (red rectangle). The sampling location of serpentinized peridotite (6K#1507) is shown by a pink star, along with previous locations where peridotite or gabbro were recovered. b Enlarged bathymetric map of the area depicted by the black-and-white rectangle in Fig. 1a, around the Umigame seamount located in the southern Izu–Ogasawara Trench. Maps in a and b were drawn using Generic Mapping Tools 5.4.592 with ETOPO1_Bed_g_gmt4.grd93, 94 (a) and grid data from the KR08-07 and KH07-02 cruises (b). c Depth profiles of seawater temperature, salinity, and dissolved oxygen (D.O.) during the DSV Shinkai 6500 dive #1507 (13 July 2017). The dive and sampling were conducted at ~6400 mbsl, which is deeper than both the carbonate (calcite) compensation depth (CCD; 4000–4500 mbsl)27 and aragonite compensation depth (ACD; 500–1500 mbsl)32.
Results
Geological setting of the Izu–Ogasawara Trench and sampling
Samples of serpentinized peridotite were collected from the Umigame seamount (26°47ʹN, 143°14ʹE) on the forearc slope of the southern IOT (Fig. 1a, b). The IOT is an erosive trench36,37, where deformation of the hangingwall occurs. Previous studies of the distribution of mafic and ultramafic rocks dredged from the IOT and geochemical and geochronological data have revealed that (i) outcrops of peridotite, gabbro, and dolerite occur from the slope base to slope top (7000–3000 mbsl) at the seamount38, (ii) ultramafic rock is exposed on the slope at >5000 mbsl1 (Fig. 1a), and (iii) the IOT comprises immature forearc mantle–crust related to subduction zone initiation38,39,40.
During the YK17-14 Leg 2 cruise (July 2017) on the R/V Yokosuka, dive #1507 by the deep submergence research vehicle (DSV) Shinkai 6500 collected 18 rock samples (14 serpentinized peridotites, 3 gabbros, and 1 basalt) from 6465 to 6429 mbsl at a water temperature of 1.7 °C, a salinity of 34.7 psu, and a dissolved oxygen content of 3.3 mL L−1 (6474 mbsl; Fig. 1c). The outcrop surveyed during dive #1507 consists of boulders of serpentinized peridotite (dominantly 10–50 cm in diameter, but up to 1–3 m) immersed in a muddy seafloor (Supplementary Fig. 1a, b). Boulder surfaces are mostly coated by black Mn deposits, although some have only thin coatings (Supplementary Fig. 1a, b). The serpentinite samples were originally mantled rocks (dunite and harzburgite). The samples are strongly serpentinized (~80%) and contain extensive fractures infilled with carbonate (Fig. 2a, b). X-ray diffraction and Raman spectra of the carbonate mineral indicate that it is pure aragonite. The aragonite is not observed on the surface of serpentinized peridotite but is limited to fractures (Fig. 2a). Unlike the serpentinite, carbonate veins have not been observed in the basalt and gabbros at the same location.
a Slice of serpentinite consisting of highly brecciated serpentine that is cemented by aragonite. b Euhedral aragonite in serpentine fractures, which implies in situ aragonite growth. c Mineral-phase map created from an elemental map using k-means clustering. Ol = olivine; Srp = serpentine; Spl = spinel; Arg = aragonite. d Three-dimensional distribution of clasts (serpentine and olivine) in an aragonite vein (total volume: 1.13 mm × 0.90 mm × 0.89 mm). Photomicrograph (e) and back-scattered electron image (f) of serpentine mesh texture, which consists of porous brown serpentine mesh cores (b-Srp) and non-porous white serpentine mesh rims (w-Srp). g FIB–SEM image showing the porosity contrast between the serpentine mesh core and rim.
Petrology of aragonite-bearing serpentinized peridotite at depths of >6400 mbsl
One serpentinized harzburgite sample (6K#1507-R14) is highly brecciated, meaning that it is difficult to reconstruct its original structure (Fig. 2c; Supplementary Fig. 2a, b). Aragonite contains clasts of serpentine, olivine, and dendritic or spherical Mn oxides (Fig. 2c). High-resolution X-ray computed tomography imaging revealed that each clast is separated from other clasts and supported by aragonite (Fig. 2d). The clasts have a mode at ~100 µm diameter, but some measure up to 3–5 mm (Supplementary Fig. 2c). The serpentinite samples consist mainly of serpentine minerals (lizardite and chrysotile; XMg = 0.91; Fig. 2e, f) that are locally intermixed with talc. Magnetite and hematite, as well as variable amounts of aragonite, are also observed with relics of primary olivine (XMg = 0.90) and spinel (Fig. 2c). The serpentine has a mesh texture consisting of brown serpentine cores and white serpentine rims (Fig. 2e). Locally, voids up to ~100 µm in size are observed in the mesh cores (Fig. 2e, f), and some of the void inner walls are lined with hematite (Supplementary Fig. 3a, b). Back-scattered electron images of the serpentine mesh texture show that the brown serpentine cores have variable porosity (Fig. 2f). High-resolution focused ion beam–scanning electron microscopy (FIB–SEM) observations revealed the presence of abundant nano- to submicron-scale pores in the serpentine mesh cores, whereas nano-scale pores are less prominent in the serpentine mesh rims (Fig. 2g). Both the serpentine mesh cores and rims are cut by aragonite veins.
In the veins, aragonite shows radial growth features (Fig. 3a). In some samples (6K#1507-R12 and 6K#1507-R14; Supplementary Table 1), aragonite has grown in fractures and is acicular (1–5 mm in length; Fig. 2b), and the crystal surfaces of aragonite growing on fracture surfaces indicate crystal growth in some domains and dissolution (e.g., etch pits) in other domains (Fig. 3b, c).
a Radiating aragonite that infills between brecciated serpentinite clasts. SEM image of aragonite surface showing growth banding (b) and dissolution etch pits (c) in a single aragonite crystal. d Selected REE + Y (REY) patterns of the aragonite samples. e A comparison of C and O isotope data of this study with those of serpentine-hosted carbonate collected during previous dredges and dives. Data for aragonite-bearing serpentinized peridotite recovered from hydrothermal fields are from Eickman et al.31 (Logachev and Gakkei ridges; 2000–4000 mbsl) and Ribeiro et al.28 (Rainbow and Saldanha fields; 2200 mbsl). Aragonite in serpentinized peridotite from the IOT is characterized by negative δ13C values. Negative δ13C values have been reported from the Mariana Trough24, where cold and methane-rich seeps are observed. The red line and pink region indicate the δ18OV-SMOW value and ±1σ range (34.5‰ ± 0.7‰) that is in equilibrium with seawater (δ18OV-SMOW = 0‰) at 1.7 °C. f Relationship between Δ14C and δ13C of aragonite. The modern deep seawater Δ14C value of DIC (−200‰ to −210‰)42 is represented by the green star. The inserted graph is a close-up view of the data. The analytical errors in e and f are substantially smaller than the symbols (Supplementary Table 1).
Aragonite geochemistry
Geochemical analysis of aragonite veins from six bulk rock samples was conducted. The geochemistry of acicular aragonite observed in 6K#1507-R12 and 6K#1507-R14 was measured separately. The aragonite shows rare earth element (REE) and Y (REY) patterns (Fig. 3d) that are characterized by negative Ce anomalies (Ce/Ce* = 0.10–0.55), depletion in LREEs relative to HREEs (PrSN/YbSN = 0.57 ± 0.41), and high Y/Ho ratios (42.6–73.2; Supplementary Table 2). There are wide variations in the concentrations of aragonite ∑REY (0.039–0.723 μg g−1) and U (0.267–1.690 μg g−1; Supplementary Table 2). The acicular aragonite has a higher ∑REY relative to aragonite veins from the same rock sample (Supplementary Table 2). The Sr/Ca ratio of the fluid reconstructed from the aragonite composition (Sr/Ca = 11.4–15.5 mmol/mol; Supplementary Table 2) is 9.68–13.13 mmol/mol, which is high compared with modern seawater (Sr/Ca = 8.7 mmol/mol)9.
Aragonite δ13CV-PDB values vary from −2.0‰ to +0.1‰ (Fig. 3e; Supplementary Table 1). δ18OV-SMOW values of the aragonite (33.80‰ ± 0.01‰ to 36.19‰ ± 0.01‰; Supplementary Table 1) are mostly in the range of aragonite δ18OV-SMOW values in equilibrium with seawater at 1.7 °C (34.5‰ ± 0.7‰; Fig. 3e), although some aragonite samples are slightly enriched in 18O (Fig. 3e). 87Sr/86Sr ratios of most aragonite samples (0.70915–0.70916; Supplementary Table 1) are similar to that of modern seawater (0.70917)41, with some having slightly higher (6K#1507-R14: 0.709195) or lower (6K#1507-R01: 0.709099) values (Supplementary Table 1).
The radiocarbon (Δ14C) contents of the aragonite samples analyzed in this study range from −991‰ to −995‰ (Fig. 3f; Supplementary Table 1). All Δ14C values of the studied aragonite are quite different from that of present-day seawater at a similar depth in the IOT (Δ14C = −200‰ to −210‰;42 Fig. 3f). Vein-filling and acicular aragonite sampled from the same rock specimen (6K#1507-R14) have similar Δ14C values, −994‰ and −995‰, respectively (Supplementary Table 1). The process blank obtained from the 14C-free standard IAEA-C1 yielded 0.0037 ± 0.0001 Fraction Modern (Δ14C = −996.3‰), indicating that the aragonite samples are nearly 14C dead (Supplementary Table 1).
Discussion
Serpentinized peridotites are commonly found along the trench-landward slope of the western Pacific margin, as well as in the IOT and Mariana trench1,43. The studied samples from the Umigame seamount were obtained from ~6400 m water depth, indicating that our observations in this study are consistent with those of previously investigated occurrences of ultramafic rock1,38,44 (Fig. 1a). Moreover, peridotite occurrence is limited to water depths of >5000 m in the IOT (Fig. 1b) and no serpentinized peridotite has been reported above the ASD (500–1500 mbsl)1,38,40, where aragonite can precipitate directly from seawater, suggesting that the recovered rocks did not originate from the shallow ocean floor. Therefore, aragonite-bearing serpentinized peridotite was formed by autochthonous processes in the hadal seafloor.
Textural relationships and the presence of olivine in aragonite veins (Fig. 2c) suggest that serpentinization was incomplete due to its sluggish kinetics, and aragonite precipitation postdated the serpentinization. The radial texture of the aragonite (Fig. 3a) indicates that it was precipitated under supersaturated conditions, although hadal seawater is undersaturated in aragonite (Fig. 1c). Both the presence of fractures and the composition of the bulk rock are inferred to play a key role in aragonite formation, as no carbonate was observed in fractures in both gabbro and basalt samples recovered adjacent to aragonite sampling points (Supplementary Fig. 4a, b), and, in particular, aragonite is not observed on rock surfaces either (Fig. 2a).
Furthermore, δ13CV-PDB values (−2.0‰ to +0.1‰; Fig. 3e) of the studied aragonite are similar to those of dissolved inorganic carbon (DIC) in seawater (δ13CV-PDB = 0‰), suggesting that the aragonite was formed from DIC derived from seawater. The similarity of aragonite 87Sr/86Sr ratios to that of modern seawater also supports a seawater origin. In addition, the REY pattern of the aragonite samples is characterized by negative Ce anomalies, positive Y anomalies, and elevated Y/Ho mass ratios (Fig. 3d), suggesting that the fluid source for the aragonite was predominantly seawater. The depletion in LREEs and variation in ∑REY imply a change in fluid source and the influence of sedimentary porewater45,46.
Hadal zone is undersaturated to precipitate aragonite directly from seawater (Fig. 1c). Calculations based on oxygen isotopic fractionation at ambient seawater temperatures (1.7 °C) indicate that the aragonite was precipitated from seawater with δ18OV-SMOW = 1.6‰ ± 0.6‰, which differs from ambient seawater (δ18OV-SMOW = 0‰) but is consistent with the δ18OV-SMOW values of serpentinizing fluids from different locations2,23,44. Thus, the geochemical evidence reveals that the chemical composition of seawater that induced aragonite formation was slightly different from that of ambient seawater.
There are two possible causes of the presence of 14C-dead carbon in the aragonite: (i) the aragonite was formed from 14C-bearing seawater and survived dissolution for some time; or (ii) the aragonite was formed more recently from almost-14C-dead seawater. During dive observations, we did not observe active venting of fluids, meaning that aragonite-supersaturated fluid is not presently forming on serpentinized peridotite. This finding implies that preexisting aragonite is being dissolved in the hadal ocean. The surface morphology of aragonite suggests that dissolution is ongoing (Fig. 3c), but aragonite dissolution in the hadal ocean (i.e., below the ACD) would be completed rapidly, as revealed by in situ carbonate dissolution experiments47. Therefore, the former scenario is unlikely, and the preservation of aragonite on the hadal seafloor suggests recent aragonite formation, which is inconsistent with the obtained 14C results. The 14C of aragonite hence represents not the age of aragonite formation but a carbon source composed of 14C-dead carbon; the deviation of Δ14C content between aragonite and modern deep seawater (Fig. 3f) suggests that aragonite formation was sourced from nearly 14C-dead carbon in seawater that had stagnated in the serpentinized peridotite. The blank-corrected 14C ages of sample 6K#1507-R13 and modern hadal water in the IOT (Δ14C = −206.6‰ ± 4.4‰)42 are 44,230 ± 600 and 1860 ± 50 BP, respectively, implying that the residence time of fluids in the serpentinized peridotites is >42 kyr.
Thermodynamic calculations of seawater–mantle rock equilibrium (i.e., with serpentinite) at 1.7 °C and 65 MPa reveal that brucite concentrations decrease with increasing seawater reaction (i.e., increasing the fluid-to-rock mass ratio, F/R; Supplementary Fig. 5). Therefore, the lack of brucite in the serpentinized peridotite from the IOT suggests that brucite was consumed during seawater–serpentinite reactions29,48. Moreover, the modeling revealed that the observed aragonite-bearing mineral assemblage (talc + serpentine + hematite + aragonite) is stable at a high F/R (= 102.5–103.5; Supplementary Fig. 5). The high F/R ratio for aragonite precipitation is consistent with seawater-like REY patterns and C–O–Sr isotope data, as this ratio implies only a small change in the composition of seawater by reactions with mantle rock. These calculations suggest that aragonite formation occurs as a consequence of seawater–serpentinite reaction under the conditions of the hadal ocean and in the presence of a high paleoseawater flux.
The occurrence of rock fragments supported within aragonite veins indicates that the flow of fluid (paleoseawater) balanced the ambient seawater pressure. The Ergun equation49, which has been used to estimate fluid velocity50,51,52,53,54, was also applied to the supported clasts in the aragonite veins (Fig. 2b). Image analysis constrained the extent of serpentinization and degree of porosity in the serpentinite clasts to 80%–100% and 0%–50%, respectively (Fig. 2c). Using these values, we obtained a fluid flow velocity of 10−2–10−1 m s−1 for 3–5-mm-diameter clasts to be suspended in the fluid (Supplementary Fig. 6). The discharge velocity is consistent with those measured in hydrothermal vents (0.02–1.99 m s−1)55. Moreover, we estimated the duration of the fluid (paleoseawater) discharge involved in the precipitation of aragonite using the estimated fluid velocity. Given a fracture length scale of 100 m, we obtained a timescale for fluid flow of 10–10,000 days. The estimated timescale for fluid flow and carbonate precipitation is largely consistent with the observation that a carbonate–brucite chimney can be produced in a year56 at a serpentinized fluid seep. These results suggest that rapid venting of paleoseawater from forearc serpentinite can be surprisingly short-lived and pulse-like.
The samples of serpentinized peridotite investigated in this study were recovered from the inner-wall trench, which is ~10 km landward of the IOT (Fig. 1a, b). At the forearc front, fluids released by compaction from subducting sediment generally have a chemical composition that is similar to that of seawater57. In accreting margins, fluid flow is largely constrained by matrix permeability, and fluid thus migrates along the décollement or as diffuse flow across the accreted overriding sediments58. In contrast, in an erosive margin such as the IOT, fluid flow across the overriding rock is controlled by faults because the bulk of the upper plate of an erosive margin has low permeability59. Fluids thus accumulate in and migrate through fractures in the overriding plate to the ocean60,61. The fracture can be created by various processes. Fluid overpressure commonly observed at the plate interface57,61,62,63 induces hydrofracturing of the base of the overriding rock in the erosive margin, which allows the migration of fluids into the overriding rock59,61,64. Moreover, present-day tectonic stresses related to tectonic erosion would induce pervasive normal faulting64,65. Either or both of these processes may create interconnected fractures across the overriding serpentinized peridotite at the erosive margin, resulting in discharge of the stagnated fluid from serpentinized peridotite to hadal seafloor. Considering that the growth rates of hydrogenetic crust (1–10 mm Myr−1)66,67 are similar in a wide range of water depths (800–5500 mbsl)68, thin (<1 mm thick) Mn coatings on the surfaces of the samples recovered from ~6400 mbsl (Supplementary Fig. 1a, b) indicate that deformation of the rocks occurred prior to 1.0–0.1 Ma.
Given the above discussion, we propose the following model of fluid flow dynamics in tectonically exposed forearc mantle: (i) Seawater trapped in subducting sediments are expelled by compaction just after subduction and accumulate in the overriding tectonically exposed forearc serpentinized peridotite (Fig. 4a, b); (ii) the seawater with dissolved carbon stagnates for >42 kyr within the serpentinized peridotite (Fig. 4b); and (iii) episodic rupture events expel these deep-seated carbon-bearing fluids and lead to aragonite precipitation (Fig. 4c). Subsequent exposure to hadal seawater leads to rapid carbonate dissolution47, meaning that these processes recycle the accumulated carbon to the ocean (Fig. 4b, c). Recent studies have revealed that subducted carbon is sequestered in the forearc crust and mantle, thereby influencing the global carbon cycle18,21,22,69,70,71. The residence time of carbon in the forearc is related to the reservoir size and determines the response of carbon flux into the atmosphere and biosphere induced by the perturbation of carbon flux17. Our estimate of the residence time of circulating carbon-bearing fluids in serpentinized peridotite (ca. > 42 kyr) is much longer than that for thermally driven hydrothermal fluid flow along fractures in the oceanic crust at mid-ocean ridge settings (less than a few years)34,72. The lower bound of residence time obtained in this study is similar to the carbon residence time in the forearc (88–8800 kyr)18,73, implying that the exposed forearc mantle may also be a large reservoir of carbon and water and may reduce carbon flux to deep regions of Earth (Fig. 4b). Compared with the residence time of carbon in the global carbon cycle in subduction zones (in the order of 10 Myr)17,19, the lower bound of residence time is much shorter, suggesting that the exposed forearc serpentinized peridotite can act as a shortened pathway for the carbon cycle and respond quickly to ongoing perturbation in subducting carbon input fluxes17. We infer that aragonite deposition on exposed forearc mantle peridotite may induce episodic carbon flux perturbation, causing an imbalance in the geological carbon cycle, ultimately influencing the atmosphere, climate, ocean, and habitability of Earth.
a Schematic illustration of the erosive convergent margin in the IOT and DSV Shinkai 6500. b Simplified illustration of the area represented by the dashed gray rectangle in a, showing fluid circulation in the tectonically exposed forearc mantle. c Fluid flow and carbonation at fracture indicated by the dashed gray rectangle in b. Schematic illustration of the episodic rupture events that allow the accumulated seawater to discharge. Each event continues for 101 to 104 days with a velocity of 10−2 to 10−1 m s−1 and induces carbonation.
Methods
Submersible conductivity–temperature–depth profiler
The depth profiles of seawater temperature, salinity, and dissolved oxygen were obtained with a submersible conductivity–temperature–depth (CTD) profiler system (SBE-19 SEACAT PROFILER CTD and SBE43 DO; Sea-Bird Electronics Inc.) mounted on the submersible research vehicle Shinkai 650074. Conductivity, water temperature, pressure, and dissolved oxygen were measured in 1 time in a second.
Scanning electron microscopy (SEM)
SEM was undertaken at the JAMSTEC on Au-coated samples with an FEI Quanta instrument operated at an accelerating voltage of 15–30 kV.
Electron probe microanalysis (EPMA)
Chemical compositions of minerals were analyzed by EPMA (JEOL JXA8500F) at the JAMSTEC. The accelerating voltage and electron beam current were 15 kV and 1–12 nA for point analysis, and 15 kV and 50 nA for elemental mapping, respectively. ZAF corrections were applied to the raw data.
Image analysis
The clast size distribution of the serpentinite was obtained from an EPMA elemental map using ImageJ software. A Ca elemental map (2 cm × 2 cm) with a pixel size of 10 μm was used to obtain the clast size distribution. The clast diameter was calculated based on the equivalent diameter. Owing to the spatial resolution of the images used for the analysis, a cut-off value of 25 square pixels was defined.
X-ray diffraction (XRD)
X-ray powder diffraction analysis was performed by XRD (Rigaku RINT-220VL), using Cu-Kα radiation. Samples were scanned with 2θ step sizes of 0.02°.
Raman microscopy
Raman microscopy was conducted with a Raman spectrophotometer (Nanophoton RAMANtouch) at the JAMSTEC using a 532 nm green laser. The laser power was 2–10 mW on the sample surface. Most spectra were collected using a 1200 grooves mm−1 grating. The Raman peak position was calibrated using a silicon wafer (520.7 cm−1).
X-ray computed tomography (X-ray CT)
A quadrangular prism (5 mm wide) was cut from the serpentinized peridotite and scanned using high-resolution X-ray computed tomography (Xradia 410 Versa ZEISS) at the Kochi Core Center, Kochi, Japan. Images were obtained under conditions of 70 kV beam energy, 8 W power, and 10 s exposure time using 360° rotation. We collected 3201 projections. The images had a pixel size of 3.0 μm and were visualized using the software program Fiji75.
Focused ion beam–SEM (FIB–SEM)
Cross-sectional microtextures were investigated using a dual-beam FIB–SEM system (Helios G4 UX; Thermo Fisher Scientific) at the JAMSTEC. A gallium ion source installed at an angle of 52° was used to mill the sample. After careful determination of the target area, a 1-μm-thick platinum layer was deposited on the area of interest to protect it from ion beam damage. FIB serial sectioning was performed using an ion beam of 30 kV and 9.1 nA. Images taken using the mirror detectors were processed with Adobe Photoshop® software to adjust the contrast and brightness.
Trace-element analyses
Aragonite sample powders weighing between 20 and 50 mg were placed into vials containing 0.5 mL of distilled water and 0.2 mL of CH3COOH. After dissolution and drying, a mixed acid solution (nitric, hydrochloric, and hydrofluoric acids) was used to dissolve the powders, which were then dried three times. The solution was diluted by a factor of 10,000 for REE measurements and by a factor of 50,000 for Mn measurements. All analyses were carried out using an ICP–MS instrument at Niigata University, Japan, using the procedures of Neo et al76. The BHVO-2, W-2a, and JB-2 standards were also analyzed. Eu, La, Gd, and Ce anomalies were calculated using shale-normalized (SN) concentrations as follows: Eu/Eu*= 2EuSN/(SmSN + GdSN)77, La/La* = LaSN/(PrSN(PrSN/NdSN)2)78, Gd/Gd* = GdSN/(TbSN(TbSN/DySN))79, and Ce/Ce* = CeSN/(PrSN2/NdSN)77. Trace-element compositions and anomalies are presented in Supplementary Table 2. The Post-Archean Australian Shale values used for normalization were taken from McLennan79.
Calculation of fluid Sr/Ca ratios
The fluid Sr/Ca molar ratio ([Sr/Ca]Fluid) was determined from:
where [Sr/Ca]Aragonite is the Sr/Ca molar ratio of aragonite, and KSr–Ca is the equilibrium partition coefficient for Sr between aragonite and fluid. The temperature (T; in K) dependent partition coefficients are given by:80
Carbon and oxygen isotope analyses
Aragonite powder samples were placed in small stainless steel thimbles and dropped into a reaction vessel containing pyrophosphoric acid at 60 °C in a vacuum to liberate CO2 gas. The CO2 was cleaned cryogenically to remove impurities such as H2O with pentane slush and collected using a liquid nitrogen cold trap. Stable-isotope measurements were carried out with a Thermo Fisher MAT-253 mass spectrometer at Niigata University. The results are reported in conventional δ notation in per mil (‰) with respect to Vienna Standard Mean Ocean Water (V-SMOW) for oxygen isotopes and Vienna Peedee Belemnite (V-PDB) for carbon isotopes. The precisions of δ13C and δ18O values for the laboratory standard CO2 gas were ±0.03‰ and ±0.05‰, and for NBS-20 were ±0.05‰ and ±0.1‰, respectively. Stable-isotope results are presented in Supplementary Table 1.
δ18O fractionation between aragonite and fluid
We used the following equilibrium oxygen isotope fractionation equation between aragonite and fluid proposed by Kim et al.:81
where α is the fractionation factor between aragonite and water, and T is the temperature in K. δ18O values of aragonite in equilibrium with seawater (Fig. 3e) were calculated using the above equation, as well as a seawater temperature of 1.7 °C and seawater δ18O = 0‰. δ18O values of the fluids were calculated using the above equation, a seawater temperature of 1.7 °C, and the measured aragonite δ18O values (Supplementally Table 1).
Strontium isotopes
Strontium isotopes were measured on an aliquot of the same sample powders used for the analysis of stable isotopes and trace elements. Aragonite samples were firstly decomposed in a mixed solution of distilled water and CH3COOH in a Teflon® vessel. Only carbonate minerals dissolve in acetic acid, which minimizes the effect of any minor silicate minerals, especially detrital components, on the strontium isotopic composition. After dissolution, the vials were centrifuged, and the supernatant was separated. Distilled water was added once again to the residue, and the supernatant was collected. The collected supernatant liquid was evaporated to dryness and nitric acid was added to the residue. Ca–Rb–Sr and REEs were separated in a first column separation (BioRad, AG50W-X8 cation exchange resin). Purification of strontium was undertaken with a second column separation (Eichrom Sr-Spec resin). Rubidium–Sr isotope analyses were carried out following the procedures of Miyazaki and Shuto82 by thermal ionization mass spectrometry with a Finnigan MAT 262 mass spectrometer at Niigata University. A tantalum (sample) and rhenium (ionization) filament combination was used for the analysis. Strontium isotopic compositions were normalized to 87Sr/86Sr = 0.1194. Repeated measurements of the strontium isotopic composition of the NIST 987 standard agree well with the known values for this standard (87Sr/86Sr = 0.710251 ± 0.000003; 2σ; n = 20). The 2σ values of the carbonate 87Sr/86Sr ratios were less than ±0.000014 (Supplementally Table 1).
Radiocarbon analysis
Hand-picked aragonite was rinsed with 0.1 M HCl acid for a few minutes. Approximately 10–15 mg of aragonite sample powders and 5 mL of phosphoric acid were introduced into a bifurcated reactor and connected to the vacuum line. After being a vacuum and sealed, the sample was reacted with phosphoric acid at 60 °C overnight to produce CO2 gas. The CO2 gas of about 1–3 mgC was cryogenically purified in a vacuum line using liquid N2, ethanol/liquid N2, and n-pentane traps. The purified CO2 of ~1 mgC was reduced to graphite by H2 with a Fe catalyst at 620 °C for 6 h. The resulting mixture of graphite and Fe powder was pressed into a target holder for AMS 14C measurements. The 14C concentrations were measured with a Tandetron AMS (model 4130-AMS, HVEE) at the Institute for Space-Earth Environmental Research, Nagoya University, Japan, by comparison to NIST oxalic acid (SRM 4990C: OxII). Each target was 14C-measured for five runs of 30 min each with the AMS. The 12C3+ beam currents were 100−200 nA during the measurement runs. The isotopic fractionation was corrected using the 13C/12C ratio measured by the AMS systems. 14C contents are reported as Δ14C (Supplementally Table 1).
Geochemical modeling
Geochemical modeling was conducted with Geochemist’s Workbench 12® software (GWB)83. The isobaric (65 MPa) thermodynamic dataset was generated based on a SUPCRT9284 speq06.dat dataset using DBCreate software85. The saturation state of minerals and redox potential of seawater at 1.7 °C and 65 MPa were calculated with the SpecE8 module in GWB. The seawater composition used was the bottom seawater composition of the Mariana Trench (Supplementary Table 3)41, with modifications to the Fe and O2(aq) concentrations. The Fe concentration was set to 1.0 × 10−6 mol kg−1 on the basis of the detection limit of the ICP-OES analyses, and the O2(aq) content (3.3 mL L−1) is the measured value in the IOT (Fig. 1c). Reaction path modeling was conducted with the REACT module in GWB by suppressing calcite, dolomite, and magnesite from the thermodynamic dataset. It is known that these suppressed minerals are difficult to be precipitated from seawater at ambient temperatures, even under supersaturated conditions. Suppression of the mineral phases was undertaken at the discretion of the operator, based on the feasibility of such minerals being precipitated, as recommended by the modeling package83. In the reaction path modeling, serpentinite is titrated step by step in 1 kg of seawater, with a composition identical to that used for calculation of mineral saturation (Supplementary Table 3). Modeling results are monitored by the fluid-rock mass ratio (F/R). In terms of the modeling on fluid infiltration into fractures, large F/R show equilibrium mineral assemblage of fluid-dominated conditions (e.g., around fracture) whereas low F/R show that of rock-dominated conditions (e.g., far from the fracture)29,70,86,87,88. The serpentinite was assumed to consist of chrysotile (85 mol%), brucite (10 mol%), and magnetite (5 mol%). We did not consider mineral solid solutions, and thus our simulation is a simplified approach.
Estimation of fluid velocities and timescales
The Ergun equation provides an estimate of fluid velocities (v; m s−1) for fluidization and elutriation:49,50,51
where Δp (Pa) is the reduction in fluid pressure; H (m) is the height of the fluidized layer; Ψ is the particle sphericity; μ (Pa s) and ρ (kg m–3) are the fluid viscosity and density, respectively; and dp (m) is the particle diameter; ε is the proportion of voids relative to particles + fluid. When the force exerted on particles by the upward fluid flow equals the gravity force on the particles, the Δp/H ratio is given by:
where ρp (kg m–3) and g (m s–2) are the particle density and acceleration due to gravity, respectively. These two equations can be combined and solved to estimate the minimum fluidization velocity (vm):
For packed aggregates, Wen and Yu89 proposed that the void proportion at the minimum fluidization velocity (εmf) is empirically related to the particle sphericity as εmf = (0.071/Ψ)(1/3). The velocity required to elutriate a spherical particle (vt) is given by:
In our calculations, μ and ρ were set to 1.17 × 10−3 (Pa s) and 1028 (kg m−3), respectively, based on the properties of seawater at 2 °C.
The serpentinite clasts exhibit variable degrees of serpentinization and reaction-induced porosity (Fig. 2c). These effects on density can be expressed as:
where φp is the porosity of a serpentinite clast; and ρSrp (kg m–3) is the density of serpentinized peridotite, which is obtained from the empirical relationship between the extent of serpentinization and density proposed by Miller and Christensen:90
where ξSrp (%) is the degree of serpentinization.
Supplementary Fig. 7 shows the relationship between porosity and serpentinization and density calculated from Eqs. (8–9), which suggests that φp has a large effect on the calculated density compared with ξSrp. Preservation of clasts in the breccia indicates that the clast density is greater than the seawater density. Therefore, the seawater density contour can be used to constrain the upper limit of φp. Mineralogical observations suggest that ξSrp ranges from 80% to 100% and that the two-dimensional porosity varies from 0% to 50% (Fig. 2c, d). From these ranges, two end-member cases for the extent of serpentinization (ξSrp; %) and porosity (φp) in the serpentinite clasts were examined: ξSrp = 80% and φp = 0 (ρp = 2672 kg m–3) as an upper limit for ρp; and ξSrp = 100% and φp = 0.5 (ρp = 1257 kg m–3) as a lower limit for ρp.
The estimated velocity can be used to estimate the timescale of fluid flow. The time-integrated volumetric fluid flux (Q; m3 fluid m–2 rock) is given by:
where t (s) is the duration of water flow, and φ is the fracture porosity. Assuming local equilibrium between the fluid and rock, the time-integrated fluid flux is given by:91
where L (m) is the characteristic length, Me (mol m–3 rock) is the moles of element e added or removed per volume of rock, and ΔCe (mol m–3 fluid) is the concentration difference of element e between the input and equilibrium fluids. Me⁄ΔCe is equivalent to the fluid–rock volume ratio and can be rewritten as Me ⁄ΔCe = (Mf/Mr)(ρr/ρ), where Mf (kg) is the mass of fluid reacted with the initial rock mass (Mr; kg), ρ (1028 kg m–3) is the seawater density at 2 °C, and ρr (kg m–3) is the density of the initial rock calculated from its empirical relationship with the extent of serpentinization (i.e., Eq. (9); ρr = ρSrp). Mf/Mr is the fluid–rock mass ratio and is equivalent to F/R in the reaction path simulation (i.e., Mf/Mr = F/R). The two equations for Q are combined and provide estimates of the timescales:
From petrological observations, we assumed that the extent of serpentinization (ξSrp) is 30%–100%. The ξSrp range constrains the ρr range to 2515–3064 kg m–3. A range of F/R of 102.5–103.5 was constrained by thermodynamic modeling (Supplementary Fig. 5), and a range of v of 10−2–10−1 was constrained by numerical modeling (Supplementary Fig. 6). The range of φ was assumed to be 0.1–0.8. Using these values and a fracture length of 100 m (L = 100), a minimum estimate of the timescale can be calculated as follows:
which is equal to 10 days. Similarly, the maximum timescale can be calculated as follows:
which is equal to 10,000 days. Thus, we constrained the timescale to be 10–10,000 days.
Data availability
The data of this study are available in Supplementary Tables and the online repository at: https://doi.org/10.6084/m9.figshare.16816099.
Code availability
The code used for thermodynamic modeling (The Geochemist’s Workbench®) can be purchased from Aqueous Solutions LLC (https://www.gwb.com/index.php).
References
Stern, R. J., Reagan, M., Ishizuka, O., Ohara, Y. & Whattam, S. To understand subduction initiation, study forearc crust: to understand forearc crust, study ophiolites. Lithosphere 4, 469–483 (2012).
Kelley, D. S. et al. An off-axis hydrothermal vent field near the Mid-Atlantic Ridge at 30°N. Nature 412, 145–149 (2001).
Früh-Green, G. L. et al. 30,000 years of hydrothermal activity at the lost city vent field. Science 301, 495–498 (2003).
Kelley, D. S. et al. A serpentinite-hosted ecosystem: the lost city hydrothermal field. Science 307, 1428–1434 (2005).
Klein, F. et al. Fluid mixing and the deep biosphere of a fossil Lost City-type hydrothermal system at the Iberia Margin. Proc. Natl. Acad. Sci. 112, 12036–12041 (2015).
Plümper, O. et al. Subduction zone forearc serpentinites as incubators for deep microbial life. Proc. Natl. Acad. Sci. 114, 4324–4329 (2017).
Vitale Brovarone, A. et al. Subduction hides high-pressure sources of energy that may feed the deep subsurface biosphere. Nat. Commun. 11, 1–11 (2020).
Hand, K. P. et al. Discovery of novel structures at 10.7 km depth in the Mariana Trench may reveal chemolithoautotrophic microbial communities. Deep Sea Res. Part I Oceanogr. Res. Pap. 160, 103238 (2020).
Coggon, R. M., Teagle, D. A. H., Smith-Duque, C. E., Alt, J. C. & Cooper, M. J. Reconstructing past seawater Mg/Ca. Science 327, 1114–1117 (2010).
Coogan, L. A., Parrish, R. R. & Roberts, N. M. W. Early hydrothermal carbon uptake by the upper oceanic crust: Insight from in situ U-Pb dating. Geology 44, 147–150 (2016).
Alt, J. C. et al. The role of serpentinites in cycling of carbon and sulfur: Seafloor serpentinization and subduction metamorphism. Lithos 178, 40–54 (2013).
Alt, J. C. & Teagle, D. A. H. The uptake of carbon during alteration of ocean crust. Geochim. Cosmochim. Acta 63, 1527–1535 (1999).
Bach, W. et al. Carbonate veins trace seawater circulation during exhumation and uplift of mantle rock: Results from ODP Leg 209. Earth Planet. Sci. Lett. 311, 242–252 (2011).
Dasgupta, R. & Hirschmann, M. M. The deep carbon cycle and melting in Earth’s interior. Earth Planet. Sci. Lett. 298, 1–13 (2010).
Kelemen, P. B. & Manning, C. E. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc. Natl. Acad. Sci. U.S.A. 112, E3997–E4006 (2015).
Plank, T. & Manning, C. E. Subducting carbon. Nature 574, 343–352 (2019).
Galvez, M. E. & Pubellier, M. How do subduction zones regulate the carbon cycle? in Deep Carbon (Orcutt, B. N., Daniel, I. & Dasgupta, R. eds.) 276–312 (Cambridge University Press, 2019). https://doi.org/10.1017/9781108677950.010
Barry, P. H. et al. Forearc carbon sink reduces long-term volatile recycling into the mantle. Nature 568, 487–492 (2019).
Horton, F. Rapid recycling of subducted sedimentary carbon revealed by Afghanistan carbonatite volcano. Nat. Geosci. 14, 508–512 (2021).
Hulme, S. M., Wheat, C. G., Fryer, P. & Mottl, M. J. Pore water chemistry of the Mariana serpentinite mud volcanoes: a window to the seismogenic zone. Geochem. Geophys. Geosyst. 11, Q01X09 (2010).
Mottl, M. J., Komor, S. C., Fryer, P. & Moyer, C. L. Deep-slab fluids fuel extremophilic Archaea on a Mariana forearc serpentinite mud volcano: ocean drilling program leg 195. Geochem. Geophys. Geosyst. 4, 1–14 (2003).
Albers, E. et al. Fluid-rock interactions in the shallow Mariana forearc: carbon cycling and redox conditions. Solid Earth 10, 907–930 (2019).
Bonatti, E., Lawrence, J. R., Hamlyn, P. R. & Breger, D. Aragonite from deep sea ultramafic rocks. Geochim. Cosmochim. Acta 44, 1207–1214 (1980).
Haggerty, J. A. Evidence from fluid seeps atop serpentine seamounts in the Mariana forearc: clues for emplacement of the seamounts and their relationship to forearc tectonics. Mar. Geol. 102, 293–309 (1991).
Ternieten, L., Früh‐Green, G. L. & Bernasconi, S. M. Distribution and sources of carbon in serpentinized mantle peridotites at the Atlantis Massif (IODP Expedition 357). J. Geophys. Res. Solid Earth 126, e2021JB021973 (2021).
Ohara, Y. et al. A serpentinite-hosted ecosystem in the Southern Mariana Forearc. Proc. Natl. Acad. Sci. 109, 2831–2835 (2012).
Feely, R. A. et al. Impact of anthropogenic CO2 on the CaCO3 system in the oceans. Science 305, 362–366 (2004).
Ribeiro da Costa, I., Barriga, F. J. A. S. & Taylor, R. N. Late seafloor carbonate precipitation in serpentinites from the Rainbow and Saldanha sites (Mid-Atlantic Ridge). Eur. J. Mineral. 20, 173–181 (2008).
Jöns, N., Kahl, W. A. & Bach, W. Reaction-induced porosity and onset of low-temperature carbonation in abyssal peridotites: Insights from 3D high-resolution microtomography. Lithos 268–271, 274–284 (2017).
Fryer, P. Serpentinite mud volcanism: observations, processes, and implications. Ann. Rev. Mar. Sci. 4, 345–373 (2012).
Eickmann, B., Bach, W., Rosner, M. & Peckmann, J. Geochemical constraints on the modes of carbonate precipitation in peridotites from the Logatchev Hydrothermal Vent Field and Gakkel Ridge. Chem. Geol. 268, 97–106 (2009).
Berger, W. H. Deep-sea carbonate: pteropod distribution and the aragonite compensation depth. Deep Sea Res. 25, 447–452 (1978).
Sulpis, O. et al. Current CaCO3 dissolution at the seafloor caused by anthropogenic CO2. Proc. Natl. Acad. Sci. U.S.A. 115, 11700–11705 (2018).
Fisher, A. T. et al. Hydrothermal recharge and discharge across 50 km guided by seamounts on a young ridge flank. Nature 421, 618–621 (2003).
Shah Walter, S. R. et al. Microbial decomposition of marine dissolved organic matter in cool oceanic crust. Nat. Geosci. 11, 334–339 (2018).
Straub, S. M., Gómez-Tuena, A. & Vannucchi, P. Subduction erosion and arc volcanism. Nat. Rev. Earth Environ. 1, 574–589 (2020).
Scholl, D. W. & Von Huene, R. Crustal recycling at modern subduction zones applied to the past—Issues of growth and preservation of continental basement crust, mantle geochemistry, and supercontinent reconstruction. Mem. Geol. Soc. Am. 200, 9–32 (2007).
Morishita, T. et al. Diversity of melt conduits in the Izu-Bonin-Mariana forearc mantle: Implications for the earliest stage of arc magmatism. Geology 39, 411–414 (2011).
Harigane, Y. et al. The earliest mantle fabrics formed during subduction zone infancy. Earth Planet. Sci. Lett. 377–378, 106–113 (2013).
Ishizuka, O. et al. The timescales of subduction initiation and subsequent evolution of an oceanic island arc. Earth Planet. Sci. Lett. 306, 229–240 (2011).
Mottl, M. J., Wheat, C. G., Fryer, P., Gharib, J. & Martin, J. B. Chemistry of springs across the Mariana forearc shows progressive devolatilization of the subducting plate. Geochim. Cosmochim. Acta 68, 4915–4933 (2004).
Kawagucci, S. et al. Hadal water biogeochemistry over the Izu-Ogasawara Trench observed with a full-depth CTD-CMS. Ocean Sci. 14, 575–588 (2018).
Stern, R. J., Ohara, Y., Ren, M., Leybourne, M. & Bowers, B. Glimpses of oceanic lithosphere of the Challenger Deep forearc segment in the southernmost Marianas: The 143°E transect, 5800–4200 m. Isl. Arc. 29, 1–17 (2020).
Sakai, R., Kusakabe, M., Noto, M. & Ishii, T. Origin of waters responsible for serpentinization of the Izu-Ogasawara-Mariana forearc seamounts in view of hydrogen and oxygen isotope ratios. Earth Planet. Sci. Lett. 100, 291–303 (1990).
Haley, B. A., Klinkhammer, G. P. & McManus, J. Rare earth elements in pore waters of marine sediments. Geochim. Cosmochim. Acta 68, 1265–1279 (2004).
Himmler, T., Bach, W., Bohrmann, G. & Peckmann, J. Rare earth elements in authigenic methane-seep carbonates as tracers for fluid composition during early diagenesis. Chem. Geol. 277, 126–136 (2010).
Honjo, S. & Erez, J. Dissolution rates of calcium carbonate in the deep ocean; an in-situ experiment in the North Atlantic Ocean. Earth Planet. Sci. Lett. 40, 287–300 (1978).
Klein, F., Humphris, S. E. & Bach, W. Brucite formation and dissolution in oceanic serpentinite. Geochem. Perspect. Lett 16, 1–5 (2020).
Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 89–94 (1952).
Cox, S. F. & Munroe, S. M. Breccia formation by particle fluidization in fault zones: Implications for transitory, rupture-controlled fluid flow regimes in hydrothermal systems. Am. J. Sci. 316, 241–278 (2016).
Masoch, S., Fondriest, M., Preto, N. & Secco, M. & Di Toro, G. Seismic cycle recorded in cockade-bearing faults (Col de Teghime, Alpine Corsica). J. Struct. Geol. 129, 103889 (2019).
Berger, A. & Herwegh, M. Cockade structures as a paleo-earthquake proxy in upper crustal hydrothermal systems. Sci. Rep. 9, 1–9 (2019).
Oliver, N. H. S. et al. Granite-related overpressure and volatile release in the mid crust: Fluidized breccias from the Cloncurry District, Australia. Geofluids 6, 346–358 (2006).
Okamoto, A. & Tsuchiya, N. Velocity of vertical fluid ascent within vein-forming fractures. Geology 37, 563–566 (2009).
Germanovich, L. N., Hurt, R. S., Smith, J. E., Genc, G. & Lowell, R. P. Measuring fluid flow and heat output in seafloor hydrothermal environments. J. Geophys. Res. Solid Earth 120, 8031–8055 (2015).
Okumura, T. et al. Brucite chimney formation and carbonate alteration at the Shinkai Seep Field, a serpentinite-hosted vent system in the southern Mariana forearc. Geochem. Geophys. Geosyst. 17, 3775–3796 (2016).
Saffer, D. M. & Tobin, H. J. Hydrogeology and mechanics of subduction zone forearcs: fluid flow and pore pressure. Annu. Rev. Earth Planet. Sci. 39, 157–186 (2011).
Spinelli, G. A., Saffer, D. M. & Underwood, M. B. Hydrogeologic responses to three-dimensional temperature variability, Costa Rica subduction margin. J. Geophys. Res. Solid Earth 111, 1–15 (2006).
Ranero, C. R. et al. Hydrogeological system of erosional convergent margins and its influence on tectonics and interplate seismogenesis. Geochem. Geophys. Geosyst. 9, Q03S04 (2008).
Bangs, N. L., McIntosh, K. D., Silver, E. A., Kluesner, J. W. & Ranero, C. R. Fluid accumulation along the Costa Rica subduction thrust and development of the seismogenic zone. J. Geophys. Res. Solid Earth 120, 67–86 (2015).
Talukder, A. R. Review of submarine cold seep plumbing systems: leakage to seepage and venting. Terra Nov 24, 255–272 (2012).
Saffer, D. M. Pore pressure development and progressive dewatering in underthrust sediments at the Costa Rican subduction margin: comparison with northern Barbados and Nankai. J. Geophys. Res. Solid Earth 108, 1–16 (2003).
Klaucke, I., Masson, D. G., Petersen, C. J., Weinrebe, W. & Ranero, C. R. Multifrequency geoacoustic imaging of fluid escape structures offshore Costa Rica: Implications for the quantification of seep processes. Geochem. Geophys. Geosyst. 9, Q04010 (2008).
Von Huene, R., Ranero, C. R. & Vannucchi, P. Generic model of subduction erosion. Geology 32, 913 (2004).
Ranero, C. R. & Von Huene, R. Subduction erosion along the Middle America convergent margin. Nature 404, 748–752 (2000).
Usui, A. et al. Modern precipitation of hydrogenetic ferromanganese minerals during on-site 15-year exposure tests. Sci. Rep. 10, 3558 (2020).
Hein, J. R. & Koschinsky, A. Deep-Ocean Ferromanganese Crusts and Nodules. Treatise on Geochemistry: Second Edition 13, (Published by Elsevier Inc., 2013).
Usui, A. et al. Continuous growth of hydrogenetic ferromanganese crusts since 17 Myr ago on Takuyo-Daigo Seamount, NW Pacific, at water depths of 800–5500 m. Ore Geol. Rev. 87, 71–87 (2017).
Peng, W. et al. Multistage CO2 sequestration in the subduction zone: Insights from exhumed carbonated serpentinites, SW Tianshan UHP belt, China. Geochim. Cosmochim. Acta 270, 218–243 (2019).
Okamoto, A. et al. Rupture of wet mantle wedge by self-promoting carbonation. Commun. Earth Environ. 2, 151 (2021).
Galvez, M. E. et al. Graphite formation by carbonate reduction during subduction. Nat. Geosci. 6, 473–477 (2013).
Kadko, D. & Moore, W. Radiochemical constraints on the crustal residence time of submarine hydrothermal fluids: endeavour ridge. Geochim. Cosmochim. Acta 52, 659–668 (1988).
Fullerton, K. M. et al. Effect of tectonic processes on biosphere–geosphere feedbacks across a convergent margin. Nat. Geosci. 14, 301–306 (2021).
JAMSTEC. YOKOSUKA YK17-14 Leg2 Cruise Data. (2017). https://doi.org/10.17596/0001691
Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682 (2012).
Neo, N., Yamazaki, S. & Miyashita, S. Data report: bulk rock compositions of samples from the IODP Expedition 309/312 sample pool, ODP Hole 1256D. in Proceedings of the IODP, 309/312 309, (Integrated Ocean Drilling Program, 2009).
Tostevin, R. et al. Effective use of cerium anomalies as a redox proxy in carbonate-dominated marine settings. Chem. Geol. 438, 146–162 (2016).
Lawrence, M. G., Greig, A., Collerson, K. D. & Kamber, B. S. Rare earth element and yttrium variability in South East Queensland waterways. Aquat. Geochem. 12, 39–72 (2006).
McLennan, S. M. Rare earth elements in sedimentary rocks: influence of provenance and sedimentary processes. in Reviews in Mineralogy & Geochemistry (eds. Lipin, B. R. & McKay, G. A.) 169–200 (De Gruyter, 1989). https://doi.org/10.1515/9781501509032-010
Kinsman, D. J. J. & Holland, H. D. The co-precipitation of cations with CaCO3—IV. The co-precipitation of Sr2+ with aragonite between 16° and 96°C. Geochim. Cosmochim. Acta 33, 1–17 (1969).
Kim, S. T., O’Neil, J. R., Hillaire-Marcel, C. & Mucci, A. Oxygen isotope fractionation between synthetic aragonite and water: Influence of temperature and Mg2+ concentration. Geochim. Cosmochim. Acta 71, 4704–4715 (2007).
Miyazaki, T. & Shuto, K. Sr and Nd isotope ratios of twelve GSJ rock reference samples. Geochem. J. 32, 345–350 (1998).
Bethke, C. M. Geochemical and Biogeochemical Reaction Modeling. (Cambridge University Press, 2007). https://doi.org/10.1017/CBO9780511619670
Johnson, J. W., Oelkers, E. H. & Helgeson, H. C. SUPCRT92: a software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000 °C. Comput. Geosci. 18, 899–947 (1992).
Kong, X. Z., Tutolo, B. M. & Saar, M. O. DBCreate: a SUPCRT92-based program for producing EQ3/6, TOUGHREACT, and GWB thermodynamic databases at user-defined T and P. Comput. Geosci. 51, 415–417 (2013).
Bach, W. & Klein, F. The petrology of seafloor rodingites: insights from geochemical reaction path modeling. Lithos 112, 103–117 (2009).
Palandri, J. L. & Reed, M. H. Geochemical models of metasomatism in ultramafic systems: serpentinization, rodingitization, and sea floor carbonate chimney precipitation. Geochim. Cosmochim. Acta 68, 1115–1133 (2004).
Reed, M. H. Hydrothermal alteration and its relationship to ore fluid composition. in Geochemistry of Hydrothermal Ore Deposits (ed. Barnes, H. L.) 303–365 (John Wiley & Sons, 1997).
Wen, C. Y. & Yu, Y. H. A generalized method for predicting the minimum fluidization velocity. AIChE J. 12, 610–612 (1966).
Miller, D. J. & Christensen, N. I. Seismic velocities of lower crustal and upper mantle rocks from the slow-spreading Mid-Atlantic Ridge, south of the Kane Transform Zone (MARK). Proc. Ocean Drill. Program, Sci. Results 153, (1997).
Bucholz, C. E. & Ague, J. J. Fluid flow and Al transport during quartz-kyanite vein formation, Unst, Shetland Islands, Scotland. J. Metamorph. Geol. 28, 19–39 (2010).
Wessel, P., Smith, W. H. F., Scharroo, R., Luis, J. & Wobbe, F. Generic Mapping Tools: Improved Version Released. Eos, Trans. Am. Geophys. Union 94, 409–410 (2013).
NOAA National Geophysical Data Center. ETOPO1 1 Arc-Minute Global Relief Model. NOAA National Centers for Environmental Information. (2009).
Amante, C. & Eakins, B. W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. NOAA Technical Memorandum NESDIS NGDC-24 (2009). https://doi.org/10.7289/V5C8276M
Acknowledgements
We thank the captain and crew of the R/V Yokosuka, Yoshihiko Tamura, and the YK17–14 science party for their support and cooperation. We thank Kazuki Yoshida, Kenta Yoshida, Otgonbayar Dandar, Rikako Imanaka-Nohara, and Takuya Matsuzaki for their assistance with the sample analyses. Osamu Ishizuka and Kenichiro Tani provided information regarding previous sampling of gabbros and peridotites from the IOT. Takuya Ishibashi, Ryo Yamada, Katsuhiko Suzuki, and Hikaru Sawada are thanked for the discussion. Comments from M. Galvez, A. Vitale Brovarone, and an anonymous reviewer helped us to substantially improve the manuscript. This research was supported by the Japan Society for the Promotion of Science (KAKENHI Grants JP18J01649, JP19K14827, JP20KK0079, JP15H05831, JP18KK0376, and JP16H06347).
Author information
Authors and Affiliations
Contributions
R.O., A.O., Y.H., and K.M. joined the YK17-14 science party and collected samples. R.O., A.O., and K.M. designed the project. M.S-K. conducted the C–O–Sr isotope and trace element analyses. R.O. and M.M. undertook the radiocarbon dating. R.O. made the petrological observations and conducted the geochemical and numerical modeling. All authors contributed to the data interpretation. R.O. prepared the draft of the manuscript. All authors were involved in revising the manuscript and approved the submitted version.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment thanks Matthieu Galvez and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: João Duarte, Joe Aslin.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Oyanagi, R., Okamoto, A., Satish-Kumar, M. et al. Hadal aragonite records venting of stagnant paleoseawater in the hydrated forearc mantle. Commun Earth Environ 2, 243 (2021). https://doi.org/10.1038/s43247-021-00317-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00317-1
This article is cited by
-
Subducted carbon weakens the forearc mantle wedge in a warm subduction zone
Nature Communications (2024)
-
Metasomatism at a metapelite–ultramafic rock contact at the subduction interface: Insights into mass transfer and fluid flow at the mantle wedge corner
Contributions to Mineralogy and Petrology (2023)
-
Progressive carbonation and Ca-metasomatism of serpentinized ultramafic rocks: insights from natural occurrences and hydrothermal experiments
Contributions to Mineralogy and Petrology (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.